Hostname: page-component-5b777bbd6c-gcwzt Total loading time: 0 Render date: 2025-06-18T20:11:43.276Z Has data issue: false hasContentIssue false
  • English
  • Français

On Thompson groups for Ważewski dendrites

Part of: Special aspects of infinite or finite groups Classical measure theory Structure and classification of infinite or finite groups Connections with other structures, applications

Published online by Cambridge University Press:  19 May 2025

MATTEO TAROCCHI
MATTEO TAROCCHI*
Affiliation:
Università degli Studi di Milano-Bicocca, Milano, Italia (EU). Current: Université Paris-Saclay, Laboratoire de Mathématiques d’Orsay, Orsay, France (EU) & Université de Rennes, IRMAR, Rennes, France (EU) e-mail: matteo.tarocchi.math@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a family of Thompson-like groups built as rearrangement groups of fractals introduced by Belk and Forrest in 2019, each acting on a Ważewski dendrite. Each of these is a finitely generated group that is dense in the full group of homeomorphisms of the dendrite (studied by Monod and Duchesne in 2019) and has infinite-index finitely generated simple commutator subgroup, with a single possible exception. More properties are discussed, including finite subgroups, the conjugacy problem, invariable generation and existence of free subgroups. We discuss many possible generalisations, among which we find the Airplane rearrangement group 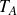$T_A$. Despite close connections with Thompson’s group F, dendrite rearrangement groups seem to share many features with Thompson’s group V.

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F38: Other groups related to topology or analysis 28A80: Fractals 20E32: Simple groups 20F05: Generators, relations, and presentations 54H11: Topological groups 20F10: Word problems, other decision problems, connections with logic and automata 20E45: Conjugacy classes
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 179 , Issue 1 , July 2025 , pp. 189 - 231
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdalaoui, E. H. E. and Naghmouchi, I.. Group action with finite orbits on local dendrites. Dyn. Syst. 36(4) (2021), pp. 714–730. doi: 10.1080/14689367.2021.1994925.CrossRefGoogle Scholar
Belk, J.. Thompson’s Group F. PhD. thesis. Cornell University (2004). url: https://arxiv.org/abs/0708.3609.Google Scholar
Belk, J. and Forrest, B.. A Thompson group for the basilica. Groups Geom. Dyn. 9(4) (2015), pp. 975–1000. doi: 10.4171/GGD/333.CrossRefGoogle Scholar
Belk, J. and Forrest, B.. Quasisymmetries of finitely ramified Julia sets. Preprint: ArXiv. 2310·17442 (2023). doi: 10.48550/arXiv.2310.17442.CrossRefGoogle Scholar
Belk, J. and Forrest, B.. Rearrangement groups of fractals. Trans. Amer. Math. Soc. 372(7) (2019), pp. 4509–4552. doi: 10.1090/tran/7386.CrossRefGoogle Scholar
Belk, J. and Matucci, F.. Conjugacy and dynamics in Thompson’s groups. Geom. Dedicata 169 (2014), pp. 239–261. doi: 10.1007/s10711-013-9853-2.CrossRefGoogle Scholar
Belk, J., Elliott, L., and Matucci, F.. A short proof of Rubin’s theorem. Israel J. Math. (2024). doi: 10.1007/s11856-024-2700-3.CrossRefGoogle Scholar
J. Belk and C. B. Matthew Zaremsky. Twisted Brin-Thompson groups. Geom. Topol. 26(3) (2022), pp. 1189–1223. doi: 10.2140/gt.2022.26.1189.CrossRefGoogle Scholar
R. Bieri and R. Strebel . On groups of PL-homeomorphisms of the real line. Math. Surveys Monogr, vol. 215. (American Mathematical Society, Providence, RI, 2016), pp. xvii+174. doi: 10.1090/surv/215.CrossRefGoogle Scholar
Bleak, C., Matucci, F., and M. Neunhöffer. Embeddings into Thompson’s group V and co $\mathcal{C}\mathcal{F}$ groups. J. London Math. Soc. (2) 94(2) (2016), pp. 583–597. doi: 10.1112/jlms/jdw044.CrossRefGoogle Scholar
M. Bonk and D. Meyer . Quasiconformal and geodesic trees. Fund. Math. 250(3) (2020), pp. 253–299. doi: 10.4064/fm749-7-2019.CrossRefGoogle Scholar
Brin, M. G.. Higher dimensional Thompson groups. Geom. Dedicata 108 (2004), pp. 163–192. doi: 10.1007/s10711-004-8122-9.CrossRefGoogle Scholar
Brown, K. S.. Finiteness properties of groups. J. Pure Appl. Algebra 44(1-3) (1987), pp. 45–75. doi: 10.1016/0022-4049(87)90015-6.CrossRefGoogle Scholar
Cameron, P. J.. Oligomorphic permutation groups. London Mathematical Society Lecture Note Series. Cambridge University Press, vol. 152 (Cambridge 1990), pp. viii+160. doi: 10.1017/CBO9780511549809.CrossRefGoogle Scholar
Cannon, J. W., Floyd, W. J., and Parry, W. R.. Introductory notes on Richard Thompson’s groups. Enseign. Math. (2) 42(3-4) (1996), pp. 215–256.Google Scholar
P.-E. Caprace and T. D. Medts . Simple locally compact groups acting on trees and their germs of automorphisms. Transform. Groups 16(2) (2011), pp. 375–411. doi: 10.1007/s00031-011-9131-z.Google Scholar
Charatonik, J. J.. Homeomorphisms of universal dendrites. Rend. Circ. Mat. Palermo (2) 44(3) (1995), pp. 457–468. doi: 10.1007/BF02844680.CrossRefGoogle Scholar
W. lodzimierz, J. Charatonik and A. Dilks. On self-homeomorphic spaces. Topology Appl. 55(3) (1994), pp. 215–238. doi: 10.1016/0166-8641(94)90038-8.CrossRefGoogle Scholar
Chatterji, I., Drutu, C. and F. Haglund. Kazhdan and Haagerup properties from the median viewpoint. Adv. Math. 225(2) (2010), pp. 882–921. doi: 10.1016/j.aim.2010.03.012.CrossRefGoogle Scholar
Duchesne, B.. A closed subgroup of the homeomorphism group of the circle with property (T). Internat. Math. Res. Notices IMRN 12 (2023), pp. 10615–10640. doi: 10.1093/imrn/rnac136.CrossRefGoogle Scholar
Duchesne, B.. Topological properties of Waz˙ewski dendrite groups. J. E´c. Polytech. Math. 7 (2020), pp. 431–477. doi: 10.5802/jep.121.CrossRefGoogle Scholar
B. Duchesne and N. Monod . Group actions on dendrites and curves. Ann. Inst. Fourier (Grenoble) 68(5) (2018), pp. 2277–2309. url: http://aif.cedram.org/item?id=AIF_2018__68_5_2277_0.Google Scholar
B. Duchesne and N. Monod . Structural properties of dendrite groups. Trans. Amer. Math. Soc. 371(3) (2019), pp. 1925–1949. doi: 10.1090/tran/7347.CrossRefGoogle Scholar
Duchesne, B., Monod, N. and Wesolek, P.. Kaleidoscopic groups: permutation groups constructed from dendrite homeomorphisms. Fund. Math. 247(3) (2019), pp. 229–274. doi: 10.4064/fm702-4-2019.CrossRefGoogle Scholar
Epstein, D. B. A.. The simplicity of certain groups of homeomorphisms. Compositio Math. 22 (1970), pp. 165–173.Google Scholar
A. Garrido and D. Colin . Reid. Discrete locally finite full groups of Cantor set homeomorphisms. Bull. London Math. Soc. 53(4) (2021), pp. 1228–1248. doi: 10.1112/blms.12496.CrossRefGoogle Scholar
Gelander, T., Golan, G., and Juschenko, K.. Invariable generation of Thompson groups. J. Algebra 478 (2016), pp. 261–270. doi: 10.1016/j.jalgebra.2017.01.019.CrossRefGoogle Scholar
E. Glasner and M. Megrelishvili . Group actions on treelike compact spaces. Sci. China Math. 62(12) (2019), pp. 2447–2462. doi: 10.1007/s11425-018-9488-9.CrossRefGoogle Scholar
G. Goffer and W. Lederle. Conjugacy and dynamics in almost automorphism groups of trees. Internat. J. Algebra Comput. 31(8) (2021), pp. 1497–1545. doi: 10.1142/S0218196721500557.CrossRefGoogle Scholar
V. Guba and M. Sapir . Diagram groups. Mem. Amer. Math. Soc. 130(620) (1997), pp. viii+117. doi: 10.1090/memo/0620.CrossRefGoogle Scholar
Higman, G.. Finitely presented infinite simple groups. Notes on Pure Mathematics, no. 8. (Australian National University, Department of Pure Mathematics, Department of Mathematics, I.A.S., Canberra, 1974), pp. vii+82.Google Scholar
Houghton, C. H.. The first cohomology of a group with permutation module coefficients. Arch. Math. (Basel) 31(3) (1978), pp. 254–258. doi: 10.1007/BF01226445.CrossRefGoogle Scholar
Kuratowski, K.. Topology, vol. II. New. Translated from the French by A. Kirkor. (Academic Press, New York-London; Pa´nstwowe Wydawnictwo Naukowe [Polish Scientific Publishers], Warsaw, 1968), pp. xiv+608.Google Scholar
Lehnert, J.. Gruppen von quasi-Automorphismen. PhD thesis. Johann Wolfgang Goethe-Universit¨at Frankfurt am Main (2008). url: https://d-nb.info/990316440/34.Google Scholar
M. Lyubich and S. Merenkov . Quasisymmetries of the basilica and the Thompson group. Geom. Funct. Anal. 28(3) (2018), pp. 727–754. doi: 10.1007/s00039-018-0452-0.CrossRefGoogle Scholar
Meier, J.. Groups, graphs and trees. An introduction to the geometry of infinite groups. London Mathematical Society Student Texts. Vol. 73 (Cambridge University Press, Cambridge. 2008), pp. xii+231. doi: 10.1017/CBO9781139167505.CrossRefGoogle Scholar
S. B., Nadler Jr. Continuum theory. Vol. 158. Monographs and Textbooks in Pure and Applied Mathematics. An introduction. (Marcel Dekker, Inc., New York 1992), pp. xiv+328.Google Scholar
V. Nekrashevych . Self-similar groups. Math. Surveys Monogr., vol. 117 (American Mathematical Society, Providence, RI, 2005), pp. xii+231. doi: 10.1090/surv/117.CrossRefGoogle Scholar
Neretin, Y. A.. On the group of homeomorphisms of the Basilica. Topology Proc. 64 (2024), pp. 121–128.Google Scholar
M. H. A.Newman. On theories with a combinatorial definition of “equivalence”. Ann. of Math. (2) 43 (1942), pp. 223–243. doi: 10.2307/1968867.CrossRefGoogle Scholar
D. Perego and M. Tarocchi . A class of rearrangement groups that are not invariably generated. Bull. London Math. Soc. 56(6) (2024), pp. 2115–2131. doi: 10.1112/blms.13046.CrossRefGoogle Scholar
Rubin, M.. On the reconstruction of topological spaces from their groups of homeomorphisms. Trans. Amer. Math. Soc. 312(2) (1989), pp. 487–538. doi: 10.2307/2001000.CrossRefGoogle Scholar
Á. Seress . Permutation group algorithms. Cambridge Tracts in Mathematics, vol. 152 (Cambridge University Press, Cambridge 2003), pp. x+264. doi: 10.1017/CBO9780511546549.CrossRefGoogle Scholar
Shi, E.. Free subgroups of dendrite homeomorphism group. Topology Appl. 159(10-11) (2012), pp. 2662–2668. doi: 10.1016/j.topol.2012.04.001.CrossRefGoogle Scholar
E. Shi and X. Ye . Periodic points for amenable group actions on dendrites. Proc. Amer. Math. Soc. 145(1) (2017), pp. 177–184. doi: 10.1090/proc/13206.Google Scholar
W. Smith . Thompson-Like groups for dendrite Julia sets. Senior project. Bard College (2013). url: https://e.math.cornell.edu/people/belk/projects/WillSmith.pdf.Google Scholar
Stein, M.. Groups of piecewise linear homeomorphisms. Trans. Amer. Math. Soc. 332(2) (1992), pp. 477–514. doi: 10.2307/2154179.CrossRefGoogle Scholar
Tarocchi, M.. Conjugacy in rearrangement groups of fractals. Preprint ArXiv.2309·16613 (2023). doi: 10.48550/arXiv.2309.16613.CrossRefGoogle Scholar
Tarocchi, M.. Generation and simplicity in the airplane rearrangement group. Groups Geom. Dyn. 18(2) (2024), pp. 603–634. doi: 10.4171/ggd/772.CrossRefGoogle Scholar
G. Thomas Whyburn . Analytic Topology. American Mathematical Society Colloquium Publications, vol. 28 (American Mathematical Society, New York, 1942), pp. x+278.CrossRefGoogle Scholar
S. Witzel and M. C. B. Zaremsky. The basilica Thompson group is not finitely presented. Groups Geom. Dyn. 13(4) (2019), pp. 1255–1270. doi: 10.4171/ggd/522.CrossRefGoogle Scholar
Zhuang, D.. Irrational stable commutator length in finitely presented groups. J. Mod. Dyn. 2(3) (2008), pp. 499–507. doi: 10.3934/jmd.2008.2.499.CrossRefGoogle Scholar