Hostname: page-component-7dd5485656-bvgqh Total loading time: 0 Render date: 2025-10-31T03:10:33.692Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractional Brownian motion with deterministic drift: how critical is drift regularity in hitting probabilities

Part of: Stochastic processes Classical measure theory Markov processes

Published online by Cambridge University Press:  20 February 2025

MOHAMED ERRAOUI  and
YOUSSEF HAKIKI
MOHAMED ERRAOUI
Affiliation:
Department of mathematics, Faculty of science El jadida, Chouaïb Doukkali University, Route Ben Maachou, 24000, El Jadida, Morocco. e-mail: erraoui.mohamed@ucd.ac.ma
YOUSSEF HAKIKI
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, W. Lafayette, IN 47907, U.S.A. e-mail: yhakiki@purdue.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 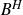$B^{H}$ be a d-dimensional fractional Brownian motion with Hurst index 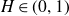$H\in(0,1)$, 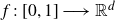$f\,:\,[0,1]\longrightarrow\mathbb{R}^{d}$ a Borel function, and 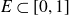$E\subset[0,1]$, 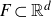$F\subset\mathbb{R}^{d}$ are given Borel sets. The focus of this paper is on hitting probabilities of the non-centered Gaussian process 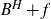$B^{H}+f$. It aims to highlight how each component f, E and F is involved in determining the upper and lower bounds of 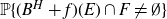$\mathbb{P}\{(B^H+f)(E)\cap F\neq \emptyset \}$. When F is a singleton and f is a general measurable drift, some new estimates are obtained for the last probability by means of suitable Hausdorff measure and capacity of the graph 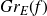$Gr_E(f)$. As application we deal with the issue of polarity of points for 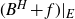$(B^H+f)\vert_E$ (the restriction of 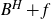$B^H+f$ to the subset 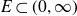$E\subset (0,\infty)$).

MSC classification

Primary: 60G22: Fractional processes, including fractional Brownian motion 60G17: Sample path properties
Secondary: 60J45: Probabilistic potential theory 28A78: Hausdorff and packing measures

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 178 , Issue 1 , January 2025 , pp. 103 - 132
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Biermé, H., Lacaux, C. and Xiao, Y.. Hitting probabilities and the Hausdorff dimension of the inverse images of anisotropic Gaussian random fields. Bull London Math. Soc. 41 (2009), 253–273.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular Variation (Cambridge University Press Cambridge, 1987).CrossRefGoogle Scholar
Bishop, C. J. and Peres, Y.. Fractals in probability and analysis. Cambridge Studies in Advanced Math. 162 (2017) (Cambridge University Press, Cambridge).Google Scholar
Chen, Z. and Xiao, Y.. On intersections of independent anisotropic Gaussian random fields. Sci. China Math. 55 (11) (2012), 2217–2232.CrossRefGoogle Scholar
Chen, Z.. Hitting Probabilities and Fractal Dimensions of Multiparameter Multifractional Brownian Motion. Acta Math. Sin. Engl. Ser. 29 (9) (2013), 1723–1742.CrossRefGoogle Scholar
Dalang, R. C. and Nualart, E.. Potential theory for hyperbolic SPDEs. Ann. Probab. 32 (3A) (2004), 2099–2148.CrossRefGoogle Scholar
Dalang, R. C., Khoshnevisan, D. and Nualart, E.. Hitting probabilities for systems of non-linear stochastic heat equations with additive noise. ALEA Lat. Am. J. Probab. Math. Stat. 3 (2007), 231–271.Google Scholar
Dalang, R. C., Khoshnevisan, D. and Nualart, E.. Hitting probabilities for systems of non-linear stochastic heat equations with multiplicative noise. Probab. Theory Related Fields. 144 (2009), 371–427.CrossRefGoogle Scholar
Erraoui, M. and Hakiki, Y.. Images of fractional Brownian motion with deterministic drift: Positive Lebesgue measure and non-empty interior. Math. Proc. Camb. Phil. Soc. 173 (2022), 693–713.CrossRefGoogle Scholar
Evans, S. N.. Perturbation of functions by the paths of a Lévy process. Math. Proc. Camb. Phil. Soc. 105 (2) (1989), 377–380.CrossRefGoogle Scholar
Falconer, K. J.. Fractal Geometry-Mathematical Foundations and Applications (John Wiley Sons, Chichester, 1990).CrossRefGoogle Scholar
Graversen, S. E.. Polar-functions for Brownian motion. Z. Wahrsch. Verw. Gebiete, 61 (2), 261–270 (1982)CrossRefGoogle Scholar
Hakiki, Y. and Viens, F.. Irregularity scales for Gaussian processes: Hausdorff dimensions and hitting probabilities (2023).Google Scholar
Hutchinson, J. E.. Fractals and self similarity. Indiana Univ. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
Kahane, J. P.. Some Random Series of Functions, Second edition. Cambridge Studies in Advanced Math. 5 (Cambridge University Press, Cambridge, 1985).Google Scholar
Kakutani, S.. Two dimensional Brownian motion and harmonic functions. Proc. Imp. Acad. Tokyo 20 (1944), 648-652.Google Scholar
Khoshnevisan, D.. Escape rates for Lévy processes. Studia Sci. Math. Hungar. 33 (1-3) (1997), 177–183.Google Scholar
Khoshnevisan, D. and Shi, Z.. Brownian sheet and capacity. Ann. Probab. 27 (1999), 1135–1159.CrossRefGoogle Scholar
Le Gall, J. F.. Sur les fonctions polaires pour le mouvement brownien. In Séminaire de Probabilités, XXII. Lecture Notes in Math. 1321 (Springer, Berlin, 1988), 186–189CrossRefGoogle Scholar
Marcus, M. and Rosen, J.. Markov Processes, Gaussian Processes, and Local Times. Cambridge Studies in Advanced Math. 100 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Mattila, P.. Geometry of sets and measures in Euclidean spaces. Fractals and rectifiability (Cambridge University Press, Cambridge, 1999).Google Scholar
Mountford, T. S.. Time inhomogeneous Markov processes and the polarity of single points. Ann. Probab. 17 (2) (1989), 573–585.CrossRefGoogle Scholar
Mörters, P. and Peres, Y.. Brownian Motion. Cambridge Series in Statistical and Probabilistic Math. vol. 30 (Cambridge University Press, 2010).Google Scholar
Peres, Y. and Sousi, P.. Brownian motion with variable drift: 0-1 laws, hitting probabilities and Hausdorff dimension. Math. Proc. Camb. Phil. Soc. 153 (2) (2012), 215–234.CrossRefGoogle Scholar
Peres, Y. and Sousi, P.. Dimension of fractional Brownian motion with variable drift. Probab. Theory Related Fields 165 (3-4) (2016), 771–794.CrossRefGoogle Scholar
Pruitt, W. E. and Taylor, S. J.. The potential kernel and hitting probabilities for the general stable process in $R^{N}$ . Trans. Amer. Math. Soc. 146 (1969), 299-321.Google Scholar
Taylor, S. J.. On the connexion between Hausdorff measures and generalised capacity. Math. Proc. Camb. Phil. Soc. 57 (3) (1961), 524–531.CrossRefGoogle Scholar
Xiao, Y.. Packing measure of the sample paths of fractional Brownian motion. Trans. Amer. Math. Soc. 348 (8) (1996), 3193–3213.CrossRefGoogle Scholar
Xiao, Y.. Sample Path Properties of Anisotropic Gaussian Random Fields. A Minicourse on Stochastic Partial Differential Equations. Lecture Notes in Math. 1962 (2009), 145-212 (New York: Springer).Google Scholar