Hostname: page-component-cb9f654ff-mwwwr Total loading time: 0 Render date: 2025-09-01T09:18:15.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Labelled seeds and the mutation group

Published online by Cambridge University Press:  11 October 2016

ALASTAIR KING  and
MATTHEW PRESSLAND
ALASTAIR KING
Affiliation:
Department of Mathematical Sciences, Claverton Down, University of Bath, BA2 7AY. e-mail: A.D.King@bath.ac.uk; mdpressland@bath.edu
MATTHEW PRESSLAND
Affiliation:
Department of Mathematical Sciences, Claverton Down, University of Bath, BA2 7AY. e-mail: A.D.King@bath.ac.uk; mdpressland@bath.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the set 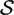${\mathcal{S}}$ of labelled seeds of a cluster algebra of rank n inside a field 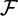${\mathcal{F}}$ as a homogeneous space for the group M n of (globally defined) mutations and relabellings. Regular equivalence relations on 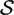${\mathcal{S}}$ are associated to subgroups W of AutM n ( 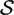${\mathcal{S}}$ ), and we thus obtain groupoids W\ 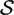${\mathcal{S}}$ . We show that for two natural choices of equivalence relation, the corresponding groups W c and W + act on 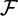${\mathcal{F}}$ , and the groupoids W c\ 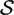${\mathcal{S}}$ and W +\ 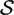${\mathcal{S}}$ act on the model field 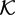${\mathcal{K}}$ =ℚ(x 1,. . .,x n ). The groupoid W +\ 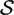${\mathcal{S}}$ is equivalent to Fock–Goncharov's cluster modular groupoid. Moreover, W c is isomorphic to the group of cluster automorphisms, and W + to the subgroup of direct cluster automorphisms, in the sense of Assem–Schiffler–Shramchenko.

We also prove that, for mutation classes whose seeds have mutation finite quivers, the stabiliser of a labelled seed under M n determines the quiver of the seed up to ‘similarity’, meaning up to taking opposites of some of the connected components. Consequently, the subgroup W c is the entire automorphism group of 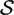${\mathcal{S}}$ in these cases.

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 163 , Issue 2 , September 2017 , pp. 193 - 217
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1] Assem, I., Schiffler, R. and Shramchenko, V. Cluster automorphisms. Proc. Lond. Math. Soc. (3) 104 (2012), no. 6, 1271–1302.CrossRefGoogle Scholar
[2] Berenstein, A., Fomin, S. and Zelevinsky, A. Cluster algebras. III. Upper bounds and double Bruhat cells. Duke Math. J. 126 (2005), no. 1, 1–52.Google Scholar
[3] Berenstein, A. and Zelevinsky, A. Quantum cluster algebras. Adv. Math. 195 (2005), no. 2, 405–455.Google Scholar
[4] Brown, R. Topology and Groupoids (BookSurge, LLC, Charleston, SC, 2006).Google Scholar
[5] Cassels, J.W.S. An Introduction to Diophantine Approximation. Cambridge Tracts in Mathematics and Mathematical Physics, no. 45 (Cambridge University Press, 1957).Google Scholar
[6] Cerulli Irelli, G., Keller, B., Labardini-Fragoso, D. and Plamondon, P.-G. Linear independence of cluster monomials for skew-symmetric cluster algebras. Compos. Math. 149 (2013), no. 10, 1753–1764.Google Scholar
[7] Derksen, H. and Owen, T. New graphs of finite mutation type. Electron. J. Combin. 15 (2008), no. 1, Research Paper 139.Google Scholar
[8] Fock, V.V. and Goncharov, A.B. Cluster ensembles, quantization and the dilogarithm. Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), no. 6, 865–930.Google Scholar
[9] Fomin, S., Shapiro, M. and Thurston, D. Cluster algebras and triangulated surfaces. I. Cluster complexes. Acta Math. 201 (2008), no. 1, 83–146.Google Scholar
[10] Fomin, S. and Zelevinsky, A. Cluster algebras. I. Foundations. J. Amer. Math. Soc. 15 (2002), no. 2, 497–529.Google Scholar
[11] Fomin, S. and Zelevinsky, A. Cluster algebras. II. Finite type classification. Invent. Math. 154 (2003), no. 1, 63–121.Google Scholar
[12] Fomin, S. and Zelevinsky, A. Cluster algebras. IV. Coefficients. Compos. Math. 143 (2007), no. 1, 112–164.Google Scholar
[13] Fulton, W. Algebraic Topology: A First Course. Graduate Texts in Mathematics, vol. 153 (Springer–Verlag, 1995).Google Scholar
[14] Gekhtman, M., Shapiro, M. and Vainshtein, A. On the properties of the exchange graph of a cluster algebra. Math. Res. Lett. 15 (2008), no. 2, 321–330.Google Scholar
[15] Keller, B. Cluster algebras, quiver representations and triangulated categories. In Triangulated Categories. London Math. Soc. Lecture Note Ser. vol. 375 (Cambridge Univ. Press, 2010), pp. 76–160.CrossRefGoogle Scholar
[16] Keller, B. Quiver mutation in Java. Java applet, available at http://www.math.jussieu.fr/~keller/quivermutation/ Google Scholar
[17] Krammer, D. A class of Garside groupoid structures on the pure braid group. Trans. Amer. Math. Soc. 360 (2008), no. 8, 4029–4061.CrossRefGoogle Scholar
[18] Ladkani, S. Which mutation classes of quivers have constant number of arrows? Preprint, arXiv:1104.0436v1 [math.CO] (2011).Google Scholar
[19] Musiker, G. and Stump, C. A compendium on the cluster algebra and quiver package in Sage. Sém. Lothar. Combin. 65 (2012), Art. B65d.Google Scholar
[20] Reiten, I. Cluster categories. In Proceedings of the International Congress of Mathematicians. vol. I (Hindustan Book Agency, New Delhi, 2010), pp. 558–594.Google Scholar