We study the set ${\mathcal{S}}$ of labelled seeds of a cluster algebra of rank n inside a field ${\mathcal{F}}$ as a homogeneous space for the group M n of (globally defined) mutations and relabellings. Regular equivalence relations on ${\mathcal{S}}$ are associated to subgroups W of AutM n ( ${\mathcal{S}}$ ), and we thus obtain groupoids W\ ${\mathcal{S}}$ . We show that for two natural choices of equivalence relation, the corresponding groups W c and W + act on ${\mathcal{F}}$ , and the groupoids W c\ ${\mathcal{S}}$ and W +\ ${\mathcal{S}}$ act on the model field ${\mathcal{K}}$ =ℚ(x 1,. . .,x n ). The groupoid W +\ ${\mathcal{S}}$ is equivalent to Fock–Goncharov's cluster modular groupoid. Moreover, W c is isomorphic to the group of cluster automorphisms, and W + to the subgroup of direct cluster automorphisms, in the sense of Assem–Schiffler–Shramchenko.

We also prove that, for mutation classes whose seeds have mutation finite quivers, the stabiliser of a labelled seed under M n determines the quiver of the seed up to ‘similarity’, meaning up to taking opposites of some of the connected components. Consequently, the subgroup W c is the entire automorphism group of ${\mathcal{S}}$ in these cases.

For a group G first order definable in a structure M, we continue the study of the “definable topological dynamics” of G (from [9] for example). The special case when all subsets of G are definable in the given structure M is simply the usual topological dynamics of the discrete group G; in particular, in this case, the words “externally definable” and “definable” can be removed in the results described below.

Here we consider the mutual interactions of three notions or objects: a certain model-theoretic invariant G*/(G*)000 M of G, which appears to be “new” in the classical discrete case and of which we give a direct description in the paper; the [externally definable] generalised Bohr compactification of G; [externally definable] strong amenability. Among other things, we essentially prove: (i) the “new” invariant G*/(G*)000 M lies in between the externally definable generalised Bohr compactification and the definable Bohr compactification, and these all coincide when G is definably strongly amenable and all types in SG (M) are definable; (ii) the kernel of the surjective homomorphism from G*/(G*)000 M to the definable Bohr compactification has naturally the structure of the quotient of a compact (Hausdorff) group by a dense normal subgroup; (iii) when Th(M) is NIP, then G is [externally] definably amenable iff it is externally definably strongly amenable.

In the situation when all types in SG (M) are definable, one can just work with the definable (instead of externally definable) objects in the above results.

Let $\mathcal{C}$ be closed symmetric monoidal Grothendieck category. We define the pure derived category with respect to the monoidal structure via a relative injective model category structure on the category C( $\mathcal{C}$ ) of unbounded chain complexes in $\mathcal{C}$ . We use λ-Purity techniques to get this. As application we define the stalkwise pure derived category of the category of quasi–coherent sheaves on a quasi-separated scheme. We also give a different approach by using the category of flat quasi–coherent sheaves.

Let A be a quasi-hereditary algebra. We prove that in many cases, a tilting module is rigid (i.e. has identical radical and socle series) if it does not have certain subquotients whose composition factors extend more than one layer in the radical series or the socle series. We apply this theorem to show that the restricted tilting modules for SL 4(K) are rigid, where K is an algebraically closed field of characteristic p ≥ 5.

Let S be a polynomial ring over a field K of characteristic zero and let M ⊂ S be an ideal given as an intersection of powers of incomparable monomial prime ideals (e.g., the case where M is a squarefree monomial ideal). In this paper we provide a very effective, sufficient condition for a monomial prime ideal P ⊂ S containing M be such that the localisation M P has non-maximal analytic spread. Our technique describes, in fact, a concrete obstruction for P to be an asymptotic prime divisor of M with respect to the integral closure filtration, allowing us to employ a theorem of McAdam as a bridge to analytic spread. As an application, we derive – with the aid of results of Brodmann and Eisenbud-Huneke – a situation where the asymptotic and conormal asymptotic depths cannot vanish locally at such primes.

In noncommutative geometry a ‘Lie algebra’ or bidirectional bicovariant differential calculus on a finite group is provided by a choice of an ad-stable generating subset $\mathcal{C}$ stable under inversion. We study the associated Killing form K. For the universal calculus associated to $\mathcal{C}$ = G \ {e} we show that the magnitude $\mu=\sum_{a,b\in\mathcal{C}}(K^{-1})_{a,b}$ of the Killing form is defined for all finite groups (even when K is not invertible) and that a finite group is Roth, meaning its conjugation representation contains every irreducible, iff μ ≠ 1/(N − 1) where N is the number of conjugacy classes. We show further that the Killing form is invertible in the Roth case, and that the Killing form restricted to the (N − 1)-dimensional subspace of invariant vectors is invertible iff the finite group is an almost-Roth group (meaning its conjugation representation has at most one missing irreducible). It is known [9, 10] that most nonabelian finite simple groups are Roth and that all are almost Roth. At the other extreme from the universal calculus we prove that the 2-cycles conjugacy class in any Sn has invertible Killing form, and the same for the generating conjugacy classes in the case of the dihedral groups D 2n with n odd. We verify invertibility of the Killing forms of all real conjugacy classes in all nonabelian finite simple groups to order 75,000, by computer, and we conjecture this to extend to all nonabelian finite simple groups.

Let k := (k 1,. . .,k s ) be a sequence of natural numbers. For a graph G, let F(G;k ) denote the number of colourings of the edges of G with colours 1,. . .,s such that, for every c ∈ {1,. . .,s}, the edges of colour c contain no clique of order k c . Write F(n;k ) to denote the maximum of F(G;k ) over all graphs G on n vertices. This problem was first considered by Erdős and Rothschild in 1974, but it has been solved only for a very small number of non-trivial cases.

We prove that, for every k and n, there is a complete multipartite graph G on n vertices with F(G;k ) = F(n;k ). Also, for every k we construct a finite optimisation problem whose maximum is equal to the limit of log2F(n;k )/ 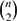${n\choose 2}$ as n tends to infinity. Our final result is a stability theorem for complete multipartite graphs G, describing the asymptotic structure of such G with F(G;k ) = F(n;k ) · 2o(n2) in terms of solutions to the optimisation problem.

We extend existing results characterizing Weil-Châtelet divisibility of locally trivial torsors over number fields to global fields of positive characteristic. Building on work of González-Avilés and Tan, we characterize when local-global divisibility holds in such contexts, providing examples showing that these results are optimal. We give an example of an elliptic curve over a global field of characteristic 2 containing a rational point which is locally divisible by 8, but is not divisible by 8 as well as examples showing that the analogous local-global principle for divisibility in the Weil-Châtelet group can also fail.

In a family of S d+1-fields (d = 2, 3, 4), we obtain the conjectured upper and lower bounds of the residues of Dedekind zeta functions except for a density zero set. For S 5-fields, we need to assume the strong Artin conjecture. We also show that there exists an infinite family of number fields with the upper and lower bounds, resp.

There was a gap in the proof of Theorem 4.1 of [1]. In this corrigendum, we correct the error.