Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-30T00:50:29.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure of fine Selmer groups over 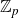$\mathbb{Z}_{p}$-extensions

Part of: Algebraic number theory: global fields Algebraic number theory: local and $p$-adic fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  04 October 2023

MENG FAI LIM
MENG FAI LIM*
Affiliation:
School of Mathematics and Statistics & Hubei Key Laboratory of Mathematical Sciences, Central China Normal University, Hubei, Wuhan, No. 152 Luoyu Road, 430079, P.R. China. e-mail: limmf@ccnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the study of the fine Selmer group of an abelian variety over a 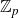$\mathbb{Z}_{p}$-extension which is not necessarily cyclotomic. It has been conjectured that these fine Selmer groups are always torsion over 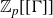$\mathbb{Z}_{p}[[ \Gamma ]]$, where 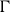$\Gamma$ is the Galois group of the 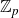$\mathbb{Z}_{p}$-extension in question. In this paper, we shall provide several strong evidences towards this conjecture. Namely, we show that the conjectural torsionness is consistent with the pseudo-nullity conjecture of Coates–Sujatha. We also show that if the conjecture is known for the cyclotomic 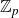$\mathbb{Z}_{p}$-extension, then it holds for almost all 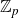$\mathbb{Z}_{p}$-extensions. We then carry out a similar study for the fine Selmer group of an elliptic modular form. When the modular forms are ordinary and come from a Hida family, we relate the torsionness of the fine Selmer groups of the specialization. This latter result allows us to show that the conjectural torsionness in certain cases is consistent with the growth number conjecture of Mazur. Finally, we end with some speculations on the torsionness of fine Selmer groups over an arbitrary p-adic Lie extension.

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11G05: Elliptic curves over global fields 11S25: Galois cohomology
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 176 , Issue 2 , March 2024 , pp. 287 - 308
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Choi, J., Kezuka, Y. and Li, Y.. Analogues of Iwasawa’s $\mu=0$ conjecture and the weak Leopoldt conjecture for a non-cyclotomic $\mathbb{Z}_2$ -extension. Asian J. Math. 23(3) (2019), 383–400.CrossRefGoogle Scholar
Coates, J. and McConnell, G.. Iwasawa theory of modular elliptic curves of analytic rank at most 1, J. London Math. Soc. (2) 50(2) (1994), 243–264.CrossRefGoogle Scholar
Coates, J. and Sujatha, R.. Fine Selmer groups for elliptic curves with complex multiplication. Algebra and number theory (Hindustan Book Agency, Delhi, 2005), 327–337.CrossRefGoogle Scholar
Coates, J. and Sujatha, R.. Fine Selmer groups of elliptic curves over p-adic Lie extensions. Math. Ann. 331(4) (2005), 809–839.CrossRefGoogle Scholar
Coates, J. and Sujatha, R.. Galois Cohomology of Elliptic Curves. Second edition (Narosa Publishing House, New Delhi; for the Tata Institute of Fundamental Research, Mumbai, 2010), xii+98 pp.Google Scholar
Coates, J., Sujatha, R. and Wintenberger, J.-P.. On the Euler–Poincaré characteristics of finite dimensional p-adic Galois representations. Publ. Math. Inst. Hautes Études Sci. 93 (2001), 107–143.Google Scholar
Cuoco, A.. Generalised lwasawa invariants in a family. Compositio Math. 51 (1984), 89–103.Google Scholar
Deligne, P.. Formes modulaires et représentations l-adiques. Séminaire Bourbaki vol. 1968/69: Exposés 347-363, Exp. No. 355. Lecture Notes in Math. 175 (Springer, Berlin, 1971), 139–172.Google Scholar
de Shalit, E.. Iwasawa theory of elliptic curves with complex multiplication. Perspectives in Mathematics, 3. (Academic Press, Inc., Boston, MA, 1987).Google Scholar
Dokchitser, T. and Dokchitser, V.. Computations in non-commutative Iwasawa theory (with an appendix by J. Coates and R. Sujatha). Proc. London Math. Soc. (3) 94(1) (2007), 211–272.CrossRefGoogle Scholar
Greenberg, R.. The Iwasawa invariants of $\Gamma$ -extensions of a fixed number field Amer. J. Math. 95(1) (1973), pp. 204–214.Google Scholar
Hachimori, Y.. Euler characteristics of fine Selmer groups J. Ramanujan Math. Soc. 25(3) (2010), 285–293.Google Scholar
Hachimori, Y. and Matsuno, K.. An analogue of Kida’s formula for the Selmer groups of elliptic curves. J. Algebraic Geom. 8(3) (1999), 581–601.Google Scholar
Hatley, J., Kundu, D., Lei, A. and Ray, J.. Control theorem for fine Selmer group and duality of fine Selmer groups attached to modular forms. Ramanujan J. 60(1) (2023), 237–258.CrossRefGoogle Scholar
Hida, H.. Galois representations into $\textrm{GL}_2(\mathbb{Z}_{p}[[ X ]])$ attached to ordinary cusp forms Invent. Math. 85 (1986), 543–613.Google Scholar
Jha, S.. Fine Selmer group of Hida deformations over non-commutative p-adic Lie extensions. Asian J. Math. 16(2) (2012), 353–366.CrossRefGoogle Scholar
Jha, S. and Sujatha, R.. On the Hida deformations of fine Selmer groups. J. Algebra 338 (2011), 180–196.CrossRefGoogle Scholar
Kato, K.. p-adic Hodge theory and values of zeta functions of modular forms In: Cohomologies p-adiques et applications arithmétiques. III. Astérisque 295, (2004), ix, pp. 117–290.Google Scholar
Kezuka, Y.. On the main conjecture of Iwasawa theory for certain non-cyclotomic $\mathbb{Z}_{p}$ -extensions. J. London Math. Soc. (2) 100(1) (2019), 107–136.CrossRefGoogle Scholar
Kleine, S.. Bounding the Iwasawa invariants of Selmer groups. Canad. J. Math. 73(5) (2021), 1390–1422.CrossRefGoogle Scholar
Kleine, S. and Müller, K.. Fine Selmer groups of congruent p-adic Galois representations. Canad. Math. Bull. 65(3) (2022), 702–722.CrossRefGoogle Scholar
Kobayashi, S.. Iwasawa theory for elliptic curves at supersingular primes. Invent. Math. 152(1) (2003), 1–36.CrossRefGoogle Scholar
Kundu, D. and Lim, M. F.. Control theorems for fine Selmer groups. J. Théor. Nombres Bordeaux 34(3) (2022), 851–880.CrossRefGoogle Scholar
Lei, A. and Palvannan, B.. Codimension two cycles in Iwasawa theory and elliptic curves with supersingular reduction. Forum Math. Sigma, 7 (2019), e25.CrossRefGoogle Scholar
Lei, A. and Palvannan, B.. Codimension two cycles in Iwasawa theory and tensor product of Hida families Math. Ann. 383(1-2) (2022), 39–75.Google Scholar
Lim, M. F.. On the pseudo-nullity of the dual fine Selmer groups. Int. J. Number Theory 11(7) (2015), 2055–2063.CrossRefGoogle Scholar
Lim, M. F.. Notes on the fine Selmer groups. Asian J. Math. 21(2) (2017), 337–361.CrossRefGoogle Scholar
Lim, M. F.. On the control theorem for fine Selmer groups and the growth of fine Tate–Shafarevich groups in $\mathbb{Z}_{p}$ -extensions Doc. Math. 25 (2020), 2445–2471.CrossRefGoogle Scholar
Lim, M. F.. On the growth of even K-groups of rings of integers in p-adic Lie extensions, Israel J. Math. 249(2) (2022), 735–767.CrossRefGoogle Scholar
Lim, M. F.. On the codescent of étale wild kernels in p-adic Lie extensions. To appear in Kyoto J. Math.Google Scholar
Lim, M. F. and Murty, V. K.. The growth of fine Selmer groups. J. Ramanujan Math. Soc. 31(1) (2016), 79–94.Google Scholar
Lim, M. F. and Sujatha, R.. Fine Selmer groups of congruent Galois representations. J. Number Theory 187 (2018), 66–91.CrossRefGoogle Scholar
Longo, M. and Vigni, S.. Plus/minus Heegner points and Iwasawa theory of elliptic curves at supersingular primes. Boll. Unione Mat. Ital. 12(3) (2019), 315–347.CrossRefGoogle Scholar
Matsumura, H.. Commutative Ring Theory Translated by Reid, M., second ed. Cambridge Stud. Adv. Math. 8 (Cambridge University Press, 1989).Google Scholar
Mattuck, A.. Abelian varieties over p-adic ground fields Ann. of Math. (2) 62 (1955), 92–119.Google Scholar
Mazur, B.. Rational points of abelian varieties with values in towers of number fields Invent. Math. 18 (1972), 183–266.CrossRefGoogle Scholar
Mazur, B.. Modular curves and arithmetic. Proc. Internat. Congr. Math. 1, 2 (Warsaw, 1983) (PWN, Warsaw, 1984), 185–211.Google Scholar
Mazur, B. and Tilouine, J.. Represéntations galoisiennes, différentielles de Kähler et “conjectures principales” Publ. Math. IHES 71 (1990), 65–103.CrossRefGoogle Scholar
Monsky, P.. Some invariants of $\mathbb{Z}_{p}^d$ -extensions. Math. Ann. 255 (1981), 229–233.CrossRefGoogle Scholar
Neukirch, J., Schmidt, A. and Wingberg, K.. Cohomology of Number Fields, 2nd edn. Grundlehren Math. Wiss. 323 (Springer–Verlag, Berlin, 2008).CrossRefGoogle Scholar
Neumann, A.. Completed group algebras without zero divisors. Arch. Math. 51(6) (1988), 496–499.CrossRefGoogle Scholar
Nguyen Quang Do, T.. Analogues supérieurs du noyau sauvage. Sém. Théor. Nombres Bordeaux (2) 4(2) (1992), 263–271.CrossRefGoogle Scholar
Nguyen Quang Do, T.. Théorie d’Iwasawa des noyaux sauvages étales d’un corps de nombres. Théorie des nombres, Années 1998/2001. Publ. Math. UFR Sci. Tech. Besançon, (Univ. Franche-Comté, Besançon, 2002), 9pp.CrossRefGoogle Scholar
Perrin-Riou, B.. Arithmétique des courbes elliptiques et théorie d’Iwasawa. Mém. Soc. Math. France (N.S.) 17 (1984), 1–130.Google Scholar
Perrin–Riou, B.. p-adic L-functions and p-adic representations. Translated from the 1995 French original by Leila Schneps and revised by the author. SMF/AMS Texts and Monographs 3 (American Mathematical Society, Providence, RI; Société Mathématique de France, Paris, 2000). xx+150 pp.Google Scholar
Pollack, R.. Tables of Iwasawa invariants of elliptic curves. Available at: http://math.bu.edu/people/rpollack/Data/data.html.Google Scholar
Pollack, R. and Weston, T.. On anticyclotomic $\mu$ -invariants of modular forms. Compositio Math. 147(5) (2011), 1353–1381.CrossRefGoogle Scholar
Rasmussen, C. and Tamagawa, A.. A finiteness conjecture on abelian varieties with constrained power torsion. Math. Res. Lett. 15(6) (2008), 1223–1231.Google Scholar
Ribet, K.. Galois representations attached to eigenforms with Nebentypus. Modular functions of one variable, V (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976) Lecture Notes in Math. 601 (Springer, Berlin, 1977), pp. 17–51.CrossRefGoogle Scholar
Rubin, K.. The “main conjectures” of Iwasawa theory for imaginary quadratic fields. Invent. Math. 103 (1991), 25–68.CrossRefGoogle Scholar
Schneider, P.. p-adic height pairings II. Invent. Math. 79(2) (1985), 329–374.CrossRefGoogle Scholar
Venjakob, O.. On the structure theory of the Iwasawa algebra of a p-adic Lie group. J. Eur. Math. Soc. 4(3) (2002), 271–311.CrossRefGoogle Scholar
Weibel, C.. An Introduction to Homological Algebra. Camb. Stud. Adv. Math. 38. (Cambridge University Press, Cambridge, 1994).Google Scholar
Wuthrich, C.. The fine Selmer group and height pairings. Ph.D. thesis University of Cambridge, (2004).Google Scholar
Wuthrich, C.. Iwasawa theory of the fine Selmer group. J. Algebraic Geom. 16(1) (2007), 83–108.Google Scholar
Wuthrich, C.. The fine Tate–Shafarevich group. Math. Proc. Camb. Phil. Soc. 142(1) (2007), 1–12.CrossRefGoogle Scholar