Contents
Research Article
Semigroup laws in varieties of solvable groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-9
-
- Article
- Export citation
On the hyperplanes of a matroid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-18
-
- Article
- Export citation
Existence theorems for H-space inverses
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-21
-
- Article
- Export citation
A class of compressible embeddings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-26
-
- Article
- Export citation
Almost periodicity and B-equicontinuity in topological dynamics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-32
-
- Article
- Export citation
On the Brunn-Minkowski coefficient of a locally compact unimodular group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-45
-
- Article
- Export citation
Finite dimensional submodules of G-modules for a compact group G
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 47-52
-
- Article
- Export citation
Ultrabarrelled groups and the closed graph theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 53-58
-
- Article
- Export citation
Arithmetic on curves with complex multiplication by the Eisenstein integers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 59-73
-
- Article
- Export citation
On the convergence factor of a Fourier series and a differentiated Fourier series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 75-85
-
- Article
- Export citation
On some results involving generalized hypergeometric polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 87-92
-
- Article
- Export citation
On a Tauberian theorem for absolute harmonic summability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 93-99
-
- Article
- Export citation
Jacobi series which converge to zero, with applications to a class of singular partial differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 101-106
-
- Article
- Export citation
Computer-calculated explicit forms for representations of the three-dimensional pure rotation group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-110
-
- Article
- Export citation
On the general quantum theory of measurement†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-122
-
- Article
- Export citation
The oscillations of a viscous gravitating sphere
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-137
-
- Article
- Export citation
An explicit determination of the empty space-times on which the wave equation satisfies Huygens' principle†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-155
-
- Article
- Export citation
Spherically symmetric differential equations, the rotation group, and tensor spherical functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 157-175
-
- Article
- Export citation
The Boltzmann-Landau transport equation: I. The first-order Chapman-Enskog approximation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-187
-
- Article
- Export citation
The Boltzmann-Landau transport equation: II. The transport coefficients
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-198
-
- Article
- Export citation
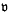 be a variety of groups. We say that the variety
be a variety of groups. We say that the variety 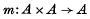
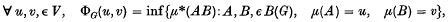
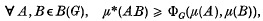
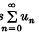
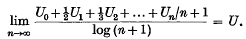
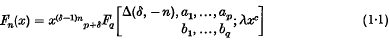
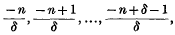
 be defined by
be defined by
 is given by
is given by


 for values of
for values of 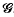 . These fields may be expanded as series of functions
. These fields may be expanded as series of functions 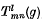 , where
, where 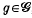 ,
,