Let G be a regular graph with even girth g = 2r ≥ 4 and valency k ≥ 3. It is well known, and easy to prove, that G must have at least n0 = n0(g, k) vertices, where

We shall be considering plane closed convex curves Γ (whose interior plus boundary will be denoted by Σ ≡ Σ(Γ)) in which we can inscribe a large set (in various senses to be made precise) of equilateral triangles or e-triangles for short; and in particular an e-triangle of side-length 1 is called an E-triangle or just an E. More formally we define the sets to be the sets of closed convex Γ for which, respectively:

: each point of Γ is the vertex of some inscribed E;

: Γ contains the vertices of some E in each orientation in the plane;

: an E can be moved round continuously, through angle 2π, with all vertices on Γ throughout.

We write and x1 = 1. In a recent paper (3), Stein and Everett consider the sequence defined by

and investigate whether

tends to a limit as n → ∞. The case b = 0 has a combinatorial interpretation (see (1)) and, in (2), they use this to prove that xn → e−1 in this case. Even for positive integral b, the number Sn has no known combinatorial interpretation, but they prove (3) that xn → x under the hypothesis that Sn+1Sn−1 ≥ Sn i.e. that Sn is convex. By computation and induction, they prove this hypothesis for b = k/5, where k = 1, 2,…, 50.

If a finite projective plane is of type (6, m), then m = 2 or 3.

It is a well-known result of V. L. Klee (2) that if a convex body K in En has all its k-dimensional sections as polytopes (k ≥ 2) then K is a polytope.

By considering the action of the Hecke operators on the logarithm of the Dedekind eta function together with the modular transformation formula for this function, Knopp (8) proved an extension of an identity of Dedekind for the classical Dedekind sums first mentioned by H. Petersson. By looking at the action of the Hecke operators on certain Lambert series studied by Apostol(l) together with the transformation formulae for these series, Parson and Rosen (9) established an analogous identity for a type of generalized Dedekind sum. A special case of this identity was initially proved by Carlitz(6). In this note an elementary proof of these identities is given. The Hecke operators are applied directly to the Dedekind sums without invoking the transformation formulae for the logarithm of the eta function or for the Lambert series. (Recently, L. Goldberg has given another elementary proof of Knopp's identity.)

A tangent-developable is a surface generated by the tangent lines of a space curve. The intersection of a tangent-developable with the normal plane at a point P of the curve generally has a cusp at that point. Thus the tangent-developable of a space curve has a cuspidal edge along the curve. The classical derivation of this phenomenon takes the trihedron (t, n, b) at P as coordinate axes to which the curve is referred. Then the intersection of the part of the tangent-developable generated by tangent lines at points close to P with the normal plane at P (i.e. the plane through P containing n and b) is given parametrically by power series

where K, T are the curvature and torsion, respectively, of the curve at P and s is arc-length measured from P ((2) p. 68). It is tacitly understood in this analysis that curvature and torsion are both defined and non-zero.

In an earlier paper (5) we showed that a finitely generated nilpotent group which is not abelian-by-finite has a primitive irreducible representation of infinite dimension over any non-absolute field. Here we are concerned primarily with the converse question: Suppose that G is a polycyclic-by-finite group with such a representation, then what can be said about G?

One of the most important constructions in topos theory ia that of the category Shv (A) of sheaves on a locale (= complete Heyting algebra) A. Normally, the objects of this category are described as ‘presheaves on A satisfying a gluing condition’; but, as Higgs(7) and Fourman and Scott(5) have observed, they may also be regarded as ‘sets structured with an A-valued equality predicate’ (briefly, ‘A-valued sets’). From the latter point of view, it is an inessential feature of the situation that every sheaf has a canonical representation as a ‘complete’ A-valued set. In this paper, our aim is to investigate those properties which A must have for us to be able to construct a topos of A-valued sets: we shall see that there is one important respect, concerning the relationship between the finitary (propositional) structure and the infinitary (quantifier) structure, in which the usual definition of a locale may be relaxed, and we shall give a number of examples (some of which will be explored more fully in a later paper (8)) to show that this relaxation is potentially useful.

Let Γ be a Fuchsian group of the first kind acting on the upper half plane H+. Let be a Ford fundamental region for Γ in H+. Let ξ be a real number (a limit point) and let L( = Lξ) = {ξ + iy|0 ≤ y < 1}. L can be broken into successive intervals each one of which can be mapped by an element of Γ into . Since L is a hyperbolic line (h-line), this gives us a set of h-arcs in which we will call the image.

Two measures are strongly equivalent if they have the same sets of zero measure and the same sets of infinite measure. Given a group G of strongly non-singular measurable transformations of a non-atomic positive measure space (X, β, p), if G is amenable, then a necessary and sufficient condition for there to be a G-invariant positive measure on (X, β) which is strongly equivalent to p is that p(E) > 0 implies inf p(gE) > 0 and also p(E) < ∞ implies

Let I be a set with |I| > 1, let Hi(i ∈ I) be nontrivial groups and let H = *i ∈ IHi be their free product. Let R be a cyclically reduced element of Hi and write

if G is (isomorphic to) H/{R}H.

This paper presents a straightforward proof of the Gel'fand-Naimark theorem for non-commutative C*-algebras with identity, established by Dauns and Hofmann(2) in the context of fields of C*-algebras, by considering instead C*-algebras in categories of sheaves. The proof differs from that of (2,3,4) in obtaining an isometric *-isomorphism

from the C*-algebra A to the C*-algebra of sections of a C*-algebra Ax in the category of sheaves on the maximal ideal space X of the centre of A, without invoking any arguments which involve completeness (3, Theorem 7·9). Instead, the results of (7) yield immediately the existence of an algebraic isomorphism, the compactness of the maximal ideal space X then being used to prove that Ax is indeed a C*-algebra in the category of sheaves on X and that the isomorphism is isometric. One recovers the representation of (2) by noting (8) that any C*-algebra in the category of sheaves on X is isomorphic to the sheaf of sections of a canonical field of C*-algebras on X.

Surface integrals of curvature arise naturally in integral geometry and geometrical probability, most often in connection with the Quermassintegrale or cross-section integrals of convex bodies. They enjoy many desirable properties, such as the ability to be determined by summing or averaging over lower-dimensional sections or projections. In fact the Quermassintegrale are the only functionals of convex bodies to meet certain, quite reasonable, requirements. The conclusion has often been drawn, especially in practical applications, that the Quermassintegrale and their associated curvature integrals have a canonical status to the exclusion of all other quantities.

In the course of their enumeration of all 4-dimensional space groups, Brown, Bülow, Neubüser, Wondratschek and Zassenhaus have introduced concepts appropriate to the study of n-dimensional crystallography for n ≥ 4 (see (2), (3)). One such concept is that of a crystal family. Families seem to be particularly useful as a framework within which to study higher dimensional crystallography, primarily because they determine a classification of all the standard crystallographic objects and overcome the traditional confusion over crystal systems (see (2); pp. 16–17, (9)). In this paper, techniques are developed for the determination of all rationally decomposable families in a given dimension from the indecomposable families of lower dimensions. These techniques place emphasis on three geometric invariants of families: the decomposition pattern; the canonical decomposition pattern; and the number of free parameters. This, it is felt, further reinforces their position as fundamental objects. The key result (Theorem 5.4) is:

a family uniquely determines, and is uniquely determined by, the constituent families in the canonical decomposition.

We give sufficient conditions on the potential V(x) which ensure that the Schrödinger operator (1 · 1) of quantum mechanics has no singular continuous spectrum This generalizes previous results.

Parametrized equations of state of the form

where s = (s1, … sr) ∈ Rr, x ∈ R, and F is smooth, are common in applied science. Often there exist multiple states x for given s, which may bifurcate as s varies.

In this paper we shall describe that part of the canonical stratification of a versal unfolding of a function germ which deals with simple singularities. These results are doubtless known to many workers in this field; see especially the papers of E. J. N. Looijenga (e.g. (12)). We fill in the details however since we have in mind some geometrical applications (given in § 2) concerning natural partitions of the spaces of binary forms, cubic surfaces and quartic curves. The first two stratifications were considered in the author's Liverpool Ph.D. thesis; the quartic curves were considered in the Liverpool thesis of C. M. Hui, where the results were obtained by specific calculation. See (4) for an illustration of the techniques employed in these theses.

This paper concerns the boundary-value problems

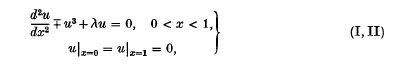
in which λ is a real parameter, u is to be a real-valued function in C2[0, 1], and problem (I) is that with the minus sign. (The differential operators 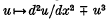are called semi-linear because the non-linearity is only in undifferentiated terms.) If we linearize the equations (for ‘ small’ solutions u) by neglecting 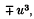, there result the eigenvalues λ = n2π2 (with n = 1,2,…) and corresponding normalized eigenfunctions

and it is well known ((2), p. 186) that the sequence {en} is complete in that it is an orthonormal basis for the real Hilbert space L2(0, 1). We shall be concerned with possible extensions of this result to the non-linear problems (I) and (II), for which non-trivial solutions (λ, u) bifurcate from the trivial solution (λ, 0) at the points {n2π2,0) in the product space 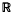× L2(0, 1). (Here 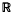denotes the real line.)

In (3), Cor. 2 to Th. 1, the first author proved that in the complex jet space Jk (n, 1) the orbits of simple singularities form canonical strata. By definition the canonical stratification is contact invariant so the proof consisted essentially of two steps: firstly, any two functions in the same canonical stratum are C0-equivalent by right-left changes of coordinates, and secondly, the right codimension (and hence the Milnor number) of an isolated complex singularity is a topological invariant.