Article contents
Autostability spectra for decidable structures
Published online by Cambridge University Press: 14 October 2016
Abstract
We study autostability spectra relative to strong constructivizations (SC-autostability spectra). For a decidable structure 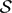 $\mathcal{S}$ , the SC-autostability spectrum of
$\mathcal{S}$ , the SC-autostability spectrum of 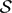 $\mathcal{S}$ is the set of all Turing degrees capable of computing isomorphisms among arbitrary decidable copies of
$\mathcal{S}$ is the set of all Turing degrees capable of computing isomorphisms among arbitrary decidable copies of 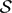 $\mathcal{S}$ . The degree of SC-autostability for
$\mathcal{S}$ . The degree of SC-autostability for 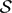 $\mathcal{S}$ is the least degree in the spectrum (if such a degree exists).
$\mathcal{S}$ is the least degree in the spectrum (if such a degree exists).
We prove that for a computable successor ordinal α, every Turing degree c.e. in and above 0 (α) is the degree of SC-autostability for some decidable structure. We show that for an infinite computable ordinal β, every Turing degree c.e. in and above 0 (2β+1) is the degree of SC-autostability for some discrete linear order. We prove that the set of all PA-degrees is an SC-autostability spectrum. We also obtain similar results for autostability spectra relative to n-constructivizations.
Information
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 28 , Special Issue 3: Mind, Mechanism and Mathematics: Computability Unchained , March 2018 , pp. 392 - 411
- Copyright
- Copyright © Cambridge University Press 2016
References
- 13
- Cited by

