Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pennemann, Karl-Heinz
2008.
Graph Transformations.
Vol. 5214,
Issue. ,
p.
508.
Hermann, Frank
Ehrig, Hartmut
Golas, Ulrike
and
Orejas, Fernando
2010.
Efficient analysis and execution of correct and complete model transformations based on triple graph grammars.
p.
22.
Radke, Hendrik
2010.
Graph Transformations.
Vol. 6372,
Issue. ,
p.
410.
Ehrig, Hartmut
Habel, Annegret
Lambers, Leen
Orejas, Fernando
and
Golas, Ulrike
2010.
Graph Transformations.
Vol. 6372,
Issue. ,
p.
330.
Biermann, Enrico
Ehrig, Hartmut
Ermel, Claudia
Golas, Ulrike
and
Taentzer, Gabriele
2010.
Graph Transformations and Model-Driven Engineering.
Vol. 5765,
Issue. ,
p.
121.
Cabot, Jordi
Clarisó, Robert
Guerra, Esther
and
de Lara, Juan
2010.
Theory and Practice of Model Transformations.
Vol. 6142,
Issue. ,
p.
45.
Hermann, Frank
Ehrig, Hartmut
Orejas, Fernando
and
Golas, Ulrike
2010.
Graph Transformations.
Vol. 6372,
Issue. ,
p.
155.
Dijkman, Remco
and
Van Gorp, Pieter
2010.
Business Process Modeling Notation.
Vol. 67,
Issue. ,
p.
16.
Taentzer, Gabriele
Ermel, Claudia
Langer, Philip
and
Wimmer, Manuel
2010.
Graph Transformations.
Vol. 6372,
Issue. ,
p.
171.
Orejas, Fernando
Ehrig, Hartmut
and
Prange, Ulrike
2010.
Reasoning with graph constraints.
Formal Aspects of Computing,
Vol. 22,
Issue. 3,
p.
385.
Poskitt, Christopher M.
and
Plump, Detlef
2010.
Graph Transformations.
Vol. 6372,
Issue. ,
p.
139.
Orejas, Fernando
2011.
Symbolic graphs for attributed graph constraints.
Journal of Symbolic Computation,
Vol. 46,
Issue. 3,
p.
294.
Ermel, Claudia
Gall, Jürgen
Lambers, Leen
and
Taentzer, Gabriele
2011.
Fundamental Approaches to Software Engineering.
Vol. 6603,
Issue. ,
p.
156.
Hülsbusch, Mathias
and
König, Barbara
2012.
Foundations of Software Science and Computational Structures.
Vol. 7213,
Issue. ,
p.
361.
Trollmann, Frank
and
Albayrak, Sahin
2012.
Expressing model relations as basis for structural consistency analysis in models@run.time.
p.
74.
Strecker, Martin
2012.
Applications of Graph Transformations with Industrial Relevance.
Vol. 7233,
Issue. ,
p.
169.
Runge, Olga
Ermel, Claudia
and
Taentzer, Gabriele
2012.
Applications of Graph Transformations with Industrial Relevance.
Vol. 7233,
Issue. ,
p.
81.
Giese, Holger
and
Lambers, Leen
2012.
Graph Transformations.
Vol. 7562,
Issue. ,
p.
249.
Kutz, Oliver
Hastings, Janna
and
Mossakowski, Till
2012.
Artificial Intelligence: Methodology, Systems, and Applications.
Vol. 7557,
Issue. ,
p.
103.
Schölzel, Hanna
Ehrig, Hartmut
Maximova, Maria
Garbriel, Karsten
and
Hermann, Frank
2012.
Satisfaction, Restriction and Amalgamation of Constraints in the Framework of M-Adhesive Categories.
Electronic Proceedings in Theoretical Computer Science,
Vol. 93,
Issue. ,
p.
83.
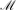 -satisfiability and
-satisfiability and 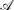 -satisfiability. We consider a number of transformations on conditions that can be composed to construct constraint-guaranteeing and constraint-preserving application conditions, weakest preconditions and strongest postconditions. The restriction of rule applications by conditions can be used to correct transformation systems by pruning transitions leading to states violating given constraints. Weakest preconditions and strongest postconditions can be used to verify the correctness of transformation systems with respect to pre- and postconditions.
-satisfiability. We consider a number of transformations on conditions that can be composed to construct constraint-guaranteeing and constraint-preserving application conditions, weakest preconditions and strongest postconditions. The restriction of rule applications by conditions can be used to correct transformation systems by pruning transitions leading to states violating given constraints. Weakest preconditions and strongest postconditions can be used to verify the correctness of transformation systems with respect to pre- and postconditions.
