Hostname: page-component-6766d58669-bp2c4 Total loading time: 0 Render date: 2026-05-16T14:00:06.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalizations of the distributed Deutsch–Jozsa promise problem

Published online by Cambridge University Press:  06 May 2015

JOZEF GRUSKA ,
DAOWEN QIU  and
SHENGGEN ZHENG
JOZEF GRUSKA
Affiliation:
Faculty of Informatics, Masaryk University, Brno 60200, Czech Republic
DAOWEN QIU
Affiliation:
Department of Computer Science, Sun Yat-sen University, Guangzhou 510006, China Email: zhengshenggen@gmail.com
SHENGGEN ZHENG*
Affiliation:
Faculty of Informatics, Masaryk University, Brno 60200, Czech Republic Department of Computer Science, Sun Yat-sen University, Guangzhou 510006, China Email: zhengshenggen@gmail.com
*
‡ Corresponding author. Zheng was supported by the Employment of Newly Graduated Doctors of Science for Scientific Excellence project/grant (CZ.1.07./2.3.00/30.0009) of Czech Republic.
Get access Rights & Permissions [Opens in a new window]

Abstract

In the distributed Deutsch–Jozsa promise problem, two parties are to determine whether their respective strings x, y ∈ {0,1}n are at the Hamming distanceH(x, y) = 0 or H(x, y) = 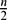$\frac{n}{2}$ . Buhrman et al. (STOC' 98) proved that the exact quantum communication complexity of this problem is O(log n) while the deterministic communication complexity is Ω(n). This was the first impressive (exponential) gap between quantum and classical communication complexity. In this paper, we generalize the above distributed Deutsch–Jozsa promise problem to determine, for any fixed 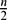$\frac{n}{2}$ ⩽ k ⩽ n, whether H(x, y) = 0 or H(x, y) = k, and show that an exponential gap between exact quantum and deterministic communication complexity still holds if k is an even such that 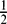$\frac{1}{2}$ n ⩽ k < (1 − λ)n, where 0 < λ < 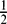$\frac{1}{2}$ is given. We also deal with a promise version of the well-known disjointness problem and show also that for this promise problem there exists an exponential gap between quantum (and also probabilistic) communication complexity and deterministic communication complexity of the promise version of such a disjointness problem. Finally, some applications to quantum, probabilistic and deterministic finite automata of the results obtained are demonstrated.

Information

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Issue 3 , March 2017 , pp. 311 - 331
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†Qiu was partially supported by the National Natural Science Foundation of China (Nos. 61272058, 61073054).

References

Aaronson, S. and Ambainis, A. (2003). Quantum search of spatial regions. In: Proceedings of 44th IEEE FOCS 200–209.Google Scholar
Ambainis, A. (2013). Superlinear advantage for exact quantum algorithms. In: Proceedings of 45th ACM STOC 891–900.Google Scholar
Ambainis, A. and Freivalds, R. (1998). One-way quantum finite automata: Strengths, weaknesses and generalizations. In: Proceedings of the 39th IEEE FOCS 332–341.Google Scholar
Ambainis, A., Gruska, J. and Zheng, S. G. (2015). Exact quantum algorithms have advantage for almost all Boolean functions. Quantum Information and Computation 15 0435–0452. Also arXiv:1404.1684.CrossRefGoogle Scholar
Ambainis, A., Iraids, A. and Smotrovs, J. (2013). Exact quantum query complexity of EXACT and THRESHOLD. In: Proceedings of 8th TQC 263–269. Also arXiv:1302.1235.Google Scholar
Ambainis, A. and Watrous, J. (2002). Two-way finite automata with quantum and classical states. Theoretical Computer Science 287 299–311.CrossRefGoogle Scholar
Ambainis, A. and Yakaryılmaz, A. (2012). Superiority of exact quantum automata for promise problems. Information Processing Letters 112 (7) 289–291.CrossRefGoogle Scholar
Bar-Yossef, Z., Jayram, T. S., Kumar, R. and Sivakumar, D. (2004) An information statistics approach to data stream and communication complexity. Journal of Computer and System Sciences 68 702–732.CrossRefGoogle Scholar
Brassard, G. (2003) Quantum communication complexity. Foundations of Physics 70 1593–1616.CrossRefGoogle Scholar
Brassard, G. and Høyer, P. (1997) An exact quantum polynomial-time algorithm for Simon's problem. In: Proceedings of the 5th Israeli Symposium on Theory of Computing and Systems 12–23.CrossRefGoogle Scholar
Buhrman, H., Cleve, R. and Wigderson, A. (1998). Quantum vs. classical communication and computation. In: Proceedings of 30th ACM STOC 63–68.Google Scholar
Buhrman, H., Cleve, R., Massar, S. and de Wolf, R. (2010). Nonlocality and communication complexity. Reviews of Modern Physics 82 665–698. Also arXiv:0907.3584.CrossRefGoogle Scholar
Buhrman, H. and de Wolf, R. (2001). Communication complexity lower bounds by polynomials. In: Proceedings of 16th IEEE Conference on Computational Complexity 120–130.Google Scholar
Buhrman, H. and de Wolf, R. (2002). Complexity measures and decision tree complexity: A survey. Theoretical Computer Science 288 21–43.CrossRefGoogle Scholar
Deutsch, D. and Jozsa, R. (1992). Rapid solution of problems by quantum computation. Proceedings of the Royal Society of London A439 553–558.Google Scholar
Frankl, P. and Rodl, V. (1987). Forbidden intersections. Transactions of the American Mathematical Society 300 (1) 259–286.CrossRefGoogle Scholar
Goldreich, O. (2006). On promise problems: A survey. In: Essays in Memory of Shimon Even, LNCS 3895, 254–290.Google Scholar
Gruska, J. (1999). Quantum Computing, McGraw-Hill, London.Google Scholar
Gruska, J. (2000). Descriptional complexity issues in quantum computing. Journal of Automata, Languages and Combinatorics 5 (3) 191–218.Google Scholar
Gruska, J., Qiu, D. W. and Zheng, S. G. (2014). Potential of quantum finite automata with exact acceptance. International Journal of Foundation of Computer Science, accepted. Also arXiv:1404.1689.Google Scholar
Hopcroft, J. E. and Ullman, J. D. (1979). Introduction to Automata Theory, Languages, and Computation, Addision-Wesley, New York.Google Scholar
Hromkovič, J. (1997). Communication Complexity and Parallel Computing, Springer, Berlin.CrossRefGoogle Scholar
Hromkovič, J. and Schintger, G. (2001). On the power of Las Vegas for one-way communication complexity, OBDDs, and finite automata. Information and Computation 169 284–296.CrossRefGoogle Scholar
Kalyanasundaram, B. and Schintger, G. (1992). The probabilistic communication complexity of set intersection. SIAM Journal on Discrete Mathematics 5 545–557.CrossRefGoogle Scholar
Klauck, H. (2000). On quantum and probabilistic communication: Las Vegas and one-way protocols. In: Proceedings of the 32th ACM STOC 644–651.Google Scholar
Kushilevitz, E. and Nisan, N. (1997). Communication Complexity, Cambridge University Press.Google Scholar
Li, L. Z. and Feng, Y. (2015). On hybrid models of quantum finite automata. Journal of Computer and System Sciences, to appear, doi:10.1016/j.jcss.2015.01.001. Also arXiv:1206.2131.CrossRefGoogle Scholar
Montanaro, A., Jozsa, R. and Mitchison, G. (2015). On exact quantum query complexity. Algorithmica 71 (4) 775–796. Also arXiv:1111.0475.CrossRefGoogle Scholar
Nielsen, M. A. and Chuang, I. L. (2000). Quantum Computation and Quantum Information. Cambridge University Press, Cambridge.Google Scholar
Qiu, D. W., Li, L. Z., Mateus, P. and Gruska, J. (2012). Quantum finite automata. CRC Handbook of Finite State Based Models and Applications, CRC Press, 113–144.Google Scholar
Qiu, D. W., Li, L. Z., Mateus, P. and Sernadas, A. (2015). Exponentially more concise quantum recognition of non-RMM regular languages. Journal of Computer and System Sciences 81 (2) 359–375.CrossRefGoogle Scholar
Razborov, A. (1992). On the distributional complexity of disjointness. Theoretical Computer Science 106 385–390.CrossRefGoogle Scholar
Razborov, A. (2003). Quantum communication complexity of symmetric predicates. Izvestiya of the Russian Academy of Sciences, Mathematics 67 159–176.Google Scholar
Yao, A. C. (1979). Some complexity questions related to distributed computing. In: Proceedings of 11th ACM STOC 209–213.Google Scholar
Yakaryılmaz, A. and Cem Say, A. C. (2010). Succinctness of two-way probabilistic and quantum finite automata. Discrete Mathematics and Theoretical Computer Science 12 (4) 19–40.Google Scholar
Yu, S. (2005). State complexity: Recent results and open problems. Fundamenta Informaticae 64 471–480.Google Scholar
Zheng, S. G., Gruska, J. and Qiu, D. W. (2014). On the state complexity of semi-quantum finite automata. RAIRO-Theoretical Informatics and Applications, 48 187–207. Earlier version in LATA'14.CrossRefGoogle Scholar
Zheng, S. G., Qiu, D. W. and Gruska, J. (2015). Power of the interactive proof systems with verifiers modeled by semi-quantum two-way finite automata. Information and Computation, to appear, doi:10.1016/j.ic.2015.02.003. Also arXiv:1304.3876.CrossRefGoogle Scholar
Zheng, S. G., Qiu, D. W., Gruska, J., Li, L. Z. and Mateus, P. (2013). State succinctness of two-way finite automata with quantum and classical states. Theoretical Computer Science 499 98–112.CrossRefGoogle Scholar
Zheng, S. G., Qiu, D. W., Li, L. Z. and Gruska, J. (2012). One-way finite automata with quantum and classical states. In: Languages Alive, LNCS 7300 273–290.Google Scholar