No CrossRef data available.
Article contents
Inquisitive split and structural completeness
Published online by Cambridge University Press: 29 May 2025
Abstract
In this paper, the notion of structural completeness is explored in the context of a generalized class of superintuitionistic logics that also involve systems that are not closed under uniform substitution. We just require that each logic must be closed under 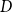 $D$-substitutions assigning to atomic formulas only
$D$-substitutions assigning to atomic formulas only 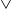 $\vee$-free formulas. For these systems, we introduce four different notions of structural completeness and study how they are related. We focus on superintuitionistic inquisitive logics that validate a schema called Split and have the disjunction property. In these logics, disjunction can be interpreted in the sense of inquisitive semantics as a question-forming operator. It is shown that a logic is structurally complete with respect to
$\vee$-free formulas. For these systems, we introduce four different notions of structural completeness and study how they are related. We focus on superintuitionistic inquisitive logics that validate a schema called Split and have the disjunction property. In these logics, disjunction can be interpreted in the sense of inquisitive semantics as a question-forming operator. It is shown that a logic is structurally complete with respect to 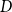 $D$-substitutions if and only if it validates Split. Various consequences of this result are explored. For example, it is shown that every superintuitionistic inquisitive logic can be characterized by a Kripke model built from
$D$-substitutions if and only if it validates Split. Various consequences of this result are explored. For example, it is shown that every superintuitionistic inquisitive logic can be characterized by a Kripke model built from 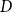 $D$-substitutions. We also formulate an algebraic counterpart of this result that says that the Lindenbaum–Tarski algebra
$D$-substitutions. We also formulate an algebraic counterpart of this result that says that the Lindenbaum–Tarski algebra 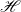 ${\mathscr{H}}$ of any inquisitive logic can be embedded into the Heyting algebra formed from left ideals of endomorphisms on
${\mathscr{H}}$ of any inquisitive logic can be embedded into the Heyting algebra formed from left ideals of endomorphisms on 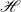 ${\mathscr{H}}$. Additionally, we resolve a conjecture concerning superintuitionistic inquisitive logics due to Miglioli et al. and show that a false conjecture about superintuitionistic logics due to Minari and Wroński becomes true in the broader space of regular generalized superintuitionistic logics.
${\mathscr{H}}$. Additionally, we resolve a conjecture concerning superintuitionistic inquisitive logics due to Miglioli et al. and show that a false conjecture about superintuitionistic logics due to Minari and Wroński becomes true in the broader space of regular generalized superintuitionistic logics.
Keywords
Information
- Type
- Special issue: WoLLIC 2023
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press


