Weak 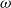$\omega$-categories are notoriously difficult to define because of the very intricate nature of their axioms. Various approaches have been explored based on different shapes given to the cells. Interestingly, homotopy type theory encompasses a definition of weak 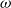$\omega$-groupoid in a globular setting, since every type carries such a structure. Starting from this remark, Brunerie could extract this definition of globular weak 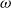$\omega$-groupoids, formulated as a type theory. By refining its rules, Finster and Mimram have then defined a type theory called 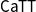$\mathsf{CaTT}$, whose models are weak 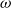$\omega$-categories. Here, we generalize this approach to monoidal weak 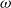$\omega$-categories. Based on the principle that they should be equivalent to weak 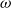$\omega$-categories with only one 0-cell, we are able to derive a type theory 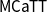$\mathsf{MCaTT}$ whose models are monoidal weak 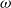$\omega$-categories. This requires changing the rules of the theory in order to encode the information carried by the unique 0-cell. The correctness of the resulting type theory is shown by defining a pair of translations between our type theory 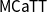$\mathsf{MCaTT}$ and the type theory 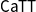$\mathsf{CaTT}$. Our main contribution is to show that these translations relate the models of our type theory to the models of the type theory 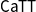$\mathsf{CaTT}$ consisting of 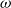$\omega$-categories with only one 0-cell by analyzing in details how the notion of models interact with the structural rules of both type theories.