Hostname: page-component-7dd5485656-gs9qr Total loading time: 0 Render date: 2025-10-31T03:40:19.220Z Has data issue: false hasContentIssue false
  • English
  • Français

On monotone modalities and adjointness

Published online by Cambridge University Press:  25 March 2011

MARTA BÍLKOVÁ ,
JIŘÍ VELEBIL  and
YDE VENEMA
MARTA BÍLKOVÁ
Affiliation:
Department of Logic, Charles University in Prague E-mail: marta.bilkova@ff.cuni.cz
JIŘÍ VELEBIL
Affiliation:
Faculty of Electrical Engineering, Czech Technical University in Prague, Czech Republic E-mail: velebil@math.feld.cvut.cz
YDE VENEMA
Affiliation:
Institute for Logic, Language and Computation, University of Amsterdam, The Netherlands E-mail: Y.Venema@uva.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

We fix a logical connection (Stone ˧ Pred : Setop → BA given by 2 as a schizophrenic object) and study coalgebraic modal logic that is induced by a functor T: Set → Set that is finitary and standard and preserves weak pullbacks and finite sets. We prove that for any such T, the cover modality nabla is a left (and its dual delta is a right) adjoint relative to 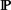ω. We then consider monotone unary modalities arising from the logical connection and show that they all are left (or right) adjoints relative to 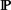ω.

Information

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 21 , Special Issue 2: Coalgebraic Logic , April 2011 , pp. 383 - 416
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adámek, J. (1983) Theory of mathematical structures, Reidel Publications.Google Scholar
Bílková, M., Palmigiano, A. and Venema, Y. (2008) Proof systems for the coalgebraic cover modality. In: Areces, C. and Goldblatt, R. (eds.) Advances in Modal Logic, Volume 7, College Publications 1–21.Google Scholar
Bonsangue, M. M. and Kurz, A. (2005) Duality for logics of transition systems. In: Sassone, V. (ed.) Foundations of Software Science and Computation Structures 2005. Springer-Verlag Lecture Notes in Computer Science 3441 455–469.CrossRefGoogle Scholar
Karazeris, P. and Velebil, J. (2009) Representability relative to a doctrine. Cah. Topol. Géom. Différ. Catég. L-1 3–22.Google Scholar
Kissig, C. and Venema, Y. (2009) Complementation of Coalgebra Automata. In: Kurz, A. et al. (eds.) Algebra and Coalgebra in Computer Science (CALCO 2009). Springer-Verlag Lecture Notes in Computer Science 5728 81–96.CrossRefGoogle Scholar
Kupke, C., Kurz, A. and Venema, Y. (2008) Completeness of the finitary Moss logic. In: Areces, C. and Goldblatt, R. (eds.) Advances in Modal Logic, Volume 7, College Publications 193–217.Google Scholar
Kurz, A. and Leal, R. (2009) Equational coalgebraic logic. In: Abramsky, S., Mislove, M. and Palamidessi, C. (eds.) MFPS XXV. Electronic Notes in Theoretical Computer Science 249 333–356.CrossRefGoogle Scholar
Moss, L. (1999) Coalgebraic logic. Ann. Pure Appl. Logic 96 277–317. (Erratum published in Ann. Pure Appl. Logic 99 241–259.)CrossRefGoogle Scholar
Pattinson, D. (2003) Coalgebraic modal logic: Soundness, completeness and decidability of local consequence. Theoretical Computer Science 309 177–193.CrossRefGoogle Scholar
Pavlović, D., Mislove, M. and Worrell, J. B. (2006) Testing semantics: Connecting processes and process logics. In: Johnson, M. and Vene, V. (eds.) Algebraic Methodology and Software Technology 2006 – Proceedings 11th International Conference, AMAST 2006. Springer-Verlag Lecture Notes in Computer Science 4019 308–322.CrossRefGoogle Scholar
Santocanale, L. (2007) Completions of μ-algebras. Ann. Pure Appl. Logic 154 127–50.CrossRefGoogle Scholar
Santocanale, L. and Venema, Y. (2007) Completeness for flat modal fixpoint logic (extended abstract). In: Dershowitz, N. and Voronkov, A. (eds.) Proceedings of the 14th International Conference on Logic for Programming, Artificial Inteligence and Reasoning (LPAR 2007). Springer-Verlag Lecture Notes in Computer Science 4790 394–408.Google Scholar
Schröder, L. (2007) A finite model construction for coalgebraic modal logic. Log. Algebr. Program. 73 97–110.CrossRefGoogle Scholar
Schröder, L. and Venema, Y. (2010) Flat coalgebraic fixed point logics. In: Gastin, P. and Laroussinie, F. (eds.) Proceedings of 21st International Conference on Concurrency Theory, CONCUR 2010. Springer-Verlag Lecture Notes in Computer Science 6269 524–538.CrossRefGoogle Scholar
Stoltenberg-Hansen, V., Lindström, I. and Griffor, E. G. (1994) Mathematical theory of domains, Cambridge Tracts in Theoretical Computer Science 22, Cambridge University Press.CrossRefGoogle Scholar
Tholen, W. (1984) Pro-categories and multiadjoint functors. Can. J. Math. 36 144–155.CrossRefGoogle Scholar
Trnková, V. (1969) Some properties of set functors. Comment. Math. Univ. Carolin. 10 323–352.Google Scholar
Venema, Y. (2006) Automata and fixed point logics: A coalgebraic perspective Inform. and Comput. 204 637–678.CrossRefGoogle Scholar