Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-02T05:29:15.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Branching-time logics and fairness, revisited

Published online by Cambridge University Press:  21 June 2022

Markus Latte Open the ORCID record for Markus Latte [Opens in a new window]
Markus Latte*
Affiliation:
Institute of Informatics, Ludwig Maximilian University of Munich, Munich, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

Emerson and Halpern (1986, Journal of the Association for Computing Machinery33, 151–178) prove that the Computation Tree Logic (CTL) cannot express the existence of a path on which a proposition holds infinitely often (fairness for short).

The scope is widened from CTL to a general branching-time logic. A path quantifier is followed by a language with temporal descriptions. In this extended setting, the said inexpressiveness is strengthened in two aspects. First, universal path quantifiers are unrestricted. In this way, they are relieved of any temporal quantifiers such as of those in 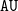$\mathtt{AU}$ and 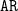$\mathtt{AR}$ from CTL. Second, existential path quantifiers are allowed with any countable language. 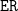Instances are the temporal quantifiers in $\mathtt{EU}$ and $\mathtt{ER}$ from CTL. By contrast, the fairness statement is an existential path quantifier with an uncountable language. Both aspects indicate that this inexpressiveness is optimal with respect to the polarity of path quantifiers and to the cardinality of their languages.

Keywords

Computation tree logicpropositional dynamic logicbranching-time logicfairnessdiagonalisationexpressivity
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Special Issue 9: In Homage to Martin Hofmann , October 2021 , pp. 1135 - 1144
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Axelsson, R., Hague, M., Kreutzer, S., Lange, M., and Latte, M. (2010a). Extended computation tree logic. In: FermÜller, C. and Voronkov, A. (eds.), Proceedings of the 17th International Conference on Logic for Programming, Artificial Intelligence and Reasoning, volume 6397 of Lecture Notes in Computer Science, pp. 67–81. Springer, Heidelberg, Germany.10.1007/978-3-642-16242-8_6CrossRefGoogle Scholar
Axelsson, R., Hague, M., Kreutzer, S., Lange, M. and Latte, M. (2010b). Extended Computation Tree Logic. arXiv.org. Avail- able at https://arxiv.org/abs/1006.3709v1.10.1007/978-3-642-16242-8_6CrossRefGoogle Scholar
Bojańczyk, M. (2008). The common fragment of ACTL and LTL. In Amadio, R. (ed.), Foundations of Software Science and Computational Structures, volume 4962 of Lecture Notes in Computer Science, pp. 172–185. Springer, Heidelberg, Germany.Google Scholar
Clarke, E. and Draghicescu, I. (1989). Expressibility results for linear-time and branching-time logics. In: de Bakker, J., de Roever, W. and Rozenberg, G. (eds.), Linear Time, Branching Time and Partial Order in Logics and Models for Concurrency, volume 354 of Lecture Notes in Computer Science, pp. 428–437. Springer, Heidelberg, Germany.10.1007/BFb0013029CrossRefGoogle Scholar
Clarke, E. M. and Emerson, E. A. (1982). Design and synthesis of synchronization skeletons using branching time temporal logic. In: Kozen, D. (ed.), Logics of Programs: Workshop, Yorktown Heights, New York, May 1981, volume 131 of Lecture Notes in Computer Science, pp. 52–71. Springer, Heidelberg, Germany.10.1007/BFb0025774CrossRefGoogle Scholar
De Nicola, R. and Vaandrager, F. (1990). Action versus state based logics for transition systems. In: Guessarian, I. (ed.), Semantics of Systems of Concurrent Processes, volume 469 of Lecture Notes in Computer Science, pp. 407–419. Springer, Heidelberg, Germany.10.1007/3-540-53479-2_17CrossRefGoogle Scholar
Demri, S., Goranko, V. and Lange, M. (2016). Temporal Logics in Computer Science: Finite-State Systems, Cambridge, UK, Cambridge University Press.10.1017/CBO9781139236119CrossRefGoogle Scholar
Emerson, E. A. and Halpern, J. Y. (1985). Decision procedures and expressiveness in the temporal logic of branching time. Journal of Computer and System Sciences 30 1–24.10.1016/0022-0000(85)90001-7CrossRefGoogle Scholar
Emerson, E. A. and Halpern, J. Y. (1986). “Sometimes” and “Not Never” revisited: On branching versus linear time temporal logic. Journal of the Association for Computing Machinery 33 151–178.10.1145/4904.4999CrossRefGoogle Scholar
Fischer, M. J. and Ladner, R. E. (1979). Propositional dynamic logic of regular programs. Journal of Computer and System Sciences 18 (2) 194–211.10.1016/0022-0000(79)90046-1CrossRefGoogle Scholar
Harel, D., Kozen, D. and Tiuryn, J. (2000). Dynamic Logic, Cambridge, MA, The MIT Press.10.7551/mitpress/2516.001.0001CrossRefGoogle Scholar
Harel, D. and Sherman, R. (1982). Looping vs. repeating in dynamic logic. Information and Control 55 (1–3) 175–192.10.1016/S0019-9958(82)90553-8CrossRefGoogle Scholar
Lamport, L. (1980). “Sometime” is sometimes “Not Never”: On the temporal logic of programs. In: Proceedings of the 7th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 174–185. New York, USA, Association for Computing Machinery.Google Scholar
Phillips, I. (1992). Recursion theory. In: Abramsky, S., Gabbay, D. and Maibaum, T. (eds.) Handbook of Logic in Computer Science, Background: Mathematical Structures, vol. 1, Oxford, UK, Oxford University Press, 79–187.Google Scholar
Streett, R. S. (1981). Propositional dynamic logic of looping and converse. In: Proceedings of the thirteenth annual ACM Symposium on Theory of Computing, pp. 375–383. New York, USA, Association for Computing Machinery.Google Scholar