Hostname: page-component-77c78cf97d-lphnv Total loading time: 0 Render date: 2026-04-23T22:55:49.146Z Has data issue: false hasContentIssue false
  • English
  • Français

Classical realizability and arithmetical formulæ

Published online by Cambridge University Press:  18 January 2016

MAURICIO GUILLERMO  and
ÉTIENNE MIQUEY
MAURICIO GUILLERMO
Affiliation:
Universidad de la República, IMERL, Facultad de Ingeniería, Montevideo, Uruguay Email: mguille@fing.edu.uy
ÉTIENNE MIQUEY
Affiliation:
Laboratoire PPS, Univ. Paris Diderot, Équipe PiR2, INRIA Universidad de la República, IMERL, Facultad de Ingeniería, Montevideo, Uruguay Email: etienne.miquey@pps.univ-paris-diderot.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we treat the specification problem in Krivine classical realizability (Krivine 2009Panoramas et synthèses27), in the case of arithmetical formulæ. In the continuity of previous works from Miquel and the first author (Guillermo 2008Jeux de réalisabilité en arithmétique classique, Ph.D. thesis, Université Paris 7; Guillermo and Miquel 2014Mathematical Structures in Computer Science, Epub ahead of print), we characterize the universal realizers of a formula as being the winning strategies for a game (defined according to the formula). In the first sections, we recall the definition of classical realizability, as well as a few technical results. In Section 5, we introduce in more details the specification problem and the intuition of the game-theoretic point of view we adopt later. We first present a game 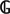1, that we prove to be adequate and complete if the language contains no instructions ‘quote’ (Krivine 2003Theoretical Computer Science308 259–276), using interaction constants to do substitution over execution threads. We then show that as soon as the language contain ‘Quote,’ the game is no more complete, and present a second game 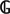2 that is both adequate and complete in the general case. In the last Section, we draw attention to a model-theoretic point of view and use our specification result to show that arithmetical formulæ are absolute for realizability models.

Information

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Issue 6 , September 2017 , pp. 1068 - 1107
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barbanera, F. and Berardi, S. (1996). A symmetric lambda calculus for classical program extraction. Information and Computation 125 (2) 103–117.CrossRefGoogle Scholar
Barendregt, H. (1984). The Lambdas Calculus: Its Syntax and Semantics, Studies in Logic and The Foundations of Mathematics, volume 103, North-Holland, Amsterdam.Google Scholar
Church, A. (1941). The Calculi of Lambda-Conversion, Annals of Mathematical Studies, volume 6, issue 4, Princeton 171–172.CrossRefGoogle Scholar
Coquand, T. (1995). A semantics of evidence for classical arithmetic. Journal of Symbolic Logic 60 (1) 325–337. doi: 10.2307/2275524. url: http://dx.doi.org/10.2307/2275524.CrossRefGoogle Scholar
Curien, P.-L. and Herbelin, H. (September 2000). The duality of computation. In: Odersky, M. and Wadler, P. (eds.) Proceedings of the Fifth ACM SIGPLAN International Conference on Functional Programming (ICFP'00), ACM, Montreal, Canada 233–243.CrossRefGoogle Scholar
Curry, H. B. and Feys, R. (1958). Combinatory Logic, volume 1, North-Holland, Amsterdam.Google Scholar
Friedman, H. (1973). Some Applications of Kleene's Methods for Intuitionistic Systems, Cambridge Summer School in Mathematical Logic, Springer Lecture Notes in Mathematics, volume 337, Springer-Verlag 113–170.Google Scholar
Friedman, H. (1978). Classically and intuitionistically provably recursive functions. Higher Set Theory 669 (1978), 21–28.CrossRefGoogle Scholar
Girard, J.-Y. (2006). Le point aveugle – cours de logique – volume I – vers la perfection, Hermann.Google Scholar
Girard, J.-Y., Lafont, Y. and Taylor, P. (1989). Proofs and Types, Cambridge tracts in theoretical computer science, volume 7, Cambridge University Press.Google Scholar
Guillermo, M. (2008). Jeux de réalisabilité en arithmétique classique, Ph.D. thesis, Université Paris 7.Google Scholar
Guillermo, M. and Miquel, A. (2014). Specifying Peirce's law in classical realizability. Mathematical Structures in Computer Science, Epub ahead of print, doi: 10.1017/S0960129514000450.Google Scholar
Howard, W.A. (1980). The formulae-as-types notion of construction. In: Hind-ley, J.R. and Seldin, J.P. (eds.) To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, Academic Press, New York, 479–490.Google Scholar
Hofstra, P.J.W. and Cockett, J.R.B. (2006). An introduction to partial lambda algebras. Available at: http://mysite.science.uottawa.ca/phofstra/lambda.pdf Google Scholar
Jean-Louis, Krivine J.-L. (2015). On the structure of classical realizability models of ZF. In: Herbelin, H., Letouzey, P. and Sozeau, M. (eds.) 20th International Conference on Types for Proofs and Programs (TYPES 2014), Leibniz International Proceedings in Informatics (LIPIcs), volume 39, Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany.Google Scholar
Jech, T. (2013). Set Theory: The Third Millennium Edition, Revised and Expanded, 3rd edition, Springer Monographs in Mathematics, Springer-Verlag Berlin Heidelberg. isbn: 9783642078996. url: http://books.google.com.uy/books?id=70N-cgAACAAJ.Google Scholar
Kleene, S.C. (1945). On the interpretation of intuitionistic number theory. Journal of Symbolic Logic 10 (4) 109–124.CrossRefGoogle Scholar
Kreisel, G. (1951). On the interpretation of non-finitist proofs–Part I. Journal of Symbolic Logic 16 (4) 241–267.Google Scholar
Kreisel, G. (1952). On the interpretation of non-finitist proofs: Part II. Interpretation of number theory. Applications. Journal of Symbolic Logic 17 (1) 43–58.CrossRefGoogle Scholar
Krivine, J.-L. (1993). Lambda-Calculus, Types and Models, Ellis Horwood series in computers and their applications, Masson.Google Scholar
Krivine, J.-L. (2000). The Curry-Howard correspondence in set theory. In: 15th Annual IEEE Symposium on Logic in Computer Science, IEEE Computer Society, Santa Barbara, CA 307–308.Google Scholar
Krivine, J.-L. (2001). Typed lambda-calculus in classical Zermelo-Fraenkel set theory. Archive for Mathematical Logic 40 (3) 189–205.CrossRefGoogle Scholar
Krivine, J.-L. (2003). Dependent choice, ‘quote’ and the clock. Theoretical Computer Science 308 (1–3) 259–276.CrossRefGoogle Scholar
Krivine, J.-L. (2007). A call-by-name lambda-calculus machine. Higher-Order and Symbolic Computation 20 (3) 199–207.CrossRefGoogle Scholar
Krivine, J.-L. (2009). Realizability in classical logic. In interactive models of computation and program behaviour. Panoramas et synthèses 27 197–229.Google Scholar
Krivine, J.-L. (2011). Realizability algebras: A program to well order R. Logical Methods in Computer Science 7 (3) 1–47.Google Scholar
Krivine, J.-L. (2012). Realizability algebras II: New models of ZF + DC. Logical Methods in Computer Science 8 (1) 1–28.Google Scholar
McCarty, D. (1984). Realizability and Recursive Mathematics, Ph.D. thesis, Carnegie-Mellon University.Google Scholar
Miquel, A. (2007). Classical program extraction in the calculus of constructions. In: Proceedings of the Computer Science Logic, 21st International Workshop, CSL 2007, 16th Annual Conference of the EACSL, Lausanne, Switzerland, September 11–15. Springer Lecture Notes in Computer Science 4646 313–327.CrossRefGoogle Scholar
Miquel, A. (2011a). Existential witness extraction in classical realizability and via a negative translation. Logical Methods for Computer Science 7 (2) (doi: 10.2168/LMCS-7(2:2)2011).Google Scholar
Miquel, A. (2011b). Forcing as a program transformation. In: Proceedings of the 26th Annual IEEE Symposium on Logic in Computer Science, IEEE Computer Society, Toronto, Ontario, Canada, 197–206.CrossRefGoogle Scholar
Myhill, J. (1973). Some properties of intuitionistic Zermelo-Fraenkel set theory. Lecture Notes in Mathematics 337 206–231.CrossRefGoogle Scholar
Oliva, P. and Streicher, T. (2008). On Krivine's realizability interpretation of classical second-order arithmetic. Fundamenta Informaticae 84 (2) 207–220.Google Scholar
Parigot, M. (1997). Proofs of strong normalisation for second order classical natural deduction. Journal of Symbolic Logic 62 (4) 1461–1479.CrossRefGoogle Scholar
Rieg, L. (June 2014). On Forcing and Classical Realizability, Theses, Ecole normale supérieure de lyon - ENS LYON. url: https://tel.archives-ouvertes.fr/tel-01061442.Google Scholar