Hostname: page-component-77f85d65b8-45ctf Total loading time: 0 Render date: 2026-04-22T19:18:25.638Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension in team semantics

Published online by Cambridge University Press:  12 March 2024

Lauri Hella Open the ORCID record for Lauri Hella [Opens in a new window] ,
Kerkko Luosto Open the ORCID record for Kerkko Luosto [Opens in a new window]  and
Jouko Väänänen Open the ORCID record for Jouko Väänänen [Opens in a new window]
Lauri Hella
Affiliation:
Tampere University, Tampere, Finland
Kerkko Luosto
Affiliation:
Tampere University, Tampere, Finland
Jouko Väänänen*
Affiliation:
University of Helsinki, Helsinki, Finland
*
Corresponding author: Jouko Väänänen; Email: jouko.vaananen@helsinki.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce three measures of complexity for families of sets. Each of the three measures, which we call dimensions, is defined in terms of the minimal number of convex subfamilies that are needed for covering the given family. For upper dimension, the subfamilies are required to contain a unique maximal set, for dual upper dimension a unique minimal set, and for cylindrical dimension both a unique maximal and a unique minimal set. In addition to considering dimensions of particular families of sets, we study the behavior of dimensions under operators that map families of sets to new families of sets. We identify natural sufficient criteria for such operators to preserve the growth class of the dimensions. We apply the theory of our dimensions for proving new hierarchy results for logics with team semantics. To this end we associate each atom with a natural notion or arity. First, we show that the standard logical operators preserve the growth classes of the families arising from the semantics of formulas in such logics. Second, we show that the upper dimension of 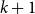$k+1$-ary dependence, inclusion, independence, anonymity, and exclusion atoms is in a strictly higher growth class than that of any k-ary atoms, whence the 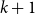$k+1$-ary atoms are not definable in terms of any atoms of smaller arity.

Keywords

team semanticsdependence logicdimensiongrowth class

Information

Type
Special Issue: Logic and Complexity
Information
Mathematical Structures in Computer Science , Volume 34 , Special Issue 5: Logic and Complexity , May 2024 , pp. 410 - 454
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

a

Supported by the Academy of Finland (grant No 322795) and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant No 101020762).

References

Abramsky, S. and Väänänen, J. (2009). From IF to BI: a tale of dependence and separation. Synthese 167 (2, Knowledge, Rationality & Action) 207–230. ISSN 0039-7857. doi: 10.1007/s11229-008-9415-6.CrossRefGoogle Scholar
Aslanyan, L. A. (1983). Length of the shortest disjunctive normal form of weakly defined Boolean functions. In: Applied Mathematics, No. 2. Erevan. Univ., Erevan, 32–40, 141–142.Google Scholar
Bollobás, B. (1986). Combinatorics, Cambridge University Press, Cambridge. ISBN 0-521-33059-9; 0-521-33703-8. Set systems, hypergraphs, families of vectors and combinatorial probability.Google Scholar
Bollobás, B. (2001). Random Graphs, 2nd edn., Cambridge Studies in Advanced Mathematics, vol. 73, Cambridge University Press, Cambridge. ISBN 0-521-80920-7; 0-521-79722-5. doi: 10.1017/CBO9780511814068.CrossRefGoogle Scholar
Ciardelli, I. (2009). Inquisitive Semantics and Intermediate Logics. Master’s thesis, University of Amsterdam.Google Scholar
Durand, A. and Kontinen, J. (2012). Hierarchies in dependence logic. ACM Transactions on Computational Logic 13 (4) Art. 31, 21. ISSN 1529-3785. doi: 10.1145/2362355.2362359.CrossRefGoogle Scholar
Engström, F. (2012). Generalized quantifiers in dependence logic. Journal of Logic, Language and Information 21 (3) 299–324. doi: 10.1007/s10849-012-9162-4.CrossRefGoogle Scholar
Galliani, P. (2012). Inclusion and exclusion dependencies in team semantics—on some logics of imperfect information. Annals of Pure and Applied Logic 163 (1) 68–84. ISSN 0168-0072. doi: 10.1016/j.apal.2011.08.005.CrossRefGoogle Scholar
Galliani, P. (2013). Epistemic operators in dependence logic. Studia Logica 101 (2) 367–397. ISSN 0039-3215. doi: 10.1007/s11225-013-9478-3.CrossRefGoogle Scholar
Galliani, P., Hannula, M. and Kontinen, J. (2013). Hierarchies in independence logic. In: Rocca, S. R. D. (ed.) Computer Science Logic 2013 (CSL 2013), CSL 2013, September 2–5, 2013, Torino, Italy, LIPIcs, vol. 23, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 263–280. doi: 10.4230/LIPIcs.CSL.2013.263.CrossRefGoogle Scholar
Glagolev, V. V. (1964). An estimate of the complexity of the contracted normal form for almost all functions of the logic of algebra. Doklady Akademii Nauk SSSR 158 770–773. ISSN 0002-3264.Google Scholar
Grädel, E. and Väänänen, J. (2013). Dependence and independence. Studia Logica 101 (2) 399–410. ISSN 0039-3215, 1572-8730. doi: 10.1007/s11225-013-9479-2.CrossRefGoogle Scholar
Grohe, M. (1996). Arity hierarchies. Annals of Pure and Applied Logic 82 (2) 103–163. ISSN 0168-0072. doi: 10.1016/0168-0072(95)00072-0.CrossRefGoogle Scholar
Hannula, M. (2018). Hierarchies in inclusion logic with lax semantics. ACM Transactions on Computational Logic 19 (3) 16:1–16:23. doi: 10.1145/320452110.1145/3204521.CrossRefGoogle Scholar
Hella, L., Luosto, K., Sano, K. and Virtema, J. (2014). The expressive power of modal dependence logic. In: Advances in Modal Logic, vol. 10, Colloquium Publications, London, 294–312.Google Scholar
Hella, L. and Stumpf, J. (2015). The expressive power of modal logic with inclusion atoms. In: Proceedings Sixth International Symposium on Games, Automata, Logics and Formal Verification, vol. 193, Electronic Proceedings in Theoretical Computer Science (EPTCS), EPTCS, [place of publication not identified], 129–143. doi: 10.4204/EPTCS.193.10.CrossRefGoogle Scholar
Kleene, S. C. (1952). Introduction to Metamathematics, D. Van Nostrand Co., Inc., New York, NY.Google Scholar
Koršunov, A. D. (1969). An upper estimate of the complexity of the shortest disjunctive normal forms of almost all Boolean functions. Kibernetika (Kiev) (6) 1–8. ISSN 0023-1274.Google Scholar
Kuznetsov, S. E. (1983). A lower bound for the length of the shortest d.n.f. of almost all Boolean functions. In: Probabilistic Methods and Cybernetics, vol. 19, Kazan. Gos. Univ., Kazan’, 44–47.Google Scholar
Lindström, P. (1966). First order predicate logic with generalized quantifiers. Theoria 32 186–195. ISSN 0040-5825. doi: 10.1111/j.1755-2567.1966.tb00600.x.CrossRefGoogle Scholar
Lück, M. and Vilander, M. (2019). On the succinctness of atoms of dependency. Logical Methods in Computer Science 15(3) Paper No. 17, 28. doi: 10.23638/LMCS-15(3:17)2019.Google Scholar
Lück, M. (2020). Team Logic: Axioms, Expressiveness, Complexity. Phd thesis, University of Hanover, Hannover, Germany. URL https://www.repo.uni-hannover.de/handle/123456789/9430.Google Scholar
Mann, A. L., Sandu, G. and Sevenster, M. (2011). Independence-Friendly Logic , London Mathematical Society Lecture Note Series, vol. 386, Cambridge University Press, Cambridge. ISBN 978-0-521-14934-1. doi: 10.1017/CBO9780511981418. A game-theoretic approach.Google Scholar
Makarov, S. V. (1964). An upper bound for the mean length of a disjunctive normal form. Diskretnyi Analiz (3), 78–80.Google Scholar
O’Donnell, R. (2014). Analysis of Boolean Functions, Cambridge University Press, New York. ISBN 978-1-107-03832-5. doi: 10.1017/CBO9781139814782.CrossRefGoogle Scholar
Quine, W. V. (1955). A way to simplify truth functions. The American Mathematical Monthly 62 0 627–631. ISSN 0002-9890. doi: 10.2307/2307285.CrossRefGoogle Scholar
Romanov, A. M. (1983). Estimate of the length of the shortest disjunctive normal form for the negation of the characteristic function of a Hamming code. Metody Diskret. Analiz. (39) 88–97. ISSN 0136-1228.Google Scholar
Rönnholm, R. (2018). Arity Fralments of Logics with Team Semantics (URN:ISBN:978-952-03-0912-1). Phd thesis, University of Tampere.Google Scholar
Weber, K. (1982). The length of random Boolean functions. Elektron. Informationsverarb. Kybernet. 18 (12) 659–668. ISSN 0013-5712.Google Scholar
Wilke, R. (2022). Reasoning about Dependence and Independence: Teams and Multiteams. Phd thesis, RWTH Aachen University, Germany. URL https://publications.rwth-aachen.de/record/842872.Google Scholar
Väänänen, J. (2011). Models and Games , Cambridge Studies in Advanced Mathematics, vol. 132, Cambridge University Press, Cambridge. ISBN 978-0-521-51812-3. doi: 10.1017/CBO9780511974885.Google Scholar
Väänänen, J. (2007). Dependence Logic, London Mathematical Society Student Texts, vol. 70, Cambridge University Press, Cambridge. ISBN 978-0-521-70015-3; 0-521-70015-9. doi: 10.1017/CBO9780511611193. A new approach to independence friendly logic.CrossRefGoogle Scholar
Väänänen, J. (2023). An atom’s worth of anonymity. Logic Journal of the IGPL 31 (6) 1078–1083.10.1093/jigpal/jzac074CrossRefGoogle Scholar
Vapnik, V. N. (1995). The Nature of Statistical Learning Theory, Springer-Verlag, New York. ISBN 0-387-94559-8. doi: 10.1007/978-1-4757-2440-0.CrossRefGoogle Scholar
Venema, Y. (2007). Algebras and coalgebras. In: Handbook of Modal Logic, Stud. Log. Pract. Reason., vol. 3, Elsevier B. V., Amsterdam, 331–426. ISBN 978-0-444-51690-9; 0-444-51690-5.10.1016/S1570-2464(07)80009-7CrossRefGoogle Scholar