Article contents
Finitary 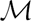 $\mathcal{M}$-adhesive categories
$\mathcal{M}$-adhesive categories
Published online by Cambridge University Press: 26 June 2014
Abstract
Finitary 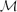 $\mathcal{M}$-adhesive categories are
$\mathcal{M}$-adhesive categories are 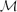 $\mathcal{M}$-adhesive categories with finite objects only, where
$\mathcal{M}$-adhesive categories with finite objects only, where 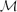 $\mathcal{M}$-adhesive categories are a slight generalisation of weak adhesive high-level replacement (HLR) categories. We say an object is finite if it has a finite number of
$\mathcal{M}$-adhesive categories are a slight generalisation of weak adhesive high-level replacement (HLR) categories. We say an object is finite if it has a finite number of 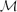 $\mathcal{M}$-subobjects. In this paper, we show that in finitary
$\mathcal{M}$-subobjects. In this paper, we show that in finitary 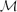 $\mathcal{M}$-adhesive categories we not only have all the well-known HLR properties of weak adhesive HLR categories, which are already valid for
$\mathcal{M}$-adhesive categories we not only have all the well-known HLR properties of weak adhesive HLR categories, which are already valid for 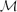 $\mathcal{M}$-adhesive categories, but also all the additional HLR requirements needed to prove classical results including the Local Church-Rosser, Parallelism, Concurrency, Embedding, Extension and Local Confluence Theorems, where the last of these is based on critical pairs. More precisely, we are able to show that finitary
$\mathcal{M}$-adhesive categories, but also all the additional HLR requirements needed to prove classical results including the Local Church-Rosser, Parallelism, Concurrency, Embedding, Extension and Local Confluence Theorems, where the last of these is based on critical pairs. More precisely, we are able to show that finitary 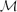 $\mathcal{M}$-adhesive categories have a unique
$\mathcal{M}$-adhesive categories have a unique 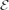 $\mathcal{E}$-
$\mathcal{E}$-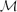 $\mathcal{M}$ factorisation and initial pushouts, and the existence of an
$\mathcal{M}$ factorisation and initial pushouts, and the existence of an 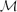 $\mathcal{M}$-initial object implies we also have finite coproducts and a unique
$\mathcal{M}$-initial object implies we also have finite coproducts and a unique 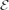 $\mathcal{E}$′-
$\mathcal{E}$′-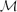 $\mathcal{M}$ pair factorisation. Moreover, we can show that the finitary restriction of each
$\mathcal{M}$ pair factorisation. Moreover, we can show that the finitary restriction of each 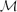 $\mathcal{M}$-adhesive category is a finitary
$\mathcal{M}$-adhesive category is a finitary 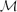 $\mathcal{M}$-adhesive category, and finitarity is preserved under functor and comma category constructions based on
$\mathcal{M}$-adhesive category, and finitarity is preserved under functor and comma category constructions based on 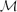 $\mathcal{M}$-adhesive categories. This means that all the classical results are also valid for corresponding finitary
$\mathcal{M}$-adhesive categories. This means that all the classical results are also valid for corresponding finitary 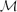 $\mathcal{M}$-adhesive transformation systems including several kinds of finitary graph and Petri net transformation systems. Finally, we discuss how some of the results can be extended to non-
$\mathcal{M}$-adhesive transformation systems including several kinds of finitary graph and Petri net transformation systems. Finally, we discuss how some of the results can be extended to non-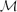 $\mathcal{M}$-adhesive categories.
$\mathcal{M}$-adhesive categories.
Information
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 24 , Issue 4: Structure Transformation , August 2014 , 240403
- Copyright
- Copyright © Cambridge University Press 2014
References
- 9
- Cited by

