Hostname: page-component-77f85d65b8-jkvpf Total loading time: 0 Render date: 2026-04-19T20:14:00.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized geometric theories and set-generated classes

Published online by Cambridge University Press:  10 November 2014

PETER ACZEL ,
HAJIME ISHIHARA ,
TAKAKO NEMOTO  and
YASUSHI SANGU
PETER ACZEL
Affiliation:
Schools of Mathematics and Computer Science, University of Manchester, Manchester, M13 9PL, United Kingdom
HAJIME ISHIHARA
Affiliation:
School of Information Science, Japan Advanced Institute of Science and Technology, Nomi, Ishikawa 923-1292, Japan
TAKAKO NEMOTO
Affiliation:
School of Information Science, Japan Advanced Institute of Science and Technology, Nomi, Ishikawa 923-1292, Japan
YASUSHI SANGU
Affiliation:
School of Information Science, Japan Advanced Institute of Science and Technology, Nomi, Ishikawa 923-1292, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce infinitary propositional theories over a set and their models which are subsets of the set, and define a generalized geometric theory as an infinitary propositional theory of a special form. The main result is that the class of models of a generalized geometric theory is set-generated. Here, a class 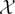$\mathcal{X}$ of subsets of a set is set-generated if there exists a subset G of 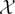$\mathcal{X}$ such that for each α ∈ 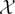$\mathcal{X}$ , and finitely enumerable subset τ of α there exists a subset β ∈ G such that τ ⊆ β ⊆ α. We show the main result in the constructive Zermelo–Fraenkel set theory (CZF) with an additional axiom, called the set generation axiom which is derivable in CZF, both from the relativized dependent choice scheme and from a regular extension axiom. We give some applications of the main result to algebra, topology and formal topology.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aczel, P. (1978) The type theoretic interpretation of constructive set theory. In: Macintyre, A., Pacholski, L. and Paris, J. (eds.) Logic Colloquium '77, North-Holland, Amsterdam 55–66.Google Scholar
Aczel, P. (1982) The type theoretic interpretation of constructive set theory: Choice principles. In: Troelstra, A.S. and van Dalen, D. (eds.) The L.E.J. Brouwer Centenary Symposium, North-Holland, Amsterdam 1–40.Google Scholar
Aczel, P. (1986) The type theoretic interpretation of constructive set theory: Inductive definitions. In: Marcus, R. B. et al. (eds.) Logic, Methodology, and Philosophy of Science VII, North-Holland, Amsterdam 17–49.Google Scholar
Aczel, P. (2006) Aspects of general topology in constructive set theory. Annals of Pure and Applied Logic 137 3–29.Google Scholar
Aczel, P. (2008) The relation reflection scheme. MLQ Mathematical Logic Quarterly 54 5–11.Google Scholar
Aczel, P. and Rathjen, M. (2001) Notes on constructive set theory. Technical Report No. 40, Institut Mittag-Leffler, The Royal Swedish Academy of Sciences.Google Scholar
Berger, J., Ishihara, H., Palmgren, E. and Schuster, P. (2012) A predicative completion of a uniform space. Annals of Pure and Applied Logic 163 975–980.Google Scholar
Bishop, E. (1967) Foundations of Constructive Mathematics, McGraw-Hill, New York.Google Scholar
Bishop, E. and Bridges, D. (1985) Constructive Analysis, Springer, Berlin.Google Scholar
Bridges, D. and Richman, F. (1987) Varieties of Constructive Mathematics, Cambridge University Press, Cambridge.Google Scholar
Bridges, D. and Vîţă, L. (2006) Techniques of Constructive Analysis, Springer, New York.Google Scholar
Crosilla, L., Ishihara, H. and Schuster, P. (2005) On constructing completions. Journal of Symbolic Logic 70 969–978.Google Scholar
Curi, G. (2012) Topological inductive definitions. Annals Pure Applied Logic 163 1471–1483.Google Scholar
Ishihara, H. and Kawai, T. (2014) Completeness and cocompleteness of the categories of basic pairs and concrete spaces. Mathematical Structures in Computer Science. to appear.Google Scholar
Ishihara, H. and Palmgren, E. (2006) Quotient topologies in constructive set theory and type theory. Annals of Pure and Applied Logic 141 257–265.Google Scholar
Martin-Löf, P. (1984) Intuitionistic Type Theory, Studies in Proof Theory volume 1, Bibliopolis, Naples.Google Scholar
Mines, R., Richman, F. and Ruitenburg, W. (1988) A Course in Constructive Algebra, Springer-Verlag, New York.Google Scholar
Myhill, J. (1975) Constructive set theory. Journal of Symbolic Logic 40 347–382.Google Scholar
Palmgren, E. (2005) Quotient spaces and coequalisers in formal topology. Journal of Universal Computer Science 11 1996–2007.Google Scholar
Palmgren, E. (2006) Maximal and partial points in formal spaces. Annals of Pure and Applied Logic 137 291–298.Google Scholar
Sambin, G. (1987) Intuitionistic formal spaces – a first communication. In: Skordev, D. (ed.) Mathematical Logic and its Applications, Plenum, New York 187–204.CrossRefGoogle Scholar
Sambin, G. (2003) Some points in formal topology. Theoretical Computer Science 305 347–408.CrossRefGoogle Scholar
Sambin, G. The Basic Picture and Positive Topology, Clarendon Press, Oxford, forthcoming.Google Scholar
Troelstra, A. S. and van Dalen, D. (1988) Constructivism in Mathematics, volume I and II, North-Holland, Amsterdam.Google Scholar
van den Berg, B. (2013) Non-deterministic inductive definitions. Archive for Mathematical Logic 52 113–135.CrossRefGoogle Scholar