Article contents
Introduction to distributive categories
Published online by Cambridge University Press: 04 March 2009
Abstract
Distributive category theory is the study of categories with two monoidal structures, one of which “distributes” over the other in some manner. When these are the product and coproduct, this distribution is taken to be the law
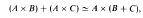
which asserts that the obvious canonical map has an inverse. A distributive category is here taken to mean a category with finite products and binary coproducts such that this law is satisfied.
In any distributive category the coproduct of the final object with itself, 1 + 1, forms a boolean algebra. Thus, maps into 1 + 1 provide a boolean logic: if each such map recognizes a unique subobject, the category is a recognizable distributive category. If, furthermore, the category is such that these recognizers classify detachable subobjects (coproduct embeddings), it is an extensive distributive category.
Extensive distributive categories can be approached in various ways. For example, recognizable distributive categories, in which coproducts are disjoint or all preinitials are isomorphic, are extensive. Also, a category X having finite products and binary coproducts satisfying the slice equation 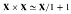 (due to Schanuel and Lawvere) is extensive. This paper describes a series of embedding theorems. Any distributive category has a full faithful embedding into a recognizable distributive category. Any recognizable distributive category can be "solidified" faithfully to produce an extensive distributive category. Any extensive distributive category can be embedded into a topos.
(due to Schanuel and Lawvere) is extensive. This paper describes a series of embedding theorems. Any distributive category has a full faithful embedding into a recognizable distributive category. Any recognizable distributive category can be "solidified" faithfully to produce an extensive distributive category. Any extensive distributive category can be embedded into a topos.
A peculiar source of extensive distributive categories is the coproduct completion of categories with familial finite products. In particular, this includes the coproduct completion of cartesian categories, which is serendipitously, therefore, also the distributive completion. Familial distributive categories can be characterized as distributive categories for which every object has a finite decomposition into indecomposables.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1993
References
- 47
- Cited by

