Article contents
Multi-amalgamation of rules with application conditions in 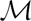 $\mathcal{M}$-adhesive categories
$\mathcal{M}$-adhesive categories
Published online by Cambridge University Press: 26 June 2014
Abstract
Amalgamation is a well-known concept for graph transformations that is used to model synchronised parallelism of rules with shared subrules and corresponding transformations. This concept is especially important for an adequate formalisation of the operational semantics of statecharts and other visual modelling languages, where typed attributed graphs are used for multiple rules with nested application conditions. However, the theory of amalgamation for the double-pushout approach has so far only been developed on a set-theoretical basis for pairs of standard graph rules without any application conditions.
For this reason, in the current paper we present the theory of amalgamation for 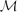 $\mathcal{M}$-adhesive categories, which form a slightly more general framework than (weak) adhesive HLR categories, for a bundle of rules with (nested) application conditions. The two main results are the Complement Rule Theorem, which shows how to construct a minimal complement rule for each subrule, and the Multi-Amalgamation Theorem, which generalises the well-known Parallelism and Amalgamation Theorems to the case of multiple synchronised parallelism. In order to apply the largest amalgamated rule, we use maximal matchings, which are computed according to the actual instance graph. The constructions are illustrated by a small but meaningful running example, while a more complex case study concerning the firing semantics of Petri nets is presented as an introductory example and to provide motivation.
$\mathcal{M}$-adhesive categories, which form a slightly more general framework than (weak) adhesive HLR categories, for a bundle of rules with (nested) application conditions. The two main results are the Complement Rule Theorem, which shows how to construct a minimal complement rule for each subrule, and the Multi-Amalgamation Theorem, which generalises the well-known Parallelism and Amalgamation Theorems to the case of multiple synchronised parallelism. In order to apply the largest amalgamated rule, we use maximal matchings, which are computed according to the actual instance graph. The constructions are illustrated by a small but meaningful running example, while a more complex case study concerning the firing semantics of Petri nets is presented as an introductory example and to provide motivation.
Information
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 24 , Issue 4: Structure Transformation , August 2014 , 240405
- Copyright
- Copyright © Cambridge University Press 2014
References
- 16
- Cited by

