1. Introduction
At least since the emergence of the fundamental correspondence between mathematical proofs and programs, it has been one of the main driving interests of proof theory to describe the computational content, and by that measuring the strength, of a mathematical theorem. In that vein, the research program of proof mining emerged in the 1990s through the work of Kohlenbach (following the spirit of Kreisel’s program of unwinding of proofs, see Kreisel (Reference Kreisel1951, Reference Kreisel1952)) which aims at providing this content by analyzing the (prima facie) noneffective proofs of mathematical theorems as they are found in the usual literature. While this is a highly nontrivial task through the prevalent use of classical logic and infinitary set-theoretical (sometimes called ideal) principles in mainstream mathematics, this research program of proof mining is nevertheless substantiated by a firm logical basis developed using central proof-theoretic tools like Gödel’s functional interpretation (see Gödel (Reference Gödel1958)) and Howard’s majorizability (see Howard (Reference Howard1973)), and their variants, and has since its inception lead to hundreds of novel applications in core mathematics and computer science. We refer to the monograph Kohlenbach (Reference Kohlenbach2008) for a detailed exposition of proof mining up to 2008 and to the surveys Kohlenbach (2017, 2019b); Kohlenbach and Oliva (Reference Kohlenbach and Oliva2003) for further details on the theoretical developments of the field as well as on applications.
In more detail, the central results of the logical foundation of proof mining are the so-called general logical metatheorems which comprise an underlying logical system together with a theorem about that system so that, for one, this corresponding system is suitably designed so that it facilitates (relatively) easy applications to large classes of objects and proofs from the core literature of the intended area of application and, for another, the associated logical metatheorem guarantees the extractability of tame and highly uniform computational information from large classes of noneffective proofs carried out in this system, the complexity of which corresponds to the logical strength of the principles used in the proof. Further, the proofs of the logical metatheorems even provide algorithms to (in principle) extract this information.Footnote 1
In the context of this enterprise of extractive proof theory, one of the prime (logical) issues actually arises in connection with the, from a mathematical perspective perhaps trivial, principle of extensionality. Concretely, working over the higher-type system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
for classical analysis over an abstract normed space
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
for classical analysis over an abstract normed space
![]() $X$
defined as in the seminal works Kohlenbach (Reference Kohlenbach2005); Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) (see Section 2 for further details), the prevalent system used in proof mining for extracting programs from proofs pertaining to the theory of normed spaces, the extensionality of an operator
$X$
defined as in the seminal works Kohlenbach (Reference Kohlenbach2005); Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) (see Section 2 for further details), the prevalent system used in proof mining for extracting programs from proofs pertaining to the theory of normed spaces, the extensionality of an operator
![]() $T:X\to X$
for the normed space (represented by)
$T:X\to X$
for the normed space (represented by)
![]() $X$
is naturally formulated as
$X$
is naturally formulated as
where equality in
![]() $X$
is internally defined using the norm of the space represented by
$X$
is internally defined using the norm of the space represented by
![]() $X$
via
$X$
via
utilizing a suitable representation of the real numbers in the underlying language. This principle, if provable in a system (say, extending
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
) that is amenable to proof mining metatheorems, would immediately entail (see e.g. the discussion in Kohlenbach (Reference Kohlenbach2008)) the extractability of a (computable) functional
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
) that is amenable to proof mining metatheorems, would immediately entail (see e.g. the discussion in Kohlenbach (Reference Kohlenbach2008)) the extractability of a (computable) functional
![]() $\omega :\mathbb{N}^3\to \mathbb{N}$
such that
$\omega :\mathbb{N}^3\to \mathbb{N}$
such that
holds for all
![]() $B$
-bounded mappings
$B$
-bounded mappings
![]() $T:X\to X$
(i.e.
$T:X\to X$
(i.e.
![]() $\lVert Tx \rVert \leq B$
for all
$\lVert Tx \rVert \leq B$
for all
![]() $x\in X$
with
$x\in X$
with
![]() $B\in \mathbb{N}$
) and all normed spaces
$B\in \mathbb{N}$
) and all normed spaces
![]() $(X,\lVert \cdot \rVert )$
axiomatized by the system,Footnote
2
where
$(X,\lVert \cdot \rVert )$
axiomatized by the system,Footnote
2
where
![]() $\overline {B}_b(0):=\{x\in X\mid \lVert x \rVert \leq b\}$
. So one could directly derive the uniform continuity on bounded sets for bounded operators
$\overline {B}_b(0):=\{x\in X\mid \lVert x \rVert \leq b\}$
. So one could directly derive the uniform continuity on bounded sets for bounded operators
![]() $T$
from its associated extensionality statement. Therefore, if discontinuous objects should be treated, one has to have issues with (and therefore has to restrict) extensionality as a principle in formal systems used in proof mining. In the practice of applying methods from proof mining, especially in the context of nonlinear analysis and fixed point theory, this has previously, more often than not, had relatively little relevance for operators of that type as for most single-valued operators considered in the respective applications, their defining properties (like e.g. nonexpansivity) immediately entail the uniform continuity and hence extensionality for these maps (as centrally also discussed in Kohlenbach (Reference Kohlenbach2005); Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008)).
$T$
from its associated extensionality statement. Therefore, if discontinuous objects should be treated, one has to have issues with (and therefore has to restrict) extensionality as a principle in formal systems used in proof mining. In the practice of applying methods from proof mining, especially in the context of nonlinear analysis and fixed point theory, this has previously, more often than not, had relatively little relevance for operators of that type as for most single-valued operators considered in the respective applications, their defining properties (like e.g. nonexpansivity) immediately entail the uniform continuity and hence extensionality for these maps (as centrally also discussed in Kohlenbach (Reference Kohlenbach2005); Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008)).
In the case of set-valued operators
![]() $T:X\to 2^X$
, this situation changes as first highlighted in Pischke (Reference Pischke2024c) where, for one, already fragments of the extensionality principle give rise to very strong uniform continuity principles excluding a wide range of natural instances of such operators and where, for another, it has been shown that the key defining properties of some of the central classes of such operators considered in the literature actually are already equivalent to the associated extensionality principle, creating an a priori dire situation for extending methods from proof mining to such objects. This issue is made even more pressing by the fact that these set-valued operators have become one of the prime foci of proof mining applications in the recent years, as exemplified by the the many case studies carried out utilizing these objects (see e.g. the many works on the seminal proximal point algorithm and its variants as in Dinis and Pinto (2020, 2021); Kohlenbach (2020, 2021, 2022); Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018); Leuştean et al. (Reference Leuştean, Nicolae and Sipoş2018); Leuştean and Pinto (Reference Leuştean and Pinto2021); Pinto (Reference Pinto2021); Pischke and Kohlenbach (Reference Pischke and Kohlenbach2024); Pischke (Reference Pischke2024b) as well as case studies on nonlinear semigroups and their relation to accretive set-valued operators as in Kohlenbach and Koutsoukou-Argyraki (Reference Kohlenbach and Koutsoukou-Argyraki2015); Pinto and Pischke (Reference Pinto and Pischke2023); Findling and Kohlenbach (Reference Findling and Kohlenbach2024); Pischke (Reference Pischke2024f) as well as other central considerations on iterations featuring these operators like in Kohlenbach (Reference Kohlenbach2019a); Kohlenbach and Powell (Reference Kohlenbach and Powell2020); Pischke (Reference Pischke2023b); Sipoş (Reference Sipoş2022, Reference Sipoş2023) among others).
$T:X\to 2^X$
, this situation changes as first highlighted in Pischke (Reference Pischke2024c) where, for one, already fragments of the extensionality principle give rise to very strong uniform continuity principles excluding a wide range of natural instances of such operators and where, for another, it has been shown that the key defining properties of some of the central classes of such operators considered in the literature actually are already equivalent to the associated extensionality principle, creating an a priori dire situation for extending methods from proof mining to such objects. This issue is made even more pressing by the fact that these set-valued operators have become one of the prime foci of proof mining applications in the recent years, as exemplified by the the many case studies carried out utilizing these objects (see e.g. the many works on the seminal proximal point algorithm and its variants as in Dinis and Pinto (2020, 2021); Kohlenbach (2020, 2021, 2022); Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018); Leuştean et al. (Reference Leuştean, Nicolae and Sipoş2018); Leuştean and Pinto (Reference Leuştean and Pinto2021); Pinto (Reference Pinto2021); Pischke and Kohlenbach (Reference Pischke and Kohlenbach2024); Pischke (Reference Pischke2024b) as well as case studies on nonlinear semigroups and their relation to accretive set-valued operators as in Kohlenbach and Koutsoukou-Argyraki (Reference Kohlenbach and Koutsoukou-Argyraki2015); Pinto and Pischke (Reference Pinto and Pischke2023); Findling and Kohlenbach (Reference Findling and Kohlenbach2024); Pischke (Reference Pischke2024f) as well as other central considerations on iterations featuring these operators like in Kohlenbach (Reference Kohlenbach2019a); Kohlenbach and Powell (Reference Kohlenbach and Powell2020); Pischke (Reference Pischke2023b); Sipoş (Reference Sipoş2022, Reference Sipoş2023) among others).
It is therefore even more surprising that, contrary to these theoretical limitations, this apparent proof-theoretic strength is rarely observed in practice. In particular, essentially none of the case studies mentioned above (besides a central illustrative example Pischke (Reference Pischke2023b)) require a quantitative treatment of extensionality at all if they did not feature a uniform continuity assumption in the first place. As first outlined in Pischke (Reference Pischke2024c), this can be explained from a proof-theoretical perspective by the empirical fact that in many proofs from the mainstream literature of m-accretive or maximally monotone operator theory, the areas where these case studies are situated in (see Takahashi (Reference Takahashi2000); Bauschke and Combettes (Reference Bauschke and Combettes2017) for canonical textbooks on these subjects), one does not require the full extensionality of the operator in question but it actually suffices to have a certain so-called intensional treatment thereof together with access to the so-called resolvent which in turn is proof-theoretically tame and can be utilized to design applicable systems with accompanying metatheorems in the usual style of proof mining for these areas (see the discussions in Pischke (Reference Pischke2024c) for further information).
If, however, the proof is not of that nature and really requires the extensionality of the operator, then a quantitative treatment of such will be necessary (as was e.g. the case in the previously mentioned application from Pischke (Reference Pischke2023b)). This might in some situations further hinder a proof-theoretic treatment as some of the central uniform continuity principles for set-valued operators, which crucially feature in many proofs in that area and naturally imply an associated extensionality statement, are not immediately recognized as proof-theoretically tame statements and instead seem to carry computational strength already due to the use of apparently logically complicated objects like for example the Hausdorff metric.
The purpose of this paper is now twofold:
-
(1) We discuss some central issues with treating the full extensionality statement in the context of an intensional approach to set-valued operators, similar to the approach towards accretive and monotone operators taken in Pischke (Reference Pischke2024c) (see also Pischke (Reference Pischke2024a)). In particular, we show that, in a way, no bound extraction result akin to the metatheorems of proof mining exists for intensional systems treating suitable classes of set-valued operators and which prove the associated full extensionality principle for the operator. This in particular puts strong emphasis on extensionality as a central logical issue for proof mining in the context of set-valued operator theory.
-
(2) Motivated by these negative results of item (1), we discuss a range of fragments of the full extensionality principle, which arise by considering said principle from a more mathematically motivated perspective, and study the relations among them, highlighting a certain robustness. Contrary to the negative results on the rather “naive” and logically motivated full extensionality principles, we illustrate how these fragments all represent the extensionality of the operator in a mathematically fruitful, and essentially equivalent, way. In particular, they allow for a computational interpretation which generates useful uniform continuity statements for set-valued operators that can be introduced in the logical systems via a collection of axioms that do not contribute to the growth of extractable bounds from proofs. In particular, we in that context illustrate how the most prominent uniform continuity principle for set-valued operators as formulated using the Hausdorff metric can be treated in a logically tame way in the context of an intensional approach to these operator, which presents the first proof-theoretically tame approach to the Hausdorff metric and hence for the first time enables proof mining applications utilizing this mapping in an essential way. This is then in particular illustrated in the later half of the paper by a case study where we extract quantitative information on the convergence of an iterative method devised in Song and Wang (Reference Song and Wang2009) for the approximation of fixed points of set-valued maps that are nonexpansive relative to the Hausdorff metric.
With these two contributions, we therefore provide highly necessary information for the practice of proof mining regarding proofs featuring the extensionality of set-valued operators as it is carried out using these intensional approaches, highlighting with (1) and (2) the subtlety of expressing mathematically meaningful notions of extensionality and uniform continuity in respective formal systems, where we in particular illustrate that even complicated uniform continuity statements using the Hausdorff metric can be approached in a proof-theoretically tame way, a fact that in this paper, as mentioned above, also immediately leads to novel applications.
2. Logical Aspects of Full Extensionality Principles for Set-Valued Operators
In this section, we discuss the main aspects of the first of the previously mentioned objectives of this paper, that is the issues with extensionality in the context of an intensional treatment of set-valued operators
![]() $T:X\to 2^X$
over a normed vector space
$T:X\to 2^X$
over a normed vector space
![]() $X$
.Footnote
3
In the context of these set-valued operators, we write
$X$
.Footnote
3
In the context of these set-valued operators, we write
for the domain of
![]() $T$
and
$T$
and
for the range of
![]() $T$
. As we are dealing with objects on normed spaces, the main system for proof mining over abstract normed spaces
$T$
. As we are dealing with objects on normed spaces, the main system for proof mining over abstract normed spaces
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
as introduced in Kohlenbach (Reference Kohlenbach2005) (see also Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008)) consequently forms a logical basis for these investigations. While this system is central for the present paper, we nevertheless only rely on a handful of key properties of it which we shortly discuss in the following. For any other background on this system, we refer to the presentation in Kohlenbach (Reference Kohlenbach2008).
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
as introduced in Kohlenbach (Reference Kohlenbach2005) (see also Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008)) consequently forms a logical basis for these investigations. While this system is central for the present paper, we nevertheless only rely on a handful of key properties of it which we shortly discuss in the following. For any other background on this system, we refer to the presentation in Kohlenbach (Reference Kohlenbach2008).
Concretely, the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
extends
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
extends
![]() $\mathscr{A}^\omega =\textrm{WE}\text{-}\textrm{PA}^\omega +\textrm{QF}\text{-}\textrm{AC}+\textrm{DC}$
, that is a weakly extensional variant of Peano arithmetic in all finite types together with the principle of quantifier-free choice in all types and the principle of dependent choice (see Kohlenbach (Reference Kohlenbach2008) and Troelstra (Reference Troelstra1973) for further details), with an additional abstract base type
$\mathscr{A}^\omega =\textrm{WE}\text{-}\textrm{PA}^\omega +\textrm{QF}\text{-}\textrm{AC}+\textrm{DC}$
, that is a weakly extensional variant of Peano arithmetic in all finite types together with the principle of quantifier-free choice in all types and the principle of dependent choice (see Kohlenbach (Reference Kohlenbach2008) and Troelstra (Reference Troelstra1973) for further details), with an additional abstract base type
![]() $X$
and additional constants and universal axioms utilizing this type to axiomatize that
$X$
and additional constants and universal axioms utilizing this type to axiomatize that
![]() $X$
is a normed space. As such, the system
$X$
is a normed space. As such, the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
operates over an extended set of types
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
operates over an extended set of types
![]() $T^X$
defined by
$T^X$
defined by
with pure types abbreviated via natural numbers through recursively defining
![]() $n+1:=0(n)$
. To induce a normed linear structure on
$n+1:=0(n)$
. To induce a normed linear structure on
![]() $X$
, one adds the constants
$X$
, one adds the constants
![]() $0_X,1_X$
of type
$0_X,1_X$
of type
![]() $X$
,
$X$
,
![]() $+_X$
of type
$+_X$
of type
![]() $X(X)(X)$
,
$X(X)(X)$
,
![]() $-_X$
of type
$-_X$
of type
![]() $X(X)$
,
$X(X)$
,
![]() $\cdot _X$
of type
$\cdot _X$
of type
![]() $X(X)(1)$
, and
$X(X)(1)$
, and
![]() $\lVert \cdot \rVert _X$
of type
$\lVert \cdot \rVert _X$
of type
![]() $1(X)$
together with suitable axioms stating that
$1(X)$
together with suitable axioms stating that
![]() $X$
with these operations is a real normed vector space with
$X$
with these operations is a real normed vector space with
![]() $1_X$
representing a unit vector and
$1_X$
representing a unit vector and
![]() $-_X$
producing the additive inverse of its argument (see Kohlenbach (2005, 2008); Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) for further details). In any way, equality at type
$-_X$
producing the additive inverse of its argument (see Kohlenbach (2005, 2008); Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) for further details). In any way, equality at type
![]() $0$
, i.e. on the natural numbers, is the only primitive relation and equality at higher types is treated as a defined notion by setting
$0$
, i.e. on the natural numbers, is the only primitive relation and equality at higher types is treated as a defined notion by setting
using a suitable representation of the real numbers as objects of type
![]() $1$
(see e.g. Kohlenbach (Reference Kohlenbach2008)) and by extending this to higher types via
$1$
(see e.g. Kohlenbach (Reference Kohlenbach2008)) and by extending this to higher types via
An intended model of this language arises from the full set-theoretic type structure
![]() $\mathscr{S}^{\omega ,X}$
defined by
$\mathscr{S}^{\omega ,X}$
defined by
for a given normed space
![]() $(X,\lVert \cdot \rVert )$
by suitably interpreting the additional constants present in
$(X,\lVert \cdot \rVert )$
by suitably interpreting the additional constants present in
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
(see Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) for further details).
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
(see Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) for further details).
Crucially, this system is suitably designed so that by an application of a negative translation together with a monotone variant of Gödel’s functional interpretation arising through a combination with Howard’s majorizability (due to the seminal work of Kohlenbach (Reference Kohlenbach1996a), see also already Kohlenbach (Reference Kohlenbach1992)), the following logical metatheorem in the style of proof mining can be established for that system:
Theorem 1. (Gerhardy and Kohlenbach Reference Gerhardy2008). Let
![]() $\rho$
be admissibleFootnote
4
and let
$\rho$
be admissibleFootnote
4
and let
![]() $B_\forall (x,u)$
/
$B_\forall (x,u)$
/
![]() $C_\exists (x,v)$
be purely universal/existential, respectively, where the types of the internal quantifiers are admissible and such that they only contain
$C_\exists (x,v)$
be purely universal/existential, respectively, where the types of the internal quantifiers are admissible and such that they only contain
![]() $x,u$
/
$x,u$
/
![]() $x,v$
freely. Assume that
$x,v$
freely. Assume that
Then there exists a partial functional
![]() $\Phi :S_{\widehat {\rho }}\rightharpoonup \mathbb{N}$
which is defined on all strongly majorizable elements of
$\Phi :S_{\widehat {\rho }}\rightharpoonup \mathbb{N}$
which is defined on all strongly majorizable elements of
![]() $S_{\widehat {\rho }}$
(see Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008)), where the corresponding restriction to these elements is bar-recursively computable and where the following holds for any model
$S_{\widehat {\rho }}$
(see Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008)), where the corresponding restriction to these elements is bar-recursively computable and where the following holds for any model
![]() $\mathscr{S}^{\omega ,X}$
defined by a nontrivial real normed vector space
$\mathscr{S}^{\omega ,X}$
defined by a nontrivial real normed vector space
![]() $(X,\lVert \cdot \rVert )$
: for all
$(X,\lVert \cdot \rVert )$
: for all
![]() $x\in S_\rho$
and
$x\in S_\rho$
and
![]() $x^*\in S_{\widehat {\rho }}$
, if
$x^*\in S_{\widehat {\rho }}$
, if
![]() $x^*\gtrsim x$
, then
$x^*\gtrsim x$
, then
Here,
![]() $\gtrsim$
is the extension due to Kohlenbach (Reference Kohlenbach2005) and Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) of the strong majorizability relation of Bezem and
$\gtrsim$
is the extension due to Kohlenbach (Reference Kohlenbach2005) and Gerhardy and Kohlenbach (Reference Gerhardy and Kohlenbach2008) of the strong majorizability relation of Bezem and
![]() $\widehat {\rho }\in T$
is the type of the majorants of objects of type
$\widehat {\rho }\in T$
is the type of the majorants of objects of type
![]() $\rho \in T^X$
.
$\rho \in T^X$
.
By an intensional approach to a set-valued operator
![]() $T$
over
$T$
over
![]() $X$
, we now understand that
$X$
, we now understand that
![]() $T$
is treated formally via its graph as coded by its characteristic function which is an object of type
$T$
is treated formally via its graph as coded by its characteristic function which is an object of type
![]() $0(X)(X)$
.Footnote
5
To generically talk about such systems here, we assume that the language of the system
$0(X)(X)$
.Footnote
5
To generically talk about such systems here, we assume that the language of the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
is extended with a new constant
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
is extended with a new constant
![]() $\chi _T$
of type
$\chi _T$
of type
![]() $0(X)(X)$
. We write
$0(X)(X)$
. We write
![]() $y\in Tx$
,
$y\in Tx$
,
![]() $(x,y)\in T$
or
$(x,y)\in T$
or
![]() $(x,y)\in \textrm{gra}T$
for the formal statement
$(x,y)\in \textrm{gra}T$
for the formal statement
![]() $\chi _Txy=_00$
in the extended language and we write
$\chi _Txy=_00$
in the extended language and we write
![]() $x\in \textrm{dom}T$
for
$x\in \textrm{dom}T$
for
![]() $\exists y^X\left (y\in Tx\right )$
. Note that inclusions in the graph of
$\exists y^X\left (y\in Tx\right )$
. Note that inclusions in the graph of
![]() $T$
are in particular quantifier-free. We denote the extension of the system
$T$
are in particular quantifier-free. We denote the extension of the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
by this constant
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
by this constant
![]() $\chi _T$
together with the characteristic function axiom
$\chi _T$
together with the characteristic function axiom
by
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
. Naturally, an intended model
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
. Naturally, an intended model
![]() $\mathscr{S}^{\omega ,X}_T$
for this extended system arises from a normed space
$\mathscr{S}^{\omega ,X}_T$
for this extended system arises from a normed space
![]() $(X,\lVert \cdot \rVert )$
and a set-valued operator
$(X,\lVert \cdot \rVert )$
and a set-valued operator
![]() $T:X\to 2^X$
by extending the induced model
$T:X\to 2^X$
by extending the induced model
![]() $\mathscr{S}^{\omega ,X}$
for the system
$\mathscr{S}^{\omega ,X}$
for the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
by interpreting
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
by interpreting
![]() $\chi _T$
via
$\chi _T$
via
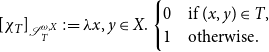 \begin{equation*} [\chi _T]_{\mathscr{S}^{\omega ,X}_T}:=\lambda x,y\in X.\begin{cases}0&\text{if }(x,y)\in T,\\1&\text{otherwise}.\end{cases} \end{equation*}
\begin{equation*} [\chi _T]_{\mathscr{S}^{\omega ,X}_T}:=\lambda x,y\in X.\begin{cases}0&\text{if }(x,y)\in T,\\1&\text{otherwise}.\end{cases} \end{equation*}
It rather immediately followsFootnote
6
that this simple extension
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
of
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
of
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
also satisfies a proof mining metatheorem akin to that presented in Theorem1.
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
also satisfies a proof mining metatheorem akin to that presented in Theorem1.
By the (full) extensionality axiom for
![]() $T$
, we now mean the following formal statement in the corresponding language of
$T$
, we now mean the following formal statement in the corresponding language of
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
:
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
:
Naturally, a system like the above might now serve as the basis for further extensions with additional constants and axioms in order to axiomatize certain specific classes of set-valued operators, like for example done in Pischke (Reference Pischke2024c) for treating (m-)accretive and (maximally) monotone operators on Hilbert spaces and in Pischke (Reference Pischke2024a) for (maximally) monotone operators on Banach spaces, but this approach is not limited by these classes of objects and rather is immediately applicable for any extension of this system by additional constants, as long as these are majorizable, and suitable axioms, as long as these have a monotone functional interpretation (see Kohlenbach (Reference Kohlenbach2008) for further details on both of these aspects).
In the following, we however want to study the behavior of a (suitably) generic but fixed extension of that very minimal base
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
which we in the following denote by
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
which we in the following denote by
![]() $\mathscr{C}^\omega$
. Crucially, we only assume for
$\mathscr{C}^\omega$
. Crucially, we only assume for
![]() $\mathscr{C}^\omega$
that is satisfies the following two properties:
$\mathscr{C}^\omega$
that is satisfies the following two properties:
-
(1) The system
 $\mathscr{C}^\omega$
satisfies a metatheorem in the style of proof mining, that is akin to Theorem1, where the conclusion is (of course) only true for a certain class of intended models
$\mathscr{C}^\omega$
satisfies a metatheorem in the style of proof mining, that is akin to Theorem1, where the conclusion is (of course) only true for a certain class of intended models
 $\mathscr{S}^{\omega ,X}_T$
, which we here fix to arise only from spaces
$\mathscr{S}^{\omega ,X}_T$
, which we here fix to arise only from spaces
 $X$
of a certain nonempty class
$X$
of a certain nonempty class
 $\mathsf{C}_{\textrm{Sp}}$
of normed spaces and from set-valued operators
$\mathsf{C}_{\textrm{Sp}}$
of normed spaces and from set-valued operators
 $T:X\to 2^X$
of an associated nonempty class
$T:X\to 2^X$
of an associated nonempty class
 $\mathsf{C}_{\textrm{Op}}(X)$
.
$\mathsf{C}_{\textrm{Op}}(X)$
. -
(2) The system
 $\mathscr{C}^\omega$
axiomatizes a class of nonempty and closed set-valued operators, that is
$\mathscr{C}^\omega$
axiomatizes a class of nonempty and closed set-valued operators, that is
 $X\in \mathsf{C}_{\textrm{Sp}}$
and
$X\in \mathsf{C}_{\textrm{Sp}}$
and
 $T\in \mathsf{C}_{\textrm{Op}}(X)$
implies that
$T\in \mathsf{C}_{\textrm{Op}}(X)$
implies that
 $T$
is closed in
$T$
is closed in
 $X\times X$
and that
$X\times X$
and that
 $\textrm{dom}T\neq \emptyset$
.
$\textrm{dom}T\neq \emptyset$
.
It should be emphasized that this in particular holds true for most systems considered for proof mining applications, in particular for the systems devised for (nonempty) m-accretive and maximally monotone operators in Pischke (Reference Pischke2024a,c) (and even for operators continuous w.r.t. the Hausdorff metric as will be discussed later on). In fact, for these classes of m-accretive or maximally monotone set-valued operators, the closedness of them in
![]() $X\times X$
is even actually equivalent to the extensionality of these mappings over respective suitable intensional systems (akin to
$X\times X$
is even actually equivalent to the extensionality of these mappings over respective suitable intensional systems (akin to
![]() $\mathscr{C}^\omega$
, i.e. extending
$\mathscr{C}^\omega$
, i.e. extending
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
and satisfying a logical metatheorem in the style of proof mining) as shown in Pischke (Reference Pischke2024a,c).
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
and satisfying a logical metatheorem in the style of proof mining) as shown in Pischke (Reference Pischke2024a,c).
We now want to investigate what consequences there are when such a system actually proves the extensionality of
![]() $T$
or fragments thereof. So, let us initially assume that
$T$
or fragments thereof. So, let us initially assume that
![]() $\mathscr{C}^\omega \vdash (E)^\chi _T$
. Then, using the bound extraction theorem, that is property (1), assumed for
$\mathscr{C}^\omega \vdash (E)^\chi _T$
. Then, using the bound extraction theorem, that is property (1), assumed for
![]() $\mathscr{C}^\omega$
, we would be able to extract a functional
$\mathscr{C}^\omega$
, we would be able to extract a functional
![]() $\omega _{X,T}:\mathbb{N}\to \mathbb{N}$
(potentially depending on
$\omega _{X,T}:\mathbb{N}\to \mathbb{N}$
(potentially depending on
![]() $X$
and
$X$
and
![]() $T$
) such that
$T$
) such that
holds for any normed space
![]() $X\in \mathsf{C}_{\textrm{Sp}}$
and operator
$X\in \mathsf{C}_{\textrm{Sp}}$
and operator
![]() $T\in \mathsf{C}_{\textrm{Op}}(X)$
. Now, any such operator has to be open in
$T\in \mathsf{C}_{\textrm{Op}}(X)$
. Now, any such operator has to be open in
![]() $X\times X$
(in a uniform way on bounded sets): given
$X\times X$
(in a uniform way on bounded sets): given
![]() $(x,z)\in T$
with
$(x,z)\in T$
with
![]() $\lVert x \rVert ,\lVert z \rVert \leq b$
and
$\lVert x \rVert ,\lVert z \rVert \leq b$
and
![]() $y,w$
such that
$y,w$
such that
we have
![]() $\lVert y \rVert ,\lVert w \rVert \leq b+1$
and so
$\lVert y \rVert ,\lVert w \rVert \leq b+1$
and so
![]() $(y,w)\in T$
. However, this provides a semantic clash with property (2) assumed for
$(y,w)\in T$
. However, this provides a semantic clash with property (2) assumed for
![]() $\mathscr{C}^\omega$
as any
$\mathscr{C}^\omega$
as any
![]() $T\in \mathsf{C}_{\textrm{Op}}(X)$
is, by that assumption, closed in
$T\in \mathsf{C}_{\textrm{Op}}(X)$
is, by that assumption, closed in
![]() $X\times X$
and hence clopen and so, since
$X\times X$
and hence clopen and so, since
![]() $X$
(and with that
$X$
(and with that
![]() $X\times X$
) is a normed space, that means any
$X\times X$
) is a normed space, that means any
![]() $T$
is either equal to
$T$
is either equal to
![]() $X\times X$
or
$X\times X$
or
![]() $\emptyset$
, the latter being excluded as
$\emptyset$
, the latter being excluded as
![]() $T$
is also assumed to be nonempty. Not only is this restriction already here so severe that it completely trivialized the semantically considered operators, but in the context of many of the central classes of set-valued operators studied in the literature of convex analysis, as is e.g. the case for m-accretive and maximally monotone operators, the analytical properties imposed on them often already further exclude the full operator
$T$
is also assumed to be nonempty. Not only is this restriction already here so severe that it completely trivialized the semantically considered operators, but in the context of many of the central classes of set-valued operators studied in the literature of convex analysis, as is e.g. the case for m-accretive and maximally monotone operators, the analytical properties imposed on them often already further exclude the full operator
![]() $X\times X$
. In such cases, there are therefore no operators
$X\times X$
. In such cases, there are therefore no operators
![]() $T\in \mathsf{C}_{\textrm{Op}}(X)$
. Consequently, if a system
$T\in \mathsf{C}_{\textrm{Op}}(X)$
. Consequently, if a system
![]() $\mathscr{C}^\omega$
with the properties (1) and (2) as above has a model based on the standard structure using spaces
$\mathscr{C}^\omega$
with the properties (1) and (2) as above has a model based on the standard structure using spaces
![]() $X\in \mathsf{C}_{\textrm{Sp}}$
and operators
$X\in \mathsf{C}_{\textrm{Sp}}$
and operators
![]() $T\in \mathsf{C}_{\textrm{Op}}(X)$
, it can not prove the extensionality of the operator
$T\in \mathsf{C}_{\textrm{Op}}(X)$
, it can not prove the extensionality of the operator
![]() $T$
.
$T$
.
A kind of internalized version of the above argument can be given using the principle of uniform boundedness
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X_-$
as introduced in Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016) (see also Kohlenbach (Reference Kohlenbach2006) as well as Kohlenbach (Reference Kohlenbach1996b), the latter being where this principle was first introduced, outside of the context of abstract types however). By the results of Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016) (see also Kohlenbach (Reference Kohlenbach2006)),
$\Sigma ^0_1\text{-}\textrm{UB}^X_-$
as introduced in Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016) (see also Kohlenbach (Reference Kohlenbach2006) as well as Kohlenbach (Reference Kohlenbach1996b), the latter being where this principle was first introduced, outside of the context of abstract types however). By the results of Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016) (see also Kohlenbach (Reference Kohlenbach2006)),
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X_-$
can be consistently added to a system that enjoys bound extraction theorems in the above sense. In particular, the system
$\Sigma ^0_1\text{-}\textrm{UB}^X_-$
can be consistently added to a system that enjoys bound extraction theorems in the above sense. In particular, the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+\Sigma ^0_1\text{-}\textrm{UB}^X_-$
enjoys the same bound extraction theorems as the system
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+\Sigma ^0_1\text{-}\textrm{UB}^X_-$
enjoys the same bound extraction theorems as the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
. Now, the principle
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
. Now, the principle
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X_-$
represents a carefully defined intensional version of the usual uniform boundedness principle
$\Sigma ^0_1\text{-}\textrm{UB}^X_-$
represents a carefully defined intensional version of the usual uniform boundedness principle
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X$
(see also Kohlenbach (Reference Kohlenbach2006) and Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016)), a necessary restriction in order to stay admissible in the context of unbounded spaces. However, as shown in Lemma 6.25 in Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016),
$\Sigma ^0_1\text{-}\textrm{UB}^X$
(see also Kohlenbach (Reference Kohlenbach2006) and Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016)), a necessary restriction in order to stay admissible in the context of unbounded spaces. However, as shown in Lemma 6.25 in Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016),
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X_-$
and
$\Sigma ^0_1\text{-}\textrm{UB}^X_-$
and
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X$
coincide for sentences that are extensional. Now, in our context, it however in particular follows that
$\Sigma ^0_1\text{-}\textrm{UB}^X$
coincide for sentences that are extensional. Now, in our context, it however in particular follows that
where, following Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016),
![]() $\textrm{Ext}(A_\exists )$
represents the extensionality of the formula
$\textrm{Ext}(A_\exists )$
represents the extensionality of the formula
![]() $A_\exists$
defined by
$A_\exists$
defined by
as by
![]() $(E)^\chi _T$
, inclusions of the form
$(E)^\chi _T$
, inclusions of the form
![]() $z\in Tx$
are extensional (and since the norm is provably extensional). Hence, by Lemma 6.25 from Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016), in the context of
$z\in Tx$
are extensional (and since the norm is provably extensional). Hence, by Lemma 6.25 from Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016), in the context of
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X_-$
we can actually apply
$\Sigma ^0_1\text{-}\textrm{UB}^X_-$
we can actually apply
![]() $\Sigma ^0_1\text{-}\textrm{UB}^X$
to
$\Sigma ^0_1\text{-}\textrm{UB}^X$
to
![]() $A_\exists$
which, by internalizing the above argument, immediately allows one to derive that
$A_\exists$
which, by internalizing the above argument, immediately allows one to derive that
![]() $T$
is open as before, i.e. we can thereby derive that
$T$
is open as before, i.e. we can thereby derive that
where
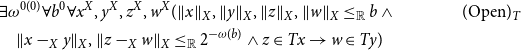 \begin{align*} &\exists \omega ^{0(0)}\forall b^0\forall x^X,y^X,z^X,w^X ( \lVert x \rVert _X, \lVert y \rVert _X, \lVert z \rVert _X, \lVert w \rVert _X\leq _{\mathbb{R}} b\;\land &&(\textrm{Open})_T\\ &\quad \lVert x-_Xy \rVert _X, \lVert z-_Xw \rVert _X\leq _{\mathbb{R}} 2^{-\omega (b)}\land z\in Tx\rightarrow w\in Ty) &&\end{align*}
\begin{align*} &\exists \omega ^{0(0)}\forall b^0\forall x^X,y^X,z^X,w^X ( \lVert x \rVert _X, \lVert y \rVert _X, \lVert z \rVert _X, \lVert w \rVert _X\leq _{\mathbb{R}} b\;\land &&(\textrm{Open})_T\\ &\quad \lVert x-_Xy \rVert _X, \lVert z-_Xw \rVert _X\leq _{\mathbb{R}} 2^{-\omega (b)}\land z\in Tx\rightarrow w\in Ty) &&\end{align*}
is a formalization of the fact that
![]() $T$
is open (uniform on bounded sets) as above. Therefore, the system
$T$
is open (uniform on bounded sets) as above. Therefore, the system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+\Sigma ^0_1\text{-}\textrm{UB}^X_-+(E)^\chi _T+(\textrm{Clsd})_T$
proves that
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+\Sigma ^0_1\text{-}\textrm{UB}^X_-+(E)^\chi _T+(\textrm{Clsd})_T$
proves that
where
![]() $(\textrm{Clsd})_T$
is some suitable formalization of the closure of
$(\textrm{Clsd})_T$
is some suitable formalization of the closure of
![]() $T$
. In particular, let us now consider the systems
$T$
. In particular, let us now consider the systems
![]() $\mathscr{V}^\omega$
or
$\mathscr{V}^\omega$
or
![]() $\mathscr{T}^\omega$
from Pischke (Reference Pischke2024c) which provide a treatment of m-accretive operators in normed spaces and maximally monotone operators in inner product spaces, respectively. There, we in particular find that the conclusions
$\mathscr{T}^\omega$
from Pischke (Reference Pischke2024c) which provide a treatment of m-accretive operators in normed spaces and maximally monotone operators in inner product spaces, respectively. There, we in particular find that the conclusions
![]() $\forall x^X,y^X\left ( y\not \in Tx\right )$
and
$\forall x^X,y^X\left ( y\not \in Tx\right )$
and
![]() $\forall x^X,y^X\left ( y\in Tx\right )$
are excluded as, for one,
$\forall x^X,y^X\left ( y\in Tx\right )$
are excluded as, for one,
![]() $T$
is provably nonempty in these cases and, for another, as the total operator is provably not accretive or monotone. Further, by utilizing special properties of the operators axiomatized therein, one has (by Theorems 3.1 and 3.3 in Pischke (Reference Pischke2024c)) that
$T$
is provably nonempty in these cases and, for another, as the total operator is provably not accretive or monotone. Further, by utilizing special properties of the operators axiomatized therein, one has (by Theorems 3.1 and 3.3 in Pischke (Reference Pischke2024c)) that
![]() $(\textrm{Clsd})_T$
is provably equivalent to
$(\textrm{Clsd})_T$
is provably equivalent to
![]() $(E)^\chi _T$
. Together, we obtain that the system
$(E)^\chi _T$
. Together, we obtain that the system
![]() $\mathscr{V}^\omega +\Sigma ^0_1\text{-}\textrm{UB}^X_-+(E)^\chi _T$
, and similarly the variant formulated with
$\mathscr{V}^\omega +\Sigma ^0_1\text{-}\textrm{UB}^X_-+(E)^\chi _T$
, and similarly the variant formulated with
![]() $\mathscr{T}^\omega$
, are actually inconsistent, while
$\mathscr{T}^\omega$
, are actually inconsistent, while
![]() $\mathscr{V}^\omega +\Sigma ^0_1\text{-}\textrm{UB}^X_-$
and
$\mathscr{V}^\omega +\Sigma ^0_1\text{-}\textrm{UB}^X_-$
and
![]() $\mathscr{T}^\omega +\Sigma ^0_1\text{-}\textrm{UB}^X_-$
still satisfy highly meaningful bound extraction theorems.
$\mathscr{T}^\omega +\Sigma ^0_1\text{-}\textrm{UB}^X_-$
still satisfy highly meaningful bound extraction theorems.
It should be noted that similar issues persist if
![]() $(E)^\chi _T$
is restricted to the domain of
$(E)^\chi _T$
is restricted to the domain of
![]() $T$
by considering the weakened extensionality principle
$T$
by considering the weakened extensionality principle
For, suppose that
![]() $\mathscr{C}^\omega \vdash (E)^{\chi _d}_T$
for the previously presumed system
$\mathscr{C}^\omega \vdash (E)^{\chi _d}_T$
for the previously presumed system
![]() $\mathscr{C}^\omega$
, then the bound extraction theorem, i.e. property (1), assumed for
$\mathscr{C}^\omega$
, then the bound extraction theorem, i.e. property (1), assumed for
![]() $\mathscr{C}^\omega$
would yield the existence of a functional
$\mathscr{C}^\omega$
would yield the existence of a functional
![]() $\omega _{X,T}:\mathbb{N}\to \mathbb{N}$
such that
$\omega _{X,T}:\mathbb{N}\to \mathbb{N}$
such that
holds for any normed space
![]() $X\in \mathsf{C}_{\textrm{Sp}}$
and any operator
$X\in \mathsf{C}_{\textrm{Sp}}$
and any operator
![]() $T\in \mathsf{C}_{\textrm{Op}}(X)$
. This still at least implies that
$T\in \mathsf{C}_{\textrm{Op}}(X)$
. This still at least implies that
![]() $Tx$
is open for any
$Tx$
is open for any
![]() $x\in \textrm{dom}T$
as if
$x\in \textrm{dom}T$
as if
![]() $z\in Tx$
with
$z\in Tx$
with
![]() $\lVert z \rVert ,\lVert x \rVert \leq b$
are given, and
$\lVert z \rVert ,\lVert x \rVert \leq b$
are given, and
![]() $w$
is such that
$w$
is such that
![]() $\lVert z-w \rVert \leq 2^{-\omega _{X,T}(b+1)}$
, then
$\lVert z-w \rVert \leq 2^{-\omega _{X,T}(b+1)}$
, then
![]() $w\in Tx$
. Again, this provides a semantic clash with property (2) assumed for
$w\in Tx$
. Again, this provides a semantic clash with property (2) assumed for
![]() $\mathscr{C}^\omega$
by which, since such a
$\mathscr{C}^\omega$
by which, since such a
![]() $T$
is closed in
$T$
is closed in
![]() $X\times X$
, any
$X\times X$
, any
![]() $Tx$
in particular is also closed so that the only operators
$Tx$
in particular is also closed so that the only operators
![]() $T\in \mathsf{C}_{\textrm{Op}}(X)$
are of the form
$T\in \mathsf{C}_{\textrm{Op}}(X)$
are of the form
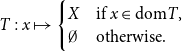 \begin{equation*} T:x\mapsto \begin{cases}X&\text{if }x\in \textrm{dom}T,\\\emptyset &\text{otherwise}.\end{cases} \end{equation*}
\begin{equation*} T:x\mapsto \begin{cases}X&\text{if }x\in \textrm{dom}T,\\\emptyset &\text{otherwise}.\end{cases} \end{equation*}
In the special case of the previously mentioned systems for, e.g., m-accretive or maximally monotone operators, this limitation on the class of axiomatized operators is now slightly less severe as it does not necessarily render models based on
![]() $\mathscr{S}^{\omega ,X}_T$
(as induced by the previously fixed classes of spaces and operators) impossible (take e.g. the normal cone operator
$\mathscr{S}^{\omega ,X}_T$
(as induced by the previously fixed classes of spaces and operators) impossible (take e.g. the normal cone operator
![]() $N_{\{x\}}$
for a given point
$N_{\{x\}}$
for a given point
![]() $x\in X$
in a Hilbert space, see Bauschke and Combettes (Reference Bauschke and Combettes2017), which is maximally monotone but of the above form and so is feasible for the previously mentioned system
$x\in X$
in a Hilbert space, see Bauschke and Combettes (Reference Bauschke and Combettes2017), which is maximally monotone but of the above form and so is feasible for the previously mentioned system
![]() $\mathscr{T}^\omega$
, for example). Nevertheless, the class is of course still extremely restrictive, presumably making any extracted results qualitatively uninteresting and so of little practical relevance. Also this result can be internalized akin to the previous discussion.
$\mathscr{T}^\omega$
, for example). Nevertheless, the class is of course still extremely restrictive, presumably making any extracted results qualitatively uninteresting and so of little practical relevance. Also this result can be internalized akin to the previous discussion.
3. Useful Fragments of the Extensionality Principle and Their Formal Treatment
All the observations made above clearly highlight that the “naive” extensionality principles
![]() $(E)^\chi _T$
and
$(E)^\chi _T$
and
![]() $(E)^{\chi _d}_T$
, derived by requiring the extensionality of the graph of
$(E)^{\chi _d}_T$
, derived by requiring the extensionality of the graph of
![]() $T$
as coded intensionally via
$T$
as coded intensionally via
![]() $\chi _T$
, is unsuitable for any applied considerations. In a way, this comes at no big surprise as the principles essentially require an inherently intensional object
$\chi _T$
, is unsuitable for any applied considerations. In a way, this comes at no big surprise as the principles essentially require an inherently intensional object
![]() $\chi _T$
to now act extensional again.
$\chi _T$
to now act extensional again.
Now, even though the use of extensionality can often be (at least partially) avoided in practice, as discussed in the introduction, there are nontrivial cases where it nevertheless features prominently, and since
![]() $(E)^\chi _T$
and
$(E)^\chi _T$
and
![]() $(E)^{\chi _d}_T$
are not amenable in any real sense to an applied proof-theoretic treatment using the intensional approach to set-valued operators, we are inclined to look for alternative formulations of extensionality to faithfully represent that property formally in this context, meanwhile being of practical, mathematical, use. Guided by the perspective of applied proof theory, we in this section study a range of fragments of the full extensionality principles, which are motivated by uniform continuity statements for set-valued operators already prominently investigated in the literature of nonlinear analysis and which in that sense all represent the extensionality of the operator in a mathematically fruitful way.
$(E)^{\chi _d}_T$
are not amenable in any real sense to an applied proof-theoretic treatment using the intensional approach to set-valued operators, we are inclined to look for alternative formulations of extensionality to faithfully represent that property formally in this context, meanwhile being of practical, mathematical, use. Guided by the perspective of applied proof theory, we in this section study a range of fragments of the full extensionality principles, which are motivated by uniform continuity statements for set-valued operators already prominently investigated in the literature of nonlinear analysis and which in that sense all represent the extensionality of the operator in a mathematically fruitful way.
3.1 A refined extensionality principle and its closed variant
We begin our investigation regarding well-behaved fragments of the full extensionality principle with a uniform continuity principle for set-valued operators based on the so-called Hausdorff-like predicate as introduced in Kohlenbach and Powell (Reference Kohlenbach and Powell2020). Concretely, in Kohlenbach and Powell (Reference Kohlenbach and Powell2020), they introduced a form of uniform continuity for a set-valued operator
![]() $T:X\to 2^X$
on a normed space
$T:X\to 2^X$
on a normed space
![]() $X$
by assuming the existence of a modulus
$X$
by assuming the existence of a modulus
![]() $\omega :\mathbb{N}\to \mathbb{N}$
such that
$\omega :\mathbb{N}\to \mathbb{N}$
such that
where
![]() $H^*$
is the aforementioned Hausdorff-like predicate defined by
$H^*$
is the aforementioned Hausdorff-like predicate defined by
This notion was introduced in Kohlenbach and Powell (Reference Kohlenbach and Powell2020) by logical motivations to avoid the use made of the full Hausdorff metric
![]() $H$
, defined by
$H$
, defined by
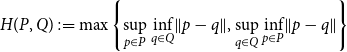 \begin{equation*} H(P,Q):=\max \left \{\sup _{p\in P}\inf _{q\in Q}\lVert p-q \rVert ,\sup _{q\in Q}\inf _{p\in P}\lVert p-q \rVert \right \} \end{equation*}
\begin{equation*} H(P,Q):=\max \left \{\sup _{p\in P}\inf _{q\in Q}\lVert p-q \rVert ,\sup _{q\in Q}\inf _{p\in P}\lVert p-q \rVert \right \} \end{equation*}
for nonempty, closed, and bounded sets
![]() $P,Q\subseteq X$
, in the proofs analyzed therein, which features there in the form of a uniform continuity assumption (and hence an associated extensionality statement). Further, the uniform continuity statement also features crucially in the only other previously mentioned proof mining case study from Pischke (Reference Pischke2023b) that had to resolve an extensionality statement for a set-valued operator. We here now want to argue that this uniform continuity statement already represents, or at least indicates, the correct refined extensionality principle for set-valued operators, which in particular then also indicates that the above uniform continuity statement represents the faithful uniform quantitative strengthening of the extensionality of a set-valued operator as suggested by the perspective of proof mining.
$P,Q\subseteq X$
, in the proofs analyzed therein, which features there in the form of a uniform continuity assumption (and hence an associated extensionality statement). Further, the uniform continuity statement also features crucially in the only other previously mentioned proof mining case study from Pischke (Reference Pischke2023b) that had to resolve an extensionality statement for a set-valued operator. We here now want to argue that this uniform continuity statement already represents, or at least indicates, the correct refined extensionality principle for set-valued operators, which in particular then also indicates that the above uniform continuity statement represents the faithful uniform quantitative strengthening of the extensionality of a set-valued operator as suggested by the perspective of proof mining.
For this, we first turn to the associated extensionality principle suggested by the above uniform continuity principle relative to
![]() $H^*$
which, following Pischke (Reference Pischke2024c) where this principle was already discussed from a logical perspective (albeit embedded in the context of systems treating monotone and accretive set-valued operators), takes the following form:
$H^*$
which, following Pischke (Reference Pischke2024c) where this principle was already discussed from a logical perspective (albeit embedded in the context of systems treating monotone and accretive set-valued operators), takes the following form:
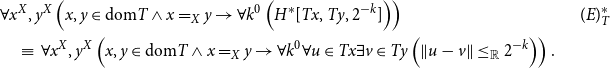 \begin{align*} &\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow \forall k^0\left ( H^*[Tx,Ty,2^{-k}]\right )\right ) && (E)^*_T\\ &\quad\equiv \;\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow \forall k^0\forall u\in Tx\exists v\in Ty\left ( \lVert u-v \rVert \leq _{\mathbb{R}}2^{-k}\right )\right ). &&\end{align*}
\begin{align*} &\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow \forall k^0\left ( H^*[Tx,Ty,2^{-k}]\right )\right ) && (E)^*_T\\ &\quad\equiv \;\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow \forall k^0\forall u\in Tx\exists v\in Ty\left ( \lVert u-v \rVert \leq _{\mathbb{R}}2^{-k}\right )\right ). &&\end{align*}
Indeed, it can be immediately recognized that the uniform continuity principle suggested by the perspective of the monotone functional interpretation of
![]() $(E)^*_T$
amounts to the above uniform continuity statement, actually in a slightly less uniform variant where
$(E)^*_T$
amounts to the above uniform continuity statement, actually in a slightly less uniform variant where
![]() $\omega$
does additionally depend on a norm upper bound
$\omega$
does additionally depend on a norm upper bound
![]() $b$
on the points from
$b$
on the points from
![]() $X$
involved. Further, as discussed in Pischke (Reference Pischke2024c), this uniform continuity principle can be formalized in a proof-theoretically tame way over a system treating such operators intensionally as outline above in the following way: A “naive” first formalization of the principle, resolving in particular the hidden quantifiers in
$X$
involved. Further, as discussed in Pischke (Reference Pischke2024c), this uniform continuity principle can be formalized in a proof-theoretically tame way over a system treating such operators intensionally as outline above in the following way: A “naive” first formalization of the principle, resolving in particular the hidden quantifiers in
![]() $x,y\in \textrm{dom}T$
, yields
$x,y\in \textrm{dom}T$
, yields
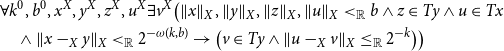 \begin{align*} &\forall k^0,b^0,x^X,y^X,z^X,u^X\exists v^X \big(\lVert x \rVert _X,\lVert y \rVert _X,\lVert z \rVert _X,\lVert u \rVert _X\lt _{\mathbb{R}}b\land z\in Ty\land u\in Tx\\ &\quad \land \lVert x-_Xy \rVert _X\lt _{\mathbb{R}}2^{-\omega (k,b)}\rightarrow \big(v\in Ty\land \lVert u-_Xv \rVert _X\leq _{\mathbb{R}}2^{-k}\big)\big) \end{align*}
\begin{align*} &\forall k^0,b^0,x^X,y^X,z^X,u^X\exists v^X \big(\lVert x \rVert _X,\lVert y \rVert _X,\lVert z \rVert _X,\lVert u \rVert _X\lt _{\mathbb{R}}b\land z\in Ty\land u\in Tx\\ &\quad \land \lVert x-_Xy \rVert _X\lt _{\mathbb{R}}2^{-\omega (k,b)}\rightarrow \big(v\in Ty\land \lVert u-_Xv \rVert _X\leq _{\mathbb{R}}2^{-k}\big)\big) \end{align*}
where
![]() $\omega$
is a suitable constant of type
$\omega$
is a suitable constant of type
![]() $0(0)(0)$
. As any such
$0(0)(0)$
. As any such
![]() $v$
naturally satisfies
$v$
naturally satisfies
![]() $\lVert v \rVert \leq \lVert u \rVert +\lVert u-v \rVert \leq \lVert u \rVert +1$
, the above statement can be further specified as
$\lVert v \rVert \leq \lVert u \rVert +\lVert u-v \rVert \leq \lVert u \rVert +1$
, the above statement can be further specified as
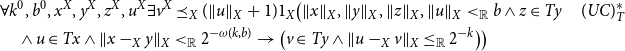 \begin{align*} &\forall k^0,b^0,x^X,y^X,z^X,u^X\exists v^X\preceq _X (\lVert u \rVert _X+1)1_X\big(\lVert x \rVert _X,\lVert y \rVert _X,\lVert z \rVert _X,\lVert u \rVert _X\lt _{\mathbb{R}}b\land z\in Ty &&(UC)^*_T\\ &\quad\land u\in Tx\land \lVert x-_Xy \rVert _X\lt _{\mathbb{R}}2^{-\omega (k,b)}\rightarrow \big(v\in Ty\land \lVert u-_Xv \rVert _X\leq _{\mathbb{R}}2^{-k}\big)\big) &&\end{align*}
\begin{align*} &\forall k^0,b^0,x^X,y^X,z^X,u^X\exists v^X\preceq _X (\lVert u \rVert _X+1)1_X\big(\lVert x \rVert _X,\lVert y \rVert _X,\lVert z \rVert _X,\lVert u \rVert _X\lt _{\mathbb{R}}b\land z\in Ty &&(UC)^*_T\\ &\quad\land u\in Tx\land \lVert x-_Xy \rVert _X\lt _{\mathbb{R}}2^{-\omega (k,b)}\rightarrow \big(v\in Ty\land \lVert u-_Xv \rVert _X\leq _{\mathbb{R}}2^{-k}\big)\big) &&\end{align*}
where
![]() $x^X\preceq _Xy^X$
means
$x^X\preceq _Xy^X$
means
![]() $\lVert x \rVert _X\leq _{\mathbb{R}}\lVert y \rVert _X$
. As the existential quantifier over
$\lVert x \rVert _X\leq _{\mathbb{R}}\lVert y \rVert _X$
. As the existential quantifier over
![]() $v$
is now bounded in terms of the preceding universal quantifiers and the inner matrix is universal, the principle
$v$
is now bounded in terms of the preceding universal quantifiers and the inner matrix is universal, the principle
![]() $(UC)^*_T$
can be recognized as a statement of type
$(UC)^*_T$
can be recognized as a statement of type
![]() $\Delta$
as defined in Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016) for languages involving abstract types (originally stemming from the earliest works on proof mining such as Kohlenbach (Reference Kohlenbach1992), see also Kohlenbach (Reference Kohlenbach2008)), a class of formulas with a particularly trivial monotone functional interpretation, which hence are admissible in the context of systems tailored for the extraction of bounds using the monotone functional interpretation.
$\Delta$
as defined in Günzel and Kohlenbach (Reference Günzel and Kohlenbach2016) for languages involving abstract types (originally stemming from the earliest works on proof mining such as Kohlenbach (Reference Kohlenbach1992), see also Kohlenbach (Reference Kohlenbach2008)), a class of formulas with a particularly trivial monotone functional interpretation, which hence are admissible in the context of systems tailored for the extraction of bounds using the monotone functional interpretation.
Now, the above extensionality principle
![]() $(E)^*_T$
seems to suggest a further extensionality principle as follows: If
$(E)^*_T$
seems to suggest a further extensionality principle as follows: If
![]() $H^*$
would be “continuous” in its last argument, we could move from
$H^*$
would be “continuous” in its last argument, we could move from
![]() $\forall k^0\left ( H^*[Tx,Ty,2^{-k}]\right )$
to
$\forall k^0\left ( H^*[Tx,Ty,2^{-k}]\right )$
to
![]() $H^*[Tx,Ty,0]$
, whereby the above statement then would in particular imply the following even more concise extensionality principle
$H^*[Tx,Ty,0]$
, whereby the above statement then would in particular imply the following even more concise extensionality principle
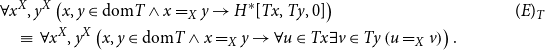 \begin{align*} &\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow H^*[Tx,Ty,0]\right ) &&(E)_T\\ &\quad\equiv \;\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow \forall u\in Tx\exists v\in Ty\left ( u=_Xv\right )\right ). &&\end{align*}
\begin{align*} &\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow H^*[Tx,Ty,0]\right ) &&(E)_T\\ &\quad\equiv \;\forall x^X,y^X\left (x,y\in \textrm{dom}T\land x=_Xy\rightarrow \forall u\in Tx\exists v\in Ty\left ( u=_Xv\right )\right ). &&\end{align*}
Here, compared to
![]() $(E)^*_T$
, the closedness of the image sets of
$(E)^*_T$
, the closedness of the image sets of
![]() $T$
is already “infused”, in a way, as it does not only allow us to conclude the existence of a sequence in
$T$
is already “infused”, in a way, as it does not only allow us to conclude the existence of a sequence in
![]() $Ty$
approximating
$Ty$
approximating
![]() $u$
but actually allows us to conclude the existence of an extensionally equal witness
$u$
but actually allows us to conclude the existence of an extensionally equal witness
![]() $v$
. Further, the above principle can be thought of as an “extensionalized version” of the principle
$v$
. Further, the above principle can be thought of as an “extensionalized version” of the principle
![]() $(E)^\chi _T$
in the sense that it posits the extensional equality of the set
$(E)^\chi _T$
in the sense that it posits the extensional equality of the set
![]() $Tx$
not as formalized by
$Tx$
not as formalized by
![]() $u\in Tx\equiv \chi (x,u)=_00$
but by the “extensionalized variant”
$u\in Tx\equiv \chi (x,u)=_00$
but by the “extensionalized variant”
![]() $u\in _E Tx\equiv \exists u'\in Tx\left (u=_Xu'\right )$
. Now, while there is certainly a subtle difference between
$u\in _E Tx\equiv \exists u'\in Tx\left (u=_Xu'\right )$
. Now, while there is certainly a subtle difference between
![]() $(E)_T$
and
$(E)_T$
and
![]() $(E)_T^*$
, the following result makes their close relationship based on the topology of the set
$(E)_T^*$
, the following result makes their close relationship based on the topology of the set
![]() $Tx$
formally precise:
$Tx$
formally precise:
Proposition 1. Over
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
, the principle
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
, the principle
![]() $(E)_T$
implies
$(E)_T$
implies
![]() $(E)_T^*$
.
$(E)_T^*$
.
Further, define the closure principle
where
![]() $y_n\to _X z$
is some formal representation of convergence in
$y_n\to _X z$
is some formal representation of convergence in
![]() $X$
, say
$X$
, say
expressing that
![]() $Tx$
is closed for any
$Tx$
is closed for any
![]() $x\in \textrm{dom}T$
. Then over
$x\in \textrm{dom}T$
. Then over
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+(\textrm{pClsd})_T$
, the principle
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+(\textrm{pClsd})_T$
, the principle
![]() $(E)^*_T$
implies
$(E)^*_T$
implies
![]() $(E)_T$
.
$(E)_T$
.
Proof. That
![]() $(E)_T$
implies
$(E)_T$
implies
![]() $(E)_T^*$
is obvious. To see that
$(E)_T^*$
is obvious. To see that
![]() $(E)^*_T$
implies
$(E)^*_T$
implies
![]() $(E)_T$
under the assumption of the closure of each
$(E)_T$
under the assumption of the closure of each
![]() $Tx$
with
$Tx$
with
![]() $x\in \textrm{dom}T$
, let
$x\in \textrm{dom}T$
, let
![]() $u\in Tx$
and
$u\in Tx$
and
![]() $y\in \textrm{dom}T$
with
$y\in \textrm{dom}T$
with
![]() $y=x$
be given. By
$y=x$
be given. By
![]() $(E)^*_T$
, for any
$(E)^*_T$
, for any
![]() $k$
of type
$k$
of type
![]() $0$
there exists a
$0$
there exists a
![]() $v_k\in Ty$
with
$v_k\in Ty$
with
![]() $\lVert u-v_k \rVert \leq 2^{-k}$
. Thus we have
$\lVert u-v_k \rVert \leq 2^{-k}$
. Thus we have
![]() $v_k\to _X u$
and by
$v_k\to _X u$
and by
![]() $(\textrm{pClsd})_T$
, there exists a
$(\textrm{pClsd})_T$
, there exists a
![]() $w\in Ty$
with
$w\in Ty$
with
![]() $w=u$
. Thus we have shown
$w=u$
. Thus we have shown
![]() $(E)_T$
.
$(E)_T$
.
So, in essence, both
![]() $(E)_T$
and
$(E)_T$
and
![]() $(E)_T^*$
represent the same extensionality principle which posits the equality of
$(E)_T^*$
represent the same extensionality principle which posits the equality of
![]() $Tx$
and
$Tx$
and
![]() $Ty$
, seen as extensional sets, for
$Ty$
, seen as extensional sets, for
![]() $x=y$
in the domain of
$x=y$
in the domain of
![]() $T$
, with the difference that
$T$
, with the difference that
![]() $(E)_T^*$
only requires a weaker approximating sequence to witness this equality which suffices in the context of closed operators.
$(E)_T^*$
only requires a weaker approximating sequence to witness this equality which suffices in the context of closed operators.
Remark 2. For the central classes of monotone and accretive operators with total resolvents, these fragments of the full extensionality principle are equivalent to suitable “extensionalized” variants of the closure of the graph of the operator as well as the resolvent identity and the maximality. Further, for these classes, removing the restriction to
![]() $\textrm{dom}T$
and the dependence on the norm-bounds from
$\textrm{dom}T$
and the dependence on the norm-bounds from
![]() $\omega$
already from the principle
$\omega$
already from the principle
![]() $(UC)^*_T$
results in a very strong uniform continuity statement which, by utilizing results of Chidume and Morales (Reference Chidume and Morales2007), implies that the operator
$(UC)^*_T$
results in a very strong uniform continuity statement which, by utilizing results of Chidume and Morales (Reference Chidume and Morales2007), implies that the operator
![]() $T$
is actually single-valued. We refer to Pischke (Reference Pischke2024e) for a further discussion of both of these aspects.
$T$
is actually single-valued. We refer to Pischke (Reference Pischke2024e) for a further discussion of both of these aspects.
Naturally, also
![]() $(E)_T$
entails its own uniform continuity principle via the perspective of the monotone functional interpretation which takes the form
$(E)_T$
entails its own uniform continuity principle via the perspective of the monotone functional interpretation which takes the form
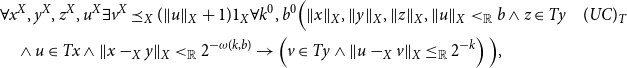 \begin{align*} &\forall x^X,y^X,z^X,u^X\exists v^X\preceq _X (\lVert u \rVert _X+1)1_X\forall k^0,b^0\Big (\lVert x \rVert _X,\lVert y \rVert _X,\lVert z \rVert _X,\lVert u \rVert _X\lt _{\mathbb{R}}b\land z\in Ty &&(UC)_T\\ &\quad\land u\in Tx\land \lVert x-_Xy \rVert _X\lt _{\mathbb{R}}2^{-\omega (k,b)}\rightarrow \left (v\in Ty\land \lVert u-_Xv \rVert _X\leq _{\mathbb{R}}2^{-k}\right )\Big ), && \end{align*}
\begin{align*} &\forall x^X,y^X,z^X,u^X\exists v^X\preceq _X (\lVert u \rVert _X+1)1_X\forall k^0,b^0\Big (\lVert x \rVert _X,\lVert y \rVert _X,\lVert z \rVert _X,\lVert u \rVert _X\lt _{\mathbb{R}}b\land z\in Ty &&(UC)_T\\ &\quad\land u\in Tx\land \lVert x-_Xy \rVert _X\lt _{\mathbb{R}}2^{-\omega (k,b)}\rightarrow \left (v\in Ty\land \lVert u-_Xv \rVert _X\leq _{\mathbb{R}}2^{-k}\right )\Big ), && \end{align*}
where we already have highlighted the natural boundedness of the quantifier over
![]() $v$
which illustrates that
$v$
which illustrates that
![]() $(UC)_T$
, similar to
$(UC)_T$
, similar to
![]() $(UC)^*_T$
before, is a statement of type
$(UC)^*_T$
before, is a statement of type
![]() $\Delta$
and so is similarly admissible in the context of systems tailored for the extraction of bounds using the monotone functional interpretation.
$\Delta$
and so is similarly admissible in the context of systems tailored for the extraction of bounds using the monotone functional interpretation.
In particular, compared to
![]() $(E)_T^\chi$
and
$(E)_T^\chi$
and
![]() $(E)_T^{\chi _d}$
, the fragments
$(E)_T^{\chi _d}$
, the fragments
![]() $(E)_T$
and
$(E)_T$
and
![]() $(E)_T^*$
are now very applicable as their uniform quantitative versions as guided by the monotone functional interpretation, that is the above uniform continuity principles
$(E)_T^*$
are now very applicable as their uniform quantitative versions as guided by the monotone functional interpretation, that is the above uniform continuity principles
![]() $(UC)_T$
and
$(UC)_T$
and
![]() $(UC)^*_T$
, are highly nontrivially populated. This also allows us to see formally that
$(UC)^*_T$
, are highly nontrivially populated. This also allows us to see formally that
![]() $(E)_T$
and hence
$(E)_T$
and hence
![]() $(E)_T^*$
are properly weaker than
$(E)_T^*$
are properly weaker than
![]() $(E)_T^{\chi _d}$
. For that, we first consider the following result which shows that any suitable operator
$(E)_T^{\chi _d}$
. For that, we first consider the following result which shows that any suitable operator
![]() $T:X\to 2^X$
that is uniformly continuous in the sense of
$T:X\to 2^X$
that is uniformly continuous in the sense of
![]() $(UC)^*_T$
is closed in
$(UC)^*_T$
is closed in
![]() $X\times X$
:
$X\times X$
:
Proposition 3. Any operator
![]() $T:X\to 2^X$
such that any set
$T:X\to 2^X$
such that any set
![]() $Tx$
is closed and which is uniformly continuous in the sense of
$Tx$
is closed and which is uniformly continuous in the sense of
![]() $(UC)^*_T$
is closed in
$(UC)^*_T$
is closed in
![]() $X\times X$
.
$X\times X$
.
Proof. As
![]() $T$
is uniformly continuous in the sense of
$T$
is uniformly continuous in the sense of
![]() $(UC)^*_T$
, there exists a
$(UC)^*_T$
, there exists a
![]() $\omega$
with
$\omega$
with
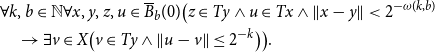 \begin{align*} &\forall k,b\in \mathbb{N}\forall x,y,z,u\in \overline {B}_b(0)\big (z\in Ty\land u\in Tx \land \lVert x-y \rVert \lt 2^{-\omega (k,b)}\\ &\quad \rightarrow \exists v\in X\big(v\in Ty\land \lVert u-v \rVert \leq 2^{-k}\big)\big ). \end{align*}
\begin{align*} &\forall k,b\in \mathbb{N}\forall x,y,z,u\in \overline {B}_b(0)\big (z\in Ty\land u\in Tx \land \lVert x-y \rVert \lt 2^{-\omega (k,b)}\\ &\quad \rightarrow \exists v\in X\big(v\in Ty\land \lVert u-v \rVert \leq 2^{-k}\big)\big ). \end{align*}
Let
![]() $(x_n,y_n)\subseteq T$
be a sequence in
$(x_n,y_n)\subseteq T$
be a sequence in
![]() $T$
such that
$T$
such that
![]() $(x_n,y_n)\to (x,y)$
for
$(x_n,y_n)\to (x,y)$
for
![]() $n\to \infty$
. As
$n\to \infty$
. As
![]() $(x_n,y_n)$
converges, the sequence is bounded and thus, using the existence of
$(x_n,y_n)$
converges, the sequence is bounded and thus, using the existence of
![]() $\omega$
, we get that for any
$\omega$
, we get that for any
![]() $n\in \mathbb{N}$
, there exists a
$n\in \mathbb{N}$
, there exists a
![]() $v_n\in Tx$
such that the sequence
$v_n\in Tx$
such that the sequence
![]() $v_n$
converges to
$v_n$
converges to
![]() $y$
. As
$y$
. As
![]() $Tx$
is closed, we have
$Tx$
is closed, we have
![]() $y\in Tx$
. Thus,
$y\in Tx$
. Thus,
![]() $T$
is closed.
$T$
is closed.
Hence, the results from Section 2 apply in this context and yield that
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+(UC)_T\not \vdash (E)^{\chi _d}_T$
as there are operators which are uniformly continuous in the sense of
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]+(UC)_T\not \vdash (E)^{\chi _d}_T$
as there are operators which are uniformly continuous in the sense of
![]() $(UC)_T$
that are not of the form
$(UC)_T$
that are not of the form
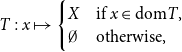 \begin{equation*} T:x\mapsto \begin{cases}X&\text{if }x\in \textrm{dom}T,\\\emptyset &\text{otherwise},\end{cases} \end{equation*}
\begin{equation*} T:x\mapsto \begin{cases}X&\text{if }x\in \textrm{dom}T,\\\emptyset &\text{otherwise},\end{cases} \end{equation*}
the most trivial example being the operator defined by
![]() $T(x):=\{x\}$
on a space that is nontrivial. So,
$T(x):=\{x\}$
on a space that is nontrivial. So,
![]() $(E)_T$
is properly weaker than
$(E)_T$
is properly weaker than
![]() $(E)^{\chi _d}_T$
.
$(E)^{\chi _d}_T$
.
Now, as mentioned before, the predicate
![]() $H^*$
and the associated uniform continuity principle for set-valued operators was introduced in Kohlenbach and Powell (Reference Kohlenbach and Powell2020) to avoid formal considerations on the Hausdorff metric. This was in particular possible as the precise value of the Hausdorff metric was not a required quantity in the proof but was only used, by means of a uniform continuity assumption, to derive certain approximation properties of the involved sets. While this was possible in Kohlenbach and Powell (Reference Kohlenbach and Powell2020), there certainly are other proofs from the literature where the value of the Hausdorff metric seems to feature much more essential in the proof and where hence a quantitative treatment thereof would be desirable to allow a more direct access to those proofs as they are found in the literature. In the next section, we provide such an access here by leveraging the strengths of the intensional approach and showing that in such a context, one can indeed treat the Hausdorff metric and its associated uniform continuity principle for a set-valued operator in a proof-theoretically tame way amenable to proof mining metatheorems.
$H^*$
and the associated uniform continuity principle for set-valued operators was introduced in Kohlenbach and Powell (Reference Kohlenbach and Powell2020) to avoid formal considerations on the Hausdorff metric. This was in particular possible as the precise value of the Hausdorff metric was not a required quantity in the proof but was only used, by means of a uniform continuity assumption, to derive certain approximation properties of the involved sets. While this was possible in Kohlenbach and Powell (Reference Kohlenbach and Powell2020), there certainly are other proofs from the literature where the value of the Hausdorff metric seems to feature much more essential in the proof and where hence a quantitative treatment thereof would be desirable to allow a more direct access to those proofs as they are found in the literature. In the next section, we provide such an access here by leveraging the strengths of the intensional approach and showing that in such a context, one can indeed treat the Hausdorff metric and its associated uniform continuity principle for a set-valued operator in a proof-theoretically tame way amenable to proof mining metatheorems.
In that section, we in particular further show that the associated extensionality principle is equivalent to
![]() $(E)^*_T$
whenever
$(E)^*_T$
whenever
![]() $H(Tx,Ty)$
is well-defined, showing that
$H(Tx,Ty)$
is well-defined, showing that
![]() $(E)_T^*$
and hence
$(E)_T^*$
and hence
![]() $(E)_T$
are very robust as extensionality principles in the sense that small perturbations yields equivalent principles. Based on this robustness and the applicability of the principles
$(E)_T$
are very robust as extensionality principles in the sense that small perturbations yields equivalent principles. Based on this robustness and the applicability of the principles
![]() $(E)_T$
and
$(E)_T$
and
![]() $(E)^*_T$
and their associated uniform continuity principles
$(E)^*_T$
and their associated uniform continuity principles
![]() $(UC)_T$
and
$(UC)_T$
and
![]() $(UC)^*_T$
as evidenced from the previous proof mining literature together with the logical motivations of this section, we thereby want to argue in this paper that
$(UC)^*_T$
as evidenced from the previous proof mining literature together with the logical motivations of this section, we thereby want to argue in this paper that
![]() $(E)_T$
and with that this cluster of related extensionality principles are the faithful and correct representation of the notion of extensionality of a set-valued operator in the context of this intensional approach.
$(E)_T$
and with that this cluster of related extensionality principles are the faithful and correct representation of the notion of extensionality of a set-valued operator in the context of this intensional approach.
3.2 An extensionality principle based on the Hausdorff metric
We now show how the Hausdorff metric and its associated extensionality and uniform continuity principles can be formally approached in the context of systems providing and intensional treatment of set-valued operators like
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
(or related systems). For that, we begin with showing that for certain sets
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
(or related systems). For that, we begin with showing that for certain sets
![]() $P,Q$
, the Hausdorff distance
$P,Q$
, the Hausdorff distance
![]() $H(P,Q)$
can indeed be treated in a proof-theoretically tame way in the context of the systems considered in the context of proof mining over normed linear spaces.Footnote
7
For this, we work over the basic system
$H(P,Q)$
can indeed be treated in a proof-theoretically tame way in the context of the systems considered in the context of proof mining over normed linear spaces.Footnote
7
For this, we work over the basic system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
for now. Now, to approach the Hausdorff metric, let concretely
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ]$
for now. Now, to approach the Hausdorff metric, let concretely
![]() $P$
now be a set in a normed space
$P$
now be a set in a normed space
![]() $X$
which is bounded, that is
$X$
which is bounded, that is
![]() $\lVert p \rVert \leq c$
for all
$\lVert p \rVert \leq c$
for all
![]() $p\in P$
with
$p\in P$
with
![]() $c\in \mathbb{N}$
. Then, we can treat the real-valued distance function
$c\in \mathbb{N}$
. Then, we can treat the real-valued distance function
by adding an additional constant
![]() $d(\cdot ,P)$
of type
$d(\cdot ,P)$
of type
![]() $1(X)$
with the following two axiom schemes:
$1(X)$
with the following two axiom schemes:
as well as (writing
![]() $c$
for the real number arising from
$c$
for the real number arising from
![]() $c$
seen as a numeral)
$c$
seen as a numeral)
where
![]() $P(p)$
is a predicate describing
$P(p)$
is a predicate describing
![]() $p\in P$
. These two axioms schemes completely characterize the facts that, for one,
$p\in P$
. These two axioms schemes completely characterize the facts that, for one,
![]() $d(x,P)$
is supposed to be a lower bound on the norm distance
$d(x,P)$
is supposed to be a lower bound on the norm distance
![]() $\lVert x-p \rVert$
from
$\lVert x-p \rVert$
from
![]() $x$
to any element
$x$
to any element
![]() $p\in P$
as governed by
$p\in P$
as governed by
![]() $P(p)$
, and for another, that
$P(p)$
, and for another, that
![]() $d(x,P)$
is arbitrarily well approximated by any such norm distance. In other words, the two schemes exactly specify that
$d(x,P)$
is arbitrarily well approximated by any such norm distance. In other words, the two schemes exactly specify that
![]() $d(x,P)$
is the greatest lower bound of all norm distances
$d(x,P)$
is the greatest lower bound of all norm distances
![]() $\lVert x-p \rVert$
for all
$\lVert x-p \rVert$
for all
![]() $p\in P$
.Footnote
8
$p\in P$
.Footnote
8
These schemes become admissible if they are instantiated with a
![]() $P$
such that the two axioms have a monotone functional interpretation. This can in particular be guaranteed if the formula
$P$
such that the two axioms have a monotone functional interpretation. This can in particular be guaranteed if the formula
![]() $P$
, besides potential parameters, is quantifier-free (as is e.g. naturally the case in the context of an intensional description of a set akin to the way we previously treated set-valued operators). Concretely, in this quantifier-free case (which will actually be the only concrete case occurring in the applications given in this paper), the axiom
$P$
, besides potential parameters, is quantifier-free (as is e.g. naturally the case in the context of an intensional description of a set akin to the way we previously treated set-valued operators). Concretely, in this quantifier-free case (which will actually be the only concrete case occurring in the applications given in this paper), the axiom
![]() $(d_P)_2$
is of type
$(d_P)_2$
is of type
![]() $\Delta$
, since the existential quantifier in
$\Delta$
, since the existential quantifier in
![]() $(d_P)_2$
is bounded (which crucially uses the boundedness of the set specified by
$(d_P)_2$
is bounded (which crucially uses the boundedness of the set specified by
![]() $P$
), and hence admissible in systems with bound extraction theorems in the style of proof mining.
$P$
), and hence admissible in systems with bound extraction theorems in the style of proof mining.
Similarly, we can add a constant
![]() $d(\cdot ,Q)$
of the same type for a second bounded set
$d(\cdot ,Q)$
of the same type for a second bounded set
![]() $Q$
(w.l.o.g. also bounded by
$Q$
(w.l.o.g. also bounded by
![]() $c$
) together with the following axioms determined as above over a (in all practical circumstances of this paper quantifier-free) predicate
$c$
) together with the following axioms determined as above over a (in all practical circumstances of this paper quantifier-free) predicate
![]() $Q(q)$
describing
$Q(q)$
describing
![]() $q\in Q$
:
$q\in Q$
:
 \begin{align*} &\forall x^X,q^X\left ( Q(q)\to d(x,Q)\leq _{\mathbb{R}} \lVert x-_Xq \rVert _X\right ),&&(d_Q)_1\\ &\forall x^X,k^0\exists q\leq _X c1_X\big( Q(q)\land \lVert x-_Xq \rVert _X\leq _{\mathbb{R}} d(x,Q)+2^{-k}\big). &&(d_Q)_2 \end{align*}
\begin{align*} &\forall x^X,q^X\left ( Q(q)\to d(x,Q)\leq _{\mathbb{R}} \lVert x-_Xq \rVert _X\right ),&&(d_Q)_1\\ &\forall x^X,k^0\exists q\leq _X c1_X\big( Q(q)\land \lVert x-_Xq \rVert _X\leq _{\mathbb{R}} d(x,Q)+2^{-k}\big). &&(d_Q)_2 \end{align*}
In the context of both
![]() $d(x,P)$
and
$d(x,P)$
and
![]() $d(x,Q)$
, we can then introduce the quantities
$d(x,Q)$
, we can then introduce the quantities
into the system by following a dual idea as the above approach towards the treatment of the infima
![]() $d(x,P)$
and
$d(x,P)$
and
![]() $d(x,Q)$
and hence adding corresponding constants (for simplicity also denoted by)
$d(x,Q)$
and hence adding corresponding constants (for simplicity also denoted by)
![]() $d(P,Q)$
and
$d(P,Q)$
and
![]() $d(Q,P)$
of type
$d(Q,P)$
of type
![]() $1$
into the language together with another set of similar axiom schemes, concretely taking
$1$
into the language together with another set of similar axiom schemes, concretely taking
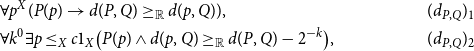 \begin{align*}& \forall p^X(P(p)\to d(P,Q)\geq _{\mathbb{R}} d(p,Q)), && (d_{P,Q})_1\\ &\forall k^0\exists p\leq _X c1_X\big( P(p)\land d(p,Q)\geq _{\mathbb{R}} d(P,Q)-2^{-k}\big), && (d_{P,Q})_2 \end{align*}
\begin{align*}& \forall p^X(P(p)\to d(P,Q)\geq _{\mathbb{R}} d(p,Q)), && (d_{P,Q})_1\\ &\forall k^0\exists p\leq _X c1_X\big( P(p)\land d(p,Q)\geq _{\mathbb{R}} d(P,Q)-2^{-k}\big), && (d_{P,Q})_2 \end{align*}
for the quantity
![]() $d(P,Q)$
as well as
$d(P,Q)$
as well as
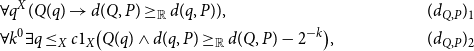 \begin{align*} &\forall q^X(Q(q)\to d(Q,P)\geq _{\mathbb{R}} d(q,P)), && (d_{Q,P})_1\\ &\forall k^0\exists q\leq _X c1_X\big( Q(q)\land d(q,P)\geq _{\mathbb{R}} d(Q,P)-2^{-k}\big), && (d_{Q,P})_2 \end{align*}
\begin{align*} &\forall q^X(Q(q)\to d(Q,P)\geq _{\mathbb{R}} d(q,P)), && (d_{Q,P})_1\\ &\forall k^0\exists q\leq _X c1_X\big( Q(q)\land d(q,P)\geq _{\mathbb{R}} d(Q,P)-2^{-k}\big), && (d_{Q,P})_2 \end{align*}
for the quantity
![]() $d(Q,P)$
.
$d(Q,P)$
.
Again, also these axiom schemes are of the form
![]() $\Delta$
if the predicates
$\Delta$
if the predicates
![]() $P$
and
$P$
and
![]() $Q$
are both quantifier-free (again making use of the fact that the existential quantifiers can be bounded as the specified sets are assumed to be bounded), and so these schemes are admissible in systems with bound extraction theorems in the style of proof mining.
$Q$
are both quantifier-free (again making use of the fact that the existential quantifiers can be bounded as the specified sets are assumed to be bounded), and so these schemes are admissible in systems with bound extraction theorems in the style of proof mining.
Lastly, we move to the concrete Hausdorff metric which can now just be introduced by a closed term involving
![]() $d(P,Q)$
and
$d(P,Q)$
and
![]() $d(Q,P)$
:
$d(Q,P)$
:
Of course, this distance can also be introduced uniformly for a family of sets described by formulas
![]() $P(p,\underline {x}),Q(q,\underline {x})$
with parameters
$P(p,\underline {x}),Q(q,\underline {x})$
with parameters
![]() $\underline {x}$
of type
$\underline {x}$
of type
![]() $\underline {\sigma }$
if the sets described by
$\underline {\sigma }$
if the sets described by
![]() $P(p,\underline {x}),Q(q,\underline {x})$
are bounded by a function
$P(p,\underline {x}),Q(q,\underline {x})$
are bounded by a function
![]() $c(\underline {x})$
pointwise in the parameters.
$c(\underline {x})$
pointwise in the parameters.
Note that the nonemptiness of the sets
![]() $P,Q$
is not needed to define these formulas but the nonemptyness is required on a semantic level in order for these formulas to actually have a model as the objects, mapping to type
$P,Q$
is not needed to define these formulas but the nonemptyness is required on a semantic level in order for these formulas to actually have a model as the objects, mapping to type
![]() $1$
, have to be interpreted by a real number (or by a function mapping into real numbers, respectively).
$1$
, have to be interpreted by a real number (or by a function mapping into real numbers, respectively).
As mentioned before, this abstract treatment is fruitful at least in the context of sets describable by quantifier-free formulas, where these constants and axioms then allow for extending a previous metatheorem of an underlying system via suitable interpretations of the constants in the modelFootnote
9
since the axioms are admissible as discussed before. Crucial for this however is the majorizability of the constants. This however can be easily achieved: For
![]() $d(\cdot ,P)$
, via the axiom
$d(\cdot ,P)$
, via the axiom
![]() $(d_P)_1$
, we have
$(d_P)_1$
, we have
where
![]() $p$
is some point witnessing that
$p$
is some point witnessing that
![]() $P$
is nonempty (and thus the nonemptyness is also important for majorization). Further, we have
$P$
is nonempty (and thus the nonemptyness is also important for majorization). Further, we have
for a suitable
![]() $q$
chosen with axiom
$q$
chosen with axiom
![]() $(d_{Q,P})_2$
. From this, majorants for
$(d_{Q,P})_2$
. From this, majorants for
![]() $d(\cdot ,P)$
and
$d(\cdot ,P)$
and
![]() $d(Q,P)$
are immediate.
$d(Q,P)$
are immediate.
By a similar reasoning,
![]() $d(\cdot ,Q)$
as well as
$d(\cdot ,Q)$
as well as
![]() $d(P,Q)$
are majorizable and this extends to any variant using additional parameters if the sets are nonempty and bounded pointwise for all parameters. Naturally, also the resulting bounding function
$d(P,Q)$
are majorizable and this extends to any variant using additional parameters if the sets are nonempty and bounded pointwise for all parameters. Naturally, also the resulting bounding function
![]() $c(\underline {x})$
then has to be majorizable as a function of type
$c(\underline {x})$
then has to be majorizable as a function of type
![]() $0(\underline {\sigma }^t)$
.
$0(\underline {\sigma }^t)$
.
We are now in particular interested in using this way of formulating the Hausdorff distance to talk about uniform continuity formulations and extensionality principles for set-valued operators
![]() $T$
treated as in the previous basic system
$T$
treated as in the previous basic system
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
. Then, the sets
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
. Then, the sets
![]() $P$
and
$P$
and
![]() $Q$
can be taken to be of the form
$Q$
can be taken to be of the form
![]() $Tx$
with a parameter
$Tx$
with a parameter
![]() $x$
of type
$x$
of type
![]() $X$
for a given set-valued operator
$X$
for a given set-valued operator
![]() $T$
which is represented in the system by an intensional description over its graph via
$T$
which is represented in the system by an intensional description over its graph via
![]() $\chi _T$
as discussed before. Formally, this is naturally represented by taking
$\chi _T$
as discussed before. Formally, this is naturally represented by taking
![]() $P(p,x):=\chi _T(x,p)=_00$
. As this resulting formulation of the set
$P(p,x):=\chi _T(x,p)=_00$
. As this resulting formulation of the set
![]() $Tx$
is quantifier-free, the above axioms in particular become admissible for bound extraction results if, as discussed before, the operator
$Tx$
is quantifier-free, the above axioms in particular become admissible for bound extraction results if, as discussed before, the operator
![]() $T$
is actually such that all
$T$
is actually such that all
![]() $Tx$
are bounded with a bounding function
$Tx$
are bounded with a bounding function
![]() $c$
of type
$c$
of type
![]() $0(X)$
that is majorizable. In the language of Pischke (Reference Pischke2024c), the existence of such a
$0(X)$
that is majorizable. In the language of Pischke (Reference Pischke2024c), the existence of such a
![]() $c$
is equivalent to the operator
$c$
is equivalent to the operator
![]() $T$
being uniformly majorizable, that is to being bounded on bounded sets. Thus, to treat such operators in the Hausdorff metric, we consider an additional constant
$T$
being uniformly majorizable, that is to being bounded on bounded sets. Thus, to treat such operators in the Hausdorff metric, we consider an additional constant
![]() $T^*$
of type
$T^*$
of type
![]() $1$
together with the axiom
$1$
together with the axiom
which serves as a majorant (and hence witness) to
![]() $c$
. Then, we can as above introduce constants
$c$
. Then, we can as above introduce constants
![]() $d(\cdot ,Tx)$
and
$d(\cdot ,Tx)$
and
![]() $d(Tx,Ty)$
for
$d(Tx,Ty)$
for
![]() $x,y\in \textrm{dom}T$
into the language using
$x,y\in \textrm{dom}T$
into the language using
![]() $\chi _T$
and
$\chi _T$
and
![]() $T^*$
to form
$T^*$
to form
![]() $H$
such that the expression
$H$
such that the expression
![]() $H(Tx,Ty)$
is represented by a term for any
$H(Tx,Ty)$
is represented by a term for any
![]() $x$
and
$x$
and
![]() $y$
.
$y$
.
With this, an extensionality statement corresponding to the Hausdorff metric now indeed can be written as a formal sentence in this extended language via
In that context, this extensionality principle
![]() $(E)_T^H$
is provably equivalent to the previous principle
$(E)_T^H$
is provably equivalent to the previous principle
![]() $(E)_T^*$
as the following result shows. For that, let
$(E)_T^*$
as the following result shows. For that, let
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T,H]$
refer to the system which results from
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T,H]$
refer to the system which results from
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
by adding the respective constants and axioms for the Hausdorff metric required to introduce
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T]$
by adding the respective constants and axioms for the Hausdorff metric required to introduce
![]() $H(Tx,Ty)$
as detailed above.
$H(Tx,Ty)$
as detailed above.
Proposition 4. Over
![]() $\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T,H]$
, the principles
$\mathscr{A}^\omega [X,\lVert \cdot \rVert ,T,H]$
, the principles
![]() $(E)_T^H$
and
$(E)_T^H$
and
![]() $(E)_T^*$
are equivalent.
$(E)_T^*$
are equivalent.
Proof. To show that
![]() $(E)_T^*$
implies
$(E)_T^*$
implies
![]() $(E)_T^H$
, let
$(E)_T^H$
, let
![]() $x=y$
for
$x=y$
for
![]() $x,y\in \textrm{dom}T$
. Fixing
$x,y\in \textrm{dom}T$
. Fixing
![]() $k$
of type
$k$
of type
![]() $0$
, let
$0$
, let
![]() $u\in Tx$
be such that
$u\in Tx$
be such that
![]() $d(u,Ty)+2^{-(k+1)}\geq d(Tx,Ty)$
, using the axioms for
$d(u,Ty)+2^{-(k+1)}\geq d(Tx,Ty)$
, using the axioms for
![]() $d(Tx,Ty)$
. Then use
$d(Tx,Ty)$
. Then use
![]() $(E)_T^*$
to pick
$(E)_T^*$
to pick
![]() $v\in Ty$
with
$v\in Ty$
with
![]() $\lVert u-v \rVert \leq 2^{-(k+1)}$
. We now have
$\lVert u-v \rVert \leq 2^{-(k+1)}$
. We now have
using the axioms for
![]() $d(u,Ty)$
. As
$d(u,Ty)$
. As
![]() $k$
was arbitrary, we have
$k$
was arbitrary, we have
![]() $d(Tx,Ty)=0$
, and similarly we can show
$d(Tx,Ty)=0$
, and similarly we can show
![]() $d(Ty,Tx)=0$
. This yields
$d(Ty,Tx)=0$
. This yields
![]() $H(Tx,Ty)=0$
, and we have shown
$H(Tx,Ty)=0$
, and we have shown
![]() $(E)_T^H$
.
$(E)_T^H$
.
To show that
![]() $(E)_T^H$
implies
$(E)_T^H$
implies
![]() $(E)_T^*$
, again let
$(E)_T^*$
, again let
![]() $x=y$
for
$x=y$
for
![]() $x,y\in \textrm{dom}T$
and fix
$x,y\in \textrm{dom}T$
and fix
![]() $k$
of type
$k$
of type
![]() $0$
as well as
$0$
as well as
![]() $u\in Tx$
. As
$u\in Tx$
. As
![]() $(E)_T^H$
implies
$(E)_T^H$
implies
![]() $H(Tx,Ty)=0$
, we have
$H(Tx,Ty)=0$
, we have
![]() $d(Tx,Ty)=0$
. Using the axioms for
$d(Tx,Ty)=0$
. Using the axioms for
![]() $d(Tx,Ty)$
, we have
$d(Tx,Ty)$
, we have
![]() $d(u,Ty)=0$
and so using the axioms for
$d(u,Ty)=0$
and so using the axioms for
![]() $d(u,Ty)$
, we have that there exists a
$d(u,Ty)$
, we have that there exists a
![]() $v\in Ty$
with
$v\in Ty$
with
Thus, we have shown
![]() $(E)_T^*$
.
$(E)_T^*$
.
Further, the monotone functional interpretation then associates to this a corresponding uniform continuity principle for set-valued operators. Further, this principle is actually the usual notion of uniform continuity for set-valued operators w.r.t. the Hausdorff metric (as commonly used in the analytic literature, see e.g. Moore and Nnoli (Reference Moore and Nnoli2001)). Concretely, the monotone functional interpretation posits the existence of a modulus
![]() $\omega$
of type
$\omega$
of type
![]() $0(0)(0)$
satisfyingFootnote
10
$0(0)(0)$
satisfyingFootnote
10
As this statement
![]() $(UC)^H_T$
is now universal based on our treatment of the Hausdorff metric, it can thus be freely added to a system with bound extraction theorems in the style of proof mining together with an accompanying constant
$(UC)^H_T$
is now universal based on our treatment of the Hausdorff metric, it can thus be freely added to a system with bound extraction theorems in the style of proof mining together with an accompanying constant
![]() $\omega$
and the preceding treatment of
$\omega$
and the preceding treatment of
![]() $H$
so that, for this extension, one retains the bound extraction results. Even further, a quantitative analysis of Proposition4 immediately yields that if
$H$
so that, for this extension, one retains the bound extraction results. Even further, a quantitative analysis of Proposition4 immediately yields that if
![]() $\omega (k,b)$
is a modulus of uniform continuity for
$\omega (k,b)$
is a modulus of uniform continuity for
![]() $T$
in the sense of
$T$
in the sense of
![]() $(UC)^H_T$
, we have that
$(UC)^H_T$
, we have that
![]() $\omega (k+1,b)$
is a corresponding modulus for the uniform continuity of
$\omega (k+1,b)$
is a corresponding modulus for the uniform continuity of
![]() $T$
in the sense of
$T$
in the sense of
![]() $(UC)^*_T$
, and similarly, we conversely have that if
$(UC)^*_T$
, and similarly, we conversely have that if
![]() $\omega (k,b)$
is a modulus of uniform continuity for
$\omega (k,b)$
is a modulus of uniform continuity for
![]() $T$
in the sense of
$T$
in the sense of
![]() $(UC)^*_T$
, then
$(UC)^*_T$
, then
![]() $\omega (k+1,b)$
is a corresponding modulus for the uniform continuity of
$\omega (k+1,b)$
is a corresponding modulus for the uniform continuity of
![]() $T$
in the sense of
$T$
in the sense of
![]() $(UC)^H_T$
(in this context where
$(UC)^H_T$
(in this context where
![]() $H(Tx,Ty)$
is well-defined).
$H(Tx,Ty)$
is well-defined).
In the next section, we will illustrate the applicability of this approach towards the Hausdorff metric by analyzing iterative methods related to set-valued mappings which are uniformly continuous w.r.t. the Hausdorff metric.
4. An Application: Quantitative Results on Mann Iterations for Nonexpansive Set-Valued Mappings in Banach Spaces
In this section, we illustrate the applicability of the treatment of the continuity principle based on the Hausdorff metric developed formally in a framework for proof mining for the first time in this paper by providing quantitative results on a Mann-type iteration of set-valued mappings which are nonexpansive w.r.t. the Hausdorff metric.
Concretely, let
![]() $X$
be a Banach space and denote by
$X$
be a Banach space and denote by
![]() $CB(X)$
the collection of nonempty, closed and bounded subsets of
$CB(X)$
the collection of nonempty, closed and bounded subsets of
![]() $X$
. We still write
$X$
. We still write
![]() $H(A,B)$
for the Hausdorff metric for
$H(A,B)$
for the Hausdorff metric for
![]() $A,B\in CB(X)$
which is well-defined and real-valued and we write
$A,B\in CB(X)$
which is well-defined and real-valued and we write
for a given set
![]() $A\in CB(X)$
as before. A set-valued map
$A\in CB(X)$
as before. A set-valued map
![]() $T:D\subseteq X\to CB(X)$
is called nonexpansive if
$T:D\subseteq X\to CB(X)$
is called nonexpansive if
for any
![]() $x,y\in D$
. We say that a point
$x,y\in D$
. We say that a point
![]() $x$
is a fixed point of
$x$
is a fixed point of
![]() $T$
if
$T$
if
![]() $x\in Tx$
, and we denote the set of fixed points of
$x\in Tx$
, and we denote the set of fixed points of
![]() $T$
by
$T$
by
![]() $F(T)$
.
$F(T)$
.
The following is a rather immediate consequence of the definition of the Hausdorff metric:
Lemma 5 (see for example Nadler (Reference Nadler1969)). Let
![]() $A,B\in CB(X)$
. For any
$A,B\in CB(X)$
. For any
![]() $a\in A$
and
$a\in A$
and
![]() $\varepsilon \gt 0$
, there exists some
$\varepsilon \gt 0$
, there exists some
![]() $b\in B$
with
$b\in B$
with
Based on this lemma, it is immediately clear that given a nonempty convex set
![]() $K$
and starting points
$K$
and starting points
![]() $x_0\in K$
,
$x_0\in K$
,
![]() $y_0\in Tx_0$
together with scalars
$y_0\in Tx_0$
together with scalars
![]() $\alpha _n\in [0,1]$
and
$\alpha _n\in [0,1]$
and
![]() $\gamma _n\in (0,\infty )$
, one can inductively define an iteration
$\gamma _n\in (0,\infty )$
, one can inductively define an iteration
where
![]() $y_{n+1}\in Tx_{n+1}$
is chosen such that
$y_{n+1}\in Tx_{n+1}$
is chosen such that
![]() $\lVert y_{n+1}-y_n \rVert \leq H(Tx_{n+1},Tx_n)+\gamma _n$
. This iteration defined in that way was studied in Song and Wang (Reference Song and Wang2009) and in the case that the set
$\lVert y_{n+1}-y_n \rVert \leq H(Tx_{n+1},Tx_n)+\gamma _n$
. This iteration defined in that way was studied in Song and Wang (Reference Song and Wang2009) and in the case that the set
![]() $K$
is additionally compact, the authors obtained the following convergence result:
$K$
is additionally compact, the authors obtained the following convergence result:
Theorem 2. (Song and Wang Reference Song and Wang2009). Let
![]() $K\subseteq X$
be nonempty, convex, and compact. Let
$K\subseteq X$
be nonempty, convex, and compact. Let
![]() $T:K\to CB(K)$
be a set-valued map that is nonexpansive and suppose that
$T:K\to CB(K)$
be a set-valued map that is nonexpansive and suppose that
![]() $F(T)\neq \emptyset$
as well as
$F(T)\neq \emptyset$
as well as
![]() $T(p)=\{p\}$
for each
$T(p)=\{p\}$
for each
![]() $p\in F(T)$
. Let
$p\in F(T)$
. Let
![]() $(x_n)$
be defined as in
$(x_n)$
be defined as in
![]() $({\dagger})$
with starting points
$({\dagger})$
with starting points
![]() $x_0\in K$
,
$x_0\in K$
,
![]() $y_0\in Tx_0$
and scalars
$y_0\in Tx_0$
and scalars
![]() $(\alpha _n)\subseteq [0,1]$
and
$(\alpha _n)\subseteq [0,1]$
and
![]() $(\gamma _n)\subseteq (0,\infty )$
such that
$(\gamma _n)\subseteq (0,\infty )$
such that
-
(1)
 $\lim _{n\to \infty } \gamma _n= 0$
,
$\lim _{n\to \infty } \gamma _n= 0$
, -
(2)
 $0\lt \liminf _{n\to \infty }\alpha _n\leq \limsup _{n\to \infty }\alpha _n\lt 1$
.
$0\lt \liminf _{n\to \infty }\alpha _n\leq \limsup _{n\to \infty }\alpha _n\lt 1$
.
Then
![]() $(x_n)$
converges strongly to a fixed point of
$(x_n)$
converges strongly to a fixed point of
![]() $T$
.
$T$
.
The main feature of the sequence exploited in the proof is that it is Fejér monotone (see in particular Combettes (Reference Combettes2001, Reference Combettes2009)). This well-studied class of sequences possesses very general convergence theorems which guarantee the weak convergence of such sequences under very mild asymptotic regularity assumptions. In compact (metric) spaces, like in the above result, the convergence is in particular strong.
These general convergence results for Fejér monotone sequences from compact sets were analyzed through the lens of proof mining in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) where, under the assumption of the existence of moduli which witness uniform quantitative reformulations of the central properties involved, a construction of a rate of metastability for the sequence in question is presented, that is a bound on the
![]() $n$
in the expression
$n$
in the expression
in terms of
![]() $k$
and
$k$
and
![]() $g$
. This noneffectively equivalent phrasing of the Cauchy property is particularly useful for more uniform and finitary considerations on convergence, as in particular also highlighted in Tao (Reference Tao2008a,b), and such a bound is in general the most one can hope for if one aims at computable information for Fejér monotone sequences as already in the most simple cases of ordinary Fejér monotonicity, there, in general, are no computable rates of convergence as one can show using methods from computability theory (essentially reducing to the seminal paper Specker (Reference Specker1949), see also Neumann Reference Neumann2015), and see Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) for a more detailed discussion of this). However, aiming for computable rates of convergence, in Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019), a general principle of metric regularity is studied (encompassing various forms of well-known regularity assumptions from nonlinear analysis and optimization like metric subregularity, weak sharp minima, error bounds, etc.) and under the assumption of such a metric regularity principle, the authors then provide a construction for a computable as well as highly uniform full rate of convergence for a given Fejér monotone iteration which moreover holds in the absence of any compactness assumptions.
$g$
. This noneffectively equivalent phrasing of the Cauchy property is particularly useful for more uniform and finitary considerations on convergence, as in particular also highlighted in Tao (Reference Tao2008a,b), and such a bound is in general the most one can hope for if one aims at computable information for Fejér monotone sequences as already in the most simple cases of ordinary Fejér monotonicity, there, in general, are no computable rates of convergence as one can show using methods from computability theory (essentially reducing to the seminal paper Specker (Reference Specker1949), see also Neumann Reference Neumann2015), and see Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) for a more detailed discussion of this). However, aiming for computable rates of convergence, in Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019), a general principle of metric regularity is studied (encompassing various forms of well-known regularity assumptions from nonlinear analysis and optimization like metric subregularity, weak sharp minima, error bounds, etc.) and under the assumption of such a metric regularity principle, the authors then provide a construction for a computable as well as highly uniform full rate of convergence for a given Fejér monotone iteration which moreover holds in the absence of any compactness assumptions.
These general but abstract proof mining results were previously successfully instantiated for many different situations in which Fejér monotone sequences occur to derive rates of metastability and rates of convergence. In particular, we want to mention the applications in the context of the composition of two firmly nonexpansive mappings in nonlinear spaces from Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2017), the proximal point algorithm in uniformly convex Banach spaces from Kohlenbach (Reference Kohlenbach2021) and in
![]() $\textrm{CAT}(0)$
-spaces as in Leuştean and Sipoş (Reference Leuştean, Nicolae and Sipoş2018a,b) as well as algorithms for finding zeros of differences of monotone operators from Pischke (Reference Pischke2023b) and Korpelevich’s extragradient method as in Pischke (Reference Pischke2023a).
$\textrm{CAT}(0)$
-spaces as in Leuştean and Sipoş (Reference Leuştean, Nicolae and Sipoş2018a,b) as well as algorithms for finding zeros of differences of monotone operators from Pischke (Reference Pischke2023b) and Korpelevich’s extragradient method as in Pischke (Reference Pischke2023a).
It is also here that we apply the results from Kohlenbach et al. (2018, 2019) to derive rates of metastability and rates of convergence (under a metric regularity assumption) for the above iteration which are, as before, not only computable in their parameters but also highly uniform. For that, we need to extract the previously mentioned moduli witnessing uniform quantitative versions of the Fejér monotonicity and asymptotic regularity which themselves arise from an application of proof mining to the respective proofs of these properties given in the course of the proof of Theorem 2 in Song and Wang (Reference Song and Wang2009). As these proofs in particular rely on the utilization of the Hausdorff metric, this application given here is in particular to be seen as a case study to illustrate the applicability of the treatment of the Hausdorff metric discussed in the previous section.
4.1 The central assumptions and their quantitative content
In this section, we now first discuss the central assumptions present in Theorem2 and in particular discuss (using the underlying logical methodology) what kind of quantitative assumptions they entail to potentially feature in the analysis of the main theorem.
The first important assumption present in Theorem2 is the compactness of the set
![]() $K$
. This compactness assumption on
$K$
. This compactness assumption on
![]() $K$
is witnessed in the following by a quantitative modulus of compactness introduced in Gerhardy (Reference Gerhardy2008) under the name of a modulus of total boundedness
Footnote
11
which takes the form of a function
$K$
is witnessed in the following by a quantitative modulus of compactness introduced in Gerhardy (Reference Gerhardy2008) under the name of a modulus of total boundedness
Footnote
11
which takes the form of a function
![]() $\gamma :\mathbb{N}\to \mathbb{N}$
such that for any
$\gamma :\mathbb{N}\to \mathbb{N}$
such that for any
![]() $k\in \mathbb{N}$
and for any
$k\in \mathbb{N}$
and for any
![]() $(x_n)\subseteq K$
:
$(x_n)\subseteq K$
:
Such a modulus exists if, and only if,
![]() $K$
is compact and we refer to Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) for various discussions on the construction of such moduli for certain concrete classes of compact sets and spaces.
$K$
is compact and we refer to Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) for various discussions on the construction of such moduli for certain concrete classes of compact sets and spaces.
As a second assumption, we find the nonemptyness of the fixed point set
![]() $F(T)$
which will be represented by a concrete witness
$F(T)$
which will be represented by a concrete witness
![]() $p_0$
(i.e.
$p_0$
(i.e.
![]() $p_0\in K$
and
$p_0\in K$
and
![]() $p_0\in Tp_0$
) in the following. As follows by the perspective of majorization, the bounds extracted later will of course only depend on an upper bound on the norm of
$p_0\in Tp_0$
) in the following. As follows by the perspective of majorization, the bounds extracted later will of course only depend on an upper bound on the norm of
![]() $p_0$
, which by the compactness and therefore the boundedness of
$p_0$
, which by the compactness and therefore the boundedness of
![]() $K$
is in particular represented by any upper bound on the diameter of
$K$
is in particular represented by any upper bound on the diameter of
![]() $K$
.
$K$
.
One of the most crucial assumptions, in some sense, is the single-valuedness of
![]() $T$
on actual fixed points, that is the assumption that
$T$
on actual fixed points, that is the assumption that
![]() $Tp=\{p\}$
if
$Tp=\{p\}$
if
![]() $p\in F(T)$
. This implication is equivalent to
$p\in F(T)$
. This implication is equivalent to
which in turn unravels into
and in that way, the logical methodology inducesFootnote
12
a modulus
![]() $\theta :\mathbb{N}\to \mathbb{N}$
bounding (and thus witnessing) such a
$\theta :\mathbb{N}\to \mathbb{N}$
bounding (and thus witnessing) such a
![]() $j$
in terms of
$j$
in terms of
![]() $k$
, that is such thatFootnote
13
$k$
, that is such thatFootnote
13
Note that by a simple compactness argument, possessing such a modulus is equivalent to the property
![]() $({*})$
in compact spaces:
$({*})$
in compact spaces:
Lemma 6. Let
![]() $K$
be compact and let
$K$
be compact and let
![]() $T:K\to CB(K)$
be a nonexpansive operator. Then
$T:K\to CB(K)$
be a nonexpansive operator. Then
![]() $T$
satisfies
$T$
satisfies
![]() $({*})$
if, and only if,
$({*})$
if, and only if,
Proof. Clearly,
![]() $({**})$
implies
$({**})$
implies
![]() $({*})$
. Conversely, suppose that
$({*})$
. Conversely, suppose that
![]() $({**})$
fails, that is suppose there exists a
$({**})$
fails, that is suppose there exists a
![]() $k\in \mathbb{N}$
such that for any
$k\in \mathbb{N}$
such that for any
![]() $j\in \mathbb{N}$
:
$j\in \mathbb{N}$
:
Then
![]() $d(p_j,Tp_j)\leq \frac {1}{j+1}$
implies that for any
$d(p_j,Tp_j)\leq \frac {1}{j+1}$
implies that for any
![]() $j\geq 1$
, there exists a
$j\geq 1$
, there exists a
![]() $q_j\in Tp_j$
such that
$q_j\in Tp_j$
such that
![]() $\lVert p_j-q_j \rVert \leq 1/j$
. Further,
$\lVert p_j-q_j \rVert \leq 1/j$
. Further,
![]() $H(\{p_{j}\},Tp_{j})\gt \frac {1}{k+1}$
now implies that there exists a
$H(\{p_{j}\},Tp_{j})\gt \frac {1}{k+1}$
now implies that there exists a
![]() $q_j'\in Tp_j$
such that
$q_j'\in Tp_j$
such that
![]() $\lVert p_j-q_j' \rVert \gt \frac {1}{k+1}$
.
$\lVert p_j-q_j' \rVert \gt \frac {1}{k+1}$
.
We now pick subsequences
![]() $p_{j_i}$
,
$p_{j_i}$
,
![]() $q_{j_i}$
and
$q_{j_i}$
and
![]() $q_{j_i}'$
such that
$q_{j_i}'$
such that
![]() $p_{j_i}\to p$
,
$p_{j_i}\to p$
,
![]() $q_{j_i}\to q$
and
$q_{j_i}\to q$
and
![]() $q_{j_i}'\to q'$
with
$q_{j_i}'\to q'$
with
![]() $p,q,$
$p,q,$
![]() $q'\in K$
. Then,
$q'\in K$
. Then,
![]() $\lVert p-q \rVert =0$
and
$\lVert p-q \rVert =0$
and
![]() $H(Tp_{j_i},Tp)\to 0$
for
$H(Tp_{j_i},Tp)\to 0$
for
![]() $i\to \infty$
as
$i\to \infty$
as
![]() $T$
is nonexpansive. Thus, in particular
$T$
is nonexpansive. Thus, in particular
![]() $d(q_{j_i},Tp),d(q'_{j_i},Tp)\to 0$
which yields
$d(q_{j_i},Tp),d(q'_{j_i},Tp)\to 0$
which yields
and thus
![]() $d(p,Tp)=d(q,Tp)=0$
. Similarly
$d(p,Tp)=d(q,Tp)=0$
. Similarly
![]() $d(q',Tp)=0$
and thus
$d(q',Tp)=0$
and thus
![]() $q'\in Tp$
. However, we have
$q'\in Tp$
. However, we have
![]() $\lVert p-q' \rVert \geq \frac {1}{k+1}$
and so
$\lVert p-q' \rVert \geq \frac {1}{k+1}$
and so
![]() $H(\{p\},Tp)\geq \lVert p-q' \rVert \geq \frac {1}{k+1}$
. This is a contradiction to
$H(\{p\},Tp)\geq \lVert p-q' \rVert \geq \frac {1}{k+1}$
. This is a contradiction to
![]() $({*})$
.
$({*})$
.
In that way, the existence of such a modulus is implied already by the assumptions in Theorem 2.
At last, we consider the assumptions on the auxiliary sequences
![]() $\gamma _n$
and
$\gamma _n$
and
![]() $\alpha _n$
. For
$\alpha _n$
. For
![]() $\gamma _n$
, where it is assumed that
$\gamma _n$
, where it is assumed that
we will later rely on a rate of convergence
![]() $\tau$
witnessing this property, i.e. on a
$\tau$
witnessing this property, i.e. on a
![]() $\tau$
satisfying
$\tau$
satisfying
For
![]() $\alpha _n$
, the assumption that
$\alpha _n$
, the assumption that
is witnessed by a value
![]() $a\in \mathbb{N}^*$
with the property
$a\in \mathbb{N}^*$
with the property
in similarity to Dinis and Pinto (Reference Dinis and Pinto2020).
Remark 7. For the previous treatment of the Hausdorff metric, it was crucial that the sets come equipped with a modulus witnessing their boundedness. Note again that the existence of such a modulus is immediate for sets of the form
![]() $Tx$
as
$Tx$
as
![]() $Tx\in CB(K)$
and thus
$Tx\in CB(K)$
and thus
![]() $Tx\subseteq K$
which is bounded as
$Tx\subseteq K$
which is bounded as
![]() $K$
is compact. In that way, for the quantitative results, we will later rely on a bound on the diameter of
$K$
is compact. In that way, for the quantitative results, we will later rely on a bound on the diameter of
![]() $K$
(as mentioned before). Note that such a bound can not be computed from the modulus of total boundedness
$K$
(as mentioned before). Note that such a bound can not be computed from the modulus of total boundedness
![]() $\gamma$
for
$\gamma$
for
![]() $K$
as this modulus is only noneffectively equivalent to the total boundedness of
$K$
as this modulus is only noneffectively equivalent to the total boundedness of
![]() $K$
in the usual sense and thus only implies the boundedness of
$K$
in the usual sense and thus only implies the boundedness of
![]() $K$
noneffectively (see Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) for a further discussion of this).
$K$
noneffectively (see Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) for a further discussion of this).
4.2 Suzuki’s lemma and its analysis
The main analytical ingredient of the convergence proof from Song and Wang (Reference Song and Wang2009) is a well-known lemma from Suzuki (Reference Suzuki2005):
Lemma 8 (Suzuki Reference Suzuki2005). Let
![]() $(x_n),(y_n)$
be bounded sequences in a Banach space
$(x_n),(y_n)$
be bounded sequences in a Banach space
![]() $X$
and let
$X$
and let
![]() $(\alpha _n)\subseteq [0,1]$
be such that
$(\alpha _n)\subseteq [0,1]$
be such that
![]() $0\lt \liminf _{n\to \infty }\alpha _n\leq \limsup _{n\in \mathbb{N}}\alpha _n\lt 1$
. Suppose that
$0\lt \liminf _{n\to \infty }\alpha _n\leq \limsup _{n\in \mathbb{N}}\alpha _n\lt 1$
. Suppose that
![]() $x_{n+1}=\alpha _nx_n+(1-\alpha _n)y_n$
as well as
$x_{n+1}=\alpha _nx_n+(1-\alpha _n)y_n$
as well as
Then
![]() $\lim _{n\to \infty }\lVert x_n-y_n \rVert =0$
.
$\lim _{n\to \infty }\lVert x_n-y_n \rVert =0$
.
This lemma was analyzed quantitatively in Dinis and Pinto (Reference Dinis and Pinto2020), and we will rely in the following on this analysis:
Lemma 9 (Dinis and Pinto 2020). Let
![]() $(x_n),(y_n)$
be sequences in a Banach space
$(x_n),(y_n)$
be sequences in a Banach space
![]() $X$
with
$X$
with
![]() $\lVert x_n \rVert ,\lVert y_n \rVert \leq b$
for some
$\lVert x_n \rVert ,\lVert y_n \rVert \leq b$
for some
![]() $b\in \mathbb{N}^*$
and let
$b\in \mathbb{N}^*$
and let
![]() $(\alpha _n)\subseteq [0,1]$
be such that there exists a
$(\alpha _n)\subseteq [0,1]$
be such that there exists a
![]() $a\in \mathbb{N}^*$
with the property
$a\in \mathbb{N}^*$
with the property
Suppose that
![]() $x_{n+1}=\alpha _nx_n+(1-\alpha _n)y_n$
as well as that there exists a monotone function
$x_{n+1}=\alpha _nx_n+(1-\alpha _n)y_n$
as well as that there exists a monotone function
![]() $\tau :\mathbb{N}\to \mathbb{N}$
such that
$\tau :\mathbb{N}\to \mathbb{N}$
such that
Then for any
![]() $k\in \mathbb{N}$
and any
$k\in \mathbb{N}$
and any
![]() $g:\mathbb{N}\to \mathbb{N}$
:
$g:\mathbb{N}\to \mathbb{N}$
:
where
![]() $\varphi _{a,\tau ,b}(k,g)=\max \{a,\tau (t(2t+1)a^t(k+1)-1)\}+(bt(2t+1)a^t(k+1)-1)t+r_0$
for
$\varphi _{a,\tau ,b}(k,g)=\max \{a,\tau (t(2t+1)a^t(k+1)-1)\}+(bt(2t+1)a^t(k+1)-1)t+r_0$
for
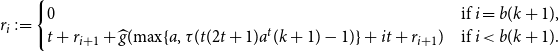 \begin{equation*} r_i:=\begin{cases}0&\text{if }i=b(k+1),\\t+r_{i+1}+\widehat {g}(\mathrm{max} \{a,\tau (t(2t+1)a^t(k+1)-1)\}+it+r_{i+1})&\text{if }i\lt b(k+1).\end{cases} \end{equation*}
\begin{equation*} r_i:=\begin{cases}0&\text{if }i=b(k+1),\\t+r_{i+1}+\widehat {g}(\mathrm{max} \{a,\tau (t(2t+1)a^t(k+1)-1)\}+it+r_{i+1})&\text{if }i\lt b(k+1).\end{cases} \end{equation*}
where
![]() $\widehat {g}(m)=t+g(m)$
and
$\widehat {g}(m)=t+g(m)$
and
![]() $t=2ba(k+1)$
.
$t=2ba(k+1)$
.
4.3 Fejér monotonicity and metastability
We now present the extractions of the quantitative versions of Fejér monotonicity and asymptotic regularity.
For this, we first need to define an appropriate notion of an approximate solution (i.e. of an approximate fixed point) as the results given in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) rely on uniform reformulations of the respective properties in terms of such approximate solutions. For our concrete situation here, note that
![]() $p$
is a fixed point of
$p$
is a fixed point of
![]() $T$
if, and only if,
$T$
if, and only if,
![]() $d(p,Tp)=0$
(as
$d(p,Tp)=0$
(as
![]() $Tp$
is closed since
$Tp$
is closed since
![]() $Tp\in CB(K)$
). In that vein, we call
$Tp\in CB(K)$
). In that vein, we call
![]() $p$
a
$p$
a
![]() $\frac {1}{k+1}$
-approximate fixed point of
$\frac {1}{k+1}$
-approximate fixed point of
![]() $T$
if
$T$
if
and define correspondingly
as the set of approximate solutions which extend the set of full solutions
Now, for the Fejér monotonicity of
![]() $(x_n)$
, we concretely strive to establish the existence of the following modulus relative to the chosen
$(x_n)$
, we concretely strive to establish the existence of the following modulus relative to the chosen
![]() $AF_k$
:
$AF_k$
:
Definition 10 (Kohlenbach et al. 2018). A function
![]() $\chi :\mathbb{N}^3\to \mathbb{N}$
is a modulus of uniform Fejér monotonicity for
$\chi :\mathbb{N}^3\to \mathbb{N}$
is a modulus of uniform Fejér monotonicity for
![]() $(x_n)$
w.r.t.
$(x_n)$
w.r.t.
![]() $(AF_k)$
if for any
$(AF_k)$
if for any
![]() $n,m,r\in \mathbb{N}$
, any
$n,m,r\in \mathbb{N}$
, any
![]() $p\in AF_{\chi (k,m,r)}$
and any
$p\in AF_{\chi (k,m,r)}$
and any
![]() $l\leq m$
:
$l\leq m$
:
For this, we can now extract the following from the proof of Fejér monotonicity given in Song and Wang (Reference Song and Wang2009) for the sequence
![]() $(x_n)$
defined as in (
$(x_n)$
defined as in (
![]() $\dagger$
).
$\dagger$
).
Lemma 11. Let
![]() $\theta$
be such that
$\theta$
be such that
Then sequence
![]() $(x_n)$
defined as in
$(x_n)$
defined as in
![]() $({\dagger})$
is uniformly Fejér monotone w.r.t.
$({\dagger})$
is uniformly Fejér monotone w.r.t.
![]() $(AF_k)$
with a modulus
$(AF_k)$
with a modulus
Proof. Let
![]() $p$
be given with
$p$
be given with
![]() $d(p,Tp)\leq \frac {1}{\chi (n,m,r)+1}$
. Then
$d(p,Tp)\leq \frac {1}{\chi (n,m,r)+1}$
. Then
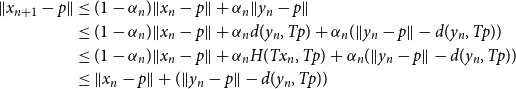 \begin{align*} \lVert x_{n+1}-p \rVert &\leq (1-\alpha _n)\lVert x_n-p \rVert +\alpha _n\lVert y_n-p \rVert \\ &\leq (1-\alpha _n)\lVert x_n-p \rVert +\alpha _nd(y_n,Tp)+\alpha _n(\lVert y_n-p \rVert -d(y_n,Tp))\\ &\leq (1-\alpha _n)\lVert x_n-p \rVert +\alpha _nH(Tx_n,Tp)+\alpha _n(\lVert y_n-p \rVert -d(y_n,Tp))\\ &\leq \lVert x_n-p \rVert +(\lVert y_n-p \rVert -d(y_n,Tp)) \end{align*}
\begin{align*} \lVert x_{n+1}-p \rVert &\leq (1-\alpha _n)\lVert x_n-p \rVert +\alpha _n\lVert y_n-p \rVert \\ &\leq (1-\alpha _n)\lVert x_n-p \rVert +\alpha _nd(y_n,Tp)+\alpha _n(\lVert y_n-p \rVert -d(y_n,Tp))\\ &\leq (1-\alpha _n)\lVert x_n-p \rVert +\alpha _nH(Tx_n,Tp)+\alpha _n(\lVert y_n-p \rVert -d(y_n,Tp))\\ &\leq \lVert x_n-p \rVert +(\lVert y_n-p \rVert -d(y_n,Tp)) \end{align*}
and by induction we get
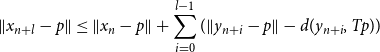 \begin{equation*} \lVert x_{n+l}-p \rVert \leq \lVert x_n-p \rVert +\sum _{i=0}^{l-1}(\lVert y_{n+i}-p \rVert -d(y_{n+i},Tp)) \end{equation*}
\begin{equation*} \lVert x_{n+l}-p \rVert \leq \lVert x_n-p \rVert +\sum _{i=0}^{l-1}(\lVert y_{n+i}-p \rVert -d(y_{n+i},Tp)) \end{equation*}
for any
![]() $l\geq 1$
. It is rather immediate to see that in general, for nonempty sets
$l\geq 1$
. It is rather immediate to see that in general, for nonempty sets
![]() $Y,Z\subseteq X$
and a point
$Y,Z\subseteq X$
and a point
![]() $x$
, we have
$x$
, we have
![]() $d(x,Y)\leq d(x,Z)+H(Y,Z)$
and instantiating this yields
$d(x,Y)\leq d(x,Z)+H(Y,Z)$
and instantiating this yields
and thus
![]() $\lVert y_{n+i}-p \rVert -d(y_{n+i},Tp)\leq H(\{p\},Tp)$
. As now
$\lVert y_{n+i}-p \rVert -d(y_{n+i},Tp)\leq H(\{p\},Tp)$
. As now
![]() $p\in AF_{\chi (n,m,r)}$
, we get
$p\in AF_{\chi (n,m,r)}$
, we get
In particular, in that case we have
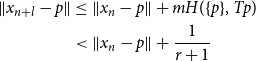 \begin{align*} \lVert x_{n+l}-p \rVert &\leq \lVert x_n-p \rVert +mH(\{p\},Tp)\\ &\lt \lVert x_n-p \rVert +\frac {1}{r+1} \end{align*}
\begin{align*} \lVert x_{n+l}-p \rVert &\leq \lVert x_n-p \rVert +mH(\{p\},Tp)\\ &\lt \lVert x_n-p \rVert +\frac {1}{r+1} \end{align*}
for
![]() $l\leq m$
.
$l\leq m$
.
Remark 12. Note that if
![]() $T$
satisfies
$T$
satisfies
![]() $({*})$
, the sequence is Fejér monotone w.r.t.
$({*})$
, the sequence is Fejér monotone w.r.t.
![]() $F(T)$
in the usual sense as can be shown by following the proof of the above Lemma 11. In particular, this result holds without any compactness assumption for
$F(T)$
in the usual sense as can be shown by following the proof of the above Lemma 11. In particular, this result holds without any compactness assumption for
![]() $K$
.
$K$
.
For the asymptotic behavior, we are interested in the following type of quantitative information:
Definition 13 (Kohlenbach et al. 2018). A function
![]() $\Phi$
is an approximate
$\Phi$
is an approximate
![]() $F$
-point bound for
$F$
-point bound for
![]() $(x_n)$
w.r.t.
$(x_n)$
w.r.t.
![]() $(AF_k)$
if for any
$(AF_k)$
if for any
![]() $k\in \mathbb{N}$
:
$k\in \mathbb{N}$
:
The construction of such a
![]() $\Phi$
for the sequence studied here relies on analyzing the proof of the statement
$\Phi$
for the sequence studied here relies on analyzing the proof of the statement
![]() $d(x_n,Tx_n)\to 0$
from Song and Wang (Reference Song and Wang2009), which relies on Suzuki’s lemma. Concretely, we get the following:
$d(x_n,Tx_n)\to 0$
from Song and Wang (Reference Song and Wang2009), which relies on Suzuki’s lemma. Concretely, we get the following:
Lemma 14. Let
![]() $b$
be a bound on the diameter of
$b$
be a bound on the diameter of
![]() $K$
and let
$K$
and let
![]() $(\alpha _n)\subseteq [0,1]$
be such that there exists an
$(\alpha _n)\subseteq [0,1]$
be such that there exists an
![]() $a\in \mathbb{N}^*$
with the property
$a\in \mathbb{N}^*$
with the property
Let
![]() $\tau$
be a monotone rate of convergence for
$\tau$
be a monotone rate of convergence for
![]() $\gamma _n\to 0$
. Let
$\gamma _n\to 0$
. Let
![]() $\varphi _{a,\tau ,b}$
be defined as in Lemma 9. Then
$\varphi _{a,\tau ,b}$
be defined as in Lemma 9. Then
![]() $(x_n)$
defined as in
$(x_n)$
defined as in
![]() $({\dagger})$
has approximate
$({\dagger})$
has approximate
![]() $F$
-points w.r.t.
$F$
-points w.r.t.
![]() $(AF_k)$
with an approximate
$(AF_k)$
with an approximate
![]() $F$
-point bound
$F$
-point bound
Proof. As in Song and Wang (Reference Song and Wang2009), we can derive
which yields that
and thus
![]() $\tau$
satisfies the assumption of Lemma 9. Applying Lemma 9, we get that for any
$\tau$
satisfies the assumption of Lemma 9. Applying Lemma 9, we get that for any
![]() $k\in \mathbb{N}$
and any
$k\in \mathbb{N}$
and any
![]() $g:\mathbb{N}\to \mathbb{N}$
:
$g:\mathbb{N}\to \mathbb{N}$
:
In particular, we get for any
![]() $k\in \mathbb{N}$
that
$k\in \mathbb{N}$
that
which yields that for this
![]() $n$
, we have
$n$
, we have
i.e.
![]() $x_n\in AF_k$
.
$x_n\in AF_k$
.
Remark 15. While the full function
![]() $\varphi _{a,\tau ,b}$
is rather complex, in the above special case of considering the constant-
$\varphi _{a,\tau ,b}$
is rather complex, in the above special case of considering the constant-
![]() $0$
function, it simplifies considerably to
$0$
function, it simplifies considerably to
for
![]() $t=2ba(k+1)$
.
$t=2ba(k+1)$
.
Lastly, we show that
![]() $F(T)$
is not only closed but that it is even sufficiently uniformly closed respective to the approximations
$F(T)$
is not only closed but that it is even sufficiently uniformly closed respective to the approximations
![]() $AF_k$
in a concrete way introduced in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018):
$AF_k$
in a concrete way introduced in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018):
Definition 16 (Kohlenbach et al. Reference Kohlenbach, Leuştean and Nicolae2018). The solution set
![]() $F$
is called uniformly closed w.r.t.
$F$
is called uniformly closed w.r.t.
![]() $(AF_k)$
with moduli
$(AF_k)$
with moduli
![]() $\delta ,\omega$
if for any
$\delta ,\omega$
if for any
![]() $k\in \mathbb{N}$
, any
$k\in \mathbb{N}$
, any
![]() $q\in AF_{\delta (k)}$
and any
$q\in AF_{\delta (k)}$
and any
![]() $p$
with
$p$
with
![]() $\lVert p-q \rVert \leq 1/(\omega (k)+1)$
, we have
$\lVert p-q \rVert \leq 1/(\omega (k)+1)$
, we have
![]() $p\in AF_k$
.
$p\in AF_k$
.
Lemma 17. The set
![]() $F=F(T)$
is uniformly closed w.r.t.
$F=F(T)$
is uniformly closed w.r.t.
![]() $(AF_k)$
with moduli
$(AF_k)$
with moduli
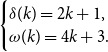 \begin{equation*} \begin{cases} \delta (k)=2k+1,\\ \omega (k)=4k+3. \end{cases} \end{equation*}
\begin{equation*} \begin{cases} \delta (k)=2k+1,\\ \omega (k)=4k+3. \end{cases} \end{equation*}
Proof. Note that we have
and thus if
![]() $q\in AF_{2k+1}$
and
$q\in AF_{2k+1}$
and
![]() $\lVert p-q \rVert \leq \frac {1}{4(k+1)}$
, then
$\lVert p-q \rVert \leq \frac {1}{4(k+1)}$
, then
![]() $d(p,Tp)\leq \frac {1}{k+1}$
, i.e.
$d(p,Tp)\leq \frac {1}{k+1}$
, i.e.
![]() $p\in AF_{k}$
.
$p\in AF_{k}$
.
Combined, we can now apply the general result from Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) to get the following quantitative version of Theorem2.
Theorem 3. Let
![]() $\gamma$
be a modulus of total boundedness for
$\gamma$
be a modulus of total boundedness for
![]() $K$
. Let
$K$
. Let
![]() $b$
be a bound on the diameter of
$b$
be a bound on the diameter of
![]() $K$
and let
$K$
and let
![]() $(\alpha _n)\subseteq [0,1]$
be such that there exists an
$(\alpha _n)\subseteq [0,1]$
be such that there exists an
![]() $a\in \mathbb{N}^*$
with the property
$a\in \mathbb{N}^*$
with the property
Let
![]() $(\gamma _n)\subseteq (0,\infty )$
be such that
$(\gamma _n)\subseteq (0,\infty )$
be such that
![]() $\gamma _n\to 0$
and let
$\gamma _n\to 0$
and let
![]() $\tau$
be a monotone rate of convergence for
$\tau$
be a monotone rate of convergence for
![]() $\gamma _n\to 0$
. Let
$\gamma _n\to 0$
. Let
![]() $\theta$
be such that
$\theta$
be such that
Let
![]() $\varphi _{a,\tau ,b}(k,0)$
be defined as in Remark 15, i.e.
$\varphi _{a,\tau ,b}(k,0)$
be defined as in Remark 15, i.e.
for
![]() $t=2ba(k+1)$
. Then,
$t=2ba(k+1)$
. Then,
![]() $(x_n)$
defined as in
$(x_n)$
defined as in
![]() $({\dagger})$
is Cauchy and moreover, for all
$({\dagger})$
is Cauchy and moreover, for all
![]() $k\in \mathbb{N}$
and all
$k\in \mathbb{N}$
and all
![]() $g:\mathbb{N}\to \mathbb{N}$
,
$g:\mathbb{N}\to \mathbb{N}$
,
where
![]() $\Psi (k,g)=\Psi _0(P,k,g)$
for
$\Psi (k,g)=\Psi _0(P,k,g)$
for
![]() $P=\gamma (4k+3)$
and with
$P=\gamma (4k+3)$
and with
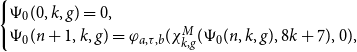 \begin{equation*} \begin{cases} \Psi _0(0,k,g)=0,\\ \Psi _0(n+1,k,g)=\varphi _{a,\tau ,b}(\chi _{k,g}^M(\Psi _0(n,k,g),8k+7),0), \end{cases} \end{equation*}
\begin{equation*} \begin{cases} \Psi _0(0,k,g)=0,\\ \Psi _0(n+1,k,g)=\varphi _{a,\tau ,b}(\chi _{k,g}^M(\Psi _0(n,k,g),8k+7),0), \end{cases} \end{equation*}
and where
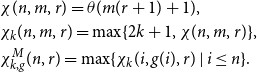 \begin{align*} &\chi (n,m,r)=\theta (m(r+1)+1),\\ &\chi _{k}(n,m,r)=\max \{2k+1,\chi (n,m,r)\},\\ &\chi _{k,g}^M(n,r)=\max \{\chi _k(i,g(i),r)\mid i\leq n\}. \end{align*}
\begin{align*} &\chi (n,m,r)=\theta (m(r+1)+1),\\ &\chi _{k}(n,m,r)=\max \{2k+1,\chi (n,m,r)\},\\ &\chi _{k,g}^M(n,r)=\max \{\chi _k(i,g(i),r)\mid i\leq n\}. \end{align*}
Proof. The result rather immediately follows from Theorem 5.3 in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) (which itself builds on Theorem 5.1 in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018)) by instantiating the bound given there with the moduli obtained in Lemmas 11, 14, and 17. Concretely,
![]() $\chi$
in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) is instantiated by
$\chi$
in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) is instantiated by
![]() $\chi$
as above and
$\chi$
as above and
![]() $\Phi$
in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) is instantiated by
$\Phi$
in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) is instantiated by
![]() $\varphi _{a,\tau ,b}(\cdot ,0)$
. Further,
$\varphi _{a,\tau ,b}(\cdot ,0)$
. Further,
![]() $\delta _F$
and
$\delta _F$
and
![]() $\omega _F$
in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) are instantiated by
$\omega _F$
in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) are instantiated by
![]() $\delta$
and
$\delta$
and
![]() $\omega$
as in Lemma 17, and we have
$\omega$
as in Lemma 17, and we have
![]() $G=H=\textrm{id}$
and thus
$G=H=\textrm{id}$
and thus
![]() $\alpha _G(k)=\beta _H(k)=k$
. Note lastly that as
$\alpha _G(k)=\beta _H(k)=k$
. Note lastly that as
![]() $\tau$
is monotone, so is
$\tau$
is monotone, so is
![]() $\varphi _{a,\tau ,b}(\cdot ,0)$
as follows by Remark 15. The bounds given here result from the ones given in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) only by immediate simplifications.
$\varphi _{a,\tau ,b}(\cdot ,0)$
as follows by Remark 15. The bounds given here result from the ones given in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018) only by immediate simplifications.
Remark 18. Theorem 3 is a full finitization of Theorem 2 in the sense of Tao as it only references finite segments of the iteration
![]() $(x_n)$
but it trivially implies back the original formulation of Theorem 2 as all the moduli naturally exist and since metastability is (noneffectively) equivalent to convergence (see also Remark 5.5 in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018)).
$(x_n)$
but it trivially implies back the original formulation of Theorem 2 as all the moduli naturally exist and since metastability is (noneffectively) equivalent to convergence (see also Remark 5.5 in Kohlenbach et al. (Reference Kohlenbach, Leuştean and Nicolae2018)).
4.4 Moduli of regularity and rates of convergence
In this section, using the results from Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019), we give constructions for rates of convergence based on the assumption of a (very general) kind of regularity notion as discussed in the introduction.
The central notion here is consequently the following instantiation of the abstract notion of a modulus of regularity from Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019):
Definition 19. Let
![]() $z\in F(T)$
and
$z\in F(T)$
and
![]() $r\gt 0$
. A function
$r\gt 0$
. A function
![]() $\phi :(0,\infty )\to (0,\infty )$
is called a modulus of regularity for
$\phi :(0,\infty )\to (0,\infty )$
is called a modulus of regularity for
![]() $T$
w.r.t
$T$
w.r.t
![]() $\overline {B}_r(z)$
if for all
$\overline {B}_r(z)$
if for all
![]() $\varepsilon \gt 0$
and all
$\varepsilon \gt 0$
and all
![]() $x\in \overline {B}_r(z)$
:
$x\in \overline {B}_r(z)$
:
If there is a
![]() $z\in F(T)$
such that
$z\in F(T)$
such that
![]() $\phi$
is a modulus of regularity w.r.t.
$\phi$
is a modulus of regularity w.r.t.
![]() $\overline {B}_r(z)$
for all
$\overline {B}_r(z)$
for all
![]() $r\gt 0$
, then
$r\gt 0$
, then
![]() $\phi$
is just called a modulus of regularity for
$\phi$
is just called a modulus of regularity for
![]() $T$
.
$T$
.
Remark 20. Note that the work Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019) is written in the context of a formal setup where instead of using sets
![]() $F$
/
$F$
/
![]() $AF_k$
as above to formulate the solutions and approximative solutions, a function
$AF_k$
as above to formulate the solutions and approximative solutions, a function
![]() $F:X\to [0,+\infty ]$
is employed and the roles of the sets
$F:X\to [0,+\infty ]$
is employed and the roles of the sets
![]() $F$
/
$F$
/
![]() $AF_k$
are (conceptually) replaced by
$AF_k$
are (conceptually) replaced by
![]() $\textrm{zer}F$
/
$\textrm{zer}F$
/
![]() $\{x\mid F(x)\leq \varepsilon \}$
for
$\{x\mid F(x)\leq \varepsilon \}$
for
![]() $\varepsilon \gt 0$
. The above notion arises from the general definition given in Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019) by using
$\varepsilon \gt 0$
. The above notion arises from the general definition given in Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019) by using
![]() $F(x):=d(x,Tx)$
but we in the following suppress this whole setup from Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019).
$F(x):=d(x,Tx)$
but we in the following suppress this whole setup from Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019).
Note that the function
![]() $d(p,Tp)$
is continuous in
$d(p,Tp)$
is continuous in
![]() $p$
if
$p$
if
![]() $T$
is nonexpansive as
$T$
is nonexpansive as
and thus
It follows from Proposition 3.3 of Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019) that any such nonexpansive map
![]() $T$
has a modulus of regularity (albeit in general being uncomputable) if
$T$
has a modulus of regularity (albeit in general being uncomputable) if
![]() $K$
is compact.
$K$
is compact.
Under the assumption of such a modulus, we now get the following result on rates of convergence:
Theorem 4. Let
![]() $z\in F(T)\neq \emptyset$
and let
$z\in F(T)\neq \emptyset$
and let
![]() $b$
be a bound on the diameter of
$b$
be a bound on the diameter of
![]() $K$
. Assume that
$K$
. Assume that
![]() $K$
is closed. Let
$K$
is closed. Let
![]() $(x_n)$
be defined as in
$(x_n)$
be defined as in
![]() $({\dagger})$
. Assume that
$({\dagger})$
. Assume that
![]() $T$
satisfies
$T$
satisfies
![]() $({*})$
. Let
$({*})$
. Let
![]() $(\alpha _n)$
with
$(\alpha _n)$
with
![]() $a$
and
$a$
and
![]() $(\gamma _n)$
with
$(\gamma _n)$
with
![]() $\tau$
as well as
$\tau$
as well as
![]() $\varphi _{a,\tau ,b}(k,0)$
be as in Theorem 3 (and Remark 15). Let
$\varphi _{a,\tau ,b}(k,0)$
be as in Theorem 3 (and Remark 15). Let
![]() $\phi$
be a modulus of regularity for
$\phi$
be a modulus of regularity for
![]() $T$
w.r.t.
$T$
w.r.t.
![]() $\overline {B}_b(z)$
. Then,
$\overline {B}_b(z)$
. Then,
![]() $(x_n)$
is Cauchy with
$(x_n)$
is Cauchy with
and further
![]() $(x_n)$
converges to a fixed point of
$(x_n)$
converges to a fixed point of
![]() $T$
with a rate of convergence
$T$
with a rate of convergence
Proof. The result is a straightforward instantiation of the general abstract Theorem 4.1 from Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019), using the previous Lemma 14 by which we have that
Note for this that the sequence
![]() $(x_n)$
is Fejér monotone w.r.t.
$(x_n)$
is Fejér monotone w.r.t.
![]() $F(T)$
by Remark 12 since
$F(T)$
by Remark 12 since
![]() $T$
satisfies
$T$
satisfies
![]() $({*})$
. That
$({*})$
. That
![]() $(x_n)$
converges to a fixed point of
$(x_n)$
converges to a fixed point of
![]() $T$
with the given rate follows from Theorem 4.1, (i) in Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019) for which we need that
$T$
with the given rate follows from Theorem 4.1, (i) in Kohlenbach et al. (Reference Kohlenbach, López-Acedo and Nicolae2019) for which we need that
![]() $K$
is complete (which follows as
$K$
is complete (which follows as
![]() $X$
is a Banach space and as
$X$
is a Banach space and as
![]() $K$
is closed) and that
$K$
is closed) and that
![]() $F(T)$
is closed which follows from the fact that
$F(T)$
is closed which follows from the fact that
![]() $d(p,Tp)$
is uniformly continuous in
$d(p,Tp)$
is uniformly continuous in
![]() $p$
and
$p$
and
![]() $F(T)=(d(\cdot ,T\cdot ))^{-1}(0)$
.
$F(T)=(d(\cdot ,T\cdot ))^{-1}(0)$
.
Remark 21. Note that the above Theorem 4 holds without any compactness assumptions on
![]() $K$
. Thus, in the presence of a modulus of regularity, the convergence result from Theorem 2 immediately holds for any closed, bounded and nonempty set
$K$
. Thus, in the presence of a modulus of regularity, the convergence result from Theorem 2 immediately holds for any closed, bounded and nonempty set
![]() $K$
and any nonexpansive mapping
$K$
and any nonexpansive mapping
![]() $T$
with
$T$
with
![]() $F(T)\neq \emptyset$
that satisfies
$F(T)\neq \emptyset$
that satisfies
![]() $({*})$
.
$({*})$
.
Finally, we look at a notion for multivalued mappings where simple instances of such moduli of regularity can be derived. Following Senter and Dotson (Reference Senter and Dotson1974), a multivalued mapping
![]() $T:K\to \textrm{CB}(K)$
is said to satisfy Condition I if there is a nondecreasing function
$T:K\to \textrm{CB}(K)$
is said to satisfy Condition I if there is a nondecreasing function
![]() $f:[0,\infty )\to [0,\infty )$
with
$f:[0,\infty )\to [0,\infty )$
with
![]() $f(0)=0$
,
$f(0)=0$
,
![]() $f(r)\gt 0$
for
$f(r)\gt 0$
for
![]() $r\in (0,\infty )$
and
$r\in (0,\infty )$
and
for all
![]() $x\in K$
. If the property that
$x\in K$
. If the property that
![]() $f(r)\gt 0$
for
$f(r)\gt 0$
for
![]() $r\in (0,\infty )$
is witnessed in a uniform and quantitative way by a function
$r\in (0,\infty )$
is witnessed in a uniform and quantitative way by a function
![]() $\phi :(0,\infty )\to (0,\infty )$
with
$\phi :(0,\infty )\to (0,\infty )$
with
for any
![]() $r,\varepsilon \gt 0$
, then such a
$r,\varepsilon \gt 0$
, then such a
![]() $\phi$
is clearly already a modulus of regularity for
$\phi$
is clearly already a modulus of regularity for
![]() $T$
. This in particular is true for mappings that satisfy Condition II of Senter and Dotson (Reference Senter and Dotson1974), i.e. where there exists a real
$T$
. This in particular is true for mappings that satisfy Condition II of Senter and Dotson (Reference Senter and Dotson1974), i.e. where there exists a real
![]() $\alpha \gt 0$
such that
$\alpha \gt 0$
such that
where then
![]() $\phi$
can be given by
$\phi$
can be given by
![]() $\phi (\varepsilon )=\alpha \varepsilon$
. Examples of mappings which satisfy Condition II are for instance discussed in Senter and Dotson (Reference Senter and Dotson1974) and for these, the above rates of convergence therefore instantiate immediately.
$\phi (\varepsilon )=\alpha \varepsilon$
. Examples of mappings which satisfy Condition II are for instance discussed in Senter and Dotson (Reference Senter and Dotson1974) and for these, the above rates of convergence therefore instantiate immediately.
Acknowledgments
I want to thank Ulrich Kohlenbach for many helpful discussions on the topic of this paper. The results of this paper stem from Chapters 11 and 12 of my doctoral dissertation Pischke (Reference Pischke2024e) written under his supervision. I also want to thank the anonymous referees for their helpful suggestions which improved the presentation of the paper.
Funding
The author was supported by the ‘Deutsche Forschungsgemeinschaft’ Project DFG KO 1737/6-2.


