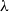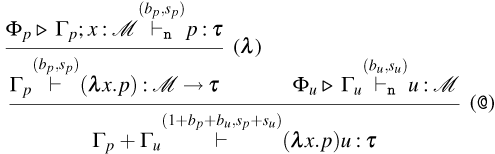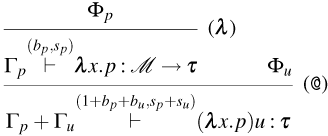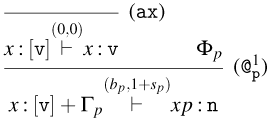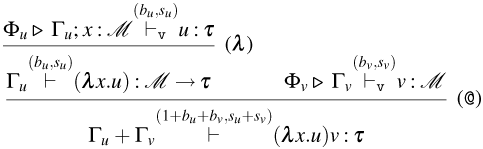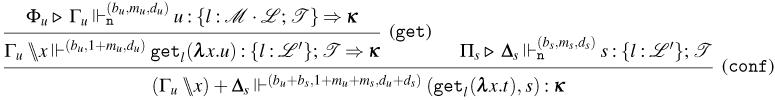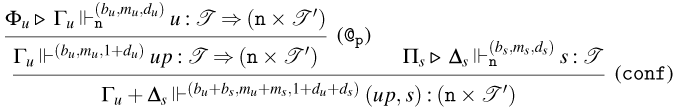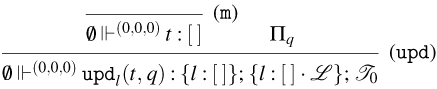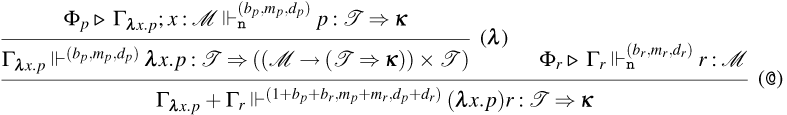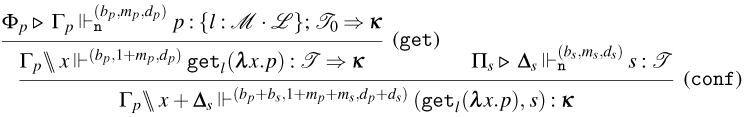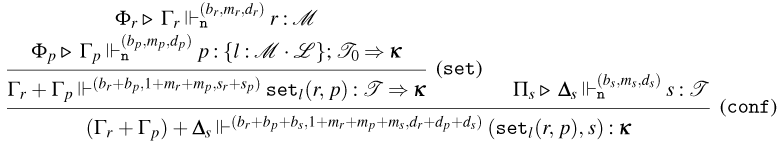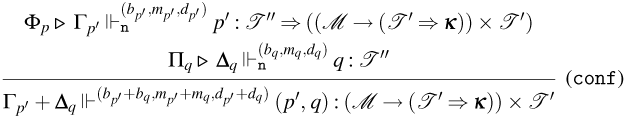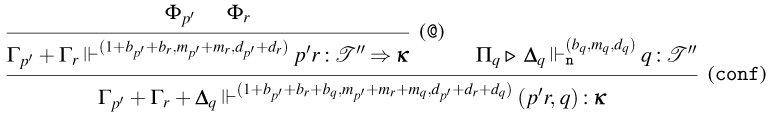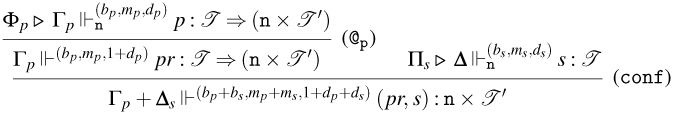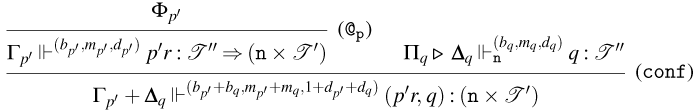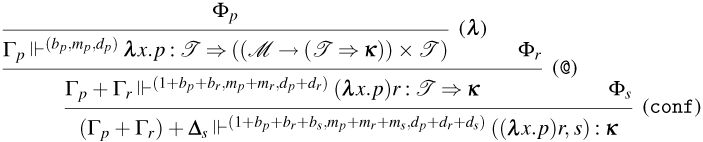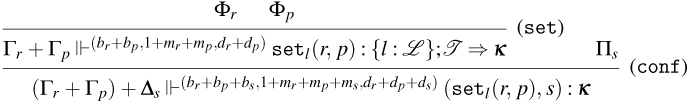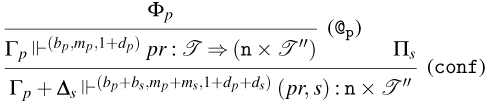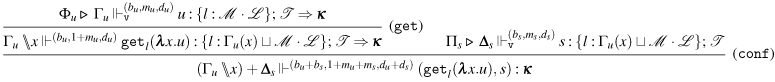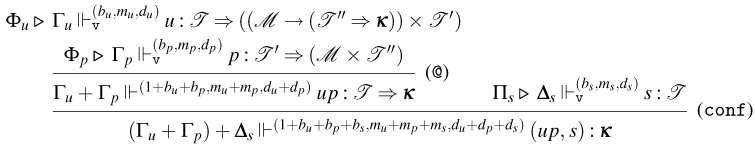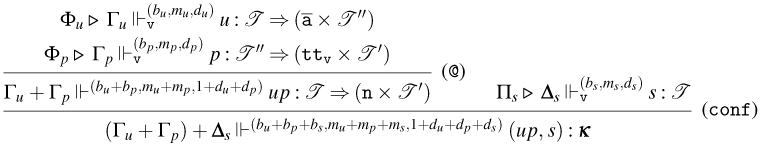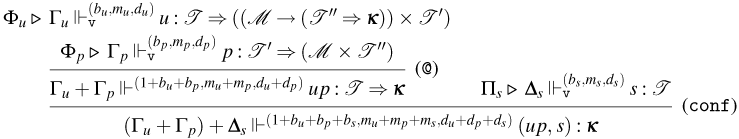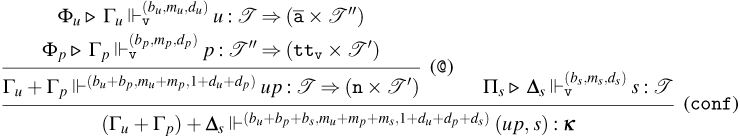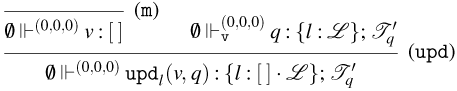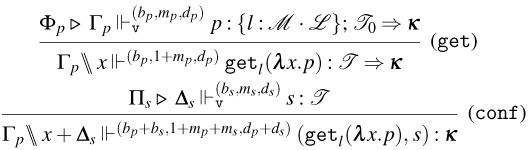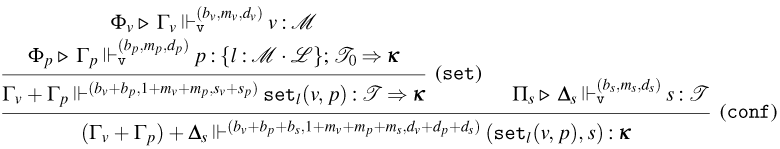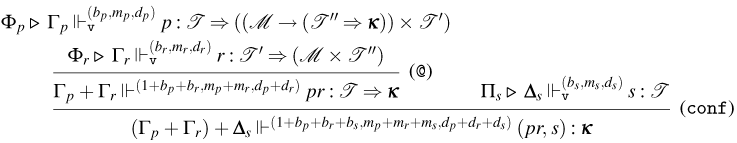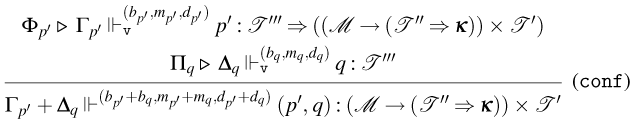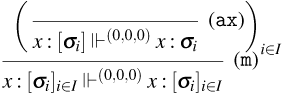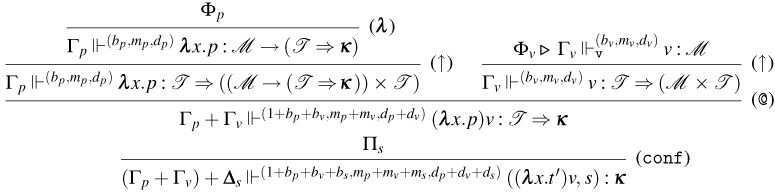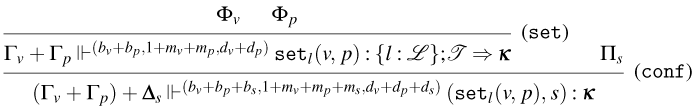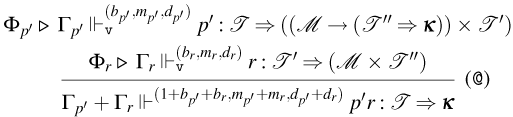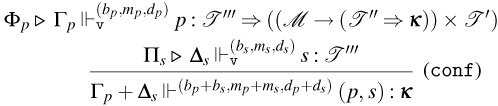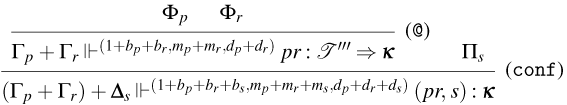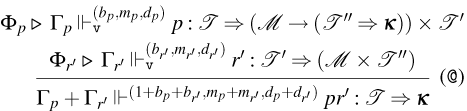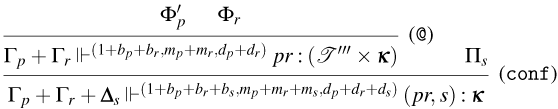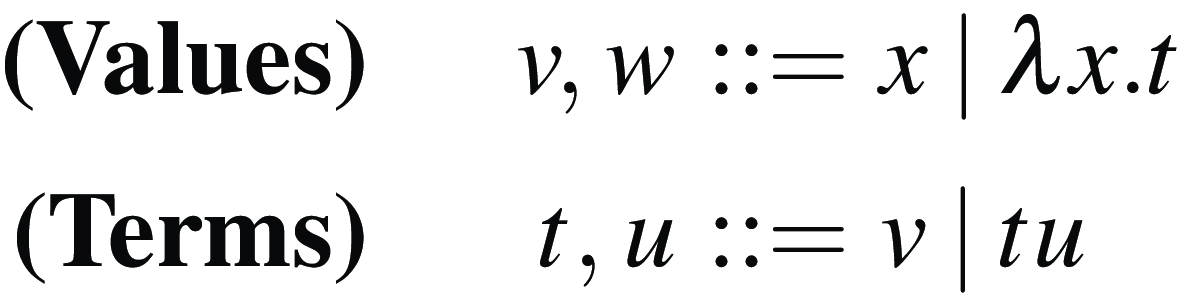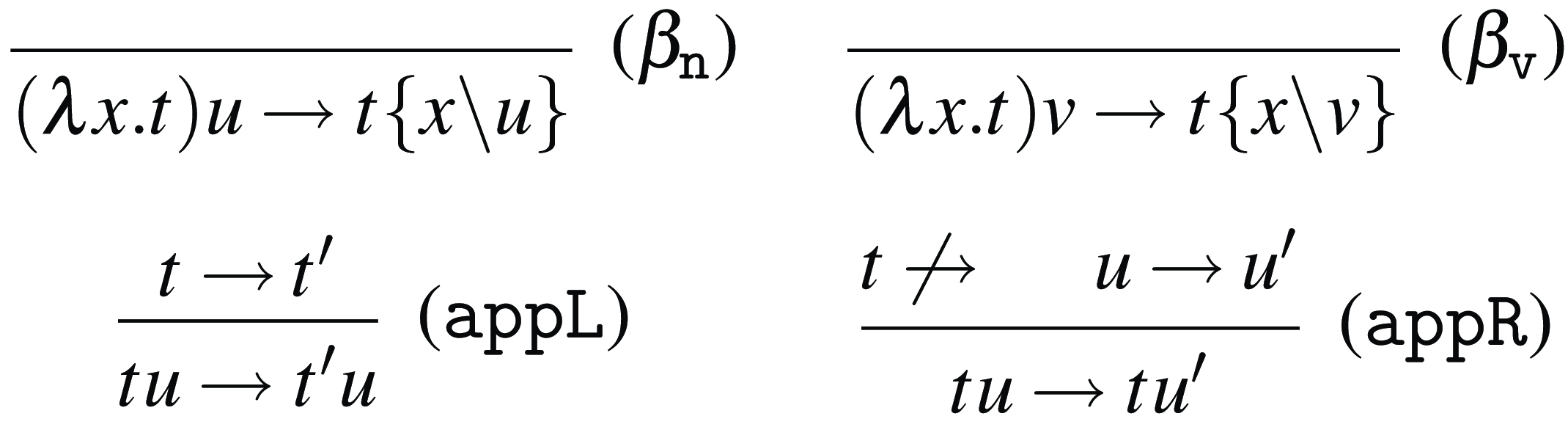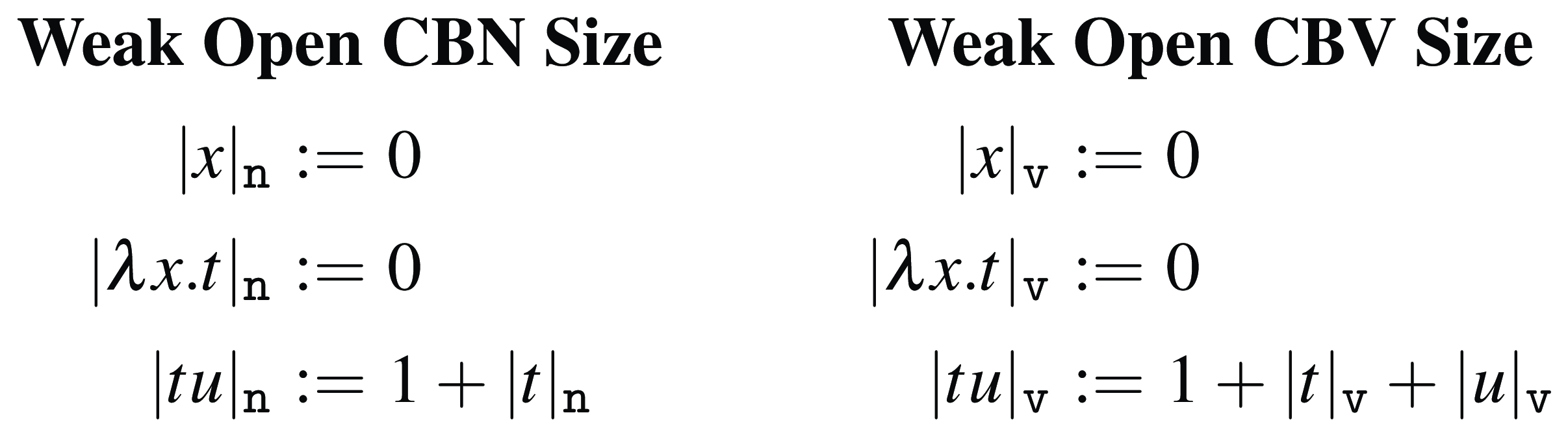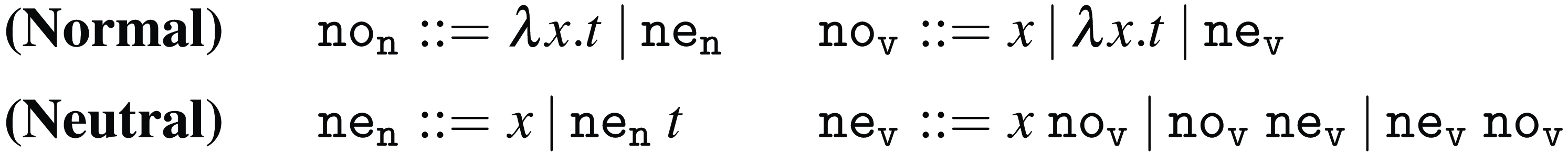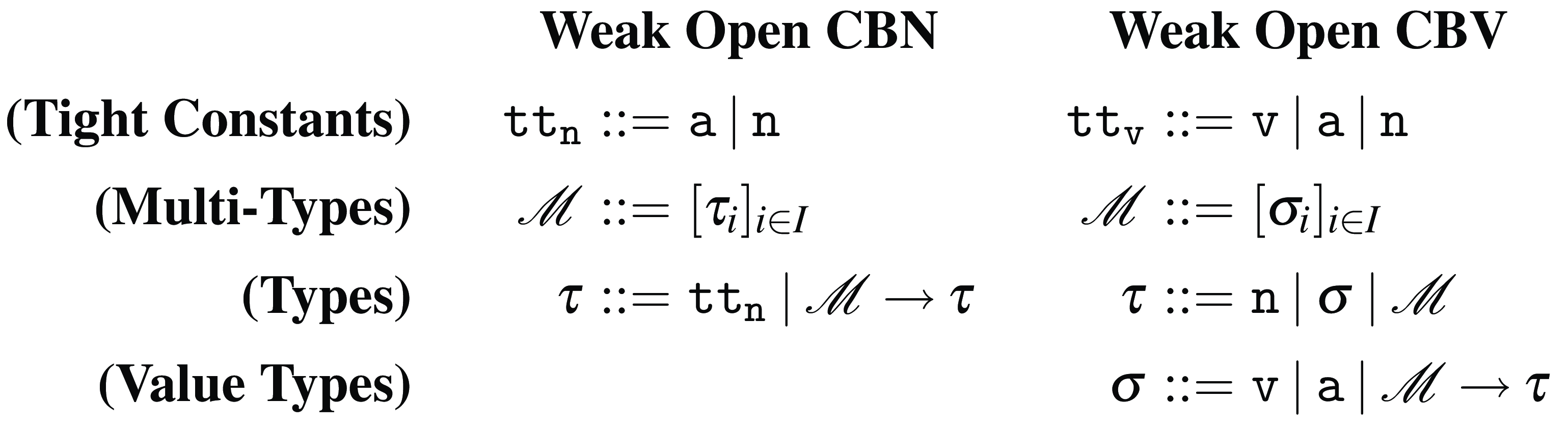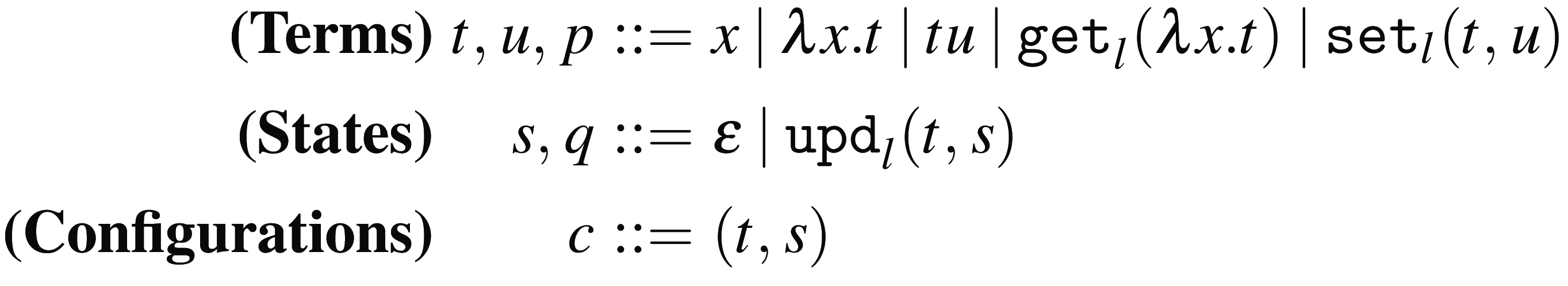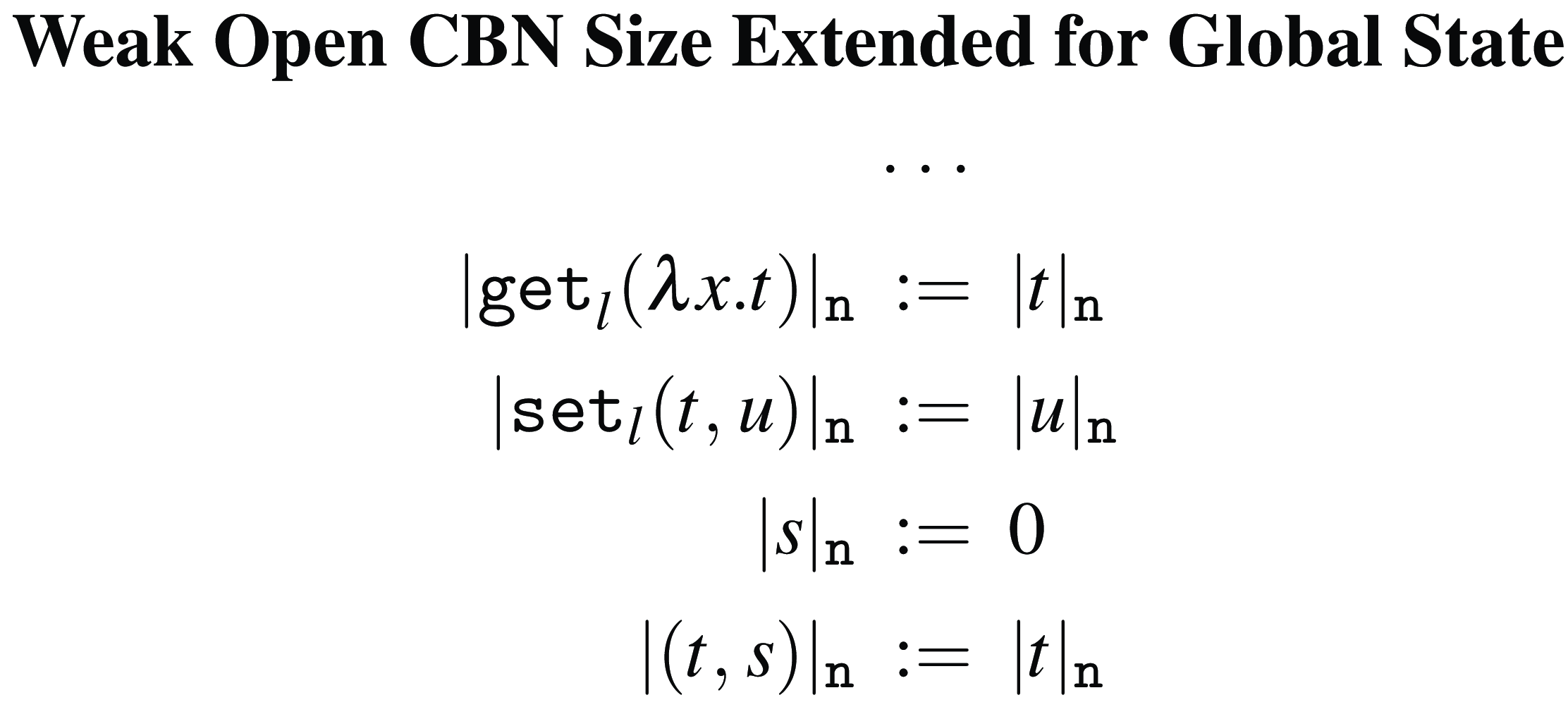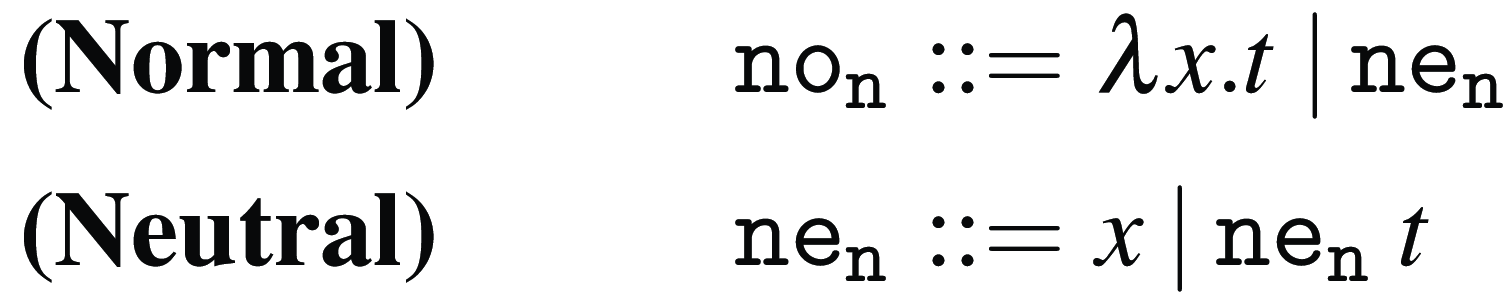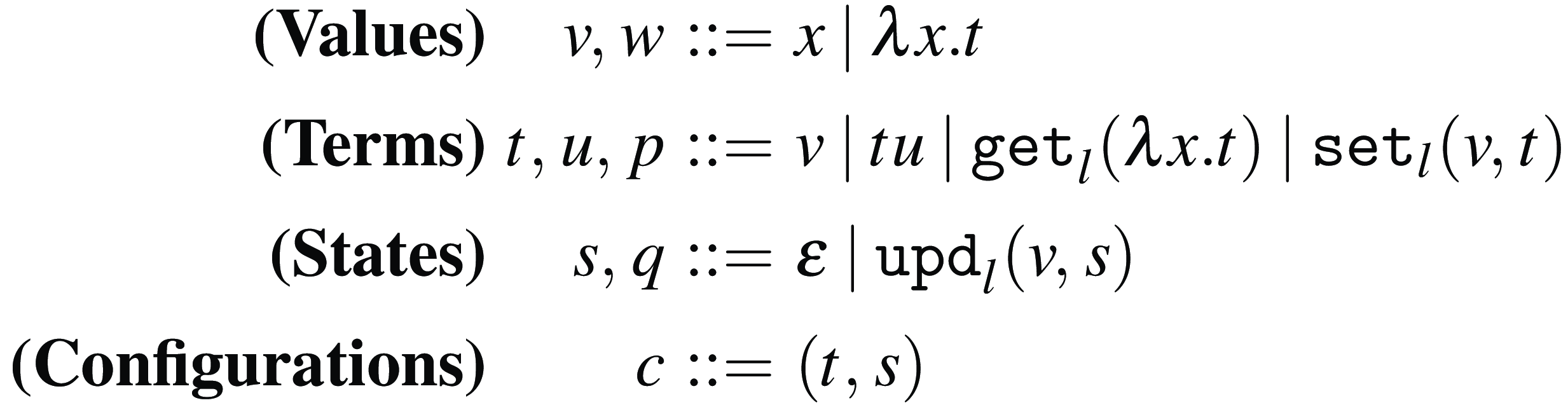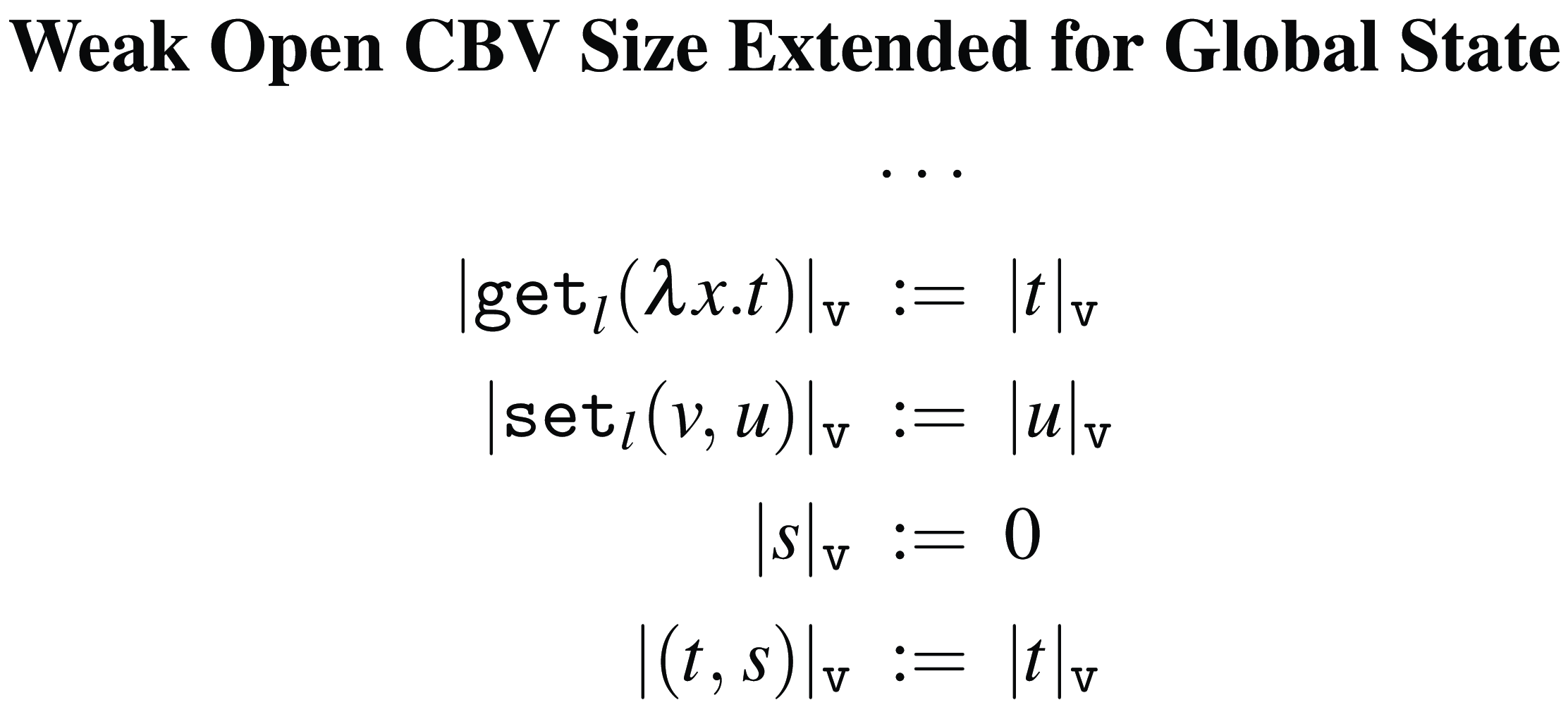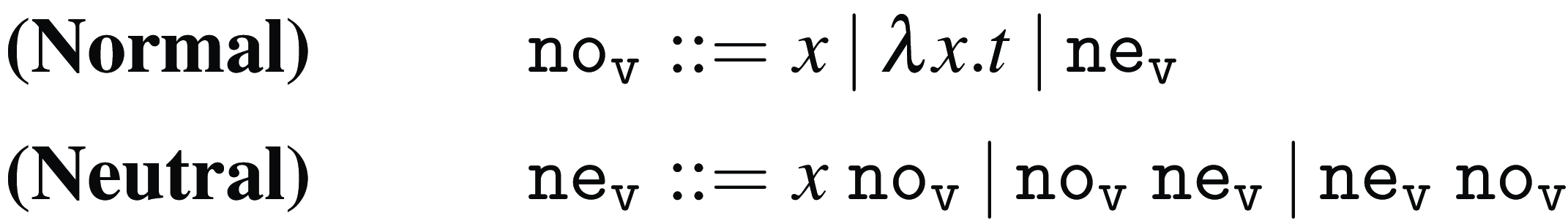1. Introduction
The main aim of this paper is to extend quantitative techniques based on multi-types to programs with effects.
Effectful programs
Programming languages produce different kinds of effects (observable interactions with the environment), such as raising and handling exceptions, reading/writing from/to a global memory, accessing a database or a file, performing pure non-deterministic or probabilistic choices, etc. The degree to which these side effects are visible to the programmer depends on each programming paradigm (Jones and Wadler, Reference Jones and Wadler1993): imperative programming usually makes invisible the distinction between pure computation and effects, while functional programming tries to keep this distinction explicit and clear. In general, dealing with side effects in a clear way facilitates the formal verification of programs, which in turn allows for the use of static analysis tools to ensure their correctness. For example, the functional programming language Haskell encapsulates side effects into monadic actions, a clean approach that is able to put in evidence the distinction between pure and effectful computations. This idea continues to attract growing attention. Indeed, for a pure function
![]() $f \;:\; A \rightarrow B$
, which for any argument of type
$f \;:\; A \rightarrow B$
, which for any argument of type
![]() $A$
returns a result of type
$A$
returns a result of type
![]() $B$
, it is possible to define an effectful function
$B$
, it is possible to define an effectful function
![]() $g$
that behaves like
$g$
that behaves like
![]() $f$
but also produces some effect along the computation, in which case we can specify that
$f$
but also produces some effect along the computation, in which case we can specify that
![]() $g \;:\; A \rightarrow T(B)$
,Footnote
1
where
$g \;:\; A \rightarrow T(B)$
,Footnote
1
where
![]() $T(B)$
makes it clear that
$T(B)$
makes it clear that
![]() $g$
returns a result of type
$g$
returns a result of type
![]() $B$
inside a useful wrapper represented by a monad that encapsulates the effect (Wadler, Reference Wadler1995). This approach allows programming languages to combine the best of both the imperative and declarative worlds: programs can produce effects, but effects are encoded in such a way that formal verification can still be performed using usual tools, by simply lifting them naturally into the monadic setting.
$B$
inside a useful wrapper represented by a monad that encapsulates the effect (Wadler, Reference Wadler1995). This approach allows programming languages to combine the best of both the imperative and declarative worlds: programs can produce effects, but effects are encoded in such a way that formal verification can still be performed using usual tools, by simply lifting them naturally into the monadic setting.
Quantitative properties
We address quantitative properties of programs with effects using multi-types, which originated in the theory of intersection type systems (Coppo and Dezani-Ciancaglini, Reference Coppo and Dezani-Ciancaglini1978). They extend simple types with a new constructor
![]() $\cap$
in such a way that a program
$\cap$
in such a way that a program
![]() $t$
is typable with
$t$
is typable with
![]() $\sigma \cap \tau$
if
$\sigma \cap \tau$
if
![]() $t$
is typable with both types
$t$
is typable with both types
![]() $\sigma$
and
$\sigma$
and
![]() $\tau$
, independently. Intersection types were first introduced as a model for capturing computational properties of the
$\tau$
, independently. Intersection types were first introduced as a model for capturing computational properties of the
![]() $\lambda$
-calculus in a broader sense. For example, termination of different evaluation strategies can be characterized by typability in some appropriate intersection type system; that is, a program
$\lambda$
-calculus in a broader sense. For example, termination of different evaluation strategies can be characterized by typability in some appropriate intersection type system; that is, a program
![]() $t$
is terminating if and only if
$t$
is terminating if and only if
![]() $t$
is typable. Naturally, intersection enjoys associativity (i.e.,
$t$
is typable. Naturally, intersection enjoys associativity (i.e.,
![]() $(\sigma \cap \tau ) \cap \rho = \sigma \cap (\tau \cap \rho )$
), commutativity (i.e.,
$(\sigma \cap \tau ) \cap \rho = \sigma \cap (\tau \cap \rho )$
), commutativity (i.e.,
![]() $\sigma \cap \tau = \tau \cap \sigma$
), and in particular, idempotency (i.e.,
$\sigma \cap \tau = \tau \cap \sigma$
), and in particular, idempotency (i.e.,
![]() $\sigma \cap \sigma = \sigma$
). Thus, an intersection of types can be naturally denoted by a set of types. By considering instead a non-idempotent intersection constructor (i.e.,
$\sigma \cap \sigma = \sigma$
). Thus, an intersection of types can be naturally denoted by a set of types. By considering instead a non-idempotent intersection constructor (i.e.,
![]() $\sigma \cap \sigma \neq \sigma$
), one naturally comes to represent an intersection type as a multi-set, which is why non-idempotent intersection types (Gardner, Reference Gardner, Hagiya and Mitchell1994; Kfoury, Reference Kfoury2000) are usually referred to as multi-types. Just like their idempotent precursors, multi-types capture interesting computational properties of the
$\sigma \cap \sigma \neq \sigma$
), one naturally comes to represent an intersection type as a multi-set, which is why non-idempotent intersection types (Gardner, Reference Gardner, Hagiya and Mitchell1994; Kfoury, Reference Kfoury2000) are usually referred to as multi-types. Just like their idempotent precursors, multi-types capture interesting computational properties of the
![]() $\lambda$
-calculus, but they also grant a substantial improvement: they provide quantitative measures about these properties (de Carvalho, Reference de Carvalho2007, Reference de Carvalho2018). For example, typability in a type system using non-idempotent intersections not only characterizes a qualitative property, such as termination for the
$\lambda$
-calculus, but they also grant a substantial improvement: they provide quantitative measures about these properties (de Carvalho, Reference de Carvalho2007, Reference de Carvalho2018). For example, typability in a type system using non-idempotent intersections not only characterizes a qualitative property, such as termination for the
![]() $\lambda$
-calculus, but also provides quantitative information such as upper bounds for the number of evaluation steps needed to reach a normal form. This shift of perspective, from idempotent to non-idempotent intersection types, goes beyond lowering the logical complexity of the proof: the quantitative information provided by typing derivations in the non-idempotent setting unveils crucial quantitative relations between typing (statics) and reduction (dynamics) of programs.
$\lambda$
-calculus, but also provides quantitative information such as upper bounds for the number of evaluation steps needed to reach a normal form. This shift of perspective, from idempotent to non-idempotent intersection types, goes beyond lowering the logical complexity of the proof: the quantitative information provided by typing derivations in the non-idempotent setting unveils crucial quantitative relations between typing (statics) and reduction (dynamics) of programs.
Upper bounds and exact split measures
Following the pioneering work by Gardner (Reference Gardner, Hagiya and Mitchell1994), Kfoury (Reference Kfoury2000), and de Carvalho (Reference de Carvalho2007, Reference de Carvalho2018), multi-types have been extensively used to reason about programming languages from a quantitative point of view. This is due to the fact that they are able to provide upper bounds for the number of steps needed to reach a normal form. However, a major drawback of this approach is the fact that the upper bound that is obtained actually bounds both the number of steps to reach a normal form and the size of this normal form. As it is well known, the size of a normal form can be exponentially bigger than the number of steps needed to reach that normal form, and thus, the resulting upper bound is not reasonable/interesting. More recently, it was shown (Accattoli et al., Reference Accattoli, Graham-Lengrand and Kesner2018, Reference Accattoli, Graham-Lengrand and Kesner2020) that it is indeed possible to extract better measures from a type system based on multi-types, thus providing exact measures instead of upper bounds. The key insight is to extract the measures only from minimal type derivations. This is achieved by introducing the key notion of tightness for type derivations. Very succinctly, minimal type derivations are obtained by imposing tightness conditions on the final judgment of type derivations. Moreover, by also splitting the set of typing rules so that terms that are consumed during evaluation (consuming) and terms that remain in the normal form (persistent) are typed differently, Accattoli et al. (Reference Accattoli, Graham-Lengrand and Kesner2018, Reference Accattoli, Graham-Lengrand and Kesner2020) show that it is not only possible to obtain exact measures but also independent ones (called exact split measures) for both the number of steps needed to reach a normal form and for its respective size. More precisely, quantitative typing systemsFootnote
2
can be equipped with counters, in such a way that any term
![]() $t$
is typable by a tight type derivation with counters
$t$
is typable by a tight type derivation with counters
![]() $b$
and
$b$
and
![]() $s$
iff
$s$
iff
![]() $t$
reaches a normal form of size
$t$
reaches a normal form of size
![]() $s$
in exactly
$s$
in exactly
![]() $b$
steps.
$b$
steps.
Evaluation strategies and open terms
Starting with Landin’s seminal work (Landin, Reference Landin1965), different incarnations of the
![]() $\lambda$
-calculus continue to be developed and deeply studied in order to provide semantics for different programming languages and proof assistants. Two of the most well-known and well-studied variants of the
$\lambda$
-calculus continue to be developed and deeply studied in order to provide semantics for different programming languages and proof assistants. Two of the most well-known and well-studied variants of the
![]() $\lambda$
-calculus can be found in Plotkin (Reference Plotkin1975): the call-by-value (CBV) and the call-by-name (CBN)
$\lambda$
-calculus can be found in Plotkin (Reference Plotkin1975): the call-by-value (CBV) and the call-by-name (CBN)
![]() $\lambda$
-calculus. The CBV
$\lambda$
-calculus. The CBV
![]() $\lambda$
-calculus, in particular, has been used in the formalization of modern programming languages, such as the call discipline of C or the operational semantics of OCaml. And, while the original formulation of CBN
$\lambda$
-calculus, in particular, has been used in the formalization of modern programming languages, such as the call discipline of C or the operational semantics of OCaml. And, while the original formulation of CBN
![]() $\lambda$
-calculus is not as widely employed, its memoized variant, commonly referred to as call-by-need (Launchbury, Reference Launchbury, Deusen and Lang1993; Ariola and Felleisen, Reference Ariola and Felleisen1997), has been used to formalize the operational semantics of lazy programming languages such as Haskell. Evaluation in the CBN and CBV
$\lambda$
-calculus is not as widely employed, its memoized variant, commonly referred to as call-by-need (Launchbury, Reference Launchbury, Deusen and Lang1993; Ariola and Felleisen, Reference Ariola and Felleisen1997), has been used to formalize the operational semantics of lazy programming languages such as Haskell. Evaluation in the CBN and CBV
![]() $\lambda$
-calculi is weak: evaluation does not occur inside abstractions. Indeed, abstractions are used to denote functions, and programming languages do not evaluate the body of functions before all parameters are consumed. Another important aspect of functional programming languages is that programs are assumed to be closed, that is, contain no free variables. The CBV and CBN
$\lambda$
-calculi is weak: evaluation does not occur inside abstractions. Indeed, abstractions are used to denote functions, and programming languages do not evaluate the body of functions before all parameters are consumed. Another important aspect of functional programming languages is that programs are assumed to be closed, that is, contain no free variables. The CBV and CBN
![]() $\lambda$
-calculi, however, are open. It has been established that the closed variant of the CBV
$\lambda$
-calculi, however, are open. It has been established that the closed variant of the CBV
![]() $\lambda$
-calculus is very well-behaved, since all normal forms are values; however, the open CBV
$\lambda$
-calculus is very well-behaved, since all normal forms are values; however, the open CBV
![]() $\lambda$
-calculus gives rise to premature normal forms (see Accattoli and Guerrieri, Reference Accattoli, Guerrieri and Igarashi2016, Reference Accattoli and Guerrieri2022, for details). If we move from the realm of programming languages into that of proof assistants like Coq, then weak evaluation is not enough. In order to talk about equality of types in Coq’s dependent type theory, strong evaluation, which relies on evaluation over open terms, is needed. In sum, and following along the lines of our previous work (Alves et al., Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), we will consider weak and open versions of Plotkin’s CBN and CBV
$\lambda$
-calculus gives rise to premature normal forms (see Accattoli and Guerrieri, Reference Accattoli, Guerrieri and Igarashi2016, Reference Accattoli and Guerrieri2022, for details). If we move from the realm of programming languages into that of proof assistants like Coq, then weak evaluation is not enough. In order to talk about equality of types in Coq’s dependent type theory, strong evaluation, which relies on evaluation over open terms, is needed. In sum, and following along the lines of our previous work (Alves et al., Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), we will consider weak and open versions of Plotkin’s CBN and CBV
![]() $\lambda$
-calculus so that our results can be easily adapted to the closed setting for both weak and strong evaluation. As shorthand, we will say Weak Open CBN and CBV whenever we mean Weak Open CBN and Weak Open CBV.
$\lambda$
-calculus so that our results can be easily adapted to the closed setting for both weak and strong evaluation. As shorthand, we will say Weak Open CBN and CBV whenever we mean Weak Open CBN and Weak Open CBV.
Contributions
This paper is about providing quantitative information for
![]() $\lambda$
-calculi with effectful computations by means of intersection types. We focus in particular on a
$\lambda$
-calculi with effectful computations by means of intersection types. We focus in particular on a
![]() $\lambda$
-calculus extended with (algebraic) operations for reading and writing on a global memory. In previous work (Alves et al., Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), inspired by the monadic approach adopted in de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021), we designed a quantitatively sound and complete tight type system for a CBV evaluation strategy equipped with global memory. Soundness means that not only a tightly typable term
$\lambda$
-calculus extended with (algebraic) operations for reading and writing on a global memory. In previous work (Alves et al., Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), inspired by the monadic approach adopted in de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021), we designed a quantitatively sound and complete tight type system for a CBV evaluation strategy equipped with global memory. Soundness means that not only a tightly typable term
![]() $t$
is always terminating but also that the tight type derivation of
$t$
is always terminating but also that the tight type derivation of
![]() $t$
provides exact (split) measures for both the number of
$t$
provides exact (split) measures for both the number of
![]() $\beta$
-steps and the number of memory accesses during the evaluation process. Moreover, the type system also provides the size of normal configurations. Dually for completeness. In this paper, we extend (Alves et al., Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023) both from an operational point of view and a denotational one.
$\beta$
-steps and the number of memory accesses during the evaluation process. Moreover, the type system also provides the size of normal configurations. Dually for completeness. In this paper, we extend (Alves et al., Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023) both from an operational point of view and a denotational one.
Extending the operational semantics
In Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), function applications were restricted to the syntactical form
![]() $vt$
, where
$vt$
, where
![]() $v$
is not an arbitrary term but a value. This follows the standard approach when considering Moggi’s CBV translation of the
$v$
is not an arbitrary term but a value. This follows the standard approach when considering Moggi’s CBV translation of the
![]() $\lambda$
-calculus, where applications are translated into CBV let-expressions (Moggi, Reference Moggi1989, Reference Moggi1991): if
$\lambda$
-calculus, where applications are translated into CBV let-expressions (Moggi, Reference Moggi1989, Reference Moggi1991): if
![]() $(\_)^v$
is the aforementioned translation, then
$(\_)^v$
is the aforementioned translation, then
![]() $(tu)^v = (\texttt {let } x = u^v \texttt { in } t^v)$
, which is syntactic sugar for
$(tu)^v = (\texttt {let } x = u^v \texttt { in } t^v)$
, which is syntactic sugar for
![]() $(\lambda x.(\lambda y.xy) (u^v)) (t^v)$
(Sabry and Wadler, Reference Sabry and Wadler1997). But the application form
$(\lambda x.(\lambda y.xy) (u^v)) (t^v)$
(Sabry and Wadler, Reference Sabry and Wadler1997). But the application form
![]() $vt$
is clearly not stable under CBN evaluation (e.g., given
$vt$
is clearly not stable under CBN evaluation (e.g., given
![]() ${\tt I} = \lambda z. z$
, the term
${\tt I} = \lambda z. z$
, the term
![]() $(\lambda x. xy)({\tt I} {\tt I})$
CBN evaluates to
$(\lambda x. xy)({\tt I} {\tt I})$
CBN evaluates to
![]() $({\tt I} {\tt I}) y$
, which is not of the desired form), which means that we cannot take this representation when considering Plotkin’s CBN
$({\tt I} {\tt I}) y$
, which is not of the desired form), which means that we cannot take this representation when considering Plotkin’s CBN
![]() $\lambda$
-calculus. A possible solution would be to base our work on Moggi’s metalanguage instead of the
$\lambda$
-calculus. A possible solution would be to base our work on Moggi’s metalanguage instead of the
![]() $\lambda$
-calculus. In this work, we show that it is possible to take the standard syntax of the
$\lambda$
-calculus. In this work, we show that it is possible to take the standard syntax of the
![]() $\lambda$
-calculus, extended with (algebraic) operations for reading and writing on a global memory, and reason not only about CBV (as in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023)) but also CBN evaluation. For this, one needs to be careful when defining the operational semantics and the typing system according to each evaluation strategy. We leave the details to the later sections of this paper, but we will present some intuition at this moment. Just like in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), we will lift reduction over terms to reduction over configurations, which are pairs consisting of a term and a state. Let
$\lambda$
-calculus, extended with (algebraic) operations for reading and writing on a global memory, and reason not only about CBV (as in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023)) but also CBN evaluation. For this, one needs to be careful when defining the operational semantics and the typing system according to each evaluation strategy. We leave the details to the later sections of this paper, but we will present some intuition at this moment. Just like in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), we will lift reduction over terms to reduction over configurations, which are pairs consisting of a term and a state. Let
![]() $t$
be some term and
$t$
be some term and
![]() $s$
some state, then
$s$
some state, then
![]() $(t, s)$
is a configuration, and we write
$(t, s)$
is a configuration, and we write
![]() $(t, s) \rightarrow (t', s')$
to denote that term
$(t, s) \rightarrow (t', s')$
to denote that term
![]() $t$
reduces to some other term
$t$
reduces to some other term
![]() $t'$
in one step and that the step changes the state from
$t'$
in one step and that the step changes the state from
![]() $s$
to
$s$
to
![]() $s'$
as a side effect. Let us focus on the behavior of applications over the following three scenarios:
$s'$
as a side effect. Let us focus on the behavior of applications over the following three scenarios:
-
(1) Applications are of the form
 $vu$
(recall that
$vu$
(recall that
 $v$
is a value), and evaluation is CBV. In this case, evaluation cannot occur on the left of applications but can occur on the right:
$v$
is a value), and evaluation is CBV. In this case, evaluation cannot occur on the left of applications but can occur on the right: \begin{equation*} \frac {{(v,s) \not \rightarrow }\quad {(u,s)\rightarrow (u',s')}} {(vu,s) \rightarrow (vu',s')}\end{equation*}
\begin{equation*} \frac {{(v,s) \not \rightarrow }\quad {(u,s)\rightarrow (u',s')}} {(vu,s) \rightarrow (vu',s')}\end{equation*}
Therefore, state
 $s$
changes with respect to the application
$s$
changes with respect to the application
 $vu$
in the same way as it changes with respect to
$vu$
in the same way as it changes with respect to
 $u$
.
$u$
. -
(2) Applications are of the form
 $tu$
, and evaluation is CBN. In this case, evaluation cannot occur on the right of application but can only occur on the left:
$tu$
, and evaluation is CBN. In this case, evaluation cannot occur on the right of application but can only occur on the left: \begin{equation*} \frac {(t,s) \rightarrow (t', s')} {(tu,s) \rightarrow (t'u,s')} \end{equation*}
\begin{equation*} \frac {(t,s) \rightarrow (t', s')} {(tu,s) \rightarrow (t'u,s')} \end{equation*}
Therefore, state
 $s$
changes with respect to the application
$s$
changes with respect to the application
 $tu$
in the same way as it changes with respect to
$tu$
in the same way as it changes with respect to
 $t$
.
$t$
. -
(3) Applications are of the form
 $tu$
, and evaluation is CBV. In this case, evaluation should first be performed on the left as much as possible, and then it should continue on the right:
$tu$
, and evaluation is CBV. In this case, evaluation should first be performed on the left as much as possible, and then it should continue on the right: \begin{equation*} \frac {(t,s) \rightarrow (t', s')} {(tu,s) \rightarrow (t'u,s')} \qquad \frac {{(t,s) \not \rightarrow }\quad {(u,s) \rightarrow (u',s')}} {(tu,s) \rightarrow (tu',s')} \end{equation*}
\begin{equation*} \frac {(t,s) \rightarrow (t', s')} {(tu,s) \rightarrow (t'u,s')} \qquad \frac {{(t,s) \not \rightarrow }\quad {(u,s) \rightarrow (u',s')}} {(tu,s) \rightarrow (tu',s')} \end{equation*}
Therefore, state
 $s$
changes with respect to the application
$s$
changes with respect to the application
 $tu$
in a compositional way. And we can see how the composition of states is essential to capture the evaluation of applications.
$tu$
in a compositional way. And we can see how the composition of states is essential to capture the evaluation of applications.
Defining reduction over configurations turns out to be crucial in order to capture the kind of results that we are interested in. Indeed, while it is possible to provide operational semantics for algebraic effects such as non-determinism, probabilistic choice, non-termination, and output, without mentioning any kind of external environment where effects occur – as was first done in Plotkin and Power (Reference Plotkin, Power, Honsell and Miculan2001) and later explored in Gavazzo et al. (Reference Gavazzo, Treglia, Vanoni and Weirich2024) – the same cannot be said for other effects, such as global state. This problem was immediately identified in Plotkin and Power (Reference Plotkin, Power, Honsell and Miculan2001), but it was only in Plotkin and Power (Reference Plotkin, Power, Bauer and Mislove2008) that the same authors provided a solution to this problem, by taking into account the coalgebraic structure of state. This then allowed them to provide an operational semantics for state based on configurations. In other words, in order to provide operational semantics for algebraic effects such as state, it is not enough to consider reduction over terms – one must consider reduction over configurations instead.
Extending the denotational semantics
In de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021) and Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), the operational semantics is based on configurations, and the associated type systems turn out to be both sound and complete. This is in contrast with the more general approach to effectful computations in Gavazzo et al. (Reference Gavazzo, Treglia, Vanoni and Weirich2024), where the operational semantics is not based on configuration, and thus, it cannot capture the particular case of the global state monad because subject expansion fails.
In this paper, we will consider an extended notion of state with a log (a mapping of locations to a history of values), which is inspired by Ahman and Uustalu (Reference Ahman, Uustalu, Matthes and Schubert2013). This is not a new notion of state: its algebraic theory can already be found in Ahman and Uustalu (Reference Ahman, Uustalu, Matthes and Schubert2013), and its coalgebraic properties (in the sense of Plotkin and Power (Reference Plotkin, Power, Bauer and Mislove2008)) were studied in Ahman and Uustalu (Reference Ahman, Uustalu, Jacobs, Silva and Staton2014). It turns out that the notion of state considered in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023) can be easily recovered from this current proposal by simply ignoring the log (update history). Moreover, by keeping track of all updates to the state, we are now able to distinguish between configurations that were indistinguishable in de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021 and Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023).
Summary
In order to gradually present our ideas, we first introduce the tight typing techniques in Section 2 for pure Weak Open CBN and CBV; that is, no effects are produced during computation. Then, in Section 3, we apply these techniques to the effectful settings by lifting reduction and typing to configurations instead of terms and by adding operations for reading and writing on a global memory. In particular, Section 3.1.1 (resp. Section 3.2.1) introduces Weak Open CBN (resp. CBV) with Global State, and Section 3.1.2 (resp. Section 3.2.2) defines a quantitative type system capturing exact measures for the length of evaluation, number of state accesses, and size of normal forms. Quantitative soundness and completeness of the type system with respect to Weak Open CBN (resp. CBV) with global state are proved in Section 3.1.2 (resp. Section 3.2.2). We discuss related work in Section 4 and conclude in Section 5. In Appendix A, we include all auxiliary lemmas, as well as all the proofs in full detail. For now, we leave the proofs in full detail for the reviewers, but we intend to significantly shorten some straightforward proofs in order to gain space in the final version.
Preliminary general notations
We start with some general notations. Given a (one-step) reduction relation
![]() $\rightarrow {\mathscr{R}}$
,
$\rightarrow {\mathscr{R}}$
,
![]() $\twoheadrightarrow {\mathscr{R}}$
denotes the reflexive-transitive closure of
$\twoheadrightarrow {\mathscr{R}}$
denotes the reflexive-transitive closure of
![]() $\rightarrow {\mathscr{R}}$
. Let
$\rightarrow {\mathscr{R}}$
. Let
![]() $S_1, \ldots , S_n$
represent
$S_1, \ldots , S_n$
represent
![]() $n$
different sets of possibly different kinds of reduction steps. We write
$n$
different sets of possibly different kinds of reduction steps. We write
![]() $t \twoheadrightarrow _{\mathscr{R}}^{(I_1, \ldots , I_n)} u$
, where
$t \twoheadrightarrow _{\mathscr{R}}^{(I_1, \ldots , I_n)} u$
, where
![]() $I_1, \ldots , I_n$
are positive integers, for a reduction sequence from
$I_1, \ldots , I_n$
are positive integers, for a reduction sequence from
![]() $t$
to
$t$
to
![]() $u$
that takes
$u$
that takes
![]() $I_1$
steps using rules from set
$I_1$
steps using rules from set
![]() $S_1$
,
$S_1$
,
![]() $I_2$
steps using rules from set
$I_2$
steps using rules from set
![]() $S_2$
, …, and
$S_2$
, …, and
![]() $I_n$
steps using rules from set
$I_n$
steps using rules from set
![]() $S_n$
. A term
$S_n$
. A term
![]() $t$
is said to be (1) in
$t$
is said to be (1) in
![]() $\mathscr{R}$
-normal form or
$\mathscr{R}$
-normal form or
![]() $\mathscr{R}$
-irreducible (written
$\mathscr{R}$
-irreducible (written
![]() $t \not \rightarrow {\mathscr{R}}$
) iff there is no
$t \not \rightarrow {\mathscr{R}}$
) iff there is no
![]() $u$
such that
$u$
such that
![]() $t \rightarrow {\mathscr{R}} u$
and (2)
$t \rightarrow {\mathscr{R}} u$
and (2)
![]() $\mathscr{R}$
-normalizing iff there is some
$\mathscr{R}$
-normalizing iff there is some
![]() $\mathscr{R}$
-normal form
$\mathscr{R}$
-normal form
![]() $u$
such that
$u$
such that
![]() $t \twoheadrightarrow _{\mathscr{R}} u$
. The reduction relation
$t \twoheadrightarrow _{\mathscr{R}} u$
. The reduction relation
![]() $\mathscr{R}$
is normalizing iff every term is
$\mathscr{R}$
is normalizing iff every term is
![]() $\mathscr{R}$
-normalizing. In general, reduction relations are non-deterministic. However, given any reduction relation
$\mathscr{R}$
-normalizing. In general, reduction relations are non-deterministic. However, given any reduction relation
![]() $\rightarrow {\mathscr{R}}$
, it is always possible to consider a deterministic subset of
$\rightarrow {\mathscr{R}}$
, it is always possible to consider a deterministic subset of
![]() $\rightarrow {\mathscr{R}}$
, which is usually referred to as an evaluation strategy. In particular, Plotkin’s CBN and CBV variants of the
$\rightarrow {\mathscr{R}}$
, which is usually referred to as an evaluation strategy. In particular, Plotkin’s CBN and CBV variants of the
![]() $\lambda$
-calculus are based on particular choices of evaluation strategies with respect to the (full)
$\lambda$
-calculus are based on particular choices of evaluation strategies with respect to the (full)
![]() $\lambda$
-calculus.
$\lambda$
-calculus.
2. Weak Open CBN and CBV
In this paper, we use the tight typing technique in Accattoli et al. (Reference Accattoli, Graham-Lengrand and Kesner2020) for obtaining quantitative bounds/measures, such as the length of reduction sequences to normal forms and the size of such normal forms. Originally, Accattoli et al. (Reference Accattoli, Graham-Lengrand and Kesner2020) consider different evaluation strategies, such as head evaluation, leftmost-outermost evaluation, the maximal strategy, and linear head evaluation. In this paper, instead, we will consider Weak Open CBN and CBV. In particular, pure Weak Open CBN and CBV (i.e., without effects) is first presented in this section, and then the general case is presented in Section 3.
2.1 Syntax and operational semantics
We now introduce the syntax of the
![]() $\lambda$
-calculus and the operational semantics for Weak Open CBN and CBV evaluations.
$\lambda$
-calculus and the operational semantics for Weak Open CBN and CBV evaluations.
The syntax of the
 $\lambda$
-calculus
$\lambda$
-calculus
The sets of values and terms of the
![]() $\lambda$
-calculus are defined by the grammars in Figure 1. The sets of free and bound variables of terms are defined as usual, and syntactic equality of terms is considered up to
$\lambda$
-calculus are defined by the grammars in Figure 1. The sets of free and bound variables of terms are defined as usual, and syntactic equality of terms is considered up to
![]() $\alpha$
-conversion (Barendregt, Reference Barendregt1985).
$\alpha$
-conversion (Barendregt, Reference Barendregt1985).
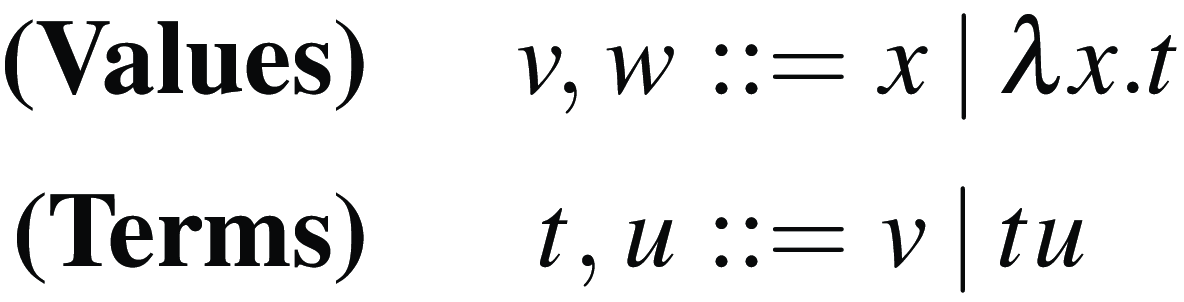
Figure 1. The syntax of the
![]() $\lambda$
-calculus.
$\lambda$
-calculus.
Evaluation in Weak Open CBN and CBV
Weak Open CBN and CBV evaluation notions are defined as subsets of the reduction rules in Figure 2. In particular, Weak CBN evaluation is denoted by
![]() ${\rightarrow }_{\texttt {n}}$
and given by rules (
${\rightarrow }_{\texttt {n}}$
and given by rules (
![]() $\beta _{\tt n}$
) and (appL), and Weak CBV evaluation is denoted by
$\beta _{\tt n}$
) and (appL), and Weak CBV evaluation is denoted by
![]() ${\rightarrow }_{\texttt {v}}$
and given by rules (
${\rightarrow }_{\texttt {v}}$
and given by rules (
![]() $\beta _{\tt v}$
) and (appL) and (appR).
$\beta _{\tt v}$
) and (appL) and (appR).
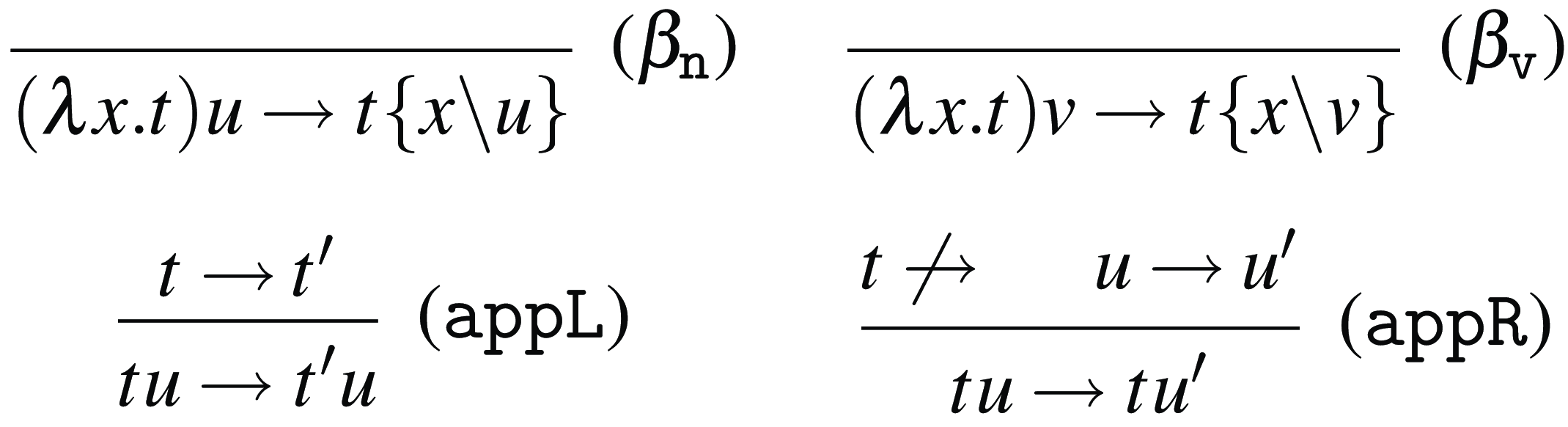
Figure 2. Reduction rules for Weak Open CBN and CBV.
Weak Open CBN and CBV size
The notions of Weak Open CBN size
![]() $|{t}|_{\texttt {n}}$
and Weak Open CBV size
$|{t}|_{\texttt {n}}$
and Weak Open CBV size
![]() $|{t}|_{\texttt {v}}$
are defined in Figure 3. Since we are considering weak versions of CBN and CBV evaluation, both variables and abstractions have size zero. The difference is in applications: in CBN, only the left side of an application is evaluated, and thus, only this left side contributes to the overall size; in CBV, both sides of applications are evaluated, and thus, both sides contribute to the overall size.
$|{t}|_{\texttt {v}}$
are defined in Figure 3. Since we are considering weak versions of CBN and CBV evaluation, both variables and abstractions have size zero. The difference is in applications: in CBN, only the left side of an application is evaluated, and thus, only this left side contributes to the overall size; in CBV, both sides of applications are evaluated, and thus, both sides contribute to the overall size.
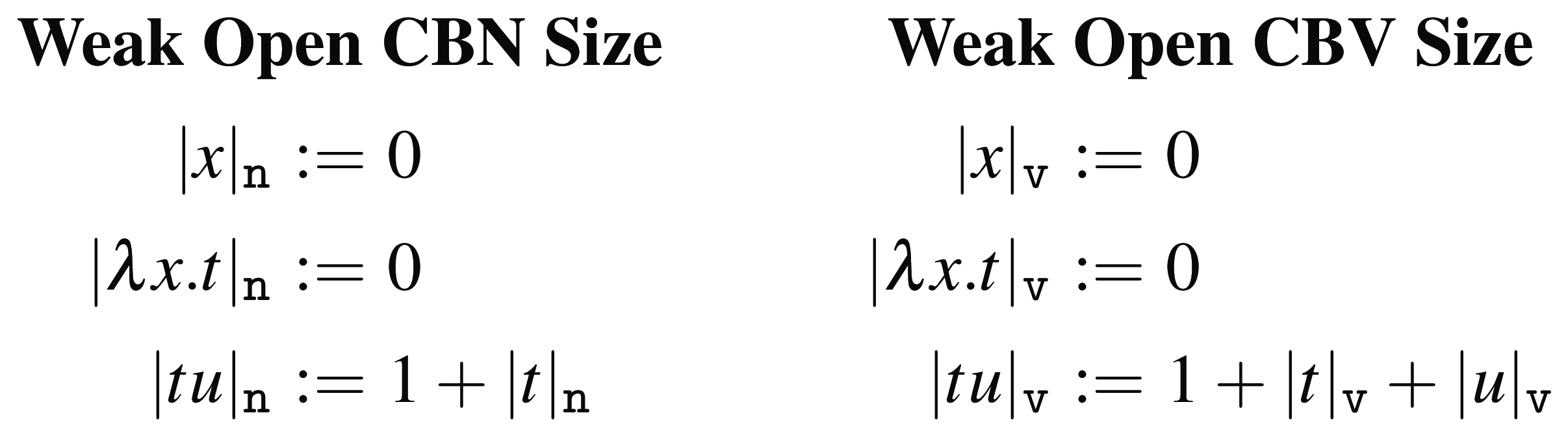
Figure 3. Weak Open CBN and CBV size.
Normal and neutral forms
In Figure 4, we present two grammars
![]() ${\tt no}_{{\tt n}}$
(CBN normal terms) and
${\tt no}_{{\tt n}}$
(CBN normal terms) and
![]() ${\tt no}_{{\tt v}}$
(CBV normal terms) that characterize all normal forms for Weak Open CBN and CBV, respectively. The key notion that allows us to define these grammars is that of neutral term. A neutral term is also a normal term; however, it has an additional property: it does not produce any new redexes when plugged into the left-hand side of some application. In Weak Open CBN evaluation, abstractions are the only normal terms that are not neutral. However, in Weak Open CBV evaluation, both abstractions and variables are (non-neutral) normal terms.
${\tt no}_{{\tt v}}$
(CBV normal terms) that characterize all normal forms for Weak Open CBN and CBV, respectively. The key notion that allows us to define these grammars is that of neutral term. A neutral term is also a normal term; however, it has an additional property: it does not produce any new redexes when plugged into the left-hand side of some application. In Weak Open CBN evaluation, abstractions are the only normal terms that are not neutral. However, in Weak Open CBV evaluation, both abstractions and variables are (non-neutral) normal terms.

Figure 4. Normal and neutral terms for Weak Open CBN and CBV.
The following propositions, whose proofs are in Sections A.1.1 and A.1.2, respectively, show that the grammars for normal and neutral terms for Weak Open CBN and CBV in Figure 4 are sound and complete.
Proposition 1 (Normal forms for Weak Open CBN).
![]() $t$
be a term. Then
$t$
be a term. Then
![]() $t \in {\tt no}_{{\tt n}}$
iff
$t \in {\tt no}_{{\tt n}}$
iff
![]() $t \not {\!\rightarrow }_{\texttt {n}}$
.
$t \not {\!\rightarrow }_{\texttt {n}}$
.
Proposition 2 (Normal forms for Weak Open CBV). Let
![]() $t$
be a term. Then
$t$
be a term. Then
![]() $t \in {\tt no}_{{\tt v}}$
iff
$t \in {\tt no}_{{\tt v}}$
iff
![]() $t \not {\!\rightarrow }_{\texttt {v}}$
.
$t \not {\!\rightarrow }_{\texttt {v}}$
.
2.2 Quantitative types for Weak Open CBN and CBV
In this section, we present the quantitative type system for Weak Open CBN and CBV. Quantitative type systems are specified by non-idempotent intersection type systems (Gardner, Reference Gardner, Hagiya and Mitchell1994; Kfoury, Reference Kfoury2000; de Carvalho, Reference de Carvalho2007), which are typing systems inspired by the resource-aware nature of linear logic. The latter was introduced by Girard (Reference Girard1987) as a refinement of intuitionistic (and classical) logic that highlights the role of formulas as resources. Due to Curry and Howard, we know that types and terms in the simply-typed
![]() $\lambda$
-calculus correspond to proofs and propositions in (the implicational fragment of) intuitionistic logic, respectively. Therefore, one can look at Girard’s translations of intuitionistic logic into linear logic (Girard, Reference Girard1987) in order to obtain resource-aware versions for CBN and CBV.
$\lambda$
-calculus correspond to proofs and propositions in (the implicational fragment of) intuitionistic logic, respectively. Therefore, one can look at Girard’s translations of intuitionistic logic into linear logic (Girard, Reference Girard1987) in order to obtain resource-aware versions for CBN and CBV.
In this section, we introduce all the necessary tools in order to present the quantitative type systems for Weak Open CBN and CBV.
Tight constants and multi-types
The types for Weak Open CBN and CBV are presented in Figure 5, where
![]() $I$
is a finite set.
$I$
is a finite set.
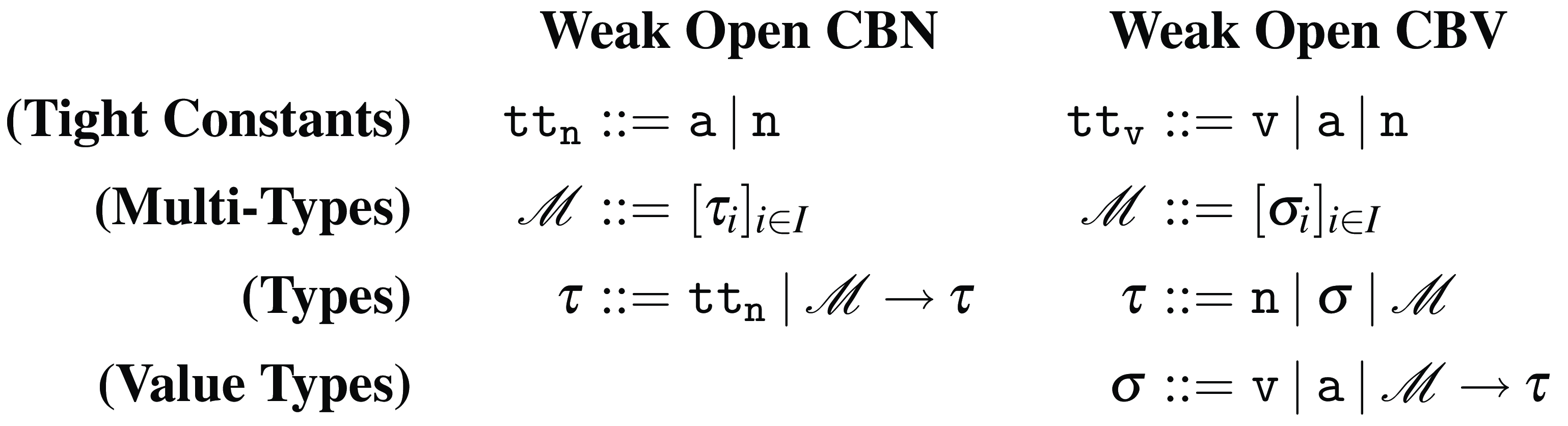
Figure 5. Types for Weak Open CBN and CBV.
Notation. Let
![]() ${\tt tt}_{0}$
be any tight constant in
${\tt tt}_{0}$
be any tight constant in
![]() ${{\tt tt}_{\tt n}}$
or
${{\tt tt}_{\tt n}}$
or
![]() ${\tt tt}_{\tt v}$
. We will write
${\tt tt}_{\tt v}$
. We will write
![]() $\overline {{{\tt tt}_{0}}}$
to denote the set
$\overline {{{\tt tt}_{0}}}$
to denote the set
![]() ${{\tt tt}_{\tt n}} \setminus {{\tt tt}_{0}}$
or
${{\tt tt}_{\tt n}} \setminus {{\tt tt}_{0}}$
or
![]() ${{\tt tt}_{\tt v}} \setminus {{\tt tt}_{0}}$
, respectively. As an example,
${{\tt tt}_{\tt v}} \setminus {{\tt tt}_{0}}$
, respectively. As an example,
![]() $\overline {{\tt a}}$
denotes
$\overline {{\tt a}}$
denotes
![]() $\{{\tt n}\}$
in Weak Open CBN and
$\{{\tt n}\}$
in Weak Open CBN and
![]() $\{{\tt v}, {\tt n}\}$
in Weak Open CBV.
$\{{\tt v}, {\tt n}\}$
in Weak Open CBV.
Tight constants are minimal types that are necessary to type normal forms in a tight (minimal) way. This means that the set of tight constants, which depends on the set of normal forms, will also depend on the underlying strategy. Terms in neutral form are typed with the neutral tight constant
![]() $\tt n$
. But, in order to type normal forms, we need to consider more tight constants:
$\tt n$
. But, in order to type normal forms, we need to consider more tight constants:
-
• Weak Open CBN. The set of tight constants for Weak Open CBN consists of the tight constants
 $\tt a$
and
$\tt a$
and
 $\tt n$
. The additional tight constant
$\tt n$
. The additional tight constant
 $\tt a$
is needed for Weak Open CBN, since abstractions are the only normal forms that are not neutral: applications of the form
$\tt a$
is needed for Weak Open CBN, since abstractions are the only normal forms that are not neutral: applications of the form
 $(\lambda x.p) u$
are never normal forms.
$(\lambda x.p) u$
are never normal forms. -
• Weak Open CBV. The set of tight constants for Weak Open CBV consists of the tight constants
 $\tt v$
,
$\tt v$
,
 $\tt a$
, and
$\tt a$
, and
 $\tt n$
. Indeed, variables that can be replaced by persistent abstractions are typed with tight constant
$\tt n$
. Indeed, variables that can be replaced by persistent abstractions are typed with tight constant
 $\tt a$
, and variables that can only be replaced by other variables are typed with tight constant
$\tt a$
, and variables that can only be replaced by other variables are typed with tight constant
 $\tt v$
.
$\tt v$
.
In Figure 5, the reader might notice that the sets of multi-types for both calculi are different. In Weak Open CBN, multi-types contain the
![]() $\tt n$
tight constant because variables can be replaced with any term, in particular, neutral terms (of type
$\tt n$
tight constant because variables can be replaced with any term, in particular, neutral terms (of type
![]() $\tt n$
). In Weak Open CBV, instead, multi-types do not contain any tight constant
$\tt n$
). In Weak Open CBV, instead, multi-types do not contain any tight constant
![]() $\tt n$
because variables can only be replaced by values (of type
$\tt n$
because variables can only be replaced by values (of type
![]() $\tt v$
or
$\tt v$
or
![]() $\tt a$
). Moreover, because in the open setting abstractions can return values and terms in neutral form, neutral tight constants can appear on the right of arrow types in both Weak Open CBN and CBV.
$\tt a$
). Moreover, because in the open setting abstractions can return values and terms in neutral form, neutral tight constants can appear on the right of arrow types in both Weak Open CBN and CBV.
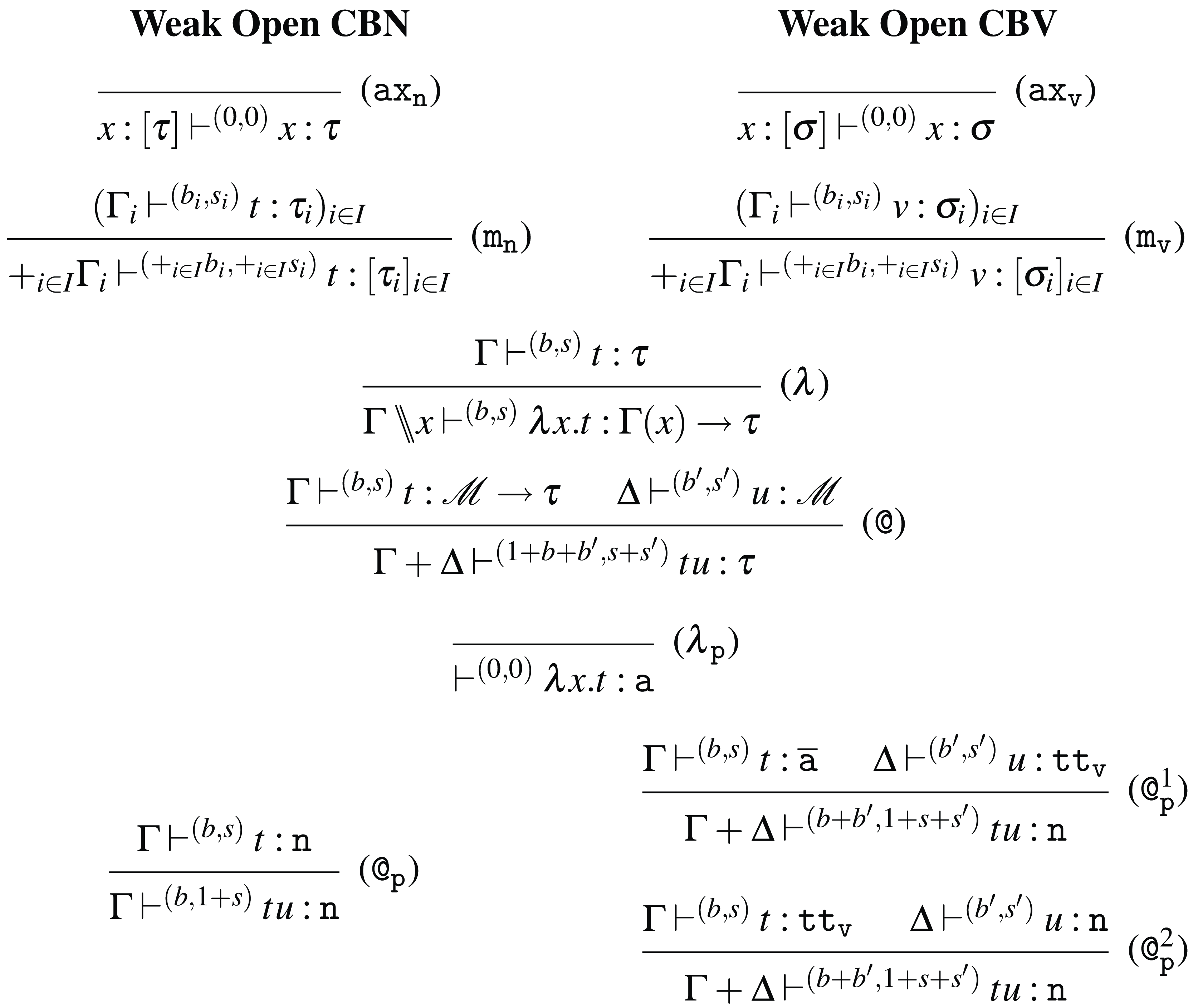
Figure 6. Typing rules for Weak Open CBN and CBV.
Typing systems for Weak Open CBN and CBV
The type systems for Weak Open CBN and CBV are defined as subsets of the typing rules in Figure 6. Let us introduce some necessary definitions:
-
• Typing environments are denoted by
 $\Gamma , \Delta$
and are defined as functions from variables to multi-types that assign the empty multi-type
$\Gamma , \Delta$
and are defined as functions from variables to multi-types that assign the empty multi-type
 $[ \, ]$
to all but a finite set of variables. The domain of a typing environment
$[ \, ]$
to all but a finite set of variables. The domain of a typing environment
 $\Gamma$
, denoted by
$\Gamma$
, denoted by
 ${\tt dom}(\Gamma )$
, is defined as
${\tt dom}(\Gamma )$
, is defined as
 ${\tt dom}(\Gamma ) := \{x \mid \Gamma (x) \not = [ \, ]\}$
. The union of typing environments
${\tt dom}(\Gamma ) := \{x \mid \Gamma (x) \not = [ \, ]\}$
. The union of typing environments
 $\Gamma$
and
$\Gamma$
and
 $\Delta$
is denoted as
$\Delta$
is denoted as
 $\Gamma + \Delta$
and defined as
$\Gamma + \Delta$
and defined as
 $(\Gamma + \Delta )(x) = \Gamma (x) \sqcup \Delta (x)$
, where
$(\Gamma + \Delta )(x) = \Gamma (x) \sqcup \Delta (x)$
, where
 $\sqcup$
denotes multi-set union. An example is
$\sqcup$
denotes multi-set union. An example is
 $(x \;:\; [ \tau _1 ], y \;:\; [ \tau _2 ]) + (x \;:\; [ \tau _1 ], z \;:\; [ \tau _2 ]) = (x \;:\; [ \tau _1, \tau _1 ], y \;:\; [ \tau _2 ], z \;:\; [ \tau _2 ])$
. This notion is extended to a finite union of environments, written
$(x \;:\; [ \tau _1 ], y \;:\; [ \tau _2 ]) + (x \;:\; [ \tau _1 ], z \;:\; [ \tau _2 ]) = (x \;:\; [ \tau _1, \tau _1 ], y \;:\; [ \tau _2 ], z \;:\; [ \tau _2 ])$
. This notion is extended to a finite union of environments, written
 $+_{i \in I} \Gamma _i$
(the empty environment is obtained when
$+_{i \in I} \Gamma _i$
(the empty environment is obtained when
 $I = \emptyset$
). We write
$I = \emptyset$
). We write
 $\Gamma \setminus x$
for the environment
$\Gamma \setminus x$
for the environment
 $(\Gamma \setminus x)(x) = [ \, ]$
and
$(\Gamma \setminus x)(x) = [ \, ]$
and
 $(\Gamma \setminus x)(y) = \Gamma (y)$
if
$(\Gamma \setminus x)(y) = \Gamma (y)$
if
 $y \not = x$
, and we write
$y \not = x$
, and we write
 $\Gamma ;\; x \;:\; \mathscr{M}$
for
$\Gamma ;\; x \;:\; \mathscr{M}$
for
 $\Gamma + (x \;:\; \mathscr{M})$
, when
$\Gamma + (x \;:\; \mathscr{M})$
, when
 $x \not \in {\tt dom}(\Gamma )$
. Notice that
$x \not \in {\tt dom}(\Gamma )$
. Notice that
 $\Gamma$
and
$\Gamma$
and
 $\Gamma ;\; x\;:\;[ \, ]$
are different notations denoting the same environment.
$\Gamma ;\; x\;:\;[ \, ]$
are different notations denoting the same environment. -
• Typing judgments have the form
 $\Gamma \vdash ^{(b,s)} t\;:\; \tau$
, where
$\Gamma \vdash ^{(b,s)} t\;:\; \tau$
, where
 $\Gamma$
is a typing environment,
$\Gamma$
is a typing environment,
 $\tau$
is a type, and
$\tau$
is a type, and
 $(b,s)$
is a counter made by two natural numbers (the meaning of
$(b,s)$
is a counter made by two natural numbers (the meaning of
 $b$
and
$b$
and
 $s$
will be made precise later). Also, if the typing environment
$s$
will be made precise later). Also, if the typing environment
 $\Gamma$
is empty, we will sometimes write
$\Gamma$
is empty, we will sometimes write
 $ \vdash ^{(b,s)} t\;:\; \tau$
instead of
$ \vdash ^{(b,s)} t\;:\; \tau$
instead of
 $\emptyset \vdash ^{(b,s)} t\;:\; \tau$
.
$\emptyset \vdash ^{(b,s)} t\;:\; \tau$
. -
• Typing rules are presented in the usual Gentzen-style layout: the typing judgments at the top of the rule are called the premises; the unique typing judgment at the bottom is its conclusion.
-
• We write
 $\triangleright\, {\Gamma }\vdash ^{(b,s)}_{\texttt {n}} t\;:\;\tau$
(resp.
$\triangleright\, {\Gamma }\vdash ^{(b,s)}_{\texttt {n}} t\;:\;\tau$
(resp.
 $\triangleright \, \Gamma \vdash ^{(b,s)}_{{\tt v}} t\;:\; \tau$
) if there is a type derivation of the judgment
$\triangleright \, \Gamma \vdash ^{(b,s)}_{{\tt v}} t\;:\; \tau$
) if there is a type derivation of the judgment
 $\Gamma \vdash ^{(b,s)} t\;:\; \tau$
(resp.
$\Gamma \vdash ^{(b,s)} t\;:\; \tau$
(resp.
 $\Gamma \vdash ^{(b,s)} t\;:\; \tau$
) using the typing rules for Weak Open CBN (resp. CBV), in which case we say that the term
$\Gamma \vdash ^{(b,s)} t\;:\; \tau$
) using the typing rules for Weak Open CBN (resp. CBV), in which case we say that the term
 $t$
of its conclusion is typable in Weak Open CBN (resp. CBV). We use letters
$t$
of its conclusion is typable in Weak Open CBN (resp. CBV). We use letters
 $\Phi , \Psi , \dots$
to name type derivations, by writing, for example,
$\Phi , \Psi , \dots$
to name type derivations, by writing, for example,
 $\Phi \triangleright \, \Gamma \vdash^{(b,s)} _{{\tt v}} t\;:\; \tau$
.
$\Phi \triangleright \, \Gamma \vdash^{(b,s)} _{{\tt v}} t\;:\; \tau$
.
We distinguish between consuming and persistent rules by subscripting the name of the latter with a
![]() $p$
. The intuitions behind the rules are the following (for now, ignore the counters
$p$
. The intuitions behind the rules are the following (for now, ignore the counters
![]() $(b,s)$
):
$(b,s)$
):
-
• Rules for Weak Open CBN:
-
– Rules (
 ${\tt ax}_{\tt n}$
), (
${\tt ax}_{\tt n}$
), (
 $\lambda$
), (@), and (
$\lambda$
), (@), and (
 ${\tt m}_{\tt n}$
). These rules are the usual ones for CBN.
${\tt m}_{\tt n}$
). These rules are the usual ones for CBN. -
– Rule (
 $\lambda _{\tt p}$
). This rule is used to type with a tight constant
$\lambda _{\tt p}$
). This rule is used to type with a tight constant
 $\tt a$
, abstractions that persist during evaluation.
$\tt a$
, abstractions that persist during evaluation. -
– Rule (@
 $_{{\tt p}}$
). This rule is used to type application terms of the form
$_{{\tt p}}$
). This rule is used to type application terms of the form
 $tu$
with the tight constant
$tu$
with the tight constant
 $\tt n$
, whenever the application constructor persists during evaluation.
$\tt n$
, whenever the application constructor persists during evaluation.
-
-
• Rules for Weak Open CBV:
-
– Rules (
 ${\tt ax}_{\tt v}$
), (
${\tt ax}_{\tt v}$
), (
 $\lambda$
), and (@). These rules are the usual ones for CBV, with the slightly less standard presentation of (@) using the fact that
$\lambda$
), and (@). These rules are the usual ones for CBV, with the slightly less standard presentation of (@) using the fact that
 $!(A \rightarrow B) = !(A) \rightarrow !(B)$
.
$!(A \rightarrow B) = !(A) \rightarrow !(B)$
. -
– Rule (
 ${\tt m}_{\tt v}$
). This rule is the exponential rule from linear logic, but, as stated before, it is introduced in the Weak Open CBV system in a restricted form: it can only be applied to values.
${\tt m}_{\tt v}$
). This rule is the exponential rule from linear logic, but, as stated before, it is introduced in the Weak Open CBV system in a restricted form: it can only be applied to values. -
– Rule (
 $\lambda _{\tt p}$
). Just like for Weak Open CBN, this rule is used to type with tight constant
$\lambda _{\tt p}$
). Just like for Weak Open CBN, this rule is used to type with tight constant
 $\tt a$
, abstractions that will persist during evaluation.
$\tt a$
, abstractions that will persist during evaluation. -
– Rules (@
 $^1_{{\tt p}}$
) and (@
$^1_{{\tt p}}$
) and (@
 $^2_{{\tt p}}$
). These rules are actually rule schemas that depend on the particular choice of tight constants. In particular, rule (@
$^2_{{\tt p}}$
). These rules are actually rule schemas that depend on the particular choice of tight constants. In particular, rule (@
 $^1_{{\tt p}}$
) unfolds into six different rules according to the particular choices of tight constants in
$^1_{{\tt p}}$
) unfolds into six different rules according to the particular choices of tight constants in
 $\overline {{\tt a}}$
and
$\overline {{\tt a}}$
and
 ${\tt tt}_{\tt v}$
, and (@
${\tt tt}_{\tt v}$
, and (@
 $^2_{{\tt p}}$
) unfolds into three different rules according to the choice of tight constant in
$^2_{{\tt p}}$
) unfolds into three different rules according to the choice of tight constant in
 ${\tt tt}_{\tt v}$
. Rules (@
${\tt tt}_{\tt v}$
. Rules (@
 $^1_{{\tt p}}$
) and (@
$^1_{{\tt p}}$
) and (@
 $^2_{{\tt p}}$
) are used to type application terms of the form
$^2_{{\tt p}}$
) are used to type application terms of the form
 $tu$
with the tight constant
$tu$
with the tight constant
 $\tt n$
, whenever the application constructor persists during evaluation. The rule depends on the types of the subterms
$\tt n$
, whenever the application constructor persists during evaluation. The rule depends on the types of the subterms
 $t$
and
$t$
and
 $u$
.
$u$
.
-
Counters
In order to keep track of the number of
![]() $\beta _{\tt n}$
-steps and
$\beta _{\tt n}$
-steps and
![]() $\beta _{\tt v}$
-steps, as well as the Weak Open CBN and CBV size of normal forms, typing judgments are decorated with counters of the form
$\beta _{\tt v}$
-steps, as well as the Weak Open CBN and CBV size of normal forms, typing judgments are decorated with counters of the form
![]() $(b,s)$
. Let
$(b,s)$
. Let
![]() $\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a typing derivation for term
$\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a typing derivation for term
![]() $t$
, then
$t$
, then
![]() $b$
is the number of
$b$
is the number of
![]() $\beta _{\tt n}$
-steps (resp.
$\beta _{\tt n}$
-steps (resp.
![]() $\beta _{\tt v}$
-steps) needed to normalize
$\beta _{\tt v}$
-steps) needed to normalize
![]() $t$
following the respective strategy, and
$t$
following the respective strategy, and
![]() $s$
is the size of the corresponding CBN (resp. CBV) normal form of
$s$
is the size of the corresponding CBN (resp. CBV) normal form of
![]() $t$
.
$t$
.
-
• Weak Open CBN. Rule (@) is the only rule that increases the counter
 $b$
for the number of
$b$
for the number of
 $\beta _{\tt n}$
-steps. Rule (@
$\beta _{\tt n}$
-steps. Rule (@
 $_{{\tt p}}$
) is the only rule that increases the counter
$_{{\tt p}}$
) is the only rule that increases the counter
 $s$
for the size of the Weak Open CBN normal form.
$s$
for the size of the Weak Open CBN normal form. -
• Weak Open CBV. Rule (@) is the only rule that increases the counter
 $b$
for the number of
$b$
for the number of
 $\beta _{\tt v}$
-steps. Rules (@
$\beta _{\tt v}$
-steps. Rules (@
 $^1_{{\tt p}}$
) and (@
$^1_{{\tt p}}$
) and (@
 $^2_{{\tt p}}$
) are the only rules that increase the counter
$^2_{{\tt p}}$
) are the only rules that increase the counter
 $s$
for the size of the Weak Open CBV normal form.
$s$
for the size of the Weak Open CBV normal form.
We call (@) a consuming application rule, and rules (@
![]() $^1_{{\tt p}}$
), (@
$^1_{{\tt p}}$
), (@
![]() $^2_{{\tt p}}$
), and (@
$^2_{{\tt p}}$
), and (@
![]() $_{{\tt p}}$
), persistent application rules. The intuition is the following:
$_{{\tt p}}$
), persistent application rules. The intuition is the following:
-
• Weak Open CBN. Consuming application rules are used to type applications that evaluate to the form
 $(\lambda x.t) u$
, and persistent application rules are used to type applications that evaluate to the form
$(\lambda x.t) u$
, and persistent application rules are used to type applications that evaluate to the form
 ${\tt ne}_{{\tt n}} t$
.
${\tt ne}_{{\tt n}} t$
. -
• Weak Open CBV. Consuming application rules are used to type applications that evaluate to the form
 $(\lambda x.t) v$
, and persistent application rules are used to type applications that evaluate to the form
$(\lambda x.t) v$
, and persistent application rules are used to type applications that evaluate to the form
 ${\tt ne}_{{\tt v}}$
.
${\tt ne}_{{\tt v}}$
.
This difference of behavior between persistent and consuming rules is captured by the rules as a tightness (minimality) constraint. If an application is not consuming, we only need to know that the terms on the left and right of the application evaluate to terms that do not interact with each other (have tight types) and will persist as an application (with a tight type) during evaluation. However, if an application is consuming, we need to know more about its form. In particular, that the term on the left of the application evaluates to an abstraction (of type
![]() $\mathscr{M} \rightarrow \tau$
) that expects an argument of a certain form (of type
$\mathscr{M} \rightarrow \tau$
) that expects an argument of a certain form (of type
![]() $\mathscr{M}$
) and that after consuming that argument, its body will have a particular form (of type
$\mathscr{M}$
) and that after consuming that argument, its body will have a particular form (of type
![]() $\tau$
).
$\tau$
).
Tightness
The same term may have different typing derivations. These will always provide upper bounds for the number of steps and the size of normal forms. The interesting aspect of tight type systems, however, is that the class of typing derivations that provide exact bounds for these measures is captured by tight derivations. The notion of tightness for types, typing environments, type judgments, and typing derivations is as follows:
-
• A type
 $\tau$
is tight if
$\tau$
is tight if
 $\tau$
is a tight constant (i.e.,
$\tau$
is a tight constant (i.e.,
 $\tau \in {{\tt tt}_{\tt v}}$
for CBV and
$\tau \in {{\tt tt}_{\tt v}}$
for CBV and
 $\tau \in {{\tt tt}_{\tt n}}$
for CBN).
$\tau \in {{\tt tt}_{\tt n}}$
for CBN). -
• A multi-type
 $\mathscr{M}$
is tight if, for all
$\mathscr{M}$
is tight if, for all
 $\sigma \in \mathscr{M}$
,
$\sigma \in \mathscr{M}$
,
 $\sigma$
is tight.
$\sigma$
is tight. -
• A typing environment
 $\Gamma$
is tight if, for all
$\Gamma$
is tight if, for all
 $x \in {\tt dom}(\Gamma )$
,
$x \in {\tt dom}(\Gamma )$
,
 $\Gamma (x)$
is tight.
$\Gamma (x)$
is tight. -
• A typing judgment
 $\Gamma \vdash ^{(b,s)} t\;:\; \tau$
is tight if
$\Gamma \vdash ^{(b,s)} t\;:\; \tau$
is tight if
 $\Gamma$
and
$\Gamma$
and
 $\tau$
are tight.
$\tau$
are tight. -
• A type derivation
 $\Phi$
is tight if its conclusion is tight.
$\Phi$
is tight if its conclusion is tight.
Soundness and completeness
The type system for Weak Open CBN (resp. CBV) is quantitatively sound and complete with respect to
![]() ${\rightarrow }_{\texttt {n}}$
(resp.
${\rightarrow }_{\texttt {n}}$
(resp.
![]() ${\rightarrow }_{\texttt {v}}$
). Quantitative soundness means that not only a tightly typable term
${\rightarrow }_{\texttt {v}}$
). Quantitative soundness means that not only a tightly typable term
![]() $t$
is terminating (qualitative) but also that exact and split measures concerning the evaluation of
$t$
is terminating (qualitative) but also that exact and split measures concerning the evaluation of
![]() $t$
to normal form (quantitative) can be extracted from its tight type derivation. More precisely, if
$t$
to normal form (quantitative) can be extracted from its tight type derivation. More precisely, if
![]() $\Phi \triangleright {\Gamma }\vdash ^{(b,s)}_{\texttt {n}} t\;:\;\tau$
(resp.
$\Phi \triangleright {\Gamma }\vdash ^{(b,s)}_{\texttt {n}} t\;:\;\tau$
(resp.
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
) is tight, then there exists
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
) is tight, then there exists
![]() $u \in {\tt no}_{{\tt n}}$
(resp.
$u \in {\tt no}_{{\tt n}}$
(resp.
![]() ${\tt no}_{{\tt v}}$
) such that
${\tt no}_{{\tt v}}$
) such that
![]() $t \twoheadrightarrow _{\tt n}^b u$
(resp.
$t \twoheadrightarrow _{\tt n}^b u$
(resp.
![]() $t \twoheadrightarrow _{\tt v}^b u$
) with
$t \twoheadrightarrow _{\tt v}^b u$
) with
![]() $|{u}|_{\texttt {n}} = s$
(resp.
$|{u}|_{\texttt {n}} = s$
(resp.
![]() $|{u}|_{\texttt {v}} = s$
). Dually for quantitative completeness. Most of the properties needed for quantitative soundness and completeness are shared between the two type systems. For this reason, we are going to present each statement only once and expect the reader to take the absence of any distinction between the two strategies as an indication of such between the statements. Also, we are going to present, in what follows, only the key properties and leave the auxiliary properties to Appendix A.1, along with their proofs.
$|{u}|_{\texttt {v}} = s$
). Dually for quantitative completeness. Most of the properties needed for quantitative soundness and completeness are shared between the two type systems. For this reason, we are going to present each statement only once and expect the reader to take the absence of any distinction between the two strategies as an indication of such between the statements. Also, we are going to present, in what follows, only the key properties and leave the auxiliary properties to Appendix A.1, along with their proofs.
To show quantitative soundness and completeness, we need to show that a term
![]() $t$
is in Weak Open CBN (resp. CBV) normal form if, and only if, the first counter, which corresponds to the number of
$t$
is in Weak Open CBN (resp. CBV) normal form if, and only if, the first counter, which corresponds to the number of
![]() $\beta _{\tt n}$
-steps (resp.
$\beta _{\tt n}$
-steps (resp.
![]() $\beta _{\tt v}$
-steps) needed to reach a normal form, is zero.
$\beta _{\tt v}$
-steps) needed to reach a normal form, is zero.
Lemma 1 (Normal forms take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a tight type derivation. Then,
$\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a tight type derivation. Then,
![]() $b = 0$
iff
$b = 0$
iff
![]() $t \in {\tt no}$
.
$t \in {\tt no}$
.
We also need to show that, given a term
![]() $t$
, the type system infers the correct Weak Open CBN (resp. CBV) size of the normal form of
$t$
, the type system infers the correct Weak Open CBN (resp. CBV) size of the normal form of
![]() $t$
.
$t$
.
Lemma 2 (Normal forms have correct size). Let
![]() $\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a tight type derivation. If
$\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a tight type derivation. If
![]() $b = 0$
, then
$b = 0$
, then
![]() $s = |t|$
.
$s = |t|$
.
Finally, we show that, for any term
![]() $t$
in Weak Open CBN (resp. CBV) normal form, there exists a tight derivation, which, moreover, infers the correct Weak Open CBN (resp. CBV) size of
$t$
in Weak Open CBN (resp. CBV) normal form, there exists a tight derivation, which, moreover, infers the correct Weak Open CBN (resp. CBV) size of
![]() $t$
.
$t$
.
Lemma 3 (All normal forms are tightly typable). If
![]() $t \in {\tt no}$
, then there exists a tight type derivation
$t \in {\tt no}$
, then there exists a tight type derivation
![]() $\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
, such that
$\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
, such that
![]() $s = |t|$
.
$s = |t|$
.
We now state a quantitative form of type preservation along evaluation.
Lemma 4 (Quantitative subject reduction). Let
![]() $\Phi _t \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a tight type derivation. If
$\Phi _t \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
be a tight type derivation. If
![]() $t \rightarrow t'$
, then there exists
$t \rightarrow t'$
, then there exists
![]() $\Phi _{t'} \triangleright \, \Gamma \vdash ^{(b-1,s)} t': \tau$
.
$\Phi _{t'} \triangleright \, \Gamma \vdash ^{(b-1,s)} t': \tau$
.
Quantitative soundness follows from the correctness of the counters for normal forms (Lemma1 and Lemma2) and quantitative subject reduction (Lemma4).
Theorem 1 (Quantitative soundness). If
![]() $\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
is a tight type derivation, then there exists
$\Phi \triangleright \, \Gamma \vdash ^{(b,s)} t\;:\; \tau$
is a tight type derivation, then there exists
![]() $u \in {\tt no}$
such that
$u \in {\tt no}$
such that
![]() $t \twoheadrightarrow ^b u$
with
$t \twoheadrightarrow ^b u$
with
![]() $|u| = s$
.
$|u| = s$
.
The following property guarantees that typability is preserved back along evaluation.
Lemma 5 (Quantitative subject expansion). Let
![]() $\Phi _{t'} \triangleright \, \Gamma \vdash ^{(b,s)} t': \tau$
be a tight type derivation. If
$\Phi _{t'} \triangleright \, \Gamma \vdash ^{(b,s)} t': \tau$
be a tight type derivation. If
![]() $t \rightarrow t'$
, then there exists
$t \rightarrow t'$
, then there exists
![]() $\Phi _t \triangleright \, \Gamma \vdash ^{(b+1, s)} t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \vdash ^{(b+1, s)} t\;:\; \tau$
.
Quantitative completeness follows from the typability of all normal forms in a tight way (Lemma3) and quantitative subject expansion (Lemma5).
Theorem 2 (Quantitative completeness). If
![]() $t \twoheadrightarrow ^b u$
with
$t \twoheadrightarrow ^b u$
with
![]() $u \in {\tt no}$
, then there exists a tight type derivation
$u \in {\tt no}$
, then there exists a tight type derivation
![]() $\Phi _t \triangleright \, \Gamma \vdash ^{(b, |u|)} t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \vdash ^{(b, |u|)} t\;:\; \tau$
.
3. Weak Open CBN and CBV with Global State
Now that we have seen how to use tight typing techniques to obtain quantitative information in the Weak Open CBN and CBV variants of the
![]() $\lambda$
-calculus without effects, we are ready to talk about the extensions of these languages with (algebraic) operations for reading and writing on a global state. To do this, we will lift reduction over terms to reduction over configurations, which are pairs consisting of a term and a state. Then, we are going to develop two types of systems: one for Weak Open CBN with Global State and another for Weak Open CBV with Global State. Since the CBN type system is, in a way, dual to the one in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023) for CBV, we are going to start by presenting the type system for Weak Open CBN with Global State first and then move to the generalization of the CBV type system in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023).
$\lambda$
-calculus without effects, we are ready to talk about the extensions of these languages with (algebraic) operations for reading and writing on a global state. To do this, we will lift reduction over terms to reduction over configurations, which are pairs consisting of a term and a state. Then, we are going to develop two types of systems: one for Weak Open CBN with Global State and another for Weak Open CBV with Global State. Since the CBN type system is, in a way, dual to the one in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023) for CBV, we are going to start by presenting the type system for Weak Open CBN with Global State first and then move to the generalization of the CBV type system in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023).
3.1 Weak Open CBN with Global State
We start by extending the syntax presented in Section 2 with operations for reading and writing on a global state and introducing the syntax for the global state and configurations. Then, also based on the CBN language introduced in Section 2, we show how to lift reduction on terms to reduction on configurations and how operations on terms interact with the global state.
3.1.1 Syntax and operational semantics
We introduce the syntax for the extension of the Weak Open CBN
![]() $\lambda$
-calculus with Global State and its operational semantics.
$\lambda$
-calculus with Global State and its operational semantics.
The syntax for Weak Open CBN with Global State
We consider a denumerable set of locations denoted by
![]() $l, l', \ldots$
. The sets of terms, states, and configurations are presented in Figure 7.
$l, l', \ldots$
. The sets of terms, states, and configurations are presented in Figure 7.
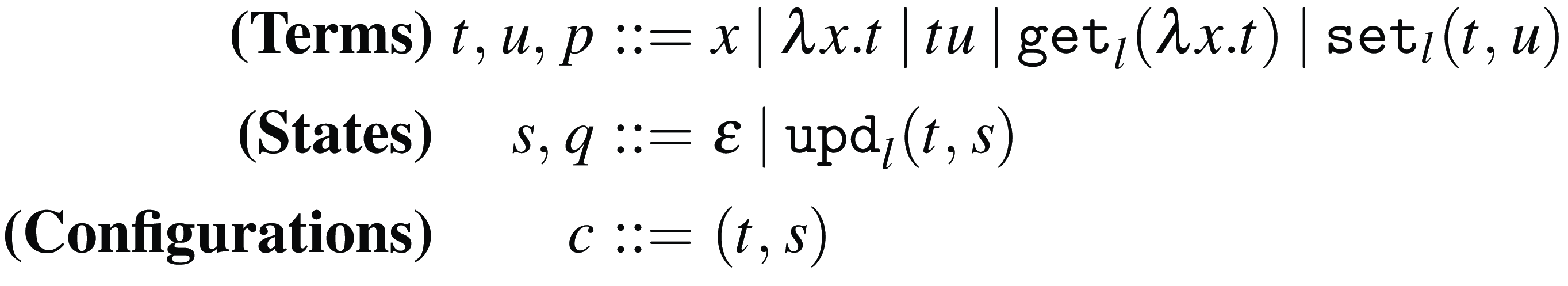
Figure 7. The extended syntax of the
![]() $\lambda$
-calculus for Weak Open CBN with Global State.
$\lambda$
-calculus for Weak Open CBN with Global State.
The set of terms of the
![]() $\lambda$
-calculus is extended with two operations:
$\lambda$
-calculus is extended with two operations:
![]() ${\tt get}_{l}(\lambda x.t)$
and
${\tt get}_{l}(\lambda x.t)$
and
![]() ${\tt set}_{l}(t,u)$
, where
${\tt set}_{l}(t,u)$
, where
![]() $l$
is a location drawn from some set of location names. The former is used to get the term at location
$l$
is a location drawn from some set of location names. The former is used to get the term at location
![]() $l$
and bind it to
$l$
and bind it to
![]() $x$
in
$x$
in
![]() $t$
. The latter is used to set a term
$t$
. The latter is used to set a term
![]() $t$
to location
$t$
to location
![]() $l$
in the state and then continue with term
$l$
in the state and then continue with term
![]() $u$
. States are either the empty state, denoted by
$u$
. States are either the empty state, denoted by
![]() $\varepsilon$
, or the result of some sequence of update operations over the empty state. Given some state
$\varepsilon$
, or the result of some sequence of update operations over the empty state. Given some state
![]() $s$
, an update over
$s$
, an update over
![]() $s$
consists in setting some term
$s$
consists in setting some term
![]() $t$
to some location
$t$
to some location
![]() $l$
, and it is denoted by
$l$
, and it is denoted by
![]() ${\tt upd}_{l}(t,s)$
. If the same location
${\tt upd}_{l}(t,s)$
. If the same location
![]() $l$
is updated twice in a row, for example,
$l$
is updated twice in a row, for example,
![]() ${\tt upd}_{l}(t,{\tt upd}_{l}(u,s))$
, only
${\tt upd}_{l}(t,{\tt upd}_{l}(u,s))$
, only
![]() $t$
(the most recent update) should be accessible at location
$t$
(the most recent update) should be accessible at location
![]() $l$
according to our operational semantics in Figure 9. Configurations are pairs consisting of a term and a state. The sets of free and bound variables of terms, states, and configuration are as expected.
$l$
according to our operational semantics in Figure 9. Configurations are pairs consisting of a term and a state. The sets of free and bound variables of terms, states, and configuration are as expected.
It is important to note that, if
![]() ${\tt upd}_{l}(t,{\tt upd}_{l}(u,s))$
is assumed to be equal to
${\tt upd}_{l}(t,{\tt upd}_{l}(u,s))$
is assumed to be equal to
![]() ${\tt upd}_{l}(t,s)$
, as in de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021) and Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), this corresponds to presenting the global state as a mapping from locations to terms, that is, the coalgebraic structure for the state monad (Plotkin and Power, Reference Plotkin, Power, Bauer and Mislove2008). We assume instead that if
${\tt upd}_{l}(t,s)$
, as in de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021) and Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), this corresponds to presenting the global state as a mapping from locations to terms, that is, the coalgebraic structure for the state monad (Plotkin and Power, Reference Plotkin, Power, Bauer and Mislove2008). We assume instead that if
![]() ${\tt upd}_{l}(t,{\tt upd}_{l}(u,s))$
is not equal to
${\tt upd}_{l}(t,{\tt upd}_{l}(u,s))$
is not equal to
![]() ${\tt upd}_{l}(t,s)$
, this corresponds to presenting the global state as a mapping from locations to lists of terms, that is, the coalgebraic structure for the state-logging monad (Ahman and Uustalu, Reference Ahman, Uustalu, Jacobs, Silva and Staton2014). We also consider the update operation to be commutative in the following sense:
${\tt upd}_{l}(t,s)$
, this corresponds to presenting the global state as a mapping from locations to lists of terms, that is, the coalgebraic structure for the state-logging monad (Ahman and Uustalu, Reference Ahman, Uustalu, Jacobs, Silva and Staton2014). We also consider the update operation to be commutative in the following sense:
The equivalence relation generated by the algebraic equation
![]() $\equiv _{\tt c}$
is denoted by
$\equiv _{\tt c}$
is denoted by
![]() $\equiv$
. We write
$\equiv$
. We write
![]() $l \in {\tt labels}(s)$
, if
$l \in {\tt labels}(s)$
, if
![]() $s \equiv {\tt upd}_{l}(t,q)$
, for some term
$s \equiv {\tt upd}_{l}(t,q)$
, for some term
![]() $t$
and state
$t$
and state
![]() $q$
. Moreover, for every location
$q$
. Moreover, for every location
![]() $l$
, these
$l$
, these
![]() $t$
and
$t$
and
![]() $q$
are unique. A consequence of the equivalence relation
$q$
are unique. A consequence of the equivalence relation
![]() $\equiv$
on states is that, whenever we want to refer to the most up-to-date content of a location in a given state
$\equiv$
on states is that, whenever we want to refer to the most up-to-date content of a location in a given state
![]() $s$
, we can always write
$s$
, we can always write
![]() $s$
so that the first update operation is the latest one over that particular location. Said differently, for every
$s$
so that the first update operation is the latest one over that particular location. Said differently, for every
![]() $l \in {\tt labels}(s)$
,
$l \in {\tt labels}(s)$
,
![]() $s \equiv {\tt upd}_{l}(u,q)$
, for some term
$s \equiv {\tt upd}_{l}(u,q)$
, for some term
![]() $u$
and some state
$u$
and some state
![]() $q$
. From now on, if
$q$
. From now on, if
![]() $s \equiv {\tt upd}_{l}(u,q)$
, we write
$s \equiv {\tt upd}_{l}(u,q)$
, we write
![]() $s(l)$
to denote the (unique) term
$s(l)$
to denote the (unique) term
![]() $u$
.
$u$
.
Weak Open CBN size
The notion of Weak Open CBN size is extended to operations, states, and configurations according to Figure 8.

Figure 8. Weak Open CBN size extended for global state.
Evaluation in Weak Open CBN with Global State
Weak Open CBN evaluation
![]() ${\rightarrow }_{\texttt {n}}$
is extended to global state by lifting it to configurations and taking into consideration the interaction between get and set operations and the global state. Evaluation for Weak Open CBN with Global State
${\rightarrow }_{\texttt {n}}$
is extended to global state by lifting it to configurations and taking into consideration the interaction between get and set operations and the global state. Evaluation for Weak Open CBN with Global State
![]() $\rightsquigarrow _{{\tt n}}$
is defined as the union of the reduction rules in Figure 9.
$\rightsquigarrow _{{\tt n}}$
is defined as the union of the reduction rules in Figure 9.
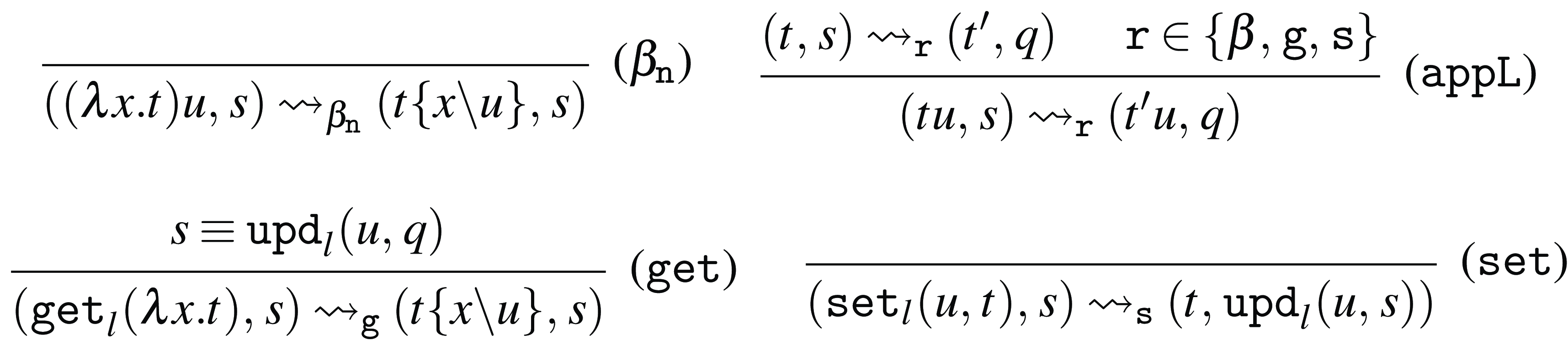
Figure 9. Reduction rule for Weak Open CBN with Global State.
Rules (
![]() $\beta _{\tt n}$
) and (appL) are the same as for the Weak Open CBN, if we take only the term part of the configuration. Rules (get) and (set) describe how the get and set operations interact with the global state. In particular, notice that, while rule (set) can always be fired, rule (get) can get stuck if it tries to interact with a location on the global state that is empty.
$\beta _{\tt n}$
) and (appL) are the same as for the Weak Open CBN, if we take only the term part of the configuration. Rules (get) and (set) describe how the get and set operations interact with the global state. In particular, notice that, while rule (set) can always be fired, rule (get) can get stuck if it tries to interact with a location on the global state that is empty.
Blocked configurations
A configuration
![]() $(t,s)$
is said to be blocked if:
$(t,s)$
is said to be blocked if:
![]() $t = {\tt get}_{l}(\lambda x.u)$
and
$t = {\tt get}_{l}(\lambda x.u)$
and
![]() $l \not \in {\tt labels}(s)$
; or
$l \not \in {\tt labels}(s)$
; or
![]() $t = up$
and
$t = up$
and
![]() $(u,s)$
is blocked. We say that
$(u,s)$
is blocked. We say that
![]() $(t,s)$
is an unblocked otherwise.
$(t,s)$
is an unblocked otherwise.
Example 1.
Let
![]() $l,l'$
be two locations such that
$l,l'$
be two locations such that
![]() $l \neq l'$
. Then, the three following configurations are all blocked:
$l \neq l'$
. Then, the three following configurations are all blocked:
Normal configurations
Clearly, blocked configurations are a kind of normal form for configurations. However, they are not the desired result of a computation – even though they are in normal form – but rather a runtime error that should be caught by the type system (i.e., blocked configurations will be untyped). A configuration
![]() $(t,s)$
is said to be normal if it is a blocked configuration or
$(t,s)$
is said to be normal if it is a blocked configuration or
![]() $t \in {\tt no}_{{\tt n}}$
, where
$t \in {\tt no}_{{\tt n}}$
, where
![]() ${\tt no}_{{\tt n}}$
is defined in Figure 10.
${\tt no}_{{\tt n}}$
is defined in Figure 10.
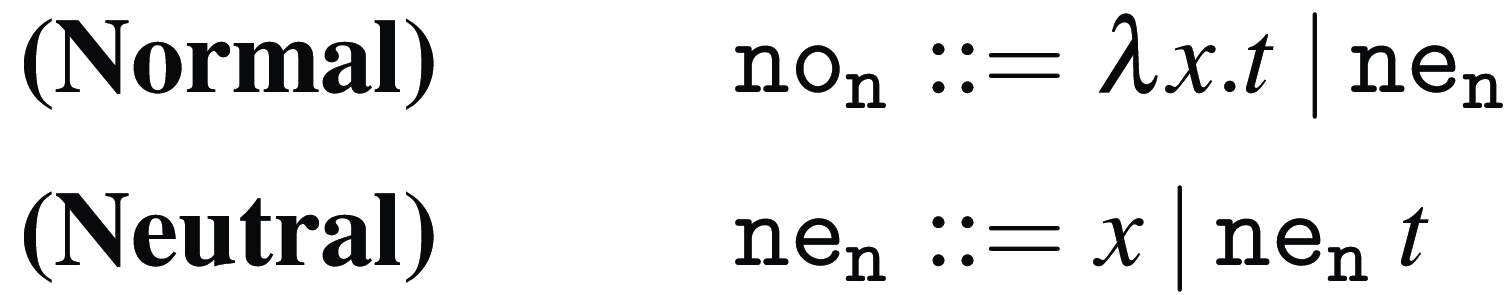
Figure 10. Normal and neutral terms for Weak Open CBN with Global State.
Example 2.
Consider the configuration
![]() $c_0 = ((\lambda x.{\tt set}_{l}(z,x)) ({\tt get}_{l}(\lambda y.y)), \varepsilon )$
. Then we can reach a normal configuration as follows:
$c_0 = ((\lambda x.{\tt set}_{l}(z,x)) ({\tt get}_{l}(\lambda y.y)), \varepsilon )$
. Then we can reach a normal configuration as follows:
 \begin{align*} ((\lambda x.{\tt set}_{l}(z,x)) ({\tt get}_{l}(\lambda y.y)), \varepsilon ) & \rightsquigarrow _{{\beta _{{\tt n}}}} ({\tt set}_{l}(z,{\tt get}_{l}(\lambda y.y)), \varepsilon ) \\ &\rightsquigarrow _{{\tt s}} ({\tt get}_{l}(\lambda y.y), {\tt upd}_{l}(z,\varepsilon ))\\ & \rightsquigarrow _{{\tt g}} (z, {\tt upd}_{l}(z,\varepsilon )) \end{align*}
\begin{align*} ((\lambda x.{\tt set}_{l}(z,x)) ({\tt get}_{l}(\lambda y.y)), \varepsilon ) & \rightsquigarrow _{{\beta _{{\tt n}}}} ({\tt set}_{l}(z,{\tt get}_{l}(\lambda y.y)), \varepsilon ) \\ &\rightsquigarrow _{{\tt s}} ({\tt get}_{l}(\lambda y.y), {\tt upd}_{l}(z,\varepsilon ))\\ & \rightsquigarrow _{{\tt g}} (z, {\tt upd}_{l}(z,\varepsilon )) \end{align*}
The following proposition, whose proof is in Appendix A.2, shows that normal configurations are indeed irreducible.

Figure 11. The CBN monadic translation for types, typing environments, and judgments.
Proposition 3.
Let
![]() $(t,s)$
be a configuration. Then
$(t,s)$
be a configuration. Then
![]() $(t,s)$
is normal iff
$(t,s)$
is normal iff
![]() $(t,s) \not \rightsquigarrow _{{\tt n}}$
.
$(t,s) \not \rightsquigarrow _{{\tt n}}$
.
3.1.2 A quantitative type system for Weak Open CBN with Global State
In this section, we present the quantitative type system for Weak Open CBN with Global State. For this, we start by introducing the CBN monadic translation of the
![]() $\lambda$
-calculus of Wadler (Reference Wadler1990) by adapting it to account for tight constants and multi-types. We then instantiate this monadic translation with the monad for global state.
$\lambda$
-calculus of Wadler (Reference Wadler1990) by adapting it to account for tight constants and multi-types. We then instantiate this monadic translation with the monad for global state.
The CBN monadic translation
In order to lift the type system for Weak Open CBN into the global state monad, we are going to follow the CBN translations of the simply-typed
![]() $\lambda$
-calculus in Wadler (Reference Wadler1990). Naturally, we will have to slightly adapt the translation in order to accommodate for multi-types. The resulting translation of the Weak Open CBN types in Figure 5 is presented in Figure 11.
$\lambda$
-calculus in Wadler (Reference Wadler1990). Naturally, we will have to slightly adapt the translation in order to accommodate for multi-types. The resulting translation of the Weak Open CBN types in Figure 5 is presented in Figure 11.
This figure deserves some comments. Notice that we choose to use two different arrows to denote our types: the first one
![]() $\Rightarrow$
is used for the global state monad, while the second one
$\Rightarrow$
is used for the global state monad, while the second one
![]() $\rightarrow$
is the usual functional arrow type. Also, the
$\rightarrow$
is the usual functional arrow type. Also, the
![]() $T$
translation is meant to be understood as a template for building the type system.
$T$
translation is meant to be understood as a template for building the type system.
State and monadic (multi-)types
The grammar for types is presented in Figure 12.

Figure 12. Types for Weak Open CBN with Global State.
State types, denoted by
![]() $\mathscr{T\;}$
, can be seen as partial functions mapping all but a finite set of locations to the empty list multi-type
$\mathscr{T\;}$
, can be seen as partial functions mapping all but a finite set of locations to the empty list multi-type
![]() $\star$
. Notice that
$\star$
. Notice that
![]() $\mathscr{T\;}$
is the set of all state types and corresponds to
$\mathscr{T\;}$
is the set of all state types and corresponds to
![]() $S$
in Figure 11. The domain of a state type
$S$
in Figure 11. The domain of a state type
![]() $\mathscr{T\;}$
is denoted by
$\mathscr{T\;}$
is denoted by
![]() ${\tt dom}(\mathscr{T\;})$
and defined as
${\tt dom}(\mathscr{T\;})$
and defined as
![]() ${\tt dom}(\mathscr{T\;}) := \{ l \mid (l\;:\;\mathscr{L\;}) \in \mathscr{T\;} \mbox{ and } \mathscr{L\;} \neq \star \}$
. We write
${\tt dom}(\mathscr{T\;}) := \{ l \mid (l\;:\;\mathscr{L\;}) \in \mathscr{T\;} \mbox{ and } \mathscr{L\;} \neq \star \}$
. We write
![]() $\mathscr{T\;}(l)$
to denote the list multi-type associated with location
$\mathscr{T\;}(l)$
to denote the list multi-type associated with location
![]() $l$
in
$l$
in
![]() $\mathscr{T\;}$
, whenever
$\mathscr{T\;}$
, whenever
![]() $l \in {\tt dom}(\mathscr{T\;})$
. To simplify the notation, we will omit
$l \in {\tt dom}(\mathscr{T\;})$
. To simplify the notation, we will omit
![]() $\star$
whenever a list multi-type is not empty; thus, for example,
$\star$
whenever a list multi-type is not empty; thus, for example,
![]() $[ \mu ] \cdot \star$
will be simply written as
$[ \mu ] \cdot \star$
will be simply written as
![]() $[ \mu ]$
. It is important to remark that the use of list multi-types is crucial in order to match the behavior exhibited by our notion of state; for example, if an empty location
$[ \mu ]$
. It is important to remark that the use of list multi-types is crucial in order to match the behavior exhibited by our notion of state; for example, if an empty location
![]() $l$
is updated twice, first with a term of type
$l$
is updated twice, first with a term of type
![]() $\mathscr{M}_1$
and then with a term of type
$\mathscr{M}_1$
and then with a term of type
![]() $\mathscr{M}_2$
, then it will be assigned type
$\mathscr{M}_2$
, then it will be assigned type
![]() $\mathscr{M}_2 \cdot (\mathscr{M}_1 \cdot \star )$
.
$\mathscr{M}_2 \cdot (\mathscr{M}_1 \cdot \star )$
.
We write
![]() $\mathscr{T\;};\; \mathscr{T\;}'$
to mean that
$\mathscr{T\;};\; \mathscr{T\;}'$
to mean that
![]() ${\tt dom}(\mathscr{T\;}) \cap {\tt dom}(\mathscr{T\;}') = \emptyset$
. Notice that
${\tt dom}(\mathscr{T\;}) \cap {\tt dom}(\mathscr{T\;}') = \emptyset$
. Notice that
![]() $\{l \;:\; \star \};\; \mathscr{T\;} = \mathscr{T\;}$
and
$\{l \;:\; \star \};\; \mathscr{T\;} = \mathscr{T\;}$
and
![]() $\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;} \neq \mathscr{T\;}$
if
$\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;} \neq \mathscr{T\;}$
if
![]() $\mathscr{L\;} \neq \star$
, so in particular
$\mathscr{L\;} \neq \star$
, so in particular
![]() $\{l \;:\; [ \, ]\};\; \mathscr{T\;} \neq \mathscr{T\;}$
. However, recall that
$\{l \;:\; [ \, ]\};\; \mathscr{T\;} \neq \mathscr{T\;}$
. However, recall that
![]() $x \;:\; [ \, ];\; \Gamma = \Gamma$
.
$x \;:\; [ \, ];\; \Gamma = \Gamma$
.
Multi-types are now multi-sets of monadic types. And monadic types are lifted types of the form
![]() $\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, where the state type
$\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, where the state type
![]() $\mathscr{T\;}\;$
is called an input state, and
$\mathscr{T\;}\;$
is called an input state, and
![]() $\tau \times \mathscr{T\;}'$
is a configuration type consisting of a type
$\tau \times \mathscr{T\;}'$
is a configuration type consisting of a type
![]() $\tau$
and a state type
$\tau$
and a state type
![]() $\mathscr{T\;}'$
called output state. When dealing with effects, it is important to distinguish between pure and monadic types. Indeed, pure types are monadic types that have the same input and output state type, for example,
$\mathscr{T\;}'$
called output state. When dealing with effects, it is important to distinguish between pure and monadic types. Indeed, pure types are monadic types that have the same input and output state type, for example,
![]() $\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})$
.
$\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})$
.
Typing system for Weak Open CBN with Global State
The type system for Weak Open CBN with Global State is defined by the typing rules in Figure 13.

Figure 13. Typing rules for Weak Open CBN with Global State.
Like in the case for Weak Open CBN and CBV, we now present some necessary definitions:
-
• The notions of typing environments are extended to global state as expected.
-
• Typing rules follow the structure introduced in the previous section.
-
• Typing judgments are of three different kinds:
-
– Term typing judgments are used to type terms and are of the form
 $\Gamma \Vdash ^{(b,m,d)} t\;:\; \mathscr{G\,}$
, where
$\Gamma \Vdash ^{(b,m,d)} t\;:\; \mathscr{G\,}$
, where
 $(b,m,d)$
is a counter,
$(b,m,d)$
is a counter,
 $\Gamma$
is a typing context, and
$\Gamma$
is a typing context, and
 $\mathscr{G\,}$
represents either a multi-type
$\mathscr{G\,}$
represents either a multi-type
 $\mathscr{M}$
or a monadic type
$\mathscr{M}$
or a monadic type
 $\mu$
.
$\mu$
. -
– State typing judgments are used to type states and are of the form
 $\Delta \Vdash ^{(b,m,d)} s\;:\; \mathscr{T\;}$
, where
$\Delta \Vdash ^{(b,m,d)} s\;:\; \mathscr{T\;}$
, where
 $(b,m,d)$
is a counter,
$(b,m,d)$
is a counter,
 $\Delta$
is a typing context, and
$\Delta$
is a typing context, and
 $\mathscr{T\;}$
a state type.
$\mathscr{T\;}$
a state type. -
– Configuration typing judgments are used to type configurations and are of the form
 $\Gamma \Vdash ^{(b,m,d)} (t,s): \kappa$
, where
$\Gamma \Vdash ^{(b,m,d)} (t,s): \kappa$
, where
 $(b,m,d)$
is a counter,
$(b,m,d)$
is a counter,
 $\Gamma$
is a typing context, and
$\Gamma$
is a typing context, and
 $\kappa$
is a configuration type.
$\kappa$
is a configuration type.
The meaning of the counters
 $b$
,
$b$
,
 $m$
, and
$m$
, and
 $s$
will again be made precise later.
$s$
will again be made precise later. -
-
• The notions of type derivation and typability are extended to global state as expected.
We distinguish between consuming and persistent rules just like before. The intuitions behind the rules are the following (again, please ignore the counters
![]() $(b,m,d)$
for now):
$(b,m,d)$
for now):
-
• Rules (ax), (
 $\lambda$
), (
$\lambda$
), (
 $\lambda _{\tt p}$
), (@
$\lambda _{\tt p}$
), (@
 $_{{\tt p}}$
), and (m). These rules are essentially the same as for Weak Open CBN, but types are now replaced by monadic types.
$_{{\tt p}}$
), and (m). These rules are essentially the same as for Weak Open CBN, but types are now replaced by monadic types. -
• Rule (@). In this rule, we can see how CBN influences the type system. Since, according to CBN, we only reduce on the left-hand side of applications, only the term
 $t$
on the left can (potentially) change the global state. Therefore, CBN tells us the following: (1)
$t$
on the left can (potentially) change the global state. Therefore, CBN tells us the following: (1)
 $t$
is reduced until reaching an abstraction
$t$
is reduced until reaching an abstraction
 $\lambda x.p$
, going from input state type
$\lambda x.p$
, going from input state type
 $\mathscr{T\;}$
to an output state type
$\mathscr{T\;}$
to an output state type
 $\mathscr{T\;}'$
; then (2) the
$\mathscr{T\;}'$
; then (2) the
 $\beta _{\tt n}$
-rule will be fired, resulting in the term
$\beta _{\tt n}$
-rule will be fired, resulting in the term
 $p \{x \setminus u\}$
; and then (3) reduction continues with
$p \{x \setminus u\}$
; and then (3) reduction continues with
 $p \{x \setminus u\}$
, thus going from input state type
$p \{x \setminus u\}$
, thus going from input state type
 $\mathscr{T\;}'$
to the output state type in the configuration type
$\mathscr{T\;}'$
to the output state type in the configuration type
 $\kappa$
. Remark that the arrow type
$\kappa$
. Remark that the arrow type
 $\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
appearing in the monadic type of
$\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
appearing in the monadic type of
 $t$
represents the fact that, after
$t$
represents the fact that, after
 $\lambda x.p$
interacts with term
$\lambda x.p$
interacts with term
 $u$
of type
$u$
of type
 $\mathscr{M}$
,
$\mathscr{M}$
,
 $p \{x \setminus u\}$
continues the computation with behavior
$p \{x \setminus u\}$
continues the computation with behavior
 $\mathscr{T\;}' \Rightarrow \kappa$
.
$\mathscr{T\;}' \Rightarrow \kappa$
. -
• Rule (get). This rule is used to type the get operation. Given some state
 $s$
,
$s$
,
 ${\tt get}_{l}(\lambda x.t)$
binds a copy of
${\tt get}_{l}(\lambda x.t)$
binds a copy of
 $s(l)$
to
$s(l)$
to
 $x$
and returns
$x$
and returns
 $t \{x \setminus s(l)\}$
. This is reflected by this typing rule: it assigns input state type
$t \{x \setminus s(l)\}$
. This is reflected by this typing rule: it assigns input state type
 $\{l \;:\; \Gamma (x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\} ;\; \mathscr{T\;}$
to
$\{l \;:\; \Gamma (x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\} ;\; \mathscr{T\;}$
to
 ${\tt get}_{l}(\lambda x.t)$
under typing context
${\tt get}_{l}(\lambda x.t)$
under typing context
 $\Gamma \setminus x$
, so that
$\Gamma \setminus x$
, so that
 $l \in {\tt labels}(s)$
(by Lemma 42), and assigns input state
$l \in {\tt labels}(s)$
(by Lemma 42), and assigns input state
 $s$
to
$s$
to
 $t$
under typing context
$t$
under typing context
 $\Gamma$
, to indicate that evaluating
$\Gamma$
, to indicate that evaluating
 $t$
consumes a copy of
$t$
consumes a copy of
 $s(l)$
. It is also important to note that the premise of the rule assigns input state
$s(l)$
. It is also important to note that the premise of the rule assigns input state
 $\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}$
to
$\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}$
to
 $t$
because
$t$
because
 $t$
has access to the same input state as
$t$
has access to the same input state as
 ${\tt get}_{l}(\lambda x.t)$
. Of course,
${\tt get}_{l}(\lambda x.t)$
. Of course,
 $t$
is not required to use the contents of location
$t$
is not required to use the contents of location
 $l$
, in which case
$l$
, in which case
 $\mathscr{M} = [ \, ]$
.
$\mathscr{M} = [ \, ]$
. -
• Rule (set). This rule is used to type the set operation, which is – in a sense – dual to the get operation. Given a state
 $s$
and terms
$s$
and terms
 $t$
and
$t$
and
 $u$
,
$u$
,
 ${\tt set}_{l}(t,u)$
(possibly) extends
${\tt set}_{l}(t,u)$
(possibly) extends
 $s$
to location
$s$
to location
 $l$
by assigning
$l$
by assigning
 $t$
to
$t$
to
 $s(l)$
and returns
$s(l)$
and returns
 $u$
, which now has access to
$u$
, which now has access to
 $t$
in location
$t$
in location
 $l$
. This is reflected by this typing rule: it assigns input state type
$l$
. This is reflected by this typing rule: it assigns input state type
 $\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;}$
to
$\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;}$
to
 ${\tt set}_{l}(t,u)$
, which is the type of the state before it is changed by set, while assuming the input state type
${\tt set}_{l}(t,u)$
, which is the type of the state before it is changed by set, while assuming the input state type
 $\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}$
for
$\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}$
for
 $u$
, where
$u$
, where
 $\mathscr{M}$
is the type of
$\mathscr{M}$
is the type of
 $t$
.
$t$
. -
• Rule (emp). This rule is used to type the empty state. By definition, the empty state has an empty set type
 $\emptyset$
because no location is set.
$\emptyset$
because no location is set. -
• Rule (upd). This rule is used to type the update operation and is very similar to rule (set). However, instead of describing the behavior of a term after a set operation, it describes the behavior of a state
 $s$
after it is updated to
$s$
after it is updated to
 ${\tt upd}_{l}(t,s)$
, for some location
${\tt upd}_{l}(t,s)$
, for some location
 $l$
and term
$l$
and term
 $t$
. Of course, if location
$t$
. Of course, if location
 $l$
was already defined in
$l$
was already defined in
 $s$
, this information is already recorded in the type
$s$
, this information is already recorded in the type
 $\{l\;:\;\mathscr{L\;}\};\; \mathscr{T\;}$
of
$\{l\;:\;\mathscr{L\;}\};\; \mathscr{T\;}$
of
 $s$
. Moreover, the new type of
$s$
. Moreover, the new type of
 ${\tt upd}_{l}(t,s)$
keeps track of this old information by adding the multi-type
${\tt upd}_{l}(t,s)$
keeps track of this old information by adding the multi-type
 $\mathscr{M}$
of the term
$\mathscr{M}$
of the term
 $t$
to the head of list multi-type
$t$
to the head of list multi-type
 $\mathscr{L\;}$
.
$\mathscr{L\;}$
. -
• Rule (conf). This rule is used to type configurations. In order to type a configuration of the form
 $(t,s)$
, both
$(t,s)$
, both
 $t$
and
$t$
and
 $s$
need to be typed. Note that
$s$
need to be typed. Note that
 $s$
is the input state of
$s$
is the input state of
 $t$
; therefore, the input state type of
$t$
; therefore, the input state type of
 $t$
needs to match the type of
$t$
needs to match the type of
 $s$
. The type of the configuration is a configuration type, and it reflects the behavior of the normal configuration reached from
$s$
. The type of the configuration is a configuration type, and it reflects the behavior of the normal configuration reached from
 $(t,s)$
.
$(t,s)$
.
Counters
Our counters are now of the form
![]() $(b,m,d)$
. This will allow us to not only keep track of the number of
$(b,m,d)$
. This will allow us to not only keep track of the number of
![]() $\beta _{\tt n}$
-steps and the size of normal configurations, just like for Weak Open CBN, but also the number of
$\beta _{\tt n}$
-steps and the size of normal configurations, just like for Weak Open CBN, but also the number of
![]() $\tt g$
/
$\tt g$
/
![]() $\tt s$
-steps. We are going to use
$\tt s$
-steps. We are going to use
![]() $d$
to denote the size of normal configurations instead of
$d$
to denote the size of normal configurations instead of
![]() $s$
to avoid confusion with notation for states. Let
$s$
to avoid confusion with notation for states. Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
. Then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
. Then
![]() $b$
is the number of
$b$
is the number of
![]() $\beta _{\tt n}$
-steps needed to normalize
$\beta _{\tt n}$
-steps needed to normalize
![]() $t$
,
$t$
,
![]() $d$
is the size of the normal configurations reached from
$d$
is the size of the normal configurations reached from
![]() $(t,s)$
, and
$(t,s)$
, and
![]() $m$
is the number of
$m$
is the number of
![]() $\tt g$
/
$\tt g$
/
![]() $\tt s$
steps. Note that, while the first and last counters depend on the interplay between consuming and persistent typing rules, the second counter is simply counting the number of get and set operations that occur during evaluation. This is due to the fact that blocked configurations are not typable (by Proposition4), and thus, get and set never get stuck. However, this is not the same thing as the total number of get and set operations in a configuration. As an example, consider configuration
$\tt s$
steps. Note that, while the first and last counters depend on the interplay between consuming and persistent typing rules, the second counter is simply counting the number of get and set operations that occur during evaluation. This is due to the fact that blocked configurations are not typable (by Proposition4), and thus, get and set never get stuck. However, this is not the same thing as the total number of get and set operations in a configuration. As an example, consider configuration
![]() $(\lambda x.{\tt get}_{l}(\lambda y.t), s)$
. This configuration has (at least) one get operation, but it is already a normal configuration. Therefore, no operation occurs during evaluation, and this should be reflected by the counter.
$(\lambda x.{\tt get}_{l}(\lambda y.t), s)$
. This configuration has (at least) one get operation, but it is already a normal configuration. Therefore, no operation occurs during evaluation, and this should be reflected by the counter.
CBN tightness
We generalize the notion of tightness for types, typing environments, type judgments, and typing derivations as follows:
-
• A type
 $\tau$
is tight if
$\tau$
is tight if
 $\tau$
is a tight constant (i.e.,
$\tau$
is a tight constant (i.e.,
 $\tau \in {{\tt tt}_{\tt n}}$
).
$\tau \in {{\tt tt}_{\tt n}}$
). -
• A multi-type is tight if, for all
 $\mu \in \mathscr{M}$
,
$\mu \in \mathscr{M}$
,
 $\mu$
is tight.
$\mu$
is tight. -
• A list multi-type
 $\mathscr{L\;}$
is tight if
$\mathscr{L\;}$
is tight if
 $\mathscr{L\;} = \star$
, or
$\mathscr{L\;} = \star$
, or
 $\mathscr{L\;} = \mathscr{M} \cdot \mathscr{L\;}'$
,
$\mathscr{L\;} = \mathscr{M} \cdot \mathscr{L\;}'$
,
 $\mathscr{M} = [ \, ]$
, and
$\mathscr{M} = [ \, ]$
, and
 $\mathscr{L\;}'$
is tight.
$\mathscr{L\;}'$
is tight. -
• A monadic type
 $\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
is tight if
$\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
is tight if
 $\tau \in {{\tt tt}_{\tt n}}$
.
$\tau \in {{\tt tt}_{\tt n}}$
. -
• A state type
 $\mathscr{T\;}$
is tight if, for all
$\mathscr{T\;}$
is tight if, for all
 $l \in {\tt dom}(\mathscr{T\;})$
,
$l \in {\tt dom}(\mathscr{T\;})$
,
 $\mathscr{T\;}(l)$
is tight. This tightness restriction on state types ensures that any information provided by the input state that is not used during evaluation is discarded by the (tight) type system.
$\mathscr{T\;}(l)$
is tight. This tightness restriction on state types ensures that any information provided by the input state that is not used during evaluation is discarded by the (tight) type system. -
• A configuration type
 $(\tau \times \mathscr{T\;})$
is tight if
$(\tau \times \mathscr{T\;})$
is tight if
 $\tau \in {{\tt tt}_{\tt n}}$
and
$\tau \in {{\tt tt}_{\tt n}}$
and
 $\mathscr{T\;}$
is tight.
$\mathscr{T\;}$
is tight. -
• A typing environment
 $\Gamma$
is tight if, for all
$\Gamma$
is tight if, for all
 $x \in {\tt dom}(\Gamma )$
, all
$x \in {\tt dom}(\Gamma )$
, all
 $\mu \in \Gamma (x)$
are of the form
$\mu \in \Gamma (x)$
are of the form
 $\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})$
, and
$\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})$
, and
 $\tau \in {{\tt tt}_{\tt n}}$
. This tightness restriction on typing environments has one crucial consequence: persistent variables cannot change the global state and thus are assigned types that reflect that fact, that is, types that have the same input and output state type (see Lemma6).
$\tau \in {{\tt tt}_{\tt n}}$
. This tightness restriction on typing environments has one crucial consequence: persistent variables cannot change the global state and thus are assigned types that reflect that fact, that is, types that have the same input and output state type (see Lemma6). -
• A term typing judgment
 $\Gamma \Vdash ^{(b,m,d)} t\;:\; \mathscr{G\,}$
is tight if
$\Gamma \Vdash ^{(b,m,d)} t\;:\; \mathscr{G\,}$
is tight if
 $\Gamma$
is tight and
$\Gamma$
is tight and
 $\mathscr{G\,}$
is tight.
$\mathscr{G\,}$
is tight. -
• A state typing judgment
 $\Delta \Vdash ^{(b,m,d)} s\;:\; \mathscr{T\;}$
is tight if
$\Delta \Vdash ^{(b,m,d)} s\;:\; \mathscr{T\;}$
is tight if
 $\Delta$
and
$\Delta$
and
 $\mathscr{T\;}$
are tight.
$\mathscr{T\;}$
are tight. -
• A configuration typing judgment
 $\Gamma \Vdash ^{(b,m,d)} (t,s): \kappa$
is tight if
$\Gamma \Vdash ^{(b,m,d)} (t,s): \kappa$
is tight if
 $\Gamma$
and
$\Gamma$
and
 $\kappa$
are tight.
$\kappa$
are tight. -
• A typing derivation
 $\Phi$
is tight if it concludes with a tight judgment.
$\Phi$
is tight if it concludes with a tight judgment.
Example 3.
Consider configuration
![]() $c_0$
from Example
2
. Let
$c_0$
from Example
2
. Let
![]() $\mu _0 = \{l \;:\; [ \, ]\} \Rightarrow ({\tt n} \times \{l\;:\;[ \, ]\})$
, and let
$\mu _0 = \{l \;:\; [ \, ]\} \Rightarrow ({\tt n} \times \{l\;:\;[ \, ]\})$
, and let
![]() $\mu _1 = \{l \;:\; \star \} \Rightarrow ({\tt n} \times \{l\;:\;[ \, ]\})$
, and recall that
$\mu _1 = \{l \;:\; \star \} \Rightarrow ({\tt n} \times \{l\;:\;[ \, ]\})$
, and recall that
![]() $\emptyset = \{l\;:\;\star \}$
. Let
$\emptyset = \{l\;:\;\star \}$
. Let
![]() $\Phi _0$
be the following typing derivation:
$\Phi _0$
be the following typing derivation:
and
![]() $\Phi _1$
be the following typing derivation:
$\Phi _1$
be the following typing derivation:
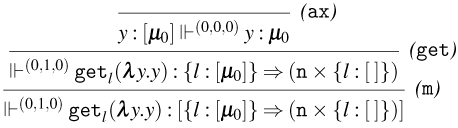
Then, we can build the following tight derivation
![]() $\Phi _{c_0}$
for
$\Phi _{c_0}$
for
![]() $c_0$
:
$c_0$
:
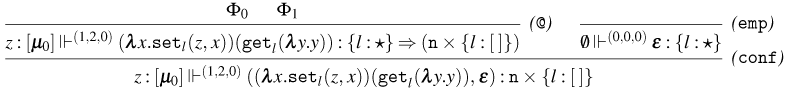
Soundness and completeness
We now extend the soundness and completeness results for Weak Open CBN to Weak Open CBN with Global State. The type system for Weak Open CBN with Global State is quantitatively sound and complete with respect to the extended reduction relation
![]() $\rightsquigarrow _{{\tt n}}$
to configurations. Quantitative soundness means that not only a tightly typable configuration
$\rightsquigarrow _{{\tt n}}$
to configurations. Quantitative soundness means that not only a tightly typable configuration
![]() $(t,s)$
is terminating (qualitative) but also that exact and split measures (quantitative) concerning the evaluation of
$(t,s)$
is terminating (qualitative) but also that exact and split measures (quantitative) concerning the evaluation of
![]() $(t,s)$
to a normal configuration can be extracted from its tight type derivation. More precisely, if
$(t,s)$
to a normal configuration can be extracted from its tight type derivation. More precisely, if
![]() $\Phi \triangleright \, \Gamma \, \Vdash _{{\tt n}}^{(b,m,d)} (t,s) \;:\; \kappa$
is a tight derivation, then there exists a normal configuration
$\Phi \triangleright \, \Gamma \, \Vdash _{{\tt n}}^{(b,m,d)} (t,s) \;:\; \kappa$
is a tight derivation, then there exists a normal configuration
![]() $(u,q)$
such that
$(u,q)$
such that
![]() $(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
with
$(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
with
![]() $|{(u,q)}|_{\texttt {n}} = d$
. Dually for quantitative completeness. The key properties necessary to show quantitative soundness and completeness for Weak Open CBN are extended to Weak Open CBN with Global State, and additional properties strictly related to the presence of the global state are necessary. All proofs are in Appendix A.2.
$|{(u,q)}|_{\texttt {n}} = d$
. Dually for quantitative completeness. The key properties necessary to show quantitative soundness and completeness for Weak Open CBN are extended to Weak Open CBN with Global State, and additional properties strictly related to the presence of the global state are necessary. All proofs are in Appendix A.2.
Correctness of the counters
To show quantitative completeness, we need to show that if a typable configuration
![]() $(t,s)$
is normal, then the counters of its tight derivation are as follows: the first counter, which corresponds to the number of
$(t,s)$
is normal, then the counters of its tight derivation are as follows: the first counter, which corresponds to the number of
![]() $\beta _{\tt n}$
-steps needed to reach a Weak Open CBN with Global State normal configuration, is zero; the second counter, which corresponds to the number of
$\beta _{\tt n}$
-steps needed to reach a Weak Open CBN with Global State normal configuration, is zero; the second counter, which corresponds to the number of
![]() $\tt g$
/
$\tt g$
/
![]() $\tt s$
-steps, is zero; and the last counter is equal to the Weak Open CBN with Global State size of
$\tt s$
-steps, is zero; and the last counter is equal to the Weak Open CBN with Global State size of
![]() $(t,s)$
.
$(t,s)$
.
Given some term
![]() $t$
in normal form, the type system will always infer a tight monadic type for
$t$
in normal form, the type system will always infer a tight monadic type for
![]() $t$
with the same input and output state types. This is due to the fact that normal forms do not interact with the state (at least in an effectful way) and is formalized as follows.
$t$
with the same input and output state types. This is due to the fact that normal forms do not interact with the state (at least in an effectful way) and is formalized as follows.
Lemma 6 (Normal forms have pure types). Let
![]() $\Phi \triangleright \, \Vdash ^{(b,m,d)}_{\tt n} t\;:\; \mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, \Vdash ^{(b,m,d)}_{\tt n} t\;:\; \mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt no}_{{\tt n}}$
, then
$t \in {\tt no}_{{\tt n}}$
, then
![]() $\mathscr{T\;} = \mathscr{T\;}'$
.
$\mathscr{T\;} = \mathscr{T\;}'$
.
A stronger crucial property can (and will) be shown for the CBV setting (Lemma 15). For the CBN setting, this weaker property is enough.
The following property shows that terms in normal form and tight states have correct size.
Lemma 7 (Normal forms and tight states have correct size).
-
(1) Let
 $\Phi \triangleright {\Gamma }\Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then, (i)
$\Phi \triangleright {\Gamma }\Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then, (i)
 $t \in {\tt no}_{{\tt n}}$
and (ii)
$t \in {\tt no}_{{\tt n}}$
and (ii)
 $d = |{t}|_{\texttt {n}}$
$d = |{t}|_{\texttt {n}}$
-
(2) Let
 $\Pi \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n}\;:\; s\;:\;\mathscr{T\;}$
be a tight derivation. Then
$\Pi \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n}\;:\; s\;:\;\mathscr{T\;}$
be a tight derivation. Then
 $b = m = d = 0$
.
$b = m = d = 0$
.
Lemma 8 (Normal forms take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then,
![]() $b = m = 0$
iff
$b = m = 0$
iff
![]() $t \in {\tt no}_{{\tt n}}$
.
$t \in {\tt no}_{{\tt n}}$
.
The fact that unblocked normal configurations also have correct size follows from Lemmas 6 and 7.
Lemma 9 (Normal configurations have correct size). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation of the following form:
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation of the following form:
where
![]() $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
![]() $\kappa = (\tau \times \mathscr{T\;}')$
,
$\kappa = (\tau \times \mathscr{T\;}')$
,
![]() $b = b_t + b_s$
,
$b = b_t + b_s$
,
![]() $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
![]() $d = d_t + d_s$
. If
$d = d_t + d_s$
. If
![]() $b_t = m_t = 0$
, then (i)
$b_t = m_t = 0$
, then (i)
![]() $d = |{(t,s)}|_{\texttt {n}}$
and
$d = |{(t,s)}|_{\texttt {n}}$
and
![]() $b = m = 0$
.
$b = m = 0$
.
The fact that this is also the case for normal configurations follows from Lemma 8.
Lemma 10 (Normal configurations take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation. Then,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation. Then,
![]() $b = m = 0$
iff
$b = m = 0$
iff
![]() $(t,s)$
is an unblocked normal configuration.
$(t,s)$
is an unblocked normal configuration.
Another important property that needs to be shown is that the type system only types unblocked configurations.
Proposition 4 (Typed configurations are unblocked). If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
, then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
, then
![]() $(t,s)$
is unblocked.
$(t,s)$
is unblocked.
This property allows us to conclude that a typable configuration
![]() $(t,s)$
that takes zero steps is such that
$(t,s)$
that takes zero steps is such that
![]() $t \in {\tt no}_{{\tt n}}$
.
$t \in {\tt no}_{{\tt n}}$
.
The following property is crucial in order to show that any state and normal form can be typed in a tight way.
Lemma 11 (Tight typability of states and normal forms).
-
(1) Let
 $s$
be a state. Then, there exists a tight derivation
$s$
be a state. Then, there exists a tight derivation
 $\Pi _s \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} s\;:\;\mathscr{T\;}$
.
$\Pi _s \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} s\;:\;\mathscr{T\;}$
. -
(2) Let
 $t \in {\tt no}_{{\tt n}}$
. Then, for any
$t \in {\tt no}_{{\tt n}}$
. Then, for any
 $\mathscr{T\;}$
, there exists a tight derivation
$\mathscr{T\;}$
, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t \;:\; \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;})$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t \;:\; \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;})$
, such that
 $d = |{t}|_{\texttt {n}}$
.
$d = |{t}|_{\texttt {n}}$
.
And the fact that any unblocked normal configuration
![]() $(t,s)$
can be typed in a tight way follows easily from Lemma 11.
$(t,s)$
can be typed in a tight way follows easily from Lemma 11.
Lemma 12 (All unblocked normal configurations are tightly typable). If
![]() $(t,s)$
is a normal but unblocked configuration, then there exists a tight typing derivation
$(t,s)$
is a normal but unblocked configuration, then there exists a tight typing derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} (t,s):\kappa$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} (t,s):\kappa$
, such that
![]() $d = |{(t,s)}|_{\texttt {n}}$
.
$d = |{(t,s)}|_{\texttt {n}}$
.
We now show a quantitative form of type preservation along evaluation for configurations.
Lemma 13 (Quantitative subject reduction). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
is a tight derivation, then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
is a tight derivation, then
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt n} (u,q):\kappa$
, where
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt n} (u,q):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt n}}}$
implies
${\tt r} ={\beta _{{\tt n}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Quantitative soundness follows from the correctness of the counters for configurations that are normal but unblocked (Lemma 7 and Lemma 10) and quantitative subject reduction (Lemma 13)
Theorem 3 (Quantitative soundness). If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
a tight derivation, then there exists
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
a tight derivation, then there exists
![]() $(u,q)$
such that
$(u,q)$
such that
![]() $u \in {\tt no}_{{\tt n}}$
and
$u \in {\tt no}_{{\tt n}}$
and
![]() $(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
with
$(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
with
![]() $b$
$b$
![]() $\beta _{{\tt n}}$
-steps,
$\beta _{{\tt n}}$
-steps,
![]() $m$
$m$
![]() ${\tt g}/{\tt s}$
-steps, and
${\tt g}/{\tt s}$
-steps, and
![]() $|{(u,q)}|_{\texttt {n}} = d$
.
$|{(u,q)}|_{\texttt {n}} = d$
.
Proof.
The proof is by induction on
![]() $b + m$
, see Appendix A.2 for details.
$b + m$
, see Appendix A.2 for details.
The following property guarantees that typability is also preserved back along evaluation.
Lemma 14 (Quantitative subject expansion). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d')}_{\tt n} (u,q):\kappa$
is a tight derivation, then
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d')}_{\tt n} (u,q):\kappa$
is a tight derivation, then
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d')}_{\tt n} (t,s):\kappa$
, where
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d')}_{\tt n} (t,s):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt n}}}$
implies
${\tt r} ={\beta _{{\tt n}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Quantitative completeness follows from the typability of all configurations normal but unblocked in a tight way (Lemma 12) and quantitative subject expansion (Lemma 14).
Theorem 4 (Quantitative completeness). If
![]() $(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
and
$(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
and
![]() $u \in {\tt no}_{{\tt n}}$
, then there exists a tight derivation
$u \in {\tt no}_{{\tt n}}$
, then there exists a tight derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {n}})}_{\tt n} (t,s):\kappa$
.
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {n}})}_{\tt n} (t,s):\kappa$
.
Example 4.
Consider again configuration
![]() $c_0$
from Example
2
and its tight derivation
$c_0$
from Example
2
and its tight derivation
![]() $\Phi _{c_0}$
from Example
3
. The first two counters of
$\Phi _{c_0}$
from Example
3
. The first two counters of
![]() $\Phi _{c_0}$
are different from
$\Phi _{c_0}$
are different from
![]() $0$
: this means that
$0$
: this means that
![]() $c_0$
is not normal but normalizes in one
$c_0$
is not normal but normalizes in one
![]() $\beta _{{\tt n}}$
-step (
$\beta _{{\tt n}}$
-step (
![]() $b = 1$
) and two
$b = 1$
) and two
![]() ${\tt g}/{\tt s}$
-steps (
${\tt g}/{\tt s}$
-steps (
![]() $m = 2$
) to a normal unblocked configuration of size
$m = 2$
) to a normal unblocked configuration of size
![]() $d = 0 = |{(z, {\tt upd}_{l}(z,\varepsilon ))}|_{\texttt {n}}$
.
$d = 0 = |{(z, {\tt upd}_{l}(z,\varepsilon ))}|_{\texttt {n}}$
.
A discussion on the subtleties of subject expansion
In this subsection, we highlight the subtleties of the type system in order to capture – in particular – subject expansion. Consider the following reduction step:
Let us assume that
![]() $c_2$
is typable. In the following, we will omit the counters decorating the typing judgments, as they are irrelevant to the discussion. Moreover, let
$c_2$
is typable. In the following, we will omit the counters decorating the typing judgments, as they are irrelevant to the discussion. Moreover, let
![]() $\mathscr{T\;} = \{l \;:\; \mathscr{M}_1 \cdot \mathscr{M}_2\}$
and
$\mathscr{T\;} = \{l \;:\; \mathscr{M}_1 \cdot \mathscr{M}_2\}$
and
![]() $\mathscr{M}_0 = [ \mathscr{T\;} \Rightarrow \kappa ]$
, for some multi-types
$\mathscr{M}_0 = [ \mathscr{T\;} \Rightarrow \kappa ]$
, for some multi-types
![]() $\mathscr{M}_1, \mathscr{M}_2$
and configuration type
$\mathscr{M}_1, \mathscr{M}_2$
and configuration type
![]() $\kappa$
, and recall that
$\kappa$
, and recall that
![]() $\{l \;:\; \star \};\; \mathscr{T\;} = \mathscr{T\;}$
. The typing derivation for configuration
$\{l \;:\; \star \};\; \mathscr{T\;} = \mathscr{T\;}$
. The typing derivation for configuration
![]() $c_2$
must be of the following form:
$c_2$
must be of the following form:

And the typing derivation for configuration
![]() $c_1$
can easily be recovered from the previous:
$c_1$
can easily be recovered from the previous:
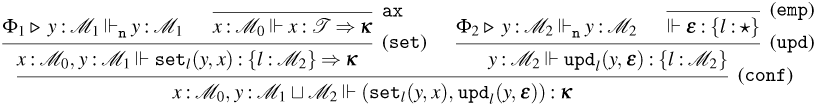
However, if we had assumed the equality
![]() ${\tt upd}_{l}(y,{\tt upd}_{l}(y,\varepsilon )) = {\tt upd}_{l}(y,\varepsilon )$
in our framework, then consequently
${\tt upd}_{l}(y,{\tt upd}_{l}(y,\varepsilon )) = {\tt upd}_{l}(y,\varepsilon )$
in our framework, then consequently
![]() $\mathscr{T\;} = \{l \;:\; \mathscr{M}_1 \cdot \mathscr{M}_2\} = \{l \;:\; \mathscr{M}_1\}$
and the
$\mathscr{T\;} = \{l \;:\; \mathscr{M}_1 \cdot \mathscr{M}_2\} = \{l \;:\; \mathscr{M}_1\}$
and the
![]() $({\tt upd})$
rule should rather look as follows:
$({\tt upd})$
rule should rather look as follows:
But then, the typing derivation for
![]() $c_2$
would be of the following form instead:
$c_2$
would be of the following form instead:
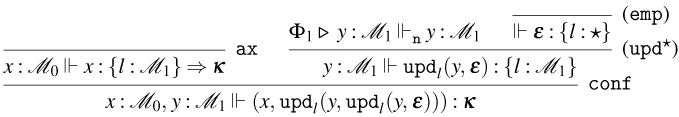
Now, observe that the type of
![]() $x$
does not contain any information about
$x$
does not contain any information about
![]() $\mathscr{M}_2$
. Therefore, rule
$\mathscr{M}_2$
. Therefore, rule
![]() $({\tt set})$
would infer a type of the form
$({\tt set})$
would infer a type of the form
![]() $\{l \;:\; \star \} \Rightarrow \kappa$
for
$\{l \;:\; \star \} \Rightarrow \kappa$
for
![]() ${\tt set}_{l}(y,x)$
, and it is then no longer possible to match
${\tt set}_{l}(y,x)$
, and it is then no longer possible to match
![]() $\{l \;:\; \star \}$
with the type of
$\{l \;:\; \star \}$
with the type of
![]() ${\tt upd}_{l}(y,\varepsilon )$
in order to build a typing derivation for
${\tt upd}_{l}(y,\varepsilon )$
in order to build a typing derivation for
![]() $c_1$
. That is, subject expansion fails because
$c_1$
. That is, subject expansion fails because
![]() ${\tt upd}_{l}(y,{\tt upd}_{l}(y,\varepsilon )) = {\tt upd}_{l}(y,\varepsilon )$
, which is an equation that clearly does not hold in the current approach.
${\tt upd}_{l}(y,{\tt upd}_{l}(y,\varepsilon )) = {\tt upd}_{l}(y,\varepsilon )$
, which is an equation that clearly does not hold in the current approach.
A comparison with previous approaches
We now compare our approach to de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021) and Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), where updates to the same location are not tracked, and thus, there is no need to use lists of types. This implies, in particular, that
![]() $\{l \;:\; \mathscr{M}\};\; \mathscr{T\;} \neq \mathscr{T\;}$
holds, for all
$\{l \;:\; \mathscr{M}\};\; \mathscr{T\;} \neq \mathscr{T\;}$
holds, for all
![]() $\mathscr{M}$
. de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021), there are two different rules for typing the state: one for typing a location as expected, and another one that allows one to “skip” typing a location whenever that location was not already typed before. The two rules can be presented in our formalist as follows:
$\mathscr{M}$
. de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021), there are two different rules for typing the state: one for typing a location as expected, and another one that allows one to “skip” typing a location whenever that location was not already typed before. The two rules can be presented in our formalist as follows:
It is worth noticing that this presentation is equivalent to requiring that
![]() $\{l \;:\; \mathscr{M}\};\; \mathscr{T\;} \neq \mathscr{T\;}$
holds only whenever
$\{l \;:\; \mathscr{M}\};\; \mathscr{T\;} \neq \mathscr{T\;}$
holds only whenever
![]() $\mathscr{M} \neq [ \, ]$
. Consequently, rule (upd
$\mathscr{M} \neq [ \, ]$
. Consequently, rule (upd
![]() $_2^\star$
) becomes redundant since rule (upd
$_2^\star$
) becomes redundant since rule (upd
![]() $_1^\star$
) now captures both behaviors. This is precisely the approach taken in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), even if there is a small inaccuracy in the definition of operation ; (it is missing the side condition requiring
$_1^\star$
) now captures both behaviors. This is precisely the approach taken in Alves et al. (Reference Alves, Kesner, Ramos, Hansen, Scedrov and de Queiroz2023), even if there is a small inaccuracy in the definition of operation ; (it is missing the side condition requiring
![]() $\mathscr{M} \neq [ \, ]$
).
$\mathscr{M} \neq [ \, ]$
).
However, even though it is possible to develop sound and complete type systems for these two alternative approaches, they lack the necessary discriminative power to distinguish configurations that have different meanings. As an example, consider the two following configurations:
Notice that location
![]() $l$
is touched (or modified) in
$l$
is touched (or modified) in
![]() $c_3$
, but no location is touched in
$c_3$
, but no location is touched in
![]() $c_4$
. Ideally, an accurate quantitative type system should be able to distinguish these two configurations, but if we consider
$c_4$
. Ideally, an accurate quantitative type system should be able to distinguish these two configurations, but if we consider
![]() $\{l \;:\; [ \, ]\};\; \mathscr{T\;} = \mathscr{T\;}$
(as discussed above), both configurations can be assigned the same type. Indeed, let
$\{l \;:\; [ \, ]\};\; \mathscr{T\;} = \mathscr{T\;}$
(as discussed above), both configurations can be assigned the same type. Indeed, let
![]() $\mathscr{M}_3 = [\emptyset \Rightarrow ({{\tt tt}_{\tt n}} \times \emptyset )]$
, for any
$\mathscr{M}_3 = [\emptyset \Rightarrow ({{\tt tt}_{\tt n}} \times \emptyset )]$
, for any
![]() ${\tt tt}_{\tt n}$
, and note that
${\tt tt}_{\tt n}$
, and note that
![]() $\{l \;:\; [ \, ]\};\; \emptyset = \emptyset$
. The typing derivation for
$\{l \;:\; [ \, ]\};\; \emptyset = \emptyset$
. The typing derivation for
![]() $c_3$
can be as follows (again, we omit the counters decorating the typing judgments):
$c_3$
can be as follows (again, we omit the counters decorating the typing judgments):
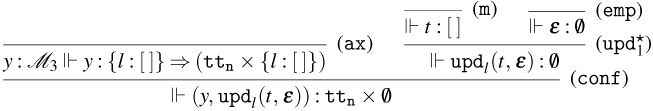
And the typing derivation for
![]() $c_4$
is as follows:
$c_4$
is as follows:
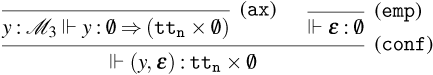
Hopefully, by requiring that
![]() $\{l \;:\; \star \};\; \mathscr{T\;} = \mathscr{T\;}$
, but not
$\{l \;:\; \star \};\; \mathscr{T\;} = \mathscr{T\;}$
, but not
![]() $\{l \;:\; [ \, ]\};\; \mathscr{T\;} = \mathscr{T\;}$
, the type system we propose in this paper is able to clearly distinguish between the two configurations above. Let us make this purpose concrete. Let
$\{l \;:\; [ \, ]\};\; \mathscr{T\;} = \mathscr{T\;}$
, the type system we propose in this paper is able to clearly distinguish between the two configurations above. Let us make this purpose concrete. Let
![]() $\mathscr{M}_4 = [\{l \;:\; [ \, ]\} \Rightarrow ({{\tt tt}_{\tt n}} \times \{l \;:\; [ \, ]\})]$
. Indeed, the type derivation for
$\mathscr{M}_4 = [\{l \;:\; [ \, ]\} \Rightarrow ({{\tt tt}_{\tt n}} \times \{l \;:\; [ \, ]\})]$
. Indeed, the type derivation for
![]() $c_3$
is now as follows:
$c_3$
is now as follows:
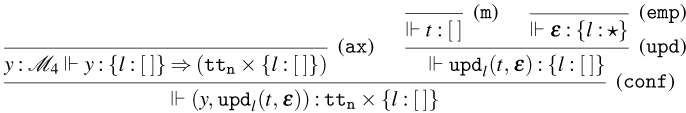
And the typing derivation for
![]() $c_4$
is as follows:
$c_4$
is as follows:
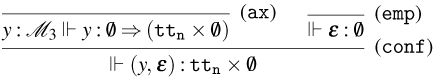
This clearly illustrates the second contribution of the paper, extending the denotational semantics of our type system.
3.2 Weak Open CBV with Global State
Now that we have presented the extension of Weak Open CBN with Global State, we will present the more subtle extension of Weak Open CBV with Global State. The extension of the basic
![]() $\lambda$
-calculus is similar to the one for Weak Open CBN with Global State, but we distinguish values from the other terms of the language, and the global state will now hold only values instead of arbitrary terms. Let us however briefly discuss this choice.
$\lambda$
-calculus is similar to the one for Weak Open CBN with Global State, but we distinguish values from the other terms of the language, and the global state will now hold only values instead of arbitrary terms. Let us however briefly discuss this choice.
It would have been possible to consider the same notion of global state as in CBN (i.e., holding arbitrary terms, and not only values), together with a unique rule for the get operator in both operational semantics have a similar shape. Indeed, the following rule (get
![]() $^\star$
) would work for both CBN and CBV:
$^\star$
) would work for both CBN and CBV:
However, from a quantitative point of view, this is not equivalent to rule that is usually adopted for CBV:
Clearly, both approaches are very different from a quantitative point of view. Suppose that the term
![]() $u$
in rule (get
$u$
in rule (get
![]() $^\star$
) evaluates to the value
$^\star$
) evaluates to the value
![]() $v$
in rule (get). If we consider rule (get
$v$
in rule (get). If we consider rule (get
![]() $^\star$
), term
$^\star$
), term
![]() $u$
will be evaluated to
$u$
will be evaluated to
![]() $v$
after it is retrieved from the global state every time. If, instead, we consider rule (get), term
$v$
after it is retrieved from the global state every time. If, instead, we consider rule (get), term
![]() $u$
must first be evaluated to
$u$
must first be evaluated to
![]() $v$
before being placed in the global and thus will only be evaluated once. This puts into question the smart duplicative behavior that is usually associated with CBV strategies but might be worth exploring in future work. For now, we will stick to the usual approach and simply adopt rule (get) in Section 3.2.1.
$v$
before being placed in the global and thus will only be evaluated once. This puts into question the smart duplicative behavior that is usually associated with CBV strategies but might be worth exploring in future work. For now, we will stick to the usual approach and simply adopt rule (get) in Section 3.2.1.
3.2.1 Syntax and operational semantics
In this section, we introduce the syntax for the extension of the
![]() $\lambda$
-calculus with global state and the operational semantics following CBV.
$\lambda$
-calculus with global state and the operational semantics following CBV.
The syntax for Weak Open CBV with Global State
The sets of values, terms, states, and configurations are presented in Figure 14.
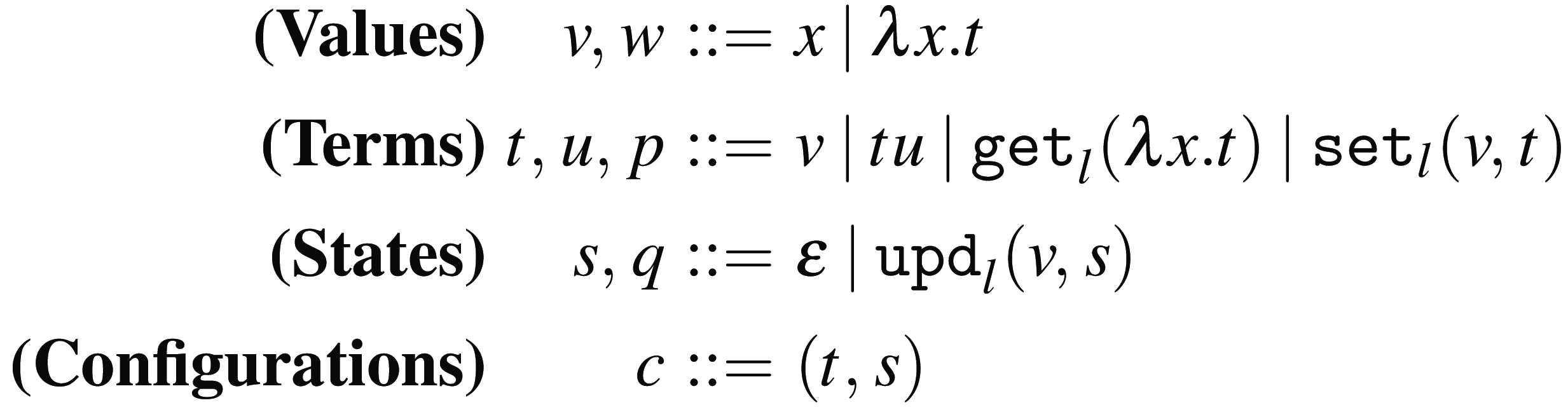
Figure 14. The extended syntax of the
![]() $\lambda$
-calculus for Weak Open CBV with Global State.
$\lambda$
-calculus for Weak Open CBV with Global State.
All notions regarding free and bound variables of terms, states, and configurations, as well as the notion of the domain of a state, are similar to the case of Weak Open CBN with Global State (c.f. Section 3.1).
Weak Open CBV size
The notion of Weak Open CBV size is extended to operations, states, and configurations according to Figure 15.

Figure 15. Weak Open CBV size extended for global state.
Evaluation and blocked configurations in Weak Open CBV with Global State
Weak Open CBV evaluation is extended to global state in the same way as we did for Weak Open CBN with Global State. The extension is denoted by
![]() $\rightsquigarrow _{{\tt v}}$
, and due to the particular nature of CBV, this notion is mutually defined with that of blocked configurations in Figure 16. Indeed, evaluation for Weak Open CBV with Global State is defined as the union of the reduction rule in Figure 16a, where the notion of blocked configurations is in Figure 16b.
$\rightsquigarrow _{{\tt v}}$
, and due to the particular nature of CBV, this notion is mutually defined with that of blocked configurations in Figure 16. Indeed, evaluation for Weak Open CBV with Global State is defined as the union of the reduction rule in Figure 16a, where the notion of blocked configurations is in Figure 16b.

Figure 16. Reduction rules and blocked configurations for Weak Open CBV with Global State.
In particular, note that reduction rule (appR) only evaluates terms on the right of applications if the term on the left is not blocked. Rule (
![]() $\beta _{\tt v}$
) and (appL) are the same as for Weak Open CBV, and rules (get) and (set) are the same as for Weak Open CBN with Global State, with the only difference being the fact that the global state only holds values.
$\beta _{\tt v}$
) and (appL) are the same as for Weak Open CBV, and rules (get) and (set) are the same as for Weak Open CBN with Global State, with the only difference being the fact that the global state only holds values.
Example 5.
All configurations in Example
1
are also blocked configurations in this setting, and so are the following ones, when assuming
![]() $l \neq l'$
:
$l \neq l'$
:
Normal configurations
The notion of normal configuration is also the same as for Weak Open CBN with Global State: a configuration
![]() $(t,s)$
is said to be normal if it is a blocked configuration or
$(t,s)$
is said to be normal if it is a blocked configuration or
![]() $t \in {\tt no}_{{\tt v}}$
, where
$t \in {\tt no}_{{\tt v}}$
, where
![]() ${\tt no}_{{\tt v}}$
is defined in Figure 17.
${\tt no}_{{\tt v}}$
is defined in Figure 17.
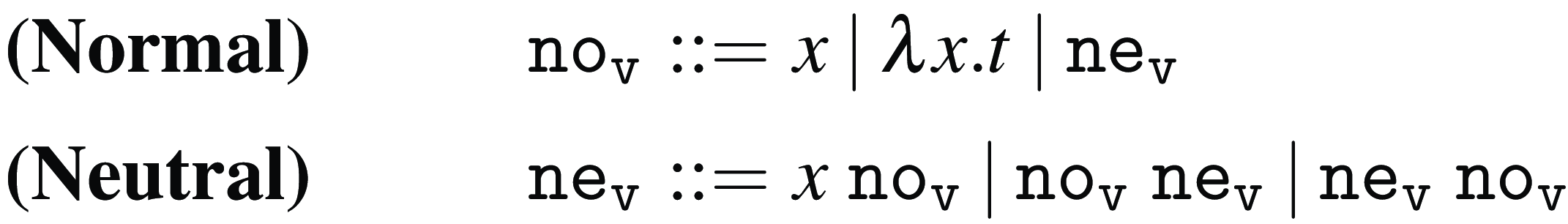
Figure 17. Normal and neutral terms for Weak Open CBV with Global State.
Example 6.
Consider configuration
![]() $c_1 = ((\lambda x.{\tt get}_{l}(\lambda y.yx)) ({\tt set}_{l}((\lambda w.w),z)), \varepsilon )$
. Then we can reach a normal configuration as follows:
$c_1 = ((\lambda x.{\tt get}_{l}(\lambda y.yx)) ({\tt set}_{l}((\lambda w.w),z)), \varepsilon )$
. Then we can reach a normal configuration as follows:
 \begin{align*} ((\lambda x.{\tt get}_{l}(\lambda y.yx)) ({\tt set}_{l}((\lambda w.w),z)), \varepsilon ) & \rightsquigarrow _{{\tt s}} ((\lambda x.{\tt get}_{l}(\lambda y.yx)) z, {\tt upd}_{l}((\lambda w.w),\varepsilon )) \\&\rightsquigarrow _{{\beta _{{\tt v}}}} ({\tt get}_{l}(\lambda y.yz), {\tt upd}_{l}((\lambda w.w),\varepsilon ))\\ & \rightsquigarrow _{{\tt g}} ((\lambda w.w) z, {\tt upd}_{l}((\lambda w.w),\varepsilon )) \\&\rightsquigarrow _{{\beta _{{\tt v}}}} (z, {\tt upd}_{l}((\lambda w.w),\varepsilon )) \end{align*}
\begin{align*} ((\lambda x.{\tt get}_{l}(\lambda y.yx)) ({\tt set}_{l}((\lambda w.w),z)), \varepsilon ) & \rightsquigarrow _{{\tt s}} ((\lambda x.{\tt get}_{l}(\lambda y.yx)) z, {\tt upd}_{l}((\lambda w.w),\varepsilon )) \\&\rightsquigarrow _{{\beta _{{\tt v}}}} ({\tt get}_{l}(\lambda y.yz), {\tt upd}_{l}((\lambda w.w),\varepsilon ))\\ & \rightsquigarrow _{{\tt g}} ((\lambda w.w) z, {\tt upd}_{l}((\lambda w.w),\varepsilon )) \\&\rightsquigarrow _{{\beta _{{\tt v}}}} (z, {\tt upd}_{l}((\lambda w.w),\varepsilon )) \end{align*}
The following proposition, whose proof is in Appendix A.3, shows that normal configurations are indeed irreducible.
Proposition 5.
Let
![]() $(t,s)$
be a configuration. Then
$(t,s)$
be a configuration. Then
![]() $(t,s)$
is normal iff
$(t,s)$
is normal iff
![]() $(t,s) \not \rightsquigarrow _{{\tt v}}$
.
$(t,s) \not \rightsquigarrow _{{\tt v}}$
.
3.2.2 A quantitative type system for Weak Open CBV with Global State
We now present the quantitative type system for Weak Open CBV with Global State. Following the same presentation as for the Weak Open CBN with Global State, we start by introducing the CBV monadic translation of the
![]() $\lambda$
-calculus of Wadler (Reference Wadler1990) by adapting it to account for tight constants and multi-types, and then instantiating the monadic translation with the monad for global state.
$\lambda$
-calculus of Wadler (Reference Wadler1990) by adapting it to account for tight constants and multi-types, and then instantiating the monadic translation with the monad for global state.
The CBV monadic translation
In order to lift the type system for Weak Open CBV into the global state monad, we are going to follow the CBV translations of the simply-typed
![]() $\lambda$
-calculus in Wadler (Reference Wadler1990). Again, we will have to slightly adapt the translation in order to accommodate for tight constants and multi-types. The resulting translation is presented in Figure 18.
$\lambda$
-calculus in Wadler (Reference Wadler1990). Again, we will have to slightly adapt the translation in order to accommodate for tight constants and multi-types. The resulting translation is presented in Figure 18.

Figure 18. The CBV monadic translation for types, typing environments, and judgments.
State and monadic (multi-)types
The grammar for types is presented in Figure 19.
Figure 19. Types for Weak Open CBV with Global State.
State Types for Weak Open CBV with Global State, and all related notions, are similar to those for Weak Open CBN with Global State.
Multi-types are multi-sets of value types. Monadic types and configuration types are exactly the same as for Weak Open CBN with Global State. Moreover, since some typing rules will apply both to value types and multi-types, we will use
![]() $\pi$
as a new auxiliary symbol ranging over both these kinds of types. All other notions related to types are common to Weak Open CBN with Global State. Note that the set of tight constants now consists of three different symbols, as in Weak Open CBV.
$\pi$
as a new auxiliary symbol ranging over both these kinds of types. All other notions related to types are common to Weak Open CBN with Global State. Note that the set of tight constants now consists of three different symbols, as in Weak Open CBV.
Typing system for Weak Open CBV with Global State
The type system for Weak Open CBV with Global State is defined by the typing rules in Figure 20.

Figure 20. Typing rules for Weak Open CBV with Global State.
The notions of typing environments, typing judgments, typing rules, and typability are the same as those for Weak Open CBN with Global State.
Like in Weak Open CBN with Global State, we distinguish between consuming and persistent rules. The intuition behind the rules is the following (again, ignore the counters
![]() $(b,m,d)$
):
$(b,m,d)$
):
-
• Rules (ax), (
 $\lambda$
), (@
$\lambda$
), (@
 $^1_{{\tt p}}$
), (@
$^1_{{\tt p}}$
), (@
 $^2_{{\tt p}}$
), and (m). These rules are essentially the same as for Weak Open CBV, but with types replaced with monadic types.
$^2_{{\tt p}}$
), and (m). These rules are essentially the same as for Weak Open CBV, but with types replaced with monadic types. -
• Rule (
 $\lambda _{\tt p}$
) is the same as for Weak Open CBV.
$\lambda _{\tt p}$
) is the same as for Weak Open CBV. -
• Rule (@). In this rule, we see how CBV, which is more intricate than the CBN, influences the type system. Note that, just like in the case of Weak Open CBN with Global State, this rule is used to type consuming applications. Therefore, CBV tells us the following: (1)
 $t$
is reduced until reaching an abstraction
$t$
is reduced until reaching an abstraction
 $\lambda x.p$
, going from input state type
$\lambda x.p$
, going from input state type
 $\mathscr{T\;}$
to an output state type
$\mathscr{T\;}$
to an output state type
 $\mathscr{T\;}''$
; then (2)
$\mathscr{T\;}''$
; then (2)
 $u$
is reduced until reaching a value
$u$
is reduced until reaching a value
 $v$
, going from the input state type
$v$
, going from the input state type
 $\mathscr{T\;}''$
to an output state type
$\mathscr{T\;}''$
to an output state type
 $\mathscr{T\;}'$
; then (3) the
$\mathscr{T\;}'$
; then (3) the
 $\beta _{\tt v}$
-rule will be fired, resulting in the term
$\beta _{\tt v}$
-rule will be fired, resulting in the term
 $p \{x \setminus v\}$
; and then (4) reduction continues with
$p \{x \setminus v\}$
; and then (4) reduction continues with
 $p \{x \setminus v\}$
, thus going from input state type
$p \{x \setminus v\}$
, thus going from input state type
 $\mathscr{T\;}'$
to the output state type in the configuration type
$\mathscr{T\;}'$
to the output state type in the configuration type
 $\kappa$
. Remark that the arrow type
$\kappa$
. Remark that the arrow type
 $\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
appearing in the monadic type of
$\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
appearing in the monadic type of
 $t$
represents the fact that, after
$t$
represents the fact that, after
 $\lambda x.p$
interacts with value
$\lambda x.p$
interacts with value
 $v$
of type
$v$
of type
 $\mathscr{M}$
,
$\mathscr{M}$
,
 $p \{x \setminus v\}$
continues the computation with behavior
$p \{x \setminus v\}$
continues the computation with behavior
 $\mathscr{T\;}' \Rightarrow \kappa$
.
$\mathscr{T\;}' \Rightarrow \kappa$
. -
• Rule (
 $\uparrow$
). In CBV, variables and abstractions are values. Rule (
$\uparrow$
). In CBV, variables and abstractions are values. Rule (
 $\uparrow$
) lifts value types and multi-types to pure types, that is, monadic types with the same input and output state types.
$\uparrow$
) lifts value types and multi-types to pure types, that is, monadic types with the same input and output state types. -
• Rules (get), (set), (emp), (upd), and (conf). These rules are essentially the same as for Weak Open CBN with Global State, with the only difference being that rules (set) and (upd) place values into locations instead of arbitrary terms.
Counters
The counters work as they did for Weak Open CBN with Global State.
CBV tightness
The notions of tightness for types, typing environments, type judgments, and typing derivations for CBV are as follows:
-
• A type
 $\tau$
is tight if
$\tau$
is tight if
 $\tau$
is a tight constant (i.e.,
$\tau$
is a tight constant (i.e.,
 $\tau \in {{\tt tt}_{\tt v}}$
).
$\tau \in {{\tt tt}_{\tt v}}$
). -
• The notions of tightness for multi-types, list multi-types, and monadic, state, and configuration types are defined just like for Weak Open CBN with Global State (Section 3.1.2).
-
• A typing environment
 $\Gamma$
is tight if, for all
$\Gamma$
is tight if, for all
 $x \in {\tt dom}(\Gamma )$
,
$x \in {\tt dom}(\Gamma )$
,
 $\Gamma (x)$
is tight.
$\Gamma (x)$
is tight. -
• The notions of tightness for typing judgments and typing derivations are defined in the same way as for Weak Open CBN with Global State (Section 3.1.2).
Example 7.
Consider configuration
![]() $c_1$
from Example
6
. Let
$c_1$
from Example
6
. Let
![]() $\mathscr{M}_0 = [ [ {\tt v} ] \rightarrow \{l\;:\;[ \, ]\} \Rightarrow ({\tt v} \times \{l\;:\;[ \, ]\}) ]$
,
$\mathscr{M}_0 = [ [ {\tt v} ] \rightarrow \{l\;:\;[ \, ]\} \Rightarrow ({\tt v} \times \{l\;:\;[ \, ]\}) ]$
,
![]() $\mathscr{T\;}_0 = \{l \;:\; [ \, ]\}$
, and
$\mathscr{T\;}_0 = \{l \;:\; [ \, ]\}$
, and
![]() $\Phi _0$
be the following typing derivation:
$\Phi _0$
be the following typing derivation:
Let
![]() $\Phi _1$
be the following typing derivation:
$\Phi _1$
be the following typing derivation:
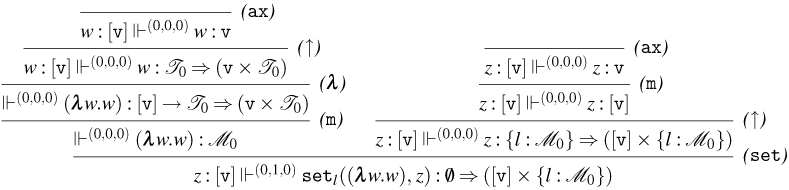
Then, we can build the following tight derivation
![]() $\Phi _{c_1}$
for
$\Phi _{c_1}$
for
![]() $c_1$
:
$c_1$
:
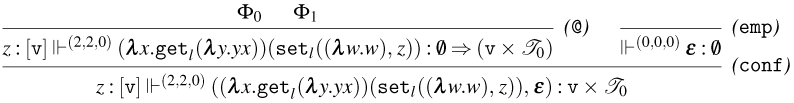
Soundness and completeness
We now extend the soundness and completeness result for Weak Open CBN to Weak Open CBV with Global State. The key properties necessary to show quantitative soundness and completeness for Weak Open CBV with Global State are the same as for Weak Open CBN with Global State. However, a stronger pureness over normal forms is necessary in order to show quantitative completeness, due to the fact that reduction happens both on the left and on the right of applications. All proofs are in Appendix A.3.
Correctness of the counters
To show quantitative completeness, we need to show that if a configuration
![]() $(t,s)$
is normal, then the counters of its tight derivation are as follows: the first counter, which corresponds to the number of
$(t,s)$
is normal, then the counters of its tight derivation are as follows: the first counter, which corresponds to the number of
![]() $\beta _{\tt v}$
-steps needed to reach a Weak Open CBV with Global State normal configuration, is zero; the second counter, which corresponds to the number of
$\beta _{\tt v}$
-steps needed to reach a Weak Open CBV with Global State normal configuration, is zero; the second counter, which corresponds to the number of
![]() $\tt g$
/
$\tt g$
/
![]() $\tt s$
-steps, is zero; and the last counter is equal to the Weak Open CBN with Global State size of
$\tt s$
-steps, is zero; and the last counter is equal to the Weak Open CBN with Global State size of
![]() $(t,s)$
.
$(t,s)$
.
Given some term
![]() $t \in {\tt no}_{{\tt v}}$
, in addition to the type system always inferring a tight monadic type for
$t \in {\tt no}_{{\tt v}}$
, in addition to the type system always inferring a tight monadic type for
![]() $t$
with the same input and output state types, such a type derivation exists for any state type.
$t$
with the same input and output state types, such a type derivation exists for any state type.
Lemma 15 (Normal forms have pure types). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt no}_{{\tt v}}$
, then (1)
$t \in {\tt no}_{{\tt v}}$
, then (1)
![]() $\mathscr{T\;} = \mathscr{T\;}'$
and, (2) for any
$\mathscr{T\;} = \mathscr{T\;}'$
and, (2) for any
![]() $\mathscr{T\;}_0$
, there exists
$\mathscr{T\;}_0$
, there exists
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;}_0 \Rightarrow (\tau \times \mathscr{T\;}_0)$
.
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;}_0 \Rightarrow (\tau \times \mathscr{T\;}_0)$
.
The previous property is a stronger version of Lemma6. It is a crucial property in order to show the quantitative versions of the usual subject reduction (Lemma 19) and subject expansion (Lemma 20) properties for CBV. We now provide an intuitive explanation of why this is the case, and point the reader to the full proofs in Appendix A.3 for a better understanding. Consider the following configuration
![]() $(tu,s)$
, such that
$(tu,s)$
, such that
![]() $(t,s) \not \rightsquigarrow _{{\tt v}}$
and
$(t,s) \not \rightsquigarrow _{{\tt v}}$
and
![]() $(u,s) \rightsquigarrow _{{\tt v}} (u',q)$
. Moreover, let us assume that
$(u,s) \rightsquigarrow _{{\tt v}} (u',q)$
. Moreover, let us assume that
![]() $s \neq q$
. Then,
$s \neq q$
. Then,
![]() $(tu,s) \rightsquigarrow _{{\tt v}} (tu',q)$
, and it is easy to see that
$(tu,s) \rightsquigarrow _{{\tt v}} (tu',q)$
, and it is easy to see that
![]() $(t,q) \not \rightsquigarrow _{{\tt v}}$
(by Proposition5). Clearly, the typability of
$(t,q) \not \rightsquigarrow _{{\tt v}}$
(by Proposition5). Clearly, the typability of
![]() $(tu,s)$
depends on the typability of
$(tu,s)$
depends on the typability of
![]() $(t,s)$
, and the typability of
$(t,s)$
, and the typability of
![]() $(tu',q)$
depends on the typability of
$(tu',q)$
depends on the typability of
![]() $(t,q)$
. However, the typability of
$(t,q)$
. However, the typability of
![]() $t$
in
$t$
in
![]() $(t,s)$
tells us that
$(t,s)$
tells us that
![]() $t$
takes
$t$
takes
![]() $s$
as its input state, and the typability of
$s$
as its input state, and the typability of
![]() $t$
in
$t$
in
![]() $(t,q)$
tells us that
$(t,q)$
tells us that
![]() $t$
should also be able to take
$t$
should also be able to take
![]() $q$
as its input state. Hopefully, this example also clarifies why this property is not necessary in the CBN setting, where evaluation only occurs on the left of applications.
$q$
as its input state. Hopefully, this example also clarifies why this property is not necessary in the CBN setting, where evaluation only occurs on the left of applications.
The following lemma tells us that unblocked normal configurations have correct size.
Lemma 16 (Tight configurations have correct size). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation of the following form:
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation of the following form:
where
![]() $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
![]() $\kappa = (\tau \times \mathscr{T\;}')$
,
$\kappa = (\tau \times \mathscr{T\;}')$
,
![]() $b = b_t + b_s$
,
$b = b_t + b_s$
,
![]() $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
![]() $d = d_t + d_s$
. If
$d = d_t + d_s$
. If
![]() $b_t = m_t = 0$
, then (i)
$b_t = m_t = 0$
, then (i)
![]() $b = m = 0$
and (ii)
$b = m = 0$
and (ii)
![]() $d = |{(t,s)}|_{\texttt {v}}$
.
$d = |{(t,s)}|_{\texttt {v}}$
.
Lemma 17 (Unblocked normal configurations take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation. Then,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation. Then,
![]() $b = m = 0$
iff
$b = m = 0$
iff
![]() $(t,s)$
is an unblocked normal configuration.
$(t,s)$
is an unblocked normal configuration.
Like in Weak Open CBN with Global State, it is also necessary to show that typed configurations that take zero steps are not blocked.
Proposition 6 (Typed configurations are unblocked). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
. Then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
. Then
![]() ${\tt tight}(\Gamma )$
implies
${\tt tight}(\Gamma )$
implies
![]() $(t,s)$
is unblocked.
$(t,s)$
is unblocked.
Moreover, we also need to show that all unblocked normal configurations are tightly typable.
Lemma 18 (All configurations in normal form are tightly typable). If
![]() $(t,s)$
is an unblocked normal configuration, then there exists a tight typing derivation
$(t,s)$
is an unblocked normal configuration, then there exists a tight typing derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, such that
![]() $d = |{(t,s)}|_{\texttt {v}}$
.
$d = |{(t,s)}|_{\texttt {v}}$
.
We now show a quantitative form of type preservation along evaluation for configurations, which relies on Lemma 15.
Lemma 19 (Quantitative subject reduction). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
is a tight derivation, there exists
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
is a tight derivation, there exists
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
, where
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt v}}}$
implies
${\tt r} ={\beta _{{\tt v}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Quantitative soundness follows from the correctness of the counters for unblocked normal configurations (Lemma 17 and Lemma 16) and quantitative subject reduction (Lemma 19).
Theorem 5 (Quantitative soundness). If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
is a tight derivation, then there exists
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
is a tight derivation, then there exists
![]() $(u,q)$
such that
$(u,q)$
such that
![]() $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
![]() $(t,s) \rightsquigarrow _{\tt v}^{(b,m)} (u,q)$
with
$(t,s) \rightsquigarrow _{\tt v}^{(b,m)} (u,q)$
with
![]() $b$
$b$
![]() $\beta _{{\tt v}}$
-steps,
$\beta _{{\tt v}}$
-steps,
![]() $m$
$m$
![]() ${\tt g}/{\tt s}$
-steps, and
${\tt g}/{\tt s}$
-steps, and
![]() $|{(u,q)}|_{\texttt {v}} = d$
.
$|{(u,q)}|_{\texttt {v}} = d$
.
The following property also relies on Lemma 15 and guarantees that typability is preserved back along evaluation.
Lemma 20 (Quantitative subject expansion). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
is a tight derivation, there exists
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
is a tight derivation, there exists
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, where
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, where
![]() ${\tt r} = {\beta _{{\tt v}}}$
implies
${\tt r} = {\beta _{{\tt v}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Quantitative completeness follows from the typability of all unblocked normal configurations in a tight way (Lemma 18) and quantitative subject expansion (Lemma 20).
Theorem 6 (Quantitative completeness). If
![]() $(t,s) \rightsquigarrow _{\tt v}^{(b,m,d)} (u,q)$
and
$(t,s) \rightsquigarrow _{\tt v}^{(b,m,d)} (u,q)$
and
![]() $u \in {\tt no}_{{\tt v}}$
, then there exists a tight derivation
$u \in {\tt no}_{{\tt v}}$
, then there exists a tight derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {v}})}_{\tt v} (t,s):\kappa$
.
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {v}})}_{\tt v} (t,s):\kappa$
.
Example 8.
Consider again configuration
![]() $c_1$
from Example
6
and its tight derivation
$c_1$
from Example
6
and its tight derivation
![]() $\Phi _{c_1}$
from Example
7
. The first two counters of
$\Phi _{c_1}$
from Example
7
. The first two counters of
![]() $\Phi _{c_1}$
are different from
$\Phi _{c_1}$
are different from
![]() $0$
: this means that
$0$
: this means that
![]() $c_1$
is not normal but normalizes in two
$c_1$
is not normal but normalizes in two
![]() $\beta _{{\tt v}}$
-steps (
$\beta _{{\tt v}}$
-steps (
![]() $b = 2$
) and two
$b = 2$
) and two
![]() ${\tt g}/{\tt s}$
-steps (
${\tt g}/{\tt s}$
-steps (
![]() $m = 2$
) to an unblocked normal configuration of size
$m = 2$
) to an unblocked normal configuration of size
![]() $d = 0 = |{(z, {\tt upd}_{l}((\lambda w.w),\varepsilon ))}|_{\texttt {v}}$
.
$d = 0 = |{(z, {\tt upd}_{l}((\lambda w.w),\varepsilon ))}|_{\texttt {v}}$
.
4. Related work
Several papers proposed quantitative approaches for different notions of CBV and CBN (without effects). There are several papers exploring exact and split measures for CBN, such as the pioneer work by Accattoli et al. (Reference Accattoli, Graham-Lengrand and Kesner2018, Reference Accattoli, Graham-Lengrand and Kesner2020), as well as others, for example, Alves et al. (Reference Alves, Kesner, Ventura, Bezem and Mahboubi2019), which explores CBN enriched with patterns, and Kesner and Vial (Reference Kesner and Vial2020), which generalized CBN to classical logic. The state of the art for CBV is as follows. The first non-idempotent intersection type system for Plotkin’s CBV is Ehrhard (Reference Ehrhard2012), where reduction is allowed under abstractions, and terms are considered to be closed. This work was further extended by Carraro and Guerrieri (Reference Carraro and Guerrieri2014), where commutation rules are added to the calculus. None of these contributions extracts quantitative bounds from the type derivations. A calculus for open CBV is proposed in Accattoli and Guerrieri (Reference Accattoli and Guerrieri2018), where fireballs – normal forms – can be erased and duplicated. Quantitative results are obtained, but no split measures. Other similar approaches appear in Guerrieri (Reference Guerrieri2018) and Accattoli et al. (Reference Accattoli, Guerrieri, Leberle, Brahám, Dubslaff and Tarifa2023). A logical characterization of CBV solvability is given in Accattoli and Guerrieri (Reference Accattoli and Guerrieri2022). The resulting non-idempotent system gives quantitative information of the solvable associated reduction relation, and exact measures are obtained. A similar notion of solvability for both CBN and CBV for generalized applications was studied in Kesner and Peyrot (Reference Kesner and Peyrot2022), together with a logical characterization provided by a quantitative system. Other non-idempotent systems for CBV were proposed (Manzonetto et al., Reference Manzonetto, Pagani and Ronchi Della Rocca2019; Kerinec et al., Reference Kerinec, Manzonetto and Ronchi Della Rocca2021), but they do not enjoy subject reduction and expansion. Exact and split measures for (strong) open CBN and CBV are developed in Kesner and Viso (Reference Kesner and Viso2022), which relate the exact measure to those of a subsuming framework called the bang calculus, which is able to encode both strategies, developed in Bucciarelli et al. (Reference Bucciarelli, Kesner, Ríos and Viso2020, Reference Bucciarelli, Kesner, Ríos and Viso2023). Dezani-Ciancaglini et al. (Reference Dezani-Ciancaglini, Giannini and Ronchi Della Rocca2009), a system with universally quantified intersection and reference types is introduced for a language belonging to the ML-family. However, intersections are idempotent and only (qualitative) soundness is proved.
With respect to CBN and CBV with effects, there has been a lot of work involving probabilistic versions of the lambda calculus. In Faggian and Ronchi Della Rocca (Reference Faggian and Ronchi Della Rocca2019), extensions of the lambda calculus with a probabilistic choice operator for CBV and CBN are introduced. However, no quantitative results are provided. In Breuvart and Dal Lago (Reference Breuvart, Dal Lago, Sabel and Thiemann2018), monadic intersection types are used to obtain a (non-exact) quantitative type system for a probabilistic calculus identical to the one in Faggian and Ronchi Della Rocca (Reference Faggian and Ronchi Della Rocca2019). More recently, in Dal Lago et al. (Reference Dal Lago, Faggian and Ronchi Della Rocca2021), non-idempotent intersection types were used to characterize almost sure termination and obtain exact split measures for a probabilistic calculus. This is done for both weak CBN and CBV, but on a closed setting, and not for other effects.
Concerning (exact) quantitative type systems for programming languages with global state, the state of the art is still underexplored. Some type systems are given in Davies and Pfenning (Reference Davies and Pfenning2000), and Benton et al. (Reference Benton, Kennedy, Beringer, Hofmann, Porto and López-Fraguas2009), but they cannot be seen as models (since termination does not imply typability) and lack quantitative results. Our work is inspired by a recent idempotent (thus only qualitative and not quantitative) type system for CBV with global memory proposed by de’Liguoro and Treglia (Reference de’Liguoro, Treglia, Veltri, Benton and Ghilezan2021) (a technical comparison to this work appears at the end of Section 3.1.2). This work was extended in Gavazzo et al. (Reference Gavazzo, Treglia, Vanoni and Weirich2024) to a generic framework for algebraic effects. However, their approach lacks any quantitative results and does not hold for global state.
Languages with global state are often closely related to concurrent languages due to the challenges and complexities involved in managing shared mutable state in concurrent settings. Indeed, if we consider locations as channels and the get and set operations as read and write, we can find some similarities between our language and concurrent languages, such as that of Gay and Vasconcelos (Reference Gay and Vasconcelos2010), where buffered channels are used in order to obtain asynchronous communication, or that of Dal Lago et al. (Reference Dal Lago, de Visme, Mazza and Yoshimizu2019), where an intersection type discipline is used to capture properties such as deadlock freedom and termination for a fragment of the
![]() $\pi$
-calculus.
$\pi$
-calculus.
5. Conclusion
This paper provides a foundational step into the development of quantitative type systems for programming languages with effects. We focus on a simple language with global memory access capabilities. Due to the inherent lack of confluence in such a framework, we fix two particular evaluation strategies: Weak Open CBN and CBV. For each language, we provide a quantitative type system characterizing termination and capturing exact measures for the number of
![]() $\beta$
-steps, memory accesses, and the size of unblocked normal configurations. This study provides a valuable insight into time and space analysis of languages with global memory, with respect to the length of evaluation and the size of unblocked normal configurations, respectively.
$\beta$
-steps, memory accesses, and the size of unblocked normal configurations. This study provides a valuable insight into time and space analysis of languages with global memory, with respect to the length of evaluation and the size of unblocked normal configurations, respectively.
In future work, we would like to explore effectful computations involving global memory in a more general framework subsuming CBN and CBV evaluation, such as the bang calculus (Bucciarelli et al., Reference Bucciarelli, Kesner, Ríos and Viso2020). Furthermore, we would like to apply our quantitative techniques to other (algebraic) effects, such as non-termination, exceptions, non-determinism, and I/O. Finally, we would also like to explore the connection between this work and that of Gay and Vasconcelos (Reference Gay and Vasconcelos2010) and Dal Lago et al. (Reference Dal Lago, de Visme, Mazza and Yoshimizu2019), in order to understand how to extract quantitative information for asynchronous communications, which is not the focus of either of these works. Finally, we would also like to take advantage of our techniques in order to study lenses (Bohannon et al., Reference Bohannon, Pierce, Vaughan and Vansummeren2006) and bidirectional programming languages (Bohannon et al., Reference Bohannon, Foster, Pierce, Pilkiewicz, Schmitt, Necula and Wadler2008).
Acknowledgments
The authors would like to thank the reviewers for their helpful suggestions that improved this work and Andrej Bauer for providing them with good references explaining the state-logging monad. The last author also acknowledges the following funding: National Funds through the Portuguese funding agency – FCT – through the individual research grant 2021.04731.BD; Base Funding - UIDB/00027/2020 of the Artificial Intelligence and Computer Science Laboratory – LIACC – funded by national funds through the FCT/MCTES (PIDDAC); European Research Network on Formal Proofs COST Action CA20111.
Competing interests
The authors declare none.
Appendix A. Proofs
A.1 Weak Open CBN and CBV
A.1.1 Weak Open CBN
Proposition 1 (Normal forms for Weak Open CBN). Let
![]() $t$
be a term. Then
$t$
be a term. Then
![]() $t \in {\tt no}_{{\tt n}}$
iff
$t \in {\tt no}_{{\tt n}}$
iff
![]() $t \not {\!\rightarrow }_{\texttt {n}}$
.
$t \not {\!\rightarrow }_{\texttt {n}}$
.
Proof. We refine the original statement as follows:
-
(1)
 $t \not {\!\rightarrow }_{\texttt {n}}$
and
$t \not {\!\rightarrow }_{\texttt {n}}$
and
 $\neg {\tt abs}(t)$
iff
$\neg {\tt abs}(t)$
iff
 $t \in {\tt ne}_{{\tt n}}$
.
$t \in {\tt ne}_{{\tt n}}$
. -
(2)
 $t \not {\!\rightarrow }_{\texttt {n}}$
iff
$t \not {\!\rightarrow }_{\texttt {n}}$
iff
 $t \in {\tt no}_{{\tt n}}$
.
$t \in {\tt no}_{{\tt n}}$
.
-
⇒) By induction over
 $t$
:
$t$
:-
(1) Let
 $t \not {\!\rightarrow }_{\texttt {n}}$
and
$t \not {\!\rightarrow }_{\texttt {n}}$
and
 $\neg {\tt abs}(t)$
:
$\neg {\tt abs}(t)$
:-
– Case
 $t = x$
. Then
$t = x$
. Then
 $x \in {\tt ne}_{{\tt n}}$
by definition.
$x \in {\tt ne}_{{\tt n}}$
by definition. -
– Case
 $t = \lambda x.u$
. Then
$t = \lambda x.u$
. Then
 ${\tt abs}(t)$
holds, which contradicts the hypothesis. Therefore, this case cannot apply.
${\tt abs}(t)$
holds, which contradicts the hypothesis. Therefore, this case cannot apply. -
– Case
 $t = u p$
. Since
$t = u p$
. Since
 $u p \not {\!\rightarrow }_{\texttt {n}}$
, no rule of
$u p \not {\!\rightarrow }_{\texttt {n}}$
, no rule of
 ${\rightarrow }_{\texttt {n}}$
applies to
${\rightarrow }_{\texttt {n}}$
applies to
 $u p$
. Then
$u p$
. Then
 $\neg {\tt abs}(u)$
, otherwise (
$\neg {\tt abs}(u)$
, otherwise (
 $\beta _{\tt n}$
) would apply, and
$\beta _{\tt n}$
) would apply, and
 $u \not {\!\rightarrow }_{\texttt {n}}$
, in which case (appL) would apply. By the i.h. (1)
$u \not {\!\rightarrow }_{\texttt {n}}$
, in which case (appL) would apply. By the i.h. (1)
 $u \in {\tt ne}_{{\tt n}}$
, therefore
$u \in {\tt ne}_{{\tt n}}$
, therefore
 $u p \in {\tt ne}_{{\tt n}}$
.
$u p \in {\tt ne}_{{\tt n}}$
.
-
-
(2) Let
 $t \not {\!\rightarrow }_{\texttt {n}}$
:
$t \not {\!\rightarrow }_{\texttt {n}}$
:-
– Case
 $t = \lambda x.u$
. Then
$t = \lambda x.u$
. Then
 $\lambda x.u \in {\tt no}_{{\tt n}}$
by definition.
$\lambda x.u \in {\tt no}_{{\tt n}}$
by definition. -
– Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
.
$t \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
.
-
-
-
⇐)
-
(1) By induction over
 $t \in {\tt ne}_{{\tt n}}$
:
$t \in {\tt ne}_{{\tt n}}$
:-
– Case
 $t = x$
. Then
$t = x$
. Then
 $x \not {\!\rightarrow }_{\texttt {n}}$
and
$x \not {\!\rightarrow }_{\texttt {n}}$
and
 $\neg {\tt abs}(x)$
by definition.
$\neg {\tt abs}(x)$
by definition. -
– Case
 $t = u p$
, such that
$t = u p$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. By the i.h. (1), we know
$u \in {\tt ne}_{{\tt n}}$
. By the i.h. (1), we know
 $u \not {\!\rightarrow }_{\texttt {n}}$
and
$u \not {\!\rightarrow }_{\texttt {n}}$
and
 $\neg {\tt abs}(u)$
. Therefore, neither (appL) nor (
$\neg {\tt abs}(u)$
. Therefore, neither (appL) nor (
 $\beta _{\tt n}$
) apply.
$\beta _{\tt n}$
) apply.
-
-
(2) Let
 $t \in {\tt no}_{{\tt n}}$
:
$t \in {\tt no}_{{\tt n}}$
:-
– Case
 $t = \lambda x.u$
. Then
$t = \lambda x.u$
. Then
 $\lambda x.u \not {\!\rightarrow }_{\texttt {n}}$
by definition.
$\lambda x.u \not {\!\rightarrow }_{\texttt {n}}$
by definition. -
– Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}}$
by definition, therefore
$t \in {\tt ne}_{{\tt n}}$
by definition, therefore
 $t \not {\!\rightarrow }_{\texttt {n}}$
, by point (1).
$t \not {\!\rightarrow }_{\texttt {n}}$
, by point (1).
-
-
Proposition 7 (Relevance). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace\overset{(b,s)}{\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
. Then
$\Phi \triangleright \, \Gamma \negmedspace\overset{(b,s)}{\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
. Then
![]() ${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
.
${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
.
Proof.
By a simple induction over
![]() $\Phi$
.
$\Phi$
.
Lemma 21 (Tight spreading). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)}{\vdash_{\texttt{n}}} \negmedspace t\;:\; \tau$
, such that
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)}{\vdash_{\texttt{n}}} \negmedspace t\;:\; \tau$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt ne}_{\texttt{n}}$
, then
$t \in {\tt ne}_{\texttt{n}}$
, then
![]() $\tau$
is a tight constant.
$\tau$
is a tight constant.
Proof.
The proof follows by induction over
![]() $t \in {\tt ne}_{{\tt n}}$
:
$t \in {\tt ne}_{{\tt n}}$
:
-
• Case
 $t = x$
. Then
$t = x$
. Then
 $\Phi \triangleright \, x \;:\; [ \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace x\;:\; \tau$
, with
$\Phi \triangleright \, x \;:\; [ \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace x\;:\; \tau$
, with
 $x \;:\; [ \tau ]$
tight, therefore
$x \;:\; [ \tau ]$
tight, therefore
 $\tau \in {{\tt tt}_{\tt n}}$
.
$\tau \in {{\tt tt}_{\tt n}}$
. -
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. Then
$u \in {\tt ne}_{{\tt n}}$
. Then
 $\Phi$
must end with rule (@) or (@
$\Phi$
must end with rule (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Case
 $\Phi$
ends with rule (@). Then
$\Phi$
ends with rule (@). Then
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M}$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
is tight,
$\Gamma = \Gamma _u + \Gamma _p$
is tight,
 $b = 1 + b_u + b_p$
, and
$b = 1 + b_u + b_p$
, and
 $s = s_u + s_p$
. Moreover,
$s = s_u + s_p$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. By the i.h. on
$\Gamma _p$
are tight. By the i.h. on
 $\Phi _u$
, we have
$\Phi _u$
, we have
 $\mathscr{M} \rightarrow \tau \in {{\tt tt}_{\tt n}}$
, which is a contradiction. Therefore, this case does not apply.
$\mathscr{M} \rightarrow \tau \in {{\tt tt}_{\tt n}}$
, which is a contradiction. Therefore, this case does not apply. -
– Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, meaning in particular that
$\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, meaning in particular that
 $\tau = {\tt n}$
. Thus, we can conclude since
$\tau = {\tt n}$
. Thus, we can conclude since
 $\tau \in {{\tt tt}_{\tt n}}$
.
$\tau \in {{\tt tt}_{\tt n}}$
.
-
Lemma 22 (Persistent abstractions have tight type). If
![]() $\Phi \triangleright \, \Gamma \negmedspace\overset{(b,s)}{\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
. If
$\Phi \triangleright \, \Gamma \negmedspace\overset{(b,s)}{\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
. If
![]() $\tau \in \overline {{\tt a}}$
, then
$\tau \in \overline {{\tt a}}$
, then
![]() $\neg {\tt abs}(t)$
.
$\neg {\tt abs}(t)$
.
Proof.
By induction over
![]() $\Phi$
:
$\Phi$
:
-
• Case
 $\Phi$
ends with rule (ax), (@), and (@
$\Phi$
ends with rule (ax), (@), and (@
 $_{{\tt p}}$
). Then
$_{{\tt p}}$
). Then
 $\neg {\tt abs}(t)$
holds by definition.
$\neg {\tt abs}(t)$
holds by definition. -
• Case
 $\Phi$
ends with rule (
$\Phi$
ends with rule (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). Then
$\lambda _{\tt p}$
). Then
 $\tau \not \in \overline {{\tt a}}$
, and then these cases hold vacuously.
$\tau \not \in \overline {{\tt a}}$
, and then these cases hold vacuously.
Lemma 1 (Normal forms take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
be a tight type derivation. Then,
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
be a tight type derivation. Then,
![]() $b = 0$
iff
$b = 0$
iff
![]() $t \in {\tt no}$
.
$t \in {\tt no}$
.
Proof.
-
⇒) We refine the original statement as follows:
-
(1) Let
 $\Phi \triangleright {\Gamma }\negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\;\tau$
be a tight derivation. Then
$\Phi \triangleright {\Gamma }\negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\;\tau$
be a tight derivation. Then
 $b=0$
and
$b=0$
and
 $\neg {\tt abs}(t)$
implies
$\neg {\tt abs}(t)$
implies
 $t \in {\tt ne}_{{\tt n}}$
.
$t \in {\tt ne}_{{\tt n}}$
. -
(2) Let
 $\Phi \triangleright {\Gamma }\negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\;\tau$
be a tight derivation. Then
$\Phi \triangleright {\Gamma }\negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\;\tau$
be a tight derivation. Then
 $b=0$
implies
$b=0$
implies
 $t \in {\tt no}_{{\tt n}}$
.
$t \in {\tt no}_{{\tt n}}$
. -
(1) Let
 $b = 0$
and
$b = 0$
and
 $\neg {\tt abs}(t)$
. The proof follows by induction over
$\neg {\tt abs}(t)$
. The proof follows by induction over
 $\Phi$
, according to the last rule of
$\Phi$
, according to the last rule of
 $\Phi$
:
$\Phi$
:-
– Rule (
 $\lambda$
) or (
$\lambda$
) or (
 $\lambda _{\tt p}$
). Then
$\lambda _{\tt p}$
). Then
 ${\tt abs}(t)$
holds, which contradicts the hypothesis. Therefore, these cases cannot apply.
${\tt abs}(t)$
holds, which contradicts the hypothesis. Therefore, these cases cannot apply. -
– Rule (ax). Then
 $t = x$
and
$t = x$
and
 $x \in {\tt ne}_{{\tt n}}$
.
$x \in {\tt ne}_{{\tt n}}$
. -
– Rule (m). Then
 $\tau \not \in {{\tt tt}_{\tt n}}$
, and thus,
$\tau \not \in {{\tt tt}_{\tt n}}$
, and thus,
 $\Phi$
is not tight, which contradicts the hypothesis. Therefore, this cannot apply.
$\Phi$
is not tight, which contradicts the hypothesis. Therefore, this cannot apply. -
– Rule (@). Then
 $b \gt 0$
so that this case holds vacuously.
$b \gt 0$
so that this case holds vacuously. -
– Rule (@
 $_{{\tt p}}$
). Then
$_{{\tt p}}$
). Then
 $t = up$
and
$t = up$
and
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi _u \triangleright \, \Gamma \negmedspace \overset {(0,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, such that
$\Phi _u \triangleright \, \Gamma \negmedspace \overset {(0,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, such that
 $\tau = {\tt n}$
. Also, since
$\tau = {\tt n}$
. Also, since
 ${\tt n} \in \overline {{\tt a}}$
then
${\tt n} \in \overline {{\tt a}}$
then
 $\neg {\tt abs}(u)$
, according to Lemma 22. Therefore, by the i.h. (1), we have
$\neg {\tt abs}(u)$
, according to Lemma 22. Therefore, by the i.h. (1), we have
 $u \in {\tt ne}_{{\tt n}}$
. Thus,
$u \in {\tt ne}_{{\tt n}}$
. Thus,
 $u p \in {\tt ne}_{{\tt n}}$
as required.
$u p \in {\tt ne}_{{\tt n}}$
as required.
-
-
(2) Let
 $b = 0$
:
$b = 0$
:-
– Case
 $t = \lambda x.u$
. Then
$t = \lambda x.u$
. Then
 $\lambda x.u \in {\tt no}_{{\tt n}}$
by definition.
$\lambda x.u \in {\tt no}_{{\tt n}}$
by definition. -
– Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}}$
, by point (1), which implies
$t \in {\tt ne}_{{\tt n}}$
, by point (1), which implies
 $t \in {\tt no}_{{\tt n}}$
.
$t \in {\tt no}_{{\tt n}}$
.
-
-
-
⇐)
-
(1) The proof follows by induction over
 $t \in {\tt ne}_{{\tt n}}$
:
$t \in {\tt ne}_{{\tt n}}$
:-
– Case
 $t = x$
. Then
$t = x$
. Then
 $b = 0$
and
$b = 0$
and
 $\neg {\tt abs}(x)$
, by definition.
$\neg {\tt abs}(x)$
, by definition. -
– Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. Then
$u \in {\tt ne}_{{\tt n}}$
. Then
 $\Phi$
must end with rule (@) or (@
$\Phi$
must end with rule (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
* Rule (@). Then
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M}$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
tight,
$\Gamma = \Gamma _u + \Gamma _p$
tight,
 $b = 1 + b_u + b_p$
, and
$b = 1 + b_u + b_p$
, and
 $s = s_u + s_p$
. Therefore,
$s = s_u + s_p$
. Therefore,
 $\mathscr{M} \rightarrow \tau$
turns to be tight by Lemma 21, which is a contradiction. Therefore, this case cannot apply.
$\mathscr{M} \rightarrow \tau$
turns to be tight by Lemma 21, which is a contradiction. Therefore, this case cannot apply. -
* Rule (@
 $_{{\tt p}}$
). Then
$_{{\tt p}}$
). Then
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi _u \triangleright \,\Gamma \negmedspace \overset {(b,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, where
$\Phi _u \triangleright \,\Gamma \negmedspace \overset {(b,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, where
 $\tau = {\tt n}$
. Therefore,
$\tau = {\tt n}$
. Therefore,
 $b = 0$
by applying point (2) to
$b = 0$
by applying point (2) to
 $\Phi _u$
. Moreover,
$\Phi _u$
. Moreover,
 $\neg {\tt abs}(up)$
trivially holds.
$\neg {\tt abs}(up)$
trivially holds.
-
-
-
(2) Case
 $t \in {\tt no}_{{\tt n}}$
:
$t \in {\tt no}_{{\tt n}}$
:-
– Case
 $t = \lambda x.u$
. Then,
$t = \lambda x.u$
. Then,
 $\Phi$
must end with (
$\Phi$
must end with (
 $\lambda$
), (m) or (
$\lambda$
), (m) or (
 $\lambda _{\tt p}$
). The first two cases cannot apply, since
$\lambda _{\tt p}$
). The first two cases cannot apply, since
 $\tau \not \in {{\tt tt}_{\tt n}}$
, and thus,
$\tau \not \in {{\tt tt}_{\tt n}}$
, and thus,
 $\Phi$
cannot be tight. For the last case,
$\Phi$
cannot be tight. For the last case,
 $b = 0$
holds by definition.
$b = 0$
holds by definition. -
– Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}}$
by definition. Therefore,
$t \in {\tt ne}_{{\tt n}}$
by definition. Therefore,
 $b = 0$
by applying point (1) to
$b = 0$
by applying point (1) to
 $t$
.
$t$
.
-
-
Lemma 2 (Normal forms have correct size). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
be a tight type derivation. If
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
be a tight type derivation. If
![]() $b = 0$
then
$b = 0$
then
![]() $s = |t|_{\texttt{n}}$
.
$s = |t|_{\texttt{n}}$
.
Proof.
The proof follows by induction over
![]() $\Phi$
, according to the last rule of
$\Phi$
, according to the last rule of
![]() $\Phi$
:
$\Phi$
:
-
• Rule (ax) or (
 $\lambda _{\tt p}$
). Then
$\lambda _{\tt p}$
). Then
 $t = x$
or
$t = x$
or
 $t = \lambda x.u$
. Moreover,
$t = \lambda x.u$
. Moreover,
 $s = 0 = |x| = |\lambda x.u|$
by definition.
$s = 0 = |x| = |\lambda x.u|$
by definition. -
• Rule (
 $\lambda$
) or (m). Then
$\lambda$
) or (m). Then
 $\tau \not \in {{\tt tt}_{\tt n}}$
, which contradicts that
$\tau \not \in {{\tt tt}_{\tt n}}$
, which contradicts that
 $\Phi$
is tight. Therefore, these cases cannot apply.
$\Phi$
is tight. Therefore, these cases cannot apply. -
• Rule (@). Then
 $b \gt 0$
; therefore, this case holds vacuously.
$b \gt 0$
; therefore, this case holds vacuously. -
• Rule (@
 $_{{\tt p}}$
). Then
$_{{\tt p}}$
). Then
 $t = up$
and
$t = up$
and
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, where
$\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, where
 $\tau = {\tt n}$
,
$\tau = {\tt n}$
,
 $b = 0$
, and
$b = 0$
, and
 $s = 1 + s_u$
. Therefore,
$s = 1 + s_u$
. Therefore,
 $s_u = |u|_{\texttt{n}}$
by applying the i.h. to
$s_u = |u|_{\texttt{n}}$
by applying the i.h. to
 $\Phi _u$
. Thus, we can conclude with
$\Phi _u$
. Thus, we can conclude with
 $s = 1+s_u = 1 + |u|_{\texttt{n}} = |up|_{\texttt{n}}$
.
$s = 1+s_u = 1 + |u|_{\texttt{n}} = |up|_{\texttt{n}}$
.
Lemma 3 (All normal forms are tightly typable). If
![]() $t \in {\tt no}_{\texttt{n}}$
, then there exists a tight type derivation
$t \in {\tt no}_{\texttt{n}}$
, then there exists a tight type derivation
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
, such that
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
, such that
![]() $s = |t|_{\texttt{n}}$
.
$s = |t|_{\texttt{n}}$
.
We refine the original statement as follows:
-
(1) If
 $t \in {\tt ne}_{{\tt n}}$
, there exists a tight derivation
$t \in {\tt ne}_{{\tt n}}$
, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t\;:\; {\tt n}$
such that
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t\;:\; {\tt n}$
such that
 $s = |{t}|_{\texttt {n}}$
.
$s = |{t}|_{\texttt {n}}$
. -
(2) If
 $t \in {\tt no}_{{\tt n}}$
, there exists a tight derivation
$t \in {\tt no}_{{\tt n}}$
, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t\;:\; {{\tt tt}_{\tt n}}$
such that
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t\;:\; {{\tt tt}_{\tt n}}$
such that
 $s = |{t}|_{\texttt {n}}$
.
$s = |{t}|_{\texttt {n}}$
.
-
(1) The proof follows by induction over
 $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:-
• Case
 $t = x$
. Then we can build
$t = x$
. Then we can build
 $\Phi$
as follows:such that
$\Phi$
as follows:such that \begin{equation*}\frac {}{x \;:\; [ {\tt n} ] \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace x\;:\; {\tt n}}({\tt ax}) \end{equation*}
\begin{equation*}\frac {}{x \;:\; [ {\tt n} ] \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace x\;:\; {\tt n}}({\tt ax}) \end{equation*}
 $\Gamma = (x \;:\; [ {\tt n} ])$
,
$\Gamma = (x \;:\; [ {\tt n} ])$
,
 $b = 0$
, and
$b = 0$
, and
 $s = 0 = |{x}|_{\texttt {n}}$
.
$s = 0 = |{x}|_{\texttt {n}}$
.
-
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. By applying the i.h. (1) to
$u \in {\tt ne}_{{\tt n}}$
. By applying the i.h. (1) to
 $\Phi _u$
, there exists a tight derivation
$\Phi _u$
, there exists a tight derivation
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, such that
 $|{t}|_{\texttt {n}} = s_u$
. Therefore, we can build
$|{t}|_{\texttt {n}} = s_u$
. Therefore, we can build
 $\Phi$
as follows:such that
$\Phi$
as follows:such that \begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}}{\Gamma _u \mathop {\vdash }\limits ^{(b_u,1+s_u)}_{} up: {\tt n}}({\tt @}_{{\tt p}}) \end{equation*}
\begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}}{\Gamma _u \mathop {\vdash }\limits ^{(b_u,1+s_u)}_{} up: {\tt n}}({\tt @}_{{\tt p}}) \end{equation*}
 $\Gamma = \Gamma _u$
,
$\Gamma = \Gamma _u$
,
 $b = b_u$
, and
$b = b_u$
, and
 $s = 1+s_u = 1 + |{u}|_{\texttt {n}} = |{up}|_{\texttt {n}}$
.
$s = 1+s_u = 1 + |{u}|_{\texttt {n}} = |{up}|_{\texttt {n}}$
.
-
-
(2) The proof follows by induction over
 $t \in {\tt no}_{{\tt n}}$
:
$t \in {\tt no}_{{\tt n}}$
:-
• Case
 $t = \lambda x.u$
. Then we can build
$t = \lambda x.u$
. Then we can build
 $\Phi$
as follows:such that
$\Phi$
as follows:such that \begin{equation*} \frac {}{\emptyset \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace \lambda x.u\;:\; {\tt a}}(\lambda _{\tt p}) \end{equation*}
\begin{equation*} \frac {}{\emptyset \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace \lambda x.u\;:\; {\tt a}}(\lambda _{\tt p}) \end{equation*}
 $\Gamma = \emptyset$
,
$\Gamma = \emptyset$
,
 $b = 0$
and
$b = 0$
and
 $s = 0 = |\lambda {x.u}|_{\texttt {n}}$
.
$s = 0 = |\lambda {x.u}|_{\texttt {n}}$
.
-
• Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}}$
by definition. Therefore,
$t \in {\tt ne}_{{\tt n}}$
by definition. Therefore,
 $s = |{t}|_{\texttt {n}}$
by applying point (1) to
$s = |{t}|_{\texttt {n}}$
by applying point (1) to
 $t$
.
$t$
.
-
Lemma 23 (Multi-types can split and merge). Let
![]() $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
![]() $b = +_{i \in I} b_i$
, and
$b = +_{i \in I} b_i$
, and
![]() $s = +_{i \in I} s_i$
. Then,
$s = +_{i \in I} s_i$
. Then,
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}$
iff (
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}$
iff (
![]() $\Phi ^i_t \triangleright \, \Gamma _i \negmedspace \overset{(b_i,s_i)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}_i)_{i \in I}$
.
$\Phi ^i_t \triangleright \, \Gamma _i \negmedspace \overset{(b_i,s_i)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}_i)_{i \in I}$
.
Proof.
-
⇒) We start by noting that
 $\Phi _t$
must end with the rule (m). Therefore, we have
$\Phi _t$
must end with the rule (m). Therefore, we have
 $\Gamma = +_{j \in J} \Gamma _j$
,
$\Gamma = +_{j \in J} \Gamma _j$
,
 $\mathscr{M} = [ \tau _j ]_{j \in J}$
,
$\mathscr{M} = [ \tau _j ]_{j \in J}$
,
 $b = +_{j \in J} b_j$
,
$b = +_{j \in J} b_j$
,
 $s = +_{j \in J} s_j$
, and
$s = +_{j \in J} s_j$
, and
 $(\Phi ^j_t \triangleright \, \Gamma _j \negmedspace \overset{(b_j,s_j)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau _j)_{j \in J}$
, for some
$(\Phi ^j_t \triangleright \, \Gamma _j \negmedspace \overset{(b_j,s_j)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau _j)_{j \in J}$
, for some
 $J$
. Let
$J$
. Let
 $\mathscr{M}_i = [ \tau _k ]_{k \in K_i}$
, for each
$\mathscr{M}_i = [ \tau _k ]_{k \in K_i}$
, for each
 $i \in I$
, such that
$i \in I$
, such that
 $J = +_{i \in I} K_i$
. Then, by using rule (m), we can build
$J = +_{i \in I} K_i$
. Then, by using rule (m), we can build
 $\Phi ^i_t \triangleright \, \Gamma _i \negmedspace \overset{(b_i,s_i)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}_i$
, for each
$\Phi ^i_t \triangleright \, \Gamma _i \negmedspace \overset{(b_i,s_i)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}_i$
, for each
 $i \in I$
, such that
$i \in I$
, such that
 $\Gamma _i = +_{k \in K_i} \Gamma _k$
,
$\Gamma _i = +_{k \in K_i} \Gamma _k$
,
 $b_i = +_{k \in K_i} b_k$
, and
$b_i = +_{k \in K_i} b_k$
, and
 $s_i = +_{k \in K_i} s_k$
. So we can conclude with
$s_i = +_{k \in K_i} s_k$
. So we can conclude with
 $\Gamma = +_{j \in J} \Gamma _j = +_{i \in I} (+_{k \in K_i} \Gamma _k) = +_{i \in I} \Gamma _i$
,
$\Gamma = +_{j \in J} \Gamma _j = +_{i \in I} (+_{k \in K_i} \Gamma _k) = +_{i \in I} \Gamma _i$
,
 $b = +_{j \in J} b_j = +_{i \in I} (+_{k \in K_i} b_k) = +_{i \in I} b_i$
, and
$b = +_{j \in J} b_j = +_{i \in I} (+_{k \in K_i} b_k) = +_{i \in I} b_i$
, and
 $s = +_{j \in J} s_j = +_{i \in I} (+_{k \in K_i} s_k) = +_{i \in I} s_i$
.
$s = +_{j \in J} s_j = +_{i \in I} (+_{k \in K_i} s_k) = +_{i \in I} s_i$
. -
⇐) We start by noting that each
 $\Phi ^i_t$
must end with the rule (m). Therefore, for each
$\Phi ^i_t$
must end with the rule (m). Therefore, for each
 $i \in I$
, we have
$i \in I$
, we have
 $\Gamma _i = +_{k \in K_i} \Gamma _k$
,
$\Gamma _i = +_{k \in K_i} \Gamma _k$
,
 $\mathscr{M}_i = [ \tau _k ]_{k \in K_i}$
,
$\mathscr{M}_i = [ \tau _k ]_{k \in K_i}$
,
 $b_i = +_{k \in K_i} b_k$
and
$b_i = +_{k \in K_i} b_k$
and
 $s_i = +_{k \in K_i} s_k$
, and the following derivations
$s_i = +_{k \in K_i} s_k$
, and the following derivations
 $(\Phi ^k_t \triangleright \, \Gamma _k \negmedspace \overset{(b_k,s_k)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau _k)_{k \in K_i}$
. Let
$(\Phi ^k_t \triangleright \, \Gamma _k \negmedspace \overset{(b_k,s_k)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau _k)_{k \in K_i}$
. Let
 $J = +_{i \in I} K_i$
and
$J = +_{i \in I} K_i$
and
 $\mathscr{M} = [ \tau _j ]_{j \in J} = [ \tau _k ]_{k \in K_i, i \in I}$
. We can use rule (m) to build
$\mathscr{M} = [ \tau _j ]_{j \in J} = [ \tau _k ]_{k \in K_i, i \in I}$
. We can use rule (m) to build
 $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(+_{j \in J} b_j, +_{j \in J} s_j)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}$
. So we can conclude with
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(+_{j \in J} b_j, +_{j \in J} s_j)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \mathscr{M}$
. So we can conclude with
 $\Gamma = +_{j \in J} \Gamma _j = +_{i \in I} (\!+_{k \in K_i} \Gamma _k) = +_{i \in I} \Gamma _i$
,
$\Gamma = +_{j \in J} \Gamma _j = +_{i \in I} (\!+_{k \in K_i} \Gamma _k) = +_{i \in I} \Gamma _i$
,
 $b = +_{j \in J} b_j = +_{i \in I} (\!+_{k \in K_i} b_k) = +_{i \in I} b_i$
, and
$b = +_{j \in J} b_j = +_{i \in I} (\!+_{k \in K_i} b_k) = +_{i \in I} b_i$
, and
 $s = +_{j \in J} s_j = +_{i \in I} (\!+_{k \in K_i} s_k) = +_{i \in I} s_i$
.
$s = +_{j \in J} s_j = +_{i \in I} (\!+_{k \in K_i} s_k) = +_{i \in I} s_i$
.
Lemma 24 (Substitution). Let
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau$
and
![]() $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, then there exists
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, then there exists
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u \negmedspace \overset {(b_t+b_u,s_t+s_u)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau$
.
$\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u \negmedspace \overset {(b_t+b_u,s_t+s_u)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau$
.
Proof.
We generalize the original statement by allowing
![]() $\Phi _{t \{x \setminus u\}}$
to conclude with either a type
$\Phi _{t \{x \setminus u\}}$
to conclude with either a type
![]() $\tau$
or a multi-type
$\tau$
or a multi-type
![]() $\mathscr{M}$
. Let
$\mathscr{M}$
. Let
![]() $\mathscr{G\,} \in \{\tau , \mathscr{M}\}$
. Then the statement is as follows:
$\mathscr{G\,} \in \{\tau , \mathscr{M}\}$
. Then the statement is as follows:
Let
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \mathscr{G\,}$
. Then, there exist
$\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \mathscr{G\,}$
. Then, there exist
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \mathscr{G\,}$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \mathscr{G\,}$
and
![]() $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
![]() $\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
![]() $b = b_t + b_u$
, and
$b = b_t + b_u$
, and
![]() $s = s_t + s_u$
.
$s = s_t + s_u$
.
The proof follows by induction over
![]() $\Phi _t$
:
$\Phi _t$
:
-
• Rule (ax). Then
 $t= y$
and we have two cases:
$t= y$
and we have two cases:-
–
 $y = x$
. Then
$y = x$
. Then
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{G\,} = \mathscr{M}$
,
$\mathscr{G\,} = \mathscr{M}$
,
 $b_t = 0$
, and
$b_t = 0$
, and
 $s_t = 0$
. Also, notice that
$s_t = 0$
. Also, notice that
 $x \{x \setminus u\} = u$
. Therefore, we can take
$x \{x \setminus u\} = u$
. Therefore, we can take
 $\Phi _{t \{x \setminus u\}} = \Phi _u$
and conclude with
$\Phi _{t \{x \setminus u\}} = \Phi _u$
and conclude with
 $\Gamma _u = \emptyset + \Gamma _u$
,
$\Gamma _u = \emptyset + \Gamma _u$
,
 $b_u = 0 + b_u$
, and
$b_u = 0 + b_u$
, and
 $s_u = 0 + s_u$
.
$s_u = 0 + s_u$
. -
–
 $y \neq x$
. Then
$y \neq x$
. Then
 $\mathscr{M} = [ \, ]$
. Therefore,
$\mathscr{M} = [ \, ]$
. Therefore,
 $\Gamma _u = \emptyset$
,
$\Gamma _u = \emptyset$
,
 $b_u = 0$
, and
$b_u = 0$
, and
 $s_u = 0$
. Also, notice that
$s_u = 0$
. Also, notice that
 $y \{x \setminus u\} = y$
. Therefore, we can take
$y \{x \setminus u\} = y$
. Therefore, we can take
 $\Phi _{t \{x \setminus u\}} = \Phi _t$
and conclude with
$\Phi _{t \{x \setminus u\}} = \Phi _t$
and conclude with
 $\Gamma _t = \Gamma _t + \emptyset$
,
$\Gamma _t = \Gamma _t + \emptyset$
,
 $b_t = b_t + 0$
, and
$b_t = b_t + 0$
, and
 $s_t = s_t + 0$
.
$s_t = s_t + 0$
.
-
-
• Rule (
 $\lambda$
). Then
$\lambda$
). Then
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
(by
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
(by
 $\alpha$
-conversion, we can assume
$\alpha$
-conversion, we can assume
 $y \neq x$
), and
$y \neq x$
), and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _p \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace p: \tau '$
, such that
$\Phi _p \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace p: \tau '$
, such that
 $\Gamma _t = (\Gamma _p;\; y \;:\; \mathscr{M\;}')$
, and
$\Gamma _t = (\Gamma _p;\; y \;:\; \mathscr{M\;}')$
, and
 $\mathscr{G\,} = \mathscr{M\;}' \rightarrow \tau '$
. By applying the i.h. to
$\mathscr{G\,} = \mathscr{M\;}' \rightarrow \tau '$
. By applying the i.h. to
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _{p \{x \setminus u\}} \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u \negmedspace \overset {(b_t + b_u, s_t + s_u)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau '$
. Therefore, we can build
$\Phi _{p \{x \setminus u\}} \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u \negmedspace \overset {(b_t + b_u, s_t + s_u)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau '$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:
$\Phi _{t \{x \setminus u\}}$
as follows: \begin{equation*} \frac {\Phi _{p \{x \setminus u\}}}{\Gamma _p + \Gamma _u \mathop {\vdash }\limits ^{(b_t + b_u, s_t + s_u)}_{} (\lambda y.p) \{x \setminus u\}\;:\; \mathscr{M\;}' \rightarrow \tau '}(\lambda )\end{equation*}
\begin{equation*} \frac {\Phi _{p \{x \setminus u\}}}{\Gamma _p + \Gamma _u \mathop {\vdash }\limits ^{(b_t + b_u, s_t + s_u)}_{} (\lambda y.p) \{x \setminus u\}\;:\; \mathscr{M\;}' \rightarrow \tau '}(\lambda )\end{equation*}
-
• Rule (
 $\tt @$
). Then
$\tt @$
). Then
 $t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
, and
$t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
, and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _r \triangleright \, \Gamma _r;\; x \;:\; \mathscr{M}_1 \negmedspace \overset {(b_r, s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _r \triangleright \, \Gamma _r;\; x \;:\; \mathscr{M}_1 \negmedspace \overset {(b_r, s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _p \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M\;}'$
, such that
$\Phi _p \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M\;}'$
, such that
 $\Gamma _t = \Gamma _r + \Gamma _p$
,
$\Gamma _t = \Gamma _r + \Gamma _p$
,
 $\mathscr{G\,} = \tau$
,
$\mathscr{G\,} = \tau$
,
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b_t = 1 + b_r + b_p$
, and
$b_t = 1 + b_r + b_p$
, and
 $s_t = s_r + s_p$
. By Lemma 23, there exist
$s_t = s_r + s_p$
. By Lemma 23, there exist
 $(\Phi ^i_u \triangleright \, \Gamma ^i_u \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_i)_{i \in \{1,2\}}$
, such that
$(\Phi ^i_u \triangleright \, \Gamma ^i_u \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_i)_{i \in \{1,2\}}$
, such that
 $\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
$\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
 $b_u = b_1 + b_2$
, and
$b_u = b_1 + b_2$
, and
 $s_u = s_1 + s_2$
. By applying the i.h. to
$s_u = s_1 + s_2$
. By applying the i.h. to
 $\Phi _r$
and
$\Phi _r$
and
 $\Phi _p$
, there exist
$\Phi _p$
, there exist
 $\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _r + \Gamma ^1_u \negmedspace \overset {(b_r+b_1, s_r+s_1)}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _r + \Gamma ^1_u \negmedspace \overset {(b_r+b_1, s_r+s_1)}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _p + \Gamma ^2_u \negmedspace \overset {(b_p + b_2, s_p + s_2)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \mathscr{M\;}'$
, respectively. Therefore, we can build
$\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _p + \Gamma ^2_u \negmedspace \overset {(b_p + b_2, s_p + s_2)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \mathscr{M\;}'$
, respectively. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{r \{x \setminus u\}}\quad \Phi _{p \{x \setminus u\}}}{(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) \mathop {\vdash }\limits ^{(1+b_r+b_p+b_1+b_2, s_r + s_p + s_1 + s_2)}_{} (r p) \{x \setminus u\}\;:\; \tau }({\mathtt {@}}) \end{equation*}
\begin{equation*} \frac {\Phi _{r \{x \setminus u\}}\quad \Phi _{p \{x \setminus u\}}}{(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) \mathop {\vdash }\limits ^{(1+b_r+b_p+b_1+b_2, s_r + s_p + s_1 + s_2)}_{} (r p) \{x \setminus u\}\;:\; \tau }({\mathtt {@}}) \end{equation*}
 $(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) = \Gamma _t + \Gamma _u$
,
$(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) = \Gamma _t + \Gamma _u$
,
 $1 + b_r + b_p + b_1 + b_2 = b_t + b_u$
, and
$1 + b_r + b_p + b_1 + b_2 = b_t + b_u$
, and
 $s_r + s_p + s_1 + s_2 = s_t + s_u$
.
$s_r + s_p + s_1 + s_2 = s_t + s_u$
.
-
• Rule (m). Then
 $\Phi _t$
has premises
$\Phi _t$
has premises
 $(\Phi _t^i \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t,s^i_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau _i)_{i \in I}$
, such that
$(\Phi _t^i \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t,s^i_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau _i)_{i \in I}$
, such that
 $\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
$\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
 $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
 $\mathscr{G\,} = [ \tau _i ]_{i \in I}$
,
$\mathscr{G\,} = [ \tau _i ]_{i \in I}$
,
 $b_t = +_{i \in I} b^i_t$
, and
$b_t = +_{i \in I} b^i_t$
, and
 $s_t = +_{i \in I} s^i_t$
. By Lemma 23, there exist
$s_t = +_{i \in I} s^i_t$
. By Lemma 23, there exist
 $(\Phi ^i_u \triangleright \, \Gamma ^i_u \negmedspace \overset {(b^i_u, s^i_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_i)_{i \in I}$
, such that
$(\Phi ^i_u \triangleright \, \Gamma ^i_u \negmedspace \overset {(b^i_u, s^i_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_i)_{i \in I}$
, such that
 $\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
$\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
 $b_u = +_{i \in I} b^i_u$
, and
$b_u = +_{i \in I} b^i_u$
, and
 $s_u = +_{i \in I} s^i_u$
. By applying the i.h. to each
$s_u = +_{i \in I} s^i_u$
. By applying the i.h. to each
 $\Phi ^i_t$
, there exist
$\Phi ^i_t$
, there exist
 $(\Phi ^i_{t \{x \setminus u\}} \triangleright \, \Gamma ^i_t + \Gamma ^i_u \negmedspace \overset {(b^i_t + b^i_u, s^i_t + s^i_u)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau _i)_{i \in I}$
. Therefore, we can build
$(\Phi ^i_{t \{x \setminus u\}} \triangleright \, \Gamma ^i_t + \Gamma ^i_u \negmedspace \overset {(b^i_t + b^i_u, s^i_t + s^i_u)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau _i)_{i \in I}$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {(\Phi ^i_{p \{x \setminus u\}})_{i \in I}}{+_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) \mathop {\vdash }\limits ^{(+_{i \in I} (b^i_t + b^i_u), +_{i \in I} (s^i_t + s^i_u))}_{} t \{x \setminus u\}\;:\; [ \tau _i ]_{i \in I}}({\tt m}) \end{equation*}
\begin{equation*} \frac {(\Phi ^i_{p \{x \setminus u\}})_{i \in I}}{+_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) \mathop {\vdash }\limits ^{(+_{i \in I} (b^i_t + b^i_u), +_{i \in I} (s^i_t + s^i_u))}_{} t \{x \setminus u\}\;:\; [ \tau _i ]_{i \in I}}({\tt m}) \end{equation*}
 $+_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) = \Gamma _t + \Gamma _u$
,
$+_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) = \Gamma _t + \Gamma _u$
,
 $+_{i \in I} (b^i_t + b^i_u) = b_t + b_u$
, and
$+_{i \in I} (b^i_t + b^i_u) = b_t + b_u$
, and
 $+_{i \in I} (s^i_t + s^i_u) = s_t + s_u$
.
$+_{i \in I} (s^i_t + s^i_u) = s_t + s_u$
.
-
• Rule (
 $\lambda _{\tt p}$
). Then
$\lambda _{\tt p}$
). Then
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
(by
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
(by
 $\alpha$
-conversion, we can assume
$\alpha$
-conversion, we can assume
 $y\neq x$
), and
$y\neq x$
), and
 $\Phi _t \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace \lambda y.p: {\tt a}$
, such that
$\Phi _t \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace \lambda y.p: {\tt a}$
, such that
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{G\,} = {\tt a}$
, and
$\mathscr{G\,} = {\tt a}$
, and
 $\mathscr{M} = \emptyset$
. Therefore,
$\mathscr{M} = \emptyset$
. Therefore,
 $\Gamma _u = \emptyset$
,
$\Gamma _u = \emptyset$
,
 $b_u = s_u = 0$
, and we can build
$b_u = s_u = 0$
, and we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {}{\emptyset \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace \lambda y. (p \{x \setminus u\}): {\tt a}}(\lambda _{\tt p}) \end{equation*}
\begin{equation*} \frac {}{\emptyset \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace \lambda y. (p \{x \setminus u\}): {\tt a}}(\lambda _{\tt p}) \end{equation*}
 $\emptyset = \Gamma _t + \Gamma _u$
,
$\emptyset = \Gamma _t + \Gamma _u$
,
 $0 = b_t + b_u$
, and
$0 = b_t + b_u$
, and
 $0 = s_t + s_u$
.
$0 = s_t + s_u$
.
-
• Rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
, and
$t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _r \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_r,s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; {\tt n}$
, such that
$\Phi _r \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_r,s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; {\tt n}$
, such that
 $\mathscr{G\,} = {\tt n}$
,
$\mathscr{G\,} = {\tt n}$
,
 $b_t = b_r$
, and
$b_t = b_r$
, and
 $s_t = 1 + s_r$
. By applying the i.h. to
$s_t = 1 + s_r$
. By applying the i.h. to
 $\Phi _r$
, there exists
$\Phi _r$
, there exists
 $\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _r + \Gamma _u \negmedspace \overset {(b_r+b_u,s_r+s_u)}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; {\tt n}$
. Therefore, we can build
$\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _r + \Gamma _u \negmedspace \overset {(b_r+b_u,s_r+s_u)}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; {\tt n}$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{r \{x \setminus u\}}}{\Gamma _t + \Gamma _u \mathop {\vdash }\limits ^{(b_r+b_u,1+s_r+s_u)}_{} (r \{x \setminus u\})(p \{x \setminus u\}): {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _{r \{x \setminus u\}}}{\Gamma _t + \Gamma _u \mathop {\vdash }\limits ^{(b_r+b_u,1+s_r+s_u)}_{} (r \{x \setminus u\})(p \{x \setminus u\}): {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
 $b_r+b_u = b_t+b_u$
, and
$b_r+b_u = b_t+b_u$
, and
 $1+s_r+s_u = s_t+s_u$
.
$1+s_r+s_u = s_t+s_u$
.
Lemma 4 (Quantitative subject reduction). Let
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
be a tight type derivation. If
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
be a tight type derivation. If
![]() $t \rightarrow t'$
, then there exists
$t \rightarrow t'$
, then there exists
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1,s)} {\vdash_{\texttt{n}}}\negmedspace t': \tau$
.
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1,s)} {\vdash_{\texttt{n}}}\negmedspace t': \tau$
.
Proof. We prove a stronger version of the statement that allows us to reason inductively:
Let
![]() $\Phi _t \triangleright {\Gamma }\negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\;\tau$
, such that
$\Phi _t \triangleright {\Gamma }\negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\;\tau$
, such that
![]() $\Gamma$
is tight, and either
$\Gamma$
is tight, and either
![]() $\tau$
is tight or
$\tau$
is tight or
![]() $\neg {\tt abs}(t)$
. If
$\neg {\tt abs}(t)$
. If
![]() $t \rightarrow t'$
, then there exists
$t \rightarrow t'$
, then there exists
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt n}}}\negmedspace t': \tau$
.
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt n}}}\negmedspace t': \tau$
.
The proof follows by induction over
![]() $t \rightarrow t'$
:
$t \rightarrow t'$
:
-
• Case
 $t = (\lambda x.p) u \rightarrow p \{x \setminus u\} = t'$
. Then
$t = (\lambda x.p) u \rightarrow p \{x \setminus u\} = t'$
. Then
 $\Phi _t$
must end with rule (@) or (@
$\Phi _t$
must end with rule (@) or (@
 $_{{\tt p}}$
). Let us assume that
$_{{\tt p}}$
). Let us assume that
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _{\lambda x.p}$
. Moreover,
$\Phi _{\lambda x.p}$
. Moreover,
 $\Phi _{\lambda x.p}$
must conclude with type
$\Phi _{\lambda x.p}$
must conclude with type
 ${\tt n} \in \overline {{\tt a}}$
. However, this is not possible according to Lemma 22. Therefore, this case does not apply. Now, let us assume that
${\tt n} \in \overline {{\tt a}}$
. However, this is not possible according to Lemma 22. Therefore, this case does not apply. Now, let us assume that
 $\Phi _t$
ends with rule (@). Then,
$\Phi _t$
ends with rule (@). Then,
 $\Phi _t$
has the following form:
$\Phi _t$
has the following form:
such that
 $\Gamma = \Gamma _p + \Gamma _u$
tight,
$\Gamma = \Gamma _p + \Gamma _u$
tight,
 $\tau \in {{\tt tt}_{\tt n}}$
,
$\tau \in {{\tt tt}_{\tt n}}$
,
 $b = 1 + b_p + b_u$
, and
$b = 1 + b_p + b_u$
, and
 $s = s_p + s_u$
. By Lemma 24, there exists
$s = s_p + s_u$
. By Lemma 24, there exists
 $\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _p + \Gamma _u \negmedspace \overset {(b_p+b_u,s_p+s_u)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau$
. Therefore, we can take
$\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _p + \Gamma _u \negmedspace \overset {(b_p+b_u,s_p+s_u)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau$
. Therefore, we can take
 $\Phi _{t'} = \Phi _{p \{x \setminus u\}}$
and conclude with
$\Phi _{t'} = \Phi _{p \{x \setminus u\}}$
and conclude with
 $b - 1 = b_p + b_u$
.
$b - 1 = b_p + b_u$
. -
• Case
 $t = up \rightarrow u'p = t'$
, such that
$t = up \rightarrow u'p = t'$
, such that
 $u \rightarrow u'$
. Then
$u \rightarrow u'$
. Then
 $\Phi _t$
must either end with (@) or (@
$\Phi _t$
must either end with (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Case
 $\Phi _t$
ends with rule (@). Then
$\Phi _t$
ends with rule (@). Then
 $\Phi _t$
has the following form:such that
$\Phi _t$
has the following form:such that \begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau \qquad \Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 +b_u+b_p,s_u+s_p)}_{} up: \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau \qquad \Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 +b_u+b_p,s_u+s_p)}_{} up: \tau }({\tt @})\end{equation*}
 $\Gamma = \Gamma _u + \Gamma _p$
tight,
$\Gamma = \Gamma _u + \Gamma _p$
tight,
 $\tau \in {{\tt tt}_{\tt n}}$
,
$\tau \in {{\tt tt}_{\tt n}}$
,
 $b = 1+b_u + b_p$
, and
$b = 1+b_u + b_p$
, and
 $s = s_u + s_p$
. Moreover,
$s = s_u + s_p$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. Also, notice that
$\Gamma _p$
are tight. Also, notice that
 $\neg {\tt abs}(u)$
since
$\neg {\tt abs}(u)$
since
 $u \rightarrow u'$
, by definition. Therefore, by applying the i.h. to
$u \rightarrow u'$
, by definition. Therefore, by applying the i.h. to
 $\Phi _u$
, there exists
$\Phi _u$
, there exists
 $\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u-1, s_u)}{\vdash _{{\tt n}}}\negmedspace u': \mathscr{M} \rightarrow \tau$
. Therefore, we can build
$\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u-1, s_u)}{\vdash _{{\tt n}}}\negmedspace u': \mathscr{M} \rightarrow \tau$
. Therefore, we can build
 $\Phi _{t'}$
as follows:Thus, we can conclude with
$\Phi _{t'}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{u'}\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,s_u+s_p)}_{} u'p: \tau }({\tt @}) \end{equation*}
\begin{equation*} \frac {\Phi _{u'}\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,s_u+s_p)}_{} u'p: \tau }({\tt @}) \end{equation*}
 $b - 1= b_u + b_p$
.
$b - 1= b_u + b_p$
.
-
– Case
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $_{{\tt p}}$
). Then
$_{{\tt p}}$
). Then
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, such that
$\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
, such that
 $s = 1 + s_u$
. By applying the i.h. to
$s = 1 + s_u$
. By applying the i.h. to
 $\Phi _u$
, there exists
$\Phi _u$
, there exists
 $\Phi _{u'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s_u)}{\vdash _{{\tt n}}}\negmedspace u': {\tt n}$
. Therefore, we can build
$\Phi _{u'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s_u)}{\vdash _{{\tt n}}}\negmedspace u': {\tt n}$
. Therefore, we can build
 $\Phi _{t'}$
as follows:Thus, we can conclude with
$\Phi _{t'}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{u'}}{\Gamma \mathop {\vdash }\limits ^{(b-1,1+s_u)}_{} u'p: {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _{u'}}{\Gamma \mathop {\vdash }\limits ^{(b-1,1+s_u)}_{} u'p: {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
 $s = 1 + s_u$
.
$s = 1 + s_u$
.
-
Theorem 1 (Quantitative soundness). If
![]() $\Phi \triangleright \, \Gamma\negmedspace \overset{{(b,s)}}{\vdash_{{\tt n}}}\negmedspace t\;:\; \tau$
is a tight type derivation, then there exists
$\Phi \triangleright \, \Gamma\negmedspace \overset{{(b,s)}}{\vdash_{{\tt n}}}\negmedspace t\;:\; \tau$
is a tight type derivation, then there exists
![]() $u \in {\tt no}_{\texttt{n}}$
such that
$u \in {\tt no}_{\texttt{n}}$
such that
![]() $t \twoheadrightarrow ^b_{\texttt{n}} u$
with
$t \twoheadrightarrow ^b_{\texttt{n}} u$
with
![]() $|u|_{\texttt{n}} = s$
.
$|u|_{\texttt{n}} = s$
.
Proof.
The proof follows by induction over
![]() $b$
:
$b$
:
-
• Case
 $b = 0$
. Then
$b = 0$
. Then
 $t \in {\tt no}_{\texttt{n}}$
by Lemma1. Moreover,
$t \in {\tt no}_{\texttt{n}}$
by Lemma1. Moreover,
 $s = |t|_{\texttt{n}}$
, by Lemma2. So we can conclude with
$s = |t|_{\texttt{n}}$
, by Lemma2. So we can conclude with
 $u = t$
.
$u = t$
. -
• Case
 $b \gt 0$
. Then
$b \gt 0$
. Then
 $t \not \in {\tt no}_{\texttt{n}}$
by Lemma1. Therefore, by Proposition1, there exists
$t \not \in {\tt no}_{\texttt{n}}$
by Lemma1. Therefore, by Proposition1, there exists
 $t'$
such that
$t'$
such that
 $t \rightarrow_{\texttt{n}} t'$
. Moreover, this derivation is also tight. By Lemma4, there exists
$t \rightarrow_{\texttt{n}} t'$
. Moreover, this derivation is also tight. By Lemma4, there exists
 $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, s)} {\vdash_{\texttt{n}}}\negmedspace t': \tau$
. By the i.h., there exists
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, s)} {\vdash_{\texttt{n}}}\negmedspace t': \tau$
. By the i.h., there exists
 $u \in {\tt no}_{\texttt{n}}$
, such that
$u \in {\tt no}_{\texttt{n}}$
, such that
 $t' \twoheadrightarrow ^{b-1}_{\texttt{n}} u$
, such that
$t' \twoheadrightarrow ^{b-1}_{\texttt{n}} u$
, such that
 $s = |u|_{\texttt{n}}$
. So we can conclude with
$s = |u|_{\texttt{n}}$
. So we can conclude with
 $t \rightarrow_{\texttt{n}} t' \twoheadrightarrow^{b-1}_{\texttt{n}} u$
, which means that
$t \rightarrow_{\texttt{n}} t' \twoheadrightarrow^{b-1}_{\texttt{n}} u$
, which means that
 $t \twoheadrightarrow ^b_{\texttt{n}} u$
, as expected.
$t \twoheadrightarrow ^b_{\texttt{n}} u$
, as expected.
Lemma 25 (Anti-substitution). Let
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau$
. Then, there exist
$\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau$
. Then, there exist
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau$
and
![]() $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
![]() $\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
![]() $b = b_t + b_u$
, and
$b = b_t + b_u$
, and
![]() $s = s_t + s_u$
.
$s = s_t + s_u$
.
Proof.
We generalize the original statement by allowing
![]() $\Phi _{t \{x \setminus u\}}$
to conclude with either a type
$\Phi _{t \{x \setminus u\}}$
to conclude with either a type
![]() $\tau$
or a multi-type
$\tau$
or a multi-type
![]() $\mathscr{M}$
. Let
$\mathscr{M}$
. Let
![]() $\mathscr{G\,} \in \{\tau , \mathscr{M}\}$
. Then the statement is as follows:
$\mathscr{G\,} \in \{\tau , \mathscr{M}\}$
. Then the statement is as follows:
Let
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \mathscr{G\,}$
. Then, there exist
$\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \mathscr{G\,}$
. Then, there exist
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \mathscr{G\,}$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \mathscr{G\,}$
and
![]() $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
![]() $\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
![]() $b = b_t + b_u$
, and
$b = b_t + b_u$
, and
![]() $s = s_t + s_u$
.
$s = s_t + s_u$
.
The proof follows by induction over
![]() $\Phi _{t \{x \setminus u\}}$
, according to the last rule of
$\Phi _{t \{x \setminus u\}}$
, according to the last rule of
![]() $\Phi _{t \{x \setminus u\}}$
:
$\Phi _{t \{x \setminus u\}}$
:
Let us assume
![]() $t = x$
, such that
$t = x$
, such that
![]() $t \{x \setminus u\} = u$
. Then, we have to consider two cases:
$t \{x \setminus u\} = u$
. Then, we have to consider two cases:
![]() $\mathscr{G\,} = \tau$
, or
$\mathscr{G\,} = \tau$
, or
![]() $\mathscr{G\,} = \mathscr{M\;}'$
. If
$\mathscr{G\,} = \mathscr{M\;}'$
. If
![]() $\Phi _{t \{x \setminus u\}}$
concludes with
$\Phi _{t \{x \setminus u\}}$
concludes with
![]() $\tau$
, we can build
$\tau$
, we can build
![]() $\Phi _t \triangleright \, x \;:\; [ \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace x\;:\; \tau$
, such that
$\Phi _t \triangleright \, x \;:\; [ \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace x\;:\; \tau$
, such that
![]() $\Gamma _t = \emptyset$
, and
$\Gamma _t = \emptyset$
, and
![]() $b_t = s_t = 0$
, by using rule (ax), and build
$b_t = s_t = 0$
, by using rule (ax), and build
![]() $\Phi _u \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \tau$
, such that
$\Phi _u \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \tau$
, such that
![]() $\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
$\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
![]() $b_u = b$
, and
$b_u = b$
, and
![]() $s_u = s$
, by applying rule (m) to
$s_u = s$
, by applying rule (m) to
![]() $\Phi _{t \{x \setminus u\}}$
. If
$\Phi _{t \{x \setminus u\}}$
. If
![]() $\Phi _{t \{x \setminus u\}}$
concludes with
$\Phi _{t \{x \setminus u\}}$
concludes with
![]() $\mathscr{M\;}' = [ \tau _i ]_{i \in I}$
, we pick
$\mathscr{M\;}' = [ \tau _i ]_{i \in I}$
, we pick
![]() $\Phi _u = \Gamma _{t \{x \setminus u\}}$
, such that
$\Phi _u = \Gamma _{t \{x \setminus u\}}$
, such that
![]() $\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
$\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
![]() $b_u = b$
, and
$b_u = b$
, and
![]() $s_u = s$
, and build
$s_u = s$
, and build
![]() $\Phi _t$
as follows:
$\Phi _t$
as follows:
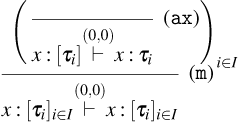
such that
![]() $\Gamma _t = \emptyset$
, and
$\Gamma _t = \emptyset$
, and
![]() $b_t = s_t = 0$
. In both cases, we can conclude with
$b_t = s_t = 0$
. In both cases, we can conclude with
![]() $\Gamma _{t \{x \setminus u\}} = \Gamma _u = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _u = \Gamma _t + \Gamma _u$
,
![]() $b = b_u = b_t + b_u$
, and
$b = b_u = b_t + b_u$
, and
![]() $s = s_u = s_t + s_u$
. From now on, we will assume
$s = s_u = s_t + s_u$
. From now on, we will assume
![]() $t \neq x$
:
$t \neq x$
:
-
• Rule (ax). Then
 $t = y$
,
$t = y$
,
 $t \{x \setminus u\} = y$
, and
$t \{x \setminus u\} = y$
, and
 $\mathscr{M} = [ \, ]$
. Therefore, we can pick
$\mathscr{M} = [ \, ]$
. Therefore, we can pick
 $\Phi _t = \Phi _{t \{x \setminus u\}}$
, such that
$\Phi _t = \Phi _{t \{x \setminus u\}}$
, such that
 $\Gamma _t = \Gamma _{t \{x \setminus u\}}$
,
$\Gamma _t = \Gamma _{t \{x \setminus u\}}$
,
 $b_t = b$
, and
$b_t = b$
, and
 $s_t = s$
, and build
$s_t = s$
, and build
 $\Phi _u \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace u\;:\; [ \, ]$
, such that
$\Phi _u \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace u\;:\; [ \, ]$
, such that
 $\Gamma _u = \emptyset$
, and
$\Gamma _u = \emptyset$
, and
 $b_u = s_u = 0$
, by using rule (m) with no premises. Thus, we can conclude with
$b_u = s_u = 0$
, by using rule (m) with no premises. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _t = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t = \Gamma _t + \Gamma _v$
,
 $b = b_t = b_t + b_v$
, and
$b = b_t = b_t + b_v$
, and
 $s = s_t = s_t + s_v$
.
$s = s_t = s_t + s_v$
. -
• Rule (
 $\lambda$
). Then
$\lambda$
). Then
 $t = \lambda y.p$
and
$t = \lambda y.p$
and
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
. Moreover,
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
. Moreover,
 $\Phi _{t \{x \setminus u\}}$
has one premise
$\Phi _{t \{x \setminus u\}}$
has one premise
 $\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus v\}};\;\; y\; :\; \mathscr{M\;}' \negmedspace \overset {(b, s)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau '$
, such that
$\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus v\}};\;\; y\; :\; \mathscr{M\;}' \negmedspace \overset {(b, s)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau '$
, such that
 $\mathscr{G\,} = \mathscr{M\;}' \rightarrow \tau '$
. By applying the i.h. to
$\mathscr{G\,} = \mathscr{M\;}' \rightarrow \tau '$
. By applying the i.h. to
 $\Phi _{p \{x \setminus u\}}$
, there exist
$\Phi _{p \{x \setminus u\}}$
, there exist
 $\Phi _p \triangleright \, (\Gamma _p;\; y\;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M} \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \tau '$
and
$\Phi _p \triangleright \, (\Gamma _p;\; y\;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M} \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \tau '$
and
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
 $(\Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}') = (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u$
,
$(\Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}') = (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u$
,
 $b = b_p + b_u$
, and
$b = b_p + b_u$
, and
 $s = s_p + s_u$
. Notice that
$s = s_p + s_u$
. Notice that
 $\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
, since we may assume (by Proposition 7) that
$\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
, since we may assume (by Proposition 7) that
 $y \not \in {\tt dom}(\Gamma _u)$
. Therefore, we can build
$y \not \in {\tt dom}(\Gamma _u)$
. Therefore, we can build
 $\Phi _t$
as follows:Thus, we can conclude with
$\Phi _t$
as follows:Thus, we can conclude with \begin{equation*}\frac {\Phi _p}{\Gamma _p;\; x \;:\; \mathscr{M} \mathop {\vdash }\limits ^{(b_p, s_p)}_{} \lambda y.p: \mathscr{M\;}' \rightarrow \tau '}(\lambda ) \end{equation*}
\begin{equation*}\frac {\Phi _p}{\Gamma _p;\; x \;:\; \mathscr{M} \mathop {\vdash }\limits ^{(b_p, s_p)}_{} \lambda y.p: \mathscr{M\;}' \rightarrow \tau '}(\lambda ) \end{equation*}
 $\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
,
 $b = b_p + b_u$
, and
$b = b_p + b_u$
, and
 $s = s_p + s_u$
.
$s = s_p + s_u$
.
-
• Rule (@). Then
 $t = rp$
and
$t = rp$
and
 $t \{x \setminus u\} = (r \{x \setminus u\}) (p \{x \setminus u\})$
. Moreover,
$t \{x \setminus u\} = (r \{x \setminus u\}) (p \{x \setminus u\})$
. Moreover,
 $\Phi _{t \{x \setminus u\}}$
has two premises
$\Phi _{t \{x \setminus u\}}$
has two premises
 $\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _{r \{x \setminus u\}} \negmedspace \overset {(b_1,s_1)}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _{r \{x \setminus u\}} \negmedspace \overset {(b_1,s_1)}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _{p \{x \setminus u\}} \negmedspace \overset {(b_2,s_2)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \mathscr{M\;}'$
, such that
$\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _{p \{x \setminus u\}} \negmedspace \overset {(b_2,s_2)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \mathscr{M\;}'$
, such that
 $\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}}$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}}$
,
 $\mathscr{G\,} = \tau$
,
$\mathscr{G\,} = \tau$
,
 $b = 1+b_1+b_2$
, and
$b = 1+b_1+b_2$
, and
 $s = s_1+s_2$
. By applying the i.h. to
$s = s_1+s_2$
. By applying the i.h. to
 $\Phi _{r \{x \setminus u\}}$
and
$\Phi _{r \{x \setminus u\}}$
and
 $\Phi _{p \{x \setminus u\}}$
, there exist
$\Phi _{p \{x \setminus u\}}$
, there exist
 $\Phi _r \triangleright \, \Gamma _r;\; x \;:\; \mathscr{M}_1 \negmedspace \overset {(b_r,s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _r \triangleright \, \Gamma _r;\; x \;:\; \mathscr{M}_1 \negmedspace \overset {(b_r,s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi ^1_u \triangleright \, \Gamma ^1_u \negmedspace \overset {(b^1_u,s^1_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_1$
, such that
$\Phi ^1_u \triangleright \, \Gamma ^1_u \negmedspace \overset {(b^1_u,s^1_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_1$
, such that
 $\Gamma _{r \{x \setminus u\}} = \Gamma _r + \Gamma ^1_u$
,
$\Gamma _{r \{x \setminus u\}} = \Gamma _r + \Gamma ^1_u$
,
 $b_1 = b_r + b^1_u$
, and
$b_1 = b_r + b^1_u$
, and
 $s_1 = s_r + s^1_u$
, and there exist
$s_1 = s_r + s^1_u$
, and there exist
 $\Phi _{p} \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M\;}'$
and
$\Phi _{p} \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M\;}'$
and
 $\Phi ^2_u \triangleright \, \Gamma ^2_u \negmedspace \overset {(b^2_u,s^2_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_2$
, such that
$\Phi ^2_u \triangleright \, \Gamma ^2_u \negmedspace \overset {(b^2_u,s^2_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_2$
, such that
 $\Gamma _{p \{x \setminus u\}} = \Gamma _p + \Gamma ^2_u$
,
$\Gamma _{p \{x \setminus u\}} = \Gamma _p + \Gamma ^2_u$
,
 $b_2 = b_p + b^2_u$
, and
$b_2 = b_p + b^2_u$
, and
 $s_2 = s_p + s^2_u$
, respectively. By Lemma 23, there exists
$s_2 = s_p + s^2_u$
, respectively. By Lemma 23, there exists
 $\Phi _u \triangleright \, \Gamma ^1_u + \Gamma ^2_u \negmedspace \overset {(b^1_u+b^2_u, s^1_u + s^2_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2$
, such that
$\Phi _u \triangleright \, \Gamma ^1_u + \Gamma ^2_u \negmedspace \overset {(b^1_u+b^2_u, s^1_u + s^2_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2$
, such that
 $\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
$\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
 $b_u = b^1_u + b^2_u$
, and
$b_u = b^1_u + b^2_u$
, and
 $s_u = s^1_u + s^2_u$
. Therefore, we can build
$s_u = s^1_u + s^2_u$
. Therefore, we can build
 $\Phi _t$
as follows:Thus, we can conclude with
$\Phi _t$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _r \qquad \Phi _p}{(\Gamma _r + \Gamma _p);\; x \;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2 \mathop {\vdash }\limits ^{(1+b_u+b_p, s_u+s_p)}_{} up: \tau }({\tt @}) \end{equation*}
\begin{equation*} \frac {\Phi _r \qquad \Phi _p}{(\Gamma _r + \Gamma _p);\; x \;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2 \mathop {\vdash }\limits ^{(1+b_u+b_p, s_u+s_p)}_{} up: \tau }({\tt @}) \end{equation*}
 $\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b = 1+b_1+b_2 = 1+b_r + b^1_u + b_p + b^2_u = b_t + b_v$
, and
$b = 1+b_1+b_2 = 1+b_r + b^1_u + b_p + b^2_u = b_t + b_v$
, and
 $s = s_1+s_2 = s_r + s^1_u + s_p + s^2_u = s_t + s_u$
.
$s = s_1+s_2 = s_r + s^1_u + s_p + s^2_u = s_t + s_u$
.
-
• Rule (m). Then,
 $\Phi _{t \{x \setminus u\}}$
has premises
$\Phi _{t \{x \setminus u\}}$
has premises
 $(\Phi _i \triangleright \, \Gamma _i \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau _i)_{i \in I}$
, such that
$(\Phi _i \triangleright \, \Gamma _i \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt n}}}\negmedspace t \{x \setminus u\}\;:\; \tau _i)_{i \in I}$
, such that
 $\mathscr{G\,} = [ \tau _i ]_{i \in I}$
,
$\mathscr{G\,} = [ \tau _i ]_{i \in I}$
,
 $\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma _i$
,
$\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma _i$
,
 $b = +_{i \in I} b_i$
, and
$b = +_{i \in I} b_i$
, and
 $s = +_{i \in I} s_i$
. By applying the i.h. to each
$s = +_{i \in I} s_i$
. By applying the i.h. to each
 $\Phi _i$
, there exist
$\Phi _i$
, there exist
 $\Phi ^i_t \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t, s^i_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau _i$
and
$\Phi ^i_t \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t, s^i_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau _i$
and
 $\Phi ^i_u \triangleright \, \Gamma ^i_u \negmedspace \overset {(b^i_u, s^i_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_i$
, such that
$\Phi ^i_u \triangleright \, \Gamma ^i_u \negmedspace \overset {(b^i_u, s^i_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}_i$
, such that
 $\Gamma _i = \Gamma ^i_t + \Gamma ^i_u$
,
$\Gamma _i = \Gamma ^i_t + \Gamma ^i_u$
,
 $b_i = b^i_t + b^i_u$
, and
$b_i = b^i_t + b^i_u$
, and
 $s_i = s^i_t + s^i_u$
, for each
$s_i = s^i_t + s^i_u$
, for each
 $i \in I$
. By Lemma 23, there exists
$i \in I$
. By Lemma 23, there exists
 $\Phi _u \triangleright \, +_{i \in I} \Gamma ^i_u \negmedspace \overset {(+_{i \in I} b^i_u, +_{i \in I} s^i_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, +_{i \in I} \Gamma ^i_u \negmedspace \overset {(+_{i \in I} b^i_u, +_{i \in I} s^i_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
 $\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
$\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
 $b_u = +_{i \in I} b^i_u$
, and
$b_u = +_{i \in I} b^i_u$
, and
 $s_u = +_{i \in I} s^i_u$
. Moreover, we can build
$s_u = +_{i \in I} s^i_u$
. Moreover, we can build
 $\Phi _t$
as follows:such that
$\Phi _t$
as follows:such that \begin{equation*} \frac {(\Phi ^i_t \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t, s^i_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau _i)_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \sqcup _{i \in I} \mathscr{M}_i \mathop {\vdash }\limits ^{(+_{i \in I} b^i_t, +_{i \in I} s^i_t)}_{} t\;:\; [ \tau _i ]_{i \in I}}({\tt m}) \end{equation*}
\begin{equation*} \frac {(\Phi ^i_t \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t, s^i_t)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau _i)_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \sqcup _{i \in I} \mathscr{M}_i \mathop {\vdash }\limits ^{(+_{i \in I} b^i_t, +_{i \in I} s^i_t)}_{} t\;:\; [ \tau _i ]_{i \in I}}({\tt m}) \end{equation*}
 $\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
$\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
 $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
 $b_t = +_{i \in I} b^i_t$
, and
$b_t = +_{i \in I} b^i_t$
, and
 $s_t = +_{i \in I} s^i_t$
. And we can conclude with
$s_t = +_{i \in I} s^i_t$
. And we can conclude with
 $\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma _i = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_u = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma _i = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_u = \Gamma _t + \Gamma _u$
,
 $b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_u) = +_{i \in I} b^i_t +_{i \in I} b^i_u = b_t + b_u$
, and
$b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_u) = +_{i \in I} b^i_t +_{i \in I} b^i_u = b_t + b_u$
, and
 $s = +_{i \in I} s_i = +_{i \in I} (s^i_t + s^i_u) = +_{i \in I} s^i_t +_{i \in I} s^i_u = s_t + s_u$
.
$s = +_{i \in I} s_i = +_{i \in I} (s^i_t + s^i_u) = +_{i \in I} s^i_t +_{i \in I} s^i_u = s_t + s_u$
.
-
• Rule (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $t = \lambda y.p$
and
$t = \lambda y.p$
and
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
. Moreover,
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
. Moreover,
 $\Gamma _{t \{x \setminus u\}} = \emptyset$
,
$\Gamma _{t \{x \setminus u\}} = \emptyset$
,
 $\tau = {\tt a}$
, and
$\tau = {\tt a}$
, and
 $b = m = 0$
. Therefore, we can build
$b = m = 0$
. Therefore, we can build
 $\Phi _{u} \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace u\;:\; [ \, ]$
, such that
$\Phi _{u} \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace u\;:\; [ \, ]$
, such that
 $\Gamma _{u} = \emptyset$
,
$\Gamma _{u} = \emptyset$
,
 $\mathscr{G\,} = {\tt a}$
,
$\mathscr{G\,} = {\tt a}$
,
 $\mathscr{M} = [ \, ]$
, and
$\mathscr{M} = [ \, ]$
, and
 $b_{u} = s_{u} = 0$
, by using rule (m) with no premises, and build
$b_{u} = s_{u} = 0$
, by using rule (m) with no premises, and build
 $\Phi _t \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace \lambda y.p: {\tt a}$
, such that
$\Phi _t \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt n}}}\negmedspace \lambda y.p: {\tt a}$
, such that
 $\Gamma _t = \emptyset$
, and
$\Gamma _t = \emptyset$
, and
 $b_t = s_t = 0$
, by using (
$b_t = s_t = 0$
, by using (
 $\lambda _{\tt p}$
). Thus, we can conclude with
$\lambda _{\tt p}$
). Thus, we can conclude with
 $\Gamma _{t \{x \setminus u\}} = \emptyset = \Gamma _t + \Gamma _u = \emptyset$
,
$\Gamma _{t \{x \setminus u\}} = \emptyset = \Gamma _t + \Gamma _u = \emptyset$
,
 $b = b_t + b_u = 0$
, and
$b = b_t + b_u = 0$
, and
 $s = s_t + s_u = 0$
.
$s = s_t + s_u = 0$
. -
• Rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $t = rp$
and
$t = rp$
and
 $t \{x \setminus u\} = (r \{x \setminus u\}) (p \{x \setminus u\})$
. Moreover,
$t \{x \setminus u\} = (r \{x \setminus u\}) (p \{x \setminus u\})$
. Moreover,
 $\Phi _{t \{x \setminus u\}}$
has one premise
$\Phi _{t \{x \setminus u\}}$
has one premise
 $\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s')}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; {\tt n}$
, such that
$\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _{t \{x \setminus u\}} \negmedspace \overset {(b,s')}{\vdash _{{\tt n}}}\negmedspace r \{x \setminus u\}\;:\; {\tt n}$
, such that
 $s = 1 + s'$
, and
$s = 1 + s'$
, and
 $\mathscr{G\,} = {\tt n}$
. By applying the i.h. to
$\mathscr{G\,} = {\tt n}$
. By applying the i.h. to
 $\Phi _{r \{x \setminus u\}}$
, there exist
$\Phi _{r \{x \setminus u\}}$
, there exist
 $\Phi _r \triangleright \, \Gamma _r;\; \mathscr{M} \negmedspace \overset {(b_r, s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; {\tt n}$
and
$\Phi _r \triangleright \, \Gamma _r;\; \mathscr{M} \negmedspace \overset {(b_r, s_r)}{\vdash _{{\tt n}}}\negmedspace r\;:\; {\tt n}$
and
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
 $\Gamma _{t \{x \setminus u\}} = \Gamma _r + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _r + \Gamma _u$
,
 $b = b_r + b_u$
, and
$b = b_r + b_u$
, and
 $s' = s_r + s_u$
. Therefore, we can build
$s' = s_r + s_u$
. Therefore, we can build
 $\Phi _t$
as follows:such that
$\Phi _t$
as follows:such that \begin{equation*} \frac {\Phi _r}{\Gamma _r;\; x \;:\; \mathscr{M} \mathop {\vdash }\limits ^{(b_r,1+s_r)}_{} rp: {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _r}{\Gamma _r;\; x \;:\; \mathscr{M} \mathop {\vdash }\limits ^{(b_r,1+s_r)}_{} rp: {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
 $\Gamma _t = \Gamma _r$
,
$\Gamma _t = \Gamma _r$
,
 $b_t = b_r$
, and
$b_t = b_r$
, and
 $s_t = 1 + s_r$
. Thus, we can conclude with
$s_t = 1 + s_r$
. Thus, we can conclude with
 $s = 1 + s' = 1 + s_r + s_u = s_t + s_u$
.
$s = 1 + s' = 1 + s_r + s_u = s_t + s_u$
.
Lemma 5 (Quantitative subject expansion). Let
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t': \tau$
be a tight type derivation. If
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{n}}}\negmedspace t': \tau$
be a tight type derivation. If
![]() $t \rightarrow_{\texttt{n}} t'$
, then there exists
$t \rightarrow_{\texttt{n}} t'$
, then there exists
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b+1, s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b+1, s)} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
.
Proof. Similarly to Lemma4, we prove a stronger version of the statement that allows us to reason inductively:
Let
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t': \tau$
, such that
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace t': \tau$
, such that
![]() $\Gamma$
is tight, and either
$\Gamma$
is tight, and either
![]() $\tau \in {{\tt tt}_{\tt n}}$
or
$\tau \in {{\tt tt}_{\tt n}}$
or
![]() $\neg {\tt abs}(t)$
. If
$\neg {\tt abs}(t)$
. If
![]() $t \rightarrow t'$
, then there exists
$t \rightarrow t'$
, then there exists
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b+1,s)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b+1,s)}{\vdash _{{\tt n}}}\negmedspace t\;:\; \tau$
.
The proof now follows by induction over
![]() $t \rightarrow t'$
:
$t \rightarrow t'$
:
-
• Case
 $t = (\lambda x.p) u \rightarrow p \{x \setminus u\} = t'$
. Then
$t = (\lambda x.p) u \rightarrow p \{x \setminus u\} = t'$
. Then
 $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau$
. By Lemma 25, there exist
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt n}}}\negmedspace p \{x \setminus u\}\;:\; \tau$
. By Lemma 25, there exist
 $\Phi _p \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \tau$
and
$\Phi _p \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \tau$
and
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M}$
, such that
 $\Gamma = \Gamma _p + \Gamma _u$
tight,
$\Gamma = \Gamma _p + \Gamma _u$
tight,
 $\tau \in {{\tt tt}_{\tt n}}$
,
$\tau \in {{\tt tt}_{\tt n}}$
,
 $b = b_p + b_u$
, and
$b = b_p + b_u$
, and
 $s = s_p + s_u$
. Therefore, we can build
$s = s_p + s_u$
. Therefore, we can build
 $\Phi _t$
as follows:
$\Phi _t$
as follows:
Thus, we can conclude with
 $b + 1 = 1 + b_p + b_u$
.
$b + 1 = 1 + b_p + b_u$
. -
• Case
 $t = up \rightarrow u'p = t'$
, such that
$t = up \rightarrow u'p = t'$
, such that
 $u \rightarrow u'$
. Then,
$u \rightarrow u'$
. Then,
 $\Phi _{t'}$
must end with rule (@) or (@
$\Phi _{t'}$
must end with rule (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Case
 $\Phi _{t'}$
ends with rule (@). Then,
$\Phi _{t'}$
ends with rule (@). Then,
 $\Phi _{t'}$
has two premises,
$\Phi _{t'}$
has two premises,
 $\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u': \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u': \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M\;}'$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt n}}}\negmedspace p: \mathscr{M\;}'$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
tight,
$\Gamma = \Gamma _u + \Gamma _p$
tight,
 $\tau \in {{\tt tt}_{\tt n}}$
,
$\tau \in {{\tt tt}_{\tt n}}$
,
 $b = 1 + b_u + b_p$
, and
$b = 1 + b_u + b_p$
, and
 $s = s_u + s_p$
. Notice that
$s = s_u + s_p$
. Notice that
 $\neg {\tt abs}(u)$
, since
$\neg {\tt abs}(u)$
, since
 $u \rightarrow u'$
. Moreover,
$u \rightarrow u'$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. Therefore, by applying the i.h. to
$\Gamma _p$
are tight. Therefore, by applying the i.h. to
 $\Phi _{u'}$
, there exists
$\Phi _{u'}$
, there exists
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(1 + b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
. Therefore, we can build
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(1 + b_u, s_u)}{\vdash _{{\tt n}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
. Therefore, we can build
 $\Phi _t$
as follows:Thus, we can conclude with
$\Phi _t$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _u \qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 + 1+ b_u + b_p, s_u + s_p)}_{} up: \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u \qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 + 1+ b_u + b_p, s_u + s_p)}_{} up: \tau }({\tt @})\end{equation*}
 $b + 1 = (1 + b_u + b_p) + 1$
.
$b + 1 = (1 + b_u + b_p) + 1$
.
-
– Case
 $\Phi _{t'}$
ends with rule (@
$\Phi _{t'}$
ends with rule (@
 $_{{\tt p}}$
). Then
$_{{\tt p}}$
). Then
 $\Phi _{t'}$
has one premise
$\Phi _{t'}$
has one premise
 $\Phi _{u'} \triangleright \, \Gamma \negmedspace \overset {(b,s_{u'})}{\vdash _{{\tt n}}}\negmedspace u': {\tt n}$
, such that
$\Phi _{u'} \triangleright \, \Gamma \negmedspace \overset {(b,s_{u'})}{\vdash _{{\tt n}}}\negmedspace u': {\tt n}$
, such that
 $s = 1 + s_{u'}$
. By applying the i.h. to
$s = 1 + s_{u'}$
. By applying the i.h. to
 $\Phi _{u'}$
, there exists
$\Phi _{u'}$
, there exists
 $\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b+1, s_{u'})}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
. Therefore, we can build
$\Phi _u \triangleright \, \Gamma \negmedspace \overset {(b+1, s_{u'})}{\vdash _{{\tt n}}}\negmedspace u\;:\; {\tt n}$
. Therefore, we can build
 $\Phi _t$
as follows:
$\Phi _t$
as follows: \begin{equation*} \frac {\Phi _u}{\Gamma \mathop {\vdash }\limits ^{(b+1,1+s_{u'})}_{} up: {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _u}{\Gamma \mathop {\vdash }\limits ^{(b+1,1+s_{u'})}_{} up: {\tt n}}({\tt @}_{{\tt p}})\end{equation*}
-
Theorem 2 (Quantitative completeness). If
![]() $t \twoheadrightarrow ^b_{\texttt{n}} u$
with
$t \twoheadrightarrow ^b_{\texttt{n}} u$
with
![]() $u \in {\tt no}_{\texttt{n}}$
, then there exists a tight type derivation
$u \in {\tt no}_{\texttt{n}}$
, then there exists a tight type derivation
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b, |u|_{\texttt{n}})} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b, |u|_{\texttt{n}})} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
.
Proof.
The proof follows by induction over
![]() $b$
:
$b$
:
-
• Case
 $b = 0$
. Then
$b = 0$
. Then
 $t = u$
, which means that
$t = u$
, which means that
 $t \in {\tt no}_{\texttt{n}}$
. Therefore, we can conclude by Lemma3.
$t \in {\tt no}_{\texttt{n}}$
. Therefore, we can conclude by Lemma3. -
• Case
 $b \gt 0$
. Then there exists
$b \gt 0$
. Then there exists
 $t'$
, such that
$t'$
, such that
 $t \rightarrow t' \twoheadrightarrow ^{b-1}_{\texttt{n}} u$
. By the i.h., there exists a tight derivation
$t \rightarrow t' \twoheadrightarrow ^{b-1}_{\texttt{n}} u$
. By the i.h., there exists a tight derivation
 $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, |u|_{\texttt{n}})} {\vdash_{\texttt{n}}}\negmedspace t'\;:\; \tau$
. By Lemma5, there exists a tight derivation
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, |u|_{\texttt{n}})} {\vdash_{\texttt{n}}}\negmedspace t'\;:\; \tau$
. By Lemma5, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \negmedspace \overset{(b, |u|_{\texttt{n}})} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
. So, we can conclude.
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b, |u|_{\texttt{n}})} {\vdash_{\texttt{n}}}\negmedspace t\;:\; \tau$
. So, we can conclude.
A.1.2 Weak Open CBV
Proposition 2 (Normal forms for Weak Open CBV). Let
![]() $t$
be a term. Then
$t$
be a term. Then
![]() $t \in {\tt no}_{{\tt v}}$
iff
$t \in {\tt no}_{{\tt v}}$
iff
![]() $t \not {\!\rightarrow }_{\texttt {v}}$
.
$t \not {\!\rightarrow }_{\texttt {v}}$
.
Proof. We refine the original statement into the two following ones:
-
(1)
 $t \not {\!\rightarrow }_{\texttt {v}}$
and
$t \not {\!\rightarrow }_{\texttt {v}}$
and
 $\neg {\tt val}(t)$
iff
$\neg {\tt val}(t)$
iff
 $t \in {\tt ne}_{{\tt v}}$
.
$t \in {\tt ne}_{{\tt v}}$
. -
(2)
 $t \not {\!\rightarrow }_{\texttt {v}}$
iff
$t \not {\!\rightarrow }_{\texttt {v}}$
iff
 $t \in {\tt no}_{{\tt v}}$
.
$t \in {\tt no}_{{\tt v}}$
.
The proof now follows by simultaneous induction over both these statements:
-
⇒) By induction over
 $t$
:
$t$
:-
(1) Let
 $t \not {\!\rightarrow }_{\texttt {v}}$
and
$t \not {\!\rightarrow }_{\texttt {v}}$
and
 $\neg {\tt val}(t)$
. We want to show that
$\neg {\tt val}(t)$
. We want to show that
 $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:-
– Case
 $t = x$
or
$t = x$
or
 $t = \lambda x.u$
. Then
$t = \lambda x.u$
. Then
 ${\tt val}(t)$
, which contradicts the hypothesis. Therefore, this cannot apply.
${\tt val}(t)$
, which contradicts the hypothesis. Therefore, this cannot apply. -
– Case
 $t = u p$
. Since
$t = u p$
. Since
 $u p \not {\!\rightarrow }_{\texttt {v}}$
, no rule of
$u p \not {\!\rightarrow }_{\texttt {v}}$
, no rule of
 ${\rightarrow }_{\texttt {v}}$
applies to
${\rightarrow }_{\texttt {v}}$
applies to
 $up$
. We consider two cases:
$up$
. We consider two cases:-
*
 ${\tt abs}(u)$
, then
${\tt abs}(u)$
, then
 $\neg {\tt val}(p)$
otherwise rule (
$\neg {\tt val}(p)$
otherwise rule (
 $\beta _{\tt v}$
) would apply. Moreover,
$\beta _{\tt v}$
) would apply. Moreover,
 $p \not {\!\rightarrow }_{\texttt {v}}$
, otherwise
$p \not {\!\rightarrow }_{\texttt {v}}$
, otherwise
 $t$
would be reducible by (appR). Therefore,
$t$
would be reducible by (appR). Therefore,
 $p \in {\tt ne}_{{\tt v}}$
by the i.h. (1). Furthermore,
$p \in {\tt ne}_{{\tt v}}$
by the i.h. (1). Furthermore,
 ${\tt val}(u)$
by definition, that is
${\tt val}(u)$
by definition, that is
 $u\in {\tt no}_{{\tt v}}$
and therefore
$u\in {\tt no}_{{\tt v}}$
and therefore
 $up \in {\tt ne}_{{\tt v}}$
.
$up \in {\tt ne}_{{\tt v}}$
. -
*
 $\neg {\tt abs}(u)$
, then
$\neg {\tt abs}(u)$
, then
 $\neg {\tt val}(u)$
or
$\neg {\tt val}(u)$
or
 $u=x$
(since variables are the only values other than abstractions). We can also conclude that
$u=x$
(since variables are the only values other than abstractions). We can also conclude that
 $u \not {\!\rightarrow }_{\texttt {v}}$
otherwise
$u \not {\!\rightarrow }_{\texttt {v}}$
otherwise
 $t$
would be reducible by (appL). And
$t$
would be reducible by (appL). And
 $p \not {\!\rightarrow }_{\texttt {v}}$
, otherwise
$p \not {\!\rightarrow }_{\texttt {v}}$
, otherwise
 $t$
would be reducible by (appR), therefore the i.h. (1), we get
$t$
would be reducible by (appR), therefore the i.h. (1), we get
 $p \in {\tt no}_{{\tt v}}$
. If
$p \in {\tt no}_{{\tt v}}$
. If
 $\neg {\tt val}(u)$
, then we can apply the i.h. (1), and get
$\neg {\tt val}(u)$
, then we can apply the i.h. (1), and get
 $u \in {\tt ne}_{{\tt v}}$
. In both cases,
$u \in {\tt ne}_{{\tt v}}$
. In both cases,
 $u p \in {\tt ne}_{{\tt v}}$
.
$u p \in {\tt ne}_{{\tt v}}$
.
-
-
-
(2) Let
 $t \not {\!\rightarrow }_{\texttt {v}}$
. We want to show that
$t \not {\!\rightarrow }_{\texttt {v}}$
. We want to show that
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
– Case
 ${\tt val}(t)$
. Then,
${\tt val}(t)$
. Then,
 $t \in {\tt no}_{{\tt v}}$
by definition.
$t \in {\tt no}_{{\tt v}}$
by definition. -
– Case
 $\neg {\tt val}(t)$
. Then,
$\neg {\tt val}(t)$
. Then,
 $t \in {\tt ne}_{{\tt v}}$
by point (1), which implies
$t \in {\tt ne}_{{\tt v}}$
by point (1), which implies
 $t \in {\tt no}_{{\tt v}}$
.
$t \in {\tt no}_{{\tt v}}$
.
-
-
-
⇐) By mutual induction over
 $t \in {\tt ne}_{{\tt v}}$
and
$t \in {\tt ne}_{{\tt v}}$
and
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
(1) Let
 $t \in {\tt ne}_{{\tt v}}$
. We want to show that
$t \in {\tt ne}_{{\tt v}}$
. We want to show that
 $t \not {\!\rightarrow }_{\texttt {v}}$
and
$t \not {\!\rightarrow }_{\texttt {v}}$
and
 $\neg {\tt val}(t)$
:
$\neg {\tt val}(t)$
:-
– Case
 $t = x p$
, such that
$t = x p$
, such that
 $p \in {\tt no}_{{\tt v}}$
. Then,
$p \in {\tt no}_{{\tt v}}$
. Then,
 $p \not {\!\rightarrow }_{\texttt {v}}$
by i.h. (2). Therefore, no rule of
$p \not {\!\rightarrow }_{\texttt {v}}$
by i.h. (2). Therefore, no rule of
 ${\rightarrow }_{\texttt {v}}$
applies to
${\rightarrow }_{\texttt {v}}$
applies to
 $xp$
. Moreover,
$xp$
. Moreover,
 $x \neg {\tt val}(p)$
.
$x \neg {\tt val}(p)$
. -
– Case
 $t = u p$
, such that
$t = u p$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
. Then,
$p \in {\tt ne}_{{\tt v}}$
. Then,
 $u \not {\!\rightarrow }_{\texttt {v}}$
, by i.h. (2), and
$u \not {\!\rightarrow }_{\texttt {v}}$
, by i.h. (2), and
 $p \not {\!\rightarrow }_{\texttt {v}}$
and
$p \not {\!\rightarrow }_{\texttt {v}}$
and
 $\neg {\tt val}(p)$
, by i.h. (1). Therefore, no rule of
$\neg {\tt val}(p)$
, by i.h. (1). Therefore, no rule of
 ${\rightarrow }_{\texttt {v}}$
applies to
${\rightarrow }_{\texttt {v}}$
applies to
 $up$
. Moreover,
$up$
. Moreover,
 $u \neg {\tt val}(p)$
.
$u \neg {\tt val}(p)$
. -
– Case
 $t = u p$
, such that
$t = u p$
, such that
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
. Then,
$p \in {\tt no}_{{\tt v}}$
. Then,
 $u \not {\!\rightarrow }_{\texttt {v}}$
and
$u \not {\!\rightarrow }_{\texttt {v}}$
and
 $\neg {\tt val}(u)$
, by i.h. (1), and
$\neg {\tt val}(u)$
, by i.h. (1), and
 $p \not {\!\rightarrow }_{\texttt {v}}$
, by i.h. (2). Therefore, no rule of
$p \not {\!\rightarrow }_{\texttt {v}}$
, by i.h. (2). Therefore, no rule of
 ${\rightarrow }_{\texttt {v}}$
applies to
${\rightarrow }_{\texttt {v}}$
applies to
 $up$
. Moreover,
$up$
. Moreover,
 $\neg {\tt val}(up)$
.
$\neg {\tt val}(up)$
.
-
-
(2) Let
 $t \in {\tt no}_{{\tt v}}$
. We want to show that
$t \in {\tt no}_{{\tt v}}$
. We want to show that
 $t \not {\!\rightarrow }_{\texttt {v}}$
:
$t \not {\!\rightarrow }_{\texttt {v}}$
:-
– Case
 ${\tt val}(t)$
. Then,
${\tt val}(t)$
. Then,
 $t \not {\!\rightarrow }_{\texttt {v}}$
, by definition.
$t \not {\!\rightarrow }_{\texttt {v}}$
, by definition. -
– Case
 $\neg {\tt val}(t)$
. Then,
$\neg {\tt val}(t)$
. Then,
 $t \in {\tt ne}_{{\tt v}}$
by definition, and thus,
$t \in {\tt ne}_{{\tt v}}$
by definition, and thus,
 $t \not {\!\rightarrow }_{\texttt {v}}$
by i.h. (1).
$t \not {\!\rightarrow }_{\texttt {v}}$
by i.h. (1).
-
-
Lemma 26 (Values are not neutral). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
. If
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
. If
![]() ${\tt val}(t)$
, then
${\tt val}(t)$
, then
![]() $\tau \neq {\tt n}$
.
$\tau \neq {\tt n}$
.
Proof.
By case analysis on
![]() ${\tt val}(t)$
:
${\tt val}(t)$
:
-
• Case
 $t = x$
. Then,
$t = x$
. Then,
 $\Phi$
must end with rule (ax) or (m). In the former case,
$\Phi$
must end with rule (ax) or (m). In the former case,
 $\tau = \sigma$
, and
$\tau = \sigma$
, and
 ${\tt n} \not \in \sigma$
. In the latter case,
${\tt n} \not \in \sigma$
. In the latter case,
 $\tau = \mathscr{M}$
, and
$\tau = \mathscr{M}$
, and
 $\mathscr{M} \neq {\tt n}$
. Thus, we can conclude that
$\mathscr{M} \neq {\tt n}$
. Thus, we can conclude that
 $\tau \neq {\tt n}$
.
$\tau \neq {\tt n}$
. -
• Case
 $t = \lambda x.t$
. Then,
$t = \lambda x.t$
. Then,
 $\Phi$
must end with rule (
$\Phi$
must end with rule (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). In the first case,
$\lambda _{\tt p}$
). In the first case,
 $\tau = \mathscr{M} \rightarrow \tau '$
, and
$\tau = \mathscr{M} \rightarrow \tau '$
, and
 $\mathscr{M} \rightarrow \tau ' \neq {\tt n}$
. In the second case,
$\mathscr{M} \rightarrow \tau ' \neq {\tt n}$
. In the second case,
 $\tau = \mathscr{M}$
, and
$\tau = \mathscr{M}$
, and
 $\mathscr{M} \neq {\tt n}$
. In the last case,
$\mathscr{M} \neq {\tt n}$
. In the last case,
 $\tau = {\tt a}$
, and
$\tau = {\tt a}$
, and
 ${\tt a} \neq {\tt n}$
.
${\tt a} \neq {\tt n}$
.
Proposition 8 (Relevance). Let
![]() $\Phi \triangleright \, \Gamma \vdash ^{(b,s)}_{\texttt{v}} t\;:\; \tau$
. Then
$\Phi \triangleright \, \Gamma \vdash ^{(b,s)}_{\texttt{v}} t\;:\; \tau$
. Then
![]() ${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
.
${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
.
Proof.
By a simple induction over
![]() $\Phi$
.
$\Phi$
.
Lemma 27 (Persistent abstractions have tight type). If
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
. If
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
. If
![]() $\tau \in \overline {{\tt a}}$
, then
$\tau \in \overline {{\tt a}}$
, then
![]() $\neg {\tt abs}(t)$
.
$\neg {\tt abs}(t)$
.
Proof.
By induction over
![]() $\Phi$
, according to the last rule of
$\Phi$
, according to the last rule of
![]() $\Phi$
:
$\Phi$
:
-
• Rule (ax), (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
). Then,
$^2_{{\tt p}}$
). Then,
 $\neg {\tt abs}(t)$
, by definition.
$\neg {\tt abs}(t)$
, by definition. -
• Rule (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $\tau \not \in \{{\tt v}, {\tt n}\} = \overline {{\tt a}}$
. Therefore, these cases hold vacuously.
$\tau \not \in \{{\tt v}, {\tt n}\} = \overline {{\tt a}}$
. Therefore, these cases hold vacuously.
Lemma 28 (Tight spreading). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
, such that
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt ne}_{\texttt{v}}$
, then
$t \in {\tt ne}_{\texttt{v}}$
, then
![]() $\tau$
is a tight constant.
$\tau$
is a tight constant.
Proof.
By induction over
![]() $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:
-
• Case
 $t = xp$
, such that
$t = xp$
, such that
 $p \in {\tt no}_{{\tt v}}$
. Then,
$p \in {\tt no}_{{\tt v}}$
. Then,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _x \triangleright \, x \;:\; [ \mathscr{M} \rightarrow \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace x\;:\; \mathscr{M} \rightarrow \delta$
and
$\Phi _x \triangleright \, x \;:\; [ \mathscr{M} \rightarrow \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace x\;:\; \mathscr{M} \rightarrow \delta$
and
 $\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\mathscr{M}$
, such that
$\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\mathscr{M}$
, such that
 $\Gamma = (x \;:\; [ \mathscr{M} \rightarrow \tau ]) + \Gamma _p$
,
$\Gamma = (x \;:\; [ \mathscr{M} \rightarrow \tau ]) + \Gamma _p$
,
 $b = 1+b_p$
and
$b = 1+b_p$
and
 $s = s_p$
. However,
$s = s_p$
. However,
 $\mathscr{M} \rightarrow \tau$
is not tight, which contradicts the tightness of
$\mathscr{M} \rightarrow \tau$
is not tight, which contradicts the tightness of
 $\Gamma$
. Therefore, this case cannot apply.
$\Gamma$
. Therefore, this case cannot apply. -
– Rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). Then,
$^2_{{\tt p}}$
). Then,
 $\tau = {\tt n}$
.
$\tau = {\tt n}$
.
-
-
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
. Then,
$p \in {\tt ne}_{{\tt v}}$
. Then,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
 $\Phi _p \triangleright \,\Gamma _p \vdash^{{(b_p,s_p)}}_{\tt v}p\;:\;\mathscr{M}$
, such that
$\Phi _p \triangleright \,\Gamma _p \vdash^{{(b_p,s_p)}}_{\tt v}p\;:\;\mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $b = 1+b_u+b_p$
, and
$b = 1+b_u+b_p$
, and
 $s = s_u+s_p$
. Therefore,
$s = s_u+s_p$
. Therefore,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. By applying the i.h. to
$\Gamma _p$
are tight. By applying the i.h. to
 $\Phi _p$
we get that
$\Phi _p$
we get that
 $\mathscr{M}\in {{\tt tt}_{\tt v}}$
, which is a contradiction. Therefore, this case cannot apply.
$\mathscr{M}\in {{\tt tt}_{\tt v}}$
, which is a contradiction. Therefore, this case cannot apply. -
– Rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). Then,
$^2_{{\tt p}}$
). Then,
 $\tau = {\tt n}$
.
$\tau = {\tt n}$
.
-
-
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
. Then,
$p \in {\tt no}_{{\tt v}}$
. Then,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
 $\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\mathscr{M}$
, such that
$\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $b = 1+b_u+b_p$
, and
$b = 1+b_u+b_p$
, and
 $s = s_u+s_p$
. Therefore,
$s = s_u+s_p$
. Therefore,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. By applying the i.h. to
$\Gamma _p$
are tight. By applying the i.h. to
 $\Phi _p$
, we get that
$\Phi _p$
, we get that
 $\mathscr{M}\in {{\tt tt}_{\tt v}}$
, which is a contradiction. Therefore, this case cannot apply.
$\mathscr{M}\in {{\tt tt}_{\tt v}}$
, which is a contradiction. Therefore, this case cannot apply. -
– Rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). Then,
$^2_{{\tt p}}$
). Then,
 $\tau = {\tt n}$
.
$\tau = {\tt n}$
.
-
Lemma 1 (Normal forms take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
be a tight type derivation. Then,
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
be a tight type derivation. Then,
![]() $b = 0$
iff
$b = 0$
iff
![]() $t \in {\tt no}_{\texttt{v}}$
.
$t \in {\tt no}_{\texttt{v}}$
.
Proof.
-
⇒) We refine the original statement into the two following ones:
-
(1) Let
 $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
be a tight derivation. Then
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
be a tight derivation. Then
 $b = 0$
and
$b = 0$
and
 $\neg {\tt val}(t)$
implies
$\neg {\tt val}(t)$
implies
 $t \in {\tt ne}_{{\tt v}}$
.
$t \in {\tt ne}_{{\tt v}}$
. -
(2) Let
 $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
be a tight derivation. Then
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
be a tight derivation. Then
 $b = 0$
implies
$b = 0$
implies
 $t \in {\tt no}_{{\tt v}}$
.
$t \in {\tt no}_{{\tt v}}$
.The proof follows by mutual induction over
 $\Phi$
for both statements, according to the last rule of
$\Phi$
for both statements, according to the last rule of
 $\Phi$
:
$\Phi$
:-
(1) Let
 $b = 0$
and
$b = 0$
and
 $\neg {\tt val}(t)$
:
$\neg {\tt val}(t)$
:-
– Rule (ax), (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 ${\tt val}(t)$
, which contradiction the hypotheses. Therefore, these cases cannot apply.
${\tt val}(t)$
, which contradiction the hypotheses. Therefore, these cases cannot apply. -
– Rule (@). Then,
 $b \gt 0$
. Therefore, this case holds vacuously.
$b \gt 0$
. Therefore, this case holds vacuously. -
– Rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $t = up$
, and
$t = up$
, and
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(0,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \overline {{\tt a}}$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(0,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \overline {{\tt a}}$
and
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(0,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(0,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $\tau = {\tt n}$
, and
$\tau = {\tt n}$
, and
 $s = 1+s_u+s_p$
. Therefore, both
$s = 1+s_u+s_p$
. Therefore, both
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. By applying the i.h. (2) to
$\Gamma _p$
are tight. By applying the i.h. (2) to
 $\Phi _u$
and
$\Phi _u$
and
 $\Phi _p$
, we have
$\Phi _p$
, we have
 $u, p \in {\tt no}_{{\tt v}}$
. Since
$u, p \in {\tt no}_{{\tt v}}$
. Since
 $\tau = {\tt n} \in \overline {{\tt a}}$
, then, by Lemma 27, we know that
$\tau = {\tt n} \in \overline {{\tt a}}$
, then, by Lemma 27, we know that
 $\neg {\tt abs}(u)$
. Therefore, either
$\neg {\tt abs}(u)$
. Therefore, either
 $u = x$
or
$u = x$
or
 $u \in {\tt ne}_{{\tt v}}$
, by definition. In both cases,
$u \in {\tt ne}_{{\tt v}}$
, by definition. In both cases,
 $u p \in {\tt ne}_{{\tt v}}$
.
$u p \in {\tt ne}_{{\tt v}}$
. -
– Rule (@
 $^2_{{\tt p}}$
). Then,
$^2_{{\tt p}}$
). Then,
 $t = up$
, and
$t = up$
, and
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(0,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; {{\tt tt}_{\tt v}}$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(0,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; {{\tt tt}_{\tt v}}$
and
 $\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(0,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\texttt{n}$
, such that
$\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(0,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\texttt{n}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $\tau = {\tt n}$
, and
$\tau = {\tt n}$
, and
 $s = 1+s_u+s_p$
. Therefore,
$s = 1+s_u+s_p$
. Therefore,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. By applying the i.h. (2) to
$\Gamma _p$
are tight. By applying the i.h. (2) to
 $\Phi _u$
, we have that
$\Phi _u$
, we have that
 $u \in {\tt no}_{{\tt v}}$
. Since
$u \in {\tt no}_{{\tt v}}$
. Since
 $\tau = {\tt n}$
, then by Lemma 26, we know that
$\tau = {\tt n}$
, then by Lemma 26, we know that
 $\neg {\tt val}(t)$
. By applying the i.h. (1) to
$\neg {\tt val}(t)$
. By applying the i.h. (1) to
 $\Phi _p$
, we have that
$\Phi _p$
, we have that
 $p \in {\tt ne}_{{\tt v}}$
. In which case,
$p \in {\tt ne}_{{\tt v}}$
. In which case,
 $u p \in {\tt ne}_{{\tt v}}$
.
$u p \in {\tt ne}_{{\tt v}}$
.
-
-
(2) Let
 $b = 0$
:
$b = 0$
:-
– Rule (ax), (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 ${\tt val}(t) \subseteq {\tt no}_{{\tt v}}$
, by definition.
${\tt val}(t) \subseteq {\tt no}_{{\tt v}}$
, by definition. -
– Rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
). Then
$^2_{{\tt p}}$
). Then
 $\neg {\tt val}(t)$
by definition. Therefore,
$\neg {\tt val}(t)$
by definition. Therefore,
 $t \in {\tt ne}_{{\tt v}} \subseteq {\tt no}_{{\tt v}}$
by i.h. (1).
$t \in {\tt ne}_{{\tt v}} \subseteq {\tt no}_{{\tt v}}$
by i.h. (1).
-
-
-
-
⇐) The proof follows by mutual induction over
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
(1) Let
 $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:-
– Case
 $t = xp$
, such that
$t = xp$
, such that
 $p \in {\tt no}_{{\tt v}}$
. Then,
$p \in {\tt no}_{{\tt v}}$
. Then,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $_{{\tt 2}}$
):
$_{{\tt 2}}$
):-
* Case
 $\Phi$
ends with (@). Then,
$\Phi$
ends with (@). Then,
 $\Phi$
has necessarily two premises
$\Phi$
has necessarily two premises
 $\Phi _x \triangleright \, x \;:\; [ \mathscr{M} \rightarrow \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace x\;:\; \mathscr{M} \rightarrow \tau$
and
$\Phi _x \triangleright \, x \;:\; [ \mathscr{M} \rightarrow \tau ] \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace x\;:\; \mathscr{M} \rightarrow \tau$
and
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M}$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M}$
, such that
 $\Gamma = (x \;:\; [ \mathscr{M} \rightarrow \tau ]) + \Gamma _p$
,
$\Gamma = (x \;:\; [ \mathscr{M} \rightarrow \tau ]) + \Gamma _p$
,
 $b = 1+b_p$
, and
$b = 1+b_p$
, and
 $s = s_p$
. However,
$s = s_p$
. However,
 $\Gamma$
is not tight, because
$\Gamma$
is not tight, because
 $\mathscr{M} \rightarrow \tau \not \in {{\tt tt}_{\tt v}}$
, which contradicts the hypothesis. Therefore, this case cannot apply.
$\mathscr{M} \rightarrow \tau \not \in {{\tt tt}_{\tt v}}$
, which contradicts the hypothesis. Therefore, this case cannot apply. -
* Case
 $\Phi$
ends with (@
$\Phi$
ends with (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _x \triangleright \, (x \;:\; [ {\tt v} ]) \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace x\;:\; {\tt v}$
and
$\Phi _x \triangleright \, (x \;:\; [ {\tt v} ]) \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace x\;:\; {\tt v}$
and
 $\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\texttt{tt}_{\texttt{v}}$
, such that
$\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\texttt{tt}_{\texttt{v}}$
, such that
 $\Gamma = (x \;:\; [ {\tt v} ]) + \Gamma _p$
,
$\Gamma = (x \;:\; [ {\tt v} ]) + \Gamma _p$
,
 $\tau = {\tt n}$
,
$\tau = {\tt n}$
,
 $b = b_p$
, and
$b = b_p$
, and
 $s = 1+s_p$
. Therefore,
$s = 1+s_p$
. Therefore,
 $\Gamma _p$
is tight. By applying the i.h. to
$\Gamma _p$
is tight. By applying the i.h. to
 $\Phi _p$
, we have that
$\Phi _p$
, we have that
 $b_p = 0$
, and thus,
$b_p = 0$
, and thus,
 $b = b_p = 0$
. We then conclude.
$b = b_p = 0$
. We then conclude. -
* Case
 $\Phi$
ends with (@
$\Phi$
ends with (@
 $^2_{{\tt p}}$
). Very similar to the previous case.
$^2_{{\tt p}}$
). Very similar to the previous case.
-
-
– Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
. Then,
$p \in {\tt ne}_{{\tt v}}$
. Then,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $_{{\tt 2}}$
):
$_{{\tt 2}}$
):-
* Case
 $\Phi$
ends with (@). Then,
$\Phi$
ends with (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau$
and
 $\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\mathscr{M}$
, such that
$\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $b = 1+b_u+b_p$
, and
$b = 1+b_u+b_p$
, and
 $s = s_u+s_p$
. Therefore,
$s = s_u+s_p$
. Therefore,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. We can then apply Lemma 28 to
$\Gamma _p$
are tight. We can then apply Lemma 28 to
 $\Phi _u$
, and we get
$\Phi _u$
, and we get
 $\mathscr{M} \rightarrow \tau$
tight, which yields to a contradiction. Therefore, this case cannot apply.
$\mathscr{M} \rightarrow \tau$
tight, which yields to a contradiction. Therefore, this case cannot apply. -
* Case
 $\Phi$
ends with (@
$\Phi$
ends with (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). Very similar to the cases for
$^2_{{\tt p}}$
). Very similar to the cases for
 $t = x p$
, such that
$t = x p$
, such that
 $p \in {\tt no}_{{\tt v}}$
.
$p \in {\tt no}_{{\tt v}}$
.
-
-
– Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
. This case is very similar to the case where
$p \in {\tt no}_{{\tt v}}$
. This case is very similar to the case where
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
.
$p \in {\tt ne}_{{\tt v}}$
.
-
-
(2) Let
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
– Case
 ${\tt val}(t)$
. Then,
${\tt val}(t)$
. Then,
 $\Phi$
must end with rule (ax), (
$\Phi$
must end with rule (ax), (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). Case
$\lambda _{\tt p}$
). Case
 $\Phi$
ends with rules (
$\Phi$
ends with rules (
 $\lambda$
) or (m) then,
$\lambda$
) or (m) then,
 $\tau \not \in {{\tt tt}_{\tt v}}$
and the statement hold vacuously. Otherwise,
$\tau \not \in {{\tt tt}_{\tt v}}$
and the statement hold vacuously. Otherwise,
 $b = 0$
, by definition.
$b = 0$
, by definition. -
– Case
 $\neg {\tt val}(t)$
. Then,
$\neg {\tt val}(t)$
. Then,
 $t \in {\tt ne}_{{\tt v}}$
, by definition. Therefore,
$t \in {\tt ne}_{{\tt v}}$
, by definition. Therefore,
 $b = 0$
, by i.h. (1).
$b = 0$
, by i.h. (1).
-
-
Lemma 2 (Normal forms have correct size). Let
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
be a tight type derivation. If
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
be a tight type derivation. If
![]() $b = 0$
then
$b = 0$
then
![]() $s = |t|_{\texttt{v}}$
.
$s = |t|_{\texttt{v}}$
.
Proof.
The proof follows by induction over
![]() $\Phi$
, according to the last rule of
$\Phi$
, according to the last rule of
![]() $\Phi$
:
$\Phi$
:
-
• Rule (ax) or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 ${\tt val}(t)$
and
${\tt val}(t)$
and
 $s = 0 = |{t}|_{\texttt {v}}$
.
$s = 0 = |{t}|_{\texttt {v}}$
. -
• Rule (
 $\lambda$
) or (m). Then,
$\lambda$
) or (m). Then,
 $\tau \not \in {{\tt tt}_{\tt v}}$
. Therefore, these cases holds vacuously.
$\tau \not \in {{\tt tt}_{\tt v}}$
. Therefore, these cases holds vacuously. -
• Rule (@). Then,
 $b \gt 0$
. Therefore, this case holds vacuously.
$b \gt 0$
. Therefore, this case holds vacuously. -
• Rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $t = up$
and
$t = up$
and
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(0,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \overline {{\tt a}}$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(0,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \overline {{\tt a}}$
and
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(0,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(0,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $\tau = {\tt n}$
,
$\tau = {\tt n}$
,
 $b = 0$
, and
$b = 0$
, and
 $s = 1+s_u+s_p$
. Therefore, in particular,
$s = 1+s_u+s_p$
. Therefore, in particular,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. Since
$\Gamma _p$
are tight. Since
 $\Phi _u$
and
$\Phi _u$
and
 $\Phi _p$
are both tight, then, by applying the i.h. to
$\Phi _p$
are both tight, then, by applying the i.h. to
 $\Phi _u$
and
$\Phi _u$
and
 $\Phi _p$
, we have
$\Phi _p$
, we have
 $s_u = |{u}|_{\texttt {v}}$
and
$s_u = |{u}|_{\texttt {v}}$
and
 $s_p = |{p}|_{\texttt {v}}$
. Therefore,
$s_p = |{p}|_{\texttt {v}}$
. Therefore,
 $s = 1 + |{u}|_{\texttt {v}} + |{p}|_{\texttt {v}} = |{up}|_{\texttt {v}}$
.
$s = 1 + |{u}|_{\texttt {v}} + |{p}|_{\texttt {v}} = |{up}|_{\texttt {v}}$
. -
• Rule (@
 $^2_{{\tt p}}$
). Very similar to the previous case.
$^2_{{\tt p}}$
). Very similar to the previous case.
Lemma 3 (All normal forms are tightly typable). If
![]() $t \in {\tt no}_{\texttt{v}}$
, then there exists a tight type derivation
$t \in {\tt no}_{\texttt{v}}$
, then there exists a tight type derivation
![]() $\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
, such that
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
, such that
![]() $s = |t|_{\texttt{v}}$
.
$s = |t|_{\texttt{v}}$
.
Proof. We are going to split the original statement into the following two:
-
(1) If
 $t \in {\tt ne}_{{\tt v}}$
, then there exists a tight derivation
$t \in {\tt ne}_{{\tt v}}$
, then there exists a tight derivation
 $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; {\tt n}$
, such that
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; {\tt n}$
, such that
 $s = |{t}|_{\texttt {v}}$
.
$s = |{t}|_{\texttt {v}}$
. -
(2) If
 $t \in {\tt no}_{{\tt v}}$
, then there exists a tight derivation
$t \in {\tt no}_{{\tt v}}$
, then there exists a tight derivation
 $\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; {{\tt tt}_{\tt v}}$
, such that
$\Phi \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; {{\tt tt}_{\tt v}}$
, such that
 $s = |{t}|_{\texttt {v}}$
.
$s = |{t}|_{\texttt {v}}$
.
The proof follows by mutual induction over
![]() $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:
-
(1) Let
 $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:-
• Case
 $t = xp$
, such that
$t = xp$
, such that
 $p \in {\tt no}_{{\tt v}}$
. By applying the i.h. (2) to
$p \in {\tt no}_{{\tt v}}$
. By applying the i.h. (2) to
 $p$
, we have a tight derivation
$p$
, we have a tight derivation
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
, such that
 $|{p}|_{\texttt {v}} = s_p$
. Therefore, we can build
$|{p}|_{\texttt {v}} = s_p$
. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:
where
 $\Gamma = (x \;:\; [ {\tt v} ]) + \Gamma _p$
,
$\Gamma = (x \;:\; [ {\tt v} ]) + \Gamma _p$
,
 $b = b_p$
, and
$b = b_p$
, and
 $s = 1+s_p = 1+0+|{p}|_{\texttt {v}} = |{xp}|_{\texttt {v}}$
.
$s = 1+s_p = 1+0+|{p}|_{\texttt {v}} = |{xp}|_{\texttt {v}}$
. -
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
. By applying the i.h. (2) to
$p \in {\tt ne}_{{\tt v}}$
. By applying the i.h. (2) to
 $u$
and i.h. (1) to
$u$
and i.h. (1) to
 $p$
, there exists a tight derivation
$p$
, there exists a tight derivation
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; {{\tt tt}_{\tt v}}$
, such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; {{\tt tt}_{\tt v}}$
, such that
 $|{u}|_{\texttt {v}} = s_u$
, and a tight derivation
$|{u}|_{\texttt {v}} = s_u$
, and a tight derivation
 $\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\texttt{n}$
, such that
$\Phi _p \triangleright \,\Gamma _p \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\;\texttt{n}$
, such that
 $|{p}|_{\texttt {v}} = s_p$
. Therefore, we can build
$|{p}|_{\texttt {v}} = s_p$
. Therefore, we can build
 $\Phi$
as follows:where
$\Phi$
as follows:where \begin{equation*} \frac {\Phi _u \qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,1+s_u+s_p)}_{} up: {\tt n}}({\tt @}^2_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _u \qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,1+s_u+s_p)}_{} up: {\tt n}}({\tt @}^2_{{\tt p}})\end{equation*}
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $b = b_u+b_p$
, and
$b = b_u+b_p$
, and
 $s = 1+s_u+s_p = 1+|{u}|_{\texttt {v}}+|{p}|_{\texttt {v}} = |{up}|_{\texttt {v}}$
, by definition.
$s = 1+s_u+s_p = 1+|{u}|_{\texttt {v}}+|{p}|_{\texttt {v}} = |{up}|_{\texttt {v}}$
, by definition.
-
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
. By the i.h. (1) to
$p \in {\tt no}_{{\tt v}}$
. By the i.h. (1) to
 $u$
and i.h. (2) to
$u$
and i.h. (2) to
 $p$
, there exists a tight derivation
$p$
, there exists a tight derivation
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; {\tt n}$
such that
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; {\tt n}$
such that
 $|{u}|_{\texttt {v}} = s_u$
, and a tight derivation
$|{u}|_{\texttt {v}} = s_u$
, and a tight derivation
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: {{\tt tt}_{\tt v}}$
such that
 $|{p}|_{\texttt {v}} = s_p$
. Therefore, we can build
$|{p}|_{\texttt {v}} = s_p$
. Therefore, we can build
 $\Phi$
as follows:where
$\Phi$
as follows:where \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,1+s_u+s_p)}_{} up: {\tt n}}({\tt @}^1_{{\tt p}}) \end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,1+s_u+s_p)}_{} up: {\tt n}}({\tt @}^1_{{\tt p}}) \end{equation*}
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $b = b_u+b_p$
, and
$b = b_u+b_p$
, and
 $s = 1 + s_u + s_p = 1+|{u}|_{\texttt {v}}+|{p}|_{\texttt {v}} =|{up}|_{\texttt {v}}$
, by definition.
$s = 1 + s_u + s_p = 1+|{u}|_{\texttt {v}}+|{p}|_{\texttt {v}} =|{up}|_{\texttt {v}}$
, by definition.
-
-
(2) Let
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
• Case
 $t = x$
. Then, we can build
$t = x$
. Then, we can build
 $\Phi$
as follows:where
$\Phi$
as follows:where \begin{equation*} \frac {}{x \;:\; [ \sigma ] \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace x\;:\; \sigma }({\tt ax})\end{equation*}
\begin{equation*} \frac {}{x \;:\; [ \sigma ] \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace x\;:\; \sigma }({\tt ax})\end{equation*}
 $\sigma \in \overline {{\tt n}}$
,
$\sigma \in \overline {{\tt n}}$
,
 $\Gamma = \emptyset$
,
$\Gamma = \emptyset$
,
 $b = 0$
, and
$b = 0$
, and
 $s = 0 = |{x}|_{\texttt {v}}$
.
$s = 0 = |{x}|_{\texttt {v}}$
.
-
• Case
 $t = \lambda x.u$
. Then we can build
$t = \lambda x.u$
. Then we can build
 $\Phi$
as follows:where
$\Phi$
as follows:where \begin{equation*} \frac {}{\emptyset \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace \lambda x.u\;:\; {\tt a}}(\lambda _{\tt p})\end{equation*}
\begin{equation*} \frac {}{\emptyset \negmedspace \overset{(0,0)} {\vdash_{}}\negmedspace \lambda x.u\;:\; {\tt a}}(\lambda _{\tt p})\end{equation*}
 $\Gamma = \emptyset$
,
$\Gamma = \emptyset$
,
 $b = 0$
, and
$b = 0$
, and
 $s = 0 = |{\lambda x.u}|_{\texttt {v}}$
.
$s = 0 = |{\lambda x.u}|_{\texttt {v}}$
.
-
• Case
 $\neg {\tt val}(t)$
. Then,
$\neg {\tt val}(t)$
. Then,
 $t \in {\tt ne}_{{\tt v}}$
, by definition. Therefore, there exists a tight derivation
$t \in {\tt ne}_{{\tt v}}$
, by definition. Therefore, there exists a tight derivation
 $\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; {\tt n}$
such that
$\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; {\tt n}$
such that
 $s = |{t}|_{\texttt {v}}$
, by the i.h. (1).
$s = |{t}|_{\texttt {v}}$
, by the i.h. (1).
-
Lemma 29 (Multi-types can split and merge). Let
![]() $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
![]() $b = +_{i \in I} b_i$
, and
$b = +_{i \in I} b_i$
, and
![]() $s = +_{i \in I} s_i$
. Then,
$s = +_{i \in I} s_i$
. Then,
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}$
iff (
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}$
iff (
![]() $\Phi ^i_t \triangleright \, \Gamma _i \negmedspace \overset{(b_i,s_i)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}_i)_{i \in I}$
.
$\Phi ^i_t \triangleright \, \Gamma _i \negmedspace \overset{(b_i,s_i)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}_i)_{i \in I}$
.
Proof. Very similar to the proof for Weak Open CBN.
Lemma 30 (Substitution). Let
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
and
![]() $\Phi _v \triangleright \, \Gamma _v \negmedspace \overset {(b_v,s_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, then there exists
$\Phi _v \triangleright \, \Gamma _v \negmedspace \overset {(b_v,s_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, then there exists
![]() $\Phi _{t \{x \setminus v\}} \triangleright \, \Gamma _t + \Gamma _v \negmedspace \overset {(b_t+b_v,s_t+s_v)}{\vdash _{{\tt v}}}\negmedspace t \{x \setminus v\}\;:\; \tau$
.
$\Phi _{t \{x \setminus v\}} \triangleright \, \Gamma _t + \Gamma _v \negmedspace \overset {(b_t+b_v,s_t+s_v)}{\vdash _{{\tt v}}}\negmedspace t \{x \setminus v\}\;:\; \tau$
.
Proof.
The proof follows by induction over
![]() $\Phi _t$
, depending on the last rule of
$\Phi _t$
, depending on the last rule of
![]() $\Phi _t$
:
$\Phi _t$
:
-
• Rule (ax). Then,
 $t = y$
. There are two cases:
$t = y$
. There are two cases:-
–
 $y = x$
. Then,
$y = x$
. Then,
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\tau = \mathscr{M}$
,
$\tau = \mathscr{M}$
,
 $t \{x \setminus v\} = v$
,
$t \{x \setminus v\} = v$
,
 $b_t = 0$
, and
$b_t = 0$
, and
 $s_t = 0$
. So we can take
$s_t = 0$
. So we can take
 $\Phi _{t \{x \setminus v\}} = \Phi _v$
and conclude with
$\Phi _{t \{x \setminus v\}} = \Phi _v$
and conclude with
 $\Gamma _t + \Gamma _v = \Gamma _v$
,
$\Gamma _t + \Gamma _v = \Gamma _v$
,
 $b_t + b_v = b_v$
, and
$b_t + b_v = b_v$
, and
 $s_t + s_v = s_v$
.
$s_t + s_v = s_v$
. -
–
 $y \neq x$
. Then
$y \neq x$
. Then
 $\mathscr{M} = [ \, ]$
,
$\mathscr{M} = [ \, ]$
,
 $\Gamma _v = \emptyset$
,
$\Gamma _v = \emptyset$
,
 $t \{x \setminus v\} = t$
,
$t \{x \setminus v\} = t$
,
 $b_v = 0$
, and
$b_v = 0$
, and
 $s_v = 0$
. So we can take
$s_v = 0$
. So we can take
 $\Phi _{t \{x \setminus v\}} = \Phi _t$
and conclude with
$\Phi _{t \{x \setminus v\}} = \Phi _t$
and conclude with
 $\Gamma _t + \Gamma _v = \Gamma _t$
,
$\Gamma _t + \Gamma _v = \Gamma _t$
,
 $b_t + b_v = b_t$
, and
$b_t + b_v = b_t$
, and
 $s_t + s_v = s_t$
.
$s_t + s_v = s_t$
.
-
-
• Rule (
 $\lambda$
). Then,
$\lambda$
). Then,
 $t = \lambda y.u$
and
$t = \lambda y.u$
and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _u \triangleright \, \Gamma _u;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \tau '$
, such that
$\Phi _u \triangleright \, \Gamma _u;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \tau '$
, such that
 $\Gamma _t = (\Gamma _u \setminus y)$
(by
$\Gamma _t = (\Gamma _u \setminus y)$
(by
 $\alpha$
-conversion), and
$\alpha$
-conversion), and
 $\tau = \Gamma _u(y) \rightarrow \tau '$
. By applying the i.h. to
$\tau = \Gamma _u(y) \rightarrow \tau '$
. By applying the i.h. to
 $\Phi _u$
, there exists
$\Phi _u$
, there exists
 $\Phi _{u \{x \setminus v\}} \triangleright \Gamma _u + \Gamma _v \negmedspace \overset{(b_t + b_v, s_t + s_v)} {\vdash_{\texttt{v}}}\negmedspace u\{x \setminus v\} \;:\; \tau$
. Therefore, we can build
$\Phi _{u \{x \setminus v\}} \triangleright \Gamma _u + \Gamma _v \negmedspace \overset{(b_t + b_v, s_t + s_v)} {\vdash_{\texttt{v}}}\negmedspace u\{x \setminus v\} \;:\; \tau$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {\Phi _{u \{x \setminus v\}}}{(\Gamma _u + \Gamma _v) \setminus y \mathop {\vdash }\limits ^{(b_t + b_v, s_t + s_v)}_{} (\lambda y.u) \{x \setminus v\}\;:\; \Gamma _u(y) \rightarrow \tau '}(\lambda )\end{equation*}
\begin{equation*} \frac {\Phi _{u \{x \setminus v\}}}{(\Gamma _u + \Gamma _v) \setminus y \mathop {\vdash }\limits ^{(b_t + b_v, s_t + s_v)}_{} (\lambda y.u) \{x \setminus v\}\;:\; \Gamma _u(y) \rightarrow \tau '}(\lambda )\end{equation*}
 $(\Gamma _u + \Gamma _v) \setminus y = (\Gamma _u \setminus y) + \Gamma _v = \Gamma _t + \Gamma _v$
, since we may assume (by
$(\Gamma _u + \Gamma _v) \setminus y = (\Gamma _u \setminus y) + \Gamma _v = \Gamma _t + \Gamma _v$
, since we may assume (by
 $\alpha$
-conversion) that
$\alpha$
-conversion) that
 $y \not \in {\tt dom}(\Gamma _v)$
.
$y \not \in {\tt dom}(\Gamma _v)$
.
-
• Rule (
 $\tt @$
). Then,
$\tt @$
). Then,
 $t = up$
and
$t = up$
and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _u \triangleright \, \Gamma _u;\; x \;:\; \mathscr{M}_1 \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _u \triangleright \, \Gamma _u;\; x \;:\; \mathscr{M}_1 \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _p \triangleright \Gamma _p;\; x \;:\; \mathscr{M}_{2} \vdash^{(b_p,s_p)}_{\texttt{v}} p:\mathscr{M\;}'$
, such that
$\Phi _p \triangleright \Gamma _p;\; x \;:\; \mathscr{M}_{2} \vdash^{(b_p,s_p)}_{\texttt{v}} p:\mathscr{M\;}'$
, such that
 $\Gamma _t = (\Gamma _u + \Gamma _p)$
,
$\Gamma _t = (\Gamma _u + \Gamma _p)$
,
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b_t = 1 + b_u + b_p$
, and
$b_t = 1 + b_u + b_p$
, and
 $s_t = s_u + s_p$
. By Lemma 29, there exist
$s_t = s_u + s_p$
. By Lemma 29, there exist
 $(\Phi ^i_v \triangleright \, \Gamma ^i_v \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_i)_{i \in \{1,2\}}$
, such that
$(\Phi ^i_v \triangleright \, \Gamma ^i_v \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_i)_{i \in \{1,2\}}$
, such that
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b_1 + b_2$
, and
$b_v = b_1 + b_2$
, and
 $s_v = s_1 + s_2$
. By applying the i.h. to
$s_v = s_1 + s_2$
. By applying the i.h. to
 $\Phi _u$
and
$\Phi _u$
and
 $\Phi _p$
, we know there exist
$\Phi _p$
, we know there exist
 $\Phi _{u \{x \setminus v\}} \triangleright \Gamma + \Gamma ^1_v \negmedspace \overset{(b_u+b_1, s_u+s_1)} {\vdash_{\texttt{v}}}\negmedspace u \{x \setminus v\} : \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _{u \{x \setminus v\}} \triangleright \Gamma + \Gamma ^1_v \negmedspace \overset{(b_u+b_1, s_u+s_1)} {\vdash_{\texttt{v}}}\negmedspace u \{x \setminus v\} : \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _{p \{x \setminus v\}} \triangleright \Delta + \Gamma ^2_v \negmedspace \overset{(b_p + b_2, s_p + s_2)} {\vdash_{\texttt{v}}}\negmedspace p\{x \setminus v\}\;:\; \mathscr{M\;}'$
, respectively. Therefore, we can build
$\Phi _{p \{x \setminus v\}} \triangleright \Delta + \Gamma ^2_v \negmedspace \overset{(b_p + b_2, s_p + s_2)} {\vdash_{\texttt{v}}}\negmedspace p\{x \setminus v\}\;:\; \mathscr{M\;}'$
, respectively. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {\Phi _{u \{x \setminus v\}}\qquad \Phi _{p \{x \setminus v\}}}{(\Gamma + \Delta ) + (\Gamma ^1_v + \Gamma ^2_v) \mathop {\vdash }\limits ^{(1+b_u+b_p+b_1+b_2, s_u + s_p + s_1 + s_2)} (u p) \{x \setminus v\}\;:\; \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _{u \{x \setminus v\}}\qquad \Phi _{p \{x \setminus v\}}}{(\Gamma + \Delta ) + (\Gamma ^1_v + \Gamma ^2_v) \mathop {\vdash }\limits ^{(1+b_u+b_p+b_1+b_2, s_u + s_p + s_1 + s_2)} (u p) \{x \setminus v\}\;:\; \tau }({\tt @})\end{equation*}
 $(\Gamma + \Delta ) + (\Gamma ^1_v + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
$(\Gamma + \Delta ) + (\Gamma ^1_v + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
 $1 + b_u + b_p + b_1 + b_2 = b_t + b_v$
, and
$1 + b_u + b_p + b_1 + b_2 = b_t + b_v$
, and
 $s_u + s_p + s_1 + s_2 = s_t + s_v$
.
$s_u + s_p + s_1 + s_2 = s_t + s_v$
.
-
• Rule (
 $\tt m$
). Then,
$\tt m$
). Then,
 $t = w$
and
$t = w$
and
 $\Phi$
has premises
$\Phi$
has premises
 $(\Phi ^i_w \triangleright \, \Gamma _i;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt v}}}\negmedspace w: \sigma _i)_{i \in I}$
, such that
$(\Phi ^i_w \triangleright \, \Gamma _i;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt v}}}\negmedspace w: \sigma _i)_{i \in I}$
, such that
 $\tau = [ \sigma _i ]_{i \in I}$
,
$\tau = [ \sigma _i ]_{i \in I}$
,
 $\Gamma _t = +_{i \in I} \Gamma _i$
,
$\Gamma _t = +_{i \in I} \Gamma _i$
,
 $b_t = +_{i \in I} b_i$
, and
$b_t = +_{i \in I} b_i$
, and
 $s_t = +_{i \in I} s_i$
. By Lemma 29, there exists
$s_t = +_{i \in I} s_i$
. By Lemma 29, there exists
 $(\Phi ^i_v \triangleright \Gamma ^i_v \negmedspace \overset{(b^i_v, s^i_v)} {\vdash_{\texttt{v}}}\negmedspace v\;:\;\mathscr{M}_{i})_{i \in I}$
, such that
$(\Phi ^i_v \triangleright \Gamma ^i_v \negmedspace \overset{(b^i_v, s^i_v)} {\vdash_{\texttt{v}}}\negmedspace v\;:\;\mathscr{M}_{i})_{i \in I}$
, such that
 $\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
$\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
 $b_v = +_{i \in I} b^i_v$
, and
$b_v = +_{i \in I} b^i_v$
, and
 $s_v = +_{i \in I} s^i_v$
. By applying the i.h. to each
$s_v = +_{i \in I} s^i_v$
. By applying the i.h. to each
 $\Phi ^i_w$
, there exist
$\Phi ^i_w$
, there exist
 $(\Phi ^i_{w \{x \setminus v\}} \triangleright \, \Gamma _i + \Gamma ^i_v \negmedspace \overset {(b_i + b^i_v, s_i + s^i_v)}{\vdash _{{\tt v}}}\negmedspace w \{x \setminus v\}\;:\; \sigma _i)_{i \in I}$
. Therefore, we can build
$(\Phi ^i_{w \{x \setminus v\}} \triangleright \, \Gamma _i + \Gamma ^i_v \negmedspace \overset {(b_i + b^i_v, s_i + s^i_v)}{\vdash _{{\tt v}}}\negmedspace w \{x \setminus v\}\;:\; \sigma _i)_{i \in I}$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {(\Phi ^i_{w \{x \setminus v\}})_{i \in I}}{+_{i \in I} (\Gamma _i + \Gamma ^i_v) \mathop {\vdash }\limits ^{(+_{i \in I} (b_i + b^i_v), +_{i \in I} (s_i + s^i_v))}_{} w \{x \setminus v\}\;:\; [ \sigma _i ]_{i \in I}}({\tt m})\end{equation*}
\begin{equation*} \frac {(\Phi ^i_{w \{x \setminus v\}})_{i \in I}}{+_{i \in I} (\Gamma _i + \Gamma ^i_v) \mathop {\vdash }\limits ^{(+_{i \in I} (b_i + b^i_v), +_{i \in I} (s_i + s^i_v))}_{} w \{x \setminus v\}\;:\; [ \sigma _i ]_{i \in I}}({\tt m})\end{equation*}
 $+_{i \in I} (\Gamma _i + \Gamma ^i_v) = +_{i \in I} \Gamma _i +_{i \in I} \Gamma ^i_v = \Gamma _t + \Gamma _v$
,
$+_{i \in I} (\Gamma _i + \Gamma ^i_v) = +_{i \in I} \Gamma _i +_{i \in I} \Gamma ^i_v = \Gamma _t + \Gamma _v$
,
 $+_{i \in I} (b_i + b^i_v) = +_{i \in I} b_i +_{i \in I} b^i_v = b_t + b_v$
, and
$+_{i \in I} (b_i + b^i_v) = +_{i \in I} b_i +_{i \in I} b^i_v = b_t + b_v$
, and
 $+_{i \in I} (s_i + s^i_v) = +_{i \in I} s_i +_{i \in I} s^i_v = s_t + s_v$
.
$+_{i \in I} (s_i + s^i_v) = +_{i \in I} s_i +_{i \in I} s^i_v = s_t + s_v$
.
-
• Rule (
 $\lambda _{\tt p}$
). Then
$\lambda _{\tt p}$
). Then
 $t = \lambda y.u$
, and
$t = \lambda y.u$
, and
 $\Phi _t \triangleright \, \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace \lambda y.u\;:\; {\tt a}$
, such that
$\Phi _t \triangleright \, \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace \lambda y.u\;:\; {\tt a}$
, such that
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\tau = {\tt a}$
,
$\tau = {\tt a}$
,
 $b_t = 0$
and
$b_t = 0$
and
 $s_t = 0$
. Therefore,
$s_t = 0$
. Therefore,
 $\mathscr{M} = [ \, ]$
,
$\mathscr{M} = [ \, ]$
,
 $\Gamma _v = \emptyset$
,
$\Gamma _v = \emptyset$
,
 $b_v = 0$
, and
$b_v = 0$
, and
 $s_v = 0$
. Also, notice that
$s_v = 0$
. Also, notice that
 $t \{x \setminus v\} = \lambda y.(u \{x \setminus v\}) = (\lambda y.u) \{x \setminus v\}$
. Therefore, we can build
$t \{x \setminus v\} = \lambda y.(u \{x \setminus v\}) = (\lambda y.u) \{x \setminus v\}$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*}\frac {}{\emptyset \mathop {\vdash }\limits ^{(0,0)}_{} (\lambda y.u) \{x \setminus v\}\;:\; {\tt a}}(\lambda _{\tt p})\end{equation*}
\begin{equation*}\frac {}{\emptyset \mathop {\vdash }\limits ^{(0,0)}_{} (\lambda y.u) \{x \setminus v\}\;:\; {\tt a}}(\lambda _{\tt p})\end{equation*}
 $\emptyset = \Gamma _t + \Gamma _v$
,
$\emptyset = \Gamma _t + \Gamma _v$
,
 $0 = b_t + b_v$
, and
$0 = b_t + b_v$
, and
 $0 = s_t + s_v$
.
$0 = s_t + s_v$
.
-
• Case
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). Very similar to the case where
$^2_{{\tt p}}$
). Very similar to the case where
 $\Phi _t$
ends with rule (@).
$\Phi _t$
ends with rule (@).
Lemma 4 (Quantitative subject reduction). Let
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
be a tight type derivation. If
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
be a tight type derivation. If
![]() $t \rightarrow t'$
, then there exists
$t \rightarrow t'$
, then there exists
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
.
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
.
Proof. We prove a stronger version of the statement that allows us to reason inductively:
Let
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
, such that
$\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
, such that
![]() $\Gamma$
is tight, and either
$\Gamma$
is tight, and either
![]() $\tau$
is tight or
$\tau$
is tight or
![]() $\neg {\tt val}(t)$
. If
$\neg {\tt val}(t)$
. If
![]() $t {\rightarrow }_{\texttt {v}} t'$
, then there exists
$t {\rightarrow }_{\texttt {v}} t'$
, then there exists
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
.
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b-1,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
.
The proof follows by induction over
![]() $t {\rightarrow }_{\texttt {v}} t'$
:
$t {\rightarrow }_{\texttt {v}} t'$
:
-
• Case
 $t = (\lambda x.u) v {\rightarrow }_{\texttt {v}} u \{x \setminus v\} = t'$
. Then,
$t = (\lambda x.u) v {\rightarrow }_{\texttt {v}} u \{x \setminus v\} = t'$
. Then,
 $\Phi _t$
must end with rule (@), (@
$\Phi _t$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
). Let us first assume that
$^2_{{\tt p}}$
). Let us first assume that
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _{\lambda x.u}$
and
$\Phi _{\lambda x.u}$
and
 $\Phi _v$
for
$\Phi _v$
for
 $\lambda x.u$
and
$\lambda x.u$
and
 $v$
, respectively. Moreover,
$v$
, respectively. Moreover,
 $\Phi _{\lambda x.u}$
must conclude with type
$\Phi _{\lambda x.u}$
must conclude with type
 $\overline {{\tt a}}$
. However, this is not possible according to Lemma 27. Now, let us assume that
$\overline {{\tt a}}$
. However, this is not possible according to Lemma 27. Now, let us assume that
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $^2_{{\tt p}}$
). Again,
$^2_{{\tt p}}$
). Again,
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _{\lambda x.u}$
and
$\Phi _{\lambda x.u}$
and
 $\Phi _v$
for
$\Phi _v$
for
 $\lambda x.u$
and
$\lambda x.u$
and
 $v$
, respectively. Moreover,
$v$
, respectively. Moreover,
 $\Phi _v$
must conclude with type
$\Phi _v$
must conclude with type
 $\tt n$
. However, this is not possible by Lemma 26. Finally, let us assume that
$\tt n$
. However, this is not possible by Lemma 26. Finally, let us assume that
 $\Phi _t$
ends with rule (@). Then,
$\Phi _t$
ends with rule (@). Then,
 $\Phi _t$
has the following form:
$\Phi _t$
has the following form:
such that
 $\Gamma = \Gamma _u + \Gamma _v$
is tight,
$\Gamma = \Gamma _u + \Gamma _v$
is tight,
 $\tau \in {{\tt tt}_{\tt v}}$
,
$\tau \in {{\tt tt}_{\tt v}}$
,
 $b = 1 + b_u + b_v$
, and
$b = 1 + b_u + b_v$
, and
 $s = s_u + s_v$
. By Lemma 30, there exists
$s = s_u + s_v$
. By Lemma 30, there exists
 $\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _u + \Gamma _v \negmedspace \overset {(b_u+b_v,s_u+s_v)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \tau$
. Therefore, we can take
$\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _u + \Gamma _v \negmedspace \overset {(b_u+b_v,s_u+s_v)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \tau$
. Therefore, we can take
 $\Phi _{t'} = \Phi _{u \{x \setminus v\}}$
and conclude with
$\Phi _{t'} = \Phi _{u \{x \setminus v\}}$
and conclude with
 $b - 1 = b_u + b_v$
.
$b - 1 = b_u + b_v$
. -
• Case
 $t = up {\rightarrow }_{\texttt {v}} u'p = t'$
, such that
$t = up {\rightarrow }_{\texttt {v}} u'p = t'$
, such that
 $u {\rightarrow }_{\texttt {v}} u'$
. Then
$u {\rightarrow }_{\texttt {v}} u'$
. Then
 $\Phi _t$
must either end with (@), (@
$\Phi _t$
must either end with (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _t$
ends with rule (@). Then,
$\Phi _t$
ends with rule (@). Then,
 $\Phi _t$
has the following form:such that
$\Phi _t$
has the following form:such that \begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau \qquad \Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 +b_u+b_p,s_u+s_p)}_{} up: \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau \qquad \Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 +b_u+b_p,s_u+s_p)}_{} up: \tau }({\tt @})\end{equation*}
 $\Gamma = \Gamma _u + \Gamma _p$
is tight,
$\Gamma = \Gamma _u + \Gamma _p$
is tight,
 $\tau \in {{\tt tt}_{\tt v}}$
,
$\tau \in {{\tt tt}_{\tt v}}$
,
 $b = 1+b_u + b_p$
, and
$b = 1+b_u + b_p$
, and
 $s = s_u + s_p$
. Moreover,
$s = s_u + s_p$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. Also, notice that
$\Gamma _p$
are tight. Also, notice that
 $\neg {\tt val}(u)$
, since
$\neg {\tt val}(u)$
, since
 $u {\rightarrow }_{\texttt {v}} u'$
holds. Therefore, by applying the i.h. to
$u {\rightarrow }_{\texttt {v}} u'$
holds. Therefore, by applying the i.h. to
 $\Phi _u$
, there exists
$\Phi _u$
, there exists
 $\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u-1, s_u)}{\vdash _{{\tt v}}}\negmedspace u': \mathscr{M} \rightarrow \tau$
. We can then build
$\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u-1, s_u)}{\vdash _{{\tt v}}}\negmedspace u': \mathscr{M} \rightarrow \tau$
. We can then build
 $\Phi _{t'}$
as follows:Thus, we can conclude with
$\Phi _{t'}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{u'}\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,s_u+s_p)}_{} u'p: \tau }({\tt @}) \end{equation*}
\begin{equation*} \frac {\Phi _{u'}\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,s_u+s_p)}_{} u'p: \tau }({\tt @}) \end{equation*}
 $b - 1= b_u + b_p$
.
$b - 1= b_u + b_p$
.
-
– Case
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases are very similar to the previous case.
$^2_{{\tt p}}$
). These cases are very similar to the previous case.
-
-
• Case
 $t = up {\rightarrow }_{\texttt {v}} up' = t'$
, such that
$t = up {\rightarrow }_{\texttt {v}} up' = t'$
, such that
 $u \not {\!\rightarrow }_{\texttt {v}}$
and
$u \not {\!\rightarrow }_{\texttt {v}}$
and
 $p {\rightarrow }_{\texttt {v}} p'$
. Then,
$p {\rightarrow }_{\texttt {v}} p'$
. Then,
 $\Phi _t$
must end with rule (@), (@
$\Phi _t$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _t$
ends with rule (@). Then,
$\Phi _t$
ends with rule (@). Then,
 $\Phi _t$
has the following form:such that
$\Phi _t$
has the following form:such that \begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau \qquad \Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1+b_u+b_p,s_u+s_p)}_{} up: \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u,s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M} \rightarrow \tau \qquad \Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p,s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1+b_u+b_p,s_u+s_p)}_{} up: \tau }({\tt @})\end{equation*}
 $\Gamma = \Gamma _u + \Gamma _p$
is tight,
$\Gamma = \Gamma _u + \Gamma _p$
is tight,
 $\tau \in {{\tt tt}_{\tt v}}$
,
$\tau \in {{\tt tt}_{\tt v}}$
,
 $b = 1 + b_u + b_p$
, and
$b = 1 + b_u + b_p$
, and
 $s = s_u + s_p$
. Moreover,
$s = s_u + s_p$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. Also, notice that
$\Gamma _p$
are tight. Also, notice that
 $\neg {\tt val}(p)$
, since
$\neg {\tt val}(p)$
, since
 $p {\rightarrow }_{\texttt {v}} p'$
holds. Therefore, by applying the i.h. to
$p {\rightarrow }_{\texttt {v}} p'$
holds. Therefore, by applying the i.h. to
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _{p'} \triangleright \, \Gamma _p \negmedspace \overset {(b_p-1, s_p)}{\vdash _{{\tt v}}}\negmedspace p': \mathscr{M}$
. Therefore, we can build
$\Phi _{p'} \triangleright \, \Gamma _p \negmedspace \overset {(b_p-1, s_p)}{\vdash _{{\tt v}}}\negmedspace p': \mathscr{M}$
. Therefore, we can build
 $\Phi _{t'}$
as follows:Thus, we can conclude with
$\Phi _{t'}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _u \qquad \Phi _{p'}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,s_u+s_p)}_{} up': \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u \qquad \Phi _{p'}}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(b_u+b_p,s_u+s_p)}_{} up': \tau }({\tt @})\end{equation*}
 $b - 1 = b_u + b_p$
.
$b - 1 = b_u + b_p$
.
-
– Case
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases are very similar to the previous case.
$^2_{{\tt p}}$
). These cases are very similar to the previous case.
-
Theorem 1 (Quantitative soundness). If
![]() $\Phi \triangleright \, \Gamma\negmedspace \overset{{(b,s)}}{\vdash_{{\tt v}}}\negmedspace t\;:\; \tau$
is a tight type derivation, then there exists
$\Phi \triangleright \, \Gamma\negmedspace \overset{{(b,s)}}{\vdash_{{\tt v}}}\negmedspace t\;:\; \tau$
is a tight type derivation, then there exists
![]() $u \in {\tt no}$
such that
$u \in {\tt no}$
such that
![]() $t \twoheadrightarrow ^b_{\texttt{v}} u$
with
$t \twoheadrightarrow ^b_{\texttt{v}} u$
with
![]() $|u|_{\texttt{v}} = s$
.
$|u|_{\texttt{v}} = s$
.
Proof.
The proof follows by induction on
![]() $b$
:
$b$
:
-
• Case
 $b = 0$
. Then
$b = 0$
. Then
 $t \in {\tt no}_{\texttt{v}}$
by Lemma1. Moreover,
$t \in {\tt no}_{\texttt{v}}$
by Lemma1. Moreover,
 $s = |t|_{\texttt{v}}$
by Lemma2. So we can conclude with
$s = |t|_{\texttt{v}}$
by Lemma2. So we can conclude with
 $u = t$
.
$u = t$
. -
• Case
 $b \gt 0$
. Then
$b \gt 0$
. Then
 $t \not \in {\tt no}_{\texttt{v}}$
by Lemma1. Therefore, by Proposition2, there exists
$t \not \in {\tt no}_{\texttt{v}}$
by Lemma1. Therefore, by Proposition2, there exists
 $t'$
such that
$t'$
such that
 $t \rightarrow t'$
. Moreover, this derivation is also tight. By Lemma4, there exists
$t \rightarrow t'$
. Moreover, this derivation is also tight. By Lemma4, there exists
 $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, s)} {\vdash_{\texttt{v}}}\negmedspace t': \tau$
. By the i.h., there exists
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, s)} {\vdash_{\texttt{v}}}\negmedspace t': \tau$
. By the i.h., there exists
 $u \in {\tt no}$
, such that
$u \in {\tt no}$
, such that
 $t' \twoheadrightarrow ^{b-1}_{\texttt{v}} u$
and
$t' \twoheadrightarrow ^{b-1}_{\texttt{v}} u$
and
 $s = |u|_{\texttt{v}}$
. We can then conclude with
$s = |u|_{\texttt{v}}$
. We can then conclude with
 $t \rightarrow t' \twoheadrightarrow ^{b-1}_{\texttt{v}} u$
, which means that
$t \rightarrow t' \twoheadrightarrow ^{b-1}_{\texttt{v}} u$
, which means that
 $t \twoheadrightarrow ^b_{\texttt{v}} u$
, as expected.
$t \twoheadrightarrow ^b_{\texttt{v}} u$
, as expected.
Lemma 31 (Anti-substitution). Let
![]() $\Phi _{t \{x \setminus v\}} \triangleright \, \Gamma _{t \{x \setminus v\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t \{x \setminus v\}\;:\; \tau$
. Then, there exist
$\Phi _{t \{x \setminus v\}} \triangleright \, \Gamma _{t \{x \setminus v\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t \{x \setminus v\}\;:\; \tau$
. Then, there exist
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_t,s_t)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
and
![]() $\Phi _v \triangleright \, \Gamma _v \negmedspace \overset {(b_v,s_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, such that
$\Phi _v \triangleright \, \Gamma _v \negmedspace \overset {(b_v,s_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, such that
![]() $\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
![]() $b = b_t + b_v$
, and
$b = b_t + b_v$
, and
![]() $s = s_t + s_v$
.
$s = s_t + s_v$
.
Proof.
The proof follows by induction over
![]() $\Phi _{t \{x \setminus v\}}$
:
$\Phi _{t \{x \setminus v\}}$
:
Let us assume
![]() $t = x$
. Then,
$t = x$
. Then,
![]() $t \{x \setminus v\} = v$
. Therefore,
$t \{x \setminus v\} = v$
. Therefore,
![]() $\tau \neq {\tt n}$
, by Lemma 26. Now, we have to consider two cases: either
$\tau \neq {\tt n}$
, by Lemma 26. Now, we have to consider two cases: either
![]() $\tau = [ \sigma _i ]_{i \in I}$
or
$\tau = [ \sigma _i ]_{i \in I}$
or
![]() $\tau$
is not a multi-type. If
$\tau$
is not a multi-type. If
![]() $\tau = [ \sigma _i ]_{i \in I}$
, we can take
$\tau = [ \sigma _i ]_{i \in I}$
, we can take
![]() $\Phi _v = \Phi _{t \{x \setminus v\}}$
and
$\Phi _v = \Phi _{t \{x \setminus v\}}$
and
![]() $\mathscr{M} = [ \sigma _i ]_{i \in I}$
, such that
$\mathscr{M} = [ \sigma _i ]_{i \in I}$
, such that
![]() $\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
$\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
![]() $b_v = b$
,
$b_v = b$
,
![]() $s_v = s$
, and build
$s_v = s$
, and build
![]() $\Phi _t$
as follows:
$\Phi _t$
as follows:
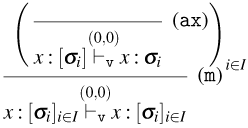
such that
![]() $\Gamma _t = \emptyset$
, and
$\Gamma _t = \emptyset$
, and
![]() $b_t = s_t = 0$
. If
$b_t = s_t = 0$
. If
![]() $\tau$
is not a multi-type, then we let
$\tau$
is not a multi-type, then we let
![]() $\mathscr{M} =[ \tau ]$
, and we build
$\mathscr{M} =[ \tau ]$
, and we build
![]() $\Phi _v \triangleright \, \Gamma _{t \{x \setminus v\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace v: [ \tau ]$
, such that
$\Phi _v \triangleright \, \Gamma _{t \{x \setminus v\}} \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace v: [ \tau ]$
, such that
![]() $\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
$\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
![]() $b_v = b$
, and
$b_v = b$
, and
![]() $s_v = s$
, from
$s_v = s$
, from
![]() $\Phi _{t \{x \setminus v\}}$
followed by rule (m), and
$\Phi _{t \{x \setminus v\}}$
followed by rule (m), and
![]() $\Phi _t \triangleright x\;:\;[\tau] \negmedspace \overset{(0,0)} {\vdash_{\texttt{v}}}\negmedspace x\;:\;\tau $
, such that
$\Phi _t \triangleright x\;:\;[\tau] \negmedspace \overset{(0,0)} {\vdash_{\texttt{v}}}\negmedspace x\;:\;\tau $
, such that
![]() $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
![]() $b_t = s_t = 0$
, by using rule (ax). In both cases, we can conclude with
$b_t = s_t = 0$
, by using rule (ax). In both cases, we can conclude with
![]() $\Gamma _{t \{x \setminus v\}} = \Gamma _v = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _v = \Gamma _t + \Gamma _v$
,
![]() $b = b_v = b_t + b_v$
, and
$b = b_v = b_t + b_v$
, and
![]() $s = s_v = s_t + s_v$
. From now on, we are going to assume
$s = s_v = s_t + s_v$
. From now on, we are going to assume
![]() $t \neq x$
:
$t \neq x$
:
-
• Rule (ax). Then,
 $t = y$
,
$t = y$
,
 $t \{x \setminus v\} = y$
, and
$t \{x \setminus v\} = y$
, and
 $\mathscr{M} = [ \, ]$
. Therefore, we can pick
$\mathscr{M} = [ \, ]$
. Therefore, we can pick
 $\Phi _t = \Phi _{t \{x \setminus v\}}$
, such that
$\Phi _t = \Phi _{t \{x \setminus v\}}$
, such that
 $\Gamma _t = \Gamma _{t \{x \setminus v\}}$
,
$\Gamma _t = \Gamma _{t \{x \setminus v\}}$
,
 $b_t = b$
, and
$b_t = b$
, and
 $s_t = s$
, and build
$s_t = s$
, and build
 $\Phi _v \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace v: [ \, ]$
, such that
$\Phi _v \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace v: [ \, ]$
, such that
 $\Gamma _v = \emptyset$
and
$\Gamma _v = \emptyset$
and
 $b_v = s_v = 0$
, by using rule (m) with no premises. Thus, we can conclude with
$b_v = s_v = 0$
, by using rule (m) with no premises. Thus, we can conclude with
 $ \Gamma _{t \{x \setminus v\}} = \Gamma _t = \Gamma _t + \Gamma _v$
, and
$ \Gamma _{t \{x \setminus v\}} = \Gamma _t = \Gamma _t + \Gamma _v$
, and
 $b = b_t = b_t + b_v$
, and
$b = b_t = b_t + b_v$
, and
 $s = s_t = s_t + s_v$
.
$s = s_t = s_t + s_v$
. -
• Rule (
 $\lambda$
). Then,
$\lambda$
). Then,
 $t = \lambda y.u$
and
$t = \lambda y.u$
and
 $t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Therefore,
$t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Therefore,
 $\Phi _{t \{x \setminus v\}}$
has one premise
$\Phi _{t \{x \setminus v\}}$
has one premise
 $\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _{t \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}' \negmedspace \overset {(b, s)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \tau '$
, such that
$\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _{t \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}' \negmedspace \overset {(b, s)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \tau '$
, such that
 $\tau = \mathscr{M\;}' \rightarrow \tau '$
. By applying the i.h. to
$\tau = \mathscr{M\;}' \rightarrow \tau '$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
, there exist
$\Phi _{u \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright (\Gamma _u;\; y\;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M} \negmedspace \overset{(b_u, s_u)} {\vdash_{\texttt{v}}}\negmedspace u\;:\; \tau'$
and
$\Phi _u \triangleright (\Gamma _u;\; y\;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M} \negmedspace \overset{(b_u, s_u)} {\vdash_{\texttt{v}}}\negmedspace u\;:\; \tau'$
and
 $\Phi _v \triangleright \Gamma _v \negmedspace \overset{(b_v, s_v)} {\vdash_{\texttt{v}}}\negmedspace\;:\; \mathscr{M}$
, such that
$\Phi _v \triangleright \Gamma _v \negmedspace \overset{(b_v, s_v)} {\vdash_{\texttt{v}}}\negmedspace\;:\; \mathscr{M}$
, such that
 $(\Gamma _{t \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}') = (\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v$
,
$(\Gamma _{t \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}') = (\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v$
,
 $b = b_u + b_v$
, and
$b = b_u + b_v$
, and
 $s = s_u + s_v$
. Notice that
$s = s_u + s_v$
. Notice that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _u + \Gamma _v$
, since we may assume (by Proposition 8), that
$\Gamma _{t \{x \setminus v\}} = \Gamma _u + \Gamma _v$
, since we may assume (by Proposition 8), that
 $y \not \in {\tt dom}(\Gamma _v)$
. Therefore, we can build
$y \not \in {\tt dom}(\Gamma _v)$
. Therefore, we can build
 $\Phi _t$
as follows:such that
$\Phi _t$
as follows:such that \begin{equation*} \frac {\Phi _u}{\Gamma _u;\; x \;:\; \mathscr{M} \mathop {\vdash _{\tt v}}\limits ^{(b_u, s_u)} \lambda y.u\;:\; \mathscr{M\;}' \rightarrow \tau '}(\lambda )\end{equation*}
\begin{equation*} \frac {\Phi _u}{\Gamma _u;\; x \;:\; \mathscr{M} \mathop {\vdash _{\tt v}}\limits ^{(b_u, s_u)} \lambda y.u\;:\; \mathscr{M\;}' \rightarrow \tau '}(\lambda )\end{equation*}
 $\Gamma _t = \Gamma _u$
,
$\Gamma _t = \Gamma _u$
,
 $b_t = b_u$
, and
$b_t = b_u$
, and
 $s_t = s_u$
. Thus, we can conclude with
$s_t = s_u$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
 $b = b_u + b_v$
, and
$b = b_u + b_v$
, and
 $s = s_u + s_v$
.
$s = s_u + s_v$
.
-
• Rule (@). Then,
 $t = up$
and
$t = up$
and
 $t \{x \setminus v\} = (u \{x \setminus v\}) (p \{x \setminus v\})$
. Moreover,
$t \{x \setminus v\} = (u \{x \setminus v\}) (p \{x \setminus v\})$
. Moreover,
 $\Phi _{t \{x \setminus v\}}$
has two premises
$\Phi _{t \{x \setminus v\}}$
has two premises
 $\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _{u \{x \setminus v\}} \negmedspace \overset {(b_1, s_1)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _{u \{x \setminus v\}} \negmedspace \overset {(b_1, s_1)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _{p \{x \setminus v\}} \triangleright \, \Gamma _{p \{x \setminus v\}} \negmedspace \overset {(s_2, s_2)}{\vdash _{{\tt v}}}\negmedspace p \{x \setminus v\}\;:\; \mathscr{M\;}'$
, such that
$\Phi _{p \{x \setminus v\}} \triangleright \, \Gamma _{p \{x \setminus v\}} \negmedspace \overset {(s_2, s_2)}{\vdash _{{\tt v}}}\negmedspace p \{x \setminus v\}\;:\; \mathscr{M\;}'$
, such that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
 $b = 1+ b_1+b_2$
, and
$b = 1+ b_1+b_2$
, and
 $s = s_1+s_2$
. By applying the i.h. to
$s = s_1+s_2$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
and
$\Phi _{u \{x \setminus v\}}$
and
 $\Phi _{p \{x \setminus v\}}$
, there exist
$\Phi _{p \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright \Gamma _u;\; x \;:\; \mathscr{M}_{1} \negmedspace \overset{(b_u,s_u)} {\vdash_{\texttt{v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau $
and
$\Phi _u \triangleright \Gamma _u;\; x \;:\; \mathscr{M}_{1} \negmedspace \overset{(b_u,s_u)} {\vdash_{\texttt{v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau $
and
 $\Phi ^1_v \triangleright \Gamma ^1_v \negmedspace \overset{(b^1_v,s^1_v)} {\vdash_{\texttt{v}}}\negmedspace v \;:\; \mathscr{M}_{1}$
, such that
$\Phi ^1_v \triangleright \Gamma ^1_v \negmedspace \overset{(b^1_v,s^1_v)} {\vdash_{\texttt{v}}}\negmedspace v \;:\; \mathscr{M}_{1}$
, such that
 $\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma ^1_v$
,
$\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma ^1_v$
,
 $b_1 = b_u + b^1_v$
, and
$b_1 = b_u + b^1_v$
, and
 $s_1 = s_u + s^1_v$
, and there exist
$s_1 = s_u + s^1_v$
, and there exist
 $\Phi _{p} \triangleright \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\; \mathscr{M\;}'$
and
$\Phi _{p} \triangleright \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p\;:\; \mathscr{M\;}'$
and
 $\Phi ^2_v \triangleright \Gamma ^2_v \negmedspace \overset{(b^2_v,s^2_v)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}_{2}$
, such that
$\Phi ^2_v \triangleright \Gamma ^2_v \negmedspace \overset{(b^2_v,s^2_v)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}_{2}$
, such that
 $\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
$\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
 $b_2 = b_p + b^2_v$
, and
$b_2 = b_p + b^2_v$
, and
 $s_2 = s_p + s^2_v$
, respectively. By Lemma 29, there exists
$s_2 = s_p + s^2_v$
, respectively. By Lemma 29, there exists
 $\Phi _v \triangleright \, \Gamma ^1_v + \Gamma ^2_v \negmedspace \overset {(b^1_v+b^2_v, s^1_v + s^2_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_1 \sqcup \mathscr{M}_2$
, such that
$\Phi _v \triangleright \, \Gamma ^1_v + \Gamma ^2_v \negmedspace \overset {(b^1_v+b^2_v, s^1_v + s^2_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_1 \sqcup \mathscr{M}_2$
, such that
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v + b^2_v$
, and
$b_v = b^1_v + b^2_v$
, and
 $s_v = s^1_v + s^2_v$
. Therefore, we can build
$s_v = s^1_v + s^2_v$
. Therefore, we can build
 $\Phi _t$
as follows:such that
$\Phi _t$
as follows:such that \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2 \mathop {\vdash _{\tt v}}\limits ^{(1+b_u+b_p, s_u+s_p)} up: \tau }({\tt @}) \end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2 \mathop {\vdash _{\tt v}}\limits ^{(1+b_u+b_p, s_u+s_p)} up: \tau }({\tt @}) \end{equation*}
 $\Gamma _t = \Gamma _u + \Gamma _p$
,
$\Gamma _t = \Gamma _u + \Gamma _p$
,
 $b_t = 1+b_u+b_p$
, and
$b_t = 1+b_u+b_p$
, and
 $s_t = s_u + s_p$
. Thus, we can conclude with
$s_t = s_u + s_p$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
 $b = 1+b_1+b_2 = 1+b_u + b^1_v + b_p + b^2_v = b_t + b_v$
, and
$b = 1+b_1+b_2 = 1+b_u + b^1_v + b_p + b^2_v = b_t + b_v$
, and
 $s = s_1+s_2 = s_u + s^1_v + s_p + s^2_v = s_t + s_v$
.
$s = s_1+s_2 = s_u + s^1_v + s_p + s^2_v = s_t + s_v$
.
-
• Rule (m). Then,
 $\Phi _{t \{x \setminus v\}}$
has premises
$\Phi _{t \{x \setminus v\}}$
has premises
 $(\Phi _i \triangleright \, \Gamma _i \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt v}}}\negmedspace t \{x \setminus v\}\;:\; \sigma _i)_{i \in I}$
, such that
$(\Phi _i \triangleright \, \Gamma _i \negmedspace \overset {(b_i,s_i)}{\vdash _{{\tt v}}}\negmedspace t \{x \setminus v\}\;:\; \sigma _i)_{i \in I}$
, such that
 $\tau = [ \sigma _i ]_{i \in I}$
,
$\tau = [ \sigma _i ]_{i \in I}$
,
 $\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i$
,
$\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i$
,
 $b = +_{i \in I} b_i$
, and
$b = +_{i \in I} b_i$
, and
 $s = +_{i \in I} s_i$
. By applying the i.h. to each
$s = +_{i \in I} s_i$
. By applying the i.h. to each
 $\Phi _i$
, there exist
$\Phi _i$
, there exist
 $\Phi ^i_t \triangleright \Gamma ^i_t;\; x\;:\; \mathscr{M}_{i} \negmedspace \overset{(b^i_t, s^i_t)} {\vdash_{\texttt{v}}}\negmedspace t \;:\; \sigma _i$
and
$\Phi ^i_t \triangleright \Gamma ^i_t;\; x\;:\; \mathscr{M}_{i} \negmedspace \overset{(b^i_t, s^i_t)} {\vdash_{\texttt{v}}}\negmedspace t \;:\; \sigma _i$
and
 $\Phi ^i_v \triangleright \, \Gamma ^i_v \negmedspace \overset {(b^i_v, s^i_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_i$
, such that
$\Phi ^i_v \triangleright \, \Gamma ^i_v \negmedspace \overset {(b^i_v, s^i_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_i$
, such that
 $\Gamma _i = \Gamma ^i_t + \Gamma ^i_v$
,
$\Gamma _i = \Gamma ^i_t + \Gamma ^i_v$
,
 $b_i = b^i_t + b^i_v$
, and
$b_i = b^i_t + b^i_v$
, and
 $s_i = s^i_t + s^i_v$
, for each
$s_i = s^i_t + s^i_v$
, for each
 $i \in I$
. By Lemma 29, there exists
$i \in I$
. By Lemma 29, there exists
 $\Phi _v \triangleright \, +_{i \in I} \Gamma ^i_v \negmedspace \overset {(+_{i \in I} b^i_v, +_{i \in I} s^i_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, such that
$\Phi _v \triangleright \, +_{i \in I} \Gamma ^i_v \negmedspace \overset {(+_{i \in I} b^i_v, +_{i \in I} s^i_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, such that
 $\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
$\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
 $b_v = +_{i \in I} b^i_v$
, and
$b_v = +_{i \in I} b^i_v$
, and
 $s_v = +_{i \in I} s^i_v$
. Moreover, we can build
$s_v = +_{i \in I} s^i_v$
. Moreover, we can build
 $\Phi _t$
as follows:such that
$\Phi _t$
as follows:such that \begin{equation*} \frac {(\Phi ^i_t \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t, s^i_t)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \sigma _i)_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \sqcup _{i \in I} \mathscr{M}_i \mathop {\vdash _{\tt v}}\limits ^{(+_{i \in I} b^i_t, +_{i \in I} s^i_t)} t\;:\; [ \sigma _i ]_{i \in I}}({\tt m})\end{equation*}
\begin{equation*} \frac {(\Phi ^i_t \triangleright \, \Gamma ^i_t;\; x \;:\; \mathscr{M}_i \negmedspace \overset {(b^i_t, s^i_t)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \sigma _i)_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \sqcup _{i \in I} \mathscr{M}_i \mathop {\vdash _{\tt v}}\limits ^{(+_{i \in I} b^i_t, +_{i \in I} s^i_t)} t\;:\; [ \sigma _i ]_{i \in I}}({\tt m})\end{equation*}
 $\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
$\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
 $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
 $b_t = +_{i \in I} b^i_t$
, and
$b_t = +_{i \in I} b^i_t$
, and
 $s_t = +_{i \in I} s^i_t$
. And we can conclude with
$s_t = +_{i \in I} s^i_t$
. And we can conclude with
 $\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_v) = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_v = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_v) = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_v = \Gamma _t + \Gamma _v$
,
 $b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_v) = +_{i \in I} b^i_t +_{i \in I} b^i_v = b_t + b_v$
, and
$b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_v) = +_{i \in I} b^i_t +_{i \in I} b^i_v = b_t + b_v$
, and
 $s = +_{i \in I} s_i = +_{i \in I} (s^i_t + s^i_v) = +_{i \in I} s^i_t +_{i \in I} s^i_v = s_t + s_v$
.
$s = +_{i \in I} s_i = +_{i \in I} (s^i_t + s^i_v) = +_{i \in I} s^i_t +_{i \in I} s^i_v = s_t + s_v$
.
-
• Rule (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $t = \lambda y.u$
and
$t = \lambda y.u$
and
 $t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Moreover,
$t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Moreover,
 $\Gamma _{t \{x \setminus v\}} = \emptyset$
,
$\Gamma _{t \{x \setminus v\}} = \emptyset$
,
 $\tau = {\tt a}$
, and
$\tau = {\tt a}$
, and
 $b = m = d = 0$
. Therefore, we can build
$b = m = d = 0$
. Therefore, we can build
 $\Phi _v \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace v: [ \, ]$
, such that
$\Phi _v \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace v: [ \, ]$
, such that
 $\Gamma _v = \emptyset$
,
$\Gamma _v = \emptyset$
,
 $\mathscr{M} = [ \, ]$
,
$\mathscr{M} = [ \, ]$
,
 $b_v = s_v = 0$
, by using rule (m) with no premises, and build
$b_v = s_v = 0$
, by using rule (m) with no premises, and build
 $\Phi _t \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace \lambda y.u\;:\; {\tt a}$
, such that
$\Phi _t \triangleright \, \emptyset \negmedspace \overset {(0,0)}{\vdash _{{\tt v}}}\negmedspace \lambda y.u\;:\; {\tt a}$
, such that
 $\Gamma _t = \emptyset$
, and
$\Gamma _t = \emptyset$
, and
 $b_t = s_t = 0$
, by using rule (
$b_t = s_t = 0$
, by using rule (
 $\lambda _{\tt p}$
). Thus, we can conclude with
$\lambda _{\tt p}$
). Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v = \emptyset$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v = \emptyset$
,
 $b = b_t + b_v = 0$
, and
$b = b_t + b_v = 0$
, and
 $s = s_t + s_v = 0$
.
$s = s_t + s_v = 0$
. -
• Rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $t = up$
and
$t = up$
and
 $t \{x \setminus v\} = (u \{x \setminus v\}) (p \{x \setminus v\})$
. Moreover,
$t \{x \setminus v\} = (u \{x \setminus v\}) (p \{x \setminus v\})$
. Moreover,
 $\Phi _{t \{x \setminus v\}}$
has two premises
$\Phi _{t \{x \setminus v\}}$
has two premises
 $\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _{u \{x \setminus v\}} \negmedspace \overset {(b_1, s_1)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \overline {{\tt a}}$
and
$\Phi _{u \{x \setminus v\}} \triangleright \, \Gamma _{u \{x \setminus v\}} \negmedspace \overset {(b_1, s_1)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \overline {{\tt a}}$
and
 $\Phi _{p \{x \setminus v\}} \triangleright \Gamma _{p \{x \setminus v\}} \negmedspace \overset{(b_2, s_2)} {\vdash_{\texttt{v}}}\negmedspace p\{x \setminus v\} \;:\; \texttt{tt}_{\texttt{v}}$
, such that
$\Phi _{p \{x \setminus v\}} \triangleright \Gamma _{p \{x \setminus v\}} \negmedspace \overset{(b_2, s_2)} {\vdash_{\texttt{v}}}\negmedspace p\{x \setminus v\} \;:\; \texttt{tt}_{\texttt{v}}$
, such that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
 $b = b_1+b_2$
, and
$b = b_1+b_2$
, and
 $s = 1+s_1+s_2$
. By applying the i.h. to
$s = 1+s_1+s_2$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
and
$\Phi _{u \{x \setminus v\}}$
and
 $\Phi _{p \{x \setminus v\}}$
, there exist
$\Phi _{p \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright \Gamma _u ;\; x \;:\; \mathscr{M}_1 \negmedspace \overset{(b_u,s_u)} {\vdash_{\texttt{v}}}\negmedspace u \;:\; {\not {{\tt a}}}$
and
$\Phi _u \triangleright \Gamma _u ;\; x \;:\; \mathscr{M}_1 \negmedspace \overset{(b_u,s_u)} {\vdash_{\texttt{v}}}\negmedspace u \;:\; {\not {{\tt a}}}$
and
 $\Phi ^1_v \triangleright \Gamma ^1_v \negmedspace \overset{(b^1_v,s^1_v)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}_{1}$
, such that
$\Phi ^1_v \triangleright \Gamma ^1_v \negmedspace \overset{(b^1_v,s^1_v)} {\vdash_{\texttt{v}}}\negmedspace v\;:\; \mathscr{M}_{1}$
, such that
 $\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma ^1_v$
,
$\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma ^1_v$
,
 $b_1 = b_u + b^1_v$
, and
$b_1 = b_u + b^1_v$
, and
 $s_1 = s_u + s^1_v$
, and there exist
$s_1 = s_u + s^1_v$
, and there exist
 $\Phi _{p} \triangleright \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p \;:\; \texttt{tt}_{\texttt{v}}$
and
$\Phi _{p} \triangleright \Gamma _p;\; x \;:\; \mathscr{M}_2 \negmedspace \overset{(b_p,s_p)} {\vdash_{\texttt{v}}}\negmedspace p \;:\; \texttt{tt}_{\texttt{v}}$
and
 $\Phi ^2_v \triangleright \Gamma ^2_v \negmedspace \overset{(b^2_v,s^2_v)} {\vdash_{\texttt{v}}}\negmedspace v \;:\; {\mathscr{M}_2}$
, such that
$\Phi ^2_v \triangleright \Gamma ^2_v \negmedspace \overset{(b^2_v,s^2_v)} {\vdash_{\texttt{v}}}\negmedspace v \;:\; {\mathscr{M}_2}$
, such that
 $\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
$\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
 $b_1 = b_p + b^2_v$
, and
$b_1 = b_p + b^2_v$
, and
 $s_2 = s_p + s^2_v$
, respectively. By Lemma 29, there exists
$s_2 = s_p + s^2_v$
, respectively. By Lemma 29, there exists
 $\Phi _v \triangleright \, \Gamma ^1_v + \Gamma ^2_v \negmedspace \overset {(b^1_v+b^2_v, s^1_v + s^2_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_1 \sqcup \mathscr{M}_2$
, such that
$\Phi _v \triangleright \, \Gamma ^1_v + \Gamma ^2_v \negmedspace \overset {(b^1_v+b^2_v, s^1_v + s^2_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}_1 \sqcup \mathscr{M}_2$
, such that
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v + b^2_v$
, and
$b_v = b^1_v + b^2_v$
, and
 $s_v = s^1_v + s^2_v$
. Therefore, we can build
$s_v = s^1_v + s^2_v$
. Therefore, we can build
 $\Phi _t$
as follows:such that
$\Phi _t$
as follows:such that \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2 \mathop {\vdash _{\tt v}}\limits ^{(b_u+b_p, 1+s_u+s_p)} up: \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M}_1 \sqcup \mathscr{M}_2 \mathop {\vdash _{\tt v}}\limits ^{(b_u+b_p, 1+s_u+s_p)} up: \tau }({\tt @})\end{equation*}
 $\Gamma _t = \Gamma _u + \Gamma _p$
,
$\Gamma _t = \Gamma _u + \Gamma _p$
,
 $b_t = b_u + b_p$
, and
$b_t = b_u + b_p$
, and
 $s_t = 1+s_u + s_p$
. Thus, we can conclude with
$s_t = 1+s_u + s_p$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
 $b = b_1+b_2 = b_u + b^1_v + b_p + b^2_v = b_t + b_v$
, and
$b = b_1+b_2 = b_u + b^1_v + b_p + b^2_v = b_t + b_v$
, and
 $s = 1+s_1+s_2=1+s_u + s^1_v + s_p + s^2_v = s_t + s_v$
.
$s = 1+s_1+s_2=1+s_u + s^1_v + s_p + s^2_v = s_t + s_v$
.
-
• Rule (@
 $^2_{{\tt p}}$
). This case is very similar to the previous case.
$^2_{{\tt p}}$
). This case is very similar to the previous case.
Lemma 5 (Quantitative subject expansion). Let
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t'\;:\; \tau$
be a tight type derivation. If
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b,s)} {\vdash_{\texttt{v}}}\negmedspace t'\;:\; \tau$
be a tight type derivation. If
![]() $t \rightarrow_{\texttt{v}} t'$
, then there exists
$t \rightarrow_{\texttt{v}} t'$
, then there exists
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b+1, s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b+1, s)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
.
Proof. Just like for the subject reduction property, we prove a stronger version of the statement that allows us to reason inductively:
Let
![]() $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
, such that
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace t': \tau$
, such that
![]() $\Gamma$
is tight, and either
$\Gamma$
is tight, and either
![]() $\tau \in {{\tt tt}_{\tt v}}$
or
$\tau \in {{\tt tt}_{\tt v}}$
or
![]() $\neg {\tt val}(t)$
. If
$\neg {\tt val}(t)$
. If
![]() $t {\rightarrow }_{\texttt {v}} t'$
, then there exists
$t {\rightarrow }_{\texttt {v}} t'$
, then there exists
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b+1,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \negmedspace \overset {(b+1,s)}{\vdash _{{\tt v}}}\negmedspace t\;:\; \tau$
.
The proof now follows by induction over
![]() $t {\rightarrow }_{\texttt {v}} t'$
:
$t {\rightarrow }_{\texttt {v}} t'$
:
-
• Case
 $t = (\lambda x.u) v {\rightarrow }_{\texttt {v}} u \{x \setminus v\} = t'$
. Then,
$t = (\lambda x.u) v {\rightarrow }_{\texttt {v}} u \{x \setminus v\} = t'$
. Then,
 $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \tau$
. By Lemma 31, there exist
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset {(b,s)}{\vdash _{{\tt v}}}\negmedspace u \{x \setminus v\}\;:\; \tau$
. By Lemma 31, there exist
 $\Phi _u \triangleright \, \Gamma _u;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \tau$
and
$\Phi _u \triangleright \, \Gamma _u;\; x \;:\; \mathscr{M} \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \tau$
and
 $\Phi _v \triangleright \, \Gamma _v \negmedspace \overset {(b_v,s_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, such that
$\Phi _v \triangleright \, \Gamma _v \negmedspace \overset {(b_v,s_v)}{\vdash _{{\tt v}}}\negmedspace v: \mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _v$
tight,
$\Gamma = \Gamma _u + \Gamma _v$
tight,
 $\tau \in {{\tt tt}_{\tt v}}$
,
$\tau \in {{\tt tt}_{\tt v}}$
,
 $b = b_u + b_v$
, and
$b = b_u + b_v$
, and
 $s = s_u + s_v$
. Therefore, we can build
$s = s_u + s_v$
. Therefore, we can build
 $\Phi _t$
as follows:
$\Phi _t$
as follows:
Thus, we can conclude with
 $b + 1 = 1 + b_u + b_v$
.
$b + 1 = 1 + b_u + b_v$
. -
• Case
 $t = up {\rightarrow }_{\texttt {v}} u'p = t'$
, such that
$t = up {\rightarrow }_{\texttt {v}} u'p = t'$
, such that
 $u {\rightarrow }_{\texttt {v}} u'$
. Then,
$u {\rightarrow }_{\texttt {v}} u'$
. Then,
 $\Phi _{t'}$
must end with rule (@), (@
$\Phi _{t'}$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _{t'}$
ends with rule (@). Then,
$\Phi _{t'}$
ends with rule (@). Then,
 $\Phi _{t'}$
has two premises,
$\Phi _{t'}$
has two premises,
 $\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u': \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _{u'} \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u': \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M\;}'$
, such that
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M\;}'$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
is tight,
$\Gamma = \Gamma _u + \Gamma _p$
is tight,
 $\tau \in {{\tt tt}_{\tt v}}$
,
$\tau \in {{\tt tt}_{\tt v}}$
,
 $b = 1 + b_u + b_p$
, and
$b = 1 + b_u + b_p$
, and
 $s = s_u + s_p$
. Notice that
$s = s_u + s_p$
. Notice that
 $\neg {\tt val}(u)$
holds, since
$\neg {\tt val}(u)$
holds, since
 $u {\rightarrow }_{\texttt {v}} u'$
. Moreover,
$u {\rightarrow }_{\texttt {v}} u'$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. Therefore, by applying the i.h. to
$\Gamma _p$
are tight. Therefore, by applying the i.h. to
 $\Phi _{u'}$
, there exists
$\Phi _{u'}$
, there exists
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(1 + b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
. Therefore, we can build
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(1 + b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
. Therefore, we can build
 $\Phi _{t'}$
as follows:Thus, we can conclude with
$\Phi _{t'}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 + 1+ b_u + b_p, s_u + s_p)}_{} up: \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 + 1+ b_u + b_p, s_u + s_p)}_{} up: \tau }({\tt @})\end{equation*}
 $b + 1 = (1 + b_u + b_p) + 1$
.
$b + 1 = (1 + b_u + b_p) + 1$
.
-
– Case
 $\Phi _{t'}$
ends with rule (@
$\Phi _{t'}$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases are very similar to the previous one.
$^2_{{\tt p}}$
). These cases are very similar to the previous one.
-
-
• Case
 $t = up {\rightarrow }_{\texttt {v}} up' = t'$
, such that
$t = up {\rightarrow }_{\texttt {v}} up' = t'$
, such that
 $u \not \rightarrow_{\texttt{v}}$
and
$u \not \rightarrow_{\texttt{v}}$
and
 $p {\rightarrow }_{\texttt {v}} p'$
. Then,
$p {\rightarrow }_{\texttt {v}} p'$
. Then,
 $\Phi _{t'}$
must end with rule (@), (@
$\Phi _{t'}$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _{t'}$
ends with rule (
$\Phi _{t'}$
ends with rule (
 $\tt @$
). Then,
$\tt @$
). Then,
 $\Phi _{t'}$
has two premises
$\Phi _{t'}$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
and
$\Phi _u \triangleright \, \Gamma _u \negmedspace \overset {(b_u, s_u)}{\vdash _{{\tt v}}}\negmedspace u\;:\; \mathscr{M\;}' \rightarrow \tau$
and
 $\Phi _{p'} \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt v}}}\negmedspace p': \mathscr{M\;}'$
, such that
$\Phi _{p'} \triangleright \, \Gamma _p \negmedspace \overset {(b_p, s_p)}{\vdash _{{\tt v}}}\negmedspace p': \mathscr{M\;}'$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
is tight,
$\Gamma = \Gamma _u + \Gamma _p$
is tight,
 $\tau \in {{\tt tt}_{\tt v}}$
,
$\tau \in {{\tt tt}_{\tt v}}$
,
 $b = 1 + b_u + b_p$
,
$b = 1 + b_u + b_p$
,
 $s_t = s_u + s_p$
. Notice that
$s_t = s_u + s_p$
. Notice that
 $\neg {\tt val}(p)$
holds, since
$\neg {\tt val}(p)$
holds, since
 $p {\rightarrow }_{\texttt {v}} p'$
. Moreover,
$p {\rightarrow }_{\texttt {v}} p'$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. Therefore, by applying the i.h. to
$\Gamma _p$
are tight. Therefore, by applying the i.h. to
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p + 1, s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M\;}' \rightarrow \tau$
. Therefore, we can build
$\Phi _p \triangleright \, \Gamma _p \negmedspace \overset {(b_p + 1, s_p)}{\vdash _{{\tt v}}}\negmedspace p: \mathscr{M\;}' \rightarrow \tau$
. Therefore, we can build
 $\Phi _t$
as follows:Thus, we can conclude with
$\Phi _t$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 + b_u + b_p + 1, s_u + s_p)}_{} up: \tau }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \mathop {\vdash }\limits ^{(1 + b_u + b_p + 1, s_u + s_p)}_{} up: \tau }({\tt @})\end{equation*}
 $b + 1 = (1 + b_u + b_p) + 1 = 1 + b_u + b_p + 1$
.
$b + 1 = (1 + b_u + b_p) + 1 = 1 + b_u + b_p + 1$
.
-
– Case
 $\Phi _{t'}$
ends with rule (@
$\Phi _{t'}$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases are very similar to the previous one.
$^2_{{\tt p}}$
). These cases are very similar to the previous one.
-
Theorem 2 (Quantitative completeness). If
![]() $t \twoheadrightarrow ^b_{\texttt{v}} u$
with
$t \twoheadrightarrow ^b_{\texttt{v}} u$
with
![]() $u \in {\tt no}_{\texttt{v}}$
, then there exists a tight type derivation
$u \in {\tt no}_{\texttt{v}}$
, then there exists a tight type derivation
![]() $\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b, |u|_{\texttt{v}})} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
.
$\Phi _t \triangleright \, \Gamma \negmedspace \overset{(b, |u|_{\texttt{v}})} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
.
Proof.
The proof follows by induction on
![]() $b$
:
$b$
:
-
• Case
 $b = 0$
. Then
$b = 0$
. Then
 $t = u$
, which means that
$t = u$
, which means that
 $t \in {\tt no}_{\texttt{v}}$
. Therefore, we conclude by Lemma3.
$t \in {\tt no}_{\texttt{v}}$
. Therefore, we conclude by Lemma3. -
• Case
 $b \gt 0$
. Then there exists
$b \gt 0$
. Then there exists
 $t'$
, such that
$t'$
, such that
 $t \rightarrow t' \twoheadrightarrow ^{b-1}_{\texttt{v}} u$
. By the i.h., there exists a tight derivation
$t \rightarrow t' \twoheadrightarrow ^{b-1}_{\texttt{v}} u$
. By the i.h., there exists a tight derivation
 $\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, |u|)} {\vdash_{\texttt{v}}}\negmedspace t': \tau$
. By Lemma5, there exists a tight derivation
$\Phi _{t'} \triangleright \, \Gamma \negmedspace \overset{(b-1, |u|)} {\vdash_{\texttt{v}}}\negmedspace t': \tau$
. By Lemma5, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \negmedspace \overset{(b, |u|)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
, and this derivation is also tight. So, we can conclude.
$\Phi \triangleright \, \Gamma \negmedspace \overset{(b, |u|)} {\vdash_{\texttt{v}}}\negmedspace t\;:\; \tau$
, and this derivation is also tight. So, we can conclude.
A.2 Weak Open CBN with Global State
Proposition 3.
Let
![]() $(t,s)$
be a configuration. Then
$(t,s)$
be a configuration. Then
![]() $(t,s)$
is normal iff
$(t,s)$
is normal iff
![]() $(t,s) \not \rightsquigarrow _{{\tt n}}$
.
$(t,s) \not \rightsquigarrow _{{\tt n}}$
.
Proof.
-
⇒) Let
 $(t, s)$
be normal. Then, either
$(t, s)$
be normal. Then, either
 $(t,s)$
is blocked or
$(t,s)$
is blocked or
 $t \in {\tt no}_{{\tt n}}$
:
$t \in {\tt no}_{{\tt n}}$
:-
– Case
 $(t,s)$
is blocked. We reason by induction on
$(t,s)$
is blocked. We reason by induction on
 $(t,s)$
:
$(t,s)$
:-
* Case
 $t = {\tt get}_{l}(\lambda x.u)$
, such that
$t = {\tt get}_{l}(\lambda x.u)$
, such that
 $l \not \in {\tt labels}(s)$
. Then,
$l \not \in {\tt labels}(s)$
. Then,
 $(t, s) \not \rightsquigarrow _{{\tt n}}$
by definition.
$(t, s) \not \rightsquigarrow _{{\tt n}}$
by definition. -
* Case
 $t = u p$
, such that
$t = u p$
, such that
 $(u,s)$
is blocked. Then,
$(u,s)$
is blocked. Then,
 $(u,s)$
is normal. By applying the i.h. to
$(u,s)$
is normal. By applying the i.h. to
 $(u,s)$
, we get
$(u,s)$
, we get
 $(u,s) \not \rightsquigarrow _{{\tt n}}$
. Therefore,
$(u,s) \not \rightsquigarrow _{{\tt n}}$
. Therefore,
 $(u p, s) \not \rightsquigarrow _{{\tt n}}$
holds.
$(u p, s) \not \rightsquigarrow _{{\tt n}}$
holds.
-
-
– Case
 $t \in {\tt no}_{{\tt n}}$
. Then
$t \in {\tt no}_{{\tt n}}$
. Then
 $(t,s)$
is unblocked by definition. We reason by induction over
$(t,s)$
is unblocked by definition. We reason by induction over
 $t \in {\tt no}_{{\tt n}}$
:
$t \in {\tt no}_{{\tt n}}$
:-
* Case
 $t = \lambda x.p$
. Then,
$t = \lambda x.p$
. Then,
 $(\lambda x.p,s) \not \rightsquigarrow _{{\tt n}}$
is straightforward.
$(\lambda x.p,s) \not \rightsquigarrow _{{\tt n}}$
is straightforward. -
* Case
 $\neg {\tt abs}(t)$
. Then,
$\neg {\tt abs}(t)$
. Then,
 $t \in {\tt ne}_{{\tt n}}$
. There are two cases:
$t \in {\tt ne}_{{\tt n}}$
. There are two cases:-
· Case
 $t = x$
. Then,
$t = x$
. Then,
 $(x,s) \not \rightsquigarrow _{{\tt n}}$
by definition.
$(x,s) \not \rightsquigarrow _{{\tt n}}$
by definition. -
· Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
. Then,
$u \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
. Then,
 $(u,s)$
is normal. By applying the i.h. to
$(u,s)$
is normal. By applying the i.h. to
 $(u,s)$
, we get
$(u,s)$
, we get
 $(u,s) \not \rightsquigarrow _{{\tt n}}$
. Therefore,
$(u,s) \not \rightsquigarrow _{{\tt n}}$
. Therefore,
 $(u p, s) \not \rightsquigarrow _{{\tt n}}$
holds.
$(u p, s) \not \rightsquigarrow _{{\tt n}}$
holds.
-
-
-
-
⇐) Let
 $(t,s) \not \rightsquigarrow _{{\tt n}}$
. We reason by induction on
$(t,s) \not \rightsquigarrow _{{\tt n}}$
. We reason by induction on
 $t$
:
$t$
:-
– Case
 $t = x$
. Then,
$t = x$
. Then,
 $t \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
. Therefore,
$t \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
. Therefore,
 $(t,s)$
is normal.
$(t,s)$
is normal. -
– Case
 $t = \lambda x.p$
. Then
$t = \lambda x.p$
. Then
 $\lambda x.p \in {\tt no}_{{\tt n}}$
. Therefore,
$\lambda x.p \in {\tt no}_{{\tt n}}$
. Therefore,
 $(t,s)$
is normal.
$(t,s)$
is normal. -
– Case
 $t = up$
. Since
$t = up$
. Since
 $(up, s) \not \rightsquigarrow _{{\tt n}}$
, then
$(up, s) \not \rightsquigarrow _{{\tt n}}$
, then
 $(u,s) \not \rightsquigarrow _{{\tt n}}$
and
$(u,s) \not \rightsquigarrow _{{\tt n}}$
and
 $\neg {\tt abs}(u)$
, otherwise rules (appL) and (
$\neg {\tt abs}(u)$
, otherwise rules (appL) and (
 $\beta _{\tt n}$
) would be applicable, respectively. By applying the i.h. to
$\beta _{\tt n}$
) would be applicable, respectively. By applying the i.h. to
 $(u,s)$
, we get
$(u,s)$
, we get
 $(u,s)$
is normal. Therefore, either
$(u,s)$
is normal. Therefore, either
 $(u, s)$
is blocked, or
$(u, s)$
is blocked, or
 $u \in {\tt ne}_{{\tt n}}$
(since
$u \in {\tt ne}_{{\tt n}}$
(since
 $u \in {\tt no}_{{\tt n}}$
and
$u \in {\tt no}_{{\tt n}}$
and
 $\neg {\tt abs}(u)$
). In the former case,
$\neg {\tt abs}(u)$
). In the former case,
 $(up, s)$
is blocked by definition. In the latter case,
$(up, s)$
is blocked by definition. In the latter case,
 $up \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
. Therefore,
$up \in {\tt ne}_{{\tt n}} \subseteq {\tt no}_{{\tt n}}$
. Therefore,
 $(up, s)$
is normal.
$(up, s)$
is normal. -
– Case
 $t = {\tt get}_{l}(\lambda x.u)$
. Since
$t = {\tt get}_{l}(\lambda x.u)$
. Since
 $({\tt get}_{l}(\lambda x.u),s) \not \rightsquigarrow _{{\tt n}}$
, then
$({\tt get}_{l}(\lambda x.u),s) \not \rightsquigarrow _{{\tt n}}$
, then
 $l \not \in {\tt labels}(s)$
. Therefore,
$l \not \in {\tt labels}(s)$
. Therefore,
 $({\tt get}_{l}(\lambda x.u),s)$
is blocked and thus normal.
$({\tt get}_{l}(\lambda x.u),s)$
is blocked and thus normal. -
– Case
 $t = {\tt set}_{l}(t,u)$
. Then
$t = {\tt set}_{l}(t,u)$
. Then
 $({\tt set}_{l}(t,u), s) \rightsquigarrow _{{\tt n}} (u, {\tt upd}_{l}(t,s))$
, which leads to a contradiction with the hypothesis. Therefore, this case cannot apply.
$({\tt set}_{l}(t,u), s) \rightsquigarrow _{{\tt n}} (u, {\tt upd}_{l}(t,s))$
, which leads to a contradiction with the hypothesis. Therefore, this case cannot apply.
-
Lemma 32 (Relevance). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{G\,}$
(resp.
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{G\,}$
(resp.
![]() $\Pi \triangleright \Delta \Vdash ^{(b',m',d')}_{\tt n} s\;:\;\mathscr{T\;}$
). Then
$\Pi \triangleright \Delta \Vdash ^{(b',m',d')}_{\tt n} s\;:\;\mathscr{T\;}$
). Then
![]() ${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
(resp.
${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
(resp.
![]() ${\tt dom}(\Delta ) \subseteq {{\tt fv}}(s)$
).
${\tt dom}(\Delta ) \subseteq {{\tt fv}}(s)$
).
Proof.
By a simple induction over
![]() $\Phi$
.
$\Phi$
.
Lemma 33.
Let
![]() $\Pi \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n} s\;:\;\mathscr{T\;}$
. If
$\Pi \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n} s\;:\;\mathscr{T\;}$
. If
![]() $l \in {\tt dom}(\mathscr{T\;})$
, then
$l \in {\tt dom}(\mathscr{T\;})$
, then
![]() $l \in {\tt labels}(s)$
.
$l \in {\tt labels}(s)$
.
Proof. The proof is exactly the same as for Weak Open CBV. Just notice that, in Weak Open CBN with Global State, we can assign the empty multi-type to any term.
Proposition 4 (Typed configurations are unblocked). If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
, then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
, then
![]() $(t,s)$
is unblocked.
$(t,s)$
is unblocked.
Proof.
The proof follows by contraposition. We assume that
![]() $(t,s)$
is blocked and show that
$(t,s)$
is blocked and show that
![]() $(t,s)$
cannot be typable. We proceed by induction on
$(t,s)$
cannot be typable. We proceed by induction on
![]() $(t,s)$
blocked:
$(t,s)$
blocked:
-
• Case
 $t = {\tt get}_{l}(\lambda x.t)$
, such that
$t = {\tt get}_{l}(\lambda x.t)$
, such that
 $l \not \in {\tt labels}(s)$
. Then, suppose that
$l \not \in {\tt labels}(s)$
. Then, suppose that
 $(t,s)$
is typable, so that the type derivation must be of the following form, where
$(t,s)$
is typable, so that the type derivation must be of the following form, where
 $\mathscr{L\;}'= \Gamma _u(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}$
:
$\mathscr{L\;}'= \Gamma _u(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}$
:
where
 $\Gamma = (\Gamma _u \setminus x) + \Delta _s$
,
$\Gamma = (\Gamma _u \setminus x) + \Delta _s$
,
 $b = b_u+b_s$
,
$b = b_u+b_s$
,
 $m = 1+m_u+m_s$
, and
$m = 1+m_u+m_s$
, and
 $d = d_u + d_s$
. Thus,
$d = d_u + d_s$
. Thus,
 $l \in {\tt dom}({\{l\;:\;\Gamma _u(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}})$
, and so, by Lemma 33, we get
$l \in {\tt dom}({\{l\;:\;\Gamma _u(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}})$
, and so, by Lemma 33, we get
 $l \in {\tt labels}(s)$
, which leads to a contradiction. Therefore,
$l \in {\tt labels}(s)$
, which leads to a contradiction. Therefore,
 $(t,s)$
is not typable.
$(t,s)$
is not typable. -
• Case
 $t = up$
, such that
$t = up$
, such that
 $(u,s)$
is blocked. Suppose that
$(u,s)$
is blocked. Suppose that
 $(t,s)$
is typable with derivation
$(t,s)$
is typable with derivation
 $\Phi$
. We have two cases:
$\Phi$
. We have two cases:-
– Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
where
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
 $b = 1+b_u + b_p + b_s$
,
$b = 1+b_u + b_p + b_s$
,
 $m = m_u + m_p + m_s$
, and
$m = m_u + m_p + m_s$
, and
 $d = d_u + d_p + d_s$
. Thus, we can build a type derivation
$d = d_u + d_p + d_s$
. Thus, we can build a type derivation
 $\Phi _{(u,s)}$
as follows:By applying the i.h. on
$\Phi _{(u,s)}$
as follows:By applying the i.h. on \begin{equation*} \frac {\Phi _u \qquad \Pi _s}{\Gamma _u + \Delta _s {\Vdash }^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): (\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) \times \mathscr{T\;}')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _u \qquad \Pi _s}{\Gamma _u + \Delta _s {\Vdash }^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): (\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) \times \mathscr{T\;}')}({\tt conf})\end{equation*}
 $(u,s)$
we get that
$(u,s)$
we get that
 $(u,s)$
is not typable, which leads to a contradiction. Therefore,
$(u,s)$
is not typable, which leads to a contradiction. Therefore,
 $(t,s)$
is not typable.
$(t,s)$
is not typable.
-
– Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
where
 $\Gamma = \Gamma _u + \Delta _s$
,
$\Gamma = \Gamma _u + \Delta _s$
,
 $b = b_u + b_s$
,
$b = b_u + b_s$
,
 $m = m_u + m_s$
, and
$m = m_u + m_s$
, and
 $d = 1+d_u + d_s$
. Therefore, we can build a type derivation
$d = 1+d_u + d_s$
. Therefore, we can build a type derivation
 $\Phi _{(u,s)}$
as follows:By applying the i.h. to
$\Phi _{(u,s)}$
as follows:By applying the i.h. to \begin{equation*} \frac {\Phi _u\qquad \Pi _s}{\Gamma _u + \Delta _s \Vdash ^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): ({\tt n} \times \mathscr{T\;}')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Pi _s}{\Gamma _u + \Delta _s \Vdash ^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): ({\tt n} \times \mathscr{T\;}')}({\tt conf})\end{equation*}
 $(u,s)$
, we get that
$(u,s)$
, we get that
 $(u,s)$
is not typable, which leads to a contradiction. Therefore,
$(u,s)$
is not typable, which leads to a contradiction. Therefore,
 $(t,s)$
is not typable.
$(t,s)$
is not typable.
-
Lemma 34 (Tight spreading). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt ne}_{{\tt n}}$
, then
$t \in {\tt ne}_{{\tt n}}$
, then
![]() $\tau = {\tt n}$
.
$\tau = {\tt n}$
.
Proof.
We proceed by induction over
![]() $t \in {\tt ne}_{{\tt n}}$
:
$t \in {\tt ne}_{{\tt n}}$
:
-
• Case
 $t = x$
. Then
$t = x$
. Then
 $\Phi$
must end with rule (ax). Therefore,
$\Phi$
must end with rule (ax). Therefore,
 $\Phi \triangleright \, x \;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')\Vdash ^{(b,m,d)}_{\tt n} x\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, and thus,
$\Phi \triangleright \, x \;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')\Vdash ^{(b,m,d)}_{\tt n} x\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, and thus,
 $\tau = {\tt n}$
.
$\tau = {\tt n}$
. -
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. Then,
$u \in {\tt ne}_{{\tt n}}$
. Then,
 $\Phi$
must end with rule (@) or (@
$\Phi$
must end with rule (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\; \mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow (\tau \times \mathscr{T\;}'))) \times \mathscr{T\;}'')$
and
$\Phi _u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\; \mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow (\tau \times \mathscr{T\;}'))) \times \mathscr{T\;}'')$
and
 $\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M}$
, where
$\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M}$
, where
 $\Gamma = \Gamma _u + \Gamma _p$
is tight,
$\Gamma = \Gamma _u + \Gamma _p$
is tight,
 $b = 1+b_u+b_p$
,
$b = 1+b_u+b_p$
,
 $m = m_u+m_p$
, and
$m = m_u+m_p$
, and
 $d = d_u+d_p$
. Moreover,
$d = d_u+d_p$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. By applying the i.h. to
$\Gamma _p$
are tight. By applying the i.h. to
 $u \in {\tt ne}_{{\tt n}}$
, we get that
$u \in {\tt ne}_{{\tt n}}$
, we get that
 $(\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow (\tau \times \mathscr{T\;}'))) = {\tt n}$
, which is a contradiction. Therefore, this case cannot apply.
$(\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow (\tau \times \mathscr{T\;}'))) = {\tt n}$
, which is a contradiction. Therefore, this case cannot apply. -
– Rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\tau = {\tt n} \in {{\tt tt}_{\tt n}}$
by definition.
$\tau = {\tt n} \in {{\tt tt}_{\tt n}}$
by definition.
-
Lemma 6 (Normal forms have pure types). Let
![]() $\Phi \,\triangleright \, \Vdash ^{(b,m,d)}_{\tt n} t\;:\; \Gamma {\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')}$
, such that
$\Phi \,\triangleright \, \Vdash ^{(b,m,d)}_{\tt n} t\;:\; \Gamma {\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')}$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt no}_{{\tt n}}$
, then
$t \in {\tt no}_{{\tt n}}$
, then
![]() $\mathscr{T\;} = \mathscr{T\;}'$
.
$\mathscr{T\;} = \mathscr{T\;}'$
.
Proof.
By induction on
![]() $t \in {\tt no}_{{\tt n}}$
. There are two cases:
$t \in {\tt no}_{{\tt n}}$
. There are two cases:
-
• Case
 $t = \lambda x.u$
. Then,
$t = \lambda x.u$
. Then,
 $\Phi$
must end with rule (
$\Phi$
must end with rule (
 $\lambda$
), (
$\lambda$
), (
 $\uparrow$
), or (
$\uparrow$
), or (
 $\lambda _{\tt p}$
):
$\lambda _{\tt p}$
):-
– Case
 $\Phi$
ends with rule (
$\Phi$
ends with rule (
 $\lambda$
) or (
$\lambda$
) or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $\mathscr{T\;} = \mathscr{T\;}'$
, by definition.
$\mathscr{T\;} = \mathscr{T\;}'$
, by definition.
-
-
• Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}}$
:
$t \in {\tt ne}_{{\tt n}}$
:-
– Case
 $t = x$
. Since
$t = x$
. Since
 $\Gamma$
is tight, then
$\Gamma$
is tight, then
 $\Phi \triangleright \, {x \;:\; [ \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}') ]}\Vdash ^{(b,m,d)}_{\tt n} x\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, {x \;:\; [ \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}') ]}\Vdash ^{(b,m,d)}_{\tt n} x\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, such that
 $\mathscr{T\;} = \mathscr{T\;}'$
.
$\mathscr{T\;} = \mathscr{T\;}'$
. -
– Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. Then,
$u \in {\tt ne}_{{\tt n}}$
. Then,
 $\Phi$
must end with rule (@) or (@
$\Phi$
must end with rule (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
* Case
 $\Phi$
ends with (@). Then,
$\Phi$
ends with (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')$
and
$\Phi _u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')$
and
 $\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M}$
, such that
$\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $b = 1 + b_u + b_p$
,
$b = 1 + b_u + b_p$
,
 $m = m_u + m_p$
, and
$m = m_u + m_p$
, and
 $d = d_u + d_p$
. By Lemma 34,
$d = d_u + d_p$
. By Lemma 34,
 $\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
should be tight, which is a contradiction. Therefore, this case cannot apply.
$\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
should be tight, which is a contradiction. Therefore, this case cannot apply. -
* Case
 $\Phi$
ends with (@
$\Phi$
ends with (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi _u \triangleright \, \Gamma \Vdash ^{(b,m,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, such that
$\Phi _u \triangleright \, \Gamma \Vdash ^{(b,m,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, such that
 $d = 1 + d_u$
. By applying the i.h. to
$d = 1 + d_u$
. By applying the i.h. to
 $\Phi _u$
, we get that
$\Phi _u$
, we get that
 $\mathscr{T\;} = \mathscr{T\;}'$
.
$\mathscr{T\;} = \mathscr{T\;}'$
.
-
-
Lemma 7 (Normal forms and tight states have correct size).
-
(1) Let
 $\Phi \triangleright {\Gamma }\Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then, (i)
$\Phi \triangleright {\Gamma }\Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then, (i)
 $t \in {\tt no}_{{\tt n}}$
and (ii)
$t \in {\tt no}_{{\tt n}}$
and (ii)
 $d = |{t}|_{\texttt {n}}$
.
$d = |{t}|_{\texttt {n}}$
. -
(2) Let
 $\Pi \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n}\;:\; s\;:\;\mathscr{T\;}$
be a tight derivation. Then
$\Pi \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n}\;:\; s\;:\;\mathscr{T\;}$
be a tight derivation. Then
 $b = m = d = 0$
.
$b = m = d = 0$
.
Proof.
-
(1) We split statement (1a) into two parts, but keep the same statement for (1b):
-
(a) If
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, then
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, then
 $t \in {\tt ne}_{{\tt n}}$
.
$t \in {\tt ne}_{{\tt n}}$
. -
(b) If
 $\mu = \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;}')$
, then
$\mu = \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;}')$
, then
 $t \in {\tt no}_{{\tt n}}$
.
$t \in {\tt no}_{{\tt n}}$
. -
(c)
 $d = |{t}|_{\texttt {n}}$
.
$d = |{t}|_{\texttt {n}}$
.
We reason by induction over
 $\Phi$
:
$\Phi$
:-
• Rule (ax). Then,
 $\Phi \triangleright \, {x \;:\; [ \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}) ]}\Vdash ^{(0,0,0)}_{\tt n} x\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, where
$\Phi \triangleright \, {x \;:\; [ \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}) ]}\Vdash ^{(0,0,0)}_{\tt n} x\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, where
 $\Gamma = (x \;:\; [ \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}) ])$
,
$\Gamma = (x \;:\; [ \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}) ])$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, and
 $d = 0$
. Thus, we can conclude with
$d = 0$
. Thus, we can conclude with
 $x \in {\tt ne}_{{\tt n}}$
(satisfying 1a), and
$x \in {\tt ne}_{{\tt n}}$
(satisfying 1a), and
 $d = 0 = |{x}|_{\texttt {n}}$
(satisfying 1c).
$d = 0 = |{x}|_{\texttt {n}}$
(satisfying 1c). -
• Rule (m). Then, the type of the conclusion is not a monadic type. Therefore, this case cannot apply.
-
• Rule (@). Then, the first counter must be greater than zero. Therefore, this case cannot apply.
-
• Rules (
 $\lambda$
) or (
$\lambda$
) or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $t = \lambda x.u$
and either
$t = \lambda x.u$
and either
 $\mu$
is not a tight monadic type, or
$\mu$
is not a tight monadic type, or
 $\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})$
and
$\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})$
and
 $d = 0$
, respectively. Thus, in the latter case, we can conclude with
$d = 0$
, respectively. Thus, in the latter case, we can conclude with
 $\lambda x.u \in {\tt no}_{{\tt n}}$
(satisfying 1b) and
$\lambda x.u \in {\tt no}_{{\tt n}}$
(satisfying 1b) and
 $|\lambda {x.u}|_{\texttt {n}} = 0 = d$
(satisfying 1c).
$|\lambda {x.u}|_{\texttt {n}} = 0 = d$
(satisfying 1c). -
• Rule (get) or (set). Then, the second counter must be greater than zero. Therefore, this case does not apply.
-
• Rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $t = up$
, and
$t = up$
, and
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi _u \triangleright \, \Gamma \Vdash ^{(0,0,d_u)}_{\tt n} u\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, such that
$\Phi _u \triangleright \, \Gamma \Vdash ^{(0,0,d_u)}_{\tt n} u\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, such that
 $d = 1 + d_u$
. By applying the i.h. to
$d = 1 + d_u$
. By applying the i.h. to
 $\Phi _u$
, we get
$\Phi _u$
, we get
 $u \in {\tt ne}_{{\tt n}}$
and
$u \in {\tt ne}_{{\tt n}}$
and
 $d_u = |{t}|_{\texttt {n}}$
. Thus, we can conclude that with
$d_u = |{t}|_{\texttt {n}}$
. Thus, we can conclude that with
 $d = 1 + d_u = 1+|{t}|_{\texttt {n}} = |{up}|_{\texttt {n}}$
(satisfying 1c) and
$d = 1 + d_u = 1+|{t}|_{\texttt {n}} = |{up}|_{\texttt {n}}$
(satisfying 1c) and
 $up \in {\tt ne}_{{\tt n}}$
(satisfying 1a).
$up \in {\tt ne}_{{\tt n}}$
(satisfying 1a).
-
-
(2) By induction over
 $\Pi$
:
$\Pi$
:-
• Case
 $\Pi$
ends with (emp). Then,
$\Pi$
ends with (emp). Then,
 $s = \varepsilon$
and
$s = \varepsilon$
and
 $\Pi \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} \varepsilon :\emptyset$
, where
$\Pi \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} \varepsilon :\emptyset$
, where
 $d = 0 = |{\varepsilon }|_{\texttt {n}}$
. Thus, we can conclude.
$d = 0 = |{\varepsilon }|_{\texttt {n}}$
. Thus, we can conclude. -
• Case
 $\Pi$
ends with (upd). Then,
$\Pi$
ends with (upd). Then,
 $s = {\tt upd}_{l}(u,q)$
and
$s = {\tt upd}_{l}(u,q)$
and
 $\Pi$
has two premises
$\Pi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
and
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
and
 $\Pi _q \triangleright \Delta _q\Vdash ^{(b_q,m_q,d_q)}_{\tt n} q\;:\;{\{l \;:\; \mathscr{L\;}\};\;\mathscr{T\;}_q}$
, where
$\Pi _q \triangleright \Delta _q\Vdash ^{(b_q,m_q,d_q)}_{\tt n} q\;:\;{\{l \;:\; \mathscr{L\;}\};\;\mathscr{T\;}_q}$
, where
 $\Delta = \Gamma _u + \Delta _q$
,
$\Delta = \Gamma _u + \Delta _q$
,
 $\mathscr{T\;} = \{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;}_q$
, and
$\mathscr{T\;} = \{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;}_q$
, and
 $d = d_{u} + d_q$
. Since we are assuming that
$d = d_{u} + d_q$
. Since we are assuming that
 $\mathscr{T\;}$
is tight, then
$\mathscr{T\;}$
is tight, then
 $\mathscr{M} = [ \, ]$
. Therefore,
$\mathscr{M} = [ \, ]$
. Therefore,
 $b_u = m_u = d_u = 0$
. By applying the i.h. to
$b_u = m_u = d_u = 0$
. By applying the i.h. to
 $\Pi _q$
, we get
$\Pi _q$
, we get
 $b_q = m_q = d_q = 0$
. Thus, we can conclude with
$b_q = m_q = d_q = 0$
. Thus, we can conclude with
 $b = b_u + b_q = m = m_u + m_q = d = d_u +d_q = 0$
.
$b = b_u + b_q = m = m_u + m_q = d = d_u +d_q = 0$
.
-
Lemma 8 (Normal forms take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mu$
be a tight derivation. Then,
![]() $b = m = 0$
iff
$b = m = 0$
iff
![]() $t \in {\tt no}_{{\tt n}}$
.
$t \in {\tt no}_{{\tt n}}$
.
Proof.
-
⇒) By Lemma 7.1.1a.
-
⇐) By induction on
 $t \in {\tt no}_{{\tt n}}$
:
$t \in {\tt no}_{{\tt n}}$
:
-
– Case
 $t = \lambda x.u$
. Then,
$t = \lambda x.u$
. Then,
 $\Phi$
must end with (
$\Phi$
must end with (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
):
$\lambda _{\tt p}$
):-
* Rule (m). Then,
 $\Phi$
does not end with a tight monadic type. Therefore, this case does not apply.
$\Phi$
does not end with a tight monadic type. Therefore, this case does not apply. -
* Rules (
 $\lambda$
) or (
$\lambda$
) or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $\mu = \mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow \mu ) \times \mathscr{T\;}')$
or
$\mu = \mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow \mu ) \times \mathscr{T\;}')$
or
 $\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;}')$
, respectively. In the former case,
$\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;}')$
, respectively. In the former case,
 $\Phi$
does not conclude with a tight type; therefore, it cannot apply. In the latter case
$\Phi$
does not conclude with a tight type; therefore, it cannot apply. In the latter case
 $b = m = 0$
by definition, and we can conclude.
$b = m = 0$
by definition, and we can conclude.
-
-
– Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}}$
:
$t \in {\tt ne}_{{\tt n}}$
:-
* Case
 $t = x$
. Then
$t = x$
. Then
 $\Phi$
must end with rule (ax) and
$\Phi$
must end with rule (ax) and
 $b = m = 0$
by definition.
$b = m = 0$
by definition. -
* Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. Then
$u \in {\tt ne}_{{\tt n}}$
. Then
 $\Phi$
must end with rule (@), (m), or (@
$\Phi$
must end with rule (@), (m), or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
· Rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')$
and
$\Phi _u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')$
and
 $\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M}$
, such that
$\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M}$
, such that
 $\Gamma = \Gamma _u + \Gamma _p$
is tight,
$\Gamma = \Gamma _u + \Gamma _p$
is tight,
 $b = 1 + b_u + b_p$
,
$b = 1 + b_u + b_p$
,
 $m = m_u + m_p$
, and
$m = m_u + m_p$
, and
 $d = d_u + d_p$
. Moreover,
$d = d_u + d_p$
. Moreover,
 $\Gamma _u$
and
$\Gamma _u$
and
 $\Gamma _p$
are tight. By applying Lemma 34 to
$\Gamma _p$
are tight. By applying Lemma 34 to
 $u$
, we get that
$u$
, we get that
 $\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}') ={\tt n}$
, which is a contradiction. Therefore, this case cannot apply.
$\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}') ={\tt n}$
, which is a contradiction. Therefore, this case cannot apply. -
· Rule (m). Then,
 $\Phi$
does not end with a tight monadic type. Therefore, this case does not apply.
$\Phi$
does not end with a tight monadic type. Therefore, this case does not apply. -
· Rule (
 ${\tt @}_{{\tt p}}$
). Then,
${\tt @}_{{\tt p}}$
). Then,
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi _u \triangleright \, \Gamma \Vdash ^{(b,m,d_u)}_{\mathtt {n}} u\;:\;\mathscr{T\;} \Rightarrow (\mathtt {n} \times {\mathscr{T\;}}^{\prime })$
, such that
$\Phi _u \triangleright \, \Gamma \Vdash ^{(b,m,d_u)}_{\mathtt {n}} u\;:\;\mathscr{T\;} \Rightarrow (\mathtt {n} \times {\mathscr{T\;}}^{\prime })$
, such that
 $d = 1 + d_u$
. By applying the i.h. to
$d = 1 + d_u$
. By applying the i.h. to
 $u$
, we have
$u$
, we have
 $b = m = 0$
. Therefore, we can conclude.
$b = m = 0$
. Therefore, we can conclude.
-
-
Lemma 9 (Normal configurations have correct size). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation of the following form:
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation of the following form:
where
![]() $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
![]() $\kappa = (\tau \times \mathscr{T\;}')$
,
$\kappa = (\tau \times \mathscr{T\;}')$
,
![]() $b = b_t + b_s$
,
$b = b_t + b_s$
,
![]() $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
![]() $d = d_t + d_s$
. If
$d = d_t + d_s$
. If
![]() $b_t = m_t = 0$
, then (i)
$b_t = m_t = 0$
, then (i)
![]() $d = |{(t,s)}|_{\texttt {n}}$
and
$d = |{(t,s)}|_{\texttt {n}}$
and
![]() $b = m = 0$
.
$b = m = 0$
.
Proof.
Since
![]() $\Gamma$
is tight, then so are
$\Gamma$
is tight, then so are
![]() $\Gamma _t$
and
$\Gamma _t$
and
![]() $\Delta _s$
. Since
$\Delta _s$
. Since
![]() $b_t = m_t = 0$
, then
$b_t = m_t = 0$
, then
![]() $t \in {\tt no}_{{\tt n}}$
by Lemma 7.1.1a and
$t \in {\tt no}_{{\tt n}}$
by Lemma 7.1.1a and
![]() $d_t = |{t}|_{\texttt {n}}$
by Lemma 7.1.1b. Therefore,
$d_t = |{t}|_{\texttt {n}}$
by Lemma 7.1.1b. Therefore,
![]() $\mathscr{T\;} = \mathscr{T\;}'$
by Lemma6. Therefore,
$\mathscr{T\;} = \mathscr{T\;}'$
by Lemma6. Therefore,
![]() $\mathscr{T\;}$
is tight and
$\mathscr{T\;}$
is tight and
![]() $b_s = m_s = d_s = 0$
by Lemma 7.2. Thus, we can conclude with
$b_s = m_s = d_s = 0$
by Lemma 7.2. Thus, we can conclude with
![]() $d = d_t + d_s = d_t = |{t}|_{\texttt {n}} = |{(t,s)}|_{\texttt {n}}$
and
$d = d_t + d_s = d_t = |{t}|_{\texttt {n}} = |{(t,s)}|_{\texttt {n}}$
and
![]() $b = b_t + b_s = m = m_t + m_s = 0$
.
$b = b_t + b_s = m = m_t + m_s = 0$
.
Lemma 10 (Normal configurations take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation. Then,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
be a tight derivation. Then,
![]() $b = m = 0$
iff
$b = m = 0$
iff
![]() $(t,s)$
is an unblocked normal configuration.
$(t,s)$
is an unblocked normal configuration.
Proof.
Derivation
![]() $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
where
![]() $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
![]() $\kappa = (\tau \times \mathscr{T\;}')$
,
$\kappa = (\tau \times \mathscr{T\;}')$
,
![]() $b = b_t + b_s$
,
$b = b_t + b_s$
,
![]() $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
![]() $d = d_t + d_s$
.
$d = d_t + d_s$
.
-
⇒) Let
 $b = m = 0$
. Then,
$b = m = 0$
. Then,
 $b_t = m_t = 0$
, and thus,
$b_t = m_t = 0$
, and thus,
 $t \in {\tt no}_{{\tt n}}$
, by Lemma 8. And we can conclude that
$t \in {\tt no}_{{\tt n}}$
, by Lemma 8. And we can conclude that
 $(t,s)$
is in normal form.
$(t,s)$
is in normal form. -
⇐) Let
 $(t,s)$
be in normal form. Then,
$(t,s)$
be in normal form. Then,
 $t \in {\tt no}_{{\tt n}}$
, by definition. Thus,
$t \in {\tt no}_{{\tt n}}$
, by definition. Thus,
 $b_t = m_t = 0$
, by Lemma 8. And we can conclude that
$b_t = m_t = 0$
, by Lemma 8. And we can conclude that
 $b = m = 0$
, by Lemma 9.
$b = m = 0$
, by Lemma 9.
Lemma 11 (Tight typability of states and normal forms).
-
(1) Let
 $s$
be a state. Then, there exists a tight derivation
$s$
be a state. Then, there exists a tight derivation
 $\Pi _s \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} s\;:\;\mathscr{T\;}$
.
$\Pi _s \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} s\;:\;\mathscr{T\;}$
. -
(2) Let
 $t \in {\tt no}_{{\tt n}}$
. Then, for any
$t \in {\tt no}_{{\tt n}}$
. Then, for any
 $\mathscr{T\;}$
, there exists a tight derivation
$\mathscr{T\;}$
, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t \;:\; \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;})$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t \;:\; \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;})$
, such that
 $d = |{t}|_{\texttt {n}}$
.
$d = |{t}|_{\texttt {n}}$
.
Proof.
-
(1) By induction on
 $s$
:
$s$
:-
• Case
 $s = \varepsilon$
. Then, we can build
$s = \varepsilon$
. Then, we can build
 $\Pi \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} \varepsilon :\emptyset$
by rule (emp), such that
$\Pi \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt n} \varepsilon :\emptyset$
by rule (emp), such that
 $\mathscr{T\;} = \emptyset$
is tight.
$\mathscr{T\;} = \emptyset$
is tight. -
• Case
 $s = {\tt upd}_{l}(t,q)$
. By applying the i.h. to
$s = {\tt upd}_{l}(t,q)$
. By applying the i.h. to
 $q$
, there exists a tight derivation
$q$
, there exists a tight derivation
 $\Pi _q \triangleright \, \Vdash ^{(0,0,0)}_{\tt n} q:{\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0}$
. Therefore, we can build
$\Pi _q \triangleright \, \Vdash ^{(0,0,0)}_{\tt n} q:{\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0}$
. Therefore, we can build
 $\Pi _s$
as follows:
$\Pi _s$
as follows:
where
 $\mathscr{T\;} = \{l \;:\; [ \, ] \cdot \mathscr{L\;}\};\; \mathscr{T\;}_0$
is tight.
$\mathscr{T\;} = \{l \;:\; [ \, ] \cdot \mathscr{L\;}\};\; \mathscr{T\;}_0$
is tight.
-
-
(2) We start by refining the original statement as follows:
-
a. Let
 $t \in {\tt ne}_{{\tt n}}$
. Then, for any
$t \in {\tt ne}_{{\tt n}}$
. Then, for any
 $\mathscr{T\;}$
, there exists a tight derivation
$\mathscr{T\;}$
, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})$
, such that
 $d = |{t}|_{\texttt {n}}$
.
$d = |{t}|_{\texttt {n}}$
. -
b. Let
 $t \in {\tt no}_{{\tt n}}$
. Then, for any
$t \in {\tt no}_{{\tt n}}$
. Then, for any
 $\mathscr{T\;}$
, there exists a tight derivation
$\mathscr{T\;}$
, there exists a tight derivation
 $\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;})$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}} \times \mathscr{T\;})$
, such that
 $d = |{t}|_{\texttt {n}}$
.
$d = |{t}|_{\texttt {n}}$
.
The proof now goes as follows:
-
a. We reason by induction over
 $t \in {\tt ne}$
:
$t \in {\tt ne}$
:-
• Case
 $t = x$
. Then we can build
$t = x$
. Then we can build
 $\Phi$
by using rule (ax), such that
$\Phi$
by using rule (ax), such that
 $b = m = d = 0 = |{x}|_{\texttt {n}}$
and
$b = m = d = 0 = |{x}|_{\texttt {n}}$
and
 ${{\tt tt}_{\tt n}} = {\tt n}$
.
${{\tt tt}_{\tt n}} = {\tt n}$
. -
• Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt n}}$
. By applying the i.h. (a.) to
$u \in {\tt ne}_{{\tt n}}$
. By applying the i.h. (a.) to
 $u$
, we get
$u$
, we get
 $\Phi _u \triangleright \, \Gamma _u\Vdash ^{(0,0,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}}' \times \mathscr{T\;})$
, such that
$\Phi _u \triangleright \, \Gamma _u\Vdash ^{(0,0,d_u)}_{\tt n} u\;:\;\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt n}}' \times \mathscr{T\;})$
, such that
 $\Gamma _u$
is tight and
$\Gamma _u$
is tight and
 $d_u = |{t}|_{\texttt {n}}$
, for any
$d_u = |{t}|_{\texttt {n}}$
, for any
 $\mathscr{T\;}$
. Moreover, since
$\mathscr{T\;}$
. Moreover, since
 $\Gamma _u$
and
$\Gamma _u$
and
 $u \in {\tt ne}_{{\tt n}}$
, then
$u \in {\tt ne}_{{\tt n}}$
, then
 ${{\tt tt}_{\tt n}} = {\tt n}$
, according to Lemma 34. Therefore, we can build
${{\tt tt}_{\tt n}} = {\tt n}$
, according to Lemma 34. Therefore, we can build
 $\Phi$
is as follows:such that
$\Phi$
is as follows:such that \begin{equation*} \frac {\Phi _u}{\Gamma _u \Vdash ^{(0,0,1+d_u)} up: \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})}({\tt @}_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _u}{\Gamma _u \Vdash ^{(0,0,1+d_u)} up: \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;})}({\tt @}_{{\tt p}})\end{equation*}
 $\Gamma = \Gamma _u$
, and
$\Gamma = \Gamma _u$
, and
 $d = 1+d_u = 1+|{u}|_{\texttt {u}} = |{up}|_{\texttt {n}}$
.
$d = 1+d_u = 1+|{u}|_{\texttt {u}} = |{up}|_{\texttt {n}}$
.
-
-
b. We reason by induction over
 $t \in {\tt no}$
:
$t \in {\tt no}$
:-
• Case
 $t = \lambda x.u$
. Then we can build
$t = \lambda x.u$
. Then we can build
 $\Phi$
by using rule (
$\Phi$
by using rule (
 $\lambda _{\tt p}$
), such that
$\lambda _{\tt p}$
), such that
 $b = m = d = 0 = |\lambda {x.u}|_{\texttt {n}}$
and
$b = m = d = 0 = |\lambda {x.u}|_{\texttt {n}}$
and
 ${{\tt tt}_{\tt n}} = {\tt a}$
.
${{\tt tt}_{\tt n}} = {\tt a}$
. -
• Case
 $\neg {\tt abs}(t)$
. Then
$\neg {\tt abs}(t)$
. Then
 $t \in {\tt ne}_{{\tt n}}$
and we can conclude by (a.).
$t \in {\tt ne}_{{\tt n}}$
and we can conclude by (a.).
-
-
Lemma 12 (All unblocked normal configurations are tightly typable). If
![]() $(t,s)$
is a normal but unblocked configuration, then there exists a tight typing derivation
$(t,s)$
is a normal but unblocked configuration, then there exists a tight typing derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} (t,s):\kappa$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(0,0,d)}_{\tt n} (t,s):\kappa$
, such that
![]() $d = |{(t,s)}|_{\texttt {n}}$
.
$d = |{(t,s)}|_{\texttt {n}}$
.
Proof. By Lemma 11.
Lemma 35.
Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $\tau = {\tt n}$
, then
$\tau = {\tt n}$
, then
![]() $\neg {\tt abs}(t)$
.
$\neg {\tt abs}(t)$
.
Proof.
By induction over
![]() $\Phi$
:
$\Phi$
:
-
• Case
 $\Phi$
ends with rule (ax), (@), (get), (set), (@
$\Phi$
ends with rule (ax), (@), (get), (set), (@
 $_{{\tt p}}$
), then
$_{{\tt p}}$
), then
 $\neg {\tt abs}(t)$
holds by definition.
$\neg {\tt abs}(t)$
holds by definition. -
• Case
 $\Phi$
ends with rule (m). Then
$\Phi$
ends with rule (m). Then
 $\Phi$
does not conclude with a monadic type. Therefore, these cases cannot apply.
$\Phi$
does not conclude with a monadic type. Therefore, these cases cannot apply. -
• Case
 $\Phi$
ends with rules (
$\Phi$
ends with rules (
 $\lambda$
) or (
$\lambda$
) or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $t = \lambda x.u$
and
$t = \lambda x.u$
and
 $\tau = \mathscr{M} \rightarrow \mu$
or
$\tau = \mathscr{M} \rightarrow \mu$
or
 $\tau = {\tt a}$
, respectively. Therefore, these case do not apply.
$\tau = {\tt a}$
, respectively. Therefore, these case do not apply.
Lemma 36 (Multi-types can split and merge). Let
![]() $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
![]() $b = +_{i \in I} b_i$
,
$b = +_{i \in I} b_i$
,
![]() $m = +_{i \in I} m_i$
, and
$m = +_{i \in I} m_i$
, and
![]() $d = +_{i \in I}$
. Then,
$d = +_{i \in I}$
. Then,
![]() $\Phi _t \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{M}$
iff
$\Phi _t \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} t\;:\;\mathscr{M}$
iff
![]() $(\Phi ^i_t \triangleright \, \Gamma _i\Vdash ^{(b_i,m_i,d_i)}_{\tt n} t\;:\;\mathscr{M}_i)_{i \in I}$
.
$(\Phi ^i_t \triangleright \, \Gamma _i\Vdash ^{(b_i,m_i,d_i)}_{\tt n} t\;:\;\mathscr{M}_i)_{i \in I}$
.
Proof. We omit this proof given its similarity with the proof for Weak Open CBN with Global State.
Lemma 37 (States can Split). Let
![]() $\Pi _s \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
$\Pi _s \triangleright \Delta \Vdash ^{(b,m,d)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
![]() $l \in {\tt dom}(\mathscr{T\;})$
. Then,
$l \in {\tt dom}(\mathscr{T\;})$
. Then,
![]() $s \equiv {\tt upd}_{l}(t,q)$
,
$s \equiv {\tt upd}_{l}(t,q)$
,
![]() $\mathscr{T\;}(l) = \mathscr{M} \cdot \mathscr{L\;}$
,
$\mathscr{T\;}(l) = \mathscr{M} \cdot \mathscr{L\;}$
,
![]() $\Phi _t \triangleright \, \Gamma _t\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{M}$
and
$\Phi _t \triangleright \, \Gamma _t\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{M}$
and
![]() $\Pi _q \triangleright \Delta _q \Vdash ^{(b_q,m_q,d_q)}_{\tt n} q\;:\;\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;}'$
, such that
$\Pi _q \triangleright \Delta _q \Vdash ^{(b_q,m_q,d_q)}_{\tt n} q\;:\;\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;}'$
, such that
![]() $\Delta = \Gamma _t + \Delta _q$
,
$\Delta = \Gamma _t + \Delta _q$
,
![]() $\mathscr{T\;} = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}'$
,
$\mathscr{T\;} = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}'$
,
![]() $b = b_t+b_q$
,
$b = b_t+b_q$
,
![]() $m = m_t+m_q$
, and
$m = m_t+m_q$
, and
![]() $d = d_t + d_q$
.
$d = d_t + d_q$
.
Proof.
The proof follows by induction on the structure of
![]() $s$
:
$s$
:
-
• Case
 $s = \varepsilon$
. Then the statement is vacuously true.
$s = \varepsilon$
. Then the statement is vacuously true. -
• Case
 $s = {\tt upd}_{l'}(u,q')$
. Then
$s = {\tt upd}_{l'}(u,q')$
. Then
 $\Phi _s$
is of the form:where
$\Phi _s$
is of the form:where \begin{equation*} \frac {\Phi _{u} \triangleright \, \Gamma _{u}\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M\;}'\qquad \Pi _{q'} \triangleright \Delta _{q'}\Vdash ^{(b_{q'}, m_{q'},d_{q'})}_{\tt n} q':\{l' \;:\; \mathscr{L\;}\};\;\mathscr{T\;}_{q'}}{\Gamma _{u} + \Delta _{q'} \Vdash ^{(b_u+b_{q'},m_u+m_{q'},d_u+d_{q'})} {\tt upd}_{l'}(u,q'): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi _{u} \triangleright \, \Gamma _{u}\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M\;}'\qquad \Pi _{q'} \triangleright \Delta _{q'}\Vdash ^{(b_{q'}, m_{q'},d_{q'})}_{\tt n} q':\{l' \;:\; \mathscr{L\;}\};\;\mathscr{T\;}_{q'}}{\Gamma _{u} + \Delta _{q'} \Vdash ^{(b_u+b_{q'},m_u+m_{q'},d_u+d_{q'})} {\tt upd}_{l'}(u,q'): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}}({\tt upd})\end{equation*}
 $\Delta = \Gamma _{u} + \Delta _{q'}$
,
$\Delta = \Gamma _{u} + \Delta _{q'}$
,
 $\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
,
$\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
,
 $b = b_u + b_{q'}$
,
$b = b_u + b_{q'}$
,
 $m = m_u + m_{q'}$
, and
$m = m_u + m_{q'}$
, and
 $d = d_u + d_{q'}$
. We consider two cases:
$d = d_u + d_{q'}$
. We consider two cases:-
– Case
 $l' = l$
. Then we simply take
$l' = l$
. Then we simply take
 $t = u$
,
$t = u$
,
 $q = q'$
,
$q = q'$
,
 $\mathscr{M\;}' = \mathscr{M}$
, and
$\mathscr{M\;}' = \mathscr{M}$
, and
 $\mathscr{L\;}' = \mathscr{L\;}$
, and we are done.
$\mathscr{L\;}' = \mathscr{L\;}$
, and we are done. -
– Case
 $l' \not = l$
. Since
$l' \not = l$
. Since
 $l \in {\tt dom}(\{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})$
and
$l \in {\tt dom}(\{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})$
and
 $l' \not = l$
, then
$l' \not = l$
, then
 $l \in {\tt dom}(\mathscr{T\;}_{q'})$
. By applying the i.h. to
$l \in {\tt dom}(\mathscr{T\;}_{q'})$
. By applying the i.h. to
 $q'$
, we have that
$q'$
, we have that
 $q' \equiv {\tt upd}_{l}(u',q'')$
,
$q' \equiv {\tt upd}_{l}(u',q'')$
,
 $(\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})(l) = \mathscr{T\;}_{q'}(l) = \mathscr{M\;}'' \cdot \mathscr{L\;}''$
,
$(\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})(l) = \mathscr{T\;}_{q'}(l) = \mathscr{M\;}'' \cdot \mathscr{L\;}''$
,
 $\Phi _{u'} \triangleright \, \Gamma _{u'}\Vdash ^{(b_{u'},m_{u'},d_{u'})}_{\tt n} u':\mathscr{M\;}''$
and
$\Phi _{u'} \triangleright \, \Gamma _{u'}\Vdash ^{(b_{u'},m_{u'},d_{u'})}_{\tt n} u':\mathscr{M\;}''$
and
 $\Pi _{q''} \triangleright \Delta _{q''}\Vdash ^{(b_{q''},m_{q''},d_{q''})}_{\tt n} q'': conjil \;:\; \mathscr{L\;}'' ;\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
, such that
$\Pi _{q''} \triangleright \Delta _{q''}\Vdash ^{(b_{q''},m_{q''},d_{q''})}_{\tt n} q'': conjil \;:\; \mathscr{L\;}'' ;\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
, such that
 $\Delta _{q'} = \Gamma _{u'} + \Delta _{q''}$
,
$\Delta _{q'} = \Gamma _{u'} + \Delta _{q''}$
,
 $\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'} = \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
,
$\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'} = \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
,
 $b_{q'} = b_{u'} + b_{q''}$
,
$b_{q'} = b_{u'} + b_{q''}$
,
 $m_{q'} = m_{u'} + m_{q''}$
, and
$m_{q'} = m_{u'} + m_{q''}$
, and
 $d_{q'} = d_{u'} + d_{q''}$
. Therefore,
$d_{q'} = d_{u'} + d_{q''}$
. Therefore,
 $\mathscr{T\;}_{q'} = \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
. But
$\mathscr{T\;}_{q'} = \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
. But
 $s = {\tt upd}_{l'}(u,{\tt upd}_{l}(u',q'')) \equiv {\tt upd}_{l}(u',{\tt upd}_{l'}(u,q''))$
, so we can take
$s = {\tt upd}_{l'}(u,{\tt upd}_{l}(u',q'')) \equiv {\tt upd}_{l}(u',{\tt upd}_{l'}(u,q''))$
, so we can take
 $t = u'$
,
$t = u'$
,
 $q = {\tt upd}_{l'}(u,q'')$
,
$q = {\tt upd}_{l'}(u,q'')$
,
 $\mathscr{M} = \mathscr{M\;}''$
,
$\mathscr{M} = \mathscr{M\;}''$
,
 $\mathscr{L\;} = \mathscr{L\;}''$
, and
$\mathscr{L\;} = \mathscr{L\;}''$
, and
 $\mathscr{T\;}' = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
, and consider
$\mathscr{T\;}' = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
, and consider
 $\Phi _q$
to be the following derivation:where
$\Phi _q$
to be the following derivation:where \begin{equation*} \frac {\Phi _{u} \triangleright \, \Gamma _{u}\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M\;}'\qquad \Pi _{q''} \triangleright \Delta _{q''}\Vdash ^{(b_{q''}, m_{q''}, d_{q''})}_{\tt n} q'':\{l' \;:\; \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}{\Gamma _{u} + \Delta _{q''} \Vdash ^{(b_u+b_{q''}, m_u + m_{q''}, d_u+d_{q''})} {\tt upd}_{l'}(u,q''): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}({\tt upd})=\end{equation*}
\begin{equation*} \frac {\Phi _{u} \triangleright \, \Gamma _{u}\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M\;}'\qquad \Pi _{q''} \triangleright \Delta _{q''}\Vdash ^{(b_{q''}, m_{q''}, d_{q''})}_{\tt n} q'':\{l' \;:\; \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}{\Gamma _{u} + \Delta _{q''} \Vdash ^{(b_u+b_{q''}, m_u + m_{q''}, d_u+d_{q''})} {\tt upd}_{l'}(u,q''): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}({\tt upd})=\end{equation*}
 $\Delta _q = \Gamma _{u} + \Delta _{q''}$
and
$\Delta _q = \Gamma _{u} + \Delta _{q''}$
and
 $\mathscr{T\;}_q=\{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
. We can then conclude with the following observations:
$\mathscr{T\;}_q=\{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
. We can then conclude with the following observations:-
*
 $\Gamma _t + \Delta _q = \Gamma _{u'} +\Gamma _{u} + \Delta _{q''} = \Gamma _{u} + \Delta _{q'} = \Delta$
,
$\Gamma _t + \Delta _q = \Gamma _{u'} +\Gamma _{u} + \Delta _{q''} = \Gamma _{u} + \Delta _{q'} = \Delta$
, -
* Since
 $\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
and
$\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
and
 $l' \not = l$
, then
$l' \not = l$
, then
 $\mathscr{T\;}(l) = \mathscr{T\;}_{q'}(l)$
and
$\mathscr{T\;}(l) = \mathscr{T\;}_{q'}(l)$
and \begin{align*} \mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}\};\; \mathscr{T\;}_{q'} & = \{l': \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}_{q'}(l)\};\; \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}' \end{align*}
\begin{align*} \mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}\};\; \mathscr{T\;}_{q'} & = \{l': \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}_{q'}(l)\};\; \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}' \end{align*}
-
*
 $b_v + b_q= b_{u'} + b_{u} + b_{q''}= b_u + b_{q'} = b$
,
$b_v + b_q= b_{u'} + b_{u} + b_{q''}= b_u + b_{q'} = b$
,
 $m_v + m_q= m_{u'} + m_{u} + m_{q''}= m_u + m_{q'} = m$
and
$m_v + m_q= m_{u'} + m_{u} + m_{q''}= m_u + m_{q'} = m$
and
 $d_v + d_q= d_{u'} + d_{u} + d_{q''}= d_u + d_{q'} = d$
.
$d_v + d_q= d_{u'} + d_{u} + d_{q''}= d_u + d_{q'} = d$
.
-
-
Lemma 38 (Substitution). If
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mu$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mu$
and
![]() $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, then
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, then
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u \Vdash ^{(b_t+b_u,m_t+m_u,d_t+d_u)} t \{x \setminus u\}\;:\; \mu$
.
$\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u \Vdash ^{(b_t+b_u,m_t+m_u,d_t+d_u)} t \{x \setminus u\}\;:\; \mu$
.
Proof.
We generalize the original statement by allowing
![]() $\Phi _t$
to conclude with either a monadic type
$\Phi _t$
to conclude with either a monadic type
![]() $\mu$
or a multi-type
$\mu$
or a multi-type
![]() $\mathscr{M}_0$
. Let
$\mathscr{M}_0$
. Let
![]() $\mathscr{G\,} \in \{\mu , \mathscr{M}_0\}$
. Then the statement is as follows:
$\mathscr{G\,} \in \{\mu , \mathscr{M}_0\}$
. Then the statement is as follows:
If
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{G\,}$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{G\,}$
and
![]() $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, then
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, then
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u\Vdash ^{(b_t+b_u,m_t+m_u,d_t+d_u)}_{\tt n} t \{x \setminus u\}\;:\;\mathscr{G\,}$
.
$\Phi _{t \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u\Vdash ^{(b_t+b_u,m_t+m_u,d_t+d_u)}_{\tt n} t \{x \setminus u\}\;:\;\mathscr{G\,}$
.
The proof follows by induction over
![]() $\Phi _t$
, according to the last rule of
$\Phi _t$
, according to the last rule of
![]() $\Phi _t$
:
$\Phi _t$
:
-
• Case
 $\mathscr{G\,} = \mu$
. Then,
$\mathscr{G\,} = \mu$
. Then,
 $\Phi _t$
must end with rule (ax), (
$\Phi _t$
must end with rule (ax), (
 $\lambda$
), (
$\lambda$
), (
 $\lambda _{\tt p}$
), (@), (get), (set), or (@
$\lambda _{\tt p}$
), (@), (get), (set), or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Rule (ax). Then,
 $t = y$
and there are two cases:
$t = y$
and there are two cases:-
*
 $y = x$
. Then,
$y = x$
. Then,
 $x \{x \setminus u\} = u$
and
$x \{x \setminus u\} = u$
and
 $\Phi _t \triangleright \, \emptyset ; (x \;:\; [ \mu ])\Vdash ^{(0,0,0)}_{\tt n} x\;:\;\mu$
, where
$\Phi _t \triangleright \, \emptyset ; (x \;:\; [ \mu ])\Vdash ^{(0,0,0)}_{\tt n} x\;:\;\mu$
, where
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{M} = [ \mu ]$
, and
$\mathscr{M} = [ \mu ]$
, and
 $b_t = m_t = d_t = 0$
. Moreover,
$b_t = m_t = d_t = 0$
. Moreover,
 $\Phi _u$
must end with rule (m), and have one premise
$\Phi _u$
must end with rule (m), and have one premise
 $\Phi '_u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mu$
. So we can take
$\Phi '_u \triangleright \, \Gamma _u\Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mu$
. So we can take
 $\Phi _{t \{x \setminus u\}} = \Phi '_u$
, and conclude with
$\Phi _{t \{x \setminus u\}} = \Phi '_u$
, and conclude with
 $\Gamma _t + \Gamma _u = \Gamma _u$
,
$\Gamma _t + \Gamma _u = \Gamma _u$
,
 $b_t + b_u = b_u$
,
$b_t + b_u = b_u$
,
 $m_t + m_u = m_u$
, and
$m_t + m_u = m_u$
, and
 $d_t + d_u = d_u$
.
$d_t + d_u = d_u$
. -
*
 $y \neq x$
. Then,
$y \neq x$
. Then,
 $y \{x \setminus u\} = y$
,
$y \{x \setminus u\} = y$
,
 $\Gamma _t = (y \;:\; [ \mu ])$
,
$\Gamma _t = (y \;:\; [ \mu ])$
,
 $\mathscr{M} = [ \, ]$
,
$\mathscr{M} = [ \, ]$
,
 $b_t = m_t = d_t = 0$
. Moreover,
$b_t = m_t = d_t = 0$
. Moreover,
 $\Phi _u$
ends with rule (m) with no premises. Therefore,
$\Phi _u$
ends with rule (m) with no premises. Therefore,
 $\Gamma _u = \emptyset$
, and
$\Gamma _u = \emptyset$
, and
 $b_u = m_u = d_u = 0$
. So we can pick
$b_u = m_u = d_u = 0$
. So we can pick
 $\Phi _{t \{x \setminus u\}} = \Phi _t$
, where
$\Phi _{t \{x \setminus u\}} = \Phi _t$
, where
 $\Gamma _t + \Gamma _u = \Gamma _t$
,
$\Gamma _t + \Gamma _u = \Gamma _t$
,
 $b_t + b_u = b_t = 0$
,
$b_t + b_u = b_t = 0$
,
 $m_t + m_u = m_t = 0$
, and
$m_t + m_u = m_t = 0$
, and
 $d_t + d_u = d_t = 0$
.
$d_t + d_u = d_t = 0$
.
-
-
– Case
 $\Phi _t$
ends with (
$\Phi _t$
ends with (
 $\lambda$
). Then
$\lambda$
). Then
 $t = \lambda y.p$
,
$t = \lambda y.p$
,
 $\mu = \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ') \times \mathscr{T\;})$
, and
$\mu = \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ') \times \mathscr{T\;})$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _p \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mu '$
, where
$\Phi _p \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mu '$
, where
 $\Gamma _t = \Gamma _p$
(since we can assume that
$\Gamma _t = \Gamma _p$
(since we can assume that
 $y\neq x$
by
$y\neq x$
by
 $\alpha$
-conversion),
$\alpha$
-conversion),
 $b_t = b_p$
,
$b_t = b_p$
,
 $m_t = m_p$
, and
$m_t = m_p$
, and
 $d_t =d_p$
. By applying the i.h. to
$d_t =d_p$
. By applying the i.h. to
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _{p \{x \setminus u\}} \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u\Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)}_{\tt n} p \{x \setminus u\}\;:\;\mu '$
. Moreover, by
$\Phi _{p \{x \setminus u\}} \triangleright \, (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u\Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)}_{\tt n} p \{x \setminus u\}\;:\;\mu '$
. Moreover, by
 $\alpha$
-conversion, we can assume since
$\alpha$
-conversion, we can assume since
 $y \not \in {\tt dom}(\Gamma _u)$
, so that
$y \not \in {\tt dom}(\Gamma _u)$
, so that
 $(\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u = \Gamma _p + \Gamma _u;\; y \;:\; \mathscr{M\;}'$
. Therefore, we can build
$(\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u = \Gamma _p + \Gamma _u;\; y \;:\; \mathscr{M\;}'$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:And we can conclude since
$\Phi _{t \{x \setminus u\}}$
as follows:And we can conclude since \begin{equation*} \frac {\Phi _{p \{x \setminus u\}}}{\Gamma _p + \Gamma _u \Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)} \lambda y.(p \{x \setminus u\}): \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ) \times \mathscr{T\;})}(\lambda )\end{equation*}
\begin{equation*} \frac {\Phi _{p \{x \setminus u\}}}{\Gamma _p + \Gamma _u \Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)} \lambda y.(p \{x \setminus u\}): \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ) \times \mathscr{T\;})}(\lambda )\end{equation*}
 $\Gamma _t + \Gamma _u = \Gamma _p + \Gamma _u$
,
$\Gamma _t + \Gamma _u = \Gamma _p + \Gamma _u$
,
 $b_t+b_u = b_p+b_u$
,
$b_t+b_u = b_p+b_u$
,
 $m_t+m_u =m_p +m_u$
,
$m_t+m_u =m_p +m_u$
,
 $d_t+d_u=d_p+d_u$
, and
$d_t+d_u=d_p+d_u$
, and
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
.
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
.
-
– Case
 $\Phi _t$
ends with (
$\Phi _t$
ends with (
 $\lambda _{\tt p}$
). Then
$\lambda _{\tt p}$
). Then
 $t = \lambda y.p$
,
$t = \lambda y.p$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})$
, and
 $\Phi _t \triangleright \, \emptyset ;\; x \;:\; [ \, ]\Vdash ^{(0,0,0)}_{\tt n} \lambda y.p:{\tt a}$
, such that
$\Phi _t \triangleright \, \emptyset ;\; x \;:\; [ \, ]\Vdash ^{(0,0,0)}_{\tt n} \lambda y.p:{\tt a}$
, such that
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{M} = [ \, ]$
, and
$\mathscr{M} = [ \, ]$
, and
 $b_t = m_t = d_t = 0$
. Therefore,
$b_t = m_t = d_t = 0$
. Therefore,
 $\Phi _u$
ends with rule (m) with no premises, and
$\Phi _u$
ends with rule (m) with no premises, and
 $\Gamma _u = \emptyset$
. Therefore, we can build
$\Gamma _u = \emptyset$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:And we can conclude with \begin{equation*} \frac {}{\emptyset \Vdash ^{(0,0,0)} (\lambda y.p) \{x \setminus u\}\;:\; \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})}(\lambda _{\tt p})\end{equation*}
\begin{equation*} \frac {}{\emptyset \Vdash ^{(0,0,0)} (\lambda y.p) \{x \setminus u\}\;:\; \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})}(\lambda _{\tt p})\end{equation*}
 $\Gamma _t + \Gamma _u = \emptyset$
,
$\Gamma _t + \Gamma _u = \emptyset$
,
 $b_t + b_u = m_t + m_u = d_t +d_u = 0$
, and
$b_t + b_u = m_t + m_u = d_t +d_u = 0$
, and
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
.
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
.
-
– Rule (@). Then
 $t = rp$
,
$t = rp$
,
 $\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _r \triangleright \, \Gamma _r;\; x \;:\; \mathscr{M}_1\Vdash ^{(b_r,m_r,d_r)}_{\tt n} r\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')$
and
$\Phi _r \triangleright \, \Gamma _r;\; x \;:\; \mathscr{M}_1\Vdash ^{(b_r,m_r,d_r)}_{\tt n} r\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')$
and
 $\Phi _p \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M}_2\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M\;}'$
, where
$\Phi _p \triangleright \, \Gamma _p;\; x \;:\; \mathscr{M}_2\Vdash ^{(b_p,m_p,d_p)}_{\tt n} p\;:\;\mathscr{M\;}'$
, where
 $\Gamma _t = \Gamma _r + \Gamma _p$
,
$\Gamma _t = \Gamma _r + \Gamma _p$
,
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b_t = 1+b_r+b_p$
,
$b_t = 1+b_r+b_p$
,
 $m_t = m_r+m_p$
, and
$m_t = m_r+m_p$
, and
 $d_t = d_r + d_p$
. By Lemma 36, there exist
$d_t = d_r + d_p$
. By Lemma 36, there exist
 $(\Phi ^i_u \triangleright \, \Gamma ^i_u\Vdash ^{(b_i,m_i,d_i)}_{\tt n} u\;:\;\mathscr{M}_i)_{i \in \{1,2\}}$
, where
$(\Phi ^i_u \triangleright \, \Gamma ^i_u\Vdash ^{(b_i,m_i,d_i)}_{\tt n} u\;:\;\mathscr{M}_i)_{i \in \{1,2\}}$
, where
 $\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
$\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
 $b_u = b_1 + b_2$
,
$b_u = b_1 + b_2$
,
 $m_u = m_1 + m_2$
, and
$m_u = m_1 + m_2$
, and
 $d_u = d_1 + d_2$
. By applying the i.h. to
$d_u = d_1 + d_2$
. By applying the i.h. to
 $\Phi _r$
and
$\Phi _r$
and
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _r + \Gamma ^1_u\Vdash ^{(b_r+b_1,m_r+m_1,d_r+d_1)}_{\tt n} r \{x \setminus u\}\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) \times \mathscr{T\;}'))$
and
$\Phi _{r \{x \setminus u\}} \triangleright \, \Gamma _r + \Gamma ^1_u\Vdash ^{(b_r+b_1,m_r+m_1,d_r+d_1)}_{\tt n} r \{x \setminus u\}\;:\;\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) \times \mathscr{T\;}'))$
and
 $\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _p + \Gamma ^2_u\Vdash ^{(b_p+b_2,m_p+m_2,d_p+d_2)}_{\tt n} p \{x \setminus u\}\;:\;\mathscr{M\;}'$
. Therefore, we can build
$\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _p + \Gamma ^2_u\Vdash ^{(b_p+b_2,m_p+m_2,d_p+d_2)}_{\tt n} p \{x \setminus u\}\;:\;\mathscr{M\;}'$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{r \{x \setminus u\}}\qquad \Phi _{p \{x \setminus u\}}}{(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) \Vdash ^{(1+b_r+b_p+b_1+b_2,m_r+m_p+m_1+m_2,d_r+d_p+d_1+d_2)} (r \{x \setminus u\})(p \{x \setminus u\}): \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _{r \{x \setminus u\}}\qquad \Phi _{p \{x \setminus u\}}}{(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) \Vdash ^{(1+b_r+b_p+b_1+b_2,m_r+m_p+m_1+m_2,d_r+d_p+d_1+d_2)} (r \{x \setminus u\})(p \{x \setminus u\}): \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
 $t \{x \setminus u\} = (rp) \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
,
$t \{x \setminus u\} = (rp) \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
,
 $\Gamma _t + \Gamma _u = (\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u)$
,
$\Gamma _t + \Gamma _u = (\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u)$
,
 $b_t + b_u = (1 + b_r+b_p)+(b_1+b_2)$
,
$b_t + b_u = (1 + b_r+b_p)+(b_1+b_2)$
,
 $m_t + m_u = (m_r+m_p)+(m_1+m_2)$
, and
$m_t + m_u = (m_r+m_p)+(m_1+m_2)$
, and
 $d_t + d_u = (d_r+d_p)+(d_1+d_2)$
.
$d_t + d_u = (d_r+d_p)+(d_1+d_2)$
.
-
– Case
 $\Phi _t$
ends with (get). Then,
$\Phi _t$
ends with (get). Then,
 $t = {\tt get}_{l}(\lambda y.p)$
,
$t = {\tt get}_{l}(\lambda y.p)$
,
 $\mu = {\{l\;:\;\mathscr{M\;}' \sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
$\mu = {\{l\;:\;\mathscr{M\;}' \sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _p \triangleright \, (\Gamma _t;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p\,:\,}{{\{l\;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
$\Phi _p \triangleright \, (\Gamma _t;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p\,:\,}{{\{l\;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
 $b_t=b_p$
,
$b_t=b_p$
,
 $m_t = 1+m_p$
, and
$m_t = 1+m_p$
, and
 $d_t=d_p$
. By applying the i.h. over
$d_t=d_p$
. By applying the i.h. over
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _{p \{x \setminus u\}} \triangleright \, (\Gamma _t;\; y \;:\; \mathscr{M\;}') + \Gamma _u\Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)}_{\tt n} p \{x \setminus u\}\;:\;{\{l\;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
. Moreover, by
$\Phi _{p \{x \setminus u\}} \triangleright \, (\Gamma _t;\; y \;:\; \mathscr{M\;}') + \Gamma _u\Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)}_{\tt n} p \{x \setminus u\}\;:\;{\{l\;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
. Moreover, by
 $\alpha$
-conversion, we can assume since
$\alpha$
-conversion, we can assume since
 $y \not \in {\tt dom}(\Gamma _u)$
, so that
$y \not \in {\tt dom}(\Gamma _u)$
, so that
 $(\Gamma _t;\; y \;:\; \mathscr{M\;}') + \Gamma _u = \Gamma _t + \Gamma _u;\; y \;:\; \mathscr{M\;}'$
. Therefore, we can build
$(\Gamma _t;\; y \;:\; \mathscr{M\;}') + \Gamma _u = \Gamma _t + \Gamma _u;\; y \;:\; \mathscr{M\;}'$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u\Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)}_{\tt n} {p \{x \setminus u\}} \;:\; {{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }}{\Gamma _t + \Gamma _u \Vdash ^{(b_p+b_u,1+m_p+m_u,d_p+d_u)} {\tt get}_{l}(\lambda y.(p \{x \setminus u\})): {\{l\;:\;\mathscr{M\;}' \sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }({\tt get})\end{equation*}
\begin{equation*} \frac {\Phi _{p \{x \setminus u\}} \triangleright \, \Gamma _t + \Gamma _u\Vdash ^{(b_p+b_u,m_p+m_u,d_p+d_u)}_{\tt n} {p \{x \setminus u\}} \;:\; {{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }}{\Gamma _t + \Gamma _u \Vdash ^{(b_p+b_u,1+m_p+m_u,d_p+d_u)} {\tt get}_{l}(\lambda y.(p \{x \setminus u\})): {\{l\;:\;\mathscr{M\;}' \sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }({\tt get})\end{equation*}
 ${\tt get}_{l}(\lambda y.p) \{x \setminus u\} = {\tt get}_{l}(\lambda y.(p \{x \setminus u\}))$
, and
${\tt get}_{l}(\lambda y.p) \{x \setminus u\} = {\tt get}_{l}(\lambda y.(p \{x \setminus u\}))$
, and
 $b_t+b_u = b_p+b_u$
,
$b_t+b_u = b_p+b_u$
,
 $m_t + m_u = 1+m_p+m_u$
,
$m_t + m_u = 1+m_p+m_u$
,
 $d_t+d_u = d_p+d_u$
.
$d_t+d_u = d_p+d_u$
.
-
– Case
 $\Phi _t$
ends with (set). Then
$\Phi _t$
ends with (set). Then
 $t = {\tt set}_{l}(r,p)$
,
$t = {\tt set}_{l}(r,p)$
,
 $\mu = {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa$
, and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r} \;:\; {\mathscr{M\;}'}$
and
$\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r} \;:\; {\mathscr{M\;}'}$
and
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p} \;:\; {\{l \;:\; {\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
, where
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p} \;:\; {\{l \;:\; {\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
, where
 $\Gamma _t = \Gamma _r + \Gamma _p$
,
$\Gamma _t = \Gamma _r + \Gamma _p$
,
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b_t = b_r+b_p$
,
$b_t = b_r+b_p$
,
 $m_t = 1+m_r + m_p$
, and
$m_t = 1+m_r + m_p$
, and
 $d_t = d_r + d_p$
. By Lemma 36, there exist
$d_t = d_r + d_p$
. By Lemma 36, there exist
 $\Phi ^1_u \triangleright \, {\Gamma ^1_u}\,\Vdash ^{(b^1_u,m^1_u,d^1_u)}_{\tt n} {u}\,:\,{\mathscr{M}_1}$
and
$\Phi ^1_u \triangleright \, {\Gamma ^1_u}\,\Vdash ^{(b^1_u,m^1_u,d^1_u)}_{\tt n} {u}\,:\,{\mathscr{M}_1}$
and
 $\Phi ^2_u \triangleright \, {\Gamma ^2_u}\,\Vdash ^{(b^2_u,m^2_u,d^2_u)}_{\tt n} {u}\,:\,{\mathscr{M}_2}$
, where
$\Phi ^2_u \triangleright \, {\Gamma ^2_u}\,\Vdash ^{(b^2_u,m^2_u,d^2_u)}_{\tt n} {u}\,:\,{\mathscr{M}_2}$
, where
 $\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
$\Gamma _u = \Gamma ^1_u + \Gamma ^2_u$
,
 $b_u = b^1_u + b^2_u$
,
$b_u = b^1_u + b^2_u$
,
 $m_u = m^1_u + m^2_u$
, and
$m_u = m^1_u + m^2_u$
, and
 $d_u = d^1_u + d^2_u$
. By applying i.h. to
$d_u = d^1_u + d^2_u$
. By applying i.h. to
 $\Phi _r$
and
$\Phi _r$
and
 $\Phi _p$
, there exist
$\Phi _p$
, there exist
 $\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _r + \Gamma ^1_u}\,\Vdash ^{(b_r+b^1_u,m_r+m^1_u,d_r+d^1_u)}_{\tt n} {r \{x \setminus u\}}\,:\,{\mathscr{M\;}'}$
and
$\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _r + \Gamma ^1_u}\,\Vdash ^{(b_r+b^1_u,m_r+m^1_u,d_r+d^1_u)}_{\tt n} {r \{x \setminus u\}}\,:\,{\mathscr{M\;}'}$
and
 $\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _p + \Gamma ^2_u}\, \Vdash ^{(b_p+b^2_u,m_p+m^2_u,d_p+d^2_u)}_{\tt n} {p \{x \setminus u\}}\,:\,{\{l \;:\; {\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
$\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _p + \Gamma ^2_u}\, \Vdash ^{(b_p+b^2_u,m_p+m^2_u,d_p+d^2_u)}_{\tt n} {p \{x \setminus u\}}\,:\,{\{l \;:\; {\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{r \{x \setminus u\}}\qquad \Phi _{p \{x \setminus u\}}}{(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) \Vdash ^{(b_r+b_p+b^1_u+b^2_u,1+m_r+m_p+m^1_u+m^2_u,d_r+d_p+d^1_u+d^2_u)} {\tt set}_{l}(r \{x \setminus u\},p \{x \setminus u\}): {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa }({\tt set})\end{equation*}
\begin{equation*} \frac {\Phi _{r \{x \setminus u\}}\qquad \Phi _{p \{x \setminus u\}}}{(\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u) \Vdash ^{(b_r+b_p+b^1_u+b^2_u,1+m_r+m_p+m^1_u+m^2_u,d_r+d_p+d^1_u+d^2_u)} {\tt set}_{l}(r \{x \setminus u\},p \{x \setminus u\}): {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa }({\tt set})\end{equation*}
 ${\tt set}_{l}(r,p) \{x \setminus u\} = {\tt set}_{l}((t \{x \setminus u\}),(p \{x \setminus u\}))$
,
${\tt set}_{l}(r,p) \{x \setminus u\} = {\tt set}_{l}((t \{x \setminus u\}),(p \{x \setminus u\}))$
,
 $\Gamma _t + \Gamma _u = (\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u)$
,
$\Gamma _t + \Gamma _u = (\Gamma _r + \Gamma _p) + (\Gamma ^1_u + \Gamma ^2_u)$
,
 $b_t + b_u = (b_r+b_p)+(b^1_u+b^2_u)$
,
$b_t + b_u = (b_r+b_p)+(b^1_u+b^2_u)$
,
 $m_t + m_u = (1+m_r+m_p)+(m^1_u+m^2_u)$
, and
$m_t + m_u = (1+m_r+m_p)+(m^1_u+m^2_u)$
, and
 $d_t + d_u = (d_r+d_p)+(d^1_u+d^2_u)$
.
$d_t + d_u = (d_r+d_p)+(d^1_u+d^2_u)$
.
-
– Case
 $\Phi _t$
ends with (@
$\Phi _t$
ends with (@
 $_{{\tt p}}$
). Then
$_{{\tt p}}$
). Then
 $t = pr$
,
$t = pr$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _p \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
,
$\Phi _p \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
,
 $b_t=b_p$
,
$b_t=b_p$
,
 $m_t=m_p$
, and
$m_t=m_p$
, and
 $d_t = 1+d_p$
. By applying the i.h. to
$d_t = 1+d_p$
. By applying the i.h. to
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _t + \Gamma _u}\,\Vdash ^{(b_p+b_u, m_p+m_u, d_p+d_u)}_{\tt n} {p \{x \setminus u\}}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
. Therefore, we can build
$\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _t + \Gamma _u}\,\Vdash ^{(b_p+b_u, m_p+m_u, d_p+d_u)}_{\tt n} {p \{x \setminus u\}}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {\Phi _{p \{x \setminus u\}}}{\Gamma _t + \Gamma _u \Vdash ^{(b_p+b_u,m_p+m_u,1+d_p+d_u)} (p \{x \setminus u\})(r \{x \setminus u\}): \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _{p \{x \setminus u\}}}{\Gamma _t + \Gamma _u \Vdash ^{(b_p+b_u,m_p+m_u,1+d_p+d_u)} (p \{x \setminus u\})(r \{x \setminus u\}): \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}_{{\tt p}})\end{equation*}
 $(pr) \{x \setminus u\} = (p \{x \setminus u\})(r \{x \setminus u\})$
,
$(pr) \{x \setminus u\} = (p \{x \setminus u\})(r \{x \setminus u\})$
,
 $b_t+b_u = b_p+b_u$
,
$b_t+b_u = b_p+b_u$
,
 $m_t+m_u =m_p+m_u$
, and
$m_t+m_u =m_p+m_u$
, and
 $d_t + d_u = 1 + d_p + d_u$
.
$d_t + d_u = 1 + d_p + d_u$
.
-
-
• Case
 $\mathscr{G\,} = \mathscr{M}_0$
. Then,
$\mathscr{G\,} = \mathscr{M}_0$
. Then,
 $\Phi _t$
must end with rule (m):
$\Phi _t$
must end with rule (m):-
– Case
 $\Phi _t$
ends with (m). Then,
$\Phi _t$
ends with (m). Then,
 $\Phi _t$
has premises
$\Phi _t$
has premises
 $(\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i}\,\Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt n} {t}\,:\,{\delta _i})_{i \in I}$
, where
$(\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i}\,\Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt n} {t}\,:\,{\delta _i})_{i \in I}$
, where
 $\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
$\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
 $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
 $\mathscr{M}_0 = [ \delta _i ]_{i \in I}$
,
$\mathscr{M}_0 = [ \delta _i ]_{i \in I}$
,
 $b_t = +_{i \in I} b^i_t$
,
$b_t = +_{i \in I} b^i_t$
,
 $m_t = +_{i \in I} m^i_t$
, and
$m_t = +_{i \in I} m^i_t$
, and
 $d_t = +_{i \in I} d^i_t$
. By Lemma 36, there exist
$d_t = +_{i \in I} d^i_t$
. By Lemma 36, there exist
 $(\Phi ^i_u \triangleright \, {\Gamma ^i_u}\,\Vdash ^{(b^i_u,m^i_u,d^i_u)}_{\tt n} {u}\,:\,{\mathscr{M}_i})_{i \in I}$
, where
$(\Phi ^i_u \triangleright \, {\Gamma ^i_u}\,\Vdash ^{(b^i_u,m^i_u,d^i_u)}_{\tt n} {u}\,:\,{\mathscr{M}_i})_{i \in I}$
, where
 $\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
$\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
 $b_u = +_{i \in I} b^i_u$
,
$b_u = +_{i \in I} b^i_u$
,
 $m_u = +_{i \in I} m^i_u$
, and
$m_u = +_{i \in I} m^i_u$
, and
 $d_u = +_{i \in I} d^i_u$
. By the i.h. over each
$d_u = +_{i \in I} d^i_u$
. By the i.h. over each
 $\Phi ^i_u$
, we have
$\Phi ^i_u$
, we have
 $(\Phi ^i_{t \{x \setminus u\}} \triangleright \, {\Gamma ^i_t + \Gamma ^i_u}\,\Vdash ^{(b^i_t+b^i_u,m^i_t+m^i_u,d^i_t+d^i_u)}_{\tt n} {t \{x \setminus u\}}\,:\,{\delta _i})_{i \in I}$
. Therefore, we can build
$(\Phi ^i_{t \{x \setminus u\}} \triangleright \, {\Gamma ^i_t + \Gamma ^i_u}\,\Vdash ^{(b^i_t+b^i_u,m^i_t+m^i_u,d^i_t+d^i_u)}_{\tt n} {t \{x \setminus u\}}\,:\,{\delta _i})_{i \in I}$
. Therefore, we can build
 $\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with
$\Phi _{t \{x \setminus u\}}$
as follows:Thus, we can conclude with \begin{equation*} \frac {(\Phi ^i_{t \{x \setminus u\}})_{i \in I}}{+_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) \Vdash ^{(+_{i \in I}(b_i+b^i_u),+_{i \in I}(m_i+m^i_u),+_{i \in I}(d_i+d^i_u))} t \{x \setminus u\}\;:\; [ \delta _i ]_{i \in I}}({\tt m}) \end{equation*}
\begin{equation*} \frac {(\Phi ^i_{t \{x \setminus u\}})_{i \in I}}{+_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) \Vdash ^{(+_{i \in I}(b_i+b^i_u),+_{i \in I}(m_i+m^i_u),+_{i \in I}(d_i+d^i_u))} t \{x \setminus u\}\;:\; [ \delta _i ]_{i \in I}}({\tt m}) \end{equation*}
 $\Gamma _t + \Gamma _u = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_u = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_u)$
,
$\Gamma _t + \Gamma _u = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_u = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_u)$
,
 $b_t + b_u = +_{i \in I} b^i_t +_{i \in I} b^i_u = +_{i \in I} (b^i_t + b^i_u)$
,
$b_t + b_u = +_{i \in I} b^i_t +_{i \in I} b^i_u = +_{i \in I} (b^i_t + b^i_u)$
,
 $m_t + m_u = +_{i \in I} m^i_t +_{i \in I} m^i_u = +_{i \in I} (m^i_t + m^i_u)$
, and
$m_t + m_u = +_{i \in I} m^i_t +_{i \in I} m^i_u = +_{i \in I} (m^i_t + m^i_u)$
, and
 $d_t + d_u = +_{i \in I} d^i_t +_{i \in I} d^i_u = +_{i \in I} (d^i_t + d^i_u)$
.
$d_t + d_u = +_{i \in I} d^i_t +_{i \in I} d^i_u = +_{i \in I} (d^i_t + d^i_u)$
.
-
Lemma 13 (Quantitative subject reduction). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
is a tight derivation, then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
is a tight derivation, then
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt n} (u,q):\kappa$
, where
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt n} (u,q):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt n}}}$
implies
${\tt r} ={\beta _{{\tt n}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Proof. We show a stronger statement of the form:
Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
,
![]() $\Gamma$
is tight, and
$\Gamma$
is tight, and
![]() $\kappa$
is tight or
$\kappa$
is tight or
![]() $\neg {\tt abs}(t)$
, there exists
$\neg {\tt abs}(t)$
, there exists
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt n} (u,q):\kappa$
, where
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt n} (u,q):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt n}}}$
implies
${\tt r} ={\beta _{{\tt n}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
We proceed by induction over
![]() $(t,s) \rightsquigarrow _{{\tt n}} (u,q)$
:
$(t,s) \rightsquigarrow _{{\tt n}} (u,q)$
:
-
• Case
 $(t,s) = ((\lambda x.p) r,s) \rightsquigarrow _{{\beta _{{\tt n}}}} (p \{x \setminus r\}, s) = (u,q)$
. Then,
$(t,s) = ((\lambda x.p) r,s) \rightsquigarrow _{{\beta _{{\tt n}}}} (p \{x \setminus r\}, s) = (u,q)$
. Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _t \triangleright \, {\Gamma _t}\,\Vdash ^{(b_t,m_t,d_t)}_{\tt n} {t}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _t \triangleright \, {\Gamma _t}\,\Vdash ^{(b_t,m_t,d_t)}_{\tt n} {t}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
$\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
 $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
 $b = b_t + b_s$
,
$b = b_t + b_s$
,
 $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
 $d = d_t + d_s$
. Then,
$d = d_t + d_s$
. Then,
 $\Phi _t$
must end with rule (@) or (@
$\Phi _t$
must end with rule (@) or (@
 $_{{\tt p}}$
). Let us assume that
$_{{\tt p}}$
). Let us assume that
 $\Phi _t$
ends with rule (@
$\Phi _t$
ends with rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _{\lambda x.p} \triangleright \, {\Gamma _{\lambda x.p}}\,\Vdash ^{(b_{\lambda x.p},m_{\lambda x.p},d_{\lambda x.p})}_{\tt n} {\lambda x.p}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
, such that
$\Phi _{\lambda x.p} \triangleright \, {\Gamma _{\lambda x.p}}\,\Vdash ^{(b_{\lambda x.p},m_{\lambda x.p},d_{\lambda x.p})}_{\tt n} {\lambda x.p}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
, such that
 $\Gamma _t = \Gamma _{\lambda x.p}$
,
$\Gamma _t = \Gamma _{\lambda x.p}$
,
 $b_t = b_{\lambda x.p}$
,
$b_t = b_{\lambda x.p}$
,
 $m_t = m_{\lambda x.p}$
, and
$m_t = m_{\lambda x.p}$
, and
 $d_t = d_{\lambda x.p}$
. However, according to Lemma 35,
$d_t = d_{\lambda x.p}$
. However, according to Lemma 35,
 $\neg {\tt abs}(\lambda x.p)$
should hold. This gives a contradiction, meaning that this case does not apply. Now, let us assume
$\neg {\tt abs}(\lambda x.p)$
should hold. This gives a contradiction, meaning that this case does not apply. Now, let us assume
 $\Phi _t$
ends with rule (@). Then,
$\Phi _t$
ends with rule (@). Then,
 $\Phi _t$
must be of the following form:
$\Phi _t$
must be of the following form:
where
 $\Gamma _t = \Gamma _{\lambda x.p} + \Gamma _r$
,
$\Gamma _t = \Gamma _{\lambda x.p} + \Gamma _r$
,
 $b_t = 1+ b_p+b_r$
,
$b_t = 1+ b_p+b_r$
,
 $m_t = m_p+m_r$
, and
$m_t = m_p+m_r$
, and
 $d_t = d_p+d_r$
. By Lemma 38, there exists
$d_t = d_p+d_r$
. By Lemma 38, there exists
 $\Phi _{p \{x \setminus r\}} \triangleright \, {\Gamma _{\lambda x.p} +\Gamma _r}\,\Vdash ^{(b_p+b_r,m_p+m_r,d_p+d_r)}_{\tt n} {p \{x \setminus r\}}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
$\Phi _{p \{x \setminus r\}} \triangleright \, {\Gamma _{\lambda x.p} +\Gamma _r}\,\Vdash ^{(b_p+b_r,m_p+m_r,d_p+d_r)}_{\tt n} {p \{x \setminus r\}}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
 $\Phi _{(u,q)}$
as follows:where
$\Phi _{(u,q)}$
as follows:where \begin{equation*} \frac {\Phi _{p \{x \setminus r\}}\qquad \Pi _s}{\Gamma _{\lambda x.p} + \Gamma _r + \Delta _s \Vdash ^{(b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)} (p \{x \setminus r\}, s): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p \{x \setminus r\}}\qquad \Pi _s}{\Gamma _{\lambda x.p} + \Gamma _r + \Delta _s \Vdash ^{(b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)} (p \{x \setminus r\}, s): \kappa }({\tt conf})\end{equation*}
 $b' = b_p+b_r+b_s$
,
$b' = b_p+b_r+b_s$
,
 $m' = m_p+m_r+m_s$
, and
$m' = m_p+m_r+m_s$
, and
 $d = d_p+d_r+d_s$
. Thus, we can conclude with
$d = d_p+d_r+d_s$
. Thus, we can conclude with
 $b - 1 = (b_t + b_s) -1 = (1+ b_p+b_r + b_s) -1 = b'$
,
$b - 1 = (b_t + b_s) -1 = (1+ b_p+b_r + b_s) -1 = b'$
,
 $m = m_t + m_s = m_p +m_r + m_s = m'$
, and
$m = m_t + m_s = m_p +m_r + m_s = m'$
, and
 $d = d_t + d_s = d_p+d_r + d_s = d'$
.
$d = d_t + d_s = d_p+d_r + d_s = d'$
.
-
• Case
 $(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt n}} (p \{x \setminus r\},s) = (u,q)$
, such that
$(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt n}} (p \{x \setminus r\},s) = (u,q)$
, such that
 $s \equiv {\tt upd}_{l}(r,s')$
. Then
$s \equiv {\tt upd}_{l}(r,s')$
. Then
 $\Phi$
must be of the following form, where
$\Phi$
must be of the following form, where
 $\mathscr{T\;} = \{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0$
:
$\mathscr{T\;} = \{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0$
:
where
 $\Gamma = \Gamma _{p}{\setminus x} + \Delta _s$
,
$\Gamma = \Gamma _{p}{\setminus x} + \Delta _s$
,
 $b = b_p + b_s$
,
$b = b_p + b_s$
,
 $m = 1+ m_p + m_s$
, and
$m = 1+ m_p + m_s$
, and
 $d = d_p + d_s$
. Since
$d = d_p + d_s$
. Since
 $\Pi _s \triangleright \, {\Delta _s}\,\Vdash ^{(b_s,m_s,d_s)}_{\tt n} {s}\,:\,{{\{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, we know, by Lemma 37, that
$\Pi _s \triangleright \, {\Delta _s}\,\Vdash ^{(b_s,m_s,d_s)}_{\tt n} {s}\,:\,{{\{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, we know, by Lemma 37, that
 $s \equiv {\tt upd}_{l}(r,s')$
,
$s \equiv {\tt upd}_{l}(r,s')$
,
 $\Phi _r \triangleright \, {\Delta _r}\, \Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\, {{\Gamma _p (x) \sqcup \mathscr{M}}}$
and
$\Phi _r \triangleright \, {\Delta _r}\, \Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\, {{\Gamma _p (x) \sqcup \mathscr{M}}}$
and
 $\Pi _{s'} \triangleright \, {\Delta _{s'}}\,\Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt n} {s'}\,:\,{{\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, such that
$\Pi _{s'} \triangleright \, {\Delta _{s'}}\,\Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt n} {s'}\,:\,{{\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, such that
 $\Delta _s = \Gamma _r + \Delta _{s'}$
,
$\Delta _s = \Gamma _r + \Delta _{s'}$
,
 $b_s = b_r + b_{s'}$
,
$b_s = b_r + b_{s'}$
,
 $m_s = m_r + m_{s'}$
, and
$m_s = m_r + m_{s'}$
, and
 $d_s = d_r + d_{s'}$
. Therefore, by Lemma 36, there exist
$d_s = d_r + d_{s'}$
. Therefore, by Lemma 36, there exist
 $\Phi ^1_r \triangleright \, {\Gamma ^1_r}\,\Vdash ^{(b^1_r,m^1_r,d^1_r)}_{\tt n} {r}\,:\,{{\Gamma _p (x)}}$
and
$\Phi ^1_r \triangleright \, {\Gamma ^1_r}\,\Vdash ^{(b^1_r,m^1_r,d^1_r)}_{\tt n} {r}\,:\,{{\Gamma _p (x)}}$
and
 $\Phi ^2_r \triangleright \, {\Gamma ^2_r}\,\Vdash ^{(b^2_r,m^2_r,d^2_r)}_{\tt n} {r}\,:\,{{\mathscr{M}}}$
, such that
$\Phi ^2_r \triangleright \, {\Gamma ^2_r}\,\Vdash ^{(b^2_r,m^2_r,d^2_r)}_{\tt n} {r}\,:\,{{\mathscr{M}}}$
, such that
 $\Gamma _r = \Gamma ^1_r + \Gamma ^2_r$
,
$\Gamma _r = \Gamma ^1_r + \Gamma ^2_r$
,
 $b_r = b^1_r+b^2_r$
,
$b_r = b^1_r+b^2_r$
,
 $m_r = m^1_r+m^2_r$
, and
$m_r = m^1_r+m^2_r$
, and
 $d_r = d^1_r+d^2_r$
. By Lemma 38 (applied to
$d_r = d^1_r+d^2_r$
. By Lemma 38 (applied to
 $\Phi _{p}$
and
$\Phi _{p}$
and
 $\Phi ^1_r$
), there exists
$\Phi ^1_r$
), there exists
 $\Phi _{p \{x \setminus r\}} \triangleright \, {\Gamma _{p}{\setminus x}+\Delta ^1_r}\,\Vdash ^{(b_p+b^1_r,m_p+m^1_r,d_p+d^1_r)}_{\tt n} {p \{x \setminus r\}}\,:\,{{\{l\;:\;\mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0} \Rightarrow \kappa }$
. Moreover, we can construct an alternative type derivation
$\Phi _{p \{x \setminus r\}} \triangleright \, {\Gamma _{p}{\setminus x}+\Delta ^1_r}\,\Vdash ^{(b_p+b^1_r,m_p+m^1_r,d_p+d^1_r)}_{\tt n} {p \{x \setminus r\}}\,:\,{{\{l\;:\;\mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0} \Rightarrow \kappa }$
. Moreover, we can construct an alternative type derivation
 $\Pi '_s$
for
$\Pi '_s$
for
 $s$
as follows:Let
$s$
as follows:Let \begin{equation*} \frac {\Phi ^2_r\quad \Pi _{s'}}{\Gamma ^2_r+ \Delta _{s'} \Vdash ^{(b^2_r+b_{s'},m^2_r+m_{s'},d^2_r+d_{s'})} {\tt upd}_{l}(r,s'): {\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}({\tt upd}) \end{equation*}
\begin{equation*} \frac {\Phi ^2_r\quad \Pi _{s'}}{\Gamma ^2_r+ \Delta _{s'} \Vdash ^{(b^2_r+b_{s'},m^2_r+m_{s'},d^2_r+d_{s'})} {\tt upd}_{l}(r,s'): {\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}({\tt upd}) \end{equation*}
 $\Pi _q = \Pi '_s$
, where
$\Pi _q = \Pi '_s$
, where
 $q = {\tt upd}_{l}(r,s') = s$
and
$q = {\tt upd}_{l}(r,s') = s$
and
 $\Delta _q = \Gamma ^2_r + \Delta _{s'}$
. Therefore, we can build
$\Delta _q = \Gamma ^2_r + \Delta _{s'}$
. Therefore, we can build
 $\Phi '$
as follows:where
$\Phi '$
as follows:where \begin{equation*} \frac {\Phi _{p\{x \setminus r\}}\qquad \Pi _q}{(\Gamma _p {\setminus x} + \Gamma ^1_r) + (\Gamma ^2_r + \Delta _{s'}) \Vdash ^{(b_p + b^1_r + b^2_r + b_{s'},m_p + m^1_r + m^2_r + m_{s'},d_p + d^1_r + d^2_r + d_{s'})} (p \{x \setminus r\}, s): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p\{x \setminus r\}}\qquad \Pi _q}{(\Gamma _p {\setminus x} + \Gamma ^1_r) + (\Gamma ^2_r + \Delta _{s'}) \Vdash ^{(b_p + b^1_r + b^2_r + b_{s'},m_p + m^1_r + m^2_r + m_{s'},d_p + d^1_r + d^2_r + d_{s'})} (p \{x \setminus r\}, s): \kappa }({\tt conf})\end{equation*}
 $b' = b_p + b^1_r + b^2_r + b_{s'}$
,
$b' = b_p + b^1_r + b^2_r + b_{s'}$
,
 $m' = m_p + m^1_r + m^2_r + m_{s'}$
, and
$m' = m_p + m^1_r + m^2_r + m_{s'}$
, and
 $d' = d_p + d^1_r + d^2_r + d_{s'}$
. Thus, we can conclude with
$d' = d_p + d^1_r + d^2_r + d_{s'}$
. Thus, we can conclude with
 $\Gamma = \Gamma _p + \Delta _s = \Gamma _p + (\Gamma _r + \Delta _{s'}) = \Gamma _p + (\Gamma ^1_r + \Gamma ^2_r) + \Delta _{s'}$
,
$\Gamma = \Gamma _p + \Delta _s = \Gamma _p + (\Gamma _r + \Delta _{s'}) = \Gamma _p + (\Gamma ^1_r + \Gamma ^2_r) + \Delta _{s'}$
,
 $b = b_p + b_s = b_p + (b_r + b_{s'}) = b_p + (b^1_r + b^2_r) + b_{s'} = b'$
,
$b = b_p + b_s = b_p + (b_r + b_{s'}) = b_p + (b^1_r + b^2_r) + b_{s'} = b'$
,
 $m - 1 = (1 + m_p + m_s) - 1 = (1 + m_p + m_r + m_{s'}) - 1 = (1 + m_p + m^1_r + m^2_r + m_{s'}) - 1 = m'$
,
$m - 1 = (1 + m_p + m_s) - 1 = (1 + m_p + m_r + m_{s'}) - 1 = (1 + m_p + m^1_r + m^2_r + m_{s'}) - 1 = m'$
,
 $d = d_p + d_s = d_p + (d_r + d_{s'}) = d_p + (d^1_r + d^2_r) + d_{s'} = d'$
.
$d = d_p + d_s = d_p + (d_r + d_{s'}) = d_p + (d^1_r + d^2_r) + d_{s'} = d'$
.
-
• Case
 $(t,s) = ({\tt set}_{l}(r,p),s) \rightsquigarrow _{{\tt n}} (p, {\tt upd}_{l}(r,s)) = (u,q)$
. Then,
$(t,s) = ({\tt set}_{l}(r,p),s) \rightsquigarrow _{{\tt n}} (p, {\tt upd}_{l}(r,s)) = (u,q)$
. Then,
 $\Phi '$
must be of the following form, where
$\Phi '$
must be of the following form, where
 $\mathscr{T\;} = \{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0$
:
$\mathscr{T\;} = \{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0$
:
where
 $\Gamma = (\Gamma _r + \Gamma _{p}) + \Delta _{s}$
,
$\Gamma = (\Gamma _r + \Gamma _{p}) + \Delta _{s}$
,
 $b = b_r+b_p+b_s$
,
$b = b_r+b_p+b_s$
,
 $m=1+m_r+m_p+m_s$
and
$m=1+m_r+m_p+m_s$
and
 $d=d_r+d_p+d_s$
. Therefore, we can build derivation
$d=d_r+d_p+d_s$
. Therefore, we can build derivation
 $\Pi _q$
for
$\Pi _q$
for
 ${\tt upd}_{l}(r,s)$
as follows:Moreover, we can build
${\tt upd}_{l}(r,s)$
as follows:Moreover, we can build \begin{equation*} \frac {\Phi _{r}\qquad \Pi _{s}}{\Gamma _r + \Delta _{s} \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} {\tt upd}_{l}(r,s): {\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}_0}}({\tt upd}) \end{equation*}
\begin{equation*} \frac {\Phi _{r}\qquad \Pi _{s}}{\Gamma _r + \Delta _{s} \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} {\tt upd}_{l}(r,s): {\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}_0}}({\tt upd}) \end{equation*}
 $\Phi '$
as follows:where
$\Phi '$
as follows:where \begin{equation*} \frac {\Phi _{p}\qquad \Pi _{q}}{\Gamma _{p} + (\Gamma _r + \Delta _{s}) \Vdash ^{(b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)} (p, {\tt upd}_{l}(r,s)): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p}\qquad \Pi _{q}}{\Gamma _{p} + (\Gamma _r + \Delta _{s}) \Vdash ^{(b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)} (p, {\tt upd}_{l}(r,s)): \kappa }({\tt conf})\end{equation*}
 $b' = b_p+b_r+b_s$
,
$b' = b_p+b_r+b_s$
,
 $m' = m_p+m_r+m_s$
, and
$m' = m_p+m_r+m_s$
, and
 $d' = d_p+d_r +d_s$
. Thus, we can conclude with
$d' = d_p+d_r +d_s$
. Thus, we can conclude with
 $\Gamma = (\Gamma _r + \Gamma _p) + \Delta _s$
,
$\Gamma = (\Gamma _r + \Gamma _p) + \Delta _s$
,
 $b = b_r + b_p + b_s = b'$
,
$b = b_r + b_p + b_s = b'$
,
 $m - 1 = (1 + m_r + m_p + m_s) - 1 = m_r + m_p + m_s = m'$
, and
$m - 1 = (1 + m_r + m_p + m_s) - 1 = m_r + m_p + m_s = m'$
, and
 $d = d_r + d_p + d_s = d'$
.
$d = d_r + d_p + d_s = d'$
.
-
• Case
 $(t,s) = (pr,s) \rightsquigarrow _{{\tt n}} (p'r,q) = (u,q)$
, such that
$(t,s) = (pr,s) \rightsquigarrow _{{\tt n}} (p'r,q) = (u,q)$
, such that
 $(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
. Then,
$(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
. Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _t \triangleright \, {\Gamma _t}\,\Vdash ^{(b_t,m_t,d_t)}_{\tt n} {t}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _t \triangleright \, {\Gamma _t}\,\Vdash ^{(b_t,m_t,d_t)}_{\tt n} {t}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
$\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
 $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
 $b = b_t + b_s$
,
$b = b_t + b_s$
,
 $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
 $d = d_t + d_s$
. Moreover,
$d = d_t + d_s$
. Moreover,
 $\Phi _t$
must end with rule (@) or (@
$\Phi _t$
must end with rule (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Case
 $\Phi _t$
ends with (@). Then,
$\Phi _t$
ends with (@). Then,
 $\Phi _t$
must be of the following form:where
$\Phi _t$
must be of the following form:where \begin{equation*} \frac {\Phi _p \triangleright \, {\Gamma _p}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')}\qquad \Phi _r \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{M}}}{\Gamma _p + \Gamma _r \Vdash ^{(1+b_p+b_r,m_p+m_r,d_p+d_r)} pr\;:\; \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _p \triangleright \, {\Gamma _p}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')}\qquad \Phi _r \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{M}}}{\Gamma _p + \Gamma _r \Vdash ^{(1+b_p+b_r,m_p+m_r,d_p+d_r)} pr\;:\; \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
 $\Gamma _t = \Gamma _p+\Gamma _r$
,
$\Gamma _t = \Gamma _p+\Gamma _r$
,
 $b_t = 1+b_p+b_r$
,
$b_t = 1+b_p+b_r$
,
 $m_t = m_p+m_r$
, and
$m_t = m_p+m_r$
, and
 $d_t = d_p+d_r$
. Therefore, we can build the following derivation for
$d_t = d_p+d_r$
. Therefore, we can build the following derivation for
 $(p,s)$
:Moreover,
$(p,s)$
:Moreover, \begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): (\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'}({\tt conf}) \end{equation*}
\begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): (\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'}({\tt conf}) \end{equation*}
 $\Gamma _p$
and
$\Gamma _p$
and
 $\Delta _s$
are tight, and
$\Delta _s$
are tight, and
 $(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
implies that
$(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
implies that
 $\neg {\tt abs}(p)$
. By applying the i.h. over
$\neg {\tt abs}(p)$
. By applying the i.h. over
 $\Phi _{(p,s)}$
, there exists derivation
$\Phi _{(p,s)}$
, there exists derivation
 $\Phi _{(p',q)}$
that must be of the following form:
$\Phi _{(p',q)}$
that must be of the following form:

such that
 $\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
and
$\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
and
 $(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
and
$(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
and
 $(b_p+b_s,m_p+m_s,d_p+d_s)$
are properly related. Therefore, we can build
$(b_p+b_s,m_p+m_s,d_p+d_s)$
are properly related. Therefore, we can build
 $\Phi '$
as follows:
$\Phi '$
as follows:
where
 $b' = 1+b_{p'}+b_r+b_q$
,
$b' = 1+b_{p'}+b_r+b_q$
,
 $m' = m_{p'}+m_r+m_q$
, and
$m' = m_{p'}+m_r+m_q$
, and
 $d' =d_{p'}+d_r+d_q$
. Thus, we can conclude with
$d' =d_{p'}+d_r+d_q$
. Thus, we can conclude with
 $\Gamma = \Gamma _t + \Delta _s = (\Gamma _{p} + \Gamma _r) + \Delta _s = (\Gamma _{p'} + \Gamma _r) + \Delta _q$
, and
$\Gamma = \Gamma _t + \Delta _s = (\Gamma _{p} + \Gamma _r) + \Delta _s = (\Gamma _{p'} + \Gamma _r) + \Delta _q$
, and
 $(1+b_{p'}+b_r+b_q,m_{p'}+m_r+m_q,d_{p'}+d_r+d_q)$
and
$(1+b_{p'}+b_r+b_q,m_{p'}+m_r+m_q,d_{p'}+d_r+d_q)$
and
 $(1+b_{p}+b_r+b_s,m_{p}+m_r+m_s,d_{p}+d_r+d_s)$
are related properly.
$(1+b_{p}+b_r+b_s,m_{p}+m_r+m_s,d_{p}+d_r+d_s)$
are related properly. -
– Case
 $\Phi _{pr}$
ends with (@
$\Phi _{pr}$
ends with (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
where
 $\Gamma = \Gamma _p + \Delta _s$
,
$\Gamma = \Gamma _p + \Delta _s$
,
 $b = b_p+b_s$
,
$b = b_p+b_s$
,
 $m = m_p+m_s$
, and
$m = m_p+m_s$
, and
 $s = d_p+d_s$
. Therefore, we can build the following derivation
$s = d_p+d_s$
. Therefore, we can build the following derivation
 $\Phi _{(p,s)}$
:Moreover,
$\Phi _{(p,s)}$
:Moreover, \begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): ({\tt n} \times \mathscr{T\;}')}({\tt conf}) \end{equation*}
\begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): ({\tt n} \times \mathscr{T\;}')}({\tt conf}) \end{equation*}
 $\Gamma _p$
and
$\Gamma _p$
and
 $\Delta _s$
are tight, and
$\Delta _s$
are tight, and
 $(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
implies that
$(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
implies that
 $\neg {\tt abs}(p)$
. By applying the i.h. over
$\neg {\tt abs}(p)$
. By applying the i.h. over
 $\Phi _{(p,s)}$
, there exists a derivation for
$\Phi _{(p,s)}$
, there exists a derivation for
 $(p',q)$
that must be of the following form:where
$(p',q)$
that must be of the following form:where \begin{equation*} \frac {\Phi _{p'} \triangleright \, {\Gamma _{p'}}\,\Vdash ^{(b_{p'},m_{p'},d_{p'})}_{\tt n} {p'}\,:\,{\mathscr{T\;}'' \Rightarrow ({\tt n} \times \mathscr{T\;}')}\qquad \Pi _q \triangleright \, {\Delta _q}\,\Vdash ^{(b_q,m_q,d_q)}_{\tt n} {q}\,:\,{\mathscr{T\;}''}}{\Gamma _{p'} + \Delta _q \Vdash ^{(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)} (p',q): ({\tt n} \times \mathscr{T\;}')}({\tt conf}) \end{equation*}
\begin{equation*} \frac {\Phi _{p'} \triangleright \, {\Gamma _{p'}}\,\Vdash ^{(b_{p'},m_{p'},d_{p'})}_{\tt n} {p'}\,:\,{\mathscr{T\;}'' \Rightarrow ({\tt n} \times \mathscr{T\;}')}\qquad \Pi _q \triangleright \, {\Delta _q}\,\Vdash ^{(b_q,m_q,d_q)}_{\tt n} {q}\,:\,{\mathscr{T\;}''}}{\Gamma _{p'} + \Delta _q \Vdash ^{(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)} (p',q): ({\tt n} \times \mathscr{T\;}')}({\tt conf}) \end{equation*}
 $\Gamma _{p'} + \Delta _q = \Gamma _p + \Delta _s$
, and
$\Gamma _{p'} + \Delta _q = \Gamma _p + \Delta _s$
, and
 $(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
and
$(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
and
 $(b_p+b_s,m_p+m_s,d_p+d_s)$
are related properly. Therefore, we can build derivation
$(b_p+b_s,m_p+m_s,d_p+d_s)$
are related properly. Therefore, we can build derivation
 $\Phi '$
as follows:
$\Phi '$
as follows:

where
 $\Gamma _{p'} + \Delta _q = \Gamma _p + \Delta _s$
,
$\Gamma _{p'} + \Delta _q = \Gamma _p + \Delta _s$
,
 $b' = b_{p'} + b_q$
,
$b' = b_{p'} + b_q$
,
 $m' = m_{p'} + m_q$
, and
$m' = m_{p'} + m_q$
, and
 $d' = 1+ d_{p'} + d_q$
. Thus, we can conclude
$d' = 1+ d_{p'} + d_q$
. Thus, we can conclude
 $\Gamma = \Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
, and
$\Gamma = \Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
, and
 $(b_{p'}+b_q,m_{p'}+m_q,1+d_{p'}+d_q)$
and
$(b_{p'}+b_q,m_{p'}+m_q,1+d_{p'}+d_q)$
and
 $(b_p+b_s,m_p+m_s,1+d_p+d_s)$
are properly related.
$(b_p+b_s,m_p+m_s,1+d_p+d_s)$
are properly related.
-
Theorem 3 (Quantitative soundness). If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
a tight derivation, then there exists
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt n} (t,s) \;:\; \kappa$
a tight derivation, then there exists
![]() $(u,q)$
such that
$(u,q)$
such that
![]() $u \in {\tt no}_{{\tt n}}$
and
$u \in {\tt no}_{{\tt n}}$
and
![]() $(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
with
$(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
with
![]() $b$
$b$
![]() $\beta _{{\tt n}}$
-steps,
$\beta _{{\tt n}}$
-steps,
![]() $m$
$m$
![]() ${\tt g}/{\tt s}$
-steps, and
${\tt g}/{\tt s}$
-steps, and
![]() $|{(u,q)}|_{\texttt {n}} = d$
.
$|{(u,q)}|_{\texttt {n}} = d$
.
Proof.
We start by noting that
![]() $\Phi$
has two premises
$\Phi$
has two premises
![]() $\Phi _t \triangleright \, \Gamma _t\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
and
$\Phi _t \triangleright \, \Gamma _t\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
and
![]() $\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, where
$\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, where
![]() $\Gamma = \Gamma _t + \Delta _s$
and
$\Gamma = \Gamma _t + \Delta _s$
and
![]() $\kappa = \tau \times \mathscr{T\;}'$
, such that
$\kappa = \tau \times \mathscr{T\;}'$
, such that
![]() $\tau$
and
$\tau$
and
![]() $\mathscr{T\;}'$
are tight. Now, the proof follows by induction on
$\mathscr{T\;}'$
are tight. Now, the proof follows by induction on
![]() $b + m$
:
$b + m$
:
-
• Case
 $b + m = 0$
. Then,
$b + m = 0$
. Then,
 $b = m = 0$
, and thus,
$b = m = 0$
, and thus,
 $b_t = m_t = b_s = m_s = 0$
. Therefore,
$b_t = m_t = b_s = m_s = 0$
. Therefore,
 $(t,s)$
is a configuration in normal form, by Lemma 10, and
$(t,s)$
is a configuration in normal form, by Lemma 10, and
 $|{(t,s)}|_{\texttt {n}} = d$
, by Lemma 9. Thus, we can conclude by taking
$|{(t,s)}|_{\texttt {n}} = d$
, by Lemma 9. Thus, we can conclude by taking
 $u = t$
and
$u = t$
and
 $q = s$
.
$q = s$
. -
• Case
 $b + m \gt 0$
. Then,
$b + m \gt 0$
. Then,
 $b \gt 0$
or
$b \gt 0$
or
 $m \gt 0$
, and thus,
$m \gt 0$
, and thus,
 $b_t + b_s \gt 0$
or
$b_t + b_s \gt 0$
or
 $m_t + m_s \gt 0$
. Note that it cannot be that
$m_t + m_s \gt 0$
. Note that it cannot be that
 $b_t = m_t = 0$
, because this would imply that
$b_t = m_t = 0$
, because this would imply that
 $b = m = 0$
by Lemma 9. Therefore, it must be the case that
$b = m = 0$
by Lemma 9. Therefore, it must be the case that
 $b_t + m_t \gt 0$
, and thus,
$b_t + m_t \gt 0$
, and thus,
 $(t,s)$
is not a configuration in normal form, by Lemma 10. Moreover, note that
$(t,s)$
is not a configuration in normal form, by Lemma 10. Moreover, note that
 $(t,s)$
cannot be a blocked configuration, by Proposition4. Therefore, by Proposition3, there exists
$(t,s)$
cannot be a blocked configuration, by Proposition4. Therefore, by Proposition3, there exists
 $(t',s')$
such that
$(t',s')$
such that
 $(t,s) \rightsquigarrow _{{\tt n}} (t',s')$
. By Lemma 13, there exists
$(t,s) \rightsquigarrow _{{\tt n}} (t',s')$
. By Lemma 13, there exists
 $\Phi ' \triangleright {\Gamma }\,\Vdash ^{(b',m',d)}_{\tt n} {(t',s')}\,:\,{\kappa }$
, such that
$\Phi ' \triangleright {\Gamma }\,\Vdash ^{(b',m',d)}_{\tt n} {(t',s')}\,:\,{\kappa }$
, such that
 $b'+m'=b+m-1$
. By the i.h., there exists
$b'+m'=b+m-1$
. By the i.h., there exists
 $(u,q)$
, such that
$(u,q)$
, such that
 $u\in {\tt no}_{{\tt n}}$
,
$u\in {\tt no}_{{\tt n}}$
,
 $(t',s') \rightsquigarrow _{\tt n}^{(b',m')} (u,q)$
and
$(t',s') \rightsquigarrow _{\tt n}^{(b',m')} (u,q)$
and
 $d = |{(u,q)}|_{\texttt {n}}$
. So we can conclude with
$d = |{(u,q)}|_{\texttt {n}}$
. So we can conclude with
 $(t,s) \rightsquigarrow _{{\tt n}} (t',s') \rightsquigarrow _{\tt n}^{(b',m')} (u,q)$
, which means that
$(t,s) \rightsquigarrow _{{\tt n}} (t',s') \rightsquigarrow _{\tt n}^{(b',m')} (u,q)$
, which means that
 $(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
, as expected.
$(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
, as expected.
Lemma 39 (Anti-substitution). If
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_{\tt n} {t \{x \setminus u\}}\,:\,{\mu }$
, then
$\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_{\tt n} {t \{x \setminus u\}}\,:\,{\mu }$
, then
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mu$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mu$
and
![]() $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)} u\;:\; \mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)} u\;:\; \mathscr{M}$
, such that
![]() $\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
![]() $b = b_t+b_u$
,
$b = b_t+b_u$
,
![]() $m = m_t+m_u$
, and
$m = m_t+m_u$
, and
![]() $d = d_t + d_u$
.
$d = d_t + d_u$
.
Proof.
We generalize the original statement by allowing
![]() $\Phi _t$
to conclude with either a monadic type
$\Phi _t$
to conclude with either a monadic type
![]() $\mu$
or a multi-type
$\mu$
or a multi-type
![]() $\mathscr{M}_0$
. Let
$\mathscr{M}_0$
. Let
![]() $\mathscr{G\,} \in \{\mu , \mathscr{M}_0\}$
. Then the statement is as follows:
$\mathscr{G\,} \in \{\mu , \mathscr{M}_0\}$
. Then the statement is as follows:
If
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_v {t \{x \setminus u\}}\,:\,{\mathscr{G\,}}$
, then there exist
$\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_v {t \{x \setminus u\}}\,:\,{\mathscr{G\,}}$
, then there exist
![]() $\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{G\,}$
and
$\Phi _t \triangleright \, \Gamma _t;\; x \;:\; \mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt n} t\;:\;\mathscr{G\,}$
and
![]() $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, such that
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, such that
![]() $\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u$
,
![]() $b = b_t+b_u$
,
$b = b_t+b_u$
,
![]() $m = m_t+m_u$
, and
$m = m_t+m_u$
, and
![]() $d = d_t + d_u$
.
$d = d_t + d_u$
.
The proof follows by induction over
![]() $\Phi _{t \{x \setminus u\}}$
, according to the last rule of
$\Phi _{t \{x \setminus u\}}$
, according to the last rule of
![]() $\Phi _{t \{x \setminus u\}}$
:
$\Phi _{t \{x \setminus u\}}$
:
-
• Case
 $\mathscr{G\,} = \mu$
. Let us assume
$\mathscr{G\,} = \mu$
. Let us assume
 $t = x$
, such that
$t = x$
, such that
 $t \{x \setminus u\} = u$
. Then,
$t \{x \setminus u\} = u$
. Then,
 $\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_{\tt n} {u}\,:\,{\mu }$
, and we can build
$\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_{\tt n} {u}\,:\,{\mu }$
, and we can build
 $\Phi _u \triangleright \, {\Gamma _u}\,\Vdash ^{(b_u,m_u,d_u)}_{\tt n} {u}\,:\,{[ \mu ]}$
, where
$\Phi _u \triangleright \, {\Gamma _u}\,\Vdash ^{(b_u,m_u,d_u)}_{\tt n} {u}\,:\,{[ \mu ]}$
, where
 $\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
$\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
 $b_u = b$
,
$b_u = b$
,
 $m_u = m$
, and
$m_u = m$
, and
 $d_u = d$
, by applying rule (m) to
$d_u = d$
, by applying rule (m) to
 $\Phi _{t \{x \setminus u\}}$
, and
$\Phi _{t \{x \setminus u\}}$
, and
 $\Phi _t \triangleright \, {x \;:\; [ \mu ]}\, \Vdash ^{(0,0,0)}_{\tt n} {x}\,:\,{\mu }$
, where
$\Phi _t \triangleright \, {x \;:\; [ \mu ]}\, \Vdash ^{(0,0,0)}_{\tt n} {x}\,:\,{\mu }$
, where
 $\Gamma _t = \emptyset$
, and
$\Gamma _t = \emptyset$
, and
 $b_t = m_t = d_t = 0$
, by using rule (ax). From now on, we are going to assume
$b_t = m_t = d_t = 0$
, by using rule (ax). From now on, we are going to assume
 $t \neq x$
and consider the last rule used in
$t \neq x$
and consider the last rule used in
 $\Phi _{t \{x \setminus u\}}$
, which must be (ax), (
$\Phi _{t \{x \setminus u\}}$
, which must be (ax), (
 $\lambda$
), (
$\lambda$
), (
 $\lambda _{\tt p}$
), (@), (get), (set), or (@
$\lambda _{\tt p}$
), (@), (get), (set), or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Rule (ax). Then,
 $t = y$
,
$t = y$
,
 $y \{x \setminus u\} = y$
, and
$y \{x \setminus u\} = y$
, and
 $\mathscr{M} = [ \, ]$
. So we can pick
$\mathscr{M} = [ \, ]$
. So we can pick
 $\Phi _t = \Phi _{t \{x \setminus u\}}$
and
$\Phi _t = \Phi _{t \{x \setminus u\}}$
and
 $\Phi _u \triangleright \, {\emptyset }\, \Vdash ^{(0,0,0)}_{\tt n} {u}\,:\,{[ \, ]}$
, where
$\Phi _u \triangleright \, {\emptyset }\, \Vdash ^{(0,0,0)}_{\tt n} {u}\,:\,{[ \, ]}$
, where
 $\Gamma _u = \emptyset$
, and
$\Gamma _u = \emptyset$
, and
 $b_u = m_u = d_u = 0$
. And we can conclude with
$b_u = m_u = d_u = 0$
. And we can conclude with
 $\Gamma _{t \{x \setminus u\}} = \Gamma _t = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _t = \Gamma _t + \Gamma _u$
,
 $b = b_t = b_t + b_u$
,
$b = b_t = b_t + b_u$
,
 $m = m_t = m_t + m_u$
, and
$m = m_t = m_t + m_u$
, and
 $d = d_t = d_t + d_u$
.
$d = d_t = d_t + d_u$
. -
– Rule (
 $\lambda$
). Then,
$\lambda$
). Then,
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
,
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
,
 $\mu = \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ') \times \mathscr{T\;})$
, and
$\mu = \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ') \times \mathscr{T\;})$
, and
 $\Phi _{t \{x \setminus u\}}$
has one premise
$\Phi _{t \{x \setminus u\}}$
has one premise
 $\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}'}\, \Vdash ^{(b_{p \{x \setminus u\}},m_{p \{x \setminus u\}},d_{p \{x \setminus u\}})}_{\tt n} {p \{x \setminus u\}}\,:\,{\mu '}$
,
$\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}'}\, \Vdash ^{(b_{p \{x \setminus u\}},m_{p \{x \setminus u\}},d_{p \{x \setminus u\}})}_{\tt n} {p \{x \setminus u\}}\,:\,{\mu '}$
,
 $b=b_{p \{x \setminus u\}}$
,
$b=b_{p \{x \setminus u\}}$
,
 $m= m_{p \{x \setminus u\}}$
, and
$m= m_{p \{x \setminus u\}}$
, and
 $d=d_{p \{x \setminus u\}}$
. By applying the i.h. to
$d=d_{p \{x \setminus u\}}$
. By applying the i.h. to
 $\Phi _{p \{x \setminus u\}}$
, there exist
$\Phi _{p \{x \setminus u\}}$
, there exist
 $\Phi _p \triangleright \, {(\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mu '}$
and
$\Phi _p \triangleright \, {(\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mu '}$
and
 $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
 $\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
,
 $b_{p \{x \setminus u\}} = b_p + b_u$
,
$b_{p \{x \setminus u\}} = b_p + b_u$
,
 $m_{p \{x \setminus u\}} = m_p + m_u$
, and
$m_{p \{x \setminus u\}} = m_p + m_u$
, and
 $d_{p \{x \setminus u\}} = d_p + d_u$
. Therefore, we can build
$d_{p \{x \setminus u\}} = d_p + d_u$
. Therefore, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _p}{\Gamma _p \Vdash ^{(b_p,m_p,d_p)} \lambda y.p: \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ') \times \mathscr{T\;})}(\lambda )\end{equation*}
\begin{equation*} \frac {\Phi _p}{\Gamma _p \Vdash ^{(b_p,m_p,d_p)} \lambda y.p: \mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow \mu ') \times \mathscr{T\;})}(\lambda )\end{equation*}
 $b_t = b_p$
,
$b_t = b_p$
,
 $m_t = m_p$
, and
$m_t = m_p$
, and
 $d_t = d_p$
. Thus, we can conclude.
$d_t = d_p$
. Thus, we can conclude.
-
– Rule (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
,
$t \{x \setminus u\} = \lambda y.(p \{x \setminus u\})$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})$
, and
 $\Phi _{t \{x \setminus u\}} \triangleright \, {\emptyset }\,\Vdash ^{(0,0,0)}_{\tt n} {\lambda y.(p \{x \setminus u\})}\,:\,{{\tt a}}$
, such that
$\Phi _{t \{x \setminus u\}} \triangleright \, {\emptyset }\,\Vdash ^{(0,0,0)}_{\tt n} {\lambda y.(p \{x \setminus u\})}\,:\,{{\tt a}}$
, such that
 $\Gamma _{t \{x \setminus u\}} = \emptyset$
and
$\Gamma _{t \{x \setminus u\}} = \emptyset$
and
 $b = m = d = 0$
. Therefore, we can build
$b = m = d = 0$
. Therefore, we can build
 $\Phi _u \triangleright \, {\emptyset }\,\Vdash ^{(0,0,0)}_{\tt n} {u}\,:\,{[ \, ]}$
, where
$\Phi _u \triangleright \, {\emptyset }\,\Vdash ^{(0,0,0)}_{\tt n} {u}\,:\,{[ \, ]}$
, where
 $\Gamma _u = \emptyset$
,
$\Gamma _u = \emptyset$
,
 $\mathscr{M} = [ \, ]$
, and
$\mathscr{M} = [ \, ]$
, and
 $b_u = m_u = d_u = 0$
. And we can build
$b_u = m_u = d_u = 0$
. And we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {}{\emptyset ;\; x \;:\; \mathscr{M} \Vdash ^{(0,0,0)} \lambda y.p: \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})}(\lambda _{\tt p}) \end{equation*}
\begin{equation*} \frac {}{\emptyset ;\; x \;:\; \mathscr{M} \Vdash ^{(0,0,0)} \lambda y.p: \mathscr{T\;} \Rightarrow ({\tt a} \times \mathscr{T\;})}(\lambda _{\tt p}) \end{equation*}
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $b_t = m_t = d_t = 0$
. Thus, we can conclude
$b_t = m_t = d_t = 0$
. Thus, we can conclude
 $\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u = \emptyset$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _t + \Gamma _u = \emptyset$
,
 $b = b_t + b_u = m = m_t + m_u = d = d_t + d_u = 0$
.
$b = b_t + b_u = m = m_t + m_u = d = d_t + d_u = 0$
.
-
– Rule (@). Then,
 $t = rp$
,
$t = rp$
,
 $\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
 $t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
. Therefore,
$t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
. Therefore,
 $\Phi _{t \{x \setminus u\}}$
has two premises
$\Phi _{t \{x \setminus u\}}$
has two premises
 $\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _{r \{x \setminus u\}};\;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_{r \{x \setminus u\}}, m_{r \{x \setminus u\}},d_{r \{x \setminus u\}})}_{\tt n} {r \{x \setminus u\}}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')}$
and
$\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _{r \{x \setminus u\}};\;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_{r \{x \setminus u\}}, m_{r \{x \setminus u\}},d_{r \{x \setminus u\}})}_{\tt n} {r \{x \setminus u\}}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')}$
and
 $\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _{p \{x \setminus u\}};\;\; x \;:\; \mathscr{M}_2}\,\Vdash ^{(b_{p \{x \setminus u\}}, m_{p \{x \setminus u\}}, d_{p \{x \setminus u\}})}_{\tt n} {p \{x \setminus u\}}\,:\,{\mathscr{M\;}'}$
, where
$\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _{p \{x \setminus u\}};\;\; x \;:\; \mathscr{M}_2}\,\Vdash ^{(b_{p \{x \setminus u\}}, m_{p \{x \setminus u\}}, d_{p \{x \setminus u\}})}_{\tt n} {p \{x \setminus u\}}\,:\,{\mathscr{M\;}'}$
, where
 $\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}}$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}}$
,
 $b = 1+b_{r \{x \setminus u\}} + b_{p \{x \setminus u\}}$
,
$b = 1+b_{r \{x \setminus u\}} + b_{p \{x \setminus u\}}$
,
 $m = m_{r \{x \setminus u\}} + m_{p \{x \setminus u\}}$
, and
$m = m_{r \{x \setminus u\}} + m_{p \{x \setminus u\}}$
, and
 $d = d_{r \{x \setminus u\}} + d_{p \{x \setminus u\}}$
. By applying the i.h. to
$d = d_{r \{x \setminus u\}} + d_{p \{x \setminus u\}}$
. By applying the i.h. to
 $\Phi _{r \{x \setminus u\}}$
, there exist
$\Phi _{r \{x \setminus u\}}$
, there exist
 $\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}_1}\, \Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')}$
and
$\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}_1}\, \Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}')}$
and
 $\Phi ^1_u \triangleright \, {\Gamma ^1_u}\,\Vdash ^{(b^1_u,m^1_u,d^1_u)}_{\tt n} {u}\,:\,{\mathscr{M}_1}$
, where
$\Phi ^1_u \triangleright \, {\Gamma ^1_u}\,\Vdash ^{(b^1_u,m^1_u,d^1_u)}_{\tt n} {u}\,:\,{\mathscr{M}_1}$
, where
 $\Gamma _{r \{x \setminus u\}} = \Gamma _r + \Gamma ^1_u$
,
$\Gamma _{r \{x \setminus u\}} = \Gamma _r + \Gamma ^1_u$
,
 $b_{r \{x \setminus u\}} = b_r + b^1_u$
,
$b_{r \{x \setminus u\}} = b_r + b^1_u$
,
 $m_{r \{x \setminus u\}} = m_r + m^1_u$
, and
$m_{r \{x \setminus u\}} = m_r + m^1_u$
, and
 $d_{r \{x \setminus u\}} = d_r + d^1_u$
. By applying the i.h. to
$d_{r \{x \setminus u\}} = d_r + d^1_u$
. By applying the i.h. to
 $\Phi _{p \{x \setminus u\}}$
, there exist
$\Phi _{p \{x \setminus u\}}$
, there exist
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\, \Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{M\;}'}$
and
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\, \Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{M\;}'}$
and
 $\Phi ^2_u \triangleright \, {\Gamma ^2_u}\,\Vdash ^{(b^2_u,m^2_u,d^2_u)}_{\tt n} {u}\,:\,{\mathscr{M}_2}$
, where
$\Phi ^2_u \triangleright \, {\Gamma ^2_u}\,\Vdash ^{(b^2_u,m^2_u,d^2_u)}_{\tt n} {u}\,:\,{\mathscr{M}_2}$
, where
 $\Gamma _{p \{x \setminus u\}} = \Gamma _p + \Gamma ^2_u$
,
$\Gamma _{p \{x \setminus u\}} = \Gamma _p + \Gamma ^2_u$
,
 $b_{p \{x \setminus u\}} = b_p + b^2_u$
,
$b_{p \{x \setminus u\}} = b_p + b^2_u$
,
 $m_{p \{x \setminus u\}} = m_p + m^2_u$
, and
$m_{p \{x \setminus u\}} = m_p + m^2_u$
, and
 $d_{p \{x \setminus u\}} = d_p + d^2_u$
. By Lemma 36, there exists
$d_{p \{x \setminus u\}} = d_p + d^2_u$
. By Lemma 36, there exists
 $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b_u = b^1_u + b^2_u$
,
$b_u = b^1_u + b^2_u$
,
 $m_u = m^1_u + m^2_u$
, and
$m_u = m^1_u + m^2_u$
, and
 $d_u = d^1_u + d^2_u$
. Moreover, we can build
$d_u = d^1_u + d^2_u$
. Moreover, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _r\qquad \Phi _p}{(\Gamma _r + \Gamma _p);\; x \;:\; \mathscr{M} \Vdash ^{(1+b_r+b_p,m_r+m_p,d_r+d_p)} rp: \mathscr{T\;} \Rightarrow \kappa }({\tt @}) \end{equation*}
\begin{equation*} \frac {\Phi _r\qquad \Phi _p}{(\Gamma _r + \Gamma _p);\; x \;:\; \mathscr{M} \Vdash ^{(1+b_r+b_p,m_r+m_p,d_r+d_p)} rp: \mathscr{T\;} \Rightarrow \kappa }({\tt @}) \end{equation*}
 $\Gamma _t = \Gamma _r + \Gamma _p$
,
$\Gamma _t = \Gamma _r + \Gamma _p$
,
 $b_t = 1+b_r+b_p$
,
$b_t = 1+b_r+b_p$
,
 $m_t = m_r+m_p$
, and
$m_t = m_r+m_p$
, and
 $d_t = d_r + d_p$
. Thus, we can conclude with
$d_t = d_r + d_p$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}} = (\Gamma _r + \Gamma ^1_u) + (\Gamma _p + \Gamma ^2_u) = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _{r \{x \setminus u\}} + \Gamma _{p \{x \setminus u\}} = (\Gamma _r + \Gamma ^1_u) + (\Gamma _p + \Gamma ^2_u) = \Gamma _t + \Gamma _u$
,
 $b = 1+b_{r \{x \setminus u\}} + b_{p \{x \setminus u\}} = 1+(b_r + b^1_u) + (b_p + b^2_u) = b_t + b_u$
,
$b = 1+b_{r \{x \setminus u\}} + b_{p \{x \setminus u\}} = 1+(b_r + b^1_u) + (b_p + b^2_u) = b_t + b_u$
,
 $m = m_{r \{x \setminus u\}} + m_{p \{x \setminus u\}} = (m_r + m^1_u) + (m_p + m^2_u) = m_t + m_u$
, and
$m = m_{r \{x \setminus u\}} + m_{p \{x \setminus u\}} = (m_r + m^1_u) + (m_p + m^2_u) = m_t + m_u$
, and
 $d = d_{r \{x \setminus u\}} + d_{p \{x \setminus u\}} = (d_r + d^1_u) + (d_p + d^2_u) = d_t + d_u$
.
$d = d_{r \{x \setminus u\}} + d_{p \{x \setminus u\}} = (d_r + d^1_u) + (d_p + d^2_u) = d_t + d_u$
.
-
– Rule (get). Then
 $t = {\tt get}_{l}(\lambda y.p)$
,
$t = {\tt get}_{l}(\lambda y.p)$
,
 $\mu = {\{l \;:\; \mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
$\mu = {\{l \;:\; \mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
 $t \{x \setminus u\} = {\tt get}_{l}(\lambda y.(p \{x \setminus u\}))$
. Therefore,
$t \{x \setminus u\} = {\tt get}_{l}(\lambda y.(p \{x \setminus u\}))$
. Therefore,
 $\Phi _{t \{x \setminus u\}}$
has one premise
$\Phi _{t \{x \setminus u\}}$
has one premise
 $\Phi _{p \{x \setminus u\}} \triangleright \Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}' \vdash^{(b_{p \{x \setminus u\}},m_{p \{x \setminus u\}}, d_{p \{x \setminus u\}})}_\texttt{n} {p \{x \setminus u\}}\,:\,{{\{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
$\Phi _{p \{x \setminus u\}} \triangleright \Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}' \vdash^{(b_{p \{x \setminus u\}},m_{p \{x \setminus u\}}, d_{p \{x \setminus u\}})}_\texttt{n} {p \{x \setminus u\}}\,:\,{{\{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
 $b=b_{p \{x \setminus u\}}$
,
$b=b_{p \{x \setminus u\}}$
,
 $m = 1+m_{p \{x \setminus u\}}$
, and
$m = 1+m_{p \{x \setminus u\}}$
, and
 $d=d_{p \{x \setminus u\}}$
. By applying the i.h. to
$d=d_{p \{x \setminus u\}}$
. By applying the i.h. to
 $\Phi _{p \{x \setminus u\}}$
, there exists
$\Phi _{p \{x \setminus u\}}$
, there exists
 $\Phi _p \triangleright \, {(\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{{\{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
and
$\Phi _p \triangleright \, {(\Gamma _p;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{{\{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
and
 $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
 $\Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}' = (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}};\;\; y \;:\; \mathscr{M\;}' = (\Gamma _p;\; y \;:\; \mathscr{M\;}') + \Gamma _u$
,
 $b_{p \{x \setminus u\}} = b_p + b_u$
,
$b_{p \{x \setminus u\}} = b_p + b_u$
,
 $m_{p \{x \setminus u\}} = m_p + m_u$
, and
$m_{p \{x \setminus u\}} = m_p + m_u$
, and
 $d_{p \{x \setminus u\}} = d_p + d_u$
. Therefore,
$d_{p \{x \setminus u\}} = d_p + d_u$
. Therefore,
 $\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
. Moreover, we can build
$\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
. Moreover, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _p}{\Gamma _p;\; x \;:\; \mathscr{M} \Vdash ^{(b_p,1+m_p,d_p)} {\tt get}_{l}(\lambda y.p): {\{l \;:\; \mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }({\tt get}) \end{equation*}
\begin{equation*} \frac {\Phi _p}{\Gamma _p;\; x \;:\; \mathscr{M} \Vdash ^{(b_p,1+m_p,d_p)} {\tt get}_{l}(\lambda y.p): {\{l \;:\; \mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }({\tt get}) \end{equation*}
 $\Gamma _t = \Gamma _p$
,
$\Gamma _t = \Gamma _p$
,
 $b_t = b_p$
,
$b_t = b_p$
,
 $m_t = m_p$
, and
$m_t = m_p$
, and
 $d_t = d_p$
. Thus, we can conclude with
$d_t = d_p$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _p + \Gamma _u$
,
 $b = b_{p \{x \setminus u\}}=b_p + b_u$
,
$b = b_{p \{x \setminus u\}}=b_p + b_u$
,
 $m = 1 + m_{p \{x \setminus u\}} = 1 + m_p + m_u$
, and
$m = 1 + m_{p \{x \setminus u\}} = 1 + m_p + m_u$
, and
 $d = d_{p \{x \setminus u\}}= d_p + d_u$
.
$d = d_{p \{x \setminus u\}}= d_p + d_u$
.
-
– Rule (set). Then,
 $t = {\tt set}_{l}(p,r)$
,
$t = {\tt set}_{l}(p,r)$
,
 $\mu = {\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
$\mu = {\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
 $t \{x \setminus u\} = {\tt set}_{l}((p \{x \setminus u\}),(r \{x \setminus u\}))$
. Therefore,
$t \{x \setminus u\} = {\tt set}_{l}((p \{x \setminus u\}),(r \{x \setminus u\}))$
. Therefore,
 $\Phi _{t \{x \setminus u\}}$
has two premises
$\Phi _{t \{x \setminus u\}}$
has two premises
 $\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _{p \{x \setminus u\}}}\,\Vdash ^{(b_{p \{x \setminus u\}},m_{p \{x \setminus u\}}, d_{p \{x \setminus u\}})}_{\tt n} {p \{x \setminus u\}}\,:\,{\mathscr{M\;}'}$
and
$\Phi _{p \{x \setminus u\}} \triangleright \, {\Gamma _{p \{x \setminus u\}}}\,\Vdash ^{(b_{p \{x \setminus u\}},m_{p \{x \setminus u\}}, d_{p \{x \setminus u\}})}_{\tt n} {p \{x \setminus u\}}\,:\,{\mathscr{M\;}'}$
and
 $\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _{r \{x \setminus u\}}}\,\Vdash ^{(b_{r \{x \setminus u\}},m_{r \{x \setminus u\}},d_{r \{x \setminus u\}})}_{\tt n} {r \{x \setminus u\}}\,:\,{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
$\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _{r \{x \setminus u\}}}\,\Vdash ^{(b_{r \{x \setminus u\}},m_{r \{x \setminus u\}},d_{r \{x \setminus u\}})}_{\tt n} {r \{x \setminus u\}}\,:\,{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
 $\Gamma _{t \{x \setminus u\}} = \Gamma _{p \{x \setminus u\}} + \Gamma _{r \{x \setminus u\}}$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _{p \{x \setminus u\}} + \Gamma _{r \{x \setminus u\}}$
,
 $b = b_{p \{x \setminus u\}} + b_{r \{x \setminus u\}}$
,
$b = b_{p \{x \setminus u\}} + b_{r \{x \setminus u\}}$
,
 $m = 1 + m_{p \{x \setminus u\}} + m_{r \{x \setminus u\}}$
, and
$m = 1 + m_{p \{x \setminus u\}} + m_{r \{x \setminus u\}}$
, and
 $d = d_{p \{x \setminus u\}} + d_{r \{x \setminus u\}}$
. By applying the i.h. to
$d = d_{p \{x \setminus u\}} + d_{r \{x \setminus u\}}$
. By applying the i.h. to
 $\Phi _{p \{x \setminus u\}}$
, there exist
$\Phi _{p \{x \setminus u\}}$
, there exist
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{M\;}'}$
and
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{M\;}'}$
and
 $\Phi ^1_u \triangleright \, {\Gamma ^1_u}\,\Vdash ^{(b^1_u,m^1_u,d^1_u)}_{\tt n} {u}\,:\,{\mathscr{M}_1}$
, where
$\Phi ^1_u \triangleright \, {\Gamma ^1_u}\,\Vdash ^{(b^1_u,m^1_u,d^1_u)}_{\tt n} {u}\,:\,{\mathscr{M}_1}$
, where
 $\Gamma _{p \{x \setminus u\}} = \Gamma _p + \Gamma ^1_u$
,
$\Gamma _{p \{x \setminus u\}} = \Gamma _p + \Gamma ^1_u$
,
 $b_{p \{x \setminus u\}} = b_p + b^1_u$
,
$b_{p \{x \setminus u\}} = b_p + b^1_u$
,
 $m_{p \{x \setminus u\}} = m_p + m^1_u$
,
$m_{p \{x \setminus u\}} = m_p + m^1_u$
,
 $d_{p \{x \setminus u\}} = d_p + d^1_u$
. By applying the i.h. to
$d_{p \{x \setminus u\}} = d_p + d^1_u$
. By applying the i.h. to
 $\Phi _{r \{x \setminus u\}}$
, there exist
$\Phi _{r \{x \setminus u\}}$
, there exist
 $\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}_2}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
and
$\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}_2}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
and
 $\Phi ^2_u \triangleright \, {\Gamma ^2_u}\, \Vdash ^{(b^2_u,m^2_u,d^2_u)}_{\tt n} {u}\,:\,{\mathscr{M}_2}$
, where
$\Phi ^2_u \triangleright \, {\Gamma ^2_u}\, \Vdash ^{(b^2_u,m^2_u,d^2_u)}_{\tt n} {u}\,:\,{\mathscr{M}_2}$
, where
 $\Gamma _{r \{x \setminus u\}} = \Gamma _r + \Gamma ^2_u$
,
$\Gamma _{r \{x \setminus u\}} = \Gamma _r + \Gamma ^2_u$
,
 $b_{r \{x \setminus u\}} = b_r + b^2_u$
,
$b_{r \{x \setminus u\}} = b_r + b^2_u$
,
 $m_{r \{x \setminus u\}} = m_r + m^2_u$
, and
$m_{r \{x \setminus u\}} = m_r + m^2_u$
, and
 $d_{r \{x \setminus u\}} = d_r + d^2_u$
. By Lemma 36, there exists
$d_{r \{x \setminus u\}} = d_r + d^2_u$
. By Lemma 36, there exists
 $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
 $b_u = b^1_u+b^2_u$
,
$b_u = b^1_u+b^2_u$
,
 $m_u = m^1_u+m^2_u$
, and
$m_u = m^1_u+m^2_u$
, and
 $d_u = d^1_u+d^2_u$
. Moreover, we can build
$d_u = d^1_u+d^2_u$
. Moreover, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _{{p}}\qquad \Phi _{{r}}}{(\Gamma _{{p}} + \Gamma _{{r}});\; x \;:\; \mathscr{M} \Vdash ^{(b_p+b_r,1+m_p+m_r,d_p+d_r)} {\tt set}_{l}({p},{r}): {\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }({\tt set})\end{equation*}
\begin{equation*} \frac {\Phi _{{p}}\qquad \Phi _{{r}}}{(\Gamma _{{p}} + \Gamma _{{r}});\; x \;:\; \mathscr{M} \Vdash ^{(b_p+b_r,1+m_p+m_r,d_p+d_r)} {\tt set}_{l}({p},{r}): {\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }({\tt set})\end{equation*}
 $\Gamma _t = \Gamma _p+ \Gamma _r$
,
$\Gamma _t = \Gamma _p+ \Gamma _r$
,
 $b_t = b_p + b_r$
,
$b_t = b_p + b_r$
,
 $m_t = 1+m_p+m_r$
, and
$m_t = 1+m_p+m_r$
, and
 $d_t = d_p + d_r$
. Thus, we can conclude with
$d_t = d_p + d_r$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus u\}} = \Gamma _{p \{x \setminus u\}}+ \Gamma _{r \{x \setminus u\}} = (\Gamma _r + \Gamma ^1_u) + (\Gamma _p + \Gamma ^2_u) = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _{p \{x \setminus u\}}+ \Gamma _{r \{x \setminus u\}} = (\Gamma _r + \Gamma ^1_u) + (\Gamma _p + \Gamma ^2_u) = \Gamma _t + \Gamma _u$
,
 $b = b_{r \{x \setminus u\}} + b_{p \{x \setminus u\}} = (b_r + b^1_u) + (b_p + b^2_u) = b_t + b_u$
,
$b = b_{r \{x \setminus u\}} + b_{p \{x \setminus u\}} = (b_r + b^1_u) + (b_p + b^2_u) = b_t + b_u$
,
 $m = 1 + m_{r \{x \setminus u\}} + m_{p \{x \setminus u\}} = 1+ (m_r + m^1_u) + (m_p + m^2_u) = m_t + m_u$
, and
$m = 1 + m_{r \{x \setminus u\}} + m_{p \{x \setminus u\}} = 1+ (m_r + m^1_u) + (m_p + m^2_u) = m_t + m_u$
, and
 $d = d_{r \{x \setminus u\}} + d_{p \{x \setminus u\}} = (d_r + d^1_u) + (d_p + d^2_u) = d_t + d_u$
.
$d = d_{r \{x \setminus u\}} + d_{p \{x \setminus u\}} = (d_r + d^1_u) + (d_p + d^2_u) = d_t + d_u$
.
-
– Rule (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $t = rp$
,
$t = rp$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
 $t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
. Therefore,
$t \{x \setminus u\} = (r \{x \setminus u\})(p \{x \setminus u\})$
. Therefore,
 $\Phi _{t \{x \setminus u\}}$
has one premise
$\Phi _{t \{x \setminus u\}}$
has one premise
 $\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b_{r \{x \setminus u\}},m_{r \{x \setminus u\}},d_{r \{x \setminus u\}})}_{\tt n} {r \{x \setminus u\}}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
,
$\Phi _{r \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b_{r \{x \setminus u\}},m_{r \{x \setminus u\}},d_{r \{x \setminus u\}})}_{\tt n} {r \{x \setminus u\}}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
,
 $b=b_{r \{x \setminus u\}}$
,
$b=b_{r \{x \setminus u\}}$
,
 $m= m_{r \{x \setminus u\}}$
, and
$m= m_{r \{x \setminus u\}}$
, and
 $d = 1 + d_{r \{x \setminus u\}}$
. By applying the i.h. to
$d = 1 + d_{r \{x \setminus u\}}$
. By applying the i.h. to
 $\Phi _{r \{x \setminus u\}}$
, there exist
$\Phi _{r \{x \setminus u\}}$
, there exist
 $\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
and
$\Phi _r \triangleright \, {\Gamma _r;\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}$
and
 $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
 $\Gamma _{t \{x \setminus u\}} = \Gamma _r + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _r + \Gamma _u$
,
 $b_{r \{x \setminus u\}} = b_r + b_u$
,
$b_{r \{x \setminus u\}} = b_r + b_u$
,
 $m_{r \{x \setminus u\}} = m_r + m_r$
, and
$m_{r \{x \setminus u\}} = m_r + m_r$
, and
 $d_{r \{x \setminus u\}} = d_r + d_u$
. Therefore, we can build
$d_{r \{x \setminus u\}} = d_r + d_u$
. Therefore, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _r}{\Gamma _r;\; x \;:\; \mathscr{M} \Vdash ^{(b_r,m_r,1+d_r)} r\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}_{{\tt p}}) \end{equation*}
\begin{equation*} \frac {\Phi _r}{\Gamma _r;\; x \;:\; \mathscr{M} \Vdash ^{(b_r,m_r,1+d_r)} r\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}_{{\tt p}}) \end{equation*}
 $b_t = b_r$
,
$b_t = b_r$
,
 $m_t = m_r$
, and
$m_t = m_r$
, and
 $d_t = 1 + d_r$
. Thus, we can conclude with
$d_t = 1 + d_r$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus u\}} = \Gamma _r + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _r + \Gamma _u$
,
 $b = b_{r \{x \setminus u\}}= b_r + b_u = b_r + b_u$
,
$b = b_{r \{x \setminus u\}}= b_r + b_u = b_r + b_u$
,
 $m = m_{r \{x \setminus u\}}= m_r + m_u = m_t + m_u$
, and
$m = m_{r \{x \setminus u\}}= m_r + m_u = m_t + m_u$
, and
 $d = 1 + d_{r \{x \setminus u\}} = 1 + d_r + d_u = d_t + d_u$
.
$d = 1 + d_{r \{x \setminus u\}} = 1 + d_r + d_u = d_t + d_u$
.
-
-
• Case
 $\mathscr{G\,} = \mathscr{M}_0 = [ \delta _i ]_{i \in I}$
. Let us assume
$\mathscr{G\,} = \mathscr{M}_0 = [ \delta _i ]_{i \in I}$
. Let us assume
 $t = x$
, such that
$t = x$
, such that
 $t \{x \setminus u\} = u$
. Then,
$t \{x \setminus u\} = u$
. Then,
 $\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_{\tt n} {u}\,:\,{[ \delta _i ]_{i \in I}}$
and we pick
$\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _{t \{x \setminus u\}}}\,\Vdash ^{(b,m,d)}_{\tt n} {u}\,:\,{[ \delta _i ]_{i \in I}}$
and we pick
 $\Phi _u = \Phi _{t \{x \setminus u\}}$
, where
$\Phi _u = \Phi _{t \{x \setminus u\}}$
, where
 $\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
$\Gamma _u = \Gamma _{t \{x \setminus u\}}$
,
 $b_u = b$
and
$b_u = b$
and
 $m_u = m$
,
$m_u = m$
,
 $d_u=d$
, and build
$d_u=d$
, and build
 $\Phi _t$
as follows:
$\Phi _t$
as follows:
where
 $\Gamma _t = \emptyset$
, and
$\Gamma _t = \emptyset$
, and
 $b_t = m_t = d_t = 0$
. In both cases, we can conclude with
$b_t = m_t = d_t = 0$
. In both cases, we can conclude with
 $\Gamma _{t \{x \setminus u\}} = \Gamma _u = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = \Gamma _u = \Gamma _t + \Gamma _u$
,
 $b = b_u = b_t + b_u$
,
$b = b_u = b_t + b_u$
,
 $m = m_u = m_t + m_u$
, and
$m = m_u = m_t + m_u$
, and
 $d =d_u= d_t + d_u$
. From now on, we are going to assume
$d =d_u= d_t + d_u$
. From now on, we are going to assume
 $t \neq x$
and consider the last rule used in
$t \neq x$
and consider the last rule used in
 $\Phi _{t \{x \setminus u\}}$
, which must be (m):
$\Phi _{t \{x \setminus u\}}$
, which must be (m):-
– Rule (m). Then,
 $\mathscr{M}_0 = [ \delta _i ]_{i \in I}$
and
$\mathscr{M}_0 = [ \delta _i ]_{i \in I}$
and
 $\Phi _{t \{x \setminus u\}}$
has premises
$\Phi _{t \{x \setminus u\}}$
has premises
 $(\Phi ^i_{t \{x \setminus u\}} \triangleright \Gamma ^i_{t \{x \setminus u\}} \Vdash^{(b_i,m_i,d_i)}_{\texttt{n}} t \{x \setminus u\} : \delta_{i})_{i \in I}$
, where
$(\Phi ^i_{t \{x \setminus u\}} \triangleright \Gamma ^i_{t \{x \setminus u\}} \Vdash^{(b_i,m_i,d_i)}_{\texttt{n}} t \{x \setminus u\} : \delta_{i})_{i \in I}$
, where
 $\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma ^i_{t \{x \setminus u\}}$
,
$\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma ^i_{t \{x \setminus u\}}$
,
 $b = +_{i \in I} b_i$
,
$b = +_{i \in I} b_i$
,
 $m = +_{i \in I} m_i$
, and
$m = +_{i \in I} m_i$
, and
 $d = +_{i \in I} d_i$
. By applying the i.h. to each
$d = +_{i \in I} d_i$
. By applying the i.h. to each
 $\Phi ^i_{t \{x \setminus u\}}$
, there exist
$\Phi ^i_{t \{x \setminus u\}}$
, there exist
 $(\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i}\, \Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt n} {t}\,:\,{\delta _i})_{i \in I}$
and
$(\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i}\, \Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt n} {t}\,:\,{\delta _i})_{i \in I}$
and
 $(\Phi ^i_u \triangleright \, {\Gamma ^i_u}\,\Vdash ^{(b^i_u,m^i_u,d^i_u)}_{\tt n} {u}\,:\,{\mathscr{M}_i})_{i \in I}$
, where
$(\Phi ^i_u \triangleright \, {\Gamma ^i_u}\,\Vdash ^{(b^i_u,m^i_u,d^i_u)}_{\tt n} {u}\,:\,{\mathscr{M}_i})_{i \in I}$
, where
 $\Gamma ^i_{t \{x \setminus u\}} = \Gamma ^i_t + \Gamma ^i_u$
,
$\Gamma ^i_{t \{x \setminus u\}} = \Gamma ^i_t + \Gamma ^i_u$
,
 $b_i = b^i_t + b^i_u$
,
$b_i = b^i_t + b^i_u$
,
 $m_i = m^i_t + m^i_u$
, and
$m_i = m^i_t + m^i_u$
, and
 $d_i = d^i_t + d^i_u$
, for each
$d_i = d^i_t + d^i_u$
, for each
 $i \in I$
. By Lemma 36, there exists
$i \in I$
. By Lemma 36, there exists
 $\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
$\Phi _u \triangleright \, \Gamma _u \Vdash ^{(b_u,m_u,d_u)}_{\tt n} u\;:\;\mathscr{M}$
, where
 $\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
$\Gamma _u = +_{i \in I} \Gamma ^i_u$
,
 $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
 $b_u = +_{i \in I} b^i_u$
,
$b_u = +_{i \in I} b^i_u$
,
 $m_u = +_{i \in I} m^i_u$
, and
$m_u = +_{i \in I} m^i_u$
, and
 $d_u = +_{i \in I} d^i_u$
. Moreover, we can build
$d_u = +_{i \in I} d^i_u$
. Moreover, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {(\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i}\,\Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt n} {t}\,:\,{\delta _i})_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \sqcup _{i \in I} \mathscr{M}_i \Vdash ^{(+_{i \in I} b_i, +_{i \in I} m_i, +_{i \in I} d_i)} t\;:\; [ \delta _i ]_{i \in I}}({\tt m})\end{equation*}
\begin{equation*} \frac {(\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i}\,\Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt n} {t}\,:\,{\delta _i})_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \sqcup _{i \in I} \mathscr{M}_i \Vdash ^{(+_{i \in I} b_i, +_{i \in I} m_i, +_{i \in I} d_i)} t\;:\; [ \delta _i ]_{i \in I}}({\tt m})\end{equation*}
 $\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
$\Gamma _t = +_{i \in I} \Gamma ^i_t$
,
 $b_t = +_{i \in I} b^i_t$
,
$b_t = +_{i \in I} b^i_t$
,
 $m_t = +_{i \in I} m^i_t$
, and
$m_t = +_{i \in I} m^i_t$
, and
 $d_t = +_{i \in I} d^i_t$
. Thus, we can conclude with
$d_t = +_{i \in I} d^i_t$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma ^i_{t \{x \setminus u\}} = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_u = \Gamma _t + \Gamma _u$
,
$\Gamma _{t \{x \setminus u\}} = +_{i \in I} \Gamma ^i_{t \{x \setminus u\}} = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_u) = +_{i \in I} \Gamma ^i_t +_{i \in I} \Gamma ^i_u = \Gamma _t + \Gamma _u$
,
 $b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_u) = +_{i \in I} b^i_t +_{i \in I} b^i_u = b_t+b_u$
,
$b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_u) = +_{i \in I} b^i_t +_{i \in I} b^i_u = b_t+b_u$
,
 $m = +_{i \in I} m_i = +_{i \in I} (m^i_t + m^i_u) = +_{i \in I} m^i_t +_{i \in I} m^i_u = m_t+m_u$
,
$m = +_{i \in I} m_i = +_{i \in I} (m^i_t + m^i_u) = +_{i \in I} m^i_t +_{i \in I} m^i_u = m_t+m_u$
,
 $d = +_{i \in I} d_i = +_{i \in I} (d^i_t + d^i_u) = +_{i \in I} d^i_t +_{i \in I} d^i_u = d_t+d_u$
.
$d = +_{i \in I} d_i = +_{i \in I} (d^i_t + d^i_u) = +_{i \in I} d^i_t +_{i \in I} d^i_u = d_t+d_u$
.
-
Lemma 14 (Quantitative subject expansion). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d')}_{\tt n} (u,q):\kappa$
is a tight derivation, then
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d')}_{\tt n} (u,q):\kappa$
is a tight derivation, then
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d')}_{\tt n} (t,s):\kappa$
, where
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d')}_{\tt n} (t,s):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt n}}}$
implies
${\tt r} ={\beta _{{\tt n}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Proof. We show a stronger statement:
Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt n}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d')}_{\tt n} (u,q):\kappa$
,
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d')}_{\tt n} (u,q):\kappa$
,
![]() $\Gamma$
is tight, and
$\Gamma$
is tight, and
![]() $\kappa$
is tight or
$\kappa$
is tight or
![]() $\neg {\tt abs}(t)$
, then
$\neg {\tt abs}(t)$
, then
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d')}_{\tt n} (t,s):\kappa$
, where
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d')}_{\tt n} (t,s):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt n}}}$
implies
${\tt r} ={\beta _{{\tt n}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
We proceed by induction on
![]() $(t, s) \rightsquigarrow _{{\tt n}} (u,q)$
:
$(t, s) \rightsquigarrow _{{\tt n}} (u,q)$
:
-
• Case
 $(t,s) = ((\lambda x.p) r,s) \rightsquigarrow _{{\beta _{{\tt n}}}} (p \{x \setminus r\}, s) = (u,q)$
. Then
$(t,s) = ((\lambda x.p) r,s) \rightsquigarrow _{{\beta _{{\tt n}}}} (p \{x \setminus r\}, s) = (u,q)$
. Then
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _{p \{x \setminus r\}} \triangleright \, {\Gamma _{p \{x \setminus r\}}}\,\Vdash ^{(b_{p \{x \setminus r\}},m_{p \{x \setminus u\}},d_{p \{x \setminus r\}})}_{\tt n} {p \{x \setminus r\}}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _{p \{x \setminus r\}} \triangleright \, {\Gamma _{p \{x \setminus r\}}}\,\Vdash ^{(b_{p \{x \setminus r\}},m_{p \{x \setminus u\}},d_{p \{x \setminus r\}})}_{\tt n} {p \{x \setminus r\}}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
$\Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}$
, such that
 $\Gamma = \Gamma _{p \{x \setminus r\}} + \Delta _s$
,
$\Gamma = \Gamma _{p \{x \setminus r\}} + \Delta _s$
,
 $b' = b_{p \{x \setminus r\}}+b_s$
,
$b' = b_{p \{x \setminus r\}}+b_s$
,
 $m' = m_{p \{x \setminus r\}} +m_s$
, and
$m' = m_{p \{x \setminus r\}} +m_s$
, and
 $d' = d_{p \{x \setminus r\}} +d_s$
. By Lemma 39, there exist
$d' = d_{p \{x \setminus r\}} +d_s$
. By Lemma 39, there exist
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\mathscr{T\;} \Rightarrow \kappa }$
and
 $\Phi _{r} \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{M}}$
, such that
$\Phi _{r} \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\,:\,{\mathscr{M}}$
, such that
 $\Gamma _{p \{x \setminus r\}} = \Gamma _p + \Gamma _r$
,
$\Gamma _{p \{x \setminus r\}} = \Gamma _p + \Gamma _r$
,
 $b_{p \{ \setminus r\}} = b_p+b_r$
,
$b_{p \{ \setminus r\}} = b_p+b_r$
,
 $m_{p \{x \setminus u\}} = m_p+m_r$
, and
$m_{p \{x \setminus u\}} = m_p+m_r$
, and
 $d_{p \{x \setminus u\}} = d_p + d_r$
. Therefore, we can build
$d_{p \{x \setminus u\}} = d_p + d_r$
. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:
such that
 $b = 1+b_p+b_r+b_s$
,
$b = 1+b_p+b_r+b_s$
,
 $m = m_p+m_r+m_s$
, and
$m = m_p+m_r+m_s$
, and
 $d = d_p+d_r+d_s$
. Thus, we can conclude with
$d = d_p+d_r+d_s$
. Thus, we can conclude with
 $\Gamma = \Gamma _{p \{x \setminus r\}} + \Delta _s = (\Gamma _p + \Gamma _r) + \Delta _s$
,
$\Gamma = \Gamma _{p \{x \setminus r\}} + \Delta _s = (\Gamma _p + \Gamma _r) + \Delta _s$
,
 $b' = b_{p \{x \setminus r\}} + b_s = b_p + b_r + b_s = (1 + b_p + b_r + b_s) - 1 = b - 1$
,
$b' = b_{p \{x \setminus r\}} + b_s = b_p + b_r + b_s = (1 + b_p + b_r + b_s) - 1 = b - 1$
,
 $m' = m_{p \{x \setminus u\}} + m_s = (m_p + m_r) + m_s = m$
, and
$m' = m_{p \{x \setminus u\}} + m_s = (m_p + m_r) + m_s = m$
, and
 $d' = d_{p \{x \setminus u\}} + d_s = (d_p + d_r) + d_s = d$
.
$d' = d_{p \{x \setminus u\}} + d_s = (d_p + d_r) + d_s = d$
. -
• Case
 $(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt n}} (p \{x \setminus r\},s) = (u,q)$
, such that
$(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt n}} (p \{x \setminus r\},s) = (u,q)$
, such that
 $q \equiv {\tt upd}_{l}(r,s') \equiv s$
. Then,
$q \equiv {\tt upd}_{l}(r,s') \equiv s$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _u \triangleright \, {\Gamma _{p \{x \setminus r\}}}\,\Vdash ^{(b_{p \{x \setminus r\}},m_{p \{x \setminus r\}},d_{p \{x \setminus r\}})}_{\tt n} {p \{x \setminus r\}}\,:\,{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _u \triangleright \, {\Gamma _{p \{x \setminus r\}}}\,\Vdash ^{(b_{p \{x \setminus r\}},m_{p \{x \setminus r\}},d_{p \{x \setminus r\}})}_{\tt n} {p \{x \setminus r\}}\,:\,{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _q$
, which must be of the following form:where
$\Pi _q$
, which must be of the following form:where \begin{equation*} \frac {\Phi ^2_r \triangleright \, {\Gamma ^2_r}\,\Vdash ^{(b^2_r,m^2_r,d^2_r)}_{\tt n} {r}\,:\,{\mathscr{M}_2}\qquad \Pi _{s'} \triangleright \, {\Delta _{s'}}\,\Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt n} {s'}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma ^2_r + \Delta _{s'} \Vdash ^{(b^2_r+b_{s'},m^2_r+m_{s'},d^2_r+d_{s'})} {\tt upd}_{l}(r,s'): \{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi ^2_r \triangleright \, {\Gamma ^2_r}\,\Vdash ^{(b^2_r,m^2_r,d^2_r)}_{\tt n} {r}\,:\,{\mathscr{M}_2}\qquad \Pi _{s'} \triangleright \, {\Delta _{s'}}\,\Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt n} {s'}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma ^2_r + \Delta _{s'} \Vdash ^{(b^2_r+b_{s'},m^2_r+m_{s'},d^2_r+d_{s'})} {\tt upd}_{l}(r,s'): \{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
 $\Gamma = \Gamma _{p \{x \setminus r\}} + (\Gamma ^2_r + \Delta _{s'})$
,
$\Gamma = \Gamma _{p \{x \setminus r\}} + (\Gamma ^2_r + \Delta _{s'})$
,
 $b' = b_{p \{x \setminus r\}} + b^2_r + b_{s'}$
,
$b' = b_{p \{x \setminus r\}} + b^2_r + b_{s'}$
,
 $m' = m_{p \{x \setminus r\}} + b^2_r + b_{s'}$
, and
$m' = m_{p \{x \setminus r\}} + b^2_r + b_{s'}$
, and
 $d' = d_{p \{x \setminus r\}} +d^2_r+d_{s'}$
. By Lemma 39, there exist
$d' = d_{p \{x \setminus r\}} +d^2_r+d_{s'}$
. By Lemma 39, there exist
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
 $\Phi ^1_r \triangleright \, {\Gamma ^1_r}\, \Vdash ^{(b^1_r,m^1_r,d^1_r)}_{\tt n} {r}\,:\,{\mathscr{M}_1}$
, such that
$\Phi ^1_r \triangleright \, {\Gamma ^1_r}\, \Vdash ^{(b^1_r,m^1_r,d^1_r)}_{\tt n} {r}\,:\,{\mathscr{M}_1}$
, such that
 $\Gamma _{p \{x \setminus r\}} = \Gamma _p + \Gamma ^1_r$
,
$\Gamma _{p \{x \setminus r\}} = \Gamma _p + \Gamma ^1_r$
,
 $b_{p \{x \setminus r\}} = b_p + b^1_r$
,
$b_{p \{x \setminus r\}} = b_p + b^1_r$
,
 $m_{p \{x \setminus r\}} = m_p + m^1_r$
, and
$m_{p \{x \setminus r\}} = m_p + m^1_r$
, and
 $d_{p \{x \setminus u\}} = d_p + d^1_r$
. Therefore, we can build
$d_{p \{x \setminus u\}} = d_p + d^1_r$
. Therefore, we can build
 $\Phi _t$
as follows:By Lemma 36, there exists
$\Phi _t$
as follows:By Lemma 36, there exists \begin{equation*} \frac {\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }}{\Gamma _p \Vdash ^{(b_p,1+m_p,d_p)} {\tt get}_{l}(\lambda x.p): \{l \;:\; {\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
\begin{equation*} \frac {\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }}{\Gamma _p \Vdash ^{(b_p,1+m_p,d_p)} {\tt get}_{l}(\lambda x.p): \{l \;:\; {\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
 $\Phi _r \triangleright \, {\Gamma ^1_r + \Gamma ^2_r}\, \Vdash ^{(b^1_r+b^2_r,m^1_r+m^2_r,d^1_r+d^2_r)}_{\tt n} {r}\,:\,{\mathscr{M}_1 \sqcup \mathscr{M}_2}$
. Therefore, we can build an alternative derivation
$\Phi _r \triangleright \, {\Gamma ^1_r + \Gamma ^2_r}\, \Vdash ^{(b^1_r+b^2_r,m^1_r+m^2_r,d^1_r+d^2_r)}_{\tt n} {r}\,:\,{\mathscr{M}_1 \sqcup \mathscr{M}_2}$
. Therefore, we can build an alternative derivation
 $\Pi '_q$
for
$\Pi '_q$
for
 $q$
as follows:Then, we can pick
$q$
as follows:Then, we can pick \begin{equation*} \frac {\Phi _r\qquad \Pi _{s'}}{(\Gamma ^1_r + \Gamma ^2_r) + \Delta _{s'} \Vdash ^{(b^1_r+b^2_r+b_{s'},m^1_r+m^2_r+m_{s'},d^1_r+d^2_r+d_{s'})} {\tt upd}_{l}(r,s'): \{l \;:\; {\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi _r\qquad \Pi _{s'}}{(\Gamma ^1_r + \Gamma ^2_r) + \Delta _{s'} \Vdash ^{(b^1_r+b^2_r+b_{s'},m^1_r+m^2_r+m_{s'},d^1_r+d^2_r+d_{s'})} {\tt upd}_{l}(r,s'): \{l \;:\; {\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
 $\Pi _s = \Pi '_q$
, and build
$\Pi _s = \Pi '_q$
, and build
 $\Phi$
as follows:where
$\Phi$
as follows:where \begin{equation*} \frac {\Phi _t\qquad \Pi _s}{\Gamma _p + (\Gamma ^1_r + \Gamma ^2_r) + \Delta _{s'} \Vdash ^{(b_p+b^1_r+b^2_r+b_{s'},1+m_p+m^1_r+m^2_r+m_{s'},d_p+d^1_r+d^2_r+d_{s'})} ({\tt get}_{l}(\lambda x.p), s): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _t\qquad \Pi _s}{\Gamma _p + (\Gamma ^1_r + \Gamma ^2_r) + \Delta _{s'} \Vdash ^{(b_p+b^1_r+b^2_r+b_{s'},1+m_p+m^1_r+m^2_r+m_{s'},d_p+d^1_r+d^2_r+d_{s'})} ({\tt get}_{l}(\lambda x.p), s): \kappa }({\tt conf})\end{equation*}
 $b = b_p+b^1_r+b^2_r+b_{s'}$
,
$b = b_p+b^1_r+b^2_r+b_{s'}$
,
 $m = 1+m_p+m^1_r+m^2_r+m_{s'}$
, and
$m = 1+m_p+m^1_r+m^2_r+m_{s'}$
, and
 $d = d_p+d^1_r+d^2_r+d_{s'}$
. Thus, we can conclude with
$d = d_p+d^1_r+d^2_r+d_{s'}$
. Thus, we can conclude with
 $\Gamma = \Gamma _{p \{x \setminus r\}} + (\Gamma ^2_r + \Delta _{s'}) = \Gamma _p + \Gamma ^1_r + \Gamma ^2_r + \Delta _{s'}$
,
$\Gamma = \Gamma _{p \{x \setminus r\}} + (\Gamma ^2_r + \Delta _{s'}) = \Gamma _p + \Gamma ^1_r + \Gamma ^2_r + \Delta _{s'}$
,
 $b' = b_{p \{x \setminus r\}} + b^2_r + b_{s'} = b_p + b^1_r + b^2_r + b_{s'} = b$
, and
$b' = b_{p \{x \setminus r\}} + b^2_r + b_{s'} = b_p + b^1_r + b^2_r + b_{s'} = b$
, and
 $m' = m_{p \{x \setminus r\}} + m^2_r + m_{s'} = m_p + m^1_r + m^2_r + m_{s'} = (1 + m_p + m^1_r + m^2_r + m_{s'}) - 1 = m - 1$
,
$m' = m_{p \{x \setminus r\}} + m^2_r + m_{s'} = m_p + m^1_r + m^2_r + m_{s'} = (1 + m_p + m^1_r + m^2_r + m_{s'}) - 1 = m - 1$
,
 $d' = d_{p \{x \setminus r\}} + d^2_r + d_{s'} = d_p + d^1_r + d^2_r + d_{s'} = d$
.
$d' = d_{p \{x \setminus r\}} + d^2_r + d_{s'} = d_p + d^1_r + d^2_r + d_{s'} = d$
.
-
• Case
 $(t,s) = ({\tt set}_{l}(r,p),s) \rightsquigarrow _{{\tt n}} (p, {\tt upd}_{l}(r,s)) = (u,q)$
. Then,
$(t,s) = ({\tt set}_{l}(r,p),s) \rightsquigarrow _{{\tt n}} (p, {\tt upd}_{l}(r,s)) = (u,q)$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _p \triangleright \, {\Gamma _p}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _p \triangleright \, {\Gamma _p}\,\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\,:\,{\{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _q$
, which must be of the following form:where
$\Pi _q$
, which must be of the following form:where \begin{equation*} \frac {\Phi _{r} \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\;:\;{\mathscr{M}}\qquad \Pi _{s} \triangleright \, {\Delta _s}\Vdash ^{(b_s,m_s,d_s)}_{\tt n} {s}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma _r + \Delta _s \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} {\tt upd}_{l}(r,s): \{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi _{r} \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt n} {r}\;:\;{\mathscr{M}}\qquad \Pi _{s} \triangleright \, {\Delta _s}\Vdash ^{(b_s,m_s,d_s)}_{\tt n} {s}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma _r + \Delta _s \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} {\tt upd}_{l}(r,s): \{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
 $\Gamma = \Gamma _p + (\Gamma _r + \Delta _s)$
,
$\Gamma = \Gamma _p + (\Gamma _r + \Delta _s)$
,
 $b' = b_p + b_r + b_s$
,
$b' = b_p + b_r + b_s$
,
 $m' = m_p + m_r + m_s$
, and
$m' = m_p + m_r + m_s$
, and
 $d' = d_p + d_r + d_s$
. Therefore, we can build
$d' = d_p + d_r + d_s$
. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:

where
 $b =b_r+b_p+b_s$
,
$b =b_r+b_p+b_s$
,
 $m = 1+m_r+m_p+m_s$
, and
$m = 1+m_r+m_p+m_s$
, and
 $d = d_r+d_p+d_s$
. Thus, we can conclude with
$d = d_r+d_p+d_s$
. Thus, we can conclude with
 $\Gamma = \Gamma _p + (\Gamma _r + \Delta _s)$
,
$\Gamma = \Gamma _p + (\Gamma _r + \Delta _s)$
,
 $b' = b_r+b_p+b_s = b$
,
$b' = b_r+b_p+b_s = b$
,
 $m' + 1 = (m_p + m_r + m_s) + 1 = m$
, and
$m' + 1 = (m_p + m_r + m_s) + 1 = m$
, and
 $d' = d_r+d_p+d_s = d$
.
$d' = d_r+d_p+d_s = d$
. -
• Case
 $(t,s) = (pr,s) \rightsquigarrow _{{\tt n}} (p'r,q) = (u,q)$
, such that
$(t,s) = (pr,s) \rightsquigarrow _{{\tt n}} (p'r,q) = (u,q)$
, such that
 $(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
. Then,
$(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _u \triangleright \, {\Gamma _u}\,\Vdash ^{(b_u,m_u,d_u)}_{\tt n} {u}\;:\;{\mathscr{T\;}' \Rightarrow \kappa }$
and
$\Phi _u \triangleright \, {\Gamma _u}\,\Vdash ^{(b_u,m_u,d_u)}_{\tt n} {u}\;:\;{\mathscr{T\;}' \Rightarrow \kappa }$
and
 $\Pi _q \triangleright \, {\Delta _q}\Vdash ^{(b_q,m_q,d_q)}_{\tt n} {q}\;:\;{\mathscr{T\;}'}$
, such that
$\Pi _q \triangleright \, {\Delta _q}\Vdash ^{(b_q,m_q,d_q)}_{\tt n} {q}\;:\;{\mathscr{T\;}'}$
, such that
 $\Gamma = \Gamma _u + \Delta _q$
,
$\Gamma = \Gamma _u + \Delta _q$
,
 $b' = b_u + b_q$
,
$b' = b_u + b_q$
,
 $m' = m_u + m_q$
, and
$m' = m_u + m_q$
, and
 $d' = d_u + d_q$
. Moreover,
$d' = d_u + d_q$
. Moreover,
 $\Phi _u$
must end with rule (@) or (@
$\Phi _u$
must end with rule (@) or (@
 $_{{\tt p}}$
):
$_{{\tt p}}$
):-
– Case
 $\Phi _u$
ends with (
$\Phi _u$
ends with (
 $\tt @$
). Then,
$\tt @$
). Then,
 $\Phi _u$
must be of the following form:
$\Phi _u$
must be of the following form:
where
 $\Gamma _u = \Gamma _{p'}+\Gamma _{r}$
,
$\Gamma _u = \Gamma _{p'}+\Gamma _{r}$
,
 $b_u = 1 + b_{p'}+b_r$
,
$b_u = 1 + b_{p'}+b_r$
,
 $m_u = m_{p'}+m_r$
, and
$m_u = m_{p'}+m_r$
, and
 $d_u =d_{p'}+d_r$
. Therefore, we can build derivation
$d_u =d_{p'}+d_r$
. Therefore, we can build derivation
 $\Phi _{(p',q)}$
as follows:Notice that
$\Phi _{(p',q)}$
as follows:Notice that \begin{equation*} \frac {\Phi _{p'}\qquad \Pi _q}{\Gamma _{p'} + \Delta _q \Vdash ^{(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)} (p', q): (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}''}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p'}\qquad \Pi _q}{\Gamma _{p'} + \Delta _q \Vdash ^{(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)} (p', q): (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}''}({\tt conf})\end{equation*}
 $\Gamma _{p'}$
and
$\Gamma _{p'}$
and
 $\Delta _q$
are tight, and
$\Delta _q$
are tight, and
 $(p, s) \rightsquigarrow _{{\tt n}} (p',q)$
implies
$(p, s) \rightsquigarrow _{{\tt n}} (p',q)$
implies
 $\neg {\tt abs}(p)$
. By applying the i.h. to
$\neg {\tt abs}(p)$
. By applying the i.h. to
 $\Phi _{(p',q)}$
, there exists
$\Phi _{(p',q)}$
, there exists
 $\Phi _{(p,s)}$
that must be of the following form:
$\Phi _{(p,s)}$
that must be of the following form:

where
 $\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
, and
$\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
, and
 $(b_p+b_s,m_p+m_s,d_p+d_s)$
and
$(b_p+b_s,m_p+m_s,d_p+d_s)$
and
 $(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are properly related. Therefore, we can build
$(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are properly related. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:
where
 $\Gamma = \Gamma _{p'} + \Gamma _r + \Delta _q = \Gamma _p + \Gamma _r + \Delta _s$
, and
$\Gamma = \Gamma _{p'} + \Gamma _r + \Delta _q = \Gamma _p + \Gamma _r + \Delta _s$
, and
 $(1 + b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)$
and
$(1 + b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)$
and
 $(1+b_{p'}+b_r + b_q, m_{p'}+m_r+m_q, d_{p'}+d_r+d_q)$
are properly related.
$(1+b_{p'}+b_r + b_q, m_{p'}+m_r+m_q, d_{p'}+d_r+d_q)$
are properly related. -
– Case
 $\Phi _{p'r}$
ends with (@
$\Phi _{p'r}$
ends with (@
 $_{{\tt p}}$
). Then,
$_{{\tt p}}$
). Then,
 $\Phi '$
must be of the following form:
$\Phi '$
must be of the following form:
where
 $\Gamma = \Gamma _{p'} + \Delta _q$
tight,
$\Gamma = \Gamma _{p'} + \Delta _q$
tight,
 $b' = b_{p'}+b_q$
,
$b' = b_{p'}+b_q$
,
 $m' = m_{p'}+m_q$
, and
$m' = m_{p'}+m_q$
, and
 $d' = 1+d_{p'}+d_q$
. Then, we can build derivation
$d' = 1+d_{p'}+d_q$
. Then, we can build derivation
 $\Phi _{(p',q)}$
as follows:Moreover,
$\Phi _{(p',q)}$
as follows:Moreover, \begin{equation*} \frac {\Phi _{p'}\qquad \Pi _q}{\Gamma _{p'} + \Delta _q \Vdash ^{(b_{p'}+b_q,m_{p'}+m_q,1+d_{p'}+d_q)} (p', q): {\tt n} \times \mathscr{T\;}''}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p'}\qquad \Pi _q}{\Gamma _{p'} + \Delta _q \Vdash ^{(b_{p'}+b_q,m_{p'}+m_q,1+d_{p'}+d_q)} (p', q): {\tt n} \times \mathscr{T\;}''}({\tt conf})\end{equation*}
 $\Gamma _{p'}$
and
$\Gamma _{p'}$
and
 $\Delta _q$
are tight, and
$\Delta _q$
are tight, and
 $(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
implies
$(p,s) \rightsquigarrow _{{\tt n}} (p',q)$
implies
 $\neg {\tt abs}(p)$
. By applying the i.h. to
$\neg {\tt abs}(p)$
. By applying the i.h. to
 $\Phi _{(p',q)}$
, there exists a derivation for
$\Phi _{(p',q)}$
, there exists a derivation for
 $\Phi _{(p,s)}$
for
$\Phi _{(p,s)}$
for
 $(p,s)$
that must be of the following form:where
$(p,s)$
that must be of the following form:where \begin{equation*} \frac {\Phi _{p} \triangleright \, {\Gamma _{p}}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\;:\;{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}'')}\qquad \Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}}{\Gamma _{p} + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p, s): {\tt n} \times \mathscr{T\;}''}({\tt conf}) \end{equation*}
\begin{equation*} \frac {\Phi _{p} \triangleright \, {\Gamma _{p}}\Vdash ^{(b_p,m_p,d_p)}_{\tt n} {p}\;:\;{\mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}'')}\qquad \Pi _s \triangleright \Delta _s\Vdash ^{(b_s,m_s,d_s)}_{\tt n} s\;:\;\mathscr{T\;}}{\Gamma _{p} + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p, s): {\tt n} \times \mathscr{T\;}''}({\tt conf}) \end{equation*}
 $\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
,
$\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
,
 $(b_p+b_s,m_p+m_s,d_p+d_s)$
and
$(b_p+b_s,m_p+m_s,d_p+d_s)$
and
 $(b_{p'}+b_q,m_{p'}+m_q,1+d_{p'}+d_q)$
are properly related. Therefore, we can build
$(b_{p'}+b_q,m_{p'}+m_q,1+d_{p'}+d_q)$
are properly related. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:

where
 $b = b_p+b_s$
,
$b = b_p+b_s$
,
 $m = m_p+m_s$
, and
$m = m_p+m_s$
, and
 $d = 1+d_p+d_s$
. Thus, we can conclude with
$d = 1+d_p+d_s$
. Thus, we can conclude with
 $\Gamma = \Gamma _{p'} + \Delta _q = \Gamma _{p} + \Delta _s$
, and
$\Gamma = \Gamma _{p'} + \Delta _q = \Gamma _{p} + \Delta _s$
, and
 $(b_p+b_s,m_p+m_s,1+d_p+d_s)$
and
$(b_p+b_s,m_p+m_s,1+d_p+d_s)$
and
 $(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are properly related.
$(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are properly related.
-
Theorem 4 (Quantitative completeness). If
![]() $(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
and
$(t,s) \rightsquigarrow _{\tt n}^{(b,m)} (u,q)$
and
![]() $u \in {\tt no}_{{\tt n}}$
, then there exists a tight derivation
$u \in {\tt no}_{{\tt n}}$
, then there exists a tight derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {n}})}_{\tt n} (t,s):\kappa$
.
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {n}})}_{\tt n} (t,s):\kappa$
.
Proof.
By induction on
![]() $b + m$
:
$b + m$
:
-
• Case
 $b + m = 0$
. Then,
$b + m = 0$
. Then,
 $b = m = 0$
, and thus,
$b = m = 0$
, and thus,
 $(t,s)=(u,q)$
. Therefore,
$(t,s)=(u,q)$
. Therefore,
 $t \in {\tt no}$
. Thus, we can conclude by Lemma 12.
$t \in {\tt no}$
. Thus, we can conclude by Lemma 12. -
• Case
 $b + m \gt 0$
. Then, there exists
$b + m \gt 0$
. Then, there exists
 $(t',s')$
, such that
$(t',s')$
, such that
 $(t,s) \rightsquigarrow _{{\tt n}}^{(1,0)} (t',s') \rightsquigarrow _{\tt n}^{(b-1,m)} (u,q)$
or
$(t,s) \rightsquigarrow _{{\tt n}}^{(1,0)} (t',s') \rightsquigarrow _{\tt n}^{(b-1,m)} (u,q)$
or
 $(t,s) \rightsquigarrow _{{\tt n}}^{(0,1)} (t',s') \rightsquigarrow _{\tt n}^{(b,m-1)} (u,q)$
. By the i.h., there exists
$(t,s) \rightsquigarrow _{{\tt n}}^{(0,1)} (t',s') \rightsquigarrow _{\tt n}^{(b,m-1)} (u,q)$
. By the i.h., there exists
 $\Phi ' \triangleright {\Gamma } \Vdash ^{(b',m',|{(u,q)}|_{\texttt {n}})}_{\tt n} {(t',s')}\;:\;{\kappa }$
tight, such that
$\Phi ' \triangleright {\Gamma } \Vdash ^{(b',m',|{(u,q)}|_{\texttt {n}})}_{\tt n} {(t',s')}\;:\;{\kappa }$
tight, such that
 $b' + m' = b + m - 1$
. By Lemma 14, we have
$b' + m' = b + m - 1$
. By Lemma 14, we have
 $\Phi \triangleright {\Gamma } \Vdash ^{(b'',m'',|{(u,q)}|_{\texttt {n}})}_{\tt n} {(t,s)}\;:\;{\kappa }$
tight, such that
$\Phi \triangleright {\Gamma } \Vdash ^{(b'',m'',|{(u,q)}|_{\texttt {n}})}_{\tt n} {(t,s)}\;:\;{\kappa }$
tight, such that
 $b'' + m'' = 1+ b' + m'$
. Therefore,
$b'' + m'' = 1+ b' + m'$
. Therefore,
 $b'' + m'' = b + m$
, since the fact that
$b'' + m'' = b + m$
, since the fact that
 $b'' = b$
, and
$b'' = b$
, and
 $m'' = m$
can be easily checked by a simple case analysis.
$m'' = m$
can be easily checked by a simple case analysis.
A.3 Weak Open CBV with Global State
Proposition 5.
Let
![]() $(t,s)$
be a configuration. Then
$(t,s)$
be a configuration. Then
![]() $(t,s)$
is normal iff
$(t,s)$
is normal iff
![]() $(t,s) \not \rightsquigarrow _{{\tt v}}$
.
$(t,s) \not \rightsquigarrow _{{\tt v}}$
.
Proof.
-
⇒) Let
 $(t, s)$
be normal. Then, either
$(t, s)$
be normal. Then, either
 $(t, s)$
is blocked or
$(t, s)$
is blocked or
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
– Case
 $(t,s)$
is blocked. We reason by induction on
$(t,s)$
is blocked. We reason by induction on
 $(t,s)$
.
$(t,s)$
.-
* Case
 $t = {\tt get}_{l}(\lambda x.u)$
, such that
$t = {\tt get}_{l}(\lambda x.u)$
, such that
 $l \not \in {\tt labels}(s)$
. Then
$l \not \in {\tt labels}(s)$
. Then
 $(t, s) \not \rightsquigarrow _{{\tt v}}$
by definition.
$(t, s) \not \rightsquigarrow _{{\tt v}}$
by definition. -
* Case
 $(t,s) = (up, s)$
, such that
$(t,s) = (up, s)$
, such that
 $(u,s)$
is blocked. Then, by applying the i.h. to
$(u,s)$
is blocked. Then, by applying the i.h. to
 $(u,s)$
, we get
$(u,s)$
, we get
 $(u,s) \not \rightsquigarrow _{{\tt v}}$
. Moreover, since
$(u,s) \not \rightsquigarrow _{{\tt v}}$
. Moreover, since
 $(u, s)$
is blocked, then necessarily
$(u, s)$
is blocked, then necessarily
 $\neg {\tt val}(u)$
. Therefore, rule (
$\neg {\tt val}(u)$
. Therefore, rule (
 $\beta _{\tt v}$
) does not apply since
$\beta _{\tt v}$
) does not apply since
 $\neg {\tt val}(u)$
, rule (appL) does not apply since
$\neg {\tt val}(u)$
, rule (appL) does not apply since
 $(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
$(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
 $(u,s)$
is blocked, and rules (get) and (set) do not apply since
$(u,s)$
is blocked, and rules (get) and (set) do not apply since
 $t$
is an application. Thus,
$t$
is an application. Thus,
 $(up, s) \not \rightsquigarrow _{{\tt v}}$
.
$(up, s) \not \rightsquigarrow _{{\tt v}}$
. -
* Case
 $(t, s) = (up, s)$
, such that
$(t, s) = (up, s)$
, such that
 $(u,s) \not \rightsquigarrow _{{\tt v}}$
,
$(u,s) \not \rightsquigarrow _{{\tt v}}$
,
 $(u,s)$
is unblocked, and
$(u,s)$
is unblocked, and
 $(p,s)$
is blocked. Then, by applying the i.h. to
$(p,s)$
is blocked. Then, by applying the i.h. to
 $(p,s)$
, we get
$(p,s)$
, we get
 $(p,s) \not \rightsquigarrow _{{\tt v}}$
. Moreover, since
$(p,s) \not \rightsquigarrow _{{\tt v}}$
. Moreover, since
 $(p,s)$
is blocked, then necessarily
$(p,s)$
is blocked, then necessarily
 $p \neq v$
. Therefore, rule (
$p \neq v$
. Therefore, rule (
 $\beta _{\tt v}$
) does not apply since
$\beta _{\tt v}$
) does not apply since
 $p \neq v$
, rule (appL) does not apply since
$p \neq v$
, rule (appL) does not apply since
 $(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
$(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
 $(p,s) \not \rightsquigarrow _{{\tt v}}$
, and rules (get) and (set) do not apply since
$(p,s) \not \rightsquigarrow _{{\tt v}}$
, and rules (get) and (set) do not apply since
 $t$
is an application. Thus, no rule applies to
$t$
is an application. Thus, no rule applies to
 $(up,s)$
, that is,
$(up,s)$
, that is,
 $(up,s) \not \rightsquigarrow _{{\tt v}}$
.
$(up,s) \not \rightsquigarrow _{{\tt v}}$
.
-
-
– Case
 $t \in {\tt no}_{{\tt v}}$
. Then,
$t \in {\tt no}_{{\tt v}}$
. Then,
 $(t,s)$
is unblocked by definition. We reason by induction on
$(t,s)$
is unblocked by definition. We reason by induction on
 $t \in {\tt no}_{{\tt v}}$
.
$t \in {\tt no}_{{\tt v}}$
.-
* Case
 ${\tt val}(t)$
. Then
${\tt val}(t)$
. Then
 $(t,s) \not \rightsquigarrow _{{\tt v}}$
by definition.
$(t,s) \not \rightsquigarrow _{{\tt v}}$
by definition. -
* Case
 $\neg {\tt val}(t)$
. Then necessarily
$\neg {\tt val}(t)$
. Then necessarily
 $t \in {\tt ne}_{{\tt v}}$
. There are three cases:
$t \in {\tt ne}_{{\tt v}}$
. There are three cases:-
· Case
 $t = xp$
, such that
$t = xp$
, such that
 $p \in {\tt no}_{{\tt v}}$
. By applying the i.h. to
$p \in {\tt no}_{{\tt v}}$
. By applying the i.h. to
 $(p,s)$
, we get
$(p,s)$
, we get
 $(p,s) \not \rightsquigarrow _{{\tt v}}$
. Therefore, no rule of
$(p,s) \not \rightsquigarrow _{{\tt v}}$
. Therefore, no rule of
 $\rightsquigarrow _{{\tt v}}$
applies to
$\rightsquigarrow _{{\tt v}}$
applies to
 $(xp, s)$
, that is,
$(xp, s)$
, that is,
 $(xp, s)\not \rightsquigarrow _{{\tt v}}$
.
$(xp, s)\not \rightsquigarrow _{{\tt v}}$
. -
· Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}} \subseteq {\tt no}_{{\tt v}}$
. Moreover,
$p \in {\tt ne}_{{\tt v}} \subseteq {\tt no}_{{\tt v}}$
. Moreover,
 $p \neq v$
, and
$p \neq v$
, and
 $(u,s)$
and
$(u,s)$
and
 $(p,s)$
are unblocked. By applying the i.h. to
$(p,s)$
are unblocked. By applying the i.h. to
 $(u,s)$
and
$(u,s)$
and
 $(p,s)$
, we get
$(p,s)$
, we get
 $(u, s) \not \rightsquigarrow _{{\tt v}}$
and
$(u, s) \not \rightsquigarrow _{{\tt v}}$
and
 $(p, s) \not \rightsquigarrow _{{\tt v}}$
, respectively. Therefore, rule (
$(p, s) \not \rightsquigarrow _{{\tt v}}$
, respectively. Therefore, rule (
 $\beta _{\tt v}$
) does not apply since
$\beta _{\tt v}$
) does not apply since
 $p \neq v$
, rule (appL) does not apply since
$p \neq v$
, rule (appL) does not apply since
 $(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
$(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
 $(p,s) \not \rightsquigarrow _{{\tt v}}$
, and rules (get) and (set) do not apply since
$(p,s) \not \rightsquigarrow _{{\tt v}}$
, and rules (get) and (set) do not apply since
 $t$
is an application. Thus,
$t$
is an application. Thus,
 $(up, s)\not \rightsquigarrow _{{\tt v}}$
.
$(up, s)\not \rightsquigarrow _{{\tt v}}$
. -
· Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
. Moreover,
$p \in {\tt no}_{{\tt v}}$
. Moreover,
 $\neg {\tt val}(u)$
and
$\neg {\tt val}(u)$
and
 $(u,s)$
and
$(u,s)$
and
 $(p,s)$
are unblocked. By applying the i.h. to
$(p,s)$
are unblocked. By applying the i.h. to
 $(u,s)$
and
$(u,s)$
and
 $(p,s)$
, we get
$(p,s)$
, we get
 $(u, s) \not \rightsquigarrow _{{\tt v}}$
and
$(u, s) \not \rightsquigarrow _{{\tt v}}$
and
 $(p, s) \not \rightsquigarrow _{{\tt v}}$
, respectively. Therefore, rule (
$(p, s) \not \rightsquigarrow _{{\tt v}}$
, respectively. Therefore, rule (
 $\beta _{\tt v}$
) does not apply since
$\beta _{\tt v}$
) does not apply since
 $\neg {\tt val}(u)$
, rule (appL) does not apply since
$\neg {\tt val}(u)$
, rule (appL) does not apply since
 $(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
$(u,s) \not \rightsquigarrow _{{\tt v}}$
, rule (appR) does not apply since
 $(p,s) \not \rightsquigarrow _{{\tt v}}$
, and rules (get) and (set) do not apply since
$(p,s) \not \rightsquigarrow _{{\tt v}}$
, and rules (get) and (set) do not apply since
 $t$
is an application. Thus,
$t$
is an application. Thus,
 $(up, s)\not \rightsquigarrow _{{\tt v}}$
.
$(up, s)\not \rightsquigarrow _{{\tt v}}$
.
-
-
-
-
⇐) Let
 $(t,s) \not \rightsquigarrow _{{\tt v}}$
. We reason by induction on
$(t,s) \not \rightsquigarrow _{{\tt v}}$
. We reason by induction on
 $t$
:
$t$
:-
– Case
 ${\tt val}(t)$
. Then,
${\tt val}(t)$
. Then,
 $t \in {\tt no}_{{\tt v}}$
by definition. Therefore,
$t \in {\tt no}_{{\tt v}}$
by definition. Therefore,
 $(t, s)$
is normal.
$(t, s)$
is normal. -
– Case
 $t = up$
:
$t = up$
:-
* Case
 $u = \lambda x.r$
and
$u = \lambda x.r$
and
 ${\tt val}(p)$
. Then, rule (
${\tt val}(p)$
. Then, rule (
 $\beta _{\tt v}$
) is applicable to
$\beta _{\tt v}$
) is applicable to
 $(up, s)$
, which leads to a contradiction with the hypothesis. Therefore, this case does not apply.
$(up, s)$
, which leads to a contradiction with the hypothesis. Therefore, this case does not apply. -
* Case
 $u = \lambda x.r$
and
$u = \lambda x.r$
and
 $p \neq v$
. Since
$p \neq v$
. Since
 $(\lambda x.r,s)\not \rightsquigarrow _{{\tt v}}$
and
$(\lambda x.r,s)\not \rightsquigarrow _{{\tt v}}$
and
 $(\lambda x.r,s)$
is unblocked by definition, therefore,
$(\lambda x.r,s)$
is unblocked by definition, therefore,
 $(p, s) \not \rightsquigarrow _{{\tt v}}$
; otherwise, rule (appR) would be applicable to
$(p, s) \not \rightsquigarrow _{{\tt v}}$
; otherwise, rule (appR) would be applicable to
 $(up, s)$
. We can then apply the i.h. to
$(up, s)$
. We can then apply the i.h. to
 $p$
, which implies that
$p$
, which implies that
 $(p, s)$
is normal. Therefore, either
$(p, s)$
is normal. Therefore, either
 $(p, s)$
is blocked, or
$(p, s)$
is blocked, or
 $p \in {\tt no}_{{\tt v}}$
. Let us first assume
$p \in {\tt no}_{{\tt v}}$
. Let us first assume
 $(p, s)$
is blocked. Then,
$(p, s)$
is blocked. Then,
 $(up, s)$
is blocked, and thus, it is normal. Let us now assume
$(up, s)$
is blocked, and thus, it is normal. Let us now assume
 $p \in {\tt no}_{{\tt v}}$
. Since
$p \in {\tt no}_{{\tt v}}$
. Since
 $p \neq v$
then
$p \neq v$
then
 $p \in {\tt ne}_{{\tt v}}$
, and
$p \in {\tt ne}_{{\tt v}}$
, and
 ${\tt val}(u)$
, and thus,
${\tt val}(u)$
, and thus,
 $u \subseteq {\tt no}_{{\tt v}}$
. Therefore,
$u \subseteq {\tt no}_{{\tt v}}$
. Therefore,
 $up \in {\tt ne}_{{\tt v}} \subseteq {\tt no}_{{\tt v}}$
. Thus,
$up \in {\tt ne}_{{\tt v}} \subseteq {\tt no}_{{\tt v}}$
. Thus,
 $(up, s)$
is normal.
$(up, s)$
is normal. -
* Case
 $\neg {\tt abs}(u)$
. Then,
$\neg {\tt abs}(u)$
. Then,
 $(u, s) \not \rightsquigarrow _{{\tt v}}$
, otherwise rule (appL) would be applicable to
$(u, s) \not \rightsquigarrow _{{\tt v}}$
, otherwise rule (appL) would be applicable to
 $(up, s)$
. We can then apply the i.h. to
$(up, s)$
. We can then apply the i.h. to
 $u$
, which implies that
$u$
, which implies that
 $(u, s)$
is normal. Therefore, either
$(u, s)$
is normal. Therefore, either
 $(u, s)$
is blocked, or
$(u, s)$
is blocked, or
 $u \in {\tt no}_{{\tt v}}$
. Let us first assume
$u \in {\tt no}_{{\tt v}}$
. Let us first assume
 $(u, s)$
is blocked. Then,
$(u, s)$
is blocked. Then,
 $(up, s)$
is blocked by definition, and thus, it is normal. Let us now assume
$(up, s)$
is blocked by definition, and thus, it is normal. Let us now assume
 $u \in {\tt no}_{{\tt v}}$
. Therefore,
$u \in {\tt no}_{{\tt v}}$
. Therefore,
 $(u, s)$
is unblocked. As a consequence,
$(u, s)$
is unblocked. As a consequence,
 $(p, s) \not \rightsquigarrow _{{\tt v}}$
, otherwise rule (appR) would be applicable to
$(p, s) \not \rightsquigarrow _{{\tt v}}$
, otherwise rule (appR) would be applicable to
 $(up, s)$
. We can then apply the i.h. to
$(up, s)$
. We can then apply the i.h. to
 $p$
, which implies that
$p$
, which implies that
 $(p, s)$
is normal. Therefore, either
$(p, s)$
is normal. Therefore, either
 $(p, s)$
is blocked, or
$(p, s)$
is blocked, or
 $p \in {\tt no}_{{\tt v}}$
. In the former case,
$p \in {\tt no}_{{\tt v}}$
. In the former case,
 $(up, s)$
is blocked by definition, and thus, it is normal. In the latter case,
$(up, s)$
is blocked by definition, and thus, it is normal. In the latter case,
 $up \in {\tt ne}_{{\tt v}}\subseteq {\tt no}_{{\tt v}}$
. Thus,
$up \in {\tt ne}_{{\tt v}}\subseteq {\tt no}_{{\tt v}}$
. Thus,
 $(up, s)$
is normal.
$(up, s)$
is normal.
-
-
Lemma 40 (Relevance). Let
![]() $\Phi \triangleright {\Gamma }\Vdash ^{(b,m,d)}_{\tt v} {t}\;:\;{\mu }$
(resp.
$\Phi \triangleright {\Gamma }\Vdash ^{(b,m,d)}_{\tt v} {t}\;:\;{\mu }$
(resp.
![]() $\Pi \triangleright \, {\Delta } \Vdash ^{(b',m',d')}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
). Then
$\Pi \triangleright \, {\Delta } \Vdash ^{(b',m',d')}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
). Then
![]() ${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
(resp.
${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(t)$
(resp.
![]() ${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(s)$
).
${\tt dom}(\Gamma ) \subseteq {{\tt fv}}(s)$
).
Proof.
By a simple induction over
![]() $\Phi$
(resp.
$\Phi$
(resp.
![]() $\Pi$
).
$\Pi$
).
Lemma 41 (Tight spreading). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt ne}_{{\tt v}}$
, then
$t \in {\tt ne}_{{\tt v}}$
, then
![]() $\tau = {\tt n}$
.
$\tau = {\tt n}$
.
Proof.
We proceed by induction on
![]() $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:
-
(1) Case
 $t = x u$
, with
$t = x u$
, with
 $u \in {\tt no}_{{\tt v}}$
.
$u \in {\tt no}_{{\tt v}}$
. -
(2) Case
 $t = u p$
, with
$t = u p$
, with
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
.
$p \in {\tt no}_{{\tt v}}$
. -
(3) Case or
 $t = up$
, with
$t = up$
, with
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
.
$p \in {\tt ne}_{{\tt v}}$
.
In all the above cases,
![]() $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
![]() $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
![]() $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):
-
• Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _l \triangleright \, \Gamma _l \vdash ^{(b_l,m_l,d_l)} t_l\;:\; \mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}''' \Rightarrow \kappa )) \times \mathscr{T\;}'')$
and
$\Phi _l \triangleright \, \Gamma _l \vdash ^{(b_l,m_l,d_l)} t_l\;:\; \mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}''' \Rightarrow \kappa )) \times \mathscr{T\;}'')$
and
 $\Phi _r \triangleright \, \Gamma _r \vdash ^{(b_r,m_r,d_r)} t_r\;:\; \mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}''')$
, such that
$\Phi _r \triangleright \, \Gamma _r \vdash ^{(b_r,m_r,d_r)} t_r\;:\; \mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}''')$
, such that
 $\Gamma = \Gamma _l + \Gamma _r$
is tight,
$\Gamma = \Gamma _l + \Gamma _r$
is tight,
 $\kappa = \tau \times \mathscr{T\;}'$
,
$\kappa = \tau \times \mathscr{T\;}'$
,
 $b = 1+b_l+b_r$
,
$b = 1+b_l+b_r$
,
 $m = m_l+m_r$
, and
$m = m_l+m_r$
, and
 $d = d_l+d_r$
:
$d = d_l+d_r$
:-
(1)
 $t_l = x$
,
$t_l = x$
,
 $t_r = u$
, and
$t_r = u$
, and
 $\Gamma _l = (x \;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ])$
. However,
$\Gamma _l = (x \;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ])$
. However,
 $\mathscr{M} \rightarrow (\mathscr{T\;}''' \Rightarrow \kappa )$
is not tight, which leads to a contradiction with
$\mathscr{M} \rightarrow (\mathscr{T\;}''' \Rightarrow \kappa )$
is not tight, which leads to a contradiction with
 $\Gamma$
tight. Therefore, this case does not apply.
$\Gamma$
tight. Therefore, this case does not apply. -
(2)
 $t_l = u$
and
$t_l = u$
and
 $t_r = p$
. By i.h. on
$t_r = p$
. By i.h. on
 $u \in {\tt ne}_{{\tt v}}$
we get
$u \in {\tt ne}_{{\tt v}}$
we get
 $\mathscr{M} \rightarrow (\mathscr{T\;}''' \Rightarrow \kappa ) = {\tt n}$
, which is a contradiction. Therefore, this case does not apply either.
$\mathscr{M} \rightarrow (\mathscr{T\;}''' \Rightarrow \kappa ) = {\tt n}$
, which is a contradiction. Therefore, this case does not apply either. -
(3)
 $t_l = u$
and
$t_l = u$
and
 $t_r = p$
. By i.h. on
$t_r = p$
. By i.h. on
 $p \in {\tt ne}_{{\tt v}}$
, we get
$p \in {\tt ne}_{{\tt v}}$
, we get
 $\mathscr{M} = {\tt n}$
, which is a contradiction. Therefore, this case does not apply either.
$\mathscr{M} = {\tt n}$
, which is a contradiction. Therefore, this case does not apply either.
-
-
• Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). Then
$^2_{{\tt p}}$
). Then
 $\tau = {\tt n}$
by definition.
$\tau = {\tt n}$
by definition.
Lemma 42.
Let
![]() $\Pi \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
. If
$\Pi \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
. If
![]() $l \in {\tt dom}(\mathscr{T\;})$
, then
$l \in {\tt dom}(\mathscr{T\;})$
, then
![]() $l \in {\tt labels}(s)$
.
$l \in {\tt labels}(s)$
.
Proof. We proceed by proving the following stronger version of the statement:
Let
![]() $\Pi \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
. If
$\Pi \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
. If
![]() $l \in {\tt dom}(\mathscr{T\;})$
, then
$l \in {\tt dom}(\mathscr{T\;})$
, then
![]() $s \equiv {\tt upd}_{l}(v,q)$
, for some value
$s \equiv {\tt upd}_{l}(v,q)$
, for some value
![]() $v$
and store
$v$
and store
![]() $q$
.
$q$
.
The proof follows by induction on
![]() $\Pi$
:
$\Pi$
:
-
• Case
 $\Pi$
ends with (
$\Pi$
ends with (
 $\tt emp$
). Then
$\tt emp$
). Then
 $\mathscr{T\;}=\emptyset$
which contradicts
$\mathscr{T\;}=\emptyset$
which contradicts
 $l \in {\tt dom}(\mathscr{T\;})$
.
$l \in {\tt dom}(\mathscr{T\;})$
. -
• Case
 $\Pi$
ends with (
$\Pi$
ends with (
 $\tt upd$
). Then
$\tt upd$
). Then
 $\Pi$
is of the following form:where
$\Pi$
is of the following form:where \begin{equation*} \frac {\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}\qquad \Pi _q \triangleright \, {\Delta _q}\Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\;:\;{\{l':\mathscr{L\;}'\};\;\mathscr{T\;}_q}}{\Gamma _v + \Delta _q \Vdash ^{(b_v+b_q,m_v+m_q,d_v+d_q)} {\tt upd}_{l'}(v,q): \{l' \;:\; \mathscr{M} \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_q}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}\qquad \Pi _q \triangleright \, {\Delta _q}\Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\;:\;{\{l':\mathscr{L\;}'\};\;\mathscr{T\;}_q}}{\Gamma _v + \Delta _q \Vdash ^{(b_v+b_q,m_v+m_q,d_v+d_q)} {\tt upd}_{l'}(v,q): \{l' \;:\; \mathscr{M} \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_q}({\tt upd})\end{equation*}
 $\Delta = \Gamma _v + \Delta _q$
,
$\Delta = \Gamma _v + \Delta _q$
,
 $s = {\tt upd}_{l'}(v,q)$
,
$s = {\tt upd}_{l'}(v,q)$
,
 $\mathscr{T\;} = \{l' \;:\; \mathscr{M} \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_q$
,
$\mathscr{T\;} = \{l' \;:\; \mathscr{M} \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_q$
,
 $b = b_v + b_q$
,
$b = b_v + b_q$
,
 $m = m_v + m_q$
, and
$m = m_v + m_q$
, and
 $d = d_v + d_q$
. We consider two cases:
$d = d_v + d_q$
. We consider two cases:-
– Case
 $l = l'$
. Then we are done.
$l = l'$
. Then we are done. -
– Case
 $l \not = l'$
.The hypothesis
$l \not = l'$
.The hypothesis
 $l \in {\tt dom}(\mathscr{T\;})$
implies
$l \in {\tt dom}(\mathscr{T\;})$
implies
 $l \in {\tt dom}(\mathscr{T\;}_q)$
, and thus,
$l \in {\tt dom}(\mathscr{T\;}_q)$
, and thus,
 $l \in {\tt dom}(\{l':\mathscr{L\;}'\};\;\mathscr{T\;}_q)$
. By the i.h. on
$l \in {\tt dom}(\{l':\mathscr{L\;}'\};\;\mathscr{T\;}_q)$
. By the i.h. on
 $\Pi _q$
, we have
$\Pi _q$
, we have
 $q \equiv {\tt upd}_{l}(w,q')$
, for some value
$q \equiv {\tt upd}_{l}(w,q')$
, for some value
 $w$
and store
$w$
and store
 $q'$
. Therefore,
$q'$
. Therefore,
 $s \equiv {\tt upd}_{l'}(v,{\tt upd}_{l}(w,q')) \equiv {\tt upd}_{l}(w,{\tt upd}_{l'}(v,q'))$
, and we thus conclude.
$s \equiv {\tt upd}_{l'}(v,{\tt upd}_{l}(w,q')) \equiv {\tt upd}_{l}(w,{\tt upd}_{l'}(v,q'))$
, and we thus conclude.
-
The correctness of the original statement now follows easily from the fact that
![]() $s \equiv {\tt upd}_{l}(v,q)$
implies
$s \equiv {\tt upd}_{l}(v,q)$
implies
![]() $l \in {\tt labels}(s)$
, by the definition of the domain of a state in Weak Open CBV with Global State (c.f. Subsection 3.2).
$l \in {\tt labels}(s)$
, by the definition of the domain of a state in Weak Open CBV with Global State (c.f. Subsection 3.2).
Lemma 15 (Normal forms have pure types). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $t \in {\tt no}_{{\tt v}}$
, then (1)
$t \in {\tt no}_{{\tt v}}$
, then (1)
![]() $\mathscr{T\;} = \mathscr{T\;}'$
and, (2) for any
$\mathscr{T\;} = \mathscr{T\;}'$
and, (2) for any
![]() $\mathscr{T\;}_0$
, there exists
$\mathscr{T\;}_0$
, there exists
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;}_0 \Rightarrow (\tau \times \mathscr{T\;}_0)$
.
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;}_0 \Rightarrow (\tau \times \mathscr{T\;}_0)$
.
Proof.
The proof follows by induction on
![]() $t$
:
$t$
:
-
• Case
 ${\tt val}(t)$
. Then,
${\tt val}(t)$
. Then,
 $\Phi$
can only end with rule (
$\Phi$
can only end with rule (
 $\uparrow$
). Therefore, (1)
$\uparrow$
). Therefore, (1)
 $\mathscr{T\;} = \mathscr{T\;}'$
, by definition. And (2)
$\mathscr{T\;} = \mathscr{T\;}'$
, by definition. And (2)
 $\Phi '$
can be built by taking the premise
$\Phi '$
can be built by taking the premise
 $\Phi$
and simply choosing
$\Phi$
and simply choosing
 $\mathscr{T\;}_0$
when applying rule (
$\mathscr{T\;}_0$
when applying rule (
 $\uparrow$
) again.
$\uparrow$
) again. -
• Case
 $\neg {\tt val}(t)$
. Then,
$\neg {\tt val}(t)$
. Then,
 $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:-
– Case
 $t = x u$
, such that
$t = x u$
, such that
 $u \in {\tt no}_{{\tt v}}$
. Then,
$u \in {\tt no}_{{\tt v}}$
. Then,
 $\Phi$
can only end with rule (@), (@
$\Phi$
can only end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
* Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _x \triangleright \, {x \;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ]}\Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;})}$
and
$\Phi _x \triangleright \, {x \;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ]}\Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;})}$
and
 $\Phi _u \triangleright \, {\Gamma _u} \Vdash ^{(b',m',d')}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
$\Phi _u \triangleright \, {\Gamma _u} \Vdash ^{(b',m',d')}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
 $\Gamma = x\;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ] + \Gamma _u$
. Note that a derivation assigning a monadic type to
$\Gamma = x\;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ] + \Gamma _u$
. Note that a derivation assigning a monadic type to
 $x$
, has to necessarily finish with (
$x$
, has to necessarily finish with (
 $\uparrow$
). However,
$\uparrow$
). However,
 $\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
is not tight, which gives a contradiction with
$\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
is not tight, which gives a contradiction with
 $\Gamma$
tight, so that this case cannot happen.
$\Gamma$
tight, so that this case cannot happen. -
* Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _x \triangleright \, {x \;:\; [ \overline {{\tt a}} ]}\, \Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;})}$
and
$\Phi _x \triangleright \, {x \;:\; [ \overline {{\tt a}} ]}\, \Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;})}$
and
 $\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b,m,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, such that
$\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b,m,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, such that
 $\Gamma = (x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u$
,
$\Gamma = (x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u$
,
 $\tau = {\tt n}$
, and
$\tau = {\tt n}$
, and
 $d = 1+d_u$
. By applying the i.h. to
$d = 1+d_u$
. By applying the i.h. to
 $\Phi _u$
, we get (1)
$\Phi _u$
, we get (1)
 $\mathscr{T\;} = \mathscr{T\;}'$
, and (2) for any
$\mathscr{T\;} = \mathscr{T\;}'$
, and (2) for any
 $\mathscr{T\;}_0$
, we have
$\mathscr{T\;}_0$
, we have
 $\Phi '_u \triangleright \, {\Gamma _u} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;}_0 \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}_0)}$
. Furthermore, we can trivially derive
$\Phi '_u \triangleright \, {\Gamma _u} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;}_0 \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}_0)}$
. Furthermore, we can trivially derive
 $\Phi '_x \triangleright \, {x \;:\; [ \overline {{\tt a}} ]}\Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;}_0 \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}_0)}$
by picking the same
$\Phi '_x \triangleright \, {x \;:\; [ \overline {{\tt a}} ]}\Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;}_0 \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}_0)}$
by picking the same
 $\mathscr{T\;}_0$
. Therefore, (2) we can build
$\mathscr{T\;}_0$
. Therefore, (2) we can build
 $\Phi '$
as follows:Thus, we can conclude.
$\Phi '$
as follows:Thus, we can conclude. \begin{equation*} \frac {\Phi '_x\qquad \Phi '_u}{(x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u \Vdash ^{(b,m,1+d_u)} x u\;:\; \mathscr{T\;}_0 \Rightarrow ({\tt n} \times \mathscr{T\;}_0)}({\tt @}^1_{{\tt p}}) \end{equation*}
\begin{equation*} \frac {\Phi '_x\qquad \Phi '_u}{(x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u \Vdash ^{(b,m,1+d_u)} x u\;:\; \mathscr{T\;}_0 \Rightarrow ({\tt n} \times \mathscr{T\;}_0)}({\tt @}^1_{{\tt p}}) \end{equation*}
-
* Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^2_{{\tt p}}$
). This case is very similar to the previous case.
$^2_{{\tt p}}$
). This case is very similar to the previous case.
-
-
– Case
 $t = u p$
, such that
$t = u p$
, such that
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
. Then,
$p \in {\tt no}_{{\tt v}}$
. Then,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
* Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b_u, m_u, s_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
$\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b_u, m_u, s_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
 $\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
$\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
 $\Gamma = \Gamma _u + \Gamma _p$
is tight. By applying Lemma 41 to
$\Gamma = \Gamma _u + \Gamma _p$
is tight. By applying Lemma 41 to
 $\Phi _u$
we get
$\Phi _u$
we get
 $\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'') = {\tt n}$
, which is a contradiction. Therefore, this case cannot hold.
$\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'') = {\tt n}$
, which is a contradiction. Therefore, this case cannot hold. -
* Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases follow easily from the i.h.
$^2_{{\tt p}}$
). These cases follow easily from the i.h.
-
-
– Case
 $t = u p$
, such that
$t = u p$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
. Then,
$p \in {\tt ne}_{{\tt v}}$
. Then,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
* Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b_u, m_u, s_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
$\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b_u, m_u, s_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
 $\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
$\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
 $\Gamma = \Gamma _u + \Gamma _p$
is tight. By applying Lemma 41 to
$\Gamma = \Gamma _u + \Gamma _p$
is tight. By applying Lemma 41 to
 $\Phi _p$
, we get
$\Phi _p$
, we get
 $\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}') = {\tt n}$
, which is a contradiction. Therefore, this case cannot hold.
$\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}') = {\tt n}$
, which is a contradiction. Therefore, this case cannot hold. -
* Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases follow easily from the i.h.
$^2_{{\tt p}}$
). These cases follow easily from the i.h.
-
-
Proposition 6 (Typed configurations are unblocked). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
. Then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
. Then
![]() ${\tt tight}(\Gamma )$
implies
${\tt tight}(\Gamma )$
implies
![]() $(t,s)$
is unblocked.
$(t,s)$
is unblocked.
Proof.
The proof follows by contraposition. We assume that
![]() $(t, s)$
is blocked and show that
$(t, s)$
is blocked and show that
![]() $\Gamma$
is not tight. We proceed by induction on
$\Gamma$
is not tight. We proceed by induction on
![]() $(t, s)$
blocked:
$(t, s)$
blocked:
-
• Case
 $t = {\tt get}_{l}(\lambda x.u)$
, such that
$t = {\tt get}_{l}(\lambda x.u)$
, such that
 $l \not \in {\tt labels}(s)$
. Then,
$l \not \in {\tt labels}(s)$
. Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
such that
 $\Gamma = (\Gamma _u \setminus x) + \Delta _s$
,
$\Gamma = (\Gamma _u \setminus x) + \Delta _s$
,
 $b = b_u+b_s$
,
$b = b_u+b_s$
,
 $m = 1+m_u+m_s$
, and
$m = 1+m_u+m_s$
, and
 $d = d_u+d_s$
. Therefore, by applying Lemma 42 to
$d = d_u+d_s$
. Therefore, by applying Lemma 42 to
 $\Pi _s$
, we get
$\Pi _s$
, we get
 $l \in {\tt labels}(s)$
, which leads to a contradiction. Therefore, this case cannot apply.
$l \in {\tt labels}(s)$
, which leads to a contradiction. Therefore, this case cannot apply. -
• Case
 $t = up$
, such that
$t = up$
, such that
 $(u,s)$
is blocked. We have three cases:
$(u,s)$
is blocked. We have three cases:-
– Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
such that
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
 $b = 1+b_u+b_p+b_s$
,
$b = 1+b_u+b_p+b_s$
,
 $m = m_u+m_p+m_s$
, and
$m = m_u+m_p+m_s$
, and
 $d_u+d_p+d_s$
. Therefore, we can build the following derivation for
$d_u+d_p+d_s$
. Therefore, we can build the following derivation for
 $(u, s)$
:such that
$(u, s)$
:such that \begin{equation*} \frac {\Phi _u\qquad \Pi _s}{\Gamma _u + \Delta _s \Vdash ^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa ) \times \mathscr{T\;}')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Pi _s}{\Gamma _u + \Delta _s \Vdash ^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa ) \times \mathscr{T\;}')}({\tt conf})\end{equation*}
 $\Gamma _u + \Delta _s$
is tight. However, by applying the i.h. to
$\Gamma _u + \Delta _s$
is tight. However, by applying the i.h. to
 $(u, s)$
, we get that
$(u, s)$
, we get that
 $\Gamma _u + \Delta _s$
is not tight. Thus,
$\Gamma _u + \Delta _s$
is not tight. Thus,
 $\Gamma$
cannot be tight, since
$\Gamma$
cannot be tight, since
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
-
– Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
such that
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
 $b = b_u+b_p+b_s$
,
$b = b_u+b_p+b_s$
,
 $m = m_u+m_p+m_s$
, and
$m = m_u+m_p+m_s$
, and
 $1+d_u+d_p+d_s$
. Therefore, we can build the following derivation for
$1+d_u+d_p+d_s$
. Therefore, we can build the following derivation for
 $(u, s)$
:such that
$(u, s)$
:such that \begin{equation*} \frac {\Phi _u\qquad \Pi _s}{\Gamma _u + \Delta _s \Vdash ^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): (\overline {{\tt a}} \times \mathscr{T\;}')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Pi _s}{\Gamma _u + \Delta _s \Vdash ^{(b_u+b_s,m_u+m_s,d_u+d_s)} (u,s): (\overline {{\tt a}} \times \mathscr{T\;}')}({\tt conf})\end{equation*}
 $\Gamma _u + \Delta _s$
is tight. However, by applying the i.h. to
$\Gamma _u + \Delta _s$
is tight. However, by applying the i.h. to
 $(u, s)$
, we get that
$(u, s)$
, we get that
 $\Gamma _u + \Delta _s$
is not tight. Thus,
$\Gamma _u + \Delta _s$
is not tight. Thus,
 $\Gamma$
cannot be tight, since
$\Gamma$
cannot be tight, since
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
-
– Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^2_{{\tt p}}$
). This case is very similar to the previous case.
$^2_{{\tt p}}$
). This case is very similar to the previous case.
-
-
• Case
 $t = up$
, such that
$t = up$
, such that
 $(u, s) \not \rightsquigarrow _{{\tt v}}$
,
$(u, s) \not \rightsquigarrow _{{\tt v}}$
,
 $(u,s)$
is unblocked, and
$(u,s)$
is unblocked, and
 $(p,s)$
is blocked. Moreover,
$(p,s)$
is blocked. Moreover,
 $\Phi$
must end in rule (@), (@
$\Phi$
must end in rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
such that
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
 $b = 1+b_u+b_p+b_s$
,
$b = 1+b_u+b_p+b_s$
,
 $m = m_u+m_p+m_s$
, and
$m = m_u+m_p+m_s$
, and
 $d = d_u+d_p+d_s$
. Since
$d = d_u+d_p+d_s$
. Since
 $(u, s) \not \rightsquigarrow _{{\tt v}}$
, then Proposition5 implies that
$(u, s) \not \rightsquigarrow _{{\tt v}}$
, then Proposition5 implies that
 $(u,s)$
is normal, that is
$(u,s)$
is normal, that is
 $u \in {\tt no}_{{\tt v}}$
or
$u \in {\tt no}_{{\tt v}}$
or
 $(u,s)$
is blocked. But we know that
$(u,s)$
is blocked. But we know that
 $(u,s)$
is unblocked; therefore,
$(u,s)$
is unblocked; therefore,
 $u \in {\tt no}_{{\tt v}}$
, which implies
$u \in {\tt no}_{{\tt v}}$
, which implies
 $\mathscr{T\;} = \mathscr{T\;}'$
, according to Lemma 15.1. Therefore, we can build the following derivation for
$\mathscr{T\;} = \mathscr{T\;}'$
, according to Lemma 15.1. Therefore, we can build the following derivation for
 $(p, s)$
:such that
$(p, s)$
:such that \begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): \mathscr{M} \times \mathscr{T\;}''}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): \mathscr{M} \times \mathscr{T\;}''}({\tt conf})\end{equation*}
 $\Gamma _p + \Delta _s$
is tight. However, by applying the i.h. to
$\Gamma _p + \Delta _s$
is tight. However, by applying the i.h. to
 $(p,s)$
, we get
$(p,s)$
, we get
 $\Gamma _p + \Delta _s$
is not tight. Thus,
$\Gamma _p + \Delta _s$
is not tight. Thus,
 $\Gamma$
cannot be tight, since
$\Gamma$
cannot be tight, since
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
-
– Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
such that
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
,
 $b = b_u+b_p+b_s$
,
$b = b_u+b_p+b_s$
,
 $m = m_u+m_p+m_s$
, and
$m = m_u+m_p+m_s$
, and
 $d = 1+d_u+d_p+d_s$
. Since
$d = 1+d_u+d_p+d_s$
. Since
 $(u, s) \not \rightsquigarrow _{{\tt v}}$
, then Proposition5 implies that
$(u, s) \not \rightsquigarrow _{{\tt v}}$
, then Proposition5 implies that
 $(u,s)$
is normal, that is
$(u,s)$
is normal, that is
 $u \in {\tt no}_{{\tt v}}$
or
$u \in {\tt no}_{{\tt v}}$
or
 $(u,s)$
is blocked. But we know that
$(u,s)$
is blocked. But we know that
 $(u,s)$
is unblocked; therefore,
$(u,s)$
is unblocked; therefore,
 $u \in {\tt no}_{{\tt v}}$
, which implies
$u \in {\tt no}_{{\tt v}}$
, which implies
 $\mathscr{T\;} = \mathscr{T\;}''$
according to Lemma 15.1. Therefore, we can build the following derivation for
$\mathscr{T\;} = \mathscr{T\;}''$
according to Lemma 15.1. Therefore, we can build the following derivation for
 $(p, s)$
:such that
$(p, s)$
:such that \begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): {{\tt tt}_{\tt v}} \times \mathscr{T\;}'}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): {{\tt tt}_{\tt v}} \times \mathscr{T\;}'}({\tt conf})\end{equation*}
 $\Gamma _p + \Delta _s$
is tight. However, by applying the i.h. to
$\Gamma _p + \Delta _s$
is tight. However, by applying the i.h. to
 $(p,s)$
, we get that
$(p,s)$
, we get that
 $\Gamma _p + \Delta _s$
is not tight. Thus, we can conclude that
$\Gamma _p + \Delta _s$
is not tight. Thus, we can conclude that
 $\Gamma$
cannot be tight, since
$\Gamma$
cannot be tight, since
 $\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
$\Gamma = (\Gamma _u + \Gamma _p) + \Delta _s$
.
-
– Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^2_{{\tt p}}$
). This case is very similar to the previous case.
$^2_{{\tt p}}$
). This case is very similar to the previous case.
-
Lemma 43.
Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
![]() $\Gamma$
is tight. If
$\Gamma$
is tight. If
![]() $\tau \in \{{\tt v}, {\tt n}\} = \overline {{\tt a}}$
, then
$\tau \in \{{\tt v}, {\tt n}\} = \overline {{\tt a}}$
, then
![]() $\neg {\tt abs}(t)$
.
$\neg {\tt abs}(t)$
.
Proof.
By induction over
![]() $\Phi$
:
$\Phi$
:
-
• Case
 $\Phi$
ends with rule (ax), (
$\Phi$
ends with rule (ax), (
 $\lambda$
), (
$\lambda$
), (
 $\lambda _{\tt p}$
), or (m). Then,
$\lambda _{\tt p}$
), or (m). Then,
 $\Phi$
does not conclude with a monadic type. Therefore, these cases hold vacuously.
$\Phi$
does not conclude with a monadic type. Therefore, these cases hold vacuously. -
• Case
 $\Phi$
ends with rule (@), (get), (set), (@
$\Phi$
ends with rule (@), (get), (set), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
). Then,
$^2_{{\tt p}}$
). Then,
 $\neg {\tt abs}(t)$
by definition. Thus, we can conclude.
$\neg {\tt abs}(t)$
by definition. Thus, we can conclude. -
• Case
 $\Phi$
ends with rule (
$\Phi$
ends with rule (
 $\uparrow$
). Let us assume
$\uparrow$
). Let us assume
 $t = \lambda x.u$
. Then,
$t = \lambda x.u$
. Then,
 $\tau = \mathscr{M} \rightarrow \mu$
,
$\tau = \mathscr{M} \rightarrow \mu$
,
 $\tau = \mathscr{M}$
, or
$\tau = \mathscr{M}$
, or
 $\tau = {\tt a}$
, depending on whether the premise(s) of
$\tau = {\tt a}$
, depending on whether the premise(s) of
 $\Phi$
end with rule(s) (
$\Phi$
end with rule(s) (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
), respectively. Thus,
$\lambda _{\tt p}$
), respectively. Thus,
 $\tau \not \in \overline {{\tt a}}$
, so we are done. Now, let us assume
$\tau \not \in \overline {{\tt a}}$
, so we are done. Now, let us assume
 $t = x$
. Then
$t = x$
. Then
 $\neg {\tt abs}(t)$
holds.
$\neg {\tt abs}(t)$
holds.
Lemma 44 (Terms in normal form and tight states have correct size).
-
(1) Let
 $\Phi \triangleright {\Gamma }\Vdash ^{(0,0,d)}_{\tt v} {t}\;:\;{\mu }$
be a tight derivation. Then, (i)
$\Phi \triangleright {\Gamma }\Vdash ^{(0,0,d)}_{\tt v} {t}\;:\;{\mu }$
be a tight derivation. Then, (i)
 $t \in {\tt no}_{{\tt v}}$
and (ii)
$t \in {\tt no}_{{\tt v}}$
and (ii)
 $d = |{t}|_{\texttt {v}}$
.
$d = |{t}|_{\texttt {v}}$
. -
(2) Let
 $\Pi \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
be a tight derivation. Then
$\Pi \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
be a tight derivation. Then
 $b = m = d = 0$
.
$b = m = d = 0$
.
Proof.
-
(1) We split statement (1.i) into two parts, but keep the same statement for (1.ii):
-
(a) If
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, then
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, then
 $t \in {\tt ne}_{{\tt v}}$
.
$t \in {\tt ne}_{{\tt v}}$
. -
(b) If
 $\mu = \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')$
, then
$\mu = \mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')$
, then
 $t \in {\tt no}_{{\tt v}}$
.
$t \in {\tt no}_{{\tt v}}$
. -
(c)
 $d = |{t}|_{\texttt {v}}$
.
$d = |{t}|_{\texttt {v}}$
.
 $\Phi$
:
$\Phi$
:-
– Case
 $\Phi$
ends with (ax), (
$\Phi$
ends with (ax), (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). Then the type of the conclusion is not a monadic type. Therefore, this case holds vacuously.
$\lambda _{\tt p}$
). Then the type of the conclusion is not a monadic type. Therefore, this case holds vacuously. -
– Case
 $\Phi$
ends with (@). Then the first counter must be greater than zero. Therefore, this case holds vacuously.
$\Phi$
ends with (@). Then the first counter must be greater than zero. Therefore, this case holds vacuously. -
– Case
 $\Phi$
ends with (
$\Phi$
ends with (
 $\uparrow$
). Then,
$\uparrow$
). Then,
 ${\tt val}(t)$
, and thus,
${\tt val}(t)$
, and thus,
 $t \subseteq {\tt no}_{{\tt v}}$
(thus satisfying 1b),
$t \subseteq {\tt no}_{{\tt v}}$
(thus satisfying 1b),
 $\mu = \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;}')$
, where
$\mu = \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;}')$
, where
 $\mathscr{T\;} = \mathscr{T\;}'$
, and
$\mathscr{T\;} = \mathscr{T\;}'$
, and
 $\Phi$
has one premise
$\Phi$
has one premise
 $\Phi ' \triangleright {\Gamma } \Vdash ^{(0,0,d)}_{\tt v} {t}\;:\;{\pi }$
, where
$\Phi ' \triangleright {\Gamma } \Vdash ^{(0,0,d)}_{\tt v} {t}\;:\;{\pi }$
, where
 $\pi = \sigma$
or
$\pi = \sigma$
or
 $\pi = \mathscr{M}$
. But,
$\pi = \mathscr{M}$
. But,
 $\mathscr{M}$
is not a tight type, so we just need to check if 1c is satisfied when
$\mathscr{M}$
is not a tight type, so we just need to check if 1c is satisfied when
 $\Phi$
concludes with type
$\Phi$
concludes with type
 $\pi \in \{{\tt v}, {\tt a}\}$
:
$\pi \in \{{\tt v}, {\tt a}\}$
:-
— Case
 $\pi = {\tt v}$
. Then
$\pi = {\tt v}$
. Then
 $\Phi$
has one premise that must end with rule (ax) and
$\Phi$
has one premise that must end with rule (ax) and
 $t = x$
. Moreover,
$t = x$
. Moreover,
 $d = 0 =|{x}|_{\texttt {v}}$
, and thus, 1c is satisfied.
$d = 0 =|{x}|_{\texttt {v}}$
, and thus, 1c is satisfied. -
— Case
 $\pi = {\tt a}$
. Then
$\pi = {\tt a}$
. Then
 $\Phi$
has one premise that must end either with (ax) or (
$\Phi$
has one premise that must end either with (ax) or (
 $\lambda _{\tt p}$
), and thus,
$\lambda _{\tt p}$
), and thus,
 $t = x$
or
$t = x$
or
 $t = \lambda x.u$
, respectively. Moreover,
$t = \lambda x.u$
, respectively. Moreover,
 $d = 0 = |{x}|_{\texttt {v}} = |{\lambda x.u}|_{\texttt {v}}$
, and thus, 1c is satisfied.
$d = 0 = |{x}|_{\texttt {v}} = |{\lambda x.u}|_{\texttt {v}}$
, and thus, 1c is satisfied.
-
-
– Case
 $\Phi$
ends with (get) or (set). Then, the second counter must be greater than zero. Therefore, this case holds vacuously.
$\Phi$
ends with (get) or (set). Then, the second counter must be greater than zero. Therefore, this case holds vacuously. -
– Case
 $\Phi$
ends with (@
$\Phi$
ends with (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $t = up$
, and
$t = up$
, and
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(0,0,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
$\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(0,0,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
 $\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(0,0,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, where
$\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(0,0,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, where
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
 $d = 1+d_u + d_p$
. By applying the i.h. to
$d = 1+d_u + d_p$
. By applying the i.h. to
 $\Phi _u$
and
$\Phi _u$
and
 $\Phi _p$
, we get
$\Phi _p$
, we get
 $u, p \in {\tt no}_{{\tt v}}$
, and
$u, p \in {\tt no}_{{\tt v}}$
, and
 $d_u = |{u}|_{\texttt {v}}$
and
$d_u = |{u}|_{\texttt {v}}$
and
 $d_p = |{p}|_{\texttt {v}}$
, respectively. Moreover,
$d_p = |{p}|_{\texttt {v}}$
, respectively. Moreover,
 $\neg {\tt abs}(u)$
, according to Lemma 43. Therefore,
$\neg {\tt abs}(u)$
, according to Lemma 43. Therefore,
 $u = x$
or
$u = x$
or
 $u \in {\tt ne}_{{\tt v}}$
. Therefore,
$u \in {\tt ne}_{{\tt v}}$
. Therefore,
 $up \in {\tt ne}_{{\tt v}}$
(satisfying 1a) Thus, we can conclude with
$up \in {\tt ne}_{{\tt v}}$
(satisfying 1a) Thus, we can conclude with
 $d = 1 + d_u + d_p = |{up}|_{\texttt {v}}$
(satisfying 1c).
$d = 1 + d_u + d_p = |{up}|_{\texttt {v}}$
(satisfying 1c). -
– Case
 $\Phi$
ends with (@
$\Phi$
ends with (@
 $^2_{{\tt p}}$
). This case is very similar to the previous case.
$^2_{{\tt p}}$
). This case is very similar to the previous case.
-
-
(2) We reason by induction over
 $\Pi$
:
$\Pi$
:-
• Case
 $\Pi$
ends with (emp). Then
$\Pi$
ends with (emp). Then
 $\Pi \triangleright \, {\emptyset }\,\Vdash ^{(0,0,0)}_{\tt v} {\varepsilon }\,:\,{\emptyset }$
, where
$\Pi \triangleright \, {\emptyset }\,\Vdash ^{(0,0,0)}_{\tt v} {\varepsilon }\,:\,{\emptyset }$
, where
 $d = 0$
.
$d = 0$
. -
• Case
 $\Pi$
ends with (upd). Then
$\Pi$
ends with (upd). Then
 $s = {\tt upd}_{l}(v,q)$
for some
$s = {\tt upd}_{l}(v,q)$
for some
 $v$
and some
$v$
and some
 $q$
, and
$q$
, and
 $\Pi$
has two premises
$\Pi$
has two premises
 $\Phi _v \triangleright \, {\Gamma _v}\,\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\,:\,{\mathscr{M}}$
and
$\Phi _v \triangleright \, {\Gamma _v}\,\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\,:\,{\mathscr{M}}$
and
 $\Pi _q \triangleright \, {\Delta _q}\,\Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\,:\,{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}_q}$
, where
$\Pi _q \triangleright \, {\Delta _q}\,\Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\,:\,{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}_q}$
, where
 $\Delta = \Gamma _v + \Delta _q$
,
$\Delta = \Gamma _v + \Delta _q$
,
 $\mathscr{T\;} = \{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}_q$
,
$\mathscr{T\;} = \{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}_q$
,
 $b = b_v + b_q$
,
$b = b_v + b_q$
,
 $m = m_v + m_q$
, and
$m = m_v + m_q$
, and
 $d = d_v+d_q$
. However, since we are assuming that
$d = d_v+d_q$
. However, since we are assuming that
 $\Pi$
is tight, then
$\Pi$
is tight, then
 $\mathscr{T\;}$
is tight, which means in particular
$\mathscr{T\;}$
is tight, which means in particular
 $\mathscr{M} = [ \, ]$
,
$\mathscr{M} = [ \, ]$
,
 $\mathscr{L\;}$
tight and
$\mathscr{L\;}$
tight and
 $\mathscr{T\;}_q$
tight. Therefore,
$\mathscr{T\;}_q$
tight. Therefore,
 $b_v = m_v = d_v = 0$
. Moreover, by applying the i.h. to
$b_v = m_v = d_v = 0$
. Moreover, by applying the i.h. to
 $\Pi _q$
, we get
$\Pi _q$
, we get
 $b_q = m_q = d_q = 0$
. Thus, we can conclude with
$b_q = m_q = d_q = 0$
. Thus, we can conclude with
 $b = b_v + b_q = m = m_v + m_q = d = d_v + d_q = 0$
.
$b = b_v + b_q = m = m_v + m_q = d = d_v + d_q = 0$
.
-
Lemma 45 (Terms in normal form take zero steps). Let
![]() $\Phi \triangleright {\Gamma }\,\Vdash ^{(b,m,d)}_{\tt v} {t}\,:\,{\mu }$
be a tight derivation. Then,
$\Phi \triangleright {\Gamma }\,\Vdash ^{(b,m,d)}_{\tt v} {t}\,:\,{\mu }$
be a tight derivation. Then,
![]() $b = m = 0$
iff
$b = m = 0$
iff
![]() $t \in {\tt no}_{{\tt v}}$
.
$t \in {\tt no}_{{\tt v}}$
.
Proof.
-
⇒) By Lemma 44.1.i.
-
⇐) By induction on
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
– Case
 $t = v$
. Then,
$t = v$
. Then,
 $\Phi$
must end with (ax), (
$\Phi$
must end with (ax), (
 $\lambda$
), (m), (
$\lambda$
), (m), (
 $\uparrow$
), or (
$\uparrow$
), or (
 $\lambda _{\tt p}$
):
$\lambda _{\tt p}$
):-
* Case
 $\Phi$
ends with (ax), (
$\Phi$
ends with (ax), (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $\Phi$
does not conclude with a monadic type. Therefore, this case holds vacuously.
$\Phi$
does not conclude with a monadic type. Therefore, this case holds vacuously. -
*
 $\Phi$
ends with (
$\Phi$
ends with (
 $\uparrow$
). Then,
$\uparrow$
). Then,
 $\mu = \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;}')$
and
$\mu = \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;}')$
and
 $\pi = {\tt v}$
or
$\pi = {\tt v}$
or
 $\pi = {\tt a}$
, depending on whether the premise(s) of
$\pi = {\tt a}$
, depending on whether the premise(s) of
 $\Phi$
end with rule(s) (ax) or (
$\Phi$
end with rule(s) (ax) or (
 $\lambda _{\tt p}$
). In both cases
$\lambda _{\tt p}$
). In both cases
 $b = m = 0$
, by definition of rules (ax) and (
$b = m = 0$
, by definition of rules (ax) and (
 $\lambda _{\tt p}$
).
$\lambda _{\tt p}$
).
-
-
– Case
 $t \neq v$
. Then,
$t \neq v$
. Then,
 $t \in {\tt ne}_{{\tt v}}$
by definition. Therefore, (1)
$t \in {\tt ne}_{{\tt v}}$
by definition. Therefore, (1)
 $t = x u$
, where
$t = x u$
, where
 $u \in {\tt no}_{{\tt v}}$
, (2)
$u \in {\tt no}_{{\tt v}}$
, (2)
 $t = u p$
, where
$t = u p$
, where
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
, (3) or
$p \in {\tt no}_{{\tt v}}$
, (3) or
 $t = up$
, where
$t = up$
, where
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
. In all cases,
$p \in {\tt ne}_{{\tt v}}$
. In all cases,
 $\Phi$
must end with rule (@), (@
$\Phi$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
* Case
 $\Phi$
ends with rule (@). Then,
$\Phi$
ends with rule (@). Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _l \triangleright \, {\Gamma _l}\,\Vdash ^{(b_l,m_l,d_l)}_{\tt v} {t_l}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
$\Phi _l \triangleright \, {\Gamma _l}\,\Vdash ^{(b_l,m_l,d_l)}_{\tt v} {t_l}\,:\,{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
 $\Phi _r \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt v} {t_r}\,:\,{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, such that
$\Phi _r \triangleright \, {\Gamma _r}\,\Vdash ^{(b_r,m_r,d_r)}_{\tt v} {t_r}\,:\,{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, such that
 $\Gamma = \Gamma _l + \Gamma _r$
tight,
$\Gamma = \Gamma _l + \Gamma _r$
tight,
 $\mu = \mathscr{T\;} \Rightarrow \kappa$
,
$\mu = \mathscr{T\;} \Rightarrow \kappa$
,
 $b = 1+b_l+b_r$
,
$b = 1+b_l+b_r$
,
 $m = m_l+m_r$
, and
$m = m_l+m_r$
, and
 $d = d_l+d_r$
:
$d = d_l+d_r$
:-
(1)
 $t_l = x$
,
$t_l = x$
,
 $t_r = u$
, and
$t_r = u$
, and
 $\Gamma _l = (x \;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ])$
. However,
$\Gamma _l = (x \;:\; [ \mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa ) ])$
. However,
 $\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
is not tight, which leads to a contradiction with
$\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
is not tight, which leads to a contradiction with
 $\Gamma$
tight. Therefore, this case does not apply.
$\Gamma$
tight. Therefore, this case does not apply. -
(2)
 $t_l = u \in {\tt ne}_{{\tt v}}$
and
$t_l = u \in {\tt ne}_{{\tt v}}$
and
 $t_r = p$
. By Lemma 41,
$t_r = p$
. By Lemma 41,
 $\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
should be equal to
$\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )$
should be equal to
 $\tt n$
, which leads to a contradiction. Therefore, this case does not apply.
$\tt n$
, which leads to a contradiction. Therefore, this case does not apply. -
(3)
 $t_l = u$
and
$t_l = u$
and
 $t_r = p \in {\tt ne}_{{\tt v}}$
. By Lemma 41,
$t_r = p \in {\tt ne}_{{\tt v}}$
. By Lemma 41,
 $\mathscr{M}$
should be equal to
$\mathscr{M}$
should be equal to
 $\tt n$
, which leads to a contradiction. Therefore, this case does not apply.
$\tt n$
, which leads to a contradiction. Therefore, this case does not apply.
-
-
* Case
 $\Phi$
ends with rule (@
$\Phi$
ends with rule (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases follow easily from the i.h.
$^2_{{\tt p}}$
). These cases follow easily from the i.h.
-
-
Lemma 16 (Tight configurations have correct size). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation of the following form:
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation of the following form:
where
![]() $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
![]() $\kappa = (\tau \times \mathscr{T\;}')$
,
$\kappa = (\tau \times \mathscr{T\;}')$
,
![]() $b = b_t + b_s$
,
$b = b_t + b_s$
,
![]() $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
![]() $d = d_t + d_s$
. If
$d = d_t + d_s$
. If
![]() $b_t = m_t = 0$
, then (i)
$b_t = m_t = 0$
, then (i)
![]() $b = m = 0$
and (ii)
$b = m = 0$
and (ii)
![]() $d = |{(t,s)}|_{\texttt {v}}$
.
$d = |{(t,s)}|_{\texttt {v}}$
.
Proof.
Since
![]() $\Gamma$
is tight, then so are
$\Gamma$
is tight, then so are
![]() $\Gamma _t$
and
$\Gamma _t$
and
![]() $\Delta _s$
. Since
$\Delta _s$
. Since
![]() $b_t = m_t = 0$
, then
$b_t = m_t = 0$
, then
![]() $t \in {\tt no}_{{\tt v}}$
by Lemma 44.1.i and
$t \in {\tt no}_{{\tt v}}$
by Lemma 44.1.i and
![]() $d_t = |{t}|_{\texttt {v}}$
by Lemma 64.1.ii. Therefore,
$d_t = |{t}|_{\texttt {v}}$
by Lemma 64.1.ii. Therefore,
![]() $\mathscr{T\;} = \mathscr{T\;}'$
by Lemma 15.1. Therefore,
$\mathscr{T\;} = \mathscr{T\;}'$
by Lemma 15.1. Therefore,
![]() $\mathscr{T\;}$
is tight and
$\mathscr{T\;}$
is tight and
![]() $b_s = m_s = d_s = 0$
by Lemma 44.2. Thus, we can conclude with
$b_s = m_s = d_s = 0$
by Lemma 44.2. Thus, we can conclude with
![]() $d = d_t + d_s = d_t = |{t}|_{\texttt {v}} = |{(t,s)}|_{\texttt {v}}$
and
$d = d_t + d_s = d_t = |{t}|_{\texttt {v}} = |{(t,s)}|_{\texttt {v}}$
and
![]() $b = b_t + b_s = m = m_t + m_s = 0$
.
$b = b_t + b_s = m = m_t + m_s = 0$
.
Lemma 17 (Unblocked normal configurations take zero steps). Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation. Then,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
be a tight derivation. Then,
![]() $b = m = 0$
iff
$b = m = 0$
iff
![]() $(t,s)$
is an unblocked normal configuration.
$(t,s)$
is an unblocked normal configuration.
Proof.
Derivation
![]() $\Phi$
must be of the following form:
$\Phi$
must be of the following form:
where
![]() $\Gamma = \Gamma _t + \Delta _s$
,
$\Gamma = \Gamma _t + \Delta _s$
,
![]() $\kappa = (\tau \times \mathscr{T\;}')$
,
$\kappa = (\tau \times \mathscr{T\;}')$
,
![]() $b = b_t + b_s$
,
$b = b_t + b_s$
,
![]() $m = m_t + m_s$
, and
$m = m_t + m_s$
, and
![]() $d = d_t + d_s$
.
$d = d_t + d_s$
.
-
⇒) Let
 $b = m = 0$
. Then,
$b = m = 0$
. Then,
 $b_t = m_t = 0$
, and thus,
$b_t = m_t = 0$
, and thus,
 $t \in {\tt no}_{{\tt n}}$
, by Lemma 45. And we can conclude that
$t \in {\tt no}_{{\tt n}}$
, by Lemma 45. And we can conclude that
 $(t,s)$
is in normal form.
$(t,s)$
is in normal form. -
⇐) Let
 $(t,s)$
be in normal form. Then,
$(t,s)$
be in normal form. Then,
 $t \in {\tt no}_{{\tt v}}$
, by definition. Thus,
$t \in {\tt no}_{{\tt v}}$
, by definition. Thus,
 $b_t = m_t = 0$
, by Lemma 16. And we can conclude that
$b_t = m_t = 0$
, by Lemma 16. And we can conclude that
 $b = m = 0$
, by Lemma 45.
$b = m = 0$
, by Lemma 45.
Lemma 46 (Tight typability of states and normal forms).
-
(1) Let
 $s$
be a state. Then, there exists a tight derivation
$s$
be a state. Then, there exists a tight derivation
 $\Phi \ \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt v} {s}\,:\,{\mathscr{T\;}}$
.
$\Phi \ \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt v} {s}\,:\,{\mathscr{T\;}}$
. -
(2) Let
 $t \in {\tt no}_{{\tt v}}$
. Then, for any
$t \in {\tt no}_{{\tt v}}$
. Then, for any
 $\mathscr{T\;}$
, there exists a tight derivation
$\mathscr{T\;}$
, there exists a tight derivation
 $\Phi \triangleright {\Gamma }\,\Vdash ^{(0,0,d)}_{\tt v} {t}\,:\,{\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;})}$
s.t.
$\Phi \triangleright {\Gamma }\,\Vdash ^{(0,0,d)}_{\tt v} {t}\,:\,{\mathscr{T\;} \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;})}$
s.t.
 $d = |{t}|_{\texttt {v}}$
.
$d = |{t}|_{\texttt {v}}$
.
Proof.
-
(1) By induction over
 $s$
:
$s$
:-
• Case
 $s = \varepsilon$
. Then, we can build
$s = \varepsilon$
. Then, we can build
 $\Pi _s \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt v} {\varepsilon }\,:\,{\emptyset }$
, by rule (emp), which is trivially tight.
$\Pi _s \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt v} {\varepsilon }\,:\,{\emptyset }$
, by rule (emp), which is trivially tight. -
• Case
 $s = {\tt upd}_{l}(v,q)$
. By applying the i.h. to
$s = {\tt upd}_{l}(v,q)$
. By applying the i.h. to
 $q$
, there exists a tight derivation
$q$
, there exists a tight derivation
 $\Pi _q \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt v} {q}\,:\,{\mathscr{T\;}_q}$
. Moreover,
$\Pi _q \triangleright \, \emptyset \Vdash ^{(0,0,0)}_{\tt v} {q}\,:\,{\mathscr{T\;}_q}$
. Moreover,
 $\mathscr{T\;}_q$
can be written as
$\mathscr{T\;}_q$
can be written as
 $\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}'_q$
, where
$\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}'_q$
, where
 $\mathscr{L\;}$
is tight and
$\mathscr{L\;}$
is tight and
 $\mathscr{T\;}'_q$
is tight.
$\mathscr{T\;}'_q$
is tight.Therefore, we can build
 $\Pi _s$
as follows:
$\Pi _s$
as follows:
We conclude since
 $\{l \;:\; {[ \, ] \cdot \mathscr{L\;}}\};\; {\mathscr{T\;}'_q}$
is tight.
$\{l \;:\; {[ \, ] \cdot \mathscr{L\;}}\};\; {\mathscr{T\;}'_q}$
is tight.
-
-
(2) We reason by induction over
 $t \in {\tt no}_{{\tt v}}$
:
$t \in {\tt no}_{{\tt v}}$
:-
• Case
 ${\tt val}(t)$
. Then, (a)
${\tt val}(t)$
. Then, (a)
 $t = x$
or (b)
$t = x$
or (b)
 $t = \lambda x.u$
. Therefore, we can build
$t = \lambda x.u$
. Therefore, we can build
 $\Phi$
by (a) rule (ax), or rule (
$\Phi$
by (a) rule (ax), or rule (
 $\lambda _{\tt p}$
), followed by rule (
$\lambda _{\tt p}$
), followed by rule (
 $\uparrow$
). Thus, we can conclude.
$\uparrow$
). Thus, we can conclude. -
• Case
 $\neg {\tt val}(t)$
. Then,
$\neg {\tt val}(t)$
. Then,
 $t \in {\tt ne}_{{\tt v}}$
:
$t \in {\tt ne}_{{\tt v}}$
:-
– Case
 $t = x u$
, such that
$t = x u$
, such that
 $u \in {\tt no}_{{\tt v}}$
. By applying the i.h. to
$u \in {\tt no}_{{\tt v}}$
. By applying the i.h. to
 $u$
, for any
$u$
, for any
 $\mathscr{T\;}'$
, there exists a tight derivation
$\mathscr{T\;}'$
, there exists a tight derivation
 $\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(0,0,|{u}|_{\texttt {v}})}_{\tt v} {u}\;:\;{\mathscr{T\;}' \Rightarrow (\tau ' \times \mathscr{T\;}')}$
, such that
$\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(0,0,|{u}|_{\texttt {v}})}_{\tt v} {u}\;:\;{\mathscr{T\;}' \Rightarrow (\tau ' \times \mathscr{T\;}')}$
, such that
 $\tau ' \in {{\tt tt}_{\tt v}}$
. Moreover, we can build
$\tau ' \in {{\tt tt}_{\tt v}}$
. Moreover, we can build
 $\Phi _x \triangleright \, {x \;:\; [ \overline {{\tt a}} ]}\Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;}' \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}')}$
. Therefore, we can build
$\Phi _x \triangleright \, {x \;:\; [ \overline {{\tt a}} ]}\Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\mathscr{T\;}' \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}')}$
. Therefore, we can build
 $\Phi$
as follows:such that
$\Phi$
as follows:such that \begin{equation*} \frac {\Phi _x\qquad \Phi _u}{(x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u \Vdash ^{(0,0,1+|{u}|_{\texttt {v}})} xu\;:\; \mathscr{T\;}' \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}^1_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _x\qquad \Phi _u}{(x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u \Vdash ^{(0,0,1+|{u}|_{\texttt {v}})} xu\;:\; \mathscr{T\;}' \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}^1_{{\tt p}})\end{equation*}
 $\Gamma = (x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u$
tight, and
$\Gamma = (x \;:\; [ \overline {{\tt a}} ]) + \Gamma _u$
tight, and
 $1 + |{u}|_{\texttt {v}} = |{x u}|_{\texttt {v}}$
.
$1 + |{u}|_{\texttt {v}} = |{x u}|_{\texttt {v}}$
.
-
– Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
 $p \in {\tt ne}_{{\tt v}}$
. By the i.h., for any
$p \in {\tt ne}_{{\tt v}}$
. By the i.h., for any
 $\mathscr{T\;}'$
, there exist
$\mathscr{T\;}'$
, there exist
 $\Phi _u \triangleright \, \Gamma _u\Vdash ^{(0,0,|{u}|_{\texttt {v}})}_{\tt v} {u}\;:\;{=\mathscr{T\;}' \Rightarrow (\tau ' \times \mathscr{T\;}')}$
tight, such that
$\Phi _u \triangleright \, \Gamma _u\Vdash ^{(0,0,|{u}|_{\texttt {v}})}_{\tt v} {u}\;:\;{=\mathscr{T\;}' \Rightarrow (\tau ' \times \mathscr{T\;}')}$
tight, such that
 $\tau ' \in {{\tt tt}_{\tt v}}$
, and
$\tau ' \in {{\tt tt}_{\tt v}}$
, and
 $\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(0,0,|{p}|_{\texttt {v}})}_{\tt v} {u}\;:\;{\mathscr{T\;}' \Rightarrow (\tau '' \times \mathscr{T\;}')}$
, such that
$\Phi _p \triangleright \, {\Gamma _p}\Vdash ^{(0,0,|{p}|_{\texttt {v}})}_{\tt v} {u}\;:\;{\mathscr{T\;}' \Rightarrow (\tau '' \times \mathscr{T\;}')}$
, such that
 $\tau '' \in {{\tt tt}_{\tt v}}$
. Moreover, since
$\tau '' \in {{\tt tt}_{\tt v}}$
. Moreover, since
 $\Gamma _p$
is tight, and
$\Gamma _p$
is tight, and
 $p \in {\tt ne}_{{\tt v}}$
, we know
$p \in {\tt ne}_{{\tt v}}$
, we know
 $\tau '' = {\tt n}$
, according to Lemma 41. Therefore, we can build
$\tau '' = {\tt n}$
, according to Lemma 41. Therefore, we can build
 $\Phi$
as follows:such that
$\Phi$
as follows:such that \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \Vdash ^{(0,0,1+|{u}|_{\texttt {v}}+|{p}|_{\texttt {v}})} up: \mathscr{T\;}' \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}^1_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{\Gamma _u + \Gamma _p \Vdash ^{(0,0,1+|{u}|_{\texttt {v}}+|{p}|_{\texttt {v}})} up: \mathscr{T\;}' \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}^1_{{\tt p}})\end{equation*}
 $\Gamma = \Gamma _u + \Gamma _p$
tight, and
$\Gamma = \Gamma _u + \Gamma _p$
tight, and
 $1 + |{u}|_{\texttt {v}} +|{p}|_{\texttt {v}} = |{up}|_{\texttt {v}}$
.
$1 + |{u}|_{\texttt {v}} +|{p}|_{\texttt {v}} = |{up}|_{\texttt {v}}$
.
-
– Case
 $t = up$
, such that
$t = up$
, such that
 $u \in {\tt ne}_{{\tt v}}$
and
$u \in {\tt ne}_{{\tt v}}$
and
 $p \in {\tt no}_{{\tt v}}$
. This case is very similar to the previous one.
$p \in {\tt no}_{{\tt v}}$
. This case is very similar to the previous one.
-
-
Lemma 18 (All configurations in normal form are tightly typable). If
![]() $(t,s)$
is an unblocked normal configuration, then there exists a tight typing derivation
$(t,s)$
is an unblocked normal configuration, then there exists a tight typing derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, such that
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, such that
![]() $d = |{(t,s)}|_{\texttt {v}}$
.
$d = |{(t,s)}|_{\texttt {v}}$
.
Proof. By Lemma 46.
Lemma 47 (Multi-types can split and merge). Let
![]() $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
![]() $b = +_{i \in I} b_i$
,
$b = +_{i \in I} b_i$
,
![]() $m = +_{i \in I} m_i$
, and
$m = +_{i \in I} m_i$
, and
![]() $d = +_{i \in I}$
. Then,
$d = +_{i \in I}$
. Then,
![]() $\Phi _t \triangleright {\Gamma }\Vdash ^{(b,m,d)}_{\tt v} {v}\;:\;{\mathscr{M}}$
iff
$\Phi _t \triangleright {\Gamma }\Vdash ^{(b,m,d)}_{\tt v} {v}\;:\;{\mathscr{M}}$
iff
![]() $(\Phi ^i_t \triangleright \, {\Gamma _i} \Vdash ^{(b_i,m_i,d_i)}_{\tt v} {v}\;:\;{=\mathscr{M}_i})_{i \in I}$
.
$(\Phi ^i_t \triangleright \, {\Gamma _i} \Vdash ^{(b_i,m_i,d_i)}_{\tt v} {v}\;:\;{=\mathscr{M}_i})_{i \in I}$
.
Proof. We omit this proof given its similarity with the proof for Weak Open CBV.
Lemma 48 (States can split). Let
![]() $\Pi _s \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
, such that
$\Pi _s \triangleright \, {\Delta }\Vdash ^{(b,m,d)}_{\tt v} {s}\;:\;{\mathscr{T\;}}$
, such that
![]() $l \in {\tt dom}(\mathscr{T\;})$
. Then,
$l \in {\tt dom}(\mathscr{T\;})$
. Then,
![]() $s \equiv {\tt upd}_{l}(v,q)$
,
$s \equiv {\tt upd}_{l}(v,q)$
,
![]() $\mathscr{T\;}(l) = \mathscr{M} \cdot \mathscr{L\;}$
,
$\mathscr{T\;}(l) = \mathscr{M} \cdot \mathscr{L\;}$
,
![]() $\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
and
$\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
and
![]() $\Pi _q \triangleright \, {\Delta _q}\Vdash ^{(b_q,m_q,d_q)}_{\tt v}3 {q}\;:\;{\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;}'}$
, such that
$\Pi _q \triangleright \, {\Delta _q}\Vdash ^{(b_q,m_q,d_q)}_{\tt v}3 {q}\;:\;{\{l \;:\; \mathscr{L\;}\};\; \mathscr{T\;}'}$
, such that
![]() $\Delta = \Gamma _v + \Delta _q$
,
$\Delta = \Gamma _v + \Delta _q$
,
![]() $\mathscr{T\;} = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}'$
,
$\mathscr{T\;} = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}'$
,
![]() $b = b_v+b_q$
,
$b = b_v+b_q$
,
![]() $m = m_v+m_q$
, and
$m = m_v+m_q$
, and
![]() $d = d_v + d_q$
.
$d = d_v + d_q$
.
Proof.
The proof follows by induction on the structure of
![]() $s$
:
$s$
:
-
• Case
 $s = \varepsilon$
. Then the statement is vacuously true.
$s = \varepsilon$
. Then the statement is vacuously true. -
• Case
 $s = {\tt upd}_{l'}(w,q')$
. Then
$s = {\tt upd}_{l'}(w,q')$
. Then
 $\Phi _s$
is of the form:where
$\Phi _s$
is of the form:where \begin{equation*} \frac {\Phi _{w} \triangleright \, {\Gamma _{w}}\Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}\qquad \Pi _{q'} \triangleright \, {\Delta _{q'}}\Vdash ^{(b_{q'}, m_{q'},d_{q'})}_{\tt v} {q'}\;:\;{\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}}}{\Gamma _{w} + \Delta _{q'} \Vdash ^{(b_w+b_{q'},m_w+m_{q'},d_w+d_{q'})} {\tt upd}_{l'}(w,q'): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi _{w} \triangleright \, {\Gamma _{w}}\Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}\qquad \Pi _{q'} \triangleright \, {\Delta _{q'}}\Vdash ^{(b_{q'}, m_{q'},d_{q'})}_{\tt v} {q'}\;:\;{\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}}}{\Gamma _{w} + \Delta _{q'} \Vdash ^{(b_w+b_{q'},m_w+m_{q'},d_w+d_{q'})} {\tt upd}_{l'}(w,q'): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}}({\tt upd})\end{equation*}
 $\Delta = \Gamma _{w} + \Delta _{q'}$
,
$\Delta = \Gamma _{w} + \Delta _{q'}$
,
 $\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
,
$\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
,
 $b = b_w + b_{q'}$
,
$b = b_w + b_{q'}$
,
 $m = m_w + m_{q'}$
, and
$m = m_w + m_{q'}$
, and
 $d = d_w + d_{q'}$
. We consider two cases:
$d = d_w + d_{q'}$
. We consider two cases:-
– Case
 $l' = l$
. Then we simply take
$l' = l$
. Then we simply take
 $v = w$
and
$v = w$
and
 $q = q'$
, and we are done.
$q = q'$
, and we are done. -
– Case
 $l' \neq l$
. Since
$l' \neq l$
. Since
 $l \in {\tt dom}(\{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})$
and
$l \in {\tt dom}(\{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})$
and
 $l' \not = l$
, then
$l' \not = l$
, then
 $l \in {\tt dom}(\mathscr{T\;}_{q'})$
. By applying the i.h. to
$l \in {\tt dom}(\mathscr{T\;}_{q'})$
. By applying the i.h. to
 $\Pi _{q'}$
, we have that
$\Pi _{q'}$
, we have that
 $q' \equiv {\tt upd}_{l}(w',q'')$
,
$q' \equiv {\tt upd}_{l}(w',q'')$
,
 $(\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})(l) = \mathscr{T\;}_{q'}(l) = \mathscr{M\;}'' \cdot \mathscr{L\;}''$
,
$(\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'})(l) = \mathscr{T\;}_{q'}(l) = \mathscr{M\;}'' \cdot \mathscr{L\;}''$
,
 $\Phi _{w'} \triangleright \, {\Gamma _{w'}}\Vdash ^{(b_{w'},m_{w'},d_{w'})}_{\tt v} {w'}\;:\;{\mathscr{M\;}''}$
and
$\Phi _{w'} \triangleright \, {\Gamma _{w'}}\Vdash ^{(b_{w'},m_{w'},d_{w'})}_{\tt v} {w'}\;:\;{\mathscr{M\;}''}$
and
 $\Pi _{q''} \triangleright \, {\Delta _{q''}}\Vdash ^{(b_{q''},m_{q''},d_{q''})}_{\tt v} {q''}\;:\;{\{l \;:\; \mathscr{L\;}''\};\; \{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}}$
, such that
$\Pi _{q''} \triangleright \, {\Delta _{q''}}\Vdash ^{(b_{q''},m_{q''},d_{q''})}_{\tt v} {q''}\;:\;{\{l \;:\; \mathscr{L\;}''\};\; \{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}}$
, such that
 $\Delta _{q'} = \Gamma _{w'} + \Delta _{q''}$
,
$\Delta _{q'} = \Gamma _{w'} + \Delta _{q''}$
,
 $\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'} = \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
,
$\{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q'} = \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \{l' \;:\; \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
,
 $b_{q'} = b_{w'} + b_{q''}$
,
$b_{q'} = b_{w'} + b_{q''}$
,
 $m_{q'} = m_{w'} + m_{q''}$
, and
$m_{q'} = m_{w'} + m_{q''}$
, and
 $d_{q'} = d_{w'} + d_{q''}$
. But
$d_{q'} = d_{w'} + d_{q''}$
. But
 $s = {\tt upd}_{l'}(w,{\tt upd}_{l}(w',q'')) \equiv {\tt upd}_{l}(w',{\tt upd}_{l'}(w,q''))$
, so we can take
$s = {\tt upd}_{l'}(w,{\tt upd}_{l}(w',q'')) \equiv {\tt upd}_{l}(w',{\tt upd}_{l'}(w,q''))$
, so we can take
 $v = w'$
,
$v = w'$
,
 $q = {\tt upd}_{l'}(w,q'')$
,
$q = {\tt upd}_{l'}(w,q'')$
,
 $\mathscr{M} = \mathscr{M\;}''$
,
$\mathscr{M} = \mathscr{M\;}''$
,
 $\mathscr{L\;} = \mathscr{L\;}''$
, and
$\mathscr{L\;} = \mathscr{L\;}''$
, and
 $\mathscr{T\;}' = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
, and consider
$\mathscr{T\;}' = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''}$
, and consider
 $\Phi _q$
to be the following derivation:where
$\Phi _q$
to be the following derivation:where \begin{equation*} \frac {\Phi _{w} \triangleright \, {\Gamma _{w}}\Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M}}\qquad \Pi _{q''} \triangleright \, {\Delta _{q''}}\Vdash ^{(b_{q''}, m_{q''}, d_{q''})}_{\tt v} {q''}\;:\;{\{l' \;:\; \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}}{\Gamma _{w} + \Delta _{q''} \Vdash ^{(b_w+b_{q''}, m_w + m_{q''}, d_w+d_{q''})} {\tt upd}_{l'}(w,q''): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}({\tt upd}) \end{equation*}
\begin{equation*} \frac {\Phi _{w} \triangleright \, {\Gamma _{w}}\Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M}}\qquad \Pi _{q''} \triangleright \, {\Delta _{q''}}\Vdash ^{(b_{q''}, m_{q''}, d_{q''})}_{\tt v} {q''}\;:\;{\{l' \;:\; \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}}{\Gamma _{w} + \Delta _{q''} \Vdash ^{(b_w+b_{q''}, m_w + m_{q''}, d_w+d_{q''})} {\tt upd}_{l'}(w,q''): \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}}({\tt upd}) \end{equation*}
 $\Delta _q = \Gamma _{w} + \Delta _{q''}$
and
$\Delta _q = \Gamma _{w} + \Delta _{q''}$
and
 $\mathscr{T\;}_q= \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
. We can then conclude with the following observations:
$\mathscr{T\;}_q= \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{L\;}''\};\; \mathscr{T\;}_{q''}$
. We can then conclude with the following observations:-
*
 $\Gamma _v + \Delta _q = \Gamma _{w'} +\Gamma _{w} + \Delta _{q''} = \Gamma _{w} + \Delta _{q'} = \Delta$
,
$\Gamma _v + \Delta _q = \Gamma _{w'} +\Gamma _{w} + \Delta _{q''} = \Gamma _{w} + \Delta _{q'} = \Delta$
, -
* Since
 $\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
and
$\mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'}$
and
 $l' \not = l$
, then
$l' \not = l$
, then
 $\mathscr{T\;}(l) = \mathscr{T\;}_{q'}(l)$
and
$\mathscr{T\;}(l) = \mathscr{T\;}_{q'}(l)$
and \begin{align*} \mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'} & = \{l': \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}_{q'}(l)\};\;\{l': \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}' \end{align*}
\begin{align*} \mathscr{T\;} = \{l' \;:\; \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q'} & = \{l': \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \{l \;:\; \mathscr{M\;}'' \cdot \mathscr{L\;}''\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}_{q'}(l)\};\;\{l': \mathscr{M\;}' \cdot \mathscr{L\;}'\};\; \mathscr{T\;}_{q''} \\ & = \{l \;:\; \mathscr{T\;}(l)\};\; \mathscr{T\;}' \end{align*}
-
*
 $b_v + b_q= b_{w'} + b_{w} + b_{q''}= b_w + b_{q'} = b$
,
$b_v + b_q= b_{w'} + b_{w} + b_{q''}= b_w + b_{q'} = b$
,
 $m_v + m_q= m_{w'} + m_{w} + m_{q''}= m_w + m_{q'} = b$
and
$m_v + m_q= m_{w'} + m_{w} + m_{q''}= m_w + m_{q'} = b$
and
 $d_v + d_q= d_{w'} + d_{w} + d_{q''}= d_w + d_{q'} = d$
.
$d_v + d_q= d_{w'} + d_{w} + d_{q''}= d_w + d_{q'} = d$
.
-
-
Lemma 49.
Let
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
. If
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
. If
![]() $t$
is a value, then
$t$
is a value, then
![]() $\tau \neq {\tt n}$
.
$\tau \neq {\tt n}$
.
Proof. By a simple inspection of the rules.
Lemma 50 (Substitution). If
![]() $\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mu }$
and
$\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mu }$
and
![]() $\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, there exists
$\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, there exists
![]() $\Phi _{t \{x \setminus v\}} \triangleright \, {\Gamma _t + \Gamma _v}\Vdash ^{(b_t+b_v,m_t+m_v,d_t+d_v)}_{\tt v} {t \{x \setminus v\}}\;:\;{\mu }$
.
$\Phi _{t \{x \setminus v\}} \triangleright \, {\Gamma _t + \Gamma _v}\Vdash ^{(b_t+b_v,m_t+m_v,d_t+d_v)}_{\tt v} {t \{x \setminus v\}}\;:\;{\mu }$
.
Proof.
We generalize the original statement by allowing
![]() $\Phi _t$
to conclude with either a monadic type
$\Phi _t$
to conclude with either a monadic type
![]() $\mu$
or a type
$\mu$
or a type
![]() $\tau$
. Let
$\tau$
. Let
![]() $\mathscr{G\,} \in \{\mu , \tau \}$
. Then the statement is as follows:
$\mathscr{G\,} \in \{\mu , \tau \}$
. Then the statement is as follows:
If
![]() $\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{G\,}}$
and
$\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{G\,}}$
and
![]() $\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{M}}$
, then
$\Phi _u \triangleright \, {\Gamma _u}\Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{M}}$
, then
![]() $\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _t + \Gamma _u}\Vdash ^{(b_t+b_u,m_t+m_u,d_t+d_u)}_{\tt v} {t \{x \setminus u\}}\;:\;{\mathscr{G\,}}$
.
$\Phi _{t \{x \setminus u\}} \triangleright \, {\Gamma _t + \Gamma _u}\Vdash ^{(b_t+b_u,m_t+m_u,d_t+d_u)}_{\tt v} {t \{x \setminus u\}}\;:\;{\mathscr{G\,}}$
.
The proof is by induction over
![]() $\Phi _t$
, according to the last rule used of
$\Phi _t$
, according to the last rule used of
![]() $\Phi _t$
:
$\Phi _t$
:
-
• Case
 $\mathscr{G\,} = \mu$
. Then,
$\mathscr{G\,} = \mu$
. Then,
 $\Phi _t$
must end with rule (@), (
$\Phi _t$
must end with rule (@), (
 $\uparrow$
), (get), (set), (@
$\uparrow$
), (get), (set), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Rule (@). Then
 $t = up$
,
$t = up$
,
 $\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1}\Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
$\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1}\Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
, where
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b_t = 1+b_u+b_p$
,
$b_t = 1+b_u+b_p$
,
 $m_t = m_u + m_p$
, and
$m_t = m_u + m_p$
, and
 $d_t = d_u + d_p$
. By Lemma 47, there exist
$d_t = d_u + d_p$
. By Lemma 47, there exist
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v}\Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}{\mathscr{M}_1}$
and
$\Phi ^1_v \triangleright \, {\Gamma ^1_v}\Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}{\mathscr{M}_1}$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
$\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
 $\Gamma _v = \Gamma ^1_v + \Gamma ^1_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^1_v$
,
 $b_v = b^1_v + b^2_v$
,
$b_v = b^1_v + b^2_v$
,
 $m_v = m^1_v + m^2_v$
, and
$m_v = m^1_v + m^2_v$
, and
 $d_v = d^1_v + d^2_v$
. By applying the i.h. to
$d_v = d^1_v + d^2_v$
. By applying the i.h. to
 $\Phi _u$
and
$\Phi _u$
and
 $\Phi _p$
, there exists
$\Phi _p$
, there exists
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^1_v}\Vdash ^{(b_u+b^1_v, m_u + m^1_v, d_u + d^1_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^1_v}\Vdash ^{(b_u+b^1_v, m_u + m^1_v, d_u + d^1_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M} \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
 $\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _p + \Gamma ^2_v} \Vdash ^{(b_p+b^2_v, m_p+m^2_v,d_p+d^2_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
. Therefore, we can build
$\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _p + \Gamma ^2_v} \Vdash ^{(b_p+b^2_v, m_p+m^2_v,d_p+d^2_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {\Phi _{u \{x \setminus v\}}\qquad \Phi _{p \{x \setminus v\}}}{(\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v) \Vdash ^{(1+b_u+b_p+b^1_v+b^2_v, m_u+m_p+m^1_v+m^2_v, d_u+d_p+d^1_v+d^2_v)} (up) \{x \setminus v\}\;:\; \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _{u \{x \setminus v\}}\qquad \Phi _{p \{x \setminus v\}}}{(\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v) \Vdash ^{(1+b_u+b_p+b^1_v+b^2_v, m_u+m_p+m^1_v+m^2_v, d_u+d_p+d^1_v+d^2_v)} (up) \{x \setminus v\}\;:\; \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
 $\Gamma _t + \Gamma _v = (\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v)$
,
$\Gamma _t + \Gamma _v = (\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v)$
,
 $b_t + b_v = 1+b_u+b_p+b^1_v+b^2_v$
,
$b_t + b_v = 1+b_u+b_p+b^1_v+b^2_v$
,
 $m_t + m_v = m_u+m_p+m^1_v+m^2_v$
, and
$m_t + m_v = m_u+m_p+m^1_v+m^2_v$
, and
 $d_t + d_v = d_u + d_p+d^1_v + d^2_v$
.
$d_t + d_v = d_u + d_p+d^1_v + d^2_v$
.
-
– Rule (
 $\uparrow$
). Then
$\uparrow$
). Then
 $t = w$
,
$t = w$
,
 $\mu = \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;})$
, and
$\mu = \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;})$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _w \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_t)}_{\tt v} {w}\;:\;{\pi }$
. By applying i.h. to
$\Phi _w \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_t)}_{\tt v} {w}\;:\;{\pi }$
. By applying i.h. to
 $\Phi _w$
, there exists
$\Phi _w$
, there exists
 $\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _w + \Gamma _v}\Vdash ^{(b_t+b_v, m_t+m_v, d_t +d_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\pi }$
. Therefore, we can build
$\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _w + \Gamma _v}\Vdash ^{(b_t+b_v, m_t+m_v, d_t +d_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\pi }$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude.
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude. \begin{equation*} \frac {\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _t + \Gamma _v} \Vdash ^{(b_t+b_v, m_t+m_v, d_t +d_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\pi }}{\Gamma _t + \Gamma _v \Vdash ^{(b_t+b_v, m_t+m_v, d_t +d_v)} w \{x \setminus v\}\;:\; \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;})}({\tt \uparrow })\end{equation*}
\begin{equation*} \frac {\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _t + \Gamma _v} \Vdash ^{(b_t+b_v, m_t+m_v, d_t +d_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\pi }}{\Gamma _t + \Gamma _v \Vdash ^{(b_t+b_v, m_t+m_v, d_t +d_v)} w \{x \setminus v\}\;:\; \mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;})}({\tt \uparrow })\end{equation*}
-
– Rule (get). Then
 $t = {\tt get}_{l}(\lambda y.u)$
,
$t = {\tt get}_{l}(\lambda y.u)$
,
 $\mu = {\{l :\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
$\mu = {\{l :\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_u,d_t)}_{\tt v} {u}\;:\;{{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
$\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_u,d_t)}_{\tt v} {u}\;:\;{{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
, where
 $\Gamma _t = \Gamma _u$
(since we can assume that
$\Gamma _t = \Gamma _u$
(since we can assume that
 $y\neq x$
by
$y\neq x$
by
 $\alpha$
-conversion), and
$\alpha$
-conversion), and
 $m_t = 1+m_u$
. By applying the i.h. to
$m_t = 1+m_u$
. By applying the i.h. to
 $\Phi _u$
, there exists
$\Phi _u$
, there exists
 $\Phi _{u \{x \setminus v\}} \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v} \Vdash ^{(b_t+b_v,1+m_u+m_v,d_t+d_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
. Moreover, by
$\Phi _{u \{x \setminus v\}} \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v} \Vdash ^{(b_t+b_v,1+m_u+m_v,d_t+d_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;}} \Rightarrow \kappa }$
. Moreover, by
 $\alpha$
-conversion, we can assume since
$\alpha$
-conversion, we can assume since
 $y \not \in {\tt dom}(\Gamma _v)$
, so that
$y \not \in {\tt dom}(\Gamma _v)$
, so that
 $(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v = \Gamma _u + \Gamma _v;\; y \;:\; \mathscr{M\;}' {= \Gamma _t +\Gamma _v;\;y\;:\;\mathscr{M\;}'}$
. Therefore, we can build
$(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v = \Gamma _u + \Gamma _v;\; y \;:\; \mathscr{M\;}' {= \Gamma _t +\Gamma _v;\;y\;:\;\mathscr{M\;}'}$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:
$\Phi _{t \{x \setminus v\}}$
as follows: -
– Rule (get). Then
 $t = {\tt get}_{l}(\lambda y.u)$
,
$t = {\tt get}_{l}(\lambda y.u)$
,
 $\mu = \{l :\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = \{l :\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_u,d_t)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }$
, where
$\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_u,d_t)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }$
, where
 $\Gamma _t = \Gamma _u$
(since we can assume that
$\Gamma _t = \Gamma _u$
(since we can assume that
 $y\neq x$
by
$y\neq x$
by
 $\alpha$
-conversion), and
$\alpha$
-conversion), and
 $m_t = 1+m_u$
. By applying the i.h. to
$m_t = 1+m_u$
. By applying the i.h. to
 $\Phi _u$
, there exists
$\Phi _u$
, there exists
 $\Phi _{u \{x \setminus v\}} \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v}\Vdash ^{(b_t+b_v,1+m_u+m_v,d_t+d_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }$
. Moreover, by
$\Phi _{u \{x \setminus v\}} \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v}\Vdash ^{(b_t+b_v,1+m_u+m_v,d_t+d_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }$
. Moreover, by
 $\alpha$
-conversion, we can assume since
$\alpha$
-conversion, we can assume since
 $y \not \in {\tt dom}(\Gamma _v)$
, so that
$y \not \in {\tt dom}(\Gamma _v)$
, so that
 $(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v = \Gamma _u + \Gamma _v;\; y \;:\; \mathscr{M\;}' = \Gamma _t +\Gamma _v;\;y\;:\;\mathscr{M\;}'$
. Therefore, we can build
$(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v = \Gamma _u + \Gamma _v;\; y \;:\; \mathscr{M\;}' = \Gamma _t +\Gamma _v;\;y\;:\;\mathscr{M\;}'$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {\Phi _{u \{x \setminus v\}}}{\Gamma _t + \Gamma _v \Vdash ^{(b_t+b_v,1+m_u+m_v,d_t+d_v)} {\tt get}_{l}(\lambda y.u \{x \setminus v\}): \{l :\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
\begin{equation*} \frac {\Phi _{u \{x \setminus v\}}}{\Gamma _t + \Gamma _v \Vdash ^{(b_t+b_v,1+m_u+m_v,d_t+d_v)} {\tt get}_{l}(\lambda y.u \{x \setminus v\}): \{l :\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
 $m_t = 1+m_u$
.
$m_t = 1+m_u$
.
-
– Rule (set). Then
 $t = {\tt set}_{l}(w,u)$
,
$t = {\tt set}_{l}(w,u)$
,
 $\mu = {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa$
, and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _w \triangleright \, {\Gamma _w;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}$
and
$\Phi _w \triangleright \, {\Gamma _w;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}$
and
 $\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
, where
$\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
, where
 $\Gamma _t = \Gamma _w + \Gamma _u$
,
$\Gamma _t = \Gamma _w + \Gamma _u$
,
 $b_t = b_w+b_u$
,
$b_t = b_w+b_u$
,
 $m_t = 1+m_w + m_u$
, and
$m_t = 1+m_w + m_u$
, and
 $d_t = d_w + d_u$
. By Lemma 47, there exist
$d_t = d_w + d_u$
. By Lemma 47, there exist
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
and
$\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
$\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v + b^2_v$
,
$b_v = b^1_v + b^2_v$
,
 $m_v = m^1_v + m^2_v$
, and
$m_v = m^1_v + m^2_v$
, and
 $d_v = d^1_v + d^2_v$
. By applying i.h. to
$d_v = d^1_v + d^2_v$
. By applying i.h. to
 $\Phi _w$
and the i.h. to
$\Phi _w$
and the i.h. to
 $\Phi _u$
, there exist
$\Phi _u$
, there exist
 $\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _w + \Gamma ^1_v} \Vdash ^{(b_w+b^1_v,m_w+m^1_v,d_w+d^1_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\mathscr{M\;}'}$
and
$\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _w + \Gamma ^1_v} \Vdash ^{(b_w+b^1_v,m_w+m^1_v,d_w+d^1_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\mathscr{M\;}'}$
and
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^2_v}\Vdash ^{(b_u+b^2_v,m_u+m^2_u,d_u+d^2_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^2_v}\Vdash ^{(b_u+b^2_v,m_u+m^2_u,d_u+d^2_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:
$\Phi _{t \{x \setminus v\}}$
as follows: -
– Rule (set). Then
 $t = {\tt set}_{l}(w,u)$
,
$t = {\tt set}_{l}(w,u)$
,
 $\mu = \{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = \{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa$
, and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _w \triangleright \, {\Gamma _w;\; x \;:\; \mathscr{M}_1}\Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}$
and
$\Phi _w \triangleright \, {\Gamma _w;\; x \;:\; \mathscr{M}_1}\Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}$
and
 $\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\; \mathscr{T\;} \Rightarrow \kappa }$
, where
$\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\; \mathscr{T\;} \Rightarrow \kappa }$
, where
 $\Gamma _t = \Gamma _w + \Gamma _u$
,
$\Gamma _t = \Gamma _w + \Gamma _u$
,
 $b_t = b_w+b_u$
,
$b_t = b_w+b_u$
,
 $m_t = 1+m_w + m_u$
, and
$m_t = 1+m_w + m_u$
, and
 $d_t = d_w + d_u$
. By Lemma 47, there exist
$d_t = d_w + d_u$
. By Lemma 47, there exist
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
and
$\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v}\Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
$\Phi ^2_v \triangleright \, {\Gamma ^2_v}\Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v + b^2_v$
,
$b_v = b^1_v + b^2_v$
,
 $m_v = m^1_v + m^2_v$
, and
$m_v = m^1_v + m^2_v$
, and
 $d_v = d^1_v + d^2_v$
. By applying i.h. to
$d_v = d^1_v + d^2_v$
. By applying i.h. to
 $\Phi _w$
and the i.h. to
$\Phi _w$
and the i.h. to
 $\Phi _u$
, there exist
$\Phi _u$
, there exist
 $\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _w + \Gamma ^1_v}\Vdash ^{(b_w+b^1_v,m_w+m^1_v,d_w+d^1_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\mathscr{M\;}'}$
and
$\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _w + \Gamma ^1_v}\Vdash ^{(b_w+b^1_v,m_w+m^1_v,d_w+d^1_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\mathscr{M\;}'}$
and
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^2_v} \Vdash ^{(b_u+b^2_v,m_u+m^2_u,d_u+d^2_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\; \mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^2_v} \Vdash ^{(b_u+b^2_v,m_u+m^2_u,d_u+d^2_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\; \mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {\Phi _{w \{x \setminus v\}}\qquad \Phi _{u \{x \setminus v\}}}{(\Gamma _w + \Gamma _u) + (\Gamma ^1_v + \Gamma ^2_v) \Vdash ^{(b_w+b_u+b^1_v+b^2_v,1+m_w+m_u+m^1_v+m^2_v,d_w+d_u+d^1_v+d^2_v)} {\tt set}_{l}(w,u) \{x \setminus v\}\;:\; \{l\;:\;\mathscr{L\;}\} \Rightarrow \kappa }({\tt set})\end{equation*}
\begin{equation*} \frac {\Phi _{w \{x \setminus v\}}\qquad \Phi _{u \{x \setminus v\}}}{(\Gamma _w + \Gamma _u) + (\Gamma ^1_v + \Gamma ^2_v) \Vdash ^{(b_w+b_u+b^1_v+b^2_v,1+m_w+m_u+m^1_v+m^2_v,d_w+d_u+d^1_v+d^2_v)} {\tt set}_{l}(w,u) \{x \setminus v\}\;:\; \{l\;:\;\mathscr{L\;}\} \Rightarrow \kappa }({\tt set})\end{equation*}
 $\Gamma _t + \Gamma _v = (\Gamma _w + \Gamma _u) + (\Gamma ^1_v + \Gamma ^2_v)$
,
$\Gamma _t + \Gamma _v = (\Gamma _w + \Gamma _u) + (\Gamma ^1_v + \Gamma ^2_v)$
,
 $b_t + b_v = b_w+b_u+b^1_v+b^2_v$
,
$b_t + b_v = b_w+b_u+b^1_v+b^2_v$
,
 $m_t + m_v = 1+m_w+m_u+m^1_v+m^2_v$
, and
$m_t + m_v = 1+m_w+m_u+m^1_v+m^2_v$
, and
 $d_t + d_v = d_w+d_u+d^1_v+d^2_v$
.
$d_t + d_v = d_w+d_u+d^1_v+d^2_v$
.
-
– Rule (@
 $^1_{{\tt p}}$
). Then
$^1_{{\tt p}}$
). Then
 $t = up$
,
$t = up$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
 $\Phi _t$
has two premises
$\Phi _t$
has two premises
 $\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
$\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, where
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, where
 $\Gamma = \Gamma _u + \Gamma _p$
,
$\Gamma = \Gamma _u + \Gamma _p$
,
 $\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
$\mathscr{M} = \mathscr{M}_1 \sqcup \mathscr{M}_2$
,
 $b_t = b_u+b_p$
,
$b_t = b_u+b_p$
,
 $m_t = m_u + m_p$
, and
$m_t = m_u + m_p$
, and
 $d_t = 1+d_u + d_p$
. By Lemma 47, there exist
$d_t = 1+d_u + d_p$
. By Lemma 47, there exist
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v}\Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
and
$\Phi ^1_v \triangleright \, {\Gamma ^1_v}\Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
$\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, where
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v + b^2_v$
,
$b_v = b^1_v + b^2_v$
,
 $m_v = m^1_v + m^2_v$
, and
$m_v = m^1_v + m^2_v$
, and
 $d_v = d^1_v + d^2_v$
. By applying the i.h. to
$d_v = d^1_v + d^2_v$
. By applying the i.h. to
 $\Phi _u$
and
$\Phi _u$
and
 $\Phi _p$
, there exist
$\Phi _p$
, there exist
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^1_v} \Vdash ^{(b_u+b^1_v, m_u + m^1_v, d_u + d^1_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _u + \Gamma ^1_v} \Vdash ^{(b_u+b^1_v, m_u + m^1_v, d_u + d^1_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
 $\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _p + \Gamma ^2_v}\Vdash ^{(b_p+b^2_v, m_p+m^2_v,d_p+d^2_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
. Therefore, we can build
$\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _p + \Gamma ^2_v}\Vdash ^{(b_p+b^2_v, m_p+m^2_v,d_p+d^2_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {\Phi _{u \{x \setminus v\}}\qquad \Phi _{p \{x \setminus v\}}}{(\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v) \Vdash ^{(b_u+b_p+b^1_v+b^2_v, m_u+m_p+m^1_v+m^2_v, 1+d_u+d_p+d^1_v+d^2_v)} (up) \{x \setminus v\}\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}^1_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _{u \{x \setminus v\}}\qquad \Phi _{p \{x \setminus v\}}}{(\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v) \Vdash ^{(b_u+b_p+b^1_v+b^2_v, m_u+m_p+m^1_v+m^2_v, 1+d_u+d_p+d^1_v+d^2_v)} (up) \{x \setminus v\}\;:\; \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')}({\tt @}^1_{{\tt p}})\end{equation*}
 $\Gamma _t + \Gamma _v = (\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v)$
,
$\Gamma _t + \Gamma _v = (\Gamma _u + \Gamma _p) + (\Gamma ^1_v + \Gamma ^2_v)$
,
 $b_t + b_v = b_u+b_p+b^1_v+b^2_v$
,
$b_t + b_v = b_u+b_p+b^1_v+b^2_v$
,
 $m_t + m_v = m_u+m_p+m^1_v+m^2_v$
, and
$m_t + m_v = m_u+m_p+m^1_v+m^2_v$
, and
 $d_t + d_v = 1+d_u + d_p+d^1_v + d^2_v$
.
$d_t + d_v = 1+d_u + d_p+d^1_v + d^2_v$
.
-
– Rule (@
 $^2_{{\tt p}}$
). This case is very similar to the previous one.
$^2_{{\tt p}}$
). This case is very similar to the previous one.
-
-
• Case
 $\mathscr{G\,} = \tau$
. Then,
$\mathscr{G\,} = \tau$
. Then,
 $\Phi _t$
must end with rule (ax), (
$\Phi _t$
must end with rule (ax), (
 $\lambda$
), (m), or (
$\lambda$
), (m), or (
 $\lambda _{\tt p}$
):
$\lambda _{\tt p}$
):-
– Rule (
 $\tt ax$
). Then,
$\tt ax$
). Then,
 $t = y$
. There are two cases:
$t = y$
. There are two cases:-
*
 $y = x$
. Then
$y = x$
. Then
 $x \{x \setminus v\} = v$
,
$x \{x \setminus v\} = v$
,
 $\tau = \sigma$
, and
$\tau = \sigma$
, and
 $\Phi _t \triangleright \, {\emptyset ; (x \;:\; [ \sigma ])} \Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\sigma }$
, where
$\Phi _t \triangleright \, {\emptyset ; (x \;:\; [ \sigma ])} \Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\sigma }$
, where
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{M} = [ \sigma ]$
, and
$\mathscr{M} = [ \sigma ]$
, and
 $b_t = m_t = d_t = 0$
. Moreover,
$b_t = m_t = d_t = 0$
. Moreover,
 $\Phi _v$
must end with rule (m) with one premise
$\Phi _v$
must end with rule (m) with one premise
 $\Phi '_v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\sigma }$
. So we can take
$\Phi '_v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\sigma }$
. So we can take
 $\Phi _{t \{x \setminus v\}} = \Phi '_v$
, and conclude with
$\Phi _{t \{x \setminus v\}} = \Phi '_v$
, and conclude with
 $\Gamma _t + \Gamma _v = \Gamma _v$
,
$\Gamma _t + \Gamma _v = \Gamma _v$
,
 $b_t + b_v = b_v$
,
$b_t + b_v = b_v$
,
 $m_t + m_v = m_v$
, and
$m_t + m_v = m_v$
, and
 $d_t + d_v = d_v$
.
$d_t + d_v = d_v$
. -
*
 $y \neq x$
. Then
$y \neq x$
. Then
 $y \{x \setminus v\} = y$
,
$y \{x \setminus v\} = y$
,
 $\tau = \sigma$
, and
$\tau = \sigma$
, and
 $\Phi _t \triangleright \, {y \;:\; [ \sigma ]}\Vdash ^{(0,0,0)}_{\tt v} {y}\;:\;{\sigma }$
, where
$\Phi _t \triangleright \, {y \;:\; [ \sigma ]}\Vdash ^{(0,0,0)}_{\tt v} {y}\;:\;{\sigma }$
, where
 $\Gamma _t = (y \;:\; [ \sigma ])$
,
$\Gamma _t = (y \;:\; [ \sigma ])$
,
 $\mathscr{M} = [ \, ]$
, and
$\mathscr{M} = [ \, ]$
, and
 $b_t = m_t = d_t = 0$
. Moreover,
$b_t = m_t = d_t = 0$
. Moreover,
 $\Phi _v$
ends with rule (m) with no premises. Therefore,
$\Phi _v$
ends with rule (m) with no premises. Therefore,
 $\Gamma _v = \emptyset$
,
$\Gamma _v = \emptyset$
,
 $b_v = m_v = d_v = 0$
. So we can pick
$b_v = m_v = d_v = 0$
. So we can pick
 $\Phi _{t \{x \setminus v\}} = \Phi _t$
, and conclude with
$\Phi _{t \{x \setminus v\}} = \Phi _t$
, and conclude with
 $\Gamma _t + \Gamma _v = \Gamma _t$
,
$\Gamma _t + \Gamma _v = \Gamma _t$
,
 $b_t + b_v = b_t$
,
$b_t + b_v = b_t$
,
 $m_t + m_v = m_t$
, and
$m_t + m_v = m_t$
, and
 $d_t + d_v = d_t$
.
$d_t + d_v = d_t$
.
-
-
– Rule (
 $\lambda$
). Then
$\lambda$
). Then
 $t = \lambda y.u$
,
$t = \lambda y.u$
,
 $\tau = \mathscr{M\;}' \rightarrow \mu$
, and
$\tau = \mathscr{M\;}' \rightarrow \mu$
, and
 $\Phi _t$
has one premise
$\Phi _t$
has one premise
 $\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {u}\;:\;{\mu }$
, where
$\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {u}\;:\;{\mu }$
, where
 $\Gamma _t = \Gamma _u$
(since we can assume that
$\Gamma _t = \Gamma _u$
(since we can assume that
 $y\neq x$
by
$y\neq x$
by
 $\alpha$
-conversion). By applying the i.h. to
$\alpha$
-conversion). By applying the i.h. to
 $\Phi _u$
, there exists
$\Phi _u$
, there exists
 $\Phi _{u \{x \setminus v\}} \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v} \Vdash ^{(b_t+b_v,m_t+m_v,d_t+d_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mu }$
. Moreover, by
$\Phi _{u \{x \setminus v\}} \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v} \Vdash ^{(b_t+b_v,m_t+m_v,d_t+d_v)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mu }$
. Moreover, by
 $\alpha$
-conversion, we can assume since
$\alpha$
-conversion, we can assume since
 $y \not \in {\tt dom}(\Gamma _v)$
, so that
$y \not \in {\tt dom}(\Gamma _v)$
, so that
 $(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v = \Gamma _u + \Gamma _v;\; y \;:\; \mathscr{M\;}'$
. Therefore, we can build
$(\Gamma _u;\; y \;:\; \mathscr{M\;}') + \Gamma _v = \Gamma _u + \Gamma _v;\; y \;:\; \mathscr{M\;}'$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude since
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude since \begin{equation*} \frac {\Phi _{u \{x \setminus v\}}}{\Gamma _u + \Gamma _v \Vdash ^{(b_t+b_v,m_t+m_v,d_t+d_v)} \lambda y.(u \{x \setminus v\}): \mathscr{M\;}' \rightarrow \mu }(\lambda )\end{equation*}
\begin{equation*} \frac {\Phi _{u \{x \setminus v\}}}{\Gamma _u + \Gamma _v \Vdash ^{(b_t+b_v,m_t+m_v,d_t+d_v)} \lambda y.(u \{x \setminus v\}): \mathscr{M\;}' \rightarrow \mu }(\lambda )\end{equation*}
 $\Gamma _t + \Gamma _v = \Gamma _u + \Gamma _v$
and
$\Gamma _t + \Gamma _v = \Gamma _u + \Gamma _v$
and
 $t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
.
$t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
.
-
– Rule (m). Then
 $t = w$
,
$t = w$
,
 $\tau = [ \sigma _i ]_{i \in I}$
, and
$\tau = [ \sigma _i ]_{i \in I}$
, and
 $\Phi _t$
has premises
$\Phi _t$
has premises
 $(\Phi ^i_w \triangleright \, {\Gamma ^i_w;\; x \;:\; \mathscr{M}_i}\Vdash ^{(b^i_w,m^i_w,d^i_w)}_{\tt v} {w}\;:\;{\sigma _i})_{i \in I}$
, where
$(\Phi ^i_w \triangleright \, {\Gamma ^i_w;\; x \;:\; \mathscr{M}_i}\Vdash ^{(b^i_w,m^i_w,d^i_w)}_{\tt v} {w}\;:\;{\sigma _i})_{i \in I}$
, where
 $\Gamma _t = +_{i \in I} \Gamma ^i_w$
,
$\Gamma _t = +_{i \in I} \Gamma ^i_w$
,
 $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
 $b_t = +_{i \in I} b^i_w$
,
$b_t = +_{i \in I} b^i_w$
,
 $m_t = +_{i \in I} m^i_w$
, and
$m_t = +_{i \in I} m^i_w$
, and
 $d_t = +_{i \in I} d^i_w$
. By Lemma 47, there exist
$d_t = +_{i \in I} d^i_w$
. By Lemma 47, there exist
 $(\Phi ^i_v \triangleright \, {\Gamma ^i_v} \Vdash ^{(b^i_v,m^i_v,d^i_v)}_{\tt v} {v}\;:\;{\mathscr{M}_i})_{i \in I}$
, where
$(\Phi ^i_v \triangleright \, {\Gamma ^i_v} \Vdash ^{(b^i_v,m^i_v,d^i_v)}_{\tt v} {v}\;:\;{\mathscr{M}_i})_{i \in I}$
, where
 $\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
$\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
 $b_v = +_{i \in I} b^i_v$
,
$b_v = +_{i \in I} b^i_v$
,
 $m_v = +_{i \in I} m^i_v$
, and
$m_v = +_{i \in I} m^i_v$
, and
 $d_v = +_{i \in I} d^i_v$
. By applying the i.h. to each
$d_v = +_{i \in I} d^i_v$
. By applying the i.h. to each
 $\Phi ^i_w$
, there exists
$\Phi ^i_w$
, there exists
 $(\Phi ^i_{w \{x \setminus v\}} \triangleright \, {\Gamma ^i_w + \Gamma ^i_v}\Vdash ^{(b^i_w+b^i_v,m^i_w+m^i_v,d^i_w+d^i_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\sigma _i})_{i \in I}$
. Therefore, we can build
$(\Phi ^i_{w \{x \setminus v\}} \triangleright \, {\Gamma ^i_w + \Gamma ^i_v}\Vdash ^{(b^i_w+b^i_v,m^i_w+m^i_v,d^i_w+d^i_v)}_{\tt v} {w \{x \setminus v\}}\;:\;{\sigma _i})_{i \in I}$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {(\Phi ^i_{w \{x \setminus v\}})_{i \in I}}{+_{i \in I} (\Gamma ^i_v + \Gamma ^i_w) \Vdash ^{(+_{i \in I}(b^i_w+b^i_v),+_{i \in I}(m^i_w+m^i_v),+_{i \in I}(d^i_w+d^i_v))} w \{x \setminus v\}\;:\; [ \tau _i ]_{i \in I}}({\tt m})({\tt m})\end{equation*}
\begin{equation*} \frac {(\Phi ^i_{w \{x \setminus v\}})_{i \in I}}{+_{i \in I} (\Gamma ^i_v + \Gamma ^i_w) \Vdash ^{(+_{i \in I}(b^i_w+b^i_v),+_{i \in I}(m^i_w+m^i_v),+_{i \in I}(d^i_w+d^i_v))} w \{x \setminus v\}\;:\; [ \tau _i ]_{i \in I}}({\tt m})({\tt m})\end{equation*}
 $\Gamma _t + \Gamma _v = +_{i \in I} \Gamma ^i_w +_{i \in I} \Gamma ^i_v = +_{i \in I} (\Gamma ^i_w + \Gamma ^i_v)$
,
$\Gamma _t + \Gamma _v = +_{i \in I} \Gamma ^i_w +_{i \in I} \Gamma ^i_v = +_{i \in I} (\Gamma ^i_w + \Gamma ^i_v)$
,
 $b_t + b_v = +_{i \in I} b^i_w +_{i \in I} b^i_v = +_{i \in I} (b^i_w + b^i_v)$
,
$b_t + b_v = +_{i \in I} b^i_w +_{i \in I} b^i_v = +_{i \in I} (b^i_w + b^i_v)$
,
 $m_t + m_v = +_{i \in I} m^i_w +_{i \in I} m^i_v = +_{i \in I} (m^i_w + m^i_v)$
, and
$m_t + m_v = +_{i \in I} m^i_w +_{i \in I} m^i_v = +_{i \in I} (m^i_w + m^i_v)$
, and
 $d_t + d_v = +_{i \in I} d^i_w +_{i \in I} d^i_v = +_{i \in I} (d^i_w + d^i_v)$
.
$d_t + d_v = +_{i \in I} d^i_w +_{i \in I} d^i_v = +_{i \in I} (d^i_w + d^i_v)$
.
-
– Rule (
 $\lambda _{\tt p}$
). Then
$\lambda _{\tt p}$
). Then
 $t = \lambda y.u$
,
$t = \lambda y.u$
,
 $\tau = {\tt a}$
, and
$\tau = {\tt a}$
, and
 $\Phi _t \triangleright \, {\emptyset ;\; x \;:\; [ \, ]} \Vdash ^{(0,0,0)}_{\tt v} {\lambda y.u}\;:\;{{\tt a}}$
, where
$\Phi _t \triangleright \, {\emptyset ;\; x \;:\; [ \, ]} \Vdash ^{(0,0,0)}_{\tt v} {\lambda y.u}\;:\;{{\tt a}}$
, where
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{M} = [ \, ]$
, and
$\mathscr{M} = [ \, ]$
, and
 $b_t = m_t = d_t = 0$
. Also, notice that
$b_t = m_t = d_t = 0$
. Also, notice that
 $t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Therefore,
$t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Therefore,
 $\Phi _v$
ends with rule (m) with no premises, and
$\Phi _v$
ends with rule (m) with no premises, and
 $\Gamma _v = \emptyset$
. Therefore, we can build
$\Gamma _v = \emptyset$
. Therefore, we can build
 $\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with
$\Phi _{t \{x \setminus v\}}$
as follows:And we can conclude with \begin{equation*} \frac {}{\emptyset \Vdash ^{(0,0,0)} (\lambda y.u) \{x \setminus v\}\;:\; {\tt a}}(\lambda _{\tt p})\end{equation*}
\begin{equation*} \frac {}{\emptyset \Vdash ^{(0,0,0)} (\lambda y.u) \{x \setminus v\}\;:\; {\tt a}}(\lambda _{\tt p})\end{equation*}
 $\Gamma _t + \Gamma _v = \emptyset$
,
$\Gamma _t + \Gamma _v = \emptyset$
,
 $b_t + b_v = m_t + m_v = d_t +d_v = 0$
.
$b_t + b_v = m_t + m_v = d_t +d_v = 0$
.
-
Lemma 19 (Quantitative subject reduction). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s) \;:\; \kappa$
is a tight derivation, then
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s) \;:\; \kappa$
is a tight derivation, then
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
, where
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt v}}}$
implies
${\tt r} ={\beta _{{\tt v}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Proof. We show a stronger statement of the form:
Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\tt \beta }_{{\tt v}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\tt \beta }_{{\tt v}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
,
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
,
![]() $\Gamma$
is tight, and (
$\Gamma$
is tight, and (
![]() $\kappa$
is tight or
$\kappa$
is tight or
![]() $\neg {\tt val}(t)$
), then
$\neg {\tt val}(t)$
), then
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
, where
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
, where
![]() ${\tt r} ={\tt \beta }_{{\tt v}}$
implies
${\tt r} ={\tt \beta }_{{\tt v}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
We proceed by induction on
![]() $(t,s) \rightsquigarrow _{{\tt v}} (u,q)$
:
$(t,s) \rightsquigarrow _{{\tt v}} (u,q)$
:
-
• Case
 $(t,s) = ((\lambda x.p) v,s) \rightsquigarrow _{{\beta _{{\tt v}}}} (p \{x \setminus v\}, s) = (u,q)$
. Then,
$(t,s) = ((\lambda x.p) v,s) \rightsquigarrow _{{\beta _{{\tt v}}}} (p \{x \setminus v\}, s) = (u,q)$
. Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _{(\lambda x.p)v} \triangleright \, {\Gamma _{(\lambda x.p)v}}\Vdash ^{(b_{(\lambda x.p)v},m_{(\lambda x.p)v},d_{(\lambda x.p)v})}_{\tt v} {(\lambda x.p)v}\;:\;{\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')}$
and
$\Phi _{(\lambda x.p)v} \triangleright \, {\Gamma _{(\lambda x.p)v}}\Vdash ^{(b_{(\lambda x.p)v},m_{(\lambda x.p)v},d_{(\lambda x.p)v})}_{\tt v} {(\lambda x.p)v}\;:\;{\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')}$
and
 $\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, such that
$\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, such that
 $\Gamma = \Gamma _{(\lambda x.p)v} + \Delta _s$
,
$\Gamma = \Gamma _{(\lambda x.p)v} + \Delta _s$
,
 $b = b_{(\lambda x.p)v}+b_s$
,
$b = b_{(\lambda x.p)v}+b_s$
,
 $m = m_{(\lambda x.p)v}+m_s$
, and
$m = m_{(\lambda x.p)v}+m_s$
, and
 $d = d_{(\lambda x.p)v}+d_s$
. Then,
$d = d_{(\lambda x.p)v}+d_s$
. Then,
 $\Phi _{(\lambda x.p)v}$
must end with rule (@), (@
$\Phi _{(\lambda x.p)v}$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
). Therefore,
$^2_{{\tt p}}$
). Therefore,
 $\Phi _{(\lambda x.p)v}$
has two premises
$\Phi _{(\lambda x.p)v}$
has two premises
 $\Phi _{\lambda x.p} \triangleright \, {\Gamma _{\lambda x.p}}\Vdash ^{(b_{\lambda x.p},m_{\lambda x.p},d_{\lambda x.p})}_{\tt v} {\lambda x.p}\;:\;{\mathscr{T\;} \Rightarrow (\tau _1 \times \mathscr{T\;}'')}$
and
$\Phi _{\lambda x.p} \triangleright \, {\Gamma _{\lambda x.p}}\Vdash ^{(b_{\lambda x.p},m_{\lambda x.p},d_{\lambda x.p})}_{\tt v} {\lambda x.p}\;:\;{\mathscr{T\;} \Rightarrow (\tau _1 \times \mathscr{T\;}'')}$
and
 $\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{T\;}'' \Rightarrow (\tau _2 \times \mathscr{T\;}')}$
, such that
$\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{T\;}'' \Rightarrow (\tau _2 \times \mathscr{T\;}')}$
, such that
 $\Gamma _{(\lambda x.p)v} = \Gamma _{\lambda x.p} + \Gamma _v$
,
$\Gamma _{(\lambda x.p)v} = \Gamma _{\lambda x.p} + \Gamma _v$
,
 $b_{(\lambda x.p)v} = b_{\lambda x.p} + b_v$
,
$b_{(\lambda x.p)v} = b_{\lambda x.p} + b_v$
,
 $m_{(\lambda x.p)v} = m_{\lambda x.p} + m_v$
, and
$m_{(\lambda x.p)v} = m_{\lambda x.p} + m_v$
, and
 $d_{(\lambda x.p)v} = 1+d_{\lambda x.p} + d_v$
. Let us first assume
$d_{(\lambda x.p)v} = 1+d_{\lambda x.p} + d_v$
. Let us first assume
 $\Phi _{(\lambda x.p)v}$
ends with (@
$\Phi _{(\lambda x.p)v}$
ends with (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $\tau _1 = \overline {{\tt a}}$
. However, according to Lemma 43
$\tau _1 = \overline {{\tt a}}$
. However, according to Lemma 43
 $\neg {\tt abs}(\lambda x.p)$
should hold. This gives a contradiction, meaning that this case does not apply. Now, let us assume
$\neg {\tt abs}(\lambda x.p)$
should hold. This gives a contradiction, meaning that this case does not apply. Now, let us assume
 $\Phi _{(\lambda x.p)v}$
ends with (@
$\Phi _{(\lambda x.p)v}$
ends with (@
 $^2_{{\tt p}}$
). Then,
$^2_{{\tt p}}$
). Then,
 $\tau _2 = {\tt n}$
. However, according to Lemma 49
$\tau _2 = {\tt n}$
. However, according to Lemma 49
 $\tau _2 \neq {\tt n}$
should holds. This gives a contradiction, meaning that this case does not apply. Finally, let us assume
$\tau _2 \neq {\tt n}$
should holds. This gives a contradiction, meaning that this case does not apply. Finally, let us assume
 $\Phi _{(\lambda x.p)v}$
ends with rule (@). Then,
$\Phi _{(\lambda x.p)v}$
ends with rule (@). Then,
 $\Phi _{(\lambda x.p) v}$
must be of the following form:
$\Phi _{(\lambda x.p) v}$
must be of the following form:
where
 $\Gamma _{(\lambda x.p)v} = \Gamma _{\lambda x.p} + \Gamma _v$
,
$\Gamma _{(\lambda x.p)v} = \Gamma _{\lambda x.p} + \Gamma _v$
,
 $\mathscr{T\;} = \mathscr{T\;}'' = \mathscr{T\;}'$
by Lemma 15,
$\mathscr{T\;} = \mathscr{T\;}'' = \mathscr{T\;}'$
by Lemma 15,
 $\tau _1 = \mathscr{M} \rightarrow (\mathscr{T\;} \Rightarrow \kappa )$
,
$\tau _1 = \mathscr{M} \rightarrow (\mathscr{T\;} \Rightarrow \kappa )$
,
 $\tau _2 = \mathscr{M}$
,
$\tau _2 = \mathscr{M}$
,
 $b = 1+b_{\lambda x.p} + b_v + b_s$
,
$b = 1+b_{\lambda x.p} + b_v + b_s$
,
 $m = m_{\lambda x.p} + m_v + m_s$
, and
$m = m_{\lambda x.p} + m_v + m_s$
, and
 $d = d_{\lambda x.p} + d_v + d_s$
. By Lemma 50, there exists
$d = d_{\lambda x.p} + d_v + d_s$
. By Lemma 50, there exists
 $\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{\lambda x.p} + \Gamma _v} \Vdash ^{(b_p+b_v,m_p+m_v,d_p+d_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
$\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{\lambda x.p} + \Gamma _v} \Vdash ^{(b_p+b_v,m_p+m_v,d_p+d_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow \kappa }$
. Therefore, we can build
 $\Phi _{(p\{x \setminus v\},s)}$
as follows:where
$\Phi _{(p\{x \setminus v\},s)}$
as follows:where \begin{equation*} \frac {\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{\lambda x.p}+\Gamma _v}\Vdash ^{(b_v+b_p,m_v+m_p,d_v+d_p)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow \kappa }\qquad \Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}}{(\Gamma _{\lambda x.p} + \Gamma _v) + \Delta _s \Vdash ^{(b_v+b_p+b_s,m_v+m_p+m_s,d_v+d_p+d_s)} (p \{x \setminus v\}, s): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{\lambda x.p}+\Gamma _v}\Vdash ^{(b_v+b_p,m_v+m_p,d_v+d_p)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow \kappa }\qquad \Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}}{(\Gamma _{\lambda x.p} + \Gamma _v) + \Delta _s \Vdash ^{(b_v+b_p+b_s,m_v+m_p+m_s,d_v+d_p+d_s)} (p \{x \setminus v\}, s): \kappa }({\tt conf})\end{equation*}
 $b' = b_v+b_{\lambda x.p}+b_s$
,
$b' = b_v+b_{\lambda x.p}+b_s$
,
 $m' = m_v+m_{\lambda x.p}+m_s$
, and
$m' = m_v+m_{\lambda x.p}+m_s$
, and
 $d' = d_v+d_{\lambda x.p}+d_s$
. Thus, we can conclude with
$d' = d_v+d_{\lambda x.p}+d_s$
. Thus, we can conclude with
 $\Gamma = \Gamma _{(\lambda x.p)v} + \Delta _s = (\Gamma _{\lambda x.p} + \Gamma _v) + \Delta _s$
,
$\Gamma = \Gamma _{(\lambda x.p)v} + \Delta _s = (\Gamma _{\lambda x.p} + \Gamma _v) + \Delta _s$
,
 $b = b_{(\lambda x.p)v} + b_s = 1 + b_{\lambda x.p} + b_v + b_s = b' - 1$
,
$b = b_{(\lambda x.p)v} + b_s = 1 + b_{\lambda x.p} + b_v + b_s = b' - 1$
,
 $m = m_{(\lambda x.p)v} + m_s = m_{\lambda x.p} + m_v + m_s = m'$
, and
$m = m_{(\lambda x.p)v} + m_s = m_{\lambda x.p} + m_v + m_s = m'$
, and
 $d = d_{(\lambda x.p)v} + d_s = d_{\lambda x.p} + d_v + d_s = d'$
.
$d = d_{(\lambda x.p)v} + d_s = d_{\lambda x.p} + d_v + d_s = d'$
.
-
• Case
 $(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt v}} (p \{x \setminus v\},s) = (u,q)$
, such that
$(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt v}} (p \{x \setminus v\},s) = (u,q)$
, such that
 $s \equiv {\tt upd}_{l}(v,s')$
. Then
$s \equiv {\tt upd}_{l}(v,s')$
. Then
 $\Phi$
must be of the following form, where
$\Phi$
must be of the following form, where
 $\mathscr{T\;} = \{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0$
:
$\mathscr{T\;} = \{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0$
:
where
 $\Gamma = \Gamma _{p} {\setminus x} + \Delta _s$
,
$\Gamma = \Gamma _{p} {\setminus x} + \Delta _s$
,
 $b = b_p + b_s$
,
$b = b_p + b_s$
,
 $m = 1+ m_p + m_s$
, and
$m = 1+ m_p + m_s$
, and
 $d = d_p + d_s$
. Since
$d = d_p + d_s$
. Since
 $\Pi _{s} \triangleright \, {\tt v} {\Delta _s}\Vdash ^{(b_s,m_s,d_s)}_{\texttt{v}} {s}\;:\;{{\{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, we know, by Lemma 48, that
$\Pi _{s} \triangleright \, {\tt v} {\Delta _s}\Vdash ^{(b_s,m_s,d_s)}_{\texttt{v}} {s}\;:\;{{\{l\;:\;\Gamma _p(x) \sqcup \mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, we know, by Lemma 48, that
 $s \equiv {\tt upd}_{l}(v,s')$
,
$s \equiv {\tt upd}_{l}(v,s')$
,
 $\Phi _v \triangleright \, {\Delta _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{{\Gamma _p(x) \sqcup \mathscr{M}}}$
and
$\Phi _v \triangleright \, {\Delta _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{{\Gamma _p(x) \sqcup \mathscr{M}}}$
and
 $\Pi _{s'} \triangleright \, {\Delta _{s'}} \Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt v} {s'}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, such that
$\Pi _{s'} \triangleright \, {\Delta _{s'}} \Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt v} {s'}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0}}$
, such that
 $\Delta _s = \Gamma _v + \Delta _{s'}$
,
$\Delta _s = \Gamma _v + \Delta _{s'}$
,
 $b_s = b_v + b_{s'}$
,
$b_s = b_v + b_{s'}$
,
 $m_s = m_v + m_{s'}$
, and
$m_s = m_v + m_{s'}$
, and
 $d_s = d_v + d_{s'}$
. Therefore, by Lemma 47, there exist
$d_s = d_v + d_{s'}$
. Therefore, by Lemma 47, there exist
 $\Phi ^1_v \triangleright \,{\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{{\Gamma _p(x)}}$
and
$\Phi ^1_v \triangleright \,{\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{{\Gamma _p(x)}}$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{{\mathscr{M}}}$
, such that
$\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{{\mathscr{M}}}$
, such that
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v+b^2_v$
,
$b_v = b^1_v+b^2_v$
,
 $m_v = m^1_v+m^2_v$
, and
$m_v = m^1_v+m^2_v$
, and
 $d_v = d^1_v+d^2_v$
. By applying Lemma 50 to
$d_v = d^1_v+d^2_v$
. By applying Lemma 50 to
 $\Phi _{p}$
and
$\Phi _{p}$
and
 $\Phi ^1_v$
, there exists
$\Phi ^1_v$
, there exists
 $\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p} {\setminus x} +\Delta ^1_v} \Vdash ^{(b_p+b^1_v,m_p+m^1_v,d_p+d^1_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{{\{l\;:\;\mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0} \Rightarrow \kappa }$
. Moreover, we can construct an alternative type derivation
$\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p} {\setminus x} +\Delta ^1_v} \Vdash ^{(b_p+b^1_v,m_p+m^1_v,d_p+d^1_v)}_{\tt v} {p \{x \setminus v\}}\;:\;{{\{l\;:\;\mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0} \Rightarrow \kappa }$
. Moreover, we can construct an alternative type derivation
 $\Pi '_s$
for
$\Pi '_s$
for
 $s$
as follows:Let
$s$
as follows:Let \begin{equation*} \frac {\Phi ^2_v\qquad \Pi _{s'}}{\Gamma ^2_v+ \Delta _{s'} \Vdash ^{(b^2_v+b_{s'},m^2_v+m_{s'},d^2_v+d_{s'})} {\tt upd}_{l}(v,s'): {\{l\;:\;\mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi ^2_v\qquad \Pi _{s'}}{\Gamma ^2_v+ \Delta _{s'} \Vdash ^{(b^2_v+b_{s'},m^2_v+m_{s'},d^2_v+d_{s'})} {\tt upd}_{l}(v,s'): {\{l\;:\;\mathscr{M} \cdot \mathscr{L\;}\};\;\mathscr{T\;}_0}}({\tt upd})\end{equation*}
 $\Pi _q = \Pi '_s$
, such that
$\Pi _q = \Pi '_s$
, such that
 $q = {\tt upd}_{l}(v,s') = s$
and
$q = {\tt upd}_{l}(v,s') = s$
and
 $\Delta _q = \Gamma ^2_v + \Delta _{s'}$
. Therefore, we can build
$\Delta _q = \Gamma ^2_v + \Delta _{s'}$
. Therefore, we can build
 $\Phi '$
as follows:where
$\Phi '$
as follows:where \begin{equation*} \frac {\Phi _{p\{x \setminus v\}}\qquad \Pi _q}{(\Gamma _p {\setminus x} + \Gamma ^1_v) + (\Gamma ^2_v + \Delta _{s'}) \Vdash ^{(b_p + b^1_v + b^2_v + b_{s'},m_p + m^1_v + m^2_v + m_{s'},d_p + d^1_v + d^2_v + d_{s'})} (p \{x \setminus v\}, s): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p\{x \setminus v\}}\qquad \Pi _q}{(\Gamma _p {\setminus x} + \Gamma ^1_v) + (\Gamma ^2_v + \Delta _{s'}) \Vdash ^{(b_p + b^1_v + b^2_v + b_{s'},m_p + m^1_v + m^2_v + m_{s'},d_p + d^1_v + d^2_v + d_{s'})} (p \{x \setminus v\}, s): \kappa }({\tt conf})\end{equation*}
 $b' = b_p + b^1_v + b^2_v + b_{s'}$
,
$b' = b_p + b^1_v + b^2_v + b_{s'}$
,
 $m' = m_p + m^1_v + m^2_v + m_{s'}$
, and
$m' = m_p + m^1_v + m^2_v + m_{s'}$
, and
 $d' = d_p + d^1_v + d^2_v + d_{s'}$
. Thus, we can conclude with
$d' = d_p + d^1_v + d^2_v + d_{s'}$
. Thus, we can conclude with
 $\Gamma = \Gamma _p {\setminus x} + \Delta _s = \Gamma _p {\setminus x}+ (\Gamma _v + \Delta _{s'}) = \Gamma _p {\setminus x} + (\Gamma ^1_v + \Gamma ^2_v) + \Delta _{s'}$
,
$\Gamma = \Gamma _p {\setminus x} + \Delta _s = \Gamma _p {\setminus x}+ (\Gamma _v + \Delta _{s'}) = \Gamma _p {\setminus x} + (\Gamma ^1_v + \Gamma ^2_v) + \Delta _{s'}$
,
 $b = b_p + b_s = b_p + (b_v + b_{s'}) = b_p + (b^1_v + b^2_v) + b_{s'} = b'$
,
$b = b_p + b_s = b_p + (b_v + b_{s'}) = b_p + (b^1_v + b^2_v) + b_{s'} = b'$
,
 $m - 1 = (1 + m_p + m_s) - 1 = (1 + m_p + m_v + m_{s'}) - 1 = (1 + m_p + m^1_v + m^2_v + m_{s'}) - 1 = m'$
,
$m - 1 = (1 + m_p + m_s) - 1 = (1 + m_p + m_v + m_{s'}) - 1 = (1 + m_p + m^1_v + m^2_v + m_{s'}) - 1 = m'$
,
 $d = d_p + d_s = d_p + (d_v + d_{s'}) = d_p + (d^1_v + d^2_v) + d_{s'} = d'$
.
$d = d_p + d_s = d_p + (d_v + d_{s'}) = d_p + (d^1_v + d^2_v) + d_{s'} = d'$
.
-
• Case
 $(t,s) = ({\tt set}_{l}(v,p),s) \rightsquigarrow _{{\tt v}} (p, {\tt upd}_{l}(v,s)) = (u,q)$
. Then,
$(t,s) = ({\tt set}_{l}(v,p),s) \rightsquigarrow _{{\tt v}} (p, {\tt upd}_{l}(v,s)) = (u,q)$
. Then,
 $\Phi$
must be of the following form, where
$\Phi$
must be of the following form, where
 $\mathscr{T\;} = \{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0$
:
$\mathscr{T\;} = \{l\;:\;\mathscr{L\;}\};\;\mathscr{T\;}_0$
:
such that
 $\Gamma = (\Gamma _v + \Gamma _{p}) + \Delta _{s}$
,
$\Gamma = (\Gamma _v + \Gamma _{p}) + \Delta _{s}$
,
 $b = b_v+b_p+b_s$
,
$b = b_v+b_p+b_s$
,
 $m=1+m_v+m_p+m_s$
and
$m=1+m_v+m_p+m_s$
and
 $d=d_v+d_p+d_s$
. Therefore, we can build derivation
$d=d_v+d_p+d_s$
. Therefore, we can build derivation
 $\Pi _q$
for
$\Pi _q$
for
 ${\tt upd}_{l}(v,s)$
as follows:Moreover, we can build
${\tt upd}_{l}(v,s)$
as follows:Moreover, we can build \begin{equation*} \frac {\Phi _{v}\qquad \Pi _{s}}{\Gamma _v + \Delta _{s} \Vdash ^{(b_v+b_s,m_v+m_s,d_v+d_s)} {\tt upd}_{l}(v,s): {\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}_0}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi _{v}\qquad \Pi _{s}}{\Gamma _v + \Delta _{s} \Vdash ^{(b_v+b_s,m_v+m_s,d_v+d_s)} {\tt upd}_{l}(v,s): {\{l \;:\; \mathscr{M} \cdot \mathscr{L\;}\};\; \mathscr{T\;}_0}}({\tt upd})\end{equation*}
 $\Phi '$
as follows:such that
$\Phi '$
as follows:such that \begin{equation*} \frac {\Phi _{p}\qquad \Pi _{q}}{\Gamma _{p} + (\Gamma _v + \Delta _{s}) \Vdash ^{(b_p+b_v+b_s,m_p+m_v+m_s,d_p+d_v+d_s)} (p, {\tt upd}_{l}(v,s)): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p}\qquad \Pi _{q}}{\Gamma _{p} + (\Gamma _v + \Delta _{s}) \Vdash ^{(b_p+b_v+b_s,m_p+m_v+m_s,d_p+d_v+d_s)} (p, {\tt upd}_{l}(v,s)): \kappa }({\tt conf})\end{equation*}
 $b' = b_p+b_v+b_s$
,
$b' = b_p+b_v+b_s$
,
 $m' = m_p+m_v+m_s$
, and
$m' = m_p+m_v+m_s$
, and
 $d' = d_p+d_v +d_s$
. Thus, we can conclude with
$d' = d_p+d_v +d_s$
. Thus, we can conclude with
 $\Gamma = (\Gamma _v + \Gamma _p) + \Delta _s$
,
$\Gamma = (\Gamma _v + \Gamma _p) + \Delta _s$
,
 $b = b_v + b_p + b_s = b'$
,
$b = b_v + b_p + b_s = b'$
,
 $m - 1 = (1 + m_v + m_p + m_s) - 1 = m_v + m_p + m_s = m'$
, and
$m - 1 = (1 + m_v + m_p + m_s) - 1 = m_v + m_p + m_s = m'$
, and
 $d = d_v + d_p + d_s = d'$
.
$d = d_v + d_p + d_s = d'$
.
-
• Case
 $(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (p'r,q) = (u, q)$
, such that
$(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (p'r,q) = (u, q)$
, such that
 $(p, s) \rightsquigarrow _{{\tt v}} (p',q)$
. Then,
$(p, s) \rightsquigarrow _{{\tt v}} (p',q)$
. Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _{pr}$
and
$\Phi _{pr}$
and
 $\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, and
$\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, and
 $\Phi _{pr}$
must end with rule (@), (@
$\Phi _{pr}$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _{pr}$
ends with rule (@). Then,
$\Phi _{pr}$
ends with rule (@). Then,
 $\Phi _{pr}$
must be of the following form:
$\Phi _{pr}$
must be of the following form:
where
 $\Gamma = (\Gamma _p + \Gamma _r) + \Delta _s$
is tight,
$\Gamma = (\Gamma _p + \Gamma _r) + \Delta _s$
is tight,
 $b = 1+b_p+b_r+b_s$
,
$b = 1+b_p+b_r+b_s$
,
 $m = m_p+m_r+m_s$
, and
$m = m_p+m_r+m_s$
, and
 $d = d_p+d_r+d_s$
. Therefore, we can build the following derivation
$d = d_p+d_r+d_s$
. Therefore, we can build the following derivation
 $\Phi _{(p,s)}$
:Since
$\Phi _{(p,s)}$
:Since \begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}'}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _p\qquad \Pi _s}{\Gamma _p + \Delta _s \Vdash ^{(b_p+b_s,m_p+m_s,d_p+d_s)} (p,s): (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}'}({\tt conf})\end{equation*}
 $\Gamma$
is tight, then
$\Gamma$
is tight, then
 $\Gamma _p$
and
$\Gamma _p$
and
 $\Delta _s$
are both tight. Moreover,
$\Delta _s$
are both tight. Moreover,
 $\neg {\tt val}(p)$
, since
$\neg {\tt val}(p)$
, since
 $(p, s) \rightsquigarrow _{{\tt v}} (p',q)$
. By applying the i.h. to
$(p, s) \rightsquigarrow _{{\tt v}} (p',q)$
. By applying the i.h. to
 $\Phi _{(p,s)}$
, there exists
$\Phi _{(p,s)}$
, there exists
 $\Phi _{(p',q)}$
that must be of the following form:
$\Phi _{(p',q)}$
that must be of the following form:

where
 $\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
, and the counters
$\Gamma _p + \Delta _s = \Gamma _{p'} + \Delta _q$
, and the counters
 $(b_p+b_s,m_p+m_s,d_p+d_s)$
and
$(b_p+b_s,m_p+m_s,d_p+d_s)$
and
 $(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are related properly. Therefore, we can build
$(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are related properly. Therefore, we can build
 $\Phi '$
as follows:
$\Phi '$
as follows:
where
 $b' = 1+b_{p'}+b_r+b_q$
,
$b' = 1+b_{p'}+b_r+b_q$
,
 $m' = m_{p'}+m_r+m_q$
, and
$m' = m_{p'}+m_r+m_q$
, and
 $d' = d_{p'}+d_r+d_q$
. Thus, we can conclude with
$d' = d_{p'}+d_r+d_q$
. Thus, we can conclude with
 $\Gamma = (\Gamma _p + \Delta _s) + \Gamma _r = (\Gamma _{p'} + \Delta _q) + \Gamma _r$
, and
$\Gamma = (\Gamma _p + \Delta _s) + \Gamma _r = (\Gamma _{p'} + \Delta _q) + \Gamma _r$
, and
 $(1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s) = (b,m,d)$
and
$(1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s) = (b,m,d)$
and
 $(b',m',d') = (1+b_{p'}+b_r+b_q,m_{p'}+m_r+m_q,d_{p'}+d_r+d_q)$
are properly related.
$(b',m',d') = (1+b_{p'}+b_r+b_q,m_{p'}+m_r+m_q,d_{p'}+d_r+d_q)$
are properly related. -
– Case
 $\Phi _{pr}$
ends with (@
$\Phi _{pr}$
ends with (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These cases are very similar to the previous case and follow easily from the i.h..
$^2_{{\tt p}}$
). These cases are very similar to the previous case and follow easily from the i.h..
-
-
• Case
 $(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (pr',q) = (u,q)$
, such that
$(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (pr',q) = (u,q)$
, such that
 $(p, s) \not \rightsquigarrow _{{\tt v}}$
,
$(p, s) \not \rightsquigarrow _{{\tt v}}$
,
 $(p,s)$
is unblocked, and
$(p,s)$
is unblocked, and
 $(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. Then,
$(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. Then,
 $\Phi$
has two premises
$\Phi$
has two premises
 $\Phi _{pr}$
and
$\Phi _{pr}$
and
 $\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, such that
$\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, such that
 $\Gamma = \Gamma _{pr} + \Delta _s$
,
$\Gamma = \Gamma _{pr} + \Delta _s$
,
 $b = 1+b_{pr}+b_s$
,
$b = 1+b_{pr}+b_s$
,
 $m = m_{pr}+m_s$
, and
$m = m_{pr}+m_s$
, and
 $d = d_{pr} +d_s$
. Then,
$d = d_{pr} +d_s$
. Then,
 $\Phi _{pr}$
must end with rule (@), (@
$\Phi _{pr}$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _{pr}$
ends with (
$\Phi _{pr}$
ends with (
 $\tt @$
). Then,
$\tt @$
). Then,
 $\Phi _{pr}$
must be of the following form:
$\Phi _{pr}$
must be of the following form:
where
 $\Gamma _{pr} = \Gamma _p + \Gamma _r$
,
$\Gamma _{pr} = \Gamma _p + \Gamma _r$
,
 $b = 1+b_p+b_r + b_s$
,
$b = 1+b_p+b_r + b_s$
,
 $m = m_p+m_r + m_s$
, and
$m = m_p+m_r + m_s$
, and
 $d = d_p+d_r+ d_s$
. Notice that, since
$d = d_p+d_r+ d_s$
. Notice that, since
 $(p, s) \not \rightsquigarrow _{{\tt v}}$
and
$(p, s) \not \rightsquigarrow _{{\tt v}}$
and
 $(p,s)$
is unblocked, then
$(p,s)$
is unblocked, then
 $p \in {\tt no}_{{\tt v}}$
, by definition. Therefore,
$p \in {\tt no}_{{\tt v}}$
, by definition. Therefore,
 $\mathscr{T\;} = \mathscr{T\;}'$
, according to Lemma 15. And, we can build derivation
$\mathscr{T\;} = \mathscr{T\;}'$
, according to Lemma 15. And, we can build derivation
 $\Phi _{(r,s)}$
as follows:Since
$\Phi _{(r,s)}$
as follows:Since \begin{equation*} \frac {\Phi _r\qquad \Pi _s}{\Gamma _r + \Delta _s \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} (r,s): (\mathscr{M} \times \mathscr{T\;}'')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _r\qquad \Pi _s}{\Gamma _r + \Delta _s \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} (r,s): (\mathscr{M} \times \mathscr{T\;}'')}({\tt conf})\end{equation*}
 $\Gamma$
is tight, then
$\Gamma$
is tight, then
 $\Gamma _r$
and
$\Gamma _r$
and
 $\Delta _s$
are both tight. Moreover,
$\Delta _s$
are both tight. Moreover,
 $\neg {\tt val}(r)$
, since
$\neg {\tt val}(r)$
, since
 $(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. By applying the i.h. to
$(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. By applying the i.h. to
 $\Phi _{(r,s)}$
, there exists
$\Phi _{(r,s)}$
, there exists
 $\Phi _{(r',q)}$
that must be of the following form:
$\Phi _{(r',q)}$
that must be of the following form:

where
 $\Gamma _r + \Delta _s = \Gamma _{r'} + \Delta _q$
, and the counters
$\Gamma _r + \Delta _s = \Gamma _{r'} + \Delta _q$
, and the counters
 $(b_r+b_s,m_r+m_s,d_r+d_s)$
and
$(b_r+b_s,m_r+m_s,d_r+d_s)$
and
 $(b_{r'}+b_q,m_{r'}+m_q,d_{r'}+d_q)$
are related properly. Moreover, there exists
$(b_{r'}+b_q,m_{r'}+m_q,d_{r'}+d_q)$
are related properly. Moreover, there exists
 $\Phi '_p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}''' \Rightarrow ((\mathscr{M} \rightsquigarrow _{{\tt v}} (\mathscr{T\;}'' \times \kappa )) \times \mathscr{T\;}''')}$
, by Lemma 15. Therefore, we can build
$\Phi '_p \triangleright \, {\Gamma _p}\Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}''' \Rightarrow ((\mathscr{M} \rightsquigarrow _{{\tt v}} (\mathscr{T\;}'' \times \kappa )) \times \mathscr{T\;}''')}$
, by Lemma 15. Therefore, we can build
 $\Phi '$
as follows:
$\Phi '$
as follows:
where
 $b' = 1+b_p+b_{r'}+b_q$
,
$b' = 1+b_p+b_{r'}+b_q$
,
 $m' = m_p+m_{r'}+m_q$
, and
$m' = m_p+m_{r'}+m_q$
, and
 $d' = d_p+d_{r'}+d_q$
. Thus, we can conclude with
$d' = d_p+d_{r'}+d_q$
. Thus, we can conclude with
 $\Gamma = (\Gamma _p + \Delta _s) + \Gamma _r = (\Gamma _p + \Delta _q) + \Gamma _{r'}$
, and
$\Gamma = (\Gamma _p + \Delta _s) + \Gamma _r = (\Gamma _p + \Delta _q) + \Gamma _{r'}$
, and
 $(1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s) = (b,m,d)$
and
$(1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s) = (b,m,d)$
and
 $(b',m',d') = (1+b_p+b_{r'}+b_q,m_p+m_{r'}+m_q,d_p+d_{r'}+d_q)$
are properly related.
$(b',m',d') = (1+b_p+b_{r'}+b_q,m_p+m_{r'}+m_q,d_p+d_{r'}+d_q)$
are properly related. -
– Case
 $\Phi _{pr}$
ends with (@
$\Phi _{pr}$
ends with (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These two cases are very similar to the previous case.
$^2_{{\tt p}}$
). These two cases are very similar to the previous case.
-
Theorem 5 (Quantitative soundness). If
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
is a tight derivation, then there exists
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
is a tight derivation, then there exists
![]() $(u,q)$
such that
$(u,q)$
such that
![]() $u \in {\tt no}_{{\tt v}}$
and
$u \in {\tt no}_{{\tt v}}$
and
![]() $(t,s) \rightsquigarrow _{\tt v}^{(b,m)} (u,q)$
with
$(t,s) \rightsquigarrow _{\tt v}^{(b,m)} (u,q)$
with
![]() $b$
$b$
![]() $\beta _{{\tt v}}$
-steps,
$\beta _{{\tt v}}$
-steps,
![]() $m$
$m$
![]() ${\tt g}/{\tt s}$
-steps, and
${\tt g}/{\tt s}$
-steps, and
![]() $|{(u,q)}|_{\texttt {v}} = d$
.
$|{(u,q)}|_{\texttt {v}} = d$
.
Proof.
We start by noting that
![]() $\Phi$
has two premises
$\Phi$
has two premises
![]() $\Phi _t \triangleright \, \Gamma _t\Vdash ^{(b_t,m_t,d_t)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
and
$\Phi _t \triangleright \, \Gamma _t\Vdash ^{(b_t,m_t,d_t)}_{\tt v} t\;:\;\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
and
![]() $\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, where
$\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, where
![]() $\Gamma = \Gamma _t + \Delta _s$
and
$\Gamma = \Gamma _t + \Delta _s$
and
![]() $\kappa = \tau \times \mathscr{T\;}'$
, such that
$\kappa = \tau \times \mathscr{T\;}'$
, such that
![]() $\tau$
and
$\tau$
and
![]() $\mathscr{T\;}'$
are tight. Now, the proof follows by induction on
$\mathscr{T\;}'$
are tight. Now, the proof follows by induction on
![]() $b+m$
:
$b+m$
:
-
• Case
 $b + m = 0$
. Then,
$b + m = 0$
. Then,
 $b = m = 0$
, and thus,
$b = m = 0$
, and thus,
 $b_t = m_t = b_s = m_s = 0$
. Therefore,
$b_t = m_t = b_s = m_s = 0$
. Therefore,
 $(t,s)$
is a configuration in normal form, by Lemma 17, and
$(t,s)$
is a configuration in normal form, by Lemma 17, and
 $|{(t,s)}|_{\texttt {v}} = d$
, by Lemma 16. Thus, we can conclude by taking
$|{(t,s)}|_{\texttt {v}} = d$
, by Lemma 16. Thus, we can conclude by taking
 $u = t$
and
$u = t$
and
 $q = s$
.
$q = s$
. -
• Case
 $b + m \gt 0$
. Then,
$b + m \gt 0$
. Then,
 $b \gt 0$
or
$b \gt 0$
or
 $m \gt 0$
, and thus,
$m \gt 0$
, and thus,
 $b_t + b_s \gt 0$
or
$b_t + b_s \gt 0$
or
 $m_t + m_s \gt 0$
. Note that it cannot be that
$m_t + m_s \gt 0$
. Note that it cannot be that
 $b_t = m_t = 0$
, because this would imply that
$b_t = m_t = 0$
, because this would imply that
 $b = m = 0$
by Lemma 16. Therefore, it must be the case that
$b = m = 0$
by Lemma 16. Therefore, it must be the case that
 $b_t + m_t \gt 0$
, and thus,
$b_t + m_t \gt 0$
, and thus,
 $t \not \in {\tt no}_{{\tt v}}$
by Lemma 45. Moreover, note that
$t \not \in {\tt no}_{{\tt v}}$
by Lemma 45. Moreover, note that
 $(t,s)$
cannot be a blocked configuration, by Proposition6. Therefore, by Proposition5, there exists
$(t,s)$
cannot be a blocked configuration, by Proposition6. Therefore, by Proposition5, there exists
 $(t',s')$
such that
$(t',s')$
such that
 $(t,s) \rightsquigarrow _{{\tt v}} (t',s')$
. By Lemma 19, there exists
$(t,s) \rightsquigarrow _{{\tt v}} (t',s')$
. By Lemma 19, there exists
 $\Phi ' \triangleright {\Gamma } \Vdash ^{(b',m',d)}_{\tt v} {(t',s')}\;:\;{\kappa }$
, such that
$\Phi ' \triangleright {\Gamma } \Vdash ^{(b',m',d)}_{\tt v} {(t',s')}\;:\;{\kappa }$
, such that
 $b'+m'=b+m-1$
. By the i.h., there exists
$b'+m'=b+m-1$
. By the i.h., there exists
 $(u,q)$
, such that
$(u,q)$
, such that
 $u\in {\tt no}_{{\tt v}}$
,
$u\in {\tt no}_{{\tt v}}$
,
 $(t',s') \rightsquigarrow _{\tt v}^{(b',m')} (u,q)$
and
$(t',s') \rightsquigarrow _{\tt v}^{(b',m')} (u,q)$
and
 $d = |{(u,q)}|_{\texttt {v}}$
. So we can conclude with
$d = |{(u,q)}|_{\texttt {v}}$
. So we can conclude with
 $(t,s) \rightsquigarrow _{{\tt v}} (t',s') \rightsquigarrow _{\tt v}^{(b',m')} (u,q)$
, which means that
$(t,s) \rightsquigarrow _{{\tt v}} (t',s') \rightsquigarrow _{\tt v}^{(b',m')} (u,q)$
, which means that
 $(t,s) \rightsquigarrow _{\tt v}^{(b,m)} (u,q)$
, as expected.
$(t,s) \rightsquigarrow _{\tt v}^{(b,m)} (u,q)$
, as expected.
Lemma 51 (Anti-substitution). If
![]() $\Phi _{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}}\Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\mu }$
, there exist
$\Phi _{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}}\Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\mu }$
, there exist
![]() $\Phi _t \triangleright \, \Gamma _t;\; x :$
$\Phi _t \triangleright \, \Gamma _t;\; x :$
![]() $\mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mu }$
and
$\mathscr{M}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mu }$
and
![]() $\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
![]() $\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
![]() $b = b_t+b_v$
,
$b = b_t+b_v$
,
![]() $m = m_t+m_v$
, and
$m = m_t+m_v$
, and
![]() $d = d_t + d_v$
.
$d = d_t + d_v$
.
Proof.
We generalize the original statement by allowing
![]() $\Phi _{t \{x \setminus v\}}$
to conclude with either a monadic type
$\Phi _{t \{x \setminus v\}}$
to conclude with either a monadic type
![]() $\mu$
or a type
$\mu$
or a type
![]() $\tau$
. Let
$\tau$
. Let
![]() $\mathscr{G\,} \in \{\mu , \tau \}$
. Then the statement is as follows:
$\mathscr{G\,} \in \{\mu , \tau \}$
. Then the statement is as follows:
If
![]() $\Phi _{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}}\Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\mathscr{G\,}}$
, there exist
$\Phi _{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}}\Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\mathscr{G\,}}$
, there exist
![]() $\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{G\,}}$
and
$\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{G\,}}$
and
![]() $\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
![]() $\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
![]() $b = b_t+b_v$
,
$b = b_t+b_v$
,
![]() $m = m_t+m_v$
, and
$m = m_t+m_v$
, and
![]() $d = d_t + d_v$
.
$d = d_t + d_v$
.
The proof is by induction over
![]() $\Phi _{t \{x \setminus v\}}$
, according to the last rule used in
$\Phi _{t \{x \setminus v\}}$
, according to the last rule used in
![]() $\Phi _{t \{x \setminus v\}}$
:
$\Phi _{t \{x \setminus v\}}$
:
-
• Case
 $\mathscr{G\,} = \mu$
. Let us assume
$\mathscr{G\,} = \mu$
. Let us assume
 $t = x$
, such that
$t = x$
, such that
 $t \{x \setminus v\} = v$
. Then
$t \{x \setminus v\} = v$
. Then
 $\mu = \mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
$\mu = \mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;}')$
, such that
 $\mathscr{T\;} = \mathscr{T\;}'$
by the fact that
$\mathscr{T\;} = \mathscr{T\;}'$
by the fact that
 $t \{x \setminus v\} = v$
, and thus,
$t \{x \setminus v\} = v$
, and thus,
 $\Phi _{t \{x \setminus v\}}$
must finish with rule (
$\Phi _{t \{x \setminus v\}}$
must finish with rule (
 $\uparrow$
), and
$\uparrow$
), and
 $\tau \neq {\tt n}$
by Lemma 49. Moreover,
$\tau \neq {\tt n}$
by Lemma 49. Moreover,
 $\Phi _{t \{x \setminus v\}}$
must necessarily end with rule (
$\Phi _{t \{x \setminus v\}}$
must necessarily end with rule (
 $\uparrow$
) with one premise
$\uparrow$
) with one premise
 $\Phi '_{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}} \Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\pi }$
, such that
$\Phi '_{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}} \Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\pi }$
, such that
 $\tau = \pi$
. By applying the i.h. to
$\tau = \pi$
. By applying the i.h. to
 $\Phi '_{t \{x \setminus v\}}$
, there exist
$\Phi '_{t \{x \setminus v\}}$
, there exist
 $\Phi '_t \triangleright \,{\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_)}_{\tt v} {t}\;:\;{\pi }$
and
$\Phi '_t \triangleright \,{\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_)}_{\tt v} {t}\;:\;{\pi }$
and
 $\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
 $b = b_t + b_v$
,
$b = b_t + b_v$
,
 $m = m_t + m_v$
, and
$m = m_t + m_v$
, and
 $d = d_t + d_v$
. Therefore, we can build
$d = d_t + d_v$
. Therefore, we can build
 $\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;})}$
, by applying rule (
$\Phi _t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}} \Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{T\;} \Rightarrow (\pi \times \mathscr{T\;})}$
, by applying rule (
 $\uparrow$
) to
$\uparrow$
) to
 $\Phi '_t$
. We can conclude since rule (
$\Phi '_t$
. We can conclude since rule (
 $\uparrow$
) leaves the typing environment and the counters of the premise unchanged. From now on, we are going to assume
$\uparrow$
) leaves the typing environment and the counters of the premise unchanged. From now on, we are going to assume
 $t \neq x$
and consider the last rule used in
$t \neq x$
and consider the last rule used in
 $\Phi _{t \{x \setminus v\}}$
, which must be (
$\Phi _{t \{x \setminus v\}}$
, which must be (
 $\uparrow$
), (@), (get), (set), (@
$\uparrow$
), (@), (get), (set), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Rule (
 $\uparrow$
). Then
$\uparrow$
). Then
 $\mu = \mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})$
and
$\mu = \mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})$
and
 $\Phi _{t \{x \setminus v\}}$
has one premise
$\Phi _{t \{x \setminus v\}}$
has one premise
 $\Phi '_{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}} \Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\tau }$
. By applying the i.h. to
$\Phi '_{t \{x \setminus v\}} \triangleright \, {\Gamma _{t \{x \setminus v\}}} \Vdash ^{(b,m,d)}_{\tt v} {t \{x \setminus v\}}\;:\;{\tau }$
. By applying the i.h. to
 $\Phi '_{t \{x \setminus v\}}$
, there exist
$\Phi '_{t \{x \setminus v\}}$
, there exist
 $\Phi '_t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\tau }$
and
$\Phi '_t \triangleright \, {\Gamma _t;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\tau }$
and
 $\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t + \Gamma _v$
,
 $b = b_t + b_u$
,
$b = b_t + b_u$
,
 $m = m_t + m_u$
, and
$m = m_t + m_u$
, and
 $d = d_t + d_u$
. Therefore, we can build
$d = d_t + d_u$
. Therefore, we can build
 $\Phi _t \triangleright \, {\Gamma _{t};\;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})}$
by taking
$\Phi _t \triangleright \, {\Gamma _{t};\;\; x \;:\; \mathscr{M}}\Vdash ^{(b_t,m_t,d_t)}_{\tt v} {t}\;:\;{\mathscr{T\;} \Rightarrow (\tau \times \mathscr{T\;})}$
by taking
 $\Phi '_t$
and applying rule (
$\Phi '_t$
and applying rule (
 $\uparrow$
). And we can conclude since rule (
$\uparrow$
). And we can conclude since rule (
 $\uparrow$
) leaves the typing environment and the counters of the premise unchanged.
$\uparrow$
) leaves the typing environment and the counters of the premise unchanged. -
– Rule (@). Then
 $t = up$
,
$t = up$
,
 $\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = \mathscr{T\;} \Rightarrow \kappa$
, and
 $t \{x \setminus v\} = (u \{x \setminus v\})(p \{x \setminus v\})$
. Moreover,
$t \{x \setminus v\} = (u \{x \setminus v\})(p \{x \setminus v\})$
. Moreover,
 $\Phi _{t \{x \setminus v\}}$
has two premises
$\Phi _{t \{x \setminus v\}}$
has two premises
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}}}\Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}}}\Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
 $\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M\;}' \times \mathscr{T\;}')}$
, where
$\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M\;}' \times \mathscr{T\;}')}$
, where
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
 $b = 1+b_u+b_p$
,
$b = 1+b_u+b_p$
,
 $m = m_u+m_p$
, and
$m = m_u+m_p$
, and
 $d = d_u+d_p$
. By applying the i.h. to
$d = d_u+d_p$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
and
$\Phi _{u \{x \setminus v\}}$
and
 $\Phi _{p \{x \setminus v\}}$
, there exist
$\Phi _{p \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b'_u,m'_u,d'_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
$\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b'_u,m'_u,d'_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow ((\mathscr{M\;}' \rightarrow (\mathscr{T\;}' \Rightarrow \kappa )) \times \mathscr{T\;}'')}$
and
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
$\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
 $\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
$\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
 $b_u = b'_u+b^1_v$
,
$b_u = b'_u+b^1_v$
,
 $m_u = m'_u + m^1_v$
, and
$m_u = m'_u + m^1_v$
, and
 $d_u = d'_u + d^1_v$
, and
$d_u = d'_u + d^1_v$
, and
 $\Phi _p \triangleright \,{\Gamma _p;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b'_p,m'_p,d'_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
and
$\Phi _p \triangleright \,{\Gamma _p;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b'_p,m'_p,d'_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow (\mathscr{M} \times \mathscr{T\;}')}$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, such that
$\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, such that
 $\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
$\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
 $b_p = b'_p+b^2_v$
,
$b_p = b'_p+b^2_v$
,
 $m_p = m'_p+m^2_v$
, and
$m_p = m'_p+m^2_v$
, and
 $d_p = d'_p+d^2_v$
. By Lemma 47, there exists
$d_p = d'_p+d^2_v$
. By Lemma 47, there exists
 $\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v, m_v, d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v}\Vdash ^{(b_v, m_v, d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v +b^2_v$
,
$b_v = b^1_v +b^2_v$
,
 $m_v = m^1_v + m^2_v$
, and
$m_v = m^1_v + m^2_v$
, and
 $d_v = d^1_v+d^2_v$
. And we can build
$d_v = d^1_v+d^2_v$
. And we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M} \Vdash ^{(1+b'_u+b'_p,m'_u+m'_p,d'_u+d'_p)} up: \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M} \Vdash ^{(1+b'_u+b'_p,m'_u+m'_p,d'_u+d'_p)} up: \mathscr{T\;} \Rightarrow \kappa }({\tt @})\end{equation*}
 $\Gamma _t = \Gamma _u + \Gamma _p$
,
$\Gamma _t = \Gamma _u + \Gamma _p$
,
 $b_t = 1+b_u+b_p$
,
$b_t = 1+b_u+b_p$
,
 $m_t = m_u+m_p$
, and
$m_t = m_u+m_p$
, and
 $d_t = d_u+d_p$
. Thus, we can conclude with
$d_t = d_u+d_p$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
 $b = 1+b_u+b_p = 1+(b'_u + b^1_v) + (b'_p + b^2_v) = 1 + b_u + b_p + b_v = b_t + b_v$
,
$b = 1+b_u+b_p = 1+(b'_u + b^1_v) + (b'_p + b^2_v) = 1 + b_u + b_p + b_v = b_t + b_v$
,
 $m = m_u+m_p=$
$m = m_u+m_p=$
 $(m'_u + m^1_v) + (m'_p + m^2_v) = m_u + m_p + m_v = m_t + m_v$
, and
$(m'_u + m^1_v) + (m'_p + m^2_v) = m_u + m_p + m_v = m_t + m_v$
, and
 $d = d_u+d_p = (d'_u + d^1_v) + (d'_p + d^2_v) = d_u + d_p + d_v = d_t + d_v$
.
$d = d_u+d_p = (d'_u + d^1_v) + (d'_p + d^2_v) = d_u + d_p + d_v = d_t + d_v$
.
-
– Rule (get). Then,
 $t = {\tt get}_{l}(\lambda y.u)$
,
$t = {\tt get}_{l}(\lambda y.u)$
,
 $\mu = \{l \;:\; \mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;};\;\mathscr{T\;}\} \Rightarrow \kappa$
, and
$\mu = \{l \;:\; \mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;};\;\mathscr{T\;}\} \Rightarrow \kappa$
, and
 $t \{x \setminus v\} = {\tt get}_{l}(\lambda y.(u \{x \setminus v\}))$
. Moreover,
$t \{x \setminus v\} = {\tt get}_{l}(\lambda y.(u \{x \setminus v\}))$
. Moreover,
 $\Phi _{t \{x \setminus v\}}$
has one premise
$\Phi _{t \{x \setminus v\}}$
has one premise
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}'} \Vdash ^{(b,m',d)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;};\;\}\mathscr{T\;} \Rightarrow \kappa }$
, such that
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}'} \Vdash ^{(b,m',d)}_{\tt v} {u \{x \setminus v\}}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;};\;\}\mathscr{T\;} \Rightarrow \kappa }$
, such that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}}$
and
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}}$
and
 $m = 1+m'$
. By applying the i.h. to
$m = 1+m'$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
, there exist
$\Phi _{u \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;};\;\}\mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;};\;\}\mathscr{T\;} \Rightarrow \kappa }$
and
 $\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
$\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
 $b = b_u + b_v$
,
$b = b_u + b_v$
,
 $m' = m_u + m_v$
, and
$m' = m_u + m_v$
, and
 $d = d_u + d_v$
. Therefore, we can build
$d = d_u + d_v$
. Therefore, we can build
 $\Phi _t$
as follows:And we can conclude with
$\Phi _t$
as follows:And we can conclude with \begin{equation*} \frac {\Phi _u \triangleright \, {\Gamma _u;\; y \;:\; \mathscr{M\;}';\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;};\;\}\mathscr{T\;} \Rightarrow \kappa }}{\Gamma _{u};\;\; x \;:\; \mathscr{M} \Vdash ^{(b_u,1+m_u,d_u)} {\tt get}_{l}(\lambda y.u)\;:\; \{l\;:\;\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
\begin{equation*} \frac {\Phi _u \triangleright \, {\Gamma _u;\; y \;:\; \mathscr{M\;}';\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\{l\;:\;\mathscr{M\;}'' \cdot \mathscr{L\;};\;\}\mathscr{T\;} \Rightarrow \kappa }}{\Gamma _{u};\;\; x \;:\; \mathscr{M} \Vdash ^{(b_u,1+m_u,d_u)} {\tt get}_{l}(\lambda y.u)\;:\; \{l\;:\;\mathscr{M\;}'\sqcup \mathscr{M\;}'' \cdot \mathscr{L\;}\};\;\mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
 $b = b_u + b_v$
,
$b = b_u + b_v$
,
 $m = 1 + m' = 1 + m_u + m_v = (1 + m_u) + m_v$
, and
$m = 1 + m' = 1 + m_u + m_v = (1 + m_u) + m_v$
, and
 $d = d_u + d_v$
.
$d = d_u + d_v$
.
-
– Rule (set). Then,
 $t = {\tt set}_{l}(w,u)$
,
$t = {\tt set}_{l}(w,u)$
,
 $\mu = {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa$
, and
$\mu = {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa$
, and
 $t \{x \setminus v\} = {\tt set}_{l}(w \{x \setminus v\},u \{x \setminus v\})$
. Moreover,
$t \{x \setminus v\} = {\tt set}_{l}(w \{x \setminus v\},u \{x \setminus v\})$
. Moreover,
 $\Phi _{t \{x \setminus v\}}$
has two premises
$\Phi _{t \{x \setminus v\}}$
has two premises
 $\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _{w \{x \setminus v\}}} \Vdash ^{(b',m',d')}_{\tt v} {w \{x \setminus v\}}\;:\;{\mathscr{M\;}'}$
and
$\Phi _{w \{x \setminus v\}} \triangleright \, {\Gamma _{w \{x \setminus v\}}} \Vdash ^{(b',m',d')}_{\tt v} {w \{x \setminus v\}}\;:\;{\mathscr{M\;}'}$
and
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}}} \Vdash ^{(b'',m'',d'')}_{\tt v} {u \{x \setminus v\}}\;:\;{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;} \mathscr{T\;} \Rightarrow \kappa }$
, such that
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}}} \Vdash ^{(b'',m'',d'')}_{\tt v} {u \{x \setminus v\}}\;:\;{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;} \mathscr{T\;} \Rightarrow \kappa }$
, such that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{w \{x \setminus v\}} + \Gamma _{u \{x \setminus v\}}$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{w \{x \setminus v\}} + \Gamma _{u \{x \setminus v\}}$
,
 $b = b'+ b''$
,
$b = b'+ b''$
,
 $m = 1 + m'+m''$
, and
$m = 1 + m'+m''$
, and
 $d = d' + d''$
. By applying the i.h. to
$d = d' + d''$
. By applying the i.h. to
 $\Phi _{w \{x \setminus v\}}$
, there exist
$\Phi _{w \{x \setminus v\}}$
, there exist
 $\Phi _w \triangleright \, {\Gamma _w;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}$
and
$\Phi _w \triangleright \, {\Gamma _w;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_w,m_w,d_w)}_{\tt v} {w}\;:\;{\mathscr{M\;}'}$
and
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
$\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
 $\Gamma _{w \{x \setminus v\}} = \Gamma _w + \Gamma ^1_v$
,
$\Gamma _{w \{x \setminus v\}} = \Gamma _w + \Gamma ^1_v$
,
 $b' = b_w + b^1_v$
,
$b' = b_w + b^1_v$
,
 $m'= m_w + m^1_v$
, and
$m'= m_w + m^1_v$
, and
 $d' = d_w+d^1_v$
. By applying the i.h. to
$d' = d_w+d^1_v$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
, there exist
$\Phi _{u \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;} \mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{{\{l\;:\;\mathscr{M\;}' \cdot \mathscr{L\;}\};\;} \mathscr{T\;} \Rightarrow \kappa }$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, such that
$\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, such that
 $\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma ^2_v$
,
$\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma ^2_v$
,
 $b'' = b_u + b^2_v$
,
$b'' = b_u + b^2_v$
,
 $m'' = m_u + m^2_v$
, and
$m'' = m_u + m^2_v$
, and
 $d'' = d_u + d^2_v$
. By Lemma 47, there exists
$d'' = d_u + d^2_v$
. By Lemma 47, there exists
 $\Phi _v \triangleright \, {\Gamma ^1_v + \Gamma ^2_v} \Vdash ^{(b^1_v + b^2_v, m^1_v+m^2_v, d^1_v + d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma ^1_v + \Gamma ^2_v} \Vdash ^{(b^1_v + b^2_v, m^1_v+m^2_v, d^1_v + d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v + b^2_v$
,
$b_v = b^1_v + b^2_v$
,
 $m_v = m^1_v + m^2_v$
, and
$m_v = m^1_v + m^2_v$
, and
 $d_v = d^1_v + d^2_v$
. Therefore, we can build
$d_v = d^1_v + d^2_v$
. Therefore, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _w\qquad \Phi _u}{(\Gamma _w + \Gamma _u);\; x \;:\; \mathscr{M} \Vdash ^{(b_w+b_u, 1+m_w+m_u,d_w+d_u)} {\tt set}_{l}(w,u): {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa }({\tt set})\end{equation*}
\begin{equation*} \frac {\Phi _w\qquad \Phi _u}{(\Gamma _w + \Gamma _u);\; x \;:\; \mathscr{M} \Vdash ^{(b_w+b_u, 1+m_w+m_u,d_w+d_u)} {\tt set}_{l}(w,u): {\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;} \Rightarrow \kappa }({\tt set})\end{equation*}
 $\Gamma _t = \Gamma _w + \Gamma _u$
,
$\Gamma _t = \Gamma _w + \Gamma _u$
,
 $b_t = b_w + b_u$
,
$b_t = b_w + b_u$
,
 $m_t = 1 + m_w + m_u$
, and
$m_t = 1 + m_w + m_u$
, and
 $d_t = d_w + d_u$
. Thus, we can conclude with
$d_t = d_w + d_u$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{w \{x \setminus v\}} + \Gamma _{u \{x \setminus v\}} = (\Gamma _w + \Gamma ^1_u) + (\Gamma _u + \Gamma ^2_v) = (\Gamma _w + \Gamma _u) + (\Gamma ^1_v + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{w \{x \setminus v\}} + \Gamma _{u \{x \setminus v\}} = (\Gamma _w + \Gamma ^1_u) + (\Gamma _u + \Gamma ^2_v) = (\Gamma _w + \Gamma _u) + (\Gamma ^1_v + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
 $b = b' + b'' = (b_w + b^1_v) + (b_u + b^2_v) = (b_w + b_u) + (b^1_v + b^2_v) = b_t + b_v$
,
$b = b' + b'' = (b_w + b^1_v) + (b_u + b^2_v) = (b_w + b_u) + (b^1_v + b^2_v) = b_t + b_v$
,
 $m = 1+ m' + m'' = 1+ (m_w + m^1_v) + (m_u + m^2_v) = (1 + m_w + m_u) + (m^1_v + m^2_v) = m_t + m_v$
, and
$m = 1+ m' + m'' = 1+ (m_w + m^1_v) + (m_u + m^2_v) = (1 + m_w + m_u) + (m^1_v + m^2_v) = m_t + m_v$
, and
 $d = d' + d'' = (d_w + d^1_v) + (d_u + d^2_v) = (d_w + d_u) + (d^1_v + d^2_v) = d_t + d_v$
.
$d = d' + d'' = (d_w + d^1_v) + (d_u + d^2_v) = (d_w + d_u) + (d^1_v + d^2_v) = d_t + d_v$
.
-
– Rule (@
 $^1_{{\tt p}}$
). Then,
$^1_{{\tt p}}$
). Then,
 $t = up$
,
$t = up$
,
 $\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
$\mu = \mathscr{T\;} \Rightarrow ({\tt n} \times \mathscr{T\;}')$
, and
 $t \{x \setminus v\} = (u \{x \setminus v\})(p \{x \setminus v\})$
. Moreover,
$t \{x \setminus v\} = (u \{x \setminus v\})(p \{x \setminus v\})$
. Moreover,
 $\Phi _{t \{x \setminus v\}}$
has two premises
$\Phi _{t \{x \setminus v\}}$
has two premises
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
 $\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, such that
$\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
, such that
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}}$
,
 $b = b_u+b_p$
,
$b = b_u+b_p$
,
 $m = m_u+m_p$
, and
$m = m_u+m_p$
, and
 $d = 1+d_u+d_p$
. By applying the i.h. to
$d = 1+d_u+d_p$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
and
$\Phi _{u \{x \setminus v\}}$
and
 $\Phi _{p \{x \setminus v\}}$
, there exist
$\Phi _{p \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b'_u,m'_u,d'_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
$\Phi _u \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b'_u,m'_u,d'_u)}_{\tt v} {u}\;:\;{\mathscr{T\;} \Rightarrow (\overline {{\tt a}} \times \mathscr{T\;}'')}$
and
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
$\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
 $\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
$\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
 $b_u = b'_u+b^1_v$
,
$b_u = b'_u+b^1_v$
,
 $m_u = m'_u + m^1_v$
, and
$m_u = m'_u + m^1_v$
, and
 $d_u = d'_u + d^1_v$
, and
$d_u = d'_u + d^1_v$
, and
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b'_p,m'_p,d'_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
and
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_2} \Vdash ^{(b'_p,m'_p,d'_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}'' \Rightarrow ({{\tt tt}_{\tt v}} \times \mathscr{T\;}')}$
and
 $\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, such that
$\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}$
, such that
 $\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
$\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^2_v$
,
 $b_p = b'_p+b^2_v$
,
$b_p = b'_p+b^2_v$
,
 $m_p = m'_p+m^2_v$
, and
$m_p = m'_p+m^2_v$
, and
 $d_p = d'_p+d^2_v$
. By Lemma 47, there exists
$d_p = d'_p+d^2_v$
. By Lemma 47, there exists
 $\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v, m_v, d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v, m_v, d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
$\Gamma _v = \Gamma ^1_v + \Gamma ^2_v$
,
 $b_v = b^1_v +b^2_v$
,
$b_v = b^1_v +b^2_v$
,
 $m_v = m^1_v + m^2_v$
, and
$m_v = m^1_v + m^2_v$
, and
 $d_v = d^1_v+d^2_v$
. Moreover, we can build
$d_v = d^1_v+d^2_v$
. Moreover, we can build
 $\Phi _t$
as follows:where
$\Phi _t$
as follows:where \begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M} \Vdash ^{(b'_u+b'_p,m'_u+m'_p,1+d'_u+d'_p)} up: \mathscr{T\;} \Rightarrow \kappa }({\tt @}^1_{{\tt p}})\end{equation*}
\begin{equation*} \frac {\Phi _u\qquad \Phi _p}{(\Gamma _u + \Gamma _p);\; x \;:\; \mathscr{M} \Vdash ^{(b'_u+b'_p,m'_u+m'_p,1+d'_u+d'_p)} up: \mathscr{T\;} \Rightarrow \kappa }({\tt @}^1_{{\tt p}})\end{equation*}
 $\Gamma _t = \Gamma _u + \Gamma _p$
,
$\Gamma _t = \Gamma _u + \Gamma _p$
,
 $b_t = b_u+b_p$
,
$b_t = b_u+b_p$
,
 $m_t = m_u+m_p$
, and
$m_t = m_u+m_p$
, and
 $d_t = 1+d_u+d_p$
. Thus, we can conclude with
$d_t = 1+d_u+d_p$
. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} + \Gamma _{p \{x \setminus v\}} = (\Gamma _u + \Gamma ^1_v) + (\Gamma _p + \Gamma ^2_v) = \Gamma _t + \Gamma _v$
,
 $b = b_u+b_p = (b'_u + b^1_v) + (b'_p + b^2_v) = b_u + b_p + b_v = b_t + b_v$
,
$b = b_u+b_p = (b'_u + b^1_v) + (b'_p + b^2_v) = b_u + b_p + b_v = b_t + b_v$
,
 $m = m_u+m_p = (m'_u + m^1_v)+$
$m = m_u+m_p = (m'_u + m^1_v)+$
 $(m'_p + m^2_v) = m_u + m_p + m_v = m_t + m_v$
, and
$(m'_p + m^2_v) = m_u + m_p + m_v = m_t + m_v$
, and
 $d = 1+d_u+d_p = 1+(d'_u + d^1_v)+ (d'_p + $
$d = 1+d_u+d_p = 1+(d'_u + d^1_v)+ (d'_p + $
 $ d^2_v) =1+d_u + d_p + d_v = d_t + d_v$
.
$ d^2_v) =1+d_u + d_p + d_v = d_t + d_v$
.
-
– Rule (@
 $^2_{{\tt p}}$
). This case is very similar to the previous case.
$^2_{{\tt p}}$
). This case is very similar to the previous case.
-
-
• Case
 $\mathscr{G\,} = \tau$
. Let us assume
$\mathscr{G\,} = \tau$
. Let us assume
 $t = x$
, such that
$t = x$
, such that
 $t \{x \setminus v\} = v$
. Then we have to consider two cases:
$t \{x \setminus v\} = v$
. Then we have to consider two cases:
 $\tau = [ \sigma _i ]_{i \in I}$
or
$\tau = [ \sigma _i ]_{i \in I}$
or
 $\tau$
is not a multi-type. If
$\tau$
is not a multi-type. If
 $\tau = [ \sigma _i ]_{i \in I}$
, we can take
$\tau = [ \sigma _i ]_{i \in I}$
, we can take
 $\Phi _v = \Phi _{t \{x \setminus v\}}$
, such that
$\Phi _v = \Phi _{t \{x \setminus v\}}$
, such that
 $\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
$\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
 $b_v = b$
,
$b_v = b$
,
 $m_v = m$
, and
$m_v = m$
, and
 $d_v = d$
, and build
$d_v = d$
, and build
 $\Phi _t$
as follows:
$\Phi _t$
as follows:
such that
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{M} = [ \sigma _i ]_{i \in I}$
, and
$\mathscr{M} = [ \sigma _i ]_{i \in I}$
, and
 $b_t = m_t = d_t = 0$
. If
$b_t = m_t = d_t = 0$
. If
 $\tau$
is not a multi-type, then we can build
$\tau$
is not a multi-type, then we can build
 $\Phi _v \triangleright \, {\Gamma _{t \{x \setminus v\}}} \Vdash ^{(b,m,d)}_{\tt v} {v}\;:\;{[ \tau ]}$
, such that
$\Phi _v \triangleright \, {\Gamma _{t \{x \setminus v\}}} \Vdash ^{(b,m,d)}_{\tt v} {v}\;:\;{[ \tau ]}$
, such that
 $\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
$\Gamma _v = \Gamma _{t \{x \setminus v\}}$
,
 $b_v = b$
,
$b_v = b$
,
 $m_v = m$
, and
$m_v = m$
, and
 $d_v = d$
, from
$d_v = d$
, from
 $\Phi _{t \{x \setminus v\}}$
followed by rule (m), and
$\Phi _{t \{x \setminus v\}}$
followed by rule (m), and
 $\Phi _t \triangleright \, {x \;:\; [ \tau ]} \Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\tau }$
, such that
$\Phi _t \triangleright \, {x \;:\; [ \tau ]} \Vdash ^{(0,0,0)}_{\tt v} {x}\;:\;{\tau }$
, such that
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $b_t = m_t = d_t = 0$
, by using rule (ax). In both cases, we can conclude with
$b_t = m_t = d_t = 0$
, by using rule (ax). In both cases, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _v = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _v = \Gamma _t + \Gamma _v$
,
 $b = b_v = b_t + b_v$
,
$b = b_v = b_t + b_v$
,
 $m = m_v = m_t + m_v$
, and
$m = m_v = m_t + m_v$
, and
 $d = d_v = d_t + d_v$
. From now on, we are going to assume
$d = d_v = d_t + d_v$
. From now on, we are going to assume
 $t \neq x$
and consider the last rule used in
$t \neq x$
and consider the last rule used in
 $\Phi _{t \{x \setminus v\}}$
, which must be (ax), (
$\Phi _{t \{x \setminus v\}}$
, which must be (ax), (
 $\lambda$
), or (
$\lambda$
), or (
 $\lambda _{\tt p}$
):
$\lambda _{\tt p}$
):-
– Rule (ax). Then
 $t = y$
,
$t = y$
,
 $\tau = \sigma$
,
$\tau = \sigma$
,
 $y \{x \setminus v\} = y$
, and
$y \{x \setminus v\} = y$
, and
 $\mathscr{M} = [ \, ]$
. Therefore, we can take
$\mathscr{M} = [ \, ]$
. Therefore, we can take
 $\Phi _t = \Phi _{t \{x \setminus v\}}$
, where
$\Phi _t = \Phi _{t \{x \setminus v\}}$
, where
 $\Gamma _t = \Gamma _{t \{x \setminus v\}}$
,
$\Gamma _t = \Gamma _{t \{x \setminus v\}}$
,
 $b_t = b$
,
$b_t = b$
,
 $m_t = m$
, and
$m_t = m$
, and
 $d_t = d$
, and build
$d_t = d$
, and build
 $\Phi _v \triangleright \, {\emptyset }\Vdash ^{(0,0,0)}_{\tt v} {v}\;:\;{[ \, ]}$
, such that
$\Phi _v \triangleright \, {\emptyset }\Vdash ^{(0,0,0)}_{\tt v} {v}\;:\;{[ \, ]}$
, such that
 $\Gamma _v = \emptyset$
, and
$\Gamma _v = \emptyset$
, and
 $b_v = m_v = d_v = 0$
, by using rule (m) with no premises. And we can conclude with
$b_v = m_v = d_v = 0$
, by using rule (m) with no premises. And we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _t = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _t = \Gamma _t + \Gamma _v$
,
 $b = b_t = b_t + b_v$
,
$b = b_t = b_t + b_v$
,
 $m = m_t = m_t + m_v$
, and
$m = m_t = m_t + m_v$
, and
 $d = d_t = d_t + d_v$
.
$d = d_t = d_t + d_v$
. -
– Rule (
 $\lambda$
). Then
$\lambda$
). Then
 $t = \lambda y.u$
,
$t = \lambda y.u$
,
 $\tau = \mathscr{M\;}' \rightarrow \mu$
, and
$\tau = \mathscr{M\;}' \rightarrow \mu$
, and
 $t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Therefore,
$t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Therefore,
 $\Phi _{t \{x \setminus v\}}$
has one premise
$\Phi _{t \{x \setminus v\}}$
has one premise
 $\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}'}\Vdash ^{(b,m,d)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mu }$
, where
$\Phi _{u \{x \setminus v\}} \triangleright \, {\Gamma _{u \{x \setminus v\}};\;\; y \;:\; \mathscr{M\;}'}\Vdash ^{(b,m,d)}_{\tt v} {u \{x \setminus v\}}\;:\;{\mu }$
, where
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}}$
. By applying the i.h. to
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}}$
. By applying the i.h. to
 $\Phi _{u \{x \setminus v\}}$
, there exist
$\Phi _{u \{x \setminus v\}}$
, there exist
 $\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mu }$
and
$\Phi _u \triangleright \, {(\Gamma _u;\; y \;:\; \mathscr{M\;}');\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {u}\;:\;{\mu }$
and
 $\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
, since we may assume that
$\Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
, since we may assume that
 $y \not \in {\tt dom}(\Gamma _v)$
by
$y \not \in {\tt dom}(\Gamma _v)$
by
 $\alpha$
-equivalence,
$\alpha$
-equivalence,
 $b = b_u + b_v$
,
$b = b_u + b_v$
,
 $m = m_u + m_v$
, and
$m = m_u + m_v$
, and
 $d = d_u + d_v$
. Therefore, we can build
$d = d_u + d_v$
. Therefore, we can build
 $\Phi _t \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {\lambda y.u}\;:\;{\mathscr{M\;}' \rightarrow \mu }$
, such that
$\Phi _t \triangleright \, {\Gamma _u;\; x \;:\; \mathscr{M}} \Vdash ^{(b_u,m_u,d_u)}_{\tt v} {\lambda y.u}\;:\;{\mathscr{M\;}' \rightarrow \mu }$
, such that
 $\Gamma _t = \Gamma _u$
,
$\Gamma _t = \Gamma _u$
,
 $b_t = b_u$
,
$b_t = b_u$
,
 $m_t = m_u$
, and
$m_t = m_u$
, and
 $d_t = d_u$
, by taking
$d_t = d_u$
, by taking
 $\Phi '_t$
and applying rule (
$\Phi '_t$
and applying rule (
 $\lambda$
). And we can conclude with
$\lambda$
). And we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = \Gamma _{u \{x \setminus v\}} = \Gamma _u + \Gamma _v$
,
 $b = b_u + b_v$
,
$b = b_u + b_v$
,
 $m = m_u + m_v$
, and
$m = m_u + m_v$
, and
 $d = d_u + d_v$
.
$d = d_u + d_v$
. -
– Rule (m). Then
 $\tau = [ \sigma _i ]_{i \in I}$
and
$\tau = [ \sigma _i ]_{i \in I}$
and
 $\Phi '_{t \{x \setminus v\}}$
has premises
$\Phi '_{t \{x \setminus v\}}$
has premises
 $(\Phi ^i_{t \{x \setminus v\}} \triangleright \, {\Gamma _i}\Vdash ^{(b_i,m_i,d_i)}_{\tt v} {t \{x \setminus v\}}\;:\;{\sigma _i})_{i \in I}$
, where
$(\Phi ^i_{t \{x \setminus v\}} \triangleright \, {\Gamma _i}\Vdash ^{(b_i,m_i,d_i)}_{\tt v} {t \{x \setminus v\}}\;:\;{\sigma _i})_{i \in I}$
, where
 $\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i$
,
$\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i$
,
 $b = +_{i \in I} b_i$
,
$b = +_{i \in I} b_i$
,
 $m = +_{i \in I} m_i$
, and
$m = +_{i \in I} m_i$
, and
 $d = +_{i \in I} d_i$
. By applying the i.h. to each
$d = +_{i \in I} d_i$
. By applying the i.h. to each
 $\Phi ^i_{t \{x \setminus v\}}$
, there exist
$\Phi ^i_{t \{x \setminus v\}}$
, there exist
 $\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i} \Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt v} {t}\;:\;{\sigma _i}$
and
$\Phi ^i_t \triangleright \, {\Gamma ^i_t;\; x \;:\; \mathscr{M}_i} \Vdash ^{(b^i_t,m^i_t,d^i_t)}_{\tt v} {t}\;:\;{\sigma _i}$
and
 $\Phi ^i_v \triangleright \, {\Gamma ^i_v} \Vdash ^{(b^i_v,m^i_v,d^i_v)}_{\tt v} {v}\;:\;{=\mathscr{M}_i}$
, such that
$\Phi ^i_v \triangleright \, {\Gamma ^i_v} \Vdash ^{(b^i_v,m^i_v,d^i_v)}_{\tt v} {v}\;:\;{=\mathscr{M}_i}$
, such that
 $\Gamma _i = \Gamma ^i_t + \Gamma ^i_v$
,
$\Gamma _i = \Gamma ^i_t + \Gamma ^i_v$
,
 $\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
$\mathscr{M} = \sqcup _{i \in I} \mathscr{M}_i$
,
 $b_i = b^i_t + b^i_v$
,
$b_i = b^i_t + b^i_v$
,
 $m_i = m^i_t + m^i_v$
, and
$m_i = m^i_t + m^i_v$
, and
 $d_i = d^i_t + d^i_v$
, for each
$d_i = d^i_t + d^i_v$
, for each
 $i \in I$
. By Lemma 47, there exists
$i \in I$
. By Lemma 47, there exists
 $\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v, m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _v \triangleright \, {\Gamma _v} \Vdash ^{(b_v, m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
$\Gamma _v = +_{i \in I} \Gamma ^i_v$
,
 $b_v = +_{i \in I} b^i_v$
,
$b_v = +_{i \in I} b^i_v$
,
 $m_v = +_{i \in I} m^i_v$
, and
$m_v = +_{i \in I} m^i_v$
, and
 $d_v = +_{i \in I} d^i_v$
. Therefore, we can build
$d_v = +_{i \in I} d^i_v$
. Therefore, we can build
 $\Phi _t$
as follows:And we can conclude
$\Phi _t$
as follows:And we can conclude \begin{equation*} \frac {(\Phi ^i_t)_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \mathscr{M} \Vdash ^{(+_{i \in I} b^i_t, +_{i \in I} m^i_t, +_{i \in I} d^i_t)} t\;:\; [ \sigma _i ]}({\tt m})\end{equation*}
\begin{equation*} \frac {(\Phi ^i_t)_{i \in I}}{+_{i \in I} \Gamma ^i_t;\; x \;:\; \mathscr{M} \Vdash ^{(+_{i \in I} b^i_t, +_{i \in I} m^i_t, +_{i \in I} d^i_t)} t\;:\; [ \sigma _i ]}({\tt m})\end{equation*}
 $\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_v) = \Gamma _t + \Gamma _v$
,
$\Gamma _{t \{x \setminus v\}} = +_{i \in I} \Gamma _i = +_{i \in I} (\Gamma ^i_t + \Gamma ^i_v) = \Gamma _t + \Gamma _v$
,
 $b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_v)$
,
$b = +_{i \in I} b_i = +_{i \in I} (b^i_t + b^i_v)$
,
 $m = +_{i \in I} m_i = +_{i \in I} (m^i_t + m^i_v)$
, and
$m = +_{i \in I} m_i = +_{i \in I} (m^i_t + m^i_v)$
, and
 $d = +_{i \in I} d_i = +_{i \in I} (d^i_t + d^i_v)$
.
$d = +_{i \in I} d_i = +_{i \in I} (d^i_t + d^i_v)$
.
-
– Rule (
 $\lambda _{\tt p}$
). Then,
$\lambda _{\tt p}$
). Then,
 $t = \lambda y.u$
,
$t = \lambda y.u$
,
 $\tau = {\tt a}$
, and
$\tau = {\tt a}$
, and
 $t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Moreover,
$t \{x \setminus v\} = \lambda y.(u \{x \setminus v\})$
. Moreover,
 $\Gamma _{t \{x \setminus v\}} = \emptyset$
and
$\Gamma _{t \{x \setminus v\}} = \emptyset$
and
 $b = m = d = 0$
. Therefore, we can build
$b = m = d = 0$
. Therefore, we can build
 $\Phi _t \triangleright \, {\emptyset } \Vdash ^{(0,0,0)}_{\tt v} {\lambda y.u}\;:\;{{\tt a}}$
using rule (
$\Phi _t \triangleright \, {\emptyset } \Vdash ^{(0,0,0)}_{\tt v} {\lambda y.u}\;:\;{{\tt a}}$
using rule (
 $\lambda _{\tt p}$
), such that
$\lambda _{\tt p}$
), such that
 $\Gamma _t = \emptyset$
,
$\Gamma _t = \emptyset$
,
 $\mathscr{M} = [ \, ]$
, and
$\mathscr{M} = [ \, ]$
, and
 $b_t = m_t = d_t = 0$
, and we can build
$b_t = m_t = d_t = 0$
, and we can build
 $\Phi _v\, \triangleright \, \Vdash ^{(0,0,0)}_{\tt v} {v}\;:\;{[ \, ]}$
, such that
$\Phi _v\, \triangleright \, \Vdash ^{(0,0,0)}_{\tt v} {v}\;:\;{[ \, ]}$
, such that
 $\Gamma _v = \emptyset$
and
$\Gamma _v = \emptyset$
and
 $b_v = m_v = d_v = 0$
, by using (m) with no premises. Thus, we can conclude with
$b_v = m_v = d_v = 0$
, by using (m) with no premises. Thus, we can conclude with
 $\Gamma _{t \{x \setminus v\}} = \emptyset = \Gamma _t + \Gamma _v$
, and
$\Gamma _{t \{x \setminus v\}} = \emptyset = \Gamma _t + \Gamma _v$
, and
 $b = 0 = b_t + b_v$
,
$b = 0 = b_t + b_v$
,
 $m = 0 = m_t + m_v$
, and
$m = 0 = m_t + m_v$
, and
 $d = 0 = d_t + d_v$
.
$d = 0 = d_t + d_v$
.
-
Lemma 20 (Quantitative subject expansion). Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
is a tight derivation, there exists
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
is a tight derivation, there exists
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, where
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, where
![]() ${\tt r} = {\beta _{{\tt v}}}$
implies
${\tt r} = {\beta _{{\tt v}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
Proof. We show a stronger statement of the form:
Let
![]() $(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
$(t,s) \rightsquigarrow _{{\tt r}} (u,q)$
, where
![]() ${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
${\tt r} \in \{{\beta _{{\tt v}}}, {\tt g}, {\tt s}\}$
. If
![]() $\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
,
$\Phi ' \triangleright \, \Gamma \Vdash ^{(b',m',d)}_{\tt v} (u,q):\kappa$
,
![]() $\Gamma$
is tight, and (
$\Gamma$
is tight, and (
![]() $\kappa$
is tight or
$\kappa$
is tight or
![]() $\neg {\tt val}(t)$
), then
$\neg {\tt val}(t)$
), then
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, where
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,d)}_{\tt v} (t,s):\kappa$
, where
![]() ${\tt r} ={\beta _{{\tt v}}}$
implies
${\tt r} ={\beta _{{\tt v}}}$
implies
![]() $b' = b - 1$
and
$b' = b - 1$
and
![]() $m' = m$
, while
$m' = m$
, while
![]() ${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
${\tt r} \in \{{\tt g}, {\tt s}\}$
implies
![]() $b'=b$
and
$b'=b$
and
![]() $m' = m - 1$
.
$m' = m - 1$
.
We proceed by induction on
![]() $(t, s) \rightsquigarrow _{{\tt v}} (u,q)$
:
$(t, s) \rightsquigarrow _{{\tt v}} (u,q)$
:
-
• Case
 $(t,s) = ((\lambda x.p) v,s) \rightsquigarrow _{{\beta _{{\tt v}}}} (p \{x \setminus v\}, s) = (u,q)$
. Then,
$(t,s) = ((\lambda x.p) v,s) \rightsquigarrow _{{\beta _{{\tt v}}}} (p \{x \setminus v\}, s) = (u,q)$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_{p \{x \setminus v\}},m_{p \{x \setminus v\}},d_{p \{x \setminus v\}})}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _{p \{x \setminus v\}} \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_{p \{x \setminus v\}},m_{p \{x \setminus v\}},d_{p \{x \setminus v\}})}_{\tt v} {p \{x \setminus v\}}\;:\;{\mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, such that
$\Pi _s \triangleright \Delta _s \Vdash ^{(b_s,m_s,d_s)}_{\tt v} s\;:\;\mathscr{T\;}$
, such that
 $\Gamma = \Gamma _{p \{x \setminus v\}} + \Delta _s$
,
$\Gamma = \Gamma _{p \{x \setminus v\}} + \Delta _s$
,
 $b' = b_{p \{x \setminus v\}} + b_s$
,
$b' = b_{p \{x \setminus v\}} + b_s$
,
 $m' = m_{p \{x \setminus v\}} +m_s$
, and
$m' = m_{p \{x \setminus v\}} +m_s$
, and
 $d' = d_{p \{x \setminus v\}}+d_s$
. By Lemma 51, there exist
$d' = d_{p \{x \setminus v\}}+d_s$
. By Lemma 51, there exist
 $\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;} \Rightarrow \kappa }$
and
 $\Phi _{v} \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
$\Phi _{v} \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}$
, such that
 $\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma _v$
,
$\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma _v$
,
 $b_{p \{x \setminus v\}} = b_p+b_v$
,
$b_{p \{x \setminus v\}} = b_p+b_v$
,
 $m_{p \{x \setminus v\}} = m_p+m_v$
, and
$m_{p \{x \setminus v\}} = m_p+m_v$
, and
 $d_{p \{x \setminus v\}} = d_p + d_v$
. Therefore, we can build
$d_{p \{x \setminus v\}} = d_p + d_v$
. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:
where
 $b = 1+b_p+b_v+b_s$
,
$b = 1+b_p+b_v+b_s$
,
 $m = m_p+m_v+m_s$
, and
$m = m_p+m_v+m_s$
, and
 $d = d_p+d_v+d_s$
. Thus, we can conclude with
$d = d_p+d_v+d_s$
. Thus, we can conclude with
 $\Gamma = \Gamma _{p \{x \setminus v\}} + \Delta _s = (\Gamma _p + \Gamma _v) + \Delta _s$
,
$\Gamma = \Gamma _{p \{x \setminus v\}} + \Delta _s = (\Gamma _p + \Gamma _v) + \Delta _s$
,
 $b' = b_{p \{x \setminus v\}} + b_s = b_p + b_v + b_s = (1 + b_p + b_v + b_s) - 1 = b - 1$
,
$b' = b_{p \{x \setminus v\}} + b_s = b_p + b_v + b_s = (1 + b_p + b_v + b_s) - 1 = b - 1$
,
 $m' = m_{p \{x \setminus v\}} + m_s = (m_p + m_v) + m_s = m$
, and
$m' = m_{p \{x \setminus v\}} + m_s = (m_p + m_v) + m_s = m$
, and
 $d' = d_{p \{x \setminus v\}} + d_s = (d_p + d_v) + d_s = d$
.
$d' = d_{p \{x \setminus v\}} + d_s = (d_p + d_v) + d_s = d$
. -
• Case
 $(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt v}} (p \{x \setminus v\},s) = (u,q)$
, such that
$(t,s) = ({\tt get}_{l}(\lambda x.p),s) \rightsquigarrow _{{\tt v}} (p \{x \setminus v\},s) = (u,q)$
, such that
 $q \equiv {\tt upd}_{l}(v,s') \equiv s$
. Then,
$q \equiv {\tt upd}_{l}(v,s') \equiv s$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _u \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_{p \{x \setminus v\}},m_{p \{x \setminus v\}},d_{p \{x \setminus v\}})}_{\tt v} {p \{x \setminus v\}}\;:\;{\{l \;:\; \mathscr{M}_2\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _u \triangleright \, {\Gamma _{p \{x \setminus v\}}} \Vdash ^{(b_{p \{x \setminus v\}},m_{p \{x \setminus v\}},d_{p \{x \setminus v\}})}_{\tt v} {p \{x \setminus v\}}\;:\;{\{l \;:\; \mathscr{M}_2\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _q$
, which must be of the following form:where
$\Pi _q$
, which must be of the following form:where \begin{equation*} \frac {\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}\qquad \Pi _{s'} \triangleright \, {\Delta _{s'}} \Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt v} {s'}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma ^2_v + \Delta _{s'} \Vdash ^{(b^2_v+b_{s'},m^2_v+m_{s'},d^2_v+d_{s'})} {\tt upd}_{l}(v,s'): \{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi ^2_v \triangleright \, {\Gamma ^2_v} \Vdash ^{(b^2_v,m^2_v,d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_2}\qquad \Pi _{s'} \triangleright \, {\Delta _{s'}} \Vdash ^{(b_{s'},m_{s'},d_{s'})}_{\tt v} {s'}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma ^2_v + \Delta _{s'} \Vdash ^{(b^2_v+b_{s'},m^2_v+m_{s'},d^2_v+d_{s'})} {\tt upd}_{l}(v,s'): \{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
 $\Gamma = \Gamma _{p \{x \setminus v\}} + (\Gamma ^2_v + \Delta _{s'})$
,
$\Gamma = \Gamma _{p \{x \setminus v\}} + (\Gamma ^2_v + \Delta _{s'})$
,
 $b' = b_{p \{x \setminus v\}} + b^2_v + b_{s'}$
,
$b' = b_{p \{x \setminus v\}} + b^2_v + b_{s'}$
,
 $m' = m_{p \{x \setminus v\}} + b^2_v + b_{s'}$
, and
$m' = m_{p \{x \setminus v\}} + b^2_v + b_{s'}$
, and
 $d' = d_{p \{x \setminus v\}} +d^2_v+d_{s'}$
. By Lemma 51, there exist
$d' = d_{p \{x \setminus v\}} +d^2_v+d_{s'}$
. By Lemma 51, there exist
 $\Phi _p \triangleright \, {(b_p,m_p,d_p)} \Vdash ^{\Gamma _p;\; x \;:\; \mathscr{M}_1}_{\tt v} {p}\;:\;{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _p \triangleright \, {(b_p,m_p,d_p)} \Vdash ^{\Gamma _p;\; x \;:\; \mathscr{M}_1}_{\tt v} {p}\;:\;{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
 $\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
$\Phi ^1_v \triangleright \, {\Gamma ^1_v} \Vdash ^{(b^1_v,m^1_v,d^1_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1}$
, such that
 $\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^1_v$
,
$\Gamma _{p \{x \setminus v\}} = \Gamma _p + \Gamma ^1_v$
,
 $b_{p \{x \setminus v\}} = b_p + b^1_v$
,
$b_{p \{x \setminus v\}} = b_p + b^1_v$
,
 $m_{p \{x \setminus v\}} = m_p + m^1_v$
, and
$m_{p \{x \setminus v\}} = m_p + m^1_v$
, and
 $d_{p \{x \setminus u\}} = d_p + d^1_v$
. Therefore, we can build
$d_{p \{x \setminus u\}} = d_p + d^1_v$
. Therefore, we can build
 $\Phi _t$
as follows:By Lemma 47, there exists
$\Phi _t$
as follows:By Lemma 47, there exists \begin{equation*} \frac {\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }}{\Gamma _p \Vdash ^{(b_p,1+m_p,d_p)} {\tt get}_{l}(\lambda x.p): \{l \;:\; {\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
\begin{equation*} \frac {\Phi _p \triangleright \, {\Gamma _p;\; x \;:\; \mathscr{M}_1} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\{l \;:\; {\mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }}{\Gamma _p \Vdash ^{(b_p,1+m_p,d_p)} {\tt get}_{l}(\lambda x.p): \{l \;:\; {\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }({\tt get})\end{equation*}
 $\Phi _v \triangleright \, {\Gamma ^1_v + \Gamma ^2_v} \Vdash ^{(b^1_v+b^2_v,m^1_v+m^2_v,d^1_v+d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1 \sqcup \mathscr{M}_2}$
. Therefore, we can build an alternative derivation
$\Phi _v \triangleright \, {\Gamma ^1_v + \Gamma ^2_v} \Vdash ^{(b^1_v+b^2_v,m^1_v+m^2_v,d^1_v+d^2_v)}_{\tt v} {v}\;:\;{\mathscr{M}_1 \sqcup \mathscr{M}_2}$
. Therefore, we can build an alternative derivation
 $\Pi '_q$
for
$\Pi '_q$
for
 $q$
as follows:Then, we can pick
$q$
as follows:Then, we can pick \begin{equation*} \frac {\Phi _v \qquad \Pi _{s'}}{(\Gamma ^1_v + \Gamma ^2_v) + \Delta _{s'} \Vdash ^{(b^1_v+b^2_v+b_{s'},m^1_v+m^2_v+m_{s'},d^1_v+d^2_v+d_{s'})} {\tt upd}_{l}(v,s'): \{l :{\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
\begin{equation*} \frac {\Phi _v \qquad \Pi _{s'}}{(\Gamma ^1_v + \Gamma ^2_v) + \Delta _{s'} \Vdash ^{(b^1_v+b^2_v+b_{s'},m^1_v+m^2_v+m_{s'},d^1_v+d^2_v+d_{s'})} {\tt upd}_{l}(v,s'): \{l :{\mathscr{M}_1 \sqcup \mathscr{M}_2 \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd})\end{equation*}
 $\Pi _s = \Pi '_q$
and build
$\Pi _s = \Pi '_q$
and build
 $\Phi$
as follows:where
$\Phi$
as follows:where \begin{equation*} \frac {\Phi _t\qquad \Pi _s}{\Gamma _p + (\Gamma ^1_v + \Gamma ^2_v) + \Delta _{s'} \Vdash ^{(b_p+b^1_v+b^2_v+b_{s'},1+m_p+m^1_v+m^2_v+m_{s'},d_p+d^1_v+d^2_v+d_{s'})} ({\tt get}_{l}(\lambda x.p), s): \kappa }({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _t\qquad \Pi _s}{\Gamma _p + (\Gamma ^1_v + \Gamma ^2_v) + \Delta _{s'} \Vdash ^{(b_p+b^1_v+b^2_v+b_{s'},1+m_p+m^1_v+m^2_v+m_{s'},d_p+d^1_v+d^2_v+d_{s'})} ({\tt get}_{l}(\lambda x.p), s): \kappa }({\tt conf})\end{equation*}
 $b = b_p+b^1_v+b^2_v+b_{s'}$
,
$b = b_p+b^1_v+b^2_v+b_{s'}$
,
 $m = 1+m_p+m^1_v+m^2_v+m_{s'}$
, and
$m = 1+m_p+m^1_v+m^2_v+m_{s'}$
, and
 $d = d_p+d^1_v+d^2_v+d_{s'}$
. Thus, we can conclude with
$d = d_p+d^1_v+d^2_v+d_{s'}$
. Thus, we can conclude with
 $\Gamma = \Gamma _{p \{x \setminus v\}} + (\Gamma ^2_v + \Delta _{s'}) = \Gamma _p + \Gamma ^1_v + \Gamma ^2_v + \Delta _{s'}$
,
$\Gamma = \Gamma _{p \{x \setminus v\}} + (\Gamma ^2_v + \Delta _{s'}) = \Gamma _p + \Gamma ^1_v + \Gamma ^2_v + \Delta _{s'}$
,
 $b' = b_{p \{x \setminus v\}} + b^2_v + b_{s'} = b_p + b^1_v + b^2_v + b_{s'} = b$
, and
$b' = b_{p \{x \setminus v\}} + b^2_v + b_{s'} = b_p + b^1_v + b^2_v + b_{s'} = b$
, and
 $m' = m_{p \{x \setminus v\}} + m^2_v + m_{s'} = m_p + m^1_v + m^2_v + m_{s'} = (1 + m_p + m^1_v + m^2_v + m_{s'}) - 1 = m - 1$
,
$m' = m_{p \{x \setminus v\}} + m^2_v + m_{s'} = m_p + m^1_v + m^2_v + m_{s'} = (1 + m_p + m^1_v + m^2_v + m_{s'}) - 1 = m - 1$
,
 $d' = d_{p \{x \setminus v\}} + d^2_v + d_{s'} = d_p + d^1_v + d^2_v + d_{s'} = d$
.
$d' = d_{p \{x \setminus v\}} + d^2_v + d_{s'} = d_p + d^1_v + d^2_v + d_{s'} = d$
.
-
• Case
 $(t,s) = ({\tt set}_{l}(v,p),s) \rightsquigarrow _{{\tt v}} (p, {\tt upd}_{l}(v,s)) = (u,q)$
. Then,
$(t,s) = ({\tt set}_{l}(v,p),s) \rightsquigarrow _{{\tt v}} (p, {\tt upd}_{l}(v,s)) = (u,q)$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _p \triangleright \, {\Gamma _p} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
$\Phi _p \triangleright \, {\Gamma _p} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;} \Rightarrow \kappa }$
and
 $\Pi _q$
, which must be of the following form:where
$\Pi _q$
, which must be of the following form:where \begin{equation*} \frac {\Phi _{v} \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}\qquad \Pi _{s} \triangleright \, {\Delta _s} \Vdash ^{(b_s,m_s,d_s)}_{\tt v} {s}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma _v + \Delta _s \Vdash ^{(b_v+b_s,m_v+m_s,d_v+d_s)} {\tt upd}_{l}(v,s): \{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd}) \end{equation*}
\begin{equation*} \frac {\Phi _{v} \triangleright \, {\Gamma _v} \Vdash ^{(b_v,m_v,d_v)}_{\tt v} {v}\;:\;{\mathscr{M}}\qquad \Pi _{s} \triangleright \, {\Delta _s} \Vdash ^{(b_s,m_s,d_s)}_{\tt v} {s}\;:\;{{\{l\;:\;\mathscr{L\;}\};\;}\mathscr{T\;}}}{\Gamma _v + \Delta _s \Vdash ^{(b_v+b_s,m_v+m_s,d_v+d_s)} {\tt upd}_{l}(v,s): \{l \;:\; {\mathscr{M} \cdot \mathscr{L\;}}\};\; \mathscr{T\;}}({\tt upd}) \end{equation*}
 $\Gamma = \Gamma _p + (\Gamma _v + \Delta _s)$
,
$\Gamma = \Gamma _p + (\Gamma _v + \Delta _s)$
,
 $b' = b_p + b_v + b_s$
,
$b' = b_p + b_v + b_s$
,
 $m' = m_p + m_v + m_s$
, and
$m' = m_p + m_v + m_s$
, and
 $d' = d_p + d_v + d_s$
. Therefore, we can build
$d' = d_p + d_v + d_s$
. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:

where
 $b =b_v+b_p+b_s$
,
$b =b_v+b_p+b_s$
,
 $m = 1+m_v+m_p+m_s$
, and
$m = 1+m_v+m_p+m_s$
, and
 $d = d_v+d_p+d_s$
. Thus, we can conclude with
$d = d_v+d_p+d_s$
. Thus, we can conclude with
 $\Gamma = \Gamma _p + (\Gamma _v + \Delta _s)$
,
$\Gamma = \Gamma _p + (\Gamma _v + \Delta _s)$
,
 $b' = b_v+b_p+b_s = b$
,
$b' = b_v+b_p+b_s = b$
,
 $m' + 1 = (m_p + m_v + m_s) + 1 = m$
, and
$m' + 1 = (m_p + m_v + m_s) + 1 = m$
, and
 $d' = d_v+d_p+d_s = d$
.
$d' = d_v+d_p+d_s = d$
. -
• Case
 $(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (p'r,q) = (u,q)$
, such that
$(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (p'r,q) = (u,q)$
, such that
 $(p,s) \rightsquigarrow _{{\tt v}} (p',q)$
. Then,
$(p,s) \rightsquigarrow _{{\tt v}} (p',q)$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _{p'r}$
and
$\Phi _{p'r}$
and
 $\Pi _q \triangleright \, {\Delta _q} \Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\;:\;{\mathscr{T\;}}$
, and
$\Pi _q \triangleright \, {\Delta _q} \Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\;:\;{\mathscr{T\;}}$
, and
 $\Phi _{p'r}$
must end with rule (@), (@
$\Phi _{p'r}$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _{p'r}$
ends with (@). Then,
$\Phi _{p'r}$
ends with (@). Then,
 $\Phi _{p'r}$
must be of the following form:
$\Phi _{p'r}$
must be of the following form:
where
 $\Gamma = (\Gamma _{p'} + \Gamma _r) + \Delta _q$
,
$\Gamma = (\Gamma _{p'} + \Gamma _r) + \Delta _q$
,
 $b' = 1+b_{p'}+b_r + b_q$
,
$b' = 1+b_{p'}+b_r + b_q$
,
 $m' = m_{p'}+m_r + m_q$
, and
$m' = m_{p'}+m_r + m_q$
, and
 $d' = d_{p'}+d_r + d_q$
. Then, we can build
$d' = d_{p'}+d_r + d_q$
. Then, we can build
 $\Phi _{(p',q)}$
as follows:Notice that
$\Phi _{(p',q)}$
as follows:Notice that \begin{equation*} \frac {\Phi _{p'}\qquad \Pi _s}{\Gamma _{p'} + \Delta _{q} \Vdash ^{(b_{p'}+b_s,m_{p'}+m_s,d_{p'}+d_s)} (p',q): ((\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{p'}\qquad \Pi _s}{\Gamma _{p'} + \Delta _{q} \Vdash ^{(b_{p'}+b_s,m_{p'}+m_s,d_{p'}+d_s)} (p',q): ((\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}')}({\tt conf})\end{equation*}
 $\neg {\tt val}(p)$
, since
$\neg {\tt val}(p)$
, since
 $(p, s) \rightsquigarrow _{{\tt v}} (p',q)$
. By applying the i.h. to
$(p, s) \rightsquigarrow _{{\tt v}} (p',q)$
. By applying the i.h. to
 $\Phi _{(p',q)}$
, there exists
$\Phi _{(p',q)}$
, there exists
 $\Phi _{(p,s)}$
that must be of the following form:
$\Phi _{(p,s)}$
that must be of the following form:

where
 $\Gamma _{p'} + \Delta _q = \Gamma _p + \Delta _s$
, and the counters
$\Gamma _{p'} + \Delta _q = \Gamma _p + \Delta _s$
, and the counters
 $(b_p+b_s,m_p+m_s,d_p+d_s)$
and
$(b_p+b_s,m_p+m_s,d_p+d_s)$
and
 $(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are related properly. Therefore, we can build
$(b_{p'}+b_q,m_{p'}+m_q,d_{p'}+d_q)$
are related properly. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:
where
 $b = 1+b_p+b_r+b_s$
,
$b = 1+b_p+b_r+b_s$
,
 $m = m_p+m_r+m_s$
, and
$m = m_p+m_r+m_s$
, and
 $d = d_p+d_r+d_s$
. Thus, we can conclude with
$d = d_p+d_r+d_s$
. Thus, we can conclude with
 $\Gamma = (\Gamma _p + \Gamma _r) + \Delta _s = (\Gamma _{p'} + \Gamma _r) + \Delta _q$
, and
$\Gamma = (\Gamma _p + \Gamma _r) + \Delta _s = (\Gamma _{p'} + \Gamma _r) + \Delta _q$
, and
 $(1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s) = (b,m,d)$
and
$(1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s) = (b,m,d)$
and
 $(b',m',d') = (1+b_{p'}+b_r+b_q,m_{p'}+m_r+m_q,d_{p'}+d_r+d_q)$
are properly related.
$(b',m',d') = (1+b_{p'}+b_r+b_q,m_{p'}+m_r+m_q,d_{p'}+d_r+d_q)$
are properly related. -
– Case
 $\Phi _{p'r}$
ends with rule (@
$\Phi _{p'r}$
ends with rule (@
 $^1_{{\tt p}}$
) and (@
$^1_{{\tt p}}$
) and (@
 $^2_{{\tt p}}$
). These cases are very similar to the previous case.
$^2_{{\tt p}}$
). These cases are very similar to the previous case.
-
-
• Case
 $(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (pr',q) = (u,q)$
, such that
$(t,s) = (pr,s) \rightsquigarrow _{{\tt v}} (pr',q) = (u,q)$
, such that
 $(p,s) \not \rightsquigarrow _{{\tt v}}$
,
$(p,s) \not \rightsquigarrow _{{\tt v}}$
,
 $(p,s)$
is unblocked, and
$(p,s)$
is unblocked, and
 $(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. Then,
$(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. Then,
 $\Phi '$
has two premises
$\Phi '$
has two premises
 $\Phi _{pr'}$
and
$\Phi _{pr'}$
and
 $\Pi _q \triangleright \, {\Delta _q} \Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\;:\;{\mathscr{T\;}}$
, and
$\Pi _q \triangleright \, {\Delta _q} \Vdash ^{(b_q,m_q,d_q)}_{\tt v} {q}\;:\;{\mathscr{T\;}}$
, and
 $\Phi _{pr'}$
must end with rule (@), (@
$\Phi _{pr'}$
must end with rule (@), (@
 $^1_{{\tt p}}$
), or (@
$^1_{{\tt p}}$
), or (@
 $^2_{{\tt p}}$
):
$^2_{{\tt p}}$
):-
– Case
 $\Phi _{pr'}$
ends with (@). Then,
$\Phi _{pr'}$
ends with (@). Then,
 $\Phi _{pr'}$
must be of the following form:
$\Phi _{pr'}$
must be of the following form:
‘’ where
 $\Gamma = (\Gamma _{p} + \Gamma _{r'}) + \Delta _q$
,
$\Gamma = (\Gamma _{p} + \Gamma _{r'}) + \Delta _q$
,
 $b' = 1+b_p+b_{r'}+b_q$
,
$b' = 1+b_p+b_{r'}+b_q$
,
 $m' = m_p+m_{r'}+m_q$
, and
$m' = m_p+m_{r'}+m_q$
, and
 $d' = d_p+d_{r'}+d_q$
. Notice that, since
$d' = d_p+d_{r'}+d_q$
. Notice that, since
 $(p, s) \not \rightsquigarrow _{{\tt v}}$
and
$(p, s) \not \rightsquigarrow _{{\tt v}}$
and
 $(p,s)$
is unblocked (therefore
$(p,s)$
is unblocked (therefore
 $(p,s)$
is an unblocked normal configuration), then
$(p,s)$
is an unblocked normal configuration), then
 $p \in {\tt no}_{{\tt v}}$
, by definition and Proposition5. Therefore,
$p \in {\tt no}_{{\tt v}}$
, by definition and Proposition5. Therefore,
 $\mathscr{T\;} = \mathscr{T\;}'$
, according to Lemma 15. And, we can build
$\mathscr{T\;} = \mathscr{T\;}'$
, according to Lemma 15. And, we can build
 $\Phi _{(r',q)}$
as follows:Since
$\Phi _{(r',q)}$
as follows:Since \begin{equation*} \frac {\Phi _{r'}\qquad \Pi _q}{\Gamma _{r'} + \Delta _q \Vdash ^{(b_{r'}+b_q,m_{r'}+m_q,d_{r'}+d_q)} (r',q): (\mathscr{M} \times \mathscr{T\;}'')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _{r'}\qquad \Pi _q}{\Gamma _{r'} + \Delta _q \Vdash ^{(b_{r'}+b_q,m_{r'}+m_q,d_{r'}+d_q)} (r',q): (\mathscr{M} \times \mathscr{T\;}'')}({\tt conf})\end{equation*}
 $\Gamma$
is tight, then
$\Gamma$
is tight, then
 $\Gamma _{r'}$
and
$\Gamma _{r'}$
and
 $\Delta _q$
are both tight. Moreover,
$\Delta _q$
are both tight. Moreover,
 $\neg {\tt val}(r)$
, since
$\neg {\tt val}(r)$
, since
 $(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. By applying the i.h. to
$(r,s) \rightsquigarrow _{{\tt v}} (r',q)$
. By applying the i.h. to
 $\Phi _{(r',q)}$
, there exists
$\Phi _{(r',q)}$
, there exists
 $\Phi _{(r,s)}$
, which must be of the following form:where
$\Phi _{(r,s)}$
, which must be of the following form:where \begin{equation*} \frac {\Phi _r \triangleright \, {\Gamma _r} \Vdash ^{(b_r,m_r,d_r)}_{\tt v} {r}\;:\;{\mathscr{T\;}''' \Rightarrow (\mathscr{M} \times \mathscr{T\;}'')}\qquad \Pi _s \triangleright \, {\Delta _s} \Vdash ^{(b_s,m_s,d_s)}_{\tt v} {s}\;:\;{\mathscr{T\;}'''}}{\Gamma _r + \Delta _s \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} (r,s): (\mathscr{M} \times \mathscr{T\;}'')}({\tt conf})\end{equation*}
\begin{equation*} \frac {\Phi _r \triangleright \, {\Gamma _r} \Vdash ^{(b_r,m_r,d_r)}_{\tt v} {r}\;:\;{\mathscr{T\;}''' \Rightarrow (\mathscr{M} \times \mathscr{T\;}'')}\qquad \Pi _s \triangleright \, {\Delta _s} \Vdash ^{(b_s,m_s,d_s)}_{\tt v} {s}\;:\;{\mathscr{T\;}'''}}{\Gamma _r + \Delta _s \Vdash ^{(b_r+b_s,m_r+m_s,d_r+d_s)} (r,s): (\mathscr{M} \times \mathscr{T\;}'')}({\tt conf})\end{equation*}
 $\Gamma _{r'} + \Delta _q = \Gamma _{r} + \Delta _s$
, and
$\Gamma _{r'} + \Delta _q = \Gamma _{r} + \Delta _s$
, and
 $(b_{r'}+b_q,m_{r'}+m_q,d_{r'}+d_q)$
and
$(b_{r'}+b_q,m_{r'}+m_q,d_{r'}+d_q)$
and
 $(b_r+b_s,m_r+m_s,d_r+d_s)$
are related properly. Moreover, there exists
$(b_r+b_s,m_r+m_s,d_r+d_s)$
are related properly. Moreover, there exists
 $\Phi '_p \triangleright \, {\Gamma _p} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}''' \Rightarrow (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}'''}$
, by Lemma 15. Therefore, we can build
$\Phi '_p \triangleright \, {\Gamma _p} \Vdash ^{(b_p,m_p,d_p)}_{\tt v} {p}\;:\;{\mathscr{T\;}''' \Rightarrow (\mathscr{M} \rightarrow (\mathscr{T\;}'' \Rightarrow \kappa )) \times \mathscr{T\;}'''}$
, by Lemma 15. Therefore, we can build
 $\Phi$
as follows:
$\Phi$
as follows:

where
 $b = 1+b_p+b_r+b_s$
,
$b = 1+b_p+b_r+b_s$
,
 $m = m_p+m_r+m_s$
, and
$m = m_p+m_r+m_s$
, and
 $d = d_p+d_r+d_s$
. Thus, we can conclude with
$d = d_p+d_r+d_s$
. Thus, we can conclude with
 $\Gamma = (\Gamma _p + \Gamma _{r'}) + \Delta _q = (\Gamma _p + \Gamma _r) + \Delta _s$
, and
$\Gamma = (\Gamma _p + \Gamma _{r'}) + \Delta _q = (\Gamma _p + \Gamma _r) + \Delta _s$
, and
 $(1+b_p+b_{r'}+b_q, m_p+m_{r'}+m_q, d_p+d_{r'}+d_q) = (b',m',d')$
and
$(1+b_p+b_{r'}+b_q, m_p+m_{r'}+m_q, d_p+d_{r'}+d_q) = (b',m',d')$
and
 $(b, m,d) = (1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)$
are properly related.
$(b, m,d) = (1+b_p+b_r+b_s,m_p+m_r+m_s,d_p+d_r+d_s)$
are properly related. -
– Case
 $\Phi _{pr'}$
ends with (@
$\Phi _{pr'}$
ends with (@
 $^1_{{\tt p}}$
) or (@
$^1_{{\tt p}}$
) or (@
 $^2_{{\tt p}}$
). These two cases are very similar to the previous case.
$^2_{{\tt p}}$
). These two cases are very similar to the previous case.
-
Theorem 6 (Quantitative completeness). If
![]() $(t,s) \rightsquigarrow _{\tt v}^{(b,m,d)} (u,q)$
and
$(t,s) \rightsquigarrow _{\tt v}^{(b,m,d)} (u,q)$
and
![]() $u \in {\tt no}_{{\tt v}}$
, then there exists a tight derivation
$u \in {\tt no}_{{\tt v}}$
, then there exists a tight derivation
![]() $\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {v}})}_{\tt v} (t,s):\kappa$
.
$\Phi \triangleright \, \Gamma \Vdash ^{(b,m,|{(u,q)}|_{\texttt {v}})}_{\tt v} (t,s):\kappa$
.
Proof.
By induction on
![]() $b + m$
:
$b + m$
:
-
• Case
 $b + m = 0$
. Then,
$b + m = 0$
. Then,
 $b = m = 0$
, and thus,
$b = m = 0$
, and thus,
 $(t,s)=(u,q)$
. Therefore,
$(t,s)=(u,q)$
. Therefore,
 $t \in {\tt no}_{{\tt v}}$
. Thus, we can conclude by Lemma 18.
$t \in {\tt no}_{{\tt v}}$
. Thus, we can conclude by Lemma 18. -
• Case
 $b + m \gt 0$
. Then, there exists
$b + m \gt 0$
. Then, there exists
 $(t',s')$
, such that
$(t',s')$
, such that
 $(t,s) \rightsquigarrow _{{\tt v}}^{(1,0)} (t',s') \rightsquigarrow _{\tt v}^{(b-1,m)} (u,q)$
or
$(t,s) \rightsquigarrow _{{\tt v}}^{(1,0)} (t',s') \rightsquigarrow _{\tt v}^{(b-1,m)} (u,q)$
or
 $(t,s) \rightsquigarrow _{{\tt v}}^{(0,1)} (t',s') \rightsquigarrow _{\tt v}^{(b,m-1)} (u,q)$
. By the i.h., there exists
$(t,s) \rightsquigarrow _{{\tt v}}^{(0,1)} (t',s') \rightsquigarrow _{\tt v}^{(b,m-1)} (u,q)$
. By the i.h., there exists
 $\Phi ' \triangleright \,{\Gamma } \Vdash ^{(b',m',|{(u,q)}|_{\texttt {v}})}_{\tt v} {(t',s')}\;:\;{\kappa }$
tight, such that
$\Phi ' \triangleright \,{\Gamma } \Vdash ^{(b',m',|{(u,q)}|_{\texttt {v}})}_{\tt v} {(t',s')}\;:\;{\kappa }$
tight, such that
 $b' + m' = b + m - 1$
. By Lemma 20, we have
$b' + m' = b + m - 1$
. By Lemma 20, we have
 $\Phi \triangleright {\Gamma } \Vdash ^{(b'',m'',|{(u,q)}|_{\texttt {v}})}_{\tt v} {(t,s)}\;:\;{\kappa }$
tight, such that
$\Phi \triangleright {\Gamma } \Vdash ^{(b'',m'',|{(u,q)}|_{\texttt {v}})}_{\tt v} {(t,s)}\;:\;{\kappa }$
tight, such that
 $b'' + m'' = 1+ b' + m'$
. Therefore,
$b'' + m'' = 1+ b' + m'$
. Therefore,
 $b'' + m'' = b + m$
, since the fact that
$b'' + m'' = b + m$
, since the fact that
 $b'' = b$
, and
$b'' = b$
, and
 $m'' = m$
can be easily checked by a simple case analysis.
$m'' = m$
can be easily checked by a simple case analysis.