No CrossRef data available.
Article contents
Semantical proofs of correctness for programs performing non-deterministic tests on real numbers
Published online by Cambridge University Press: 27 October 2010
Abstract
We consider a functional language that performs non-deterministic tests on real numbers and define a denotational semantics for that language based on Smyth powerdomains. The semantics is only an approximate one because the denotation of a program for a real number may not be precise enough to tell which real number the program computes. However, for many first-order total functions f : 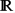 n →
n → 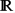 , there exists a program for f whose denotation is precise enough to show that the program indeed computes the function f. In practice, it is not difficult to find programs like this that possess a faithful denotation. We provide a few examples of such programs and the corresponding proofs of correctness.
, there exists a program for f whose denotation is precise enough to show that the program indeed computes the function f. In practice, it is not difficult to find programs like this that possess a faithful denotation. We provide a few examples of such programs and the corresponding proofs of correctness.
Information
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 20 , Special Issue 5: Theory and Applications of Models of Computation (TAMC 2008–2009) , October 2010 , pp. 723 - 751
- Copyright
- Copyright © Cambridge University Press 2010

