Hostname: page-component-89b8bd64d-5bvrz Total loading time: 0 Render date: 2026-05-07T20:38:04.936Z Has data issue: false hasContentIssue false
  • English
  • Français

Set-syllogistics meet combinatorics

Published online by Cambridge University Press:  11 May 2015

EUGENIO G. OMODEO ,
ALBERTO POLICRITI  and
ALEXANDRU I. TOMESCU
EUGENIO G. OMODEO
Affiliation:
Dipartimento di Matematica e Geoscienze, Università di Trieste, Via Valerio 12/1, I-34127, Trieste, Italy Email: eomodeo@units.it
ALBERTO POLICRITI
Affiliation:
Dipartimento di Matematica e Informatica, Università di Udine, Via delle Scienze 206, I-33100, Udine, Italy Email: alberto.policriti@uniud.it
ALEXANDRU I. TOMESCU
Affiliation:
Helsinki Institute for Information Technology HIIT, Department of Computer Science, University of Helsinki, P.O. 68 (Gustaf Hällströmin katu 2b), FI-00014, Helsinki, Finland Email: tomescu@cs.helsinki.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers ∃*∀* prenex sentences of pure first-order predicate calculus with equality. This is the set of formulas which Ramsey's treated in a famous article of 1930. We demonstrate that the satisfiability problem and the problem of existence of arbitrarily large models for these formulas can be reduced to the satisfiability problem for ∃*∀* prenex sentences of Set Theory (in the relators ∈, =).

We present two satisfiability-preserving (in a broad sense) translations Φ ↦ 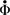$\dot{\Phi}$ and Φ ↦ Φσ of ∃*∀* sentences from pure logic to well-founded Set Theory, so that if 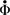$\dot{\Phi}$ is satisfiable (in the domain of Set Theory) then so is Φ, and if Φσ is satisfiable (again, in the domain of Set Theory) then Φ can be satisfied in arbitrarily large finite structures of pure logic.

It turns out that | 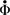$\dot{\Phi}$ | = 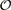$\mathcal{O}$ (|Φ|) and |Φσ| = 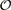$\mathcal{O}$ (|Φ|2).

Our main result makes use of the fact that ∃*∀* sentences, even though constituting a decidable fragment of Set Theory, offer ways to describe infinite sets. Such a possibility is exploited to glue together infinitely many models of increasing cardinalities of a given ∃*∀* logical formula, within a single pair of infinite sets.

Information

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Special Issue 2: Special Issue: XIV ICTCS , February 2017 , pp. 296 - 310
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Börger, E., Grädel, E. and Gurevich, Y. (1997). The Classical Decision Problem, Perspectives in Mathematical Logic, Springer.Google Scholar
Breban, M., Ferro, A., Omodeo, E. G. and Schwartz, J. T. (1981). Decision Procedures for elementary sublanguages of set theory. II: Formulas involving restricted quantifiers, together with ordinal, integer, map, and domain notions. Communications on Pure and Applied Mathematics 34 177–195.Google Scholar
Cantone, D. (2012). Decision procedures for elementary sublanguages of set theory. XVII. Commonly occurring decidable extensions of multi-level syllogistic. In: Davis, M. and Schonberg, Ed (eds.) From Linear Operators to Computational Biology: Essays in Memory of Jacob T. Schwartz, Springer 131–167.Google Scholar
Cantone, D., Omodeo, E. G. and Policriti, A. (2001). Set Theory for Computing. From Decision Procedures to Declarative Programming with Sets, Monographs in Computer Science, Springer-Verlag.Google Scholar
Ferro, A., Omodeo, E. G. and Schwartz, J. T. (1980). Decision procedures for elementary sublanguages of set theory. I. Multi-level syllogistic and some extensions. Communications on Pure and Applied Mathematics 33 (5) 599–608.Google Scholar
Omodeo, E. G. and Policriti, A. (1995). Solvable set/hyperset contexts: I. Some decision procedures for the pure, finite case. Communications on Pure and Applied Mathematics 48 (9-10) 1123–1155. (Special issue in honor of Jacob T. Schwartz.)Google Scholar
Omodeo, E. G. and Policriti, A. (2010). The Bernays-Schönfinkel-Ramsey class for set theory: Semidecidability. Journal of Symbolic Logic 75 (2) 459–480.Google Scholar
Omodeo, E. G. and Policriti, A. (2012). The Bernays-Schönfinkel-Ramsey class for set theory: Decidability. Journal of Symbolic Logic 77 (3) 896–918.Google Scholar
Omodeo, E. G. and Tomescu, A. I. (2014). Set graphs. III. Proof pearl: Claw-free graphs mirrored into transitive hereditarily finite sets. Journal of Automated Reasoning 52 (1) 1–29. doi: 10.1007/s10817-012-9272-3.CrossRefGoogle Scholar
Omodeo, E. G., Policriti, A. and Tomescu, A. I. (2009). Statements of ill-founded infinity in set theory. In: Cégielski, P. (ed.) Studies in Weak Arithmetics, No. 196 in Lecture Notes, Center for the Study of Language and Information, Stanford University 173–199.Google Scholar
Omodeo, E. G., Policriti, A. and Tomescu, A. I. (2012). Infinity, in short. Journal of Logic and Computation 22 (6) 1391–1403.Google Scholar
Parlamento, F. and Policriti, A. (1988). The logically simplest form of the infinity axiom. Proceedings of the American Mathematical Society 103 (1) 274–276.Google Scholar
Parlamento, F. and Policriti, A. (1991). Expressing innity without foundation. The Journal of Symbolic Logic 56 1230–1235.Google Scholar
Parlamento, F. and Policriti, A. (1993). Undecidability results for restricted universally quantified formulae of set theory. Communications on Pure and Applied Mathematics 46 (1) 57–73.Google Scholar
Plummer, D. and Lovász, L. (1986). Matching Theory, North-Holland Mathematics Studies, Elsevier Science.Google Scholar
Radziszowski, S. P. (2014). Small Ramsey numbers. The Electronic Journal of Combinatorics. Submitted: June 11, 1994; Revision #14: January 12, 2014.Google Scholar
Ramsey, F. P. (1930). On a problem of formal logic. Proceedings of the London Mathematical Society 30 264–286. (Read on December 13, 1928.)Google Scholar
Schwartz, J. T., Cantone, D. and Omodeo, E. G. (2011). Computational Logic and Set Theory – Applying Formalized Logic to Analysis, Springer.CrossRefGoogle Scholar