No CrossRef data available.
Article contents
Unique decomposition of homogeneous languages and application to isothetic regions
Published online by Cambridge University Press: 10 October 2018
Abstract
A language is said to be homogeneous when all its words have the same length. Homogeneous languages thus form a monoid under concatenation. It becomes freely commutative under the simultaneous actions of every permutation group 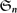 on the collection of homogeneous languages of length n ∈ ℕ. One recovers the isothetic regions from (Haucourt 2017, to appear (online since October 2017)) by considering the alphabet of connected subsets of the space |G|, viz the geometric realization of a finite graph G. Factoring the geometric model of a conservative program amounts to parallelize it, and there exists an efficient factoring algorithm for isothetic regions. Yet, from the theoretical point of view, one wishes to go beyond the class of conservative programs, which implies relaxing the finiteness hypothesis on the graph G. Provided that the collections of n-dimensional isothetic regions over G (denoted by
on the collection of homogeneous languages of length n ∈ ℕ. One recovers the isothetic regions from (Haucourt 2017, to appear (online since October 2017)) by considering the alphabet of connected subsets of the space |G|, viz the geometric realization of a finite graph G. Factoring the geometric model of a conservative program amounts to parallelize it, and there exists an efficient factoring algorithm for isothetic regions. Yet, from the theoretical point of view, one wishes to go beyond the class of conservative programs, which implies relaxing the finiteness hypothesis on the graph G. Provided that the collections of n-dimensional isothetic regions over G (denoted by  |G|) are co-unital distributive lattices, the prime decomposition of isothetic regions is given by an algorithm which is, unfortunately, very inefficient. Nevertheless, if the collections
|G|) are co-unital distributive lattices, the prime decomposition of isothetic regions is given by an algorithm which is, unfortunately, very inefficient. Nevertheless, if the collections  |G| satisfy the stronger property of being Boolean algebras, then the efficient factoring algorithm is available again. We relate the algebraic properties of the collections
|G| satisfy the stronger property of being Boolean algebras, then the efficient factoring algorithm is available again. We relate the algebraic properties of the collections  |G| to the geometric properties of the space |G|. On the way, the algebraic structure
|G| to the geometric properties of the space |G|. On the way, the algebraic structure  |G| is proven to be the universal tensor product, in the category of semilattices with zero, of n copies of the algebraic structure
|G| is proven to be the universal tensor product, in the category of semilattices with zero, of n copies of the algebraic structure  |G|.
|G|.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2018

