No CrossRef data available.
Article contents
CONTROLLING LIPSCHITZ FUNCTIONS
Published online by Cambridge University Press: 02 August 2018
Abstract
Given any positive integers 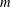 $m$ and
$m$ and 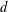 $d$, we say a sequence of points
$d$, we say a sequence of points 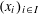 $(x_{i})_{i\in I}$ in
$(x_{i})_{i\in I}$ in 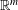 $\mathbb{R}^{m}$ is Lipschitz-
$\mathbb{R}^{m}$ is Lipschitz-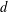 $d$-controlling if one can select suitable values
$d$-controlling if one can select suitable values 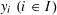 $y_{i}\;(i\in I)$ such that for every Lipschitz function
$y_{i}\;(i\in I)$ such that for every Lipschitz function 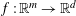 $f\,:\,\mathbb{R}^{m}\,\rightarrow \,\mathbb{R}^{d}$ there exists
$f\,:\,\mathbb{R}^{m}\,\rightarrow \,\mathbb{R}^{d}$ there exists 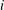 $i$ with
$i$ with 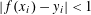 $|f(x_{i})\,-\,y_{i}|\,<\,1$. We conjecture that for every
$|f(x_{i})\,-\,y_{i}|\,<\,1$. We conjecture that for every 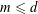 $m\leqslant d$, a sequence
$m\leqslant d$, a sequence 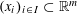 $(x_{i})_{i\in I}\subset \mathbb{R}^{m}$ is
$(x_{i})_{i\in I}\subset \mathbb{R}^{m}$ is 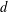 $d$-controlling if and only if
$d$-controlling if and only if 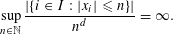 $$\begin{eqnarray}\displaystyle \sup _{n\in \mathbb{N}}\frac{|\{i\in I:|x_{i}|\leqslant n\}|}{n^{d}}=\infty . & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sup _{n\in \mathbb{N}}\frac{|\{i\in I:|x_{i}|\leqslant n\}|}{n^{d}}=\infty . & & \displaystyle \nonumber\end{eqnarray}$$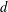 $d$-controlling. We also prove the conjecture for
$d$-controlling. We also prove the conjecture for 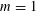 $m=1$.
$m=1$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018

