Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T03:21:57.308Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERPOLATION OF HILBERT AND SOBOLEV SPACES: QUANTITATIVE ESTIMATES AND COUNTEREXAMPLES

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear function spaces and their duals

Published online by Cambridge University Press:  19 November 2014

S. N. Chandler-Wilde ,
D. P. Hewett  and
A. Moiola
S. N. Chandler-Wilde
Affiliation:
Department of Mathematics and Statistics, University of Reading, PO Box 220, Whiteknights, Reading RG6 6AX, U.K. email s.n.chandler-wilde@reading.ac.uk
D. P. Hewett
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, U.K. email hewett@maths.ox.ac.uk
A. Moiola
Affiliation:
Department of Mathematics and Statistics, University of Reading, PO Box 220, Whiteknights, Reading RG6 6AX, U.K. email a.moiola@reading.ac.uk
Get access

Abstract

This paper provides an overview of interpolation of Banach and Hilbert spaces, with a focus on establishing when equivalence of norms is in fact equality of norms in the key results of the theory. 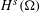(In brief, our conclusion for the Hilbert space case is that, with the right normalizations, all the key results hold with equality of norms.) In the final section we apply the Hilbert space results to the Sobolev spaces $H^{s}({\rm\Omega})$ and 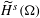$\widetilde{H}^{s}({\rm\Omega})$, for 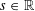$s\in \mathbb{R}$ and an open 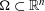${\rm\Omega}\subset \mathbb{R}^{n}$. We exhibit examples in one and two dimensions of sets 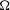${\rm\Omega}$ for which these scales of Sobolev spaces are not interpolation scales. In the cases where they are interpolation scales (in particular, if 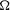${\rm\Omega}$ is Lipschitz) we exhibit examples that show that, in general, the interpolation norm does not coincide with the intrinsic Sobolev norm and, in fact, the ratio of these two norms can be arbitrarily large.

MSC classification

Primary: 46B70: Interpolation between normed linear spaces 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Research Article
Information
Mathematika , Volume 61 , Issue 2 , May 2015 , pp. 414 - 443
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, R. A., Sobolev Spaces, Academic Press (New York, 1973).Google Scholar
Ameur, Y., A new proof of Donoghue’s interpolation theorem. J. Funct. Spaces Appl. 2 2004, 253–265.CrossRefGoogle Scholar
Ameur, Y., Interpolation and operator constructions. Preprint, 2014, arXiv:1401.6090 (accessed 20/10/2014).Google Scholar
Bennet, C. and Sharpley, R., Interpolation of Operators, Academic Press (New York, 1988).Google Scholar
Bergh, J. and Löfström, J., Interpolation Spaces: An Introduction, Springer (Berlin, 1976).CrossRefGoogle Scholar
Bramble, J. H., Multigrid Methods, Chapman & Hall (New York, 1993).Google Scholar
Calderón, A. P., Lebesgue spaces of differentiable functions and distributions. Proc. Sympos. Pure Math. 4 1961, 33–49.CrossRefGoogle Scholar
Chandler-Wilde, S. N. and Hewett, D. P., Acoustic scattering by fractal screens: mathematical formulations and wavenumber-explicit continuity and coercivity estimates. University of Reading Preprint, 2013, MPS-2013-17; arXiv:1401.2786 (accessed 20/10/2014).Google Scholar
Chandler-Wilde, S. N., Hewett, D. P. and Moiola, A., Sobolev spaces on subsets of $\mathbb{R}^{n}$ with application to boundary integral equations on fractal screens (in preparation).Google Scholar
Donoghue, W., The interpolation of quadratic norms. Acta Math. 118 1967, 251–270.CrossRefGoogle Scholar
Dunford, N. and Schwarz, J. T., Linear Operators, Part II. Spectral Theory, John Wiley (New York, 1963).Google Scholar
Jones, P. W., Quasiconformal mappings and extendability of functions in Sobolev spaces. Acta Math. 147 1981, 71–88.CrossRefGoogle Scholar
Kato, T., Perturbation Theory for Linear Operators, 2nd edn, Springer (Berlin, 1980).Google Scholar
Kress, R., Linear Integral Equations, 2nd edn, Springer (New York, 1999).CrossRefGoogle Scholar
Lions, J.-L. and Magenes, E., Non-Homogeneous Boundary Value Problems and Applications I, Springer (Berlin, 1972).Google Scholar
Maz’ya, V. G., Sobolev Spaces with Applications to Elliptic Partial Differential Equations, 2nd edn, Springer (New York, 2011).CrossRefGoogle Scholar
McCarthy, J. E., Geometric interpolation between Hilbert spaces. Ark. Mat. 30 1992, 321–330.CrossRefGoogle Scholar
McLean, W., Strongly Elliptic Systems and Boundary Integral Equations, Cambridge University Press (Cambridge, 2000).Google Scholar
Peetre, J., A Theory of Interpolation of Normed Spaces (Notas de Matemática 39), Instituto de Matemática Pura e Aplicada, Conselho Nacional de Pesquisas (Rio de Janeiro, 1968).Google Scholar
Rogers, L. G., Degree-independent Sobolev extension on locally uniform domains. J. Funct. Anal. 235 2006, 619–665.CrossRefGoogle Scholar
Rychkov, V. S., On restrictions and extensions of the Besov and Triebel–Lizorkin spaces with respect to Lipschitz domains. J. Lond. Math. Soc. 60 1999, 237–257.CrossRefGoogle Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions, Vol. 1, Princeton University Press (Princeton, NJ, 1970).Google Scholar
Tartar, L., An Introduction to Sobolev Spaces and Interpolation Spaces, Springer (Berlin, 2007).Google Scholar
Triebel, H., Interpolation Theory, Function Spaces, Differential Operators, North-Holland (Amsterdam, 1978).Google Scholar