Article contents
DISSOLVING OF CUSP FORMS: HIGHER-ORDER FERMI’S GOLDEN RULES
Published online by Cambridge University Press: 21 January 2013
Abstract
For a hyperbolic surface, embedded eigenvalues of the Laplace operator are unstable and tend to dissolve into scattering poles i.e. become resonances. A sufficient dissolving condition was identified by Phillips–Sarnak and is elegantly expressed in Fermi’s golden rule. We prove formulas for higher approximations and obtain necessary and sufficient conditions for dissolving a cusp form with eigenfunction 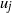 $u_j$ into a resonance. In the framework of perturbations in character varieties, we relate the result to the special values of the
$u_j$ into a resonance. In the framework of perturbations in character varieties, we relate the result to the special values of the  $L$-series
$L$-series 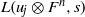 $L(u_j\otimes F^n, s)$. This is the Rankin–Selberg convolution of
$L(u_j\otimes F^n, s)$. This is the Rankin–Selberg convolution of 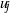 $u_j$ with
$u_j$ with 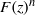 $F(z)^n$, where
$F(z)^n$, where 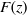 $F(z)$is the antiderivative of a weight two cusp form. In an example we show that the above-mentioned conditions force the embedded eigenvalue to become a resonance in a punctured neighborhood of the deformation space.
$F(z)$is the antiderivative of a weight two cusp form. In an example we show that the above-mentioned conditions force the embedded eigenvalue to become a resonance in a punctured neighborhood of the deformation space.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2013 University College London
References
- 6
- Cited by

