Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cherednichenko, Kirill D.
and
Evans, James A.
2016.
Full Two-Scale Asymptotic Expansion and Higher-Order Constitutive Laws in the Homogenization of the System of Quasi-static Maxwell Equations.
Multiscale Modeling & Simulation,
Vol. 14,
Issue. 4,
p.
1513.
Milton, Graeme W.
2016.
Analytic materials.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 472,
Issue. 2195,
p.
20160613.
Cooper, Shane
2018.
Quasi-periodic two-scale homogenisation and effective spatial dispersion in high-contrast media.
Calculus of Variations and Partial Differential Equations,
Vol. 57,
Issue. 3,
Cherednichenko, Kirill
and
Cooper, Shane
2018.
ASYMPTOTIC BEHAVIOUR OF THE SPECTRA OF SYSTEMS OF MAXWELL EQUATIONS IN PERIODIC COMPOSITE MEDIA WITH HIGH CONTRAST.
Mathematika,
Vol. 64,
Issue. 2,
p.
583.
Ohlberger, Mario
and
Verfurth, Barbara
2018.
A New Heterogeneous Multiscale Method for the Helmholtz Equation with High Contrast.
Multiscale Modeling & Simulation,
Vol. 16,
Issue. 1,
p.
385.
Ammari, Habib
Lee, Hyundae
and
Zhang, Hai
2019.
Bloch Waves in Bubbly Crystal Near the First Band Gap: A High-Frequency Homogenization Approach.
SIAM Journal on Mathematical Analysis,
Vol. 51,
Issue. 1,
p.
45.
Pellet, Xavier
Scardia, Lucia
and
Zeppieri, Caterina Ida
2019.
Homogenization of High-contrast Mumford--Shah Energies.
SIAM Journal on Mathematical Analysis,
Vol. 51,
Issue. 3,
p.
1696.
Verfürth, Barbara
2019.
Heterogeneous Multiscale Method for the Maxwell equations with high contrast.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 53,
Issue. 1,
p.
35.
Vial, Benjamin
and
Hao, Yang
2019.
Enhanced tunability in ferroelectric composites through local field enhancement and the effect of disorder.
Journal of Applied Physics,
Vol. 126,
Issue. 4,
Kamotski, I. V.
and
Smyshlyaev, V. P.
2019.
Two-scale homogenization for a general class of high contrast PDE systems with periodic coefficients.
Applicable Analysis,
Vol. 98,
Issue. 1-2,
p.
64.
Poelstra, Klaas Hendrik
Schweizer, Ben
and
Urban, Maik
2021.
The geometric average of curl-free fields in periodic geometries.
Analysis,
Vol. 41,
Issue. 3,
p.
179.
Rodionov, S. A.
and
Merzlikin, A. M.
2022.
Effective Refractive Index of 2D Porous Composite Materials.
Journal of Experimental and Theoretical Physics,
Vol. 134,
Issue. 5,
p.
600.
Murai, Naoki
Noguchi, Yuki
Matsushima, Kei
and
Yamada, Takayuki
2023.
Multiscale topology optimization of electromagnetic metamaterials using a high-contrast homogenization method.
Computer Methods in Applied Mechanics and Engineering,
Vol. 403,
Issue. ,
p.
115728.
Cao, Xinlin
Ghandriche, Ahcene
and
Sini, Mourad
2023.
The electromagnetic waves generated by a cluster of nanoparticles with high refractive indices.
Journal of the London Mathematical Society,
Vol. 108,
Issue. 4,
p.
1531.
Cao, Xinlin
and
Sini, Mourad
2023.
The effective permittivity and permeability generated by a cluster of moderately contrasting nanoparticles.
Journal of Differential Equations,
Vol. 367,
Issue. ,
p.
549.
Davoli, Elisa
Kružík, Martin
and
Pagliari, Valerio
2024.
Homogenization of high-contrast composites under differential constraints.
Advances in Calculus of Variations,
Vol. 17,
Issue. 2,
p.
277.
Cao, Xinlin
Ghandriche, Ahcene
and
Sini, Mourad
2025.
Effective medium theory for Van-der-Waals heterostructures.
Journal of Differential Equations,
Vol. 433,
Issue. ,
p.
113260.
Cherednichenko, Kirill
Kiselev, Alexander V.
Velčić, Igor
and
Žubrinić, Josip
2025.
Effective Behaviour of Critical-Contrast PDEs: Micro-Resonances, Frequency Conversion, and Time Dispersive Properties. II.
Communications in Mathematical Physics,
Vol. 406,
Issue. 4,
 ${\it\epsilon}$ have a high degree of contrast between each other. We assume that the ratio between the permittivities of the components with low and high values of
${\it\epsilon}$ have a high degree of contrast between each other. We assume that the ratio between the permittivities of the components with low and high values of  ${\it\epsilon}$ is of the order
${\it\epsilon}$ is of the order 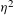 ${\it\eta}^{2}$, where
${\it\eta}^{2}$, where 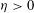 ${\it\eta}>0$ is the period of the medium. We determine the asymptotic behaviour of the electromagnetic response of such a medium in the “homogenization limit”, as
${\it\eta}>0$ is the period of the medium. We determine the asymptotic behaviour of the electromagnetic response of such a medium in the “homogenization limit”, as 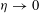 ${\it\eta}\rightarrow 0$, and derive the limit system of Maxwell equations in
${\it\eta}\rightarrow 0$, and derive the limit system of Maxwell equations in 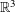 $\mathbb{R}^{3}$. Our results extend a number of conclusions of a paper by Zhikov [On gaps in the spectrum of some divergent elliptic operators with periodic coefficients. St. Petersburg Math. J.16(5) (2004), 719–773] to the case of the full system of Maxwell equations.
$\mathbb{R}^{3}$. Our results extend a number of conclusions of a paper by Zhikov [On gaps in the spectrum of some divergent elliptic operators with periodic coefficients. St. Petersburg Math. J.16(5) (2004), 719–773] to the case of the full system of Maxwell equations.
