Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-17T21:57:22.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Measures of Hausdorff-type, and Brownian motion

Part of: Markov processes

Published online by Cambridge University Press:  26 February 2010

R. Kaufman
R. Kaufman
Affiliation:
University of Illinois, Urbana, Illinois, U.S.A.
Get access

Extract

In this paper X(t) denotes Brownian motion on the line 0 ≤ t < ∞, E is a compact subset of (0, ∞) and F a compact subset of ( -∞, ∞). Then δ(E, F) is the supremum of the numbers c such that

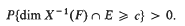
In [4, 5] some lower and upper bounds for δ were found in terms of dim E and dim F, and it seemed possible that δ(E, F) could be determined entirely by these constants; this much is false, as the examples in our last paragraph will demonstrate. Here we shall show that δ(E, F) depends on a certain metric character η(E × F). However, η is not calculated relative to the Euclidean metric: the set F must be compressed to compensate for the oscillations of most paths X(t). Fortunately, η(E × F) can be calculated for a large enough class of sets E and F, by means of sequences of integers, to test any conjectures (and disprove most of them). In passing from η to δ we present a slight variation of Frostman's theory [3II].

MSC classification

Secondary: 60J65: Brownian motion
Type
Research Article
Information
Mathematika , Volume 19 , Issue 1 , June 1972 , pp. 115 - 119
Copyright
Copyright © University College London 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Besicovitch, A. S. and Moran, P. A. P., “The measure of product and cylinder sets”, J. London Math. Soc., 20 (1945), 110–120.Google Scholar
2.Hawkes, J., “On the Hausdorff dimension of the intersection of the range of a stable process with a Borel Set”, Z. Warschein., 19 (1971), 90–102.CrossRefGoogle Scholar
3.Kahane, J.-P. and Salem, R., “Ensembles parfaits et series trigonométriques (Paris, Hermann, 1963).Google Scholar
4.Kaufman, R., “On the zeroes of some random functions, Studia Math., 34 (1970), 291–297.CrossRefGoogle Scholar
5.Kaufman, R., “Brownian motion and dimension of perfect sets”, Canadian J. Math., 22 (1970), 674–680.CrossRefGoogle Scholar
6.Kaufman, R., “Perfect sets in some groups”, Studia Math., 34 (1970), 17–21.CrossRefGoogle Scholar
7.Schreiber, J.-P., “Fonction de Peano et dimension de Hausdorff”, Enseignement Math., 13 (1968), 325–328.Google Scholar
8.Taylor, S. J. and Wendel, J. G., “The exact Hausdorff measure of the zero set of a stable process”, Z. Warschein., 6 (1966), 170–180.CrossRefGoogle Scholar