Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T07:40:33.219Z Has data issue: false hasContentIssue false
  • English
  • Français

SPECTRAL THEORETIC CHARACTERIZATION OF THE MASSLESS DIRAC ACTION

Part of: Spectral theory and eigenvalue problems Elliptic equations and systems Equations of mathematical physics and other areas of application Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  08 March 2016

Robert J. Downes  and
Dmitri Vassiliev
Robert J. Downes
Affiliation:
Department of War Studies, King’s College London, Strand, London WC2R 2LS, U.K. email robert.downes@kcl.ac.uk
Dmitri Vassiliev
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, U.K. email D.Vassiliev@ucl.ac.uk http://www.homepages.ucl.ac.uk/∼ucahdva/

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider an elliptic self-adjoint first-order differential operator 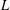$L$ acting on pairs (2-columns) of complex-valued half-densities over a connected compact three-dimensional manifold without boundary. The principal symbol of the operator 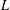$L$ is assumed to be trace-free and the subprincipal symbol is assumed to be zero. Given a positive scalar weight function, we study the weighted eigenvalue problem for the operator 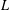$L$ . The corresponding counting function (number of eigenvalues between zero and a positive $\unicode[STIX]{x1D706}$ ) is known to admit, under appropriate assumptions on periodic trajectories, a two-term asymptotic expansion as 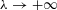$\unicode[STIX]{x1D706}\rightarrow +\infty$ and we have recently derived an explicit formula for the second asymptotic coefficient. The purpose of this paper is to establish the geometric meaning of the second asymptotic coefficient. To this end, we identify the geometric objects encoded within our eigenvalue problem—metric, non-vanishing spinor field and topological charge—and express our asymptotic coefficients in terms of these geometric objects. We prove that the second asymptotic coefficient of the counting function has the geometric meaning of the massless Dirac action.

MSC classification

Primary: 35P20: Asymptotic distribution of eigenvalues and eigenfunctions
Secondary: 35J46: First-order elliptic systems 35R01: Partial differential equations on manifolds 35Q41: Time-dependent Schrödinger equations, Dirac equations
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 701 - 718
Creative Commons
Creative Common License - CCCreative Common License - BY
This article is distributed with Open Access under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided that the original work is properly cited.
Copyright
Copyright © University College London 2016

References

Atiyah, M. F., Patodi, V. K. and Singer, I. M., Spectral asymmetry and Riemannian geometry III. Math. Proc. Cambridge Philos. Soc. 79 1976, 71–99.CrossRefGoogle Scholar
Bismut, J.-M. and Freed, D. S., The analysis of elliptic families. II. Dirac operators, eta invariants, and the holonomy theorem. Commun. Math. Phys. 107 1986, 103–163.CrossRefGoogle Scholar
Chervova, O., Downes, R. J. and Vassiliev, D., The spectral function of a first order elliptic system. J. Spectr. Theory 3 2013, 317–360.CrossRefGoogle Scholar
Chervova, O., Downes, R. J. and Vassiliev, D., Spectral theoretic characterization of the massless Dirac operator. J. Lond. Math. Soc. (2) 89 2014, 301–320.CrossRefGoogle Scholar
Chervova, O. and Vassiliev, D., The stationary Weyl equation and Cosserat elasticity. J. Phys. A 43 2010, 335203.CrossRefGoogle Scholar
Duistermaat, J. J. and Hörmander, L., Fourier integral operators II. Acta Math. 128 1972, 183–269.Google Scholar
Erdős, L. and Solovej, J. P., The kernel of Dirac operators on S3 and ℝ3 . Rev. Math. Phys. 13 2001, 1247–1280.CrossRefGoogle Scholar
Heath-Brown, D. R., Lattice points in the sphere. In Number Theory in Progress: Proceedings of the International Conference on Number Theory held in Honor of the 60th Birthday of Andrzej Schinzel, (eds Győry, K., Iwaniec, H. and Urbanowicz, J.), Walter de Gruyter (Berlin, 1999), 883–892.CrossRefGoogle Scholar
Safarov, Yu. and Vassiliev, D., The Asymptotic Distribution of Eigenvalues of Partial Differential Operators, American Mathematical Society (Providence, RI, 1997).Google Scholar