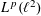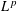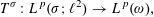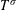Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alexis, Michel
Luna-Garcia, Jose Luis
Sawyer, Eric T.
and
Uriarte-Tuero, Ignacio
2025.
The T1 theorem for the Hilbert transform fails when p ≠ 2.
Journal d'Analyse Mathématique,
Vol. 156,
Issue. 1,
p.
27.