Article contents
ZEROS OF THE MÖBIUS FUNCTION OF PERMUTATIONS
Published online by Cambridge University Press: 14 August 2019
Abstract
We show that if a permutation  $\unicode[STIX]{x1D70B}$ contains two intervals of length 2, where one interval is an ascent and the other a descent, then the Möbius function
$\unicode[STIX]{x1D70B}$ contains two intervals of length 2, where one interval is an ascent and the other a descent, then the Möbius function 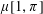 $\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]$ of the interval
$\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]$ of the interval 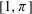 $[1,\unicode[STIX]{x1D70B}]$ is zero. As a consequence, we prove that the proportion of permutations of length
$[1,\unicode[STIX]{x1D70B}]$ is zero. As a consequence, we prove that the proportion of permutations of length  $n$ with principal Möbius function equal to zero is asymptotically bounded below by
$n$ with principal Möbius function equal to zero is asymptotically bounded below by 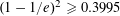 $(1-1/e)^{2}\geqslant 0.3995$. This is the first result determining the value of
$(1-1/e)^{2}\geqslant 0.3995$. This is the first result determining the value of 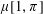 $\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]$ for an asymptotically positive proportion of permutations
$\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]$ for an asymptotically positive proportion of permutations  $\unicode[STIX]{x1D70B}$. We further establish other general conditions on a permutation
$\unicode[STIX]{x1D70B}$. We further establish other general conditions on a permutation  $\unicode[STIX]{x1D70B}$ that ensure
$\unicode[STIX]{x1D70B}$ that ensure 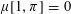 $\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]=0$, including the occurrence in
$\unicode[STIX]{x1D707}[1,\unicode[STIX]{x1D70B}]=0$, including the occurrence in  $\unicode[STIX]{x1D70B}$ of any interval of the form
$\unicode[STIX]{x1D70B}$ of any interval of the form 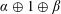 $\unicode[STIX]{x1D6FC}\oplus 1\oplus \unicode[STIX]{x1D6FD}$.
$\unicode[STIX]{x1D6FC}\oplus 1\oplus \unicode[STIX]{x1D6FD}$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
Footnotes
V. Jelínek and J. Kynčl were supported by project 16-01602Y of the Czech Science Foundation (GAČR). J. Kynčl was also supported by Charles University project UNCE/SCI/004.
References
- 2
- Cited by

