Introduction
The ability to design a material with desired properties a priori using computational methods has been promised by computational materials science for many years.[Reference Sinnott1] This problem can be framed as selecting the optimal composite material structure that meets certain quality metrics from a space of candidates.[Reference Seko, Togo, Hayashi, Tsuda, Chaput and Tanaka2,Reference Balachandran, Xue, Theiler, Hogden and Lookman3] One example is the structural determination of a substitutional alloy problem in solid-state materials design,[Reference Okhotnikov, Charpentier and Cadars4,Reference Ju, Shiga, Feng, Hou, Tsuda and Shiomi5] where optimal atoms (or vacancies) assignment in a crystal structure is determined to maximize or minimize a target property.
To accelerate this process, researchers have emphasized data-driven and machine learning approaches as the fourth paradigm of science.[Reference Agrawal and Choudhary6,Reference Drosback7] Data-driven materials design approaches are iterative design algorithms. Given a space of candidates S, the algorithm aims to find the optimal candidate p bst that optimizes a black-box function f (p) (usually the target property). Starting with a random selection, and within a predefined number of iterations, the algorithm evaluates a set of selected candidates and obtains feedback for a more informed selection on the next iteration. The function f (p) is evaluated by experiment or simulation and it is computationally expensive to query. It is necessary to reach the optimal candidate with as few queries as possible[Reference Dieb, Tsuda and Tanaka8] (Fig. 1).
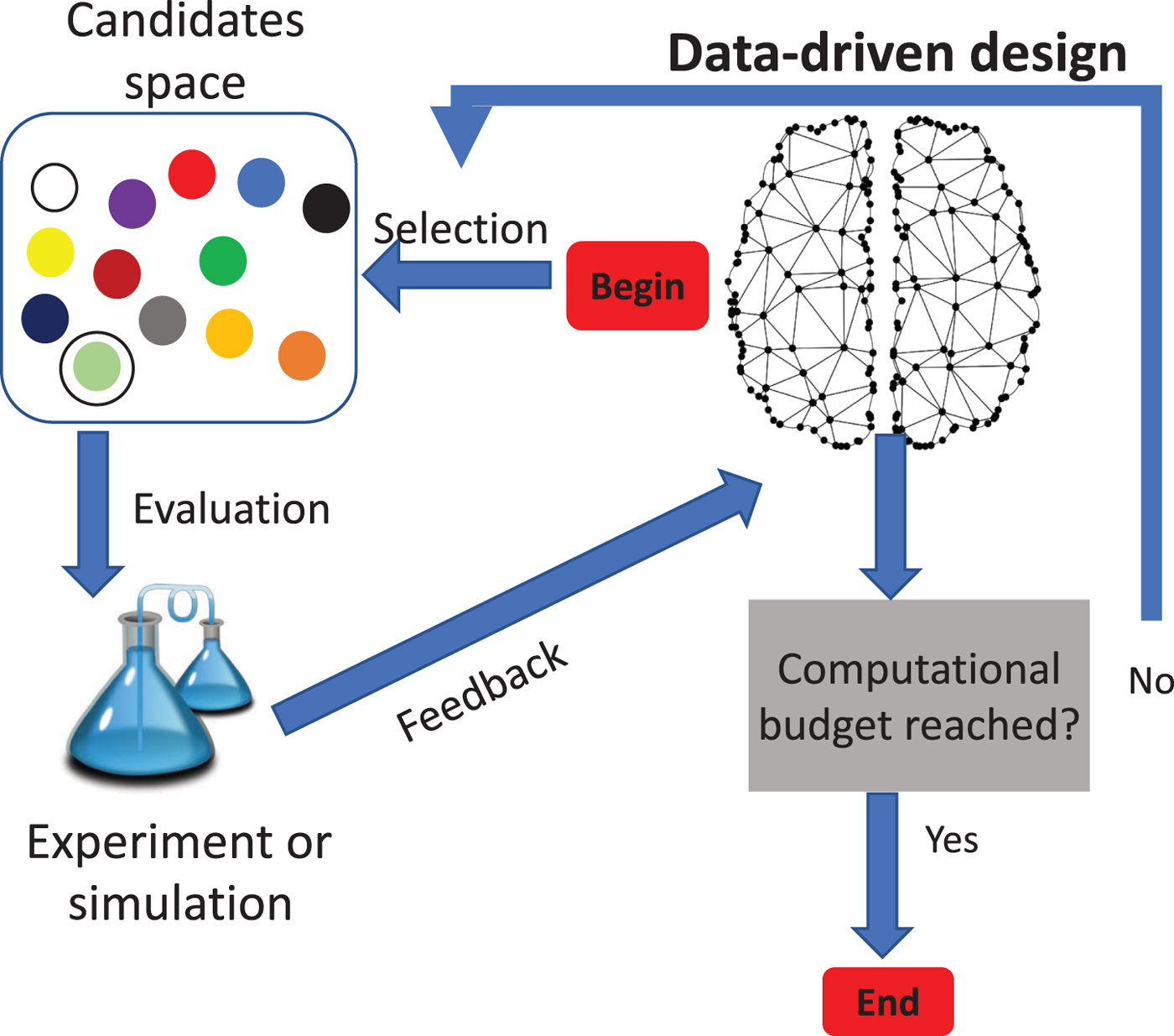
Figure 1. A data-driven materials design approach. Starting randomly, an algorithm selects a candidate set for experimentation within a computational budget. The experimental feedback is then used for a more informed selection in the next iteration.
Several methods have been applied for data-driven materials design. Evolutionary algorithms, such as genetic algorithms[Reference Patra, Meenakshisundaram, Hung and Simmons9,Reference Paszkowicz, Harris and Johnston10] that use human evolution mechanisms (such as crossover and mutation), have been used to solve optimization problems at a large scale. Genetic algorithms need adequate data available a priori to tune many parameters for optimal performance. However, a priori data are often limited in materials design and discovery.
Another approach is Bayesian optimization (BO)[Reference Snoek, Larochelle and Adams11,Reference Jones, Schonlau and Welch12] that iteratively selects an optimal candidate from a search space that optimizes an expensive black-box function f (p). A deceive advantage of BO is that, it uses the predicated merit of the candidate as well as the uncertainty of the prediction when selecting the next promising candidate. This feature has been successful in several materials design problems.[Reference Seko, Togo, Hayashi, Tsuda, Chaput and Tanaka2,Reference Ju, Shiga, Feng, Hou, Tsuda and Shiomi5,Reference Ueno, Rhone, Hou, Mizoguchi and Tsuda13–Reference Aggarwal, Demkowicz and Marzouk15] However, as the uncertainty of the prediction needs to be assessed for all candidates in the search space, excessive computation in BO faces serious challenges in large-scale problems, a common case in materials design.
The recent success of Monte Carlo tree search (MCTS)[Reference Browne, Powley, Whitehouse, Lucas, Cowling, Rohlfshagen, Tavener, Perez, Samothrakis and Colton16] in computer games[Reference Silver, Huang, Maddison, Guez, Sifre, van den Driessche, Schrittwieser, Antonoglou, Panneershelvam, Lanctot, Dieleman, Grewe, Nham, Kalchbrenner, Sutskever, Lillicrap, Leach, Kavukcuoglu, Graepel and Hassabis17,Reference Mehat and Cazenave18] has encouraged researchers to apply it to natural science domains. For example, Yang et al. used MCTS for de novo molecular generation by selecting an optimal design with a predefined desired criterion from a vast chemical space.[Reference Yang, Zhang, Yoshizoe, Terayama and Tsuda19] Segler et al. applied MCTS to discover retrosynthetic routes to plan the syntheses of small organic molecules.[Reference Segler, Preuss and Waller20]
MCTS has also been applied in materials science and engineering. In this study, we reviewed the utilization of MCTS in materials design and discovery, particularly, to analyze its ability to solve large-scale optimization problems. To the best of our knowledge, no such review has been published yet. This paper is organized into four sections. The section “Monte Carlo tree search” presents the MCTS algorithm. In the section “Applications in materials design”, we discuss the utilization of several variations of MCTS for finding optimal materials design. Finally, “Concluding remarks” section summarizes the paper with forward-looking remarks.
Monte Carlo tree search
MCTS[Reference Browne, Powley, Whitehouse, Lucas, Cowling, Rohlfshagen, Tavener, Perez, Samothrakis and Colton16] is an iterative, guided, random best-first tree search algorithm that systemically searches a space of candidates to obtain an optimal solution that maximizes the black-box function f (p). A distinguishing feature of MCTS is that it encodes the search space into a shallow tree that iteratively expands in the direction of the promising solutions, eliminating the need to construct a full tree. MCTS then utilizes guided randomization to obtain full solutions from this shallow tree.
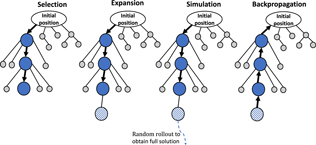
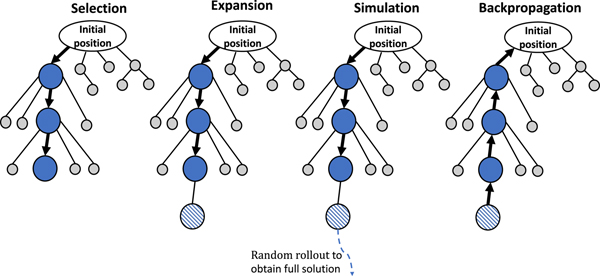
Within a computational budget, MCTS explores the search space over multiple iterations. Initially, only the root node exists. Then, each iteration consists of four steps: selection, expansion, simulation, and back-propagation (Fig. 2). In the selection step, the tree is traversed from the root to the most promising leaf using a comparative score. The chosen leaf is then expanded by adding a child node to it in the expansion step. Only partial solutions can be obtained from this shallow tree. In the simulation step, a full solution is generated by random rollout[Reference Browne, Powley, Whitehouse, Lucas, Cowling, Rohlfshagen, Tavener, Perez, Samothrakis and Colton16] starting from a node; the remaining variables are randomly determined. The merit of the obtained solution is evaluated. In the back-propagation step, the nodes’ information is updated along the path back to the root. MCTS balances exploration against exploitation using a hyper parameter that depends on the range of maximum and minimum merits values of the candidates.
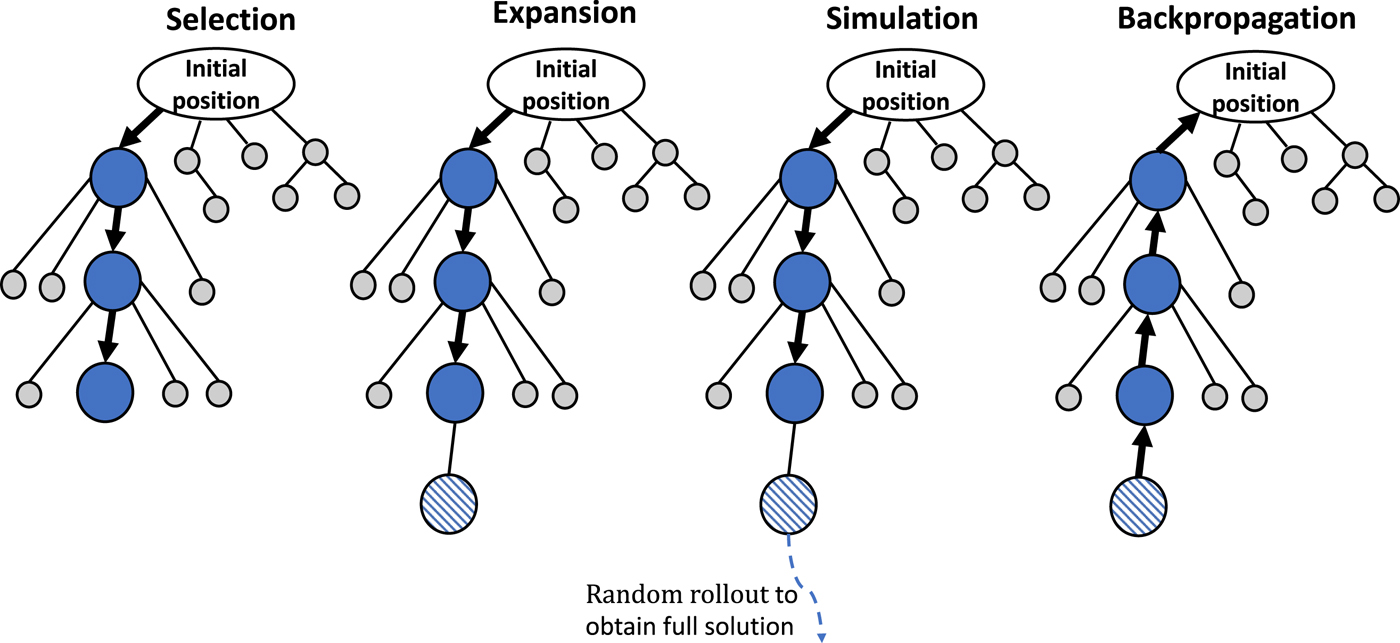
Figure 2. MCTS encodes the search space as a shallow decision tree. MCTS repeats four steps. In the selection step, a promising leaf node is chosen by following the child node with the best score. The expansion step adds a child node to the selected node. During simulation, a full solution is created by random rollout and its merit is evaluated. The back-propagation step updates information for the nodes along the path back to the root for better selection in the next iteration.
Applications in materials design
A Python package for an optimal atom assignment problem
An open source implementation of MCTS was developed by Dieb et al. using the Python programing language.[Reference Dieb, Ju, Yoshizoe, Hou, Shiomi and Tsuda21] The package MDTS (materials design using tree search) is available at https://github.com/tsudalab/MDTS. MDTS solves structure determination problems by optimal atom (or vacancy) assignment with composition constraints. This method assumes a material structure P with n positions {p 1, p 2, …, p n} that need to be assigned with several types of atoms (or vacancies). It searches for the optimal configuration p bst (subject to composition constraints) that maximizes a black-box function f (p)(usually the target property). MDTS uses the MCTS model to encode the candidate space into a tree where a node at level l represents a possible atom assignment in the position l in the structure. MDTS uses the upper confidence bound (UCB) score[Reference Browne, Powley, Whitehouse, Lucas, Cowling, Rohlfshagen, Tavener, Perez, Samothrakis and Colton16] to compare child nodes when traversing the tree. The UCB score is computed following Eq. (1):
 $${\rm uc}{\rm b}_i = \displaystyle{{z_i} \over {v_i}} + C\sqrt {\displaystyle{{2\,{\rm ln}\,v_{{\rm parent}}} \over {v_i}}} $$
$${\rm uc}{\rm b}_i = \displaystyle{{z_i} \over {v_i}} + C\sqrt {\displaystyle{{2\,{\rm ln}\,v_{{\rm parent}}} \over {v_i}}} $$where z i is the accumulated merit of the node (i.e., the sum of the immediate merits of all downstream nodes), v i is the visit count of the node, v parent is the visit count of the parent node, and C is the constant to balance exploration and exploitation.
MDTS adaptively sets C at each node following similar idea to[Reference Kocsis and Szepesvári22]:
where J is a meta-parameter initially set to one, which increases whenever the algorithm encounters a dead-end leaf, to allow for more exploration. The parameters f max and f min are the maximum and minimum immediate merits in the downstream nodes, respectively. The automatic setting of C allows MDTS to work parameter-free with optimal performance on several applications. For example, MDTS successfully designed large silicon–germanium (Si–Ge) alloy structures when BO could not be used due to its high computational cost.
Grain boundary segregation
Analysis of the grain boundary segregation behavior of impurities, dopants, and vacancies is very important for broad materials development due to its effect on material properties. Kiyohara et al.[Reference Kiyohara and Mizoguchi23] recently applied the MCTS method to determine a stable segregation configuration of copper Σ5[001]/(210) and Σ37[001]/(750) with silver impurities. A binary Monte Carlo tree was constructed where a node represented either a copper or silver atom assigned to a segregation site; the process searched for an optimum candidate with minimal segregation energy. A stable copper Σ5[001]/(210) configuration was reached by searching only 1% of all candidate configurations (Fig. 3). This result was identical to a previous study using theoretical calculations, where empirical potentials for copper–silver alloys were generated to systematically investigate the segregation.[Reference Kiyohara and Mizoguchi24] The optimal solution of copper Σ37[001]/(750) (which had a significantly larger search space) was achieved after exploring only 0.34% of the search space.

Figure 3. (a) The promising configuration of the grain boundary structure of copper Σ5[001]/(210) up to the 16th site. Yellow and gray circles represent silver and copper atoms, respectively. (b) Strain map at each site at the grain boundary. The sites with a positive strain are larger spatially (red); the reverse holds for the negative strain (blue). Reprinted from Kiyohara and Mizoguchi[Reference Kiyohara and Mizoguchi23]; with the permission of AIP Publishing.
It is reported that the search efficiency was significantly affected by the order of the search (a search by order of segregation energy was more efficient than a random search). Additionally, the analysis of the search path and the number of rollouts were important for understanding the background of the search.
Optimizing the energy gap for graphene nanoflakes
The study of the band gap in graphene is important for nanoelectronic applications. Cao et al. investigated the optimization of graphene nanoflakes' (GNFs) energy gaps by selecting the optimal structure.[Reference Cao, Zhao, Liao and Yang25] This study was challenged by the large number of candidate structures increasing as the number of carbon atoms (N c) in the graphene increased and the expensive computation of the energy gap (E g) for a specific structure. The researchers proposed an effective tight-binding model for the electronic properties of the hydrogen-terminated GNFs focusing on the effect of carbon atom local bonding. The parameters of this model were fit using first-principles calculation results on structures with N c ≤ 34. For larger search spaces (N c > 34), they used the MCTS method in combination with the congruence check to search for larger GNFs structures with large E g based on the properties of the smaller GNFs.
Using this approach, they efficiently obtained optimal structures with the largest E g for each N c. The reported results were confirmed with first-principles calculations.
Surface/interface roughness optimization
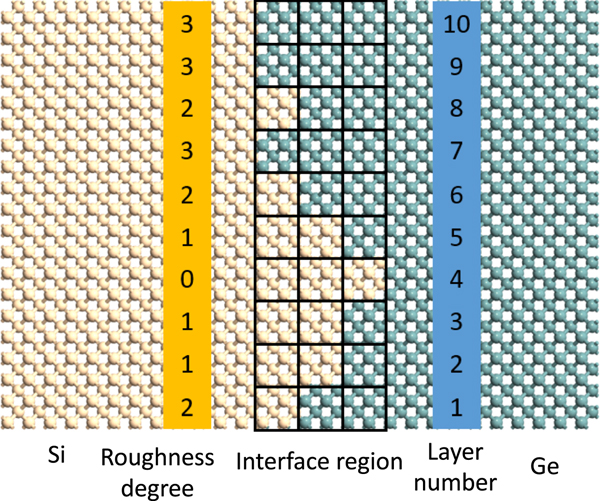
More recently, Ju et al.[Reference Ju, Dieb, Tsuda and Shiomi26] employed MCTS to study the effect of surface/interface design in nanostructures for optimal thermal transport. They investigated the limits of inhibition and enhancement of phonon transport in the interfacial roughness between a silicon–germanium (Si–Ge) bi-layer nanofilm (Fig. 4). In this setting, the number of possible roughness configurations increased exponentially with the number of layers in the nanofilm and the degree of roughness (e.g., there were 1,048,576 candidates for 10 layers and four degrees).

Figure 4. Interfacial roughness in a bi-layer nanofilm of Si–Ge. The number of possible configurations increased exponentially with the number of layers and the degree of roughness.
Researchers used the MDTS package[Reference Dieb, Ju, Yoshizoe, Hou, Shiomi and Tsuda21] with the atomistic Green's function[Reference Zhang, Fisher and Mingo27,Reference Wang, Wang and Zeng28] to search for candidates with maximum and minimum interfacial thermal conductance. The reported optimal surface/interface roughness configurations were non-intuitive, and they were in the middle range between flat and very rough. This study confirmed the scalability and efficiency of MCTS because it applied MCTS to a large search space.
Determination of boron-doping in a graphene structure
Tuning material properties by incorporating additional elements is a common practice in materials science and engineering. Both optimal composition and spatial distribution of incorporated atoms affect the target property. Dieb et al. investigated the most stable structures of doped boron atoms in graphene (for a boron concentration up to 31.25%) using a MCTS-based method in conjunction with atomistic simulations.[Reference Dieb, Hou and Tsuda29] They considered a supercell constructed of a hexagonal unit cell of graphene and carbon substituted by boron.
To increase the efficiency of MCTS, researchers engineered the rollout in the expansion step with a more sophisticated solution using BO[Reference Snoek, Larochelle and Adams11,Reference Jones, Schonlau and Welch12] (i.e., a Bayesian rollout). In this mechanism, a random pool of full candidates is enumerated under the expanded node with a predefined size, Z. BO is then used iteratively to select the optimal candidate from the pool. BO maintains a Gaussian process (GP)[Reference Rasmussen and Williams30] as the surrogate model of the objective function. As the MCTS progresses, more data points are observed and included in the GP for training, which optimizes the model for the target function (Fig. 5).

Figure 5. Bayesian rollout. A random pool of full candidates is generated under the expanded node. Initially, GP uses a random selection of data points for evaluation. As the search progresses down the tree, more observations are accumulated in the GP for a more informed future selection. To determine the next selection, the Bayesian rollout uses an acquisition function that considers the predicted value and prediction uncertainty.
Using this method, researchers have reported atomic structures of the most stable configurations of B–graphene at different B concentrations. The stability of these structures has also been verified by the density functional theory calculations with the use of the Vienna Ab initio Simulation Package (VASP).[Reference Kresse and Furthmuller31]
Concluding remarks
Our review of MCTS in materials design and discovery confirmed that MCTS can successfully solve large-scale optimization problems in materials design. An interesting feature of MCTS is that it does not require a complicated descriptor or a large dataset to tune many parameters. Instead, a single hyper parameter can be tuned automatically and adaptively based on the target application. On the other hand, MCTS can be most useful when experimenting (simulation) time is short. A significantly long experiment time will wipe out the advantage of quick design time of MCTS. Additionally, current implementations of MCTS are only available for discrete search spaces. Enhancing MCTS for continuous spaces can support a wider range of materials design applications.
MCTS may have potential not yet fully exploited in materials science. A recent trend of combining MCTS with other machine learning methods, such Bayesian learning and neural networks, has emerged to increase MCTS's efficiency, and this has shown promising results.
Acknowledgment
This work was supported by the “Materials research by Information Integration” Initiative (MI2I) project, the CREST Grant No. JPMJCR16Q5 from the Japan Science and Technology Agency (JST), and KAKENHI Grants No. 16H04274 from the Japan Society for the Promotion of Science (JSPS).