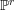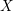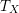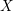1 Introduction
Projective spaces are the simplest algebraic varieties. They can be characterized in many ways. A very famous one is given by the Hartshorne’s conjecture, which was proved by Mori.
Theorem A. [Reference Mori25, Theorem 8]
Let
![]() $X$
be a projective manifold defined over an algebraically closed field
$X$
be a projective manifold defined over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() ${\geqslant}0$
. Then
${\geqslant}0$
. Then
![]() $X$
is a projective space if and only if
$X$
is a projective space if and only if
![]() $T_{X}$
is ample.
$T_{X}$
is ample.
This result has been generalized, over the field of complex number, by several authors (see [Reference Andreatta and Wiśniewski1, Reference Campana and Peternell12, Reference Wahl27]).
Theorem B. [Reference Andreatta and Wiśniewski1, Theorem]
Let
![]() $X$
be a projective manifold of dimension
$X$
be a projective manifold of dimension
![]() $n$
. If
$n$
. If
![]() $T_{X}$
contains an ample locally free subsheaf
$T_{X}$
contains an ample locally free subsheaf
![]() ${\mathcal{E}}$
of rank
${\mathcal{E}}$
of rank
![]() $r$
, then
$r$
, then
![]() $X\cong \mathbb{P}^{n}$
and
$X\cong \mathbb{P}^{n}$
and
![]() ${\mathcal{E}}\cong {\mathcal{O}}_{\mathbb{P}^{n}}(1)^{\oplus r}$
or
${\mathcal{E}}\cong {\mathcal{O}}_{\mathbb{P}^{n}}(1)^{\oplus r}$
or
![]() ${\mathcal{E}}\cong T_{\mathbb{P}^{n}}$
.
${\mathcal{E}}\cong T_{\mathbb{P}^{n}}$
.
This theorem was successively proved for
![]() $r=1$
by Wahl [Reference Wahl27] and later for
$r=1$
by Wahl [Reference Wahl27] and later for
![]() $r\geqslant n-2$
by Campana and Peternell [Reference Campana and Peternell12]. The proof was finally completed by Andreatta and Wiśniewski [Reference Andreatta and Wiśniewski1]. The main aim of the present article is to prove the following generalization.
$r\geqslant n-2$
by Campana and Peternell [Reference Campana and Peternell12]. The proof was finally completed by Andreatta and Wiśniewski [Reference Andreatta and Wiśniewski1]. The main aim of the present article is to prove the following generalization.
Theorem 1.1. Let
![]() $X$
be a projective manifold of dimension
$X$
be a projective manifold of dimension
![]() $n$
. Suppose that
$n$
. Suppose that
![]() $T_{X}$
contains an ample subsheaf
$T_{X}$
contains an ample subsheaf
![]() ${\mathcal{F}}$
of positive rank
${\mathcal{F}}$
of positive rank
![]() $r$
, then
$r$
, then
![]() $(X,{\mathcal{F}})$
is isomorphic to
$(X,{\mathcal{F}})$
is isomorphic to
![]() $(\mathbb{P}^{n},T_{\mathbb{P}^{n}})$
or
$(\mathbb{P}^{n},T_{\mathbb{P}^{n}})$
or
![]() $(\mathbb{P}^{n},{\mathcal{O}}_{\mathbb{P}^{n}}(1)^{\oplus r})$
.
$(\mathbb{P}^{n},{\mathcal{O}}_{\mathbb{P}^{n}}(1)^{\oplus r})$
.
We refer to Section 2.1 for the basic definition and properties of ample sheaves. Comparing with Theorem B, we do not require a priori the locally freeness of the subsheaf
![]() ${\mathcal{F}}$
in Theorem 1.1. In the case where the Picard number of
${\mathcal{F}}$
in Theorem 1.1. In the case where the Picard number of
![]() $X$
is one, Theorem 1.1 is proved in [Reference Aprodu, Kebekus and Peternell2]. In fact, in [Reference Aprodu, Kebekus and Peternell2], it was shown that the subsheaf
$X$
is one, Theorem 1.1 is proved in [Reference Aprodu, Kebekus and Peternell2]. In fact, in [Reference Aprodu, Kebekus and Peternell2], it was shown that the subsheaf
![]() ${\mathcal{F}}$
must be locally free under the additional assumption
${\mathcal{F}}$
must be locally free under the additional assumption
![]() $\unicode[STIX]{x1D70C}(X)=1$
, and then Theorem B immediately implies Theorem 1.1. In particular, to prove Theorem 1.1, it suffices to show that
$\unicode[STIX]{x1D70C}(X)=1$
, and then Theorem B immediately implies Theorem 1.1. In particular, to prove Theorem 1.1, it suffices to show that
![]() $X$
is isomorphic to some projective space if its tangent bundle contains an ample subsheaf
$X$
is isomorphic to some projective space if its tangent bundle contains an ample subsheaf
![]() ${\mathcal{F}}$
; then, the locally freeness of
${\mathcal{F}}$
; then, the locally freeness of
![]() ${\mathcal{F}}$
follows from [Reference Aprodu, Kebekus and Peternell2]. An interesting and important special case of Theorem 1.1 is when the subsheaf
${\mathcal{F}}$
follows from [Reference Aprodu, Kebekus and Peternell2]. An interesting and important special case of Theorem 1.1 is when the subsheaf
![]() ${\mathcal{F}}$
comes from the image of an ample vector bundle
${\mathcal{F}}$
comes from the image of an ample vector bundle
![]() $E$
over
$E$
over
![]() $X$
. This confirms a conjecture of Litt [Reference Litt23, Conjecture 2].
$X$
. This confirms a conjecture of Litt [Reference Litt23, Conjecture 2].
Corollary 1.2. Let
![]() $X$
be a projective manifold of dimension
$X$
be a projective manifold of dimension
![]() $n$
, and let
$n$
, and let
![]() $E$
be an ample vector bundle on
$E$
be an ample vector bundle on
![]() $X$
. If there exists a nonzero map
$X$
. If there exists a nonzero map
![]() $E\rightarrow T_{X}$
, then
$E\rightarrow T_{X}$
, then
![]() $X\cong \mathbb{P}^{n}$
.
$X\cong \mathbb{P}^{n}$
.
As an application, we derive the classification of projective manifolds containing a
![]() $\mathbb{P}^{r}$
-bundle as an ample divisor. This problem has attracted a great deal of interest over the past few decades (see [Reference Bădescu6–Reference Beltrametti and Sommese8, Reference Fania, Sato and Sommese13, Reference Sommese26], etc.). Recently, in [Reference Litt23, Corollary 7], Litt proved that it can be reduced to Corollary 1.2. To be more precise, we have the following classification theorem.
$\mathbb{P}^{r}$
-bundle as an ample divisor. This problem has attracted a great deal of interest over the past few decades (see [Reference Bădescu6–Reference Beltrametti and Sommese8, Reference Fania, Sato and Sommese13, Reference Sommese26], etc.). Recently, in [Reference Litt23, Corollary 7], Litt proved that it can be reduced to Corollary 1.2. To be more precise, we have the following classification theorem.
Theorem 1.3. Let
![]() $X$
be a projective manifold of dimension
$X$
be a projective manifold of dimension
![]() $n\geqslant 3$
, and let
$n\geqslant 3$
, and let
![]() $A$
be an ample divisor on
$A$
be an ample divisor on
![]() $X$
. Assume that
$X$
. Assume that
![]() $A$
is a
$A$
is a
![]() $\mathbb{P}^{r}$
-bundle,
$\mathbb{P}^{r}$
-bundle,
![]() $p:A\rightarrow B$
, over a manifold
$p:A\rightarrow B$
, over a manifold
![]() $B$
of dimension
$B$
of dimension
![]() $b>0$
. Then one of the following holds.
$b>0$
. Then one of the following holds.
(i)
 $(X,A)=(\mathbb{P}(E),H)$
for some ample vector bundle
$(X,A)=(\mathbb{P}(E),H)$
for some ample vector bundle
 $E$
over
$E$
over
 $B$
such that
$B$
such that
 $H\in |{\mathcal{O}}_{\mathbb{P}(E)}(1)|$
.
$H\in |{\mathcal{O}}_{\mathbb{P}(E)}(1)|$
.
 $p$
is equal to the restriction to
$p$
is equal to the restriction to
 $A$
of the induced projection
$A$
of the induced projection
 $\mathbb{P}(E)\rightarrow B$
.
$\mathbb{P}(E)\rightarrow B$
.(ii)
 $(X,A)=(\mathbb{P}(E),H)$
for some ample vector bundle
$(X,A)=(\mathbb{P}(E),H)$
for some ample vector bundle
 $E$
over
$E$
over
 $\mathbb{P}^{1}$
such that
$\mathbb{P}^{1}$
such that
 $H\in |{\mathcal{O}}_{\mathbb{P}(E)}(1)|$
.
$H\in |{\mathcal{O}}_{\mathbb{P}(E)}(1)|$
.
 $H=\mathbb{P}^{1}\times \mathbb{P}^{n-2}$
, and
$H=\mathbb{P}^{1}\times \mathbb{P}^{n-2}$
, and
 $p$
is the projection to the second factor.
$p$
is the projection to the second factor.(iii)
 $(X,A)=(Q^{3},H)$
, where
$(X,A)=(Q^{3},H)$
, where
 $Q^{3}$
is a smooth quadric threefold and
$Q^{3}$
is a smooth quadric threefold and
 $H$
is a smooth quadric surface with
$H$
is a smooth quadric surface with
 $H\in |{\mathcal{O}}_{Q^{3}}(1)|$
.
$H\in |{\mathcal{O}}_{Q^{3}}(1)|$
.
 $p$
is the projection to one of the factors of
$p$
is the projection to one of the factors of
 $H\cong \mathbb{P}^{1}\times \mathbb{P}^{1}$
.
$H\cong \mathbb{P}^{1}\times \mathbb{P}^{1}$
.(iv)
 $(X,A)=(\mathbb{P}^{3},H)$
.
$(X,A)=(\mathbb{P}^{3},H)$
.
 $H$
is a smooth quadric surface and
$H$
is a smooth quadric surface and
 $H\in |{\mathcal{O}}_{\mathbb{P}^{3}}(2)|$
, and
$H\in |{\mathcal{O}}_{\mathbb{P}^{3}}(2)|$
, and
 $p$
is again a projection to one of the factors of
$p$
is again a projection to one of the factors of
 $H\cong \mathbb{P}^{1}\times \mathbb{P}^{1}$
.
$H\cong \mathbb{P}^{1}\times \mathbb{P}^{1}$
.
Convention.
Throughout, we work over the field
![]() $\mathbb{C}$
of complex numbers unless otherwise stated. Varieties are always assumed to be integral separated schemes of finite type over
$\mathbb{C}$
of complex numbers unless otherwise stated. Varieties are always assumed to be integral separated schemes of finite type over
![]() $\mathbb{C}$
. If
$\mathbb{C}$
. If
![]() $D$
is a Weil divisor on a projective normal variety
$D$
is a Weil divisor on a projective normal variety
![]() $X$
, we denote by
$X$
, we denote by
![]() ${\mathcal{O}}_{X}(D)$
the reflexive sheaf associated to
${\mathcal{O}}_{X}(D)$
the reflexive sheaf associated to
![]() $D$
. Given a coherent sheaf
$D$
. Given a coherent sheaf
![]() ${\mathcal{F}}$
on a variety
${\mathcal{F}}$
on a variety
![]() $X$
of generic rank
$X$
of generic rank
![]() $r$
, then we denote by
$r$
, then we denote by
![]() ${\mathcal{F}}^{\vee }$
the sheaf
${\mathcal{F}}^{\vee }$
the sheaf
![]() ${\mathcal{H}}om_{{\mathcal{O}}_{X}}({\mathcal{F}},{\mathcal{O}}_{X})$
, and by
${\mathcal{H}}om_{{\mathcal{O}}_{X}}({\mathcal{F}},{\mathcal{O}}_{X})$
, and by
![]() $\det ({\mathcal{F}})$
the sheaf
$\det ({\mathcal{F}})$
the sheaf
![]() $(\wedge ^{r}{\mathcal{F}})^{\vee \vee }$
. We denote by
$(\wedge ^{r}{\mathcal{F}})^{\vee \vee }$
. We denote by
![]() ${\mathcal{F}}(x)={\mathcal{F}}_{x}\otimes _{{\mathcal{O}}_{X,x}}k(x)$
the fiber of
${\mathcal{F}}(x)={\mathcal{F}}_{x}\otimes _{{\mathcal{O}}_{X,x}}k(x)$
the fiber of
![]() ${\mathcal{F}}$
at
${\mathcal{F}}$
at
![]() $x\in X$
. If
$x\in X$
. If
![]() ${\mathcal{F}}$
is a coherent sheaf on a variety
${\mathcal{F}}$
is a coherent sheaf on a variety
![]() $X$
, we denote by
$X$
, we denote by
![]() $\mathbb{P}({\mathcal{F}})$
the Grothendieck projectivization
$\mathbb{P}({\mathcal{F}})$
the Grothendieck projectivization
![]() $\text{Proj}(\bigoplus _{m\geqslant 0}\text{Sym}^{m}{\mathcal{F}})$
. If
$\text{Proj}(\bigoplus _{m\geqslant 0}\text{Sym}^{m}{\mathcal{F}})$
. If
![]() $f:X\rightarrow Y$
is a morphism between projective normal varieties, we denote by
$f:X\rightarrow Y$
is a morphism between projective normal varieties, we denote by
![]() $\unicode[STIX]{x1D6FA}_{X/Y}^{1}$
the relative differential sheaf. Moreover, if
$\unicode[STIX]{x1D6FA}_{X/Y}^{1}$
the relative differential sheaf. Moreover, if
![]() $Y$
is smooth, we denote by
$Y$
is smooth, we denote by
![]() $K_{X/Y}$
the relative canonical divisor
$K_{X/Y}$
the relative canonical divisor
![]() $K_{X}-f^{\ast }K_{Y}$
, and by
$K_{X}-f^{\ast }K_{Y}$
, and by
![]() $\unicode[STIX]{x1D714}_{X/Y}$
the reflexive sheaf
$\unicode[STIX]{x1D714}_{X/Y}$
the reflexive sheaf
![]() $\unicode[STIX]{x1D714}_{X}\otimes f^{\ast }\unicode[STIX]{x1D714}_{Y}^{\vee }$
.
$\unicode[STIX]{x1D714}_{X}\otimes f^{\ast }\unicode[STIX]{x1D714}_{Y}^{\vee }$
.
2 Ample sheaves and rational curves
Let
![]() $X$
be a projective manifold. In this section, we gather some results about the behavior of an ample subsheaf
$X$
be a projective manifold. In this section, we gather some results about the behavior of an ample subsheaf
![]() ${\mathcal{F}}\subset T_{X}$
with respect to a family of minimal rational curves on
${\mathcal{F}}\subset T_{X}$
with respect to a family of minimal rational curves on
![]() $X$
.
$X$
.
2.1 Ample sheaves
Recall that an invertible sheaf
![]() ${\mathcal{L}}$
on a quasi-projective variety
${\mathcal{L}}$
on a quasi-projective variety
![]() $X$
is said to be ample if for every coherent sheaf
$X$
is said to be ample if for every coherent sheaf
![]() ${\mathcal{G}}$
on
${\mathcal{G}}$
on
![]() $X$
, there is an integer
$X$
, there is an integer
![]() $n_{0}>0$
such that for every
$n_{0}>0$
such that for every
![]() $n\geqslant n_{0}$
, the sheaf
$n\geqslant n_{0}$
, the sheaf
![]() ${\mathcal{G}}\otimes {\mathcal{L}}^{n}$
is generated by its global sections (see [Reference Hartshorne18, Section II.7]). In general, a coherent sheaf
${\mathcal{G}}\otimes {\mathcal{L}}^{n}$
is generated by its global sections (see [Reference Hartshorne18, Section II.7]). In general, a coherent sheaf
![]() ${\mathcal{F}}$
on a quasi-projective variety
${\mathcal{F}}$
on a quasi-projective variety
![]() $X$
is said to be ample if the invertible sheaf
$X$
is said to be ample if the invertible sheaf
![]() ${\mathcal{O}}_{\mathbb{P}({\mathcal{F}})}(1)$
is ample on
${\mathcal{O}}_{\mathbb{P}({\mathcal{F}})}(1)$
is ample on
![]() $\mathbb{P}({\mathcal{F}})$
[Reference Kubota22].
$\mathbb{P}({\mathcal{F}})$
[Reference Kubota22].
Well-known properties of ampleness of locally free sheaves still hold in this general setting.
(i) A sheaf
 ${\mathcal{F}}$
on a quasi-projective variety
${\mathcal{F}}$
on a quasi-projective variety
 $X$
is ample if and only if, for any coherent sheaf
$X$
is ample if and only if, for any coherent sheaf
 ${\mathcal{G}}$
on
${\mathcal{G}}$
on
 $X$
,
$X$
,
 ${\mathcal{G}}\otimes \text{Sym}^{m}{\mathcal{F}}$
is globally generated for
${\mathcal{G}}\otimes \text{Sym}^{m}{\mathcal{F}}$
is globally generated for
 $m\gg 1$
(see [Reference Kubota22, Theorem 1]).
$m\gg 1$
(see [Reference Kubota22, Theorem 1]).(ii) If
 $i:Y\rightarrow X$
is an immersion, and
$i:Y\rightarrow X$
is an immersion, and
 ${\mathcal{F}}$
is an ample sheaf on
${\mathcal{F}}$
is an ample sheaf on
 $X$
, then
$X$
, then
 $i^{\ast }{\mathcal{F}}$
is an ample sheaf on
$i^{\ast }{\mathcal{F}}$
is an ample sheaf on
 $Y$
(see [Reference Kubota22, Proposition 6]).
$Y$
(see [Reference Kubota22, Proposition 6]).(iii) If
 $\unicode[STIX]{x1D70B}:Y\rightarrow X$
is a finite morphism with
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
is a finite morphism with
 $X$
and
$X$
and
 $Y$
quasi-projective varieties, and
$Y$
quasi-projective varieties, and
 ${\mathcal{F}}$
is a coherent sheaf on
${\mathcal{F}}$
is a coherent sheaf on
 $X$
, then
$X$
, then
 ${\mathcal{F}}$
is ample if and only if
${\mathcal{F}}$
is ample if and only if
 $\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}$
is ample. Note that
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}$
is ample. Note that
 $\mathbb{P}(\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}})=\mathbb{P}({\mathcal{F}})\times _{X}Y$
, and
$\mathbb{P}(\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}})=\mathbb{P}({\mathcal{F}})\times _{X}Y$
, and
 ${\mathcal{O}}_{\mathbb{P}({\mathcal{F}})}(1)$
pulls back, by a finite morphism, to
${\mathcal{O}}_{\mathbb{P}({\mathcal{F}})}(1)$
pulls back, by a finite morphism, to
 ${\mathcal{O}}_{\mathbb{P}(\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}})}(1)$
.
${\mathcal{O}}_{\mathbb{P}(\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}})}(1)$
.(iv) Any quotient of an ample sheaf is ample (see [Reference Kubota22, Proposition 1]). In particular, the image of an ample sheaf under a nonzero map is also ample.
(v) If
 ${\mathcal{F}}$
is a locally free ample sheaf of rank
${\mathcal{F}}$
is a locally free ample sheaf of rank
 $r$
, then the
$r$
, then the
 $s$
th exterior power
$s$
th exterior power
 $\wedge ^{s}{\mathcal{F}}$
is ample for any
$\wedge ^{s}{\mathcal{F}}$
is ample for any
 $1\leqslant s\leqslant r$
(see [Reference Hartshorne17, Corollary 5.3]).
$1\leqslant s\leqslant r$
(see [Reference Hartshorne17, Corollary 5.3]).(vi) If
 ${\mathcal{L}}$
is an ample invertible sheaf on a quasi-projective variety
${\mathcal{L}}$
is an ample invertible sheaf on a quasi-projective variety
 $X$
, then
$X$
, then
 ${\mathcal{L}}^{m}$
is very ample for some
${\mathcal{L}}^{m}$
is very ample for some
 $m>0$
; that is, there is an immersion
$m>0$
; that is, there is an immersion
 $i:X\rightarrow \mathbb{P}^{n}$
for some
$i:X\rightarrow \mathbb{P}^{n}$
for some
 $n$
such that
$n$
such that
 ${\mathcal{L}}^{m}=i^{\ast }{\mathcal{O}}_{\mathbb{P}^{n}}(1)$
(see [Reference Hartshorne18, II, Theorem 7.6]).
${\mathcal{L}}^{m}=i^{\ast }{\mathcal{O}}_{\mathbb{P}^{n}}(1)$
(see [Reference Hartshorne18, II, Theorem 7.6]).
2.2 Minimal rational curves
Let
![]() $X$
be a normal projective variety. By
$X$
be a normal projective variety. By
![]() $\text{Hom}(\mathbb{P}^{1},X)$
we denote the open subscheme
$\text{Hom}(\mathbb{P}^{1},X)$
we denote the open subscheme
![]() $\subset \text{Hilb}(\mathbb{P}^{1}\times X)$
of morphisms from
$\subset \text{Hilb}(\mathbb{P}^{1}\times X)$
of morphisms from
![]() $\mathbb{P}^{1}$
to
$\mathbb{P}^{1}$
to
![]() $X$
. Let
$X$
. Let
![]() $\text{Hom}_{1}(\mathbb{P}^{1},X)\subset \text{Hom}(\mathbb{P}^{1},X)$
be the open subscheme corresponding to those morphisms
$\text{Hom}_{1}(\mathbb{P}^{1},X)\subset \text{Hom}(\mathbb{P}^{1},X)$
be the open subscheme corresponding to those morphisms
![]() $f:\mathbb{P}^{1}\rightarrow X$
that are birational onto their image. The group
$f:\mathbb{P}^{1}\rightarrow X$
that are birational onto their image. The group
![]() $\text{Aut}(\mathbb{P}^{1})$
acts on
$\text{Aut}(\mathbb{P}^{1})$
acts on
![]() $\text{Hom}_{1}(\mathbb{P}^{1},X)$
and its quotient “really parametrizes” morphisms from
$\text{Hom}_{1}(\mathbb{P}^{1},X)$
and its quotient “really parametrizes” morphisms from
![]() $\mathbb{P}^{1}$
into
$\mathbb{P}^{1}$
into
![]() $X$
. It can be proved that the quotient exists, and its normalization is denoted
$X$
. It can be proved that the quotient exists, and its normalization is denoted
![]() $\text{RatCurves}^{n}(X)$
and called the space of rational curve on
$\text{RatCurves}^{n}(X)$
and called the space of rational curve on
![]() $X$
. For more details we refer to [Reference Kollár19].
$X$
. For more details we refer to [Reference Kollár19].
Let
![]() ${\mathcal{V}}$
be an irreducible component of
${\mathcal{V}}$
be an irreducible component of
![]() $\text{RatCurves}^{n}(X)$
.
$\text{RatCurves}^{n}(X)$
.
![]() ${\mathcal{V}}$
is said to be a covering family of rational curves on
${\mathcal{V}}$
is said to be a covering family of rational curves on
![]() $X$
if the corresponding universal family dominates
$X$
if the corresponding universal family dominates
![]() $X$
. A covering family
$X$
. A covering family
![]() ${\mathcal{V}}$
of rational curves on
${\mathcal{V}}$
of rational curves on
![]() $X$
is called minimal if its general members have minimal anticanonical degree. If
$X$
is called minimal if its general members have minimal anticanonical degree. If
![]() $X$
is a uniruled projective manifold, then
$X$
is a uniruled projective manifold, then
![]() $X$
carries a minimal covering family of rational curves. We fix such a family
$X$
carries a minimal covering family of rational curves. We fix such a family
![]() ${\mathcal{V}}$
, and let
${\mathcal{V}}$
, and let
![]() $[\ell ]\in {\mathcal{V}}$
be a general point. Then, the tangent bundle
$[\ell ]\in {\mathcal{V}}$
be a general point. Then, the tangent bundle
![]() $T_{X}$
can be decomposed on the normalization of
$T_{X}$
can be decomposed on the normalization of
![]() $\ell$
as
$\ell$
as
![]() ${\mathcal{O}}_{\mathbb{P}^{1}}(2)\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(1)^{\oplus d}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}^{\oplus (n-d-1)}$
, where
${\mathcal{O}}_{\mathbb{P}^{1}}(2)\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(1)^{\oplus d}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}^{\oplus (n-d-1)}$
, where
![]() $d+2=\det (T_{X})\cdot \ell \geqslant 2$
is the anticanonical degree of
$d+2=\det (T_{X})\cdot \ell \geqslant 2$
is the anticanonical degree of
![]() ${\mathcal{V}}$
.
${\mathcal{V}}$
.
Let
![]() $\bar{{\mathcal{V}}}$
be the normalization of the closure of
$\bar{{\mathcal{V}}}$
be the normalization of the closure of
![]() ${\mathcal{V}}$
in
${\mathcal{V}}$
in
![]() $\text{Chow}(X)$
. We define the following equivalence relation on
$\text{Chow}(X)$
. We define the following equivalence relation on
![]() $X$
. Two points
$X$
. Two points
![]() $x$
,
$x$
,
![]() $y\in X$
are
$y\in X$
are
![]() $\bar{{\mathcal{V}}}$
-equivalent if they can be connected by a chain of
$\bar{{\mathcal{V}}}$
-equivalent if they can be connected by a chain of
![]() $1$
-cycle from
$1$
-cycle from
![]() $\bar{{\mathcal{V}}}$
. By [Reference Campana10] (see also [Reference Kollár, Miyaoka and Mori.21]), there exists a proper surjective morphism
$\bar{{\mathcal{V}}}$
. By [Reference Campana10] (see also [Reference Kollár, Miyaoka and Mori.21]), there exists a proper surjective morphism
![]() $\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
from an open subset of
$\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
from an open subset of
![]() $X$
onto a normal variety
$X$
onto a normal variety
![]() $T_{0}$
whose fibers are
$T_{0}$
whose fibers are
![]() $\bar{{\mathcal{V}}}$
-equivalence classes. We call this map the
$\bar{{\mathcal{V}}}$
-equivalence classes. We call this map the
![]() $\bar{{\mathcal{V}}}$
-rationally connected quotient of
$\bar{{\mathcal{V}}}$
-rationally connected quotient of
![]() $X$
.
$X$
.
The first step toward Theorem 1.1 is the following result, which was essentially proved in [Reference Araujo3].
Theorem 2.1. [Reference Araujo, Druel and Kovács5, Proposition 2.7]
Let
![]() $X$
be a projective uniruled manifold, and let
$X$
be a projective uniruled manifold, and let
![]() ${\mathcal{V}}$
be a minimal covering family of rational curves on
${\mathcal{V}}$
be a minimal covering family of rational curves on
![]() $X$
. If
$X$
. If
![]() $T_{X}$
contains a subsheaf
$T_{X}$
contains a subsheaf
![]() ${\mathcal{F}}$
of rank
${\mathcal{F}}$
of rank
![]() $r$
such that
$r$
such that
![]() ${\mathcal{F}}|_{\ell }$
is an ample vector bundle for a general member
${\mathcal{F}}|_{\ell }$
is an ample vector bundle for a general member
![]() $[\ell ]\in {\mathcal{V}}$
, then there exists a dense open subset
$[\ell ]\in {\mathcal{V}}$
, then there exists a dense open subset
![]() $X_{0}$
of
$X_{0}$
of
![]() $X$
and a
$X$
and a
![]() $\mathbb{P}^{d+1}$
-bundle
$\mathbb{P}^{d+1}$
-bundle
![]() $\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
such that any curve on
$\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
such that any curve on
![]() $X$
parametrized by
$X$
parametrized by
![]() ${\mathcal{V}}$
and meeting
${\mathcal{V}}$
and meeting
![]() $X_{0}$
is a line on a fiber of
$X_{0}$
is a line on a fiber of
![]() $\unicode[STIX]{x1D711}_{0}$
. In particular,
$\unicode[STIX]{x1D711}_{0}$
. In particular,
![]() $\unicode[STIX]{x1D711}_{0}$
is the
$\unicode[STIX]{x1D711}_{0}$
is the
![]() $\bar{{\mathcal{V}}}$
-rationally connected quotient of
$\bar{{\mathcal{V}}}$
-rationally connected quotient of
![]() $X$
.
$X$
.
Recall that the singular locus
![]() $\text{Sing}({\mathcal{S}})$
of a coherent sheaf
$\text{Sing}({\mathcal{S}})$
of a coherent sheaf
![]() ${\mathcal{S}}$
over
${\mathcal{S}}$
over
![]() $X$
is the set of all points of
$X$
is the set of all points of
![]() $X$
where
$X$
where
![]() ${\mathcal{S}}$
is not locally free.
${\mathcal{S}}$
is not locally free.
Remark 2.2. The hypothesis in Theorem 2.1 that
![]() ${\mathcal{F}}$
is locally free over a general member of
${\mathcal{F}}$
is locally free over a general member of
![]() ${\mathcal{V}}$
is automatically satisfied. In fact, since
${\mathcal{V}}$
is automatically satisfied. In fact, since
![]() ${\mathcal{F}}$
is torsion-free and
${\mathcal{F}}$
is torsion-free and
![]() $X$
is smooth,
$X$
is smooth,
![]() ${\mathcal{F}}$
is locally free in codimension one. By [Reference Kollár19, II, Proposition 3.7], a general member of
${\mathcal{F}}$
is locally free in codimension one. By [Reference Kollár19, II, Proposition 3.7], a general member of
![]() ${\mathcal{V}}$
is disjoint from
${\mathcal{V}}$
is disjoint from
![]() $\text{Sing}({\mathcal{F}})$
; hence,
$\text{Sing}({\mathcal{F}})$
; hence,
![]() ${\mathcal{F}}$
is locally free over a general member of
${\mathcal{F}}$
is locally free over a general member of
![]() ${\mathcal{V}}$
.
${\mathcal{V}}$
.
As an immediate application of Theorem 2.1, we can derive a weak version of [Reference Aprodu, Kebekus and Peternell2, Theorem 4.2].
Corollary 2.3. Let
![]() $X$
be a projective uniruled manifold with
$X$
be a projective uniruled manifold with
![]() $\unicode[STIX]{x1D70C}(X)=1$
, and let
$\unicode[STIX]{x1D70C}(X)=1$
, and let
![]() ${\mathcal{V}}$
be a minimal covering family of rational curves on
${\mathcal{V}}$
be a minimal covering family of rational curves on
![]() $X$
. If
$X$
. If
![]() $T_{X}$
contains a subsheaf
$T_{X}$
contains a subsheaf
![]() ${\mathcal{F}}$
of rank
${\mathcal{F}}$
of rank
![]() $r$
such that
$r$
such that
![]() ${\mathcal{F}}|_{\ell }$
is ample for a general member
${\mathcal{F}}|_{\ell }$
is ample for a general member
![]() $[\ell ]\in {\mathcal{V}}$
, then
$[\ell ]\in {\mathcal{V}}$
, then
![]() $X\cong \mathbb{P}^{n}$
.
$X\cong \mathbb{P}^{n}$
.
Corollary 2.4. [Reference Aprodu, Kebekus and Peternell2, Corollary 4.3]
Let
![]() $X$
be a projective manifold with
$X$
be a projective manifold with
![]() $\unicode[STIX]{x1D70C}(X)=1$
. Assume that
$\unicode[STIX]{x1D70C}(X)=1$
. Assume that
![]() $T_{X}$
contains an ample subsheaf, then
$T_{X}$
contains an ample subsheaf, then
![]() $X\cong \mathbb{P}^{n}$
.
$X\cong \mathbb{P}^{n}$
.
Proof. Since the tangent bundle
![]() $T_{X}$
contains an ample subsheaf
$T_{X}$
contains an ample subsheaf
![]() ${\mathcal{F}}$
,
${\mathcal{F}}$
,
![]() $X$
is uniruled (see [Reference Miyaoka24, Corollary 8.6]), and it carries a minimal covering family
$X$
is uniruled (see [Reference Miyaoka24, Corollary 8.6]), and it carries a minimal covering family
![]() ${\mathcal{V}}$
of rational curves. Note that the restriction
${\mathcal{V}}$
of rational curves. Note that the restriction
![]() ${\mathcal{F}}|_{C}$
is ample for any curve
${\mathcal{F}}|_{C}$
is ample for any curve
![]() $C\subset X$
; thus, we can deduce the result from Corollary 2.3.☐
$C\subset X$
; thus, we can deduce the result from Corollary 2.3.☐
Remark 2.5. Our approach above is quite different from that in [Reference Aprodu, Kebekus and Peternell2]. The proof in [Reference Aprodu, Kebekus and Peternell2] is based on a careful analysis of the singular locus of
![]() ${\mathcal{F}}$
, and the locally freeness of
${\mathcal{F}}$
, and the locally freeness of
![]() ${\mathcal{F}}$
has been proved. Even though our argument does not tell anything about the singular locus of
${\mathcal{F}}$
has been proved. Even though our argument does not tell anything about the singular locus of
![]() ${\mathcal{F}}$
, it has the advantage of giving a rough description of the geometric structure of projective manifolds whose tangent bundle contains a “positive” subsheaf.
${\mathcal{F}}$
, it has the advantage of giving a rough description of the geometric structure of projective manifolds whose tangent bundle contains a “positive” subsheaf.
3 Foliations and Pfaff fields
Let
![]() ${\mathcal{S}}$
be a subsheaf of
${\mathcal{S}}$
be a subsheaf of
![]() $T_{X}$
on a quasi-projective manifold
$T_{X}$
on a quasi-projective manifold
![]() $X$
. We denote by
$X$
. We denote by
![]() ${\mathcal{S}}^{\text{reg}}$
the largest open subset of
${\mathcal{S}}^{\text{reg}}$
the largest open subset of
![]() $X$
such that
$X$
such that
![]() ${\mathcal{S}}$
is a subbundle of
${\mathcal{S}}$
is a subbundle of
![]() $T_{X}$
over
$T_{X}$
over
![]() ${\mathcal{S}}^{\text{reg}}$
. Note that, in general,
${\mathcal{S}}^{\text{reg}}$
. Note that, in general,
![]() $\text{Sing}({\mathcal{S}})$
is a proper subset of
$\text{Sing}({\mathcal{S}})$
is a proper subset of
![]() $X\setminus {\mathcal{S}}^{\text{reg}}$
.
$X\setminus {\mathcal{S}}^{\text{reg}}$
.
Definition 3.1. Let
![]() $X$
be a quasi-projective manifold, and let
$X$
be a quasi-projective manifold, and let
![]() ${\mathcal{S}}\subsetneq T_{X}$
be a coherent subsheaf of positive rank.
${\mathcal{S}}\subsetneq T_{X}$
be a coherent subsheaf of positive rank.
![]() ${\mathcal{S}}$
is called a foliation if it satisfies the following conditions.
${\mathcal{S}}$
is called a foliation if it satisfies the following conditions.
(i)
 ${\mathcal{S}}$
is saturated in
${\mathcal{S}}$
is saturated in
 $T_{X}$
; that is,
$T_{X}$
; that is,
 $T_{X}/{\mathcal{S}}$
is torsion-free.
$T_{X}/{\mathcal{S}}$
is torsion-free.(ii) The sheaf
 ${\mathcal{S}}$
is closed under the Lie bracket.
${\mathcal{S}}$
is closed under the Lie bracket.
In addition,
![]() ${\mathcal{S}}$
is called an algebraically integrable foliation if the following holds.
${\mathcal{S}}$
is called an algebraically integrable foliation if the following holds.
(iii) For a general point
 $x\in X$
, there exists a projective subvariety
$x\in X$
, there exists a projective subvariety
 $F_{x}$
passing through
$F_{x}$
passing through
 $x$
such that We call
$x$
such that We call $$\begin{eqnarray}{\mathcal{S}}|_{F_{x}\cap {\mathcal{S}}^{\text{reg}}}=T_{F_{x}}|_{F_{x}\cap {\mathcal{S}}^{\text{reg}}}\subset T_{X}|_{F_{x}\cap {\mathcal{S}}^{\text{reg}}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}|_{F_{x}\cap {\mathcal{S}}^{\text{reg}}}=T_{F_{x}}|_{F_{x}\cap {\mathcal{S}}^{\text{reg}}}\subset T_{X}|_{F_{x}\cap {\mathcal{S}}^{\text{reg}}}.\end{eqnarray}$$
 $F_{x}$
the
$F_{x}$
the
 ${\mathcal{S}}$
-leaf through
${\mathcal{S}}$
-leaf through
 $x$
.
$x$
.
Remark 3.2. Let
![]() $X$
be a projective manifold, and let
$X$
be a projective manifold, and let
![]() ${\mathcal{S}}$
be a saturated subsheaf of
${\mathcal{S}}$
be a saturated subsheaf of
![]() $T_{X}$
. To show that
$T_{X}$
. To show that
![]() ${\mathcal{S}}$
is an algebraically integrable foliation, it is sufficient to show that it is an algebraically integrable foliation over a Zariski open subset of
${\mathcal{S}}$
is an algebraically integrable foliation, it is sufficient to show that it is an algebraically integrable foliation over a Zariski open subset of
![]() $X$
.
$X$
.
Example 3.3. Let
![]() $X\rightarrow Y$
be a fibration with
$X\rightarrow Y$
be a fibration with
![]() $X$
and
$X$
and
![]() $Y$
projective manifolds. Then
$Y$
projective manifolds. Then
![]() $T_{X/Y}\subset T_{X}$
defines an algebraically integrable foliation on
$T_{X/Y}\subset T_{X}$
defines an algebraically integrable foliation on
![]() $X$
such that the general leaves are the fibers.
$X$
such that the general leaves are the fibers.
Example 3.4. [Reference Araujo and Druel4, 4.1]
Let
![]() ${\mathcal{F}}$
be a subsheaf
${\mathcal{F}}$
be a subsheaf
![]() ${\mathcal{O}}_{\mathbb{P}^{n}}(1)^{\oplus r}$
of
${\mathcal{O}}_{\mathbb{P}^{n}}(1)^{\oplus r}$
of
![]() $T_{\mathbb{P}^{n}}$
on
$T_{\mathbb{P}^{n}}$
on
![]() $\mathbb{P}^{n}$
. Then
$\mathbb{P}^{n}$
. Then
![]() ${\mathcal{F}}$
is an algebraically integrable foliation and it is defined by a linear projection
${\mathcal{F}}$
is an algebraically integrable foliation and it is defined by a linear projection
![]() $\mathbb{P}^{n}{\dashrightarrow}\mathbb{P}^{n-r}$
. The set of points of indeterminacy
$\mathbb{P}^{n}{\dashrightarrow}\mathbb{P}^{n-r}$
. The set of points of indeterminacy
![]() $S$
of this rational map is an (
$S$
of this rational map is an (
![]() $r-1$
)-dimensional linear subspace. Let
$r-1$
)-dimensional linear subspace. Let
![]() $x\not \in S$
be a point. Then the leaf passing through
$x\not \in S$
be a point. Then the leaf passing through
![]() $x$
is the
$x$
is the
![]() $r$
-dimensional linear subspace
$r$
-dimensional linear subspace
![]() $L$
of
$L$
of
![]() $\mathbb{P}^{n}$
containing both
$\mathbb{P}^{n}$
containing both
![]() $x$
and
$x$
and
![]() $S$
.
$S$
.
Definition 3.5. Let
![]() $X$
be a projective variety, and
$X$
be a projective variety, and
![]() $r$
a positive integer. A Pfaff field of rank
$r$
a positive integer. A Pfaff field of rank
![]() $r$
on
$r$
on
![]() $X$
is a nonzero map
$X$
is a nonzero map
![]() $\unicode[STIX]{x2202}:\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{L}}$
, where
$\unicode[STIX]{x2202}:\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{L}}$
, where
![]() ${\mathcal{L}}$
is an invertible sheaf on
${\mathcal{L}}$
is an invertible sheaf on
![]() $X$
.
$X$
.
Lemma 3.6. [Reference Araujo, Druel and Kovács5, Proposition 4.5]
Let
![]() $X$
be a projective variety, and let
$X$
be a projective variety, and let
![]() $n:\widetilde{X}\rightarrow X$
be its normalization. Let
$n:\widetilde{X}\rightarrow X$
be its normalization. Let
![]() ${\mathcal{L}}$
be an invertible sheaf on
${\mathcal{L}}$
be an invertible sheaf on
![]() $X$
, let
$X$
, let
![]() $r$
be a positive integer, and let
$r$
be a positive integer, and let
![]() $\unicode[STIX]{x2202}:\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{L}}$
be a Pfaff field. Then
$\unicode[STIX]{x2202}:\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{L}}$
be a Pfaff field. Then
![]() $\unicode[STIX]{x2202}$
can be extended uniquely to a Pfaff field
$\unicode[STIX]{x2202}$
can be extended uniquely to a Pfaff field
![]() $\widetilde{\unicode[STIX]{x2202}}:\unicode[STIX]{x1D6FA}_{\widetilde{X}}^{r}\rightarrow n^{\ast }{\mathcal{L}}$
.
$\widetilde{\unicode[STIX]{x2202}}:\unicode[STIX]{x1D6FA}_{\widetilde{X}}^{r}\rightarrow n^{\ast }{\mathcal{L}}$
.
Let
![]() $X$
be a projective manifold, and let
$X$
be a projective manifold, and let
![]() ${\mathcal{S}}\subset T_{X}$
be a subsheaf with positive rank
${\mathcal{S}}\subset T_{X}$
be a subsheaf with positive rank
![]() $r$
. We denote by
$r$
. We denote by
![]() $K_{{\mathcal{S}}}$
the canonical class
$K_{{\mathcal{S}}}$
the canonical class
![]() $-c_{1}(\det ({\mathcal{S}}))$
of
$-c_{1}(\det ({\mathcal{S}}))$
of
![]() ${\mathcal{S}}$
. Then there is a natural associated Pfaff field of rank
${\mathcal{S}}$
. Then there is a natural associated Pfaff field of rank
![]() $r$
:
$r$
:
Lemma 3.7. [Reference Araujo and Druel4, Lemma 3.2]
Let
![]() $X$
be a projective manifold, and let
$X$
be a projective manifold, and let
![]() ${\mathcal{S}}$
be an algebraically integrable foliation on
${\mathcal{S}}$
be an algebraically integrable foliation on
![]() $X$
. Then there is a unique irreducible projective subvariety
$X$
. Then there is a unique irreducible projective subvariety
![]() $W$
of
$W$
of
![]() $\text{Chow}(X)$
whose general point parametrizes a general leaf of
$\text{Chow}(X)$
whose general point parametrizes a general leaf of
![]() ${\mathcal{S}}$
.
${\mathcal{S}}$
.
Remark 3.8. Let
![]() $X$
be a projective manifold, and let
$X$
be a projective manifold, and let
![]() ${\mathcal{S}}$
be an algebraically integrable foliation of rank
${\mathcal{S}}$
be an algebraically integrable foliation of rank
![]() $r$
on
$r$
on
![]() $X$
. Let
$X$
. Let
![]() $W$
be the subvariety of
$W$
be the subvariety of
![]() $\text{Chow}(X)$
provided in Lemma 3.7. Let
$\text{Chow}(X)$
provided in Lemma 3.7. Let
![]() $Z\subset W$
be a general closed subvariety of
$Z\subset W$
be a general closed subvariety of
![]() $W$
, and let
$W$
, and let
![]() $U\subset Z\times X$
be the universal cycle over
$U\subset Z\times X$
be the universal cycle over
![]() $Z$
. Let
$Z$
. Let
![]() $\widetilde{Z}$
and
$\widetilde{Z}$
and
![]() $\widetilde{U}$
be the normalizations of
$\widetilde{U}$
be the normalizations of
![]() $Z$
and
$Z$
and
![]() $U$
, respectively. We claim that the Pfaff field
$U$
, respectively. We claim that the Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
can be extended to a Pfaff field
$\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
can be extended to a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}\rightarrow n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
.
$\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}\rightarrow n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
.

Let
![]() $V$
be the universal cycle over
$V$
be the universal cycle over
![]() $W$
with
$W$
with
![]() $v:V\rightarrow X$
. From the proof of [Reference Araujo and Druel4, Lemma 3.2], we know that the Pfaff field
$v:V\rightarrow X$
. From the proof of [Reference Araujo and Druel4, Lemma 3.2], we know that the Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
extends to be a Pfaff field
$\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
extends to be a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{V}^{r}\rightarrow v^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
. It induces a Pfaff field
$\unicode[STIX]{x1D6FA}_{V}^{r}\rightarrow v^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
. It induces a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{U}^{r}\rightarrow p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
. Note that
$\unicode[STIX]{x1D6FA}_{U}^{r}\rightarrow p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
. Note that
![]() $U$
is irreducible since
$U$
is irreducible since
![]() $Z$
is a general subvariety. By Lemma 3.6, it can be uniquely extended to a Pfaff field
$Z$
is a general subvariety. By Lemma 3.6, it can be uniquely extended to a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{\widetilde{U}}^{r}\rightarrow n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
.
$\unicode[STIX]{x1D6FA}_{\widetilde{U}}^{r}\rightarrow n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
.
Let
![]() ${\mathcal{K}}$
be the kernel of the morphism
${\mathcal{K}}$
be the kernel of the morphism
![]() $\unicode[STIX]{x1D6FA}_{\widetilde{U}}^{r}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}$
. Let
$\unicode[STIX]{x1D6FA}_{\widetilde{U}}^{r}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}$
. Let
![]() $F$
be a general fiber of
$F$
be a general fiber of
![]() $\widetilde{q}$
such that its image under
$\widetilde{q}$
such that its image under
![]() $p\circ n$
is an
$p\circ n$
is an
![]() ${\mathcal{S}}$
-leaf and the morphism
${\mathcal{S}}$
-leaf and the morphism
![]() $p\circ n$
restricted on
$p\circ n$
restricted on
![]() $F$
is finite and birational. Let
$F$
is finite and birational. Let
![]() $x\in F$
be a point such that
$x\in F$
be a point such that
![]() $F$
is smooth at
$F$
is smooth at
![]() $x$
and
$x$
and
![]() $p\circ n$
is an isomorphism at a neighborhood of
$p\circ n$
is an isomorphism at a neighborhood of
![]() $x$
. Then the composite map
$x$
. Then the composite map
![]() $\unicode[STIX]{x1D6FA}_{\widetilde{U}}^{r}|_{F}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}|_{F}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{F}^{r}$
implies that the composite map
$\unicode[STIX]{x1D6FA}_{\widetilde{U}}^{r}|_{F}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}|_{F}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{F}^{r}$
implies that the composite map
vanishes in a neighborhood of
![]() $x$
; hence, it vanishes generically over
$x$
; hence, it vanishes generically over
![]() $\widetilde{U}$
. Since the sheaf
$\widetilde{U}$
. Since the sheaf
![]() $n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
is torsion-free, it vanishes identically and finally yields a Pfaff field
$n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
is torsion-free, it vanishes identically and finally yields a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}\rightarrow n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
.
$\unicode[STIX]{x1D6FA}_{\widetilde{U}/\widetilde{Z}}^{r}\rightarrow n^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{S}}})$
.
Let
![]() $X$
be a projective manifold, and let
$X$
be a projective manifold, and let
![]() ${\mathcal{S}}\subset T_{X}$
be a subsheaf. We define its saturation
${\mathcal{S}}\subset T_{X}$
be a subsheaf. We define its saturation
![]() $\overline{{\mathcal{S}}}$
as the kernel of the natural surjection
$\overline{{\mathcal{S}}}$
as the kernel of the natural surjection
![]() $T_{X}{\twoheadrightarrow}(T_{X}/{\mathcal{S}})/(torsion)$
. Then
$T_{X}{\twoheadrightarrow}(T_{X}/{\mathcal{S}})/(torsion)$
. Then
![]() $\overline{{\mathcal{S}}}$
is obviously saturated.
$\overline{{\mathcal{S}}}$
is obviously saturated.
Theorem 3.9. Let
![]() $X$
be a projective manifold. Assume that
$X$
be a projective manifold. Assume that
![]() $T_{X}$
contains an ample subsheaf
$T_{X}$
contains an ample subsheaf
![]() ${\mathcal{F}}$
of rank
${\mathcal{F}}$
of rank
![]() $r<\dim (X)$
. Then its saturation
$r<\dim (X)$
. Then its saturation
![]() $\overline{{\mathcal{F}}}$
defines an algebraically integrable foliation on
$\overline{{\mathcal{F}}}$
defines an algebraically integrable foliation on
![]() $X$
, and the
$X$
, and the
![]() $\overline{{\mathcal{F}}}$
-leaf passing through a general point is isomorphic to
$\overline{{\mathcal{F}}}$
-leaf passing through a general point is isomorphic to
![]() $\mathbb{P}^{r}$
.
$\mathbb{P}^{r}$
.
Proof. Let
![]() $\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
be as the morphism provided in Theorem 2.1. Since
$\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
be as the morphism provided in Theorem 2.1. Since
![]() ${\mathcal{F}}$
is locally free in codimension one, we may assume that no fiber of
${\mathcal{F}}$
is locally free in codimension one, we may assume that no fiber of
![]() $\unicode[STIX]{x1D711}_{0}$
is completely contained in
$\unicode[STIX]{x1D711}_{0}$
is completely contained in
![]() $\text{Sing}({\mathcal{F}})$
.
$\text{Sing}({\mathcal{F}})$
.
The first step is to show that
![]() ${\mathcal{F}}|_{X_{0}}\subset T_{X_{0}/T_{0}}$
. Since
${\mathcal{F}}|_{X_{0}}\subset T_{X_{0}/T_{0}}$
. Since
![]() $\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
is smooth, we get a short exact sequence of vector bundles,
$\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
is smooth, we get a short exact sequence of vector bundles,
The composite map
![]() ${\mathcal{F}}|_{X_{0}}\rightarrow T_{X}|_{X_{0}}\rightarrow \unicode[STIX]{x1D711}_{0}^{\ast }T_{T_{0}}$
vanishes on a Zariski open subset of every fiber. Since
${\mathcal{F}}|_{X_{0}}\rightarrow T_{X}|_{X_{0}}\rightarrow \unicode[STIX]{x1D711}_{0}^{\ast }T_{T_{0}}$
vanishes on a Zariski open subset of every fiber. Since
![]() $\unicode[STIX]{x1D711}_{0}^{\ast }T_{T_{0}}$
is torsion-free, it vanishes identically, and it follows that
$\unicode[STIX]{x1D711}_{0}^{\ast }T_{T_{0}}$
is torsion-free, it vanishes identically, and it follows that
![]() ${\mathcal{F}}|_{X_{0}}\subset T_{X_{0}/T_{0}}$
.
${\mathcal{F}}|_{X_{0}}\subset T_{X_{0}/T_{0}}$
.
Next, we show that, after shrinking
![]() $X_{0}$
and
$X_{0}$
and
![]() $T_{0}$
if necessary,
$T_{0}$
if necessary,
![]() ${\mathcal{F}}$
is actually locally free over
${\mathcal{F}}$
is actually locally free over
![]() $X_{0}$
. By the generic flatness theorem [Reference Grothendieck15, Théorème 6.9.1], after shrinking
$X_{0}$
. By the generic flatness theorem [Reference Grothendieck15, Théorème 6.9.1], after shrinking
![]() $T_{0}$
, we can suppose that
$T_{0}$
, we can suppose that
![]() $(T_{X}/{\mathcal{F}})|_{X_{0}}$
is flat over
$(T_{X}/{\mathcal{F}})|_{X_{0}}$
is flat over
![]() $T_{0}$
. Let
$T_{0}$
. Let
![]() $F\cong \mathbb{P}^{d+1}$
be an arbitrary fiber of
$F\cong \mathbb{P}^{d+1}$
be an arbitrary fiber of
![]() $\unicode[STIX]{x1D711}_{0}$
. The short exact sequence of sheaves
$\unicode[STIX]{x1D711}_{0}$
. The short exact sequence of sheaves
induces a long exact sequence of sheaves
Since
![]() $(T_{X}/{\mathcal{F}})|_{X_{0}}$
is flat over
$(T_{X}/{\mathcal{F}})|_{X_{0}}$
is flat over
![]() $T_{0}$
, it follows that
$T_{0}$
, it follows that
![]() ${\mathcal{F}}|_{F}$
is a subsheaf of
${\mathcal{F}}|_{F}$
is a subsheaf of
![]() $T_{X}|_{F}$
; in particular,
$T_{X}|_{F}$
; in particular,
![]() ${\mathcal{F}}|_{F}$
is torsion-free. Without loss of generality, we may assume that the restrictions of
${\mathcal{F}}|_{F}$
is torsion-free. Without loss of generality, we may assume that the restrictions of
![]() ${\mathcal{F}}$
on all fibers of
${\mathcal{F}}$
on all fibers of
![]() $\unicode[STIX]{x1D711}_{0}$
are torsion-free. By Remark 2.5, the restrictions of
$\unicode[STIX]{x1D711}_{0}$
are torsion-free. By Remark 2.5, the restrictions of
![]() ${\mathcal{F}}$
on all fibers of
${\mathcal{F}}$
on all fibers of
![]() $\unicode[STIX]{x1D711}_{0}$
are locally free. This yields, in particular, that the dimension of the fibers of
$\unicode[STIX]{x1D711}_{0}$
are locally free. This yields, in particular, that the dimension of the fibers of
![]() ${\mathcal{F}}$
is constant on every fiber of
${\mathcal{F}}$
is constant on every fiber of
![]() $\unicode[STIX]{x1D711}_{0}$
due to
$\unicode[STIX]{x1D711}_{0}$
due to
![]() ${\mathcal{F}}(x)=({\mathcal{F}}|_{F})(x)$
. Note that no fiber of
${\mathcal{F}}(x)=({\mathcal{F}}|_{F})(x)$
. Note that no fiber of
![]() $\unicode[STIX]{x1D711}_{0}$
is contained in
$\unicode[STIX]{x1D711}_{0}$
is contained in
![]() $\text{Sing}({\mathcal{F}})$
. We conclude that the dimension of the fibers
$\text{Sing}({\mathcal{F}})$
. We conclude that the dimension of the fibers
![]() ${\mathcal{F}}(x)$
of
${\mathcal{F}}(x)$
of
![]() ${\mathcal{F}}$
is constant over
${\mathcal{F}}$
is constant over
![]() $X_{0}$
. Hence,
$X_{0}$
. Hence,
![]() ${\mathcal{F}}$
is locally free over
${\mathcal{F}}$
is locally free over
![]() $X_{0}$
.
$X_{0}$
.
Now, we claim that
![]() $\overline{{\mathcal{F}}}$
actually defines an algebraically integrable foliation on
$\overline{{\mathcal{F}}}$
actually defines an algebraically integrable foliation on
![]() $X_{0}$
. Let
$X_{0}$
. Let
![]() $F\cong \mathbb{P}^{d+1}$
be an arbitrary fiber of
$F\cong \mathbb{P}^{d+1}$
be an arbitrary fiber of
![]() $\unicode[STIX]{x1D711}_{0}$
. We know that
$\unicode[STIX]{x1D711}_{0}$
. We know that
![]() $(F,{\mathcal{F}}|_{F})$
is isomorphic to
$(F,{\mathcal{F}}|_{F})$
is isomorphic to
![]() $(\mathbb{P}^{d+1},T_{\mathbb{P}^{d+1}})$
or
$(\mathbb{P}^{d+1},T_{\mathbb{P}^{d+1}})$
or
![]() $(\mathbb{P}^{d+1},{\mathcal{O}}_{\mathbb{P}^{d+1}}(1)^{\oplus r})$
(cf. Theorem B); therefore,
$(\mathbb{P}^{d+1},{\mathcal{O}}_{\mathbb{P}^{d+1}}(1)^{\oplus r})$
(cf. Theorem B); therefore,
![]() ${\mathcal{F}}$
defines an algebraically integrable foliation over
${\mathcal{F}}$
defines an algebraically integrable foliation over
![]() $X_{0}$
(cf. Example 3.4). Note that we have
$X_{0}$
(cf. Example 3.4). Note that we have
![]() ${\mathcal{F}}|_{X_{0}}=\overline{{\mathcal{F}}}|_{X_{0}}$
, since
${\mathcal{F}}|_{X_{0}}=\overline{{\mathcal{F}}}|_{X_{0}}$
, since
![]() ${\mathcal{F}}|_{X_{0}}$
is saturated in
${\mathcal{F}}|_{X_{0}}$
is saturated in
![]() $T_{X_{0}}$
. Hence,
$T_{X_{0}}$
. Hence,
![]() $\overline{{\mathcal{F}}}$
also defines an algebraically integrable foliation over
$\overline{{\mathcal{F}}}$
also defines an algebraically integrable foliation over
![]() $X$
(cf. Remark 3.2).☐
$X$
(cf. Remark 3.2).☐
Remark 3.10. Since
![]() ${\mathcal{F}}$
is locally free on
${\mathcal{F}}$
is locally free on
![]() $X_{0}$
, it follows that
$X_{0}$
, it follows that
![]() ${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})|_{X_{0}}$
is isomorphic to
${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})|_{X_{0}}$
is isomorphic to
![]() $\wedge ^{r}({\mathcal{F}}|_{X_{0}})$
and the invertible sheaf
$\wedge ^{r}({\mathcal{F}}|_{X_{0}})$
and the invertible sheaf
![]() ${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample over
${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample over
![]() $X_{0}$
. Moreover, as
$X_{0}$
. Moreover, as
![]() ${\mathcal{F}}$
is locally free in codimension one, there exists an open subset
${\mathcal{F}}$
is locally free in codimension one, there exists an open subset
![]() $X^{\prime }\subset X$
containing
$X^{\prime }\subset X$
containing
![]() $X_{0}$
such that
$X_{0}$
such that
![]() $\text{codim}(X\setminus X^{\prime })\geqslant 2$
and
$\text{codim}(X\setminus X^{\prime })\geqslant 2$
and
![]() ${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample on
${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample on
![]() $X^{\prime }$
.
$X^{\prime }$
.
4 Proof of main theorem
The aim of this section is to prove Theorem 1.1. Let
![]() $X$
be a normal projective variety, and let
$X$
be a normal projective variety, and let
![]() $X\rightarrow C$
be a surjective morphism with connected fibers onto a smooth curve. Let
$X\rightarrow C$
be a surjective morphism with connected fibers onto a smooth curve. Let
![]() $\unicode[STIX]{x1D6E5}$
be an effective Weil divisor on
$\unicode[STIX]{x1D6E5}$
be an effective Weil divisor on
![]() $X$
such that
$X$
such that
![]() $(X,\unicode[STIX]{x1D6E5})$
is log-canonical over the generic point of
$(X,\unicode[STIX]{x1D6E5})$
is log-canonical over the generic point of
![]() $C$
. In [Reference Araujo and Druel4, Theorem 5.1], it was proved that
$C$
. In [Reference Araujo and Druel4, Theorem 5.1], it was proved that
![]() $-(K_{X/C}+\unicode[STIX]{x1D6E5})$
cannot be ample. In the next theorem, we give a variant of this result which is the key ingredient in our proof of Theorem 1.1.
$-(K_{X/C}+\unicode[STIX]{x1D6E5})$
cannot be ample. In the next theorem, we give a variant of this result which is the key ingredient in our proof of Theorem 1.1.
Theorem 4.1. Let
![]() $X$
be a normal projective variety, and let
$X$
be a normal projective variety, and let
![]() $f:X\rightarrow C$
be a surjective morphism with connected fibers onto a smooth curve. Let
$f:X\rightarrow C$
be a surjective morphism with connected fibers onto a smooth curve. Let
![]() $\unicode[STIX]{x1D6E5}$
be a Weil divisor on
$\unicode[STIX]{x1D6E5}$
be a Weil divisor on
![]() $X$
such that
$X$
such that
![]() $K_{X}+\unicode[STIX]{x1D6E5}$
is Cartier and
$K_{X}+\unicode[STIX]{x1D6E5}$
is Cartier and
![]() $\unicode[STIX]{x1D6E5}^{\text{hor}}$
is reduced. Assume that there exists an open subset
$\unicode[STIX]{x1D6E5}^{\text{hor}}$
is reduced. Assume that there exists an open subset
![]() $C_{0}$
such that the pair
$C_{0}$
such that the pair
![]() $(X,\unicode[STIX]{x1D6E5}^{\text{hor}})$
is snc over
$(X,\unicode[STIX]{x1D6E5}^{\text{hor}})$
is snc over
![]() $X_{0}=f^{-1}(C_{0})$
. If
$X_{0}=f^{-1}(C_{0})$
. If
![]() $X^{\prime }\subset X$
is an open subset such that no fiber of
$X^{\prime }\subset X$
is an open subset such that no fiber of
![]() $f$
is completely contained in
$f$
is completely contained in
![]() $X\setminus X^{\prime }$
and
$X\setminus X^{\prime }$
and
![]() $X_{0}\subset X^{\prime }$
, then the invertible sheaf
$X_{0}\subset X^{\prime }$
, then the invertible sheaf
![]() ${\mathcal{O}}_{X}(-K_{X/C}-\unicode[STIX]{x1D6E5})$
is not ample over
${\mathcal{O}}_{X}(-K_{X/C}-\unicode[STIX]{x1D6E5})$
is not ample over
![]() $X^{\prime }$
.
$X^{\prime }$
.
Proof. To prove the theorem, we assume, to the contrary, that the invertible sheaf
![]() ${\mathcal{O}}_{X}(-K_{X/C}-\unicode[STIX]{x1D6E5})$
is ample over
${\mathcal{O}}_{X}(-K_{X/C}-\unicode[STIX]{x1D6E5})$
is ample over
![]() $X^{\prime }$
. Let
$X^{\prime }$
. Let
![]() $A$
be an ample divisor supported on
$A$
be an ample divisor supported on
![]() $C_{0}$
. Then, for some
$C_{0}$
. Then, for some
![]() $m\gg 1$
, the sheaf
$m\gg 1$
, the sheaf
![]() ${\mathcal{O}}_{X}(-m(K_{X/C}+\unicode[STIX]{x1D6E5})-f^{\ast }A)$
is very ample over
${\mathcal{O}}_{X}(-m(K_{X/C}+\unicode[STIX]{x1D6E5})-f^{\ast }A)$
is very ample over
![]() $X^{\prime }$
(see [Reference Grothendieck14, Corollaire 4.5.11]). It follows that there exists a prime divisor
$X^{\prime }$
(see [Reference Grothendieck14, Corollaire 4.5.11]). It follows that there exists a prime divisor
![]() $D^{\prime }$
on
$D^{\prime }$
on
![]() $X^{\prime }$
such that the pair
$X^{\prime }$
such that the pair
![]() $(X^{\prime },\unicode[STIX]{x1D6E5}^{\text{hor}}|_{X^{\prime }}+D^{\prime })$
is snc over
$(X^{\prime },\unicode[STIX]{x1D6E5}^{\text{hor}}|_{X^{\prime }}+D^{\prime })$
is snc over
![]() $X_{0}$
and
$X_{0}$
and
This implies that there exists a rational function
![]() $h\in K(X^{\prime })=K(X)$
such that the restriction of the Cartier divisor
$h\in K(X^{\prime })=K(X)$
such that the restriction of the Cartier divisor
![]() $D=\text{div}(h)-m(K_{X/C}+\unicode[STIX]{x1D6E5})-f^{\ast }A$
on
$D=\text{div}(h)-m(K_{X/C}+\unicode[STIX]{x1D6E5})-f^{\ast }A$
on
![]() $X^{\prime }$
is
$X^{\prime }$
is
![]() $D^{\prime }$
, and
$D^{\prime }$
, and
![]() $D^{\text{hor}}$
is the closure of
$D^{\text{hor}}$
is the closure of
![]() $D^{\prime }$
in
$D^{\prime }$
in
![]() $X$
. Note that we can write
$X$
. Note that we can write
![]() $D=D_{+}-D_{-}$
for some effective divisors
$D=D_{+}-D_{-}$
for some effective divisors
![]() $D_{+}$
and
$D_{+}$
and
![]() $D_{-}$
with no common components. Then we have
$D_{-}$
with no common components. Then we have
![]() $\operatorname{Supp}(D_{-})\subset X\setminus X^{\prime }$
. In particular, no fiber of
$\operatorname{Supp}(D_{-})\subset X\setminus X^{\prime }$
. In particular, no fiber of
![]() $f$
is supported on
$f$
is supported on
![]() $D_{-}$
. By [Reference Kollár20, Theorem 4.15], there exists a log-resolution
$D_{-}$
. By [Reference Kollár20, Theorem 4.15], there exists a log-resolution
![]() $\unicode[STIX]{x1D707}:\widetilde{X}\rightarrow X$
such that we have the following.
$\unicode[STIX]{x1D707}:\widetilde{X}\rightarrow X$
such that we have the following.
(i) The induced morphism
 $\widetilde{f}=f\circ \unicode[STIX]{x1D707}:\widetilde{X}\rightarrow C$
is prepared (cf. [Reference Campana11, Section 4.3]).
$\widetilde{f}=f\circ \unicode[STIX]{x1D707}:\widetilde{X}\rightarrow C$
is prepared (cf. [Reference Campana11, Section 4.3]).(ii) The birational morphism
 $\unicode[STIX]{x1D707}$
is an isomorphism over
$\unicode[STIX]{x1D707}$
is an isomorphism over
 $X_{0}$
.
$X_{0}$
.(iii)
 $\unicode[STIX]{x1D707}_{\ast }^{-1}\unicode[STIX]{x1D6E5}^{\text{hor}}+\unicode[STIX]{x1D707}_{\ast }^{-1}D^{\text{hor}}$
is a snc divisor.
$\unicode[STIX]{x1D707}_{\ast }^{-1}\unicode[STIX]{x1D6E5}^{\text{hor}}+\unicode[STIX]{x1D707}_{\ast }^{-1}D^{\text{hor}}$
is a snc divisor.
Let
![]() $E$
be the exceptional divisor of
$E$
be the exceptional divisor of
![]() $\unicode[STIX]{x1D707}$
. Note that we have
$\unicode[STIX]{x1D707}$
. Note that we have
![]() $\widetilde{f}_{\ast }(E)\not =C$
. Moreover, we also have
$\widetilde{f}_{\ast }(E)\not =C$
. Moreover, we also have
where
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
are effective
$E_{-}$
are effective
![]() $\unicode[STIX]{x1D707}$
-exceptional divisors with no common components.
$\unicode[STIX]{x1D707}$
-exceptional divisors with no common components.
Set
![]() $\widetilde{D}=m\unicode[STIX]{x1D707}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}_{\ast }^{-1}D_{+}+mE_{-}$
. Then
$\widetilde{D}=m\unicode[STIX]{x1D707}_{\ast }^{-1}\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}_{\ast }^{-1}D_{+}+mE_{-}$
. Then
![]() $\widetilde{D}^{\text{hor}}=m\unicode[STIX]{x1D707}_{\ast }^{-1}\unicode[STIX]{x1D6E5}^{\text{hor}}+\unicode[STIX]{x1D707}_{\ast }^{-1}D^{\text{hor}}$
is an snc effective divisor with coefficients
$\widetilde{D}^{\text{hor}}=m\unicode[STIX]{x1D707}_{\ast }^{-1}\unicode[STIX]{x1D6E5}^{\text{hor}}+\unicode[STIX]{x1D707}_{\ast }^{-1}D^{\text{hor}}$
is an snc effective divisor with coefficients
![]() ${\leqslant}m$
. Since
${\leqslant}m$
. Since
![]() $D$
is linearly equivalent to
$D$
is linearly equivalent to
![]() $-m(K_{X/C}+\unicode[STIX]{x1D6E5})-f^{\ast }A$
, we can write
$-m(K_{X/C}+\unicode[STIX]{x1D6E5})-f^{\ast }A$
, we can write
After multiplying by some positive
![]() $l$
divisible by the denominators of the coefficients of
$l$
divisible by the denominators of the coefficients of
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
, we may assume that
$E_{-}$
, we may assume that
![]() $\text{lm}\,E_{+}$
and
$\text{lm}\,E_{+}$
and
![]() $\text{lm}\,E_{-}$
are integer coefficients. By replacing
$\text{lm}\,E_{-}$
are integer coefficients. By replacing
![]() $\widetilde{D}$
by
$\widetilde{D}$
by
![]() $l\widetilde{D}$
, the weak positivity theorem [Reference Campana11, Theorem 4.13] implies that the direct image sheaf
$l\widetilde{D}$
, the weak positivity theorem [Reference Campana11, Theorem 4.13] implies that the direct image sheaf
 $$\begin{eqnarray}\displaystyle \widetilde{f}_{\ast }(\unicode[STIX]{x1D714}_{\widetilde{X}/C}^{\text{lm}}\otimes {\mathcal{O}}_{\widetilde{X}}(\widetilde{D})) & \simeq & \displaystyle \widetilde{f}_{\ast }({\mathcal{O}}_{\widetilde{X}}(-l\widetilde{f}^{\ast }A+\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{O}}_{C}(-lA)\otimes \widetilde{f}_{\ast }{\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{f}_{\ast }(\unicode[STIX]{x1D714}_{\widetilde{X}/C}^{\text{lm}}\otimes {\mathcal{O}}_{\widetilde{X}}(\widetilde{D})) & \simeq & \displaystyle \widetilde{f}_{\ast }({\mathcal{O}}_{\widetilde{X}}(-l\widetilde{f}^{\ast }A+\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{O}}_{C}(-lA)\otimes \widetilde{f}_{\ast }{\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-})\nonumber\end{eqnarray}$$
is weakly positive.
Observe that
![]() $\widetilde{f}_{\ast }({\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))={\mathcal{O}}_{C}$
. Indeed,
$\widetilde{f}_{\ast }({\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))={\mathcal{O}}_{C}$
. Indeed,
![]() $E_{+}$
is a
$E_{+}$
is a
![]() $\unicode[STIX]{x1D707}$
-exceptional divisor. It follows that
$\unicode[STIX]{x1D707}$
-exceptional divisor. It follows that
![]() $\unicode[STIX]{x1D707}_{\ast }({\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))={\mathcal{O}}_{X}(lD_{-})$
. Note that we have
$\unicode[STIX]{x1D707}_{\ast }({\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))={\mathcal{O}}_{X}(lD_{-})$
. Note that we have
![]() $f_{\ast }({\mathcal{O}}_{X}(lD_{-}))={\mathcal{O}}_{C}(P)$
for some effective divisor
$f_{\ast }({\mathcal{O}}_{X}(lD_{-}))={\mathcal{O}}_{C}(P)$
for some effective divisor
![]() $P$
on
$P$
on
![]() $C$
such that
$C$
such that
![]() $\operatorname{Supp}(P)\subset f(\operatorname{Supp}(D_{-}))$
. Let
$\operatorname{Supp}(P)\subset f(\operatorname{Supp}(D_{-}))$
. Let
![]() $V$
be an open subset of
$V$
be an open subset of
![]() $C$
, and let
$C$
, and let
![]() $\unicode[STIX]{x1D706}\in H^{0}(V,{\mathcal{O}}_{C}(P))$
. That is,
$\unicode[STIX]{x1D706}\in H^{0}(V,{\mathcal{O}}_{C}(P))$
. That is,
![]() $\unicode[STIX]{x1D706}$
is a rational function on
$\unicode[STIX]{x1D706}$
is a rational function on
![]() $C$
such that
$C$
such that
![]() $\text{div}(\unicode[STIX]{x1D706})+P\geqslant 0$
over
$\text{div}(\unicode[STIX]{x1D706})+P\geqslant 0$
over
![]() $V$
. It follows that
$V$
. It follows that
![]() $\text{div}(\unicode[STIX]{x1D706}\circ f)+lD_{-}\geqslant 0$
over
$\text{div}(\unicode[STIX]{x1D706}\circ f)+lD_{-}\geqslant 0$
over
![]() $f^{-1}(V)$
. Since there is no fiber of
$f^{-1}(V)$
. Since there is no fiber of
![]() $f$
completely supported on
$f$
completely supported on
![]() $D_{-}$
, the rational function
$D_{-}$
, the rational function
![]() $\unicode[STIX]{x1D706}\circ f$
is regular over
$\unicode[STIX]{x1D706}\circ f$
is regular over
![]() $f^{-1}(V)$
. Consequently, the rational function
$f^{-1}(V)$
. Consequently, the rational function
![]() $\unicode[STIX]{x1D706}$
is regular over
$\unicode[STIX]{x1D706}$
is regular over
![]() $V$
. This implies that the natural inclusion
$V$
. This implies that the natural inclusion
![]() ${\mathcal{O}}_{C}\rightarrow {\mathcal{O}}_{C}(P)$
is surjective, which yields
${\mathcal{O}}_{C}\rightarrow {\mathcal{O}}_{C}(P)$
is surjective, which yields
![]() $\widetilde{f}_{\ast }({\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))={\mathcal{O}}_{C}$
. However, this shows that
$\widetilde{f}_{\ast }({\mathcal{O}}_{\widetilde{X}}(\text{lm}\,E_{+}+l\unicode[STIX]{x1D707}_{\ast }^{-1}D_{-}))={\mathcal{O}}_{C}$
. However, this shows that
![]() ${\mathcal{O}}_{C}(-lA)$
is weakly positive, which is a contradiction. Hence,
${\mathcal{O}}_{C}(-lA)$
is weakly positive, which is a contradiction. Hence,
![]() ${\mathcal{O}}_{X}(-K_{X/C}-\unicode[STIX]{x1D6E5})$
is not ample over
${\mathcal{O}}_{X}(-K_{X/C}-\unicode[STIX]{x1D6E5})$
is not ample over
![]() $X^{\prime }$
.☐
$X^{\prime }$
.☐
Lemma 4.2. Let
![]() $X$
be a normal projective variety, and let
$X$
be a normal projective variety, and let
![]() $f:X\rightarrow C$
be a surjective morphism with reduced and connected fibers onto a smooth curve
$f:X\rightarrow C$
be a surjective morphism with reduced and connected fibers onto a smooth curve
![]() $C$
. Let
$C$
. Let
![]() $D$
be a Cartier divisor on
$D$
be a Cartier divisor on
![]() $X$
. If there exists a nonzero morphism
$X$
. If there exists a nonzero morphism
![]() $\unicode[STIX]{x1D6FA}_{X/C}^{r}\rightarrow {\mathcal{O}}_{X}(D)$
, where
$\unicode[STIX]{x1D6FA}_{X/C}^{r}\rightarrow {\mathcal{O}}_{X}(D)$
, where
![]() $r$
is the relative dimension of
$r$
is the relative dimension of
![]() $f$
, then there exists an effective Weil divisor
$f$
, then there exists an effective Weil divisor
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $X$
such that
$X$
such that
![]() $K_{X/C}+\unicode[STIX]{x1D6E5}=D$
.
$K_{X/C}+\unicode[STIX]{x1D6E5}=D$
.
Proof. Since all of the fibers of
![]() $f$
are reduced, the sheaf
$f$
are reduced, the sheaf
![]() $\unicode[STIX]{x1D6FA}_{X/C}^{r}$
is locally free in codimension one. Hence, the reflexive hull of
$\unicode[STIX]{x1D6FA}_{X/C}^{r}$
is locally free in codimension one. Hence, the reflexive hull of
![]() $\unicode[STIX]{x1D6FA}_{X/C}^{r}$
is
$\unicode[STIX]{x1D6FA}_{X/C}^{r}$
is
![]() $\unicode[STIX]{x1D714}_{X/C}\simeq {\mathcal{O}}_{X}(K_{X/C})$
. Note that
$\unicode[STIX]{x1D714}_{X/C}\simeq {\mathcal{O}}_{X}(K_{X/C})$
. Note that
![]() ${\mathcal{O}}_{X}(D)$
is reflexive; the nonzero morphism
${\mathcal{O}}_{X}(D)$
is reflexive; the nonzero morphism
![]() $\unicode[STIX]{x1D6FA}_{X/C}^{r}\rightarrow {\mathcal{O}}_{X}(D)$
induces a nonzero morphism
$\unicode[STIX]{x1D6FA}_{X/C}^{r}\rightarrow {\mathcal{O}}_{X}(D)$
induces a nonzero morphism
![]() $\unicode[STIX]{x1D714}_{X/C}\rightarrow {\mathcal{O}}_{X}(D)$
. This shows that there exists an effective divisor
$\unicode[STIX]{x1D714}_{X/C}\rightarrow {\mathcal{O}}_{X}(D)$
. This shows that there exists an effective divisor
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $X$
such that
$X$
such that
![]() $K_{X/C}+\unicode[STIX]{x1D6E5}=D$
.☐
$K_{X/C}+\unicode[STIX]{x1D6E5}=D$
.☐
As an application of Theorem 4.1, we derive a special property about foliations defined by an ample subsheaf of
![]() $T_{X}$
. A similar result was established for Fano foliations with mild singularities in the work of Araujo and Druel (see [Reference Araujo and Druel4, Proposition 5.3]), and we follow the same strategy.
$T_{X}$
. A similar result was established for Fano foliations with mild singularities in the work of Araujo and Druel (see [Reference Araujo and Druel4, Proposition 5.3]), and we follow the same strategy.
Proposition 4.3. Let
![]() $X$
be a projective manifold. If
$X$
be a projective manifold. If
![]() ${\mathcal{F}}\subset T_{X}$
is an ample subsheaf of rank
${\mathcal{F}}\subset T_{X}$
is an ample subsheaf of rank
![]() $r<n=\dim (X)$
, then there is a common point in the closure of general leaves of
$r<n=\dim (X)$
, then there is a common point in the closure of general leaves of
![]() $\overline{{\mathcal{F}}}$
.
$\overline{{\mathcal{F}}}$
.
Proof. Since
![]() ${\mathcal{F}}$
is torsion-free and
${\mathcal{F}}$
is torsion-free and
![]() $X$
is smooth,
$X$
is smooth,
![]() ${\mathcal{F}}$
is locally free over an open subset
${\mathcal{F}}$
is locally free over an open subset
![]() $X^{\prime }\subset X$
such that
$X^{\prime }\subset X$
such that
![]() $\text{codim}(X\setminus X^{\prime })\geqslant 2$
. In particular,
$\text{codim}(X\setminus X^{\prime })\geqslant 2$
. In particular,
![]() ${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample over
${\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample over
![]() $X^{\prime }$
. By Theorem 2.1, there exist an open subset
$X^{\prime }$
. By Theorem 2.1, there exist an open subset
![]() $X_{0}\subset X$
and a
$X_{0}\subset X$
and a
![]() $\mathbb{P}^{d+1}$
-bundle
$\mathbb{P}^{d+1}$
-bundle
![]() $\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
. Moreover, from the proof of Theorem 3.9, the saturation
$\unicode[STIX]{x1D711}_{0}:X_{0}\rightarrow T_{0}$
. Moreover, from the proof of Theorem 3.9, the saturation
![]() $\overline{{\mathcal{F}}}$
defines an algebraically integrable foliation on
$\overline{{\mathcal{F}}}$
defines an algebraically integrable foliation on
![]() $X$
, and we may assume that
$X$
, and we may assume that
![]() ${\mathcal{F}}$
is locally free over
${\mathcal{F}}$
is locally free over
![]() $X_{0}$
. In particular, we have
$X_{0}$
. In particular, we have
![]() $X_{0}\subset X^{\prime }$
. In view of Lemma 3.7, we denote by
$X_{0}\subset X^{\prime }$
. In view of Lemma 3.7, we denote by
![]() $W$
the subvariety of
$W$
the subvariety of
![]() $\text{Chow}(X)$
parametrizing the general leaves of
$\text{Chow}(X)$
parametrizing the general leaves of
![]() $\overline{{\mathcal{F}}}$
, and by
$\overline{{\mathcal{F}}}$
, and by
![]() $V$
the normalization of the universal cycle over
$V$
the normalization of the universal cycle over
![]() $W$
. Let
$W$
. Let
![]() $p:V\rightarrow X$
and
$p:V\rightarrow X$
and
![]() $\unicode[STIX]{x1D70B}:V\rightarrow W$
be the natural projections. Note that there exists an open subset
$\unicode[STIX]{x1D70B}:V\rightarrow W$
be the natural projections. Note that there exists an open subset
![]() $W_{0}$
of
$W_{0}$
of
![]() $W$
such that
$W$
such that
![]() $p(\unicode[STIX]{x1D70B}^{-1}(W_{0}))\subset X_{0}$
.
$p(\unicode[STIX]{x1D70B}^{-1}(W_{0}))\subset X_{0}$
.
To prove our proposition, we assume to the contrary that there is no common point in the general leaves of
![]() $\overline{{\mathcal{F}}}$
.
$\overline{{\mathcal{F}}}$
.
First, we show that there exists a smooth curve
![]() $C$
with a finite morphism
$C$
with a finite morphism
![]() $n:C\rightarrow n(C)\subset W$
such that we have the following.
$n:C\rightarrow n(C)\subset W$
such that we have the following.
(i) Let
 $U$
be the normalization of the fiber product
$U$
be the normalization of the fiber product
 $V\times _{W}C$
with projection
$V\times _{W}C$
with projection
 $\unicode[STIX]{x1D70B}:U\rightarrow C$
. Then the induced morphism
$\unicode[STIX]{x1D70B}:U\rightarrow C$
. Then the induced morphism
 $\widetilde{p}:U\rightarrow X$
is finite onto its image.
$\widetilde{p}:U\rightarrow X$
is finite onto its image.(ii) There exists an open subset
 $C_{0}$
of
$C_{0}$
of
 $C$
such that the image of
$C$
such that the image of
 $U_{0}$
under
$U_{0}$
under
 $p$
is contained in
$p$
is contained in
 $X_{0}$
. In particular,
$X_{0}$
. In particular,
 $U_{0}=\unicode[STIX]{x1D70B}^{-1}(C_{0})$
is a
$U_{0}=\unicode[STIX]{x1D70B}^{-1}(C_{0})$
is a
 $\mathbb{P}^{r}$
-bundle over
$\mathbb{P}^{r}$
-bundle over
 $C_{0}$
.
$C_{0}$
.(iii) For any point
 $c\in C$
, the image of the fiber
$c\in C$
, the image of the fiber
 $\unicode[STIX]{x1D70B}^{-1}(c)$
under
$\unicode[STIX]{x1D70B}^{-1}(c)$
under
 $\widetilde{p}$
is not contained in
$\widetilde{p}$
is not contained in
 $X\setminus X^{\prime }$
.
$X\setminus X^{\prime }$
.(iv) All of the fibers of
 $\unicode[STIX]{x1D70B}$
are reduced.
$\unicode[STIX]{x1D70B}$
are reduced.
Note that we have
![]() $X\setminus X^{\prime }=\operatorname{Sing}({\mathcal{F}})$
and
$X\setminus X^{\prime }=\operatorname{Sing}({\mathcal{F}})$
and
![]() $\text{codim}(\operatorname{Sing}({\mathcal{F}}))\geqslant 2$
. We consider the subset
$\text{codim}(\operatorname{Sing}({\mathcal{F}}))\geqslant 2$
. We consider the subset
Since
![]() $\unicode[STIX]{x1D70B}$
is equidimensional, it is a surjective universally open morphism (see [Reference Grothendieck16, Théorème 14.4.4]). Therefore, the subset
$\unicode[STIX]{x1D70B}$
is equidimensional, it is a surjective universally open morphism (see [Reference Grothendieck16, Théorème 14.4.4]). Therefore, the subset
![]() $Z$
is closed. Note that the general fiber of
$Z$
is closed. Note that the general fiber of
![]() $\unicode[STIX]{x1D70B}$
is disjoint from
$\unicode[STIX]{x1D70B}$
is disjoint from
![]() $p^{-1}(\operatorname{Sing}({\mathcal{F}}))$
, so
$p^{-1}(\operatorname{Sing}({\mathcal{F}}))$
, so
![]() $\text{codim}(Z)\geqslant 1$
. Moreover, by the definition of
$\text{codim}(Z)\geqslant 1$
. Moreover, by the definition of
![]() $Z$
, we have
$Z$
, we have
![]() $p(\unicode[STIX]{x1D70B}^{-1}(Z))\subset \operatorname{Sing}({\mathcal{F}})$
and
$p(\unicode[STIX]{x1D70B}^{-1}(Z))\subset \operatorname{Sing}({\mathcal{F}})$
and
![]() $\text{codim}(\operatorname{Sing}({\mathcal{F}}))\geqslant 2$
. Hence, we can choose some very ample divisors
$\text{codim}(\operatorname{Sing}({\mathcal{F}}))\geqslant 2$
. Hence, we can choose some very ample divisors
![]() $H_{i}$
$H_{i}$
![]() $(1\leqslant i\leqslant n)$
on
$(1\leqslant i\leqslant n)$
on
![]() $X$
such that the curve
$X$
such that the curve
![]() $B$
defined by the complete intersection
$B$
defined by the complete intersection
![]() $\widetilde{p}^{\ast }H_{1}\cap \cdots \cap \widetilde{p}^{\ast }H_{n}$
satisfies the following conditions.
$\widetilde{p}^{\ast }H_{1}\cap \cdots \cap \widetilde{p}^{\ast }H_{n}$
satisfies the following conditions.
- (i ′ )
There is no common point in the closure of the general fibers of
 $\unicode[STIX]{x1D70B}$
over
$\unicode[STIX]{x1D70B}$
over
 $\unicode[STIX]{x1D70B}(B)$
.
$\unicode[STIX]{x1D70B}(B)$
.- (ii ′ )
 $\unicode[STIX]{x1D70B}(B)\cap W_{0}\not =\emptyset$
.
$\unicode[STIX]{x1D70B}(B)\cap W_{0}\not =\emptyset$
.- (iii ′ )
 $\unicode[STIX]{x1D70B}(B)\subset W\setminus Z$
.
$\unicode[STIX]{x1D70B}(B)\subset W\setminus Z$
.
Let
![]() $B^{\prime }\rightarrow B$
be the normalization, and let
$B^{\prime }\rightarrow B$
be the normalization, and let
![]() $V_{B^{\prime }}$
be the normalization of the fiber product
$V_{B^{\prime }}$
be the normalization of the fiber product
![]() $V\times _{B}B^{\prime }$
. The induced morphism
$V\times _{B}B^{\prime }$
. The induced morphism
![]() $V_{B^{\prime }}\rightarrow V$
is denoted by
$V_{B^{\prime }}\rightarrow V$
is denoted by
![]() $\unicode[STIX]{x1D707}$
. Then it is easy to check that
$\unicode[STIX]{x1D707}$
. Then it is easy to check that
![]() $B^{\prime }$
satisfies (i), (ii) and (iii). By [Reference Bosch, Lütkebohmert and Raynaud9, Theorem 2.1], there exists a finite morphism
$B^{\prime }$
satisfies (i), (ii) and (iii). By [Reference Bosch, Lütkebohmert and Raynaud9, Theorem 2.1], there exists a finite morphism
![]() $C\rightarrow B^{\prime }$
such that all of the fibers of
$C\rightarrow B^{\prime }$
such that all of the fibers of
![]() $U\rightarrow C$
are reduced, where
$U\rightarrow C$
are reduced, where
![]() $U$
is the normalization of
$U$
is the normalization of
![]() $U\times _{B^{\prime }}C$
. Then we see at once that
$U\times _{B^{\prime }}C$
. Then we see at once that
![]() $C$
is the desired curve.
$C$
is the desired curve.
The next step is to get a contradiction by applying Theorem 4.1. From Remark 3.8, we see that the Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})$
extends to a Pfaff field
$\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow {\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})$
extends to a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{V_{B^{\prime }}/B^{\prime }}^{r}\rightarrow \unicode[STIX]{x1D707}^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})$
, and it induces a Pfaff field
$\unicode[STIX]{x1D6FA}_{V_{B^{\prime }}/B^{\prime }}^{r}\rightarrow \unicode[STIX]{x1D707}^{\ast }p^{\ast }{\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})$
, and it induces a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{U/C}^{r}\rightarrow \widetilde{p}^{\ast }{\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})$
. The natural inclusion
$\unicode[STIX]{x1D6FA}_{U/C}^{r}\rightarrow \widetilde{p}^{\ast }{\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})$
. The natural inclusion
![]() ${\mathcal{F}}{\hookrightarrow}\overline{{\mathcal{F}}}$
induces a morphism
${\mathcal{F}}{\hookrightarrow}\overline{{\mathcal{F}}}$
induces a morphism
![]() ${\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})\rightarrow {\mathcal{O}}_{X}(K_{{\mathcal{F}}})$
. This implies that we have a Pfaff field
${\mathcal{O}}_{X}(K_{\overline{{\mathcal{F}}}})\rightarrow {\mathcal{O}}_{X}(K_{{\mathcal{F}}})$
. This implies that we have a Pfaff field
![]() $\unicode[STIX]{x1D6FA}_{U/C}^{r}\rightarrow \widetilde{p}^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{F}}})$
. By Lemma 4.2, there exists an effective Weil divisor
$\unicode[STIX]{x1D6FA}_{U/C}^{r}\rightarrow \widetilde{p}^{\ast }{\mathcal{O}}_{X}(K_{{\mathcal{F}}})$
. By Lemma 4.2, there exists an effective Weil divisor
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $U$
such that
$U$
such that
![]() $K_{U/C}+\unicode[STIX]{x1D6E5}=\widetilde{p}^{\ast }K_{{\mathcal{F}}}$
.
$K_{U/C}+\unicode[STIX]{x1D6E5}=\widetilde{p}^{\ast }K_{{\mathcal{F}}}$
.
Let
![]() $\unicode[STIX]{x1D6E5}^{\text{hor}}$
be the
$\unicode[STIX]{x1D6E5}^{\text{hor}}$
be the
![]() $\unicode[STIX]{x1D70B}$
-horizontal part of
$\unicode[STIX]{x1D70B}$
-horizontal part of
![]() $\unicode[STIX]{x1D6E5}$
. After shrinking
$\unicode[STIX]{x1D6E5}$
. After shrinking
![]() $C_{0}$
, we may assume that
$C_{0}$
, we may assume that
![]() $\unicode[STIX]{x1D6E5}|_{U_{0}}=\unicode[STIX]{x1D6E5}^{\text{hor}}|_{U_{0}}$
. According to the proof of Theorem 3.9, for any fiber
$\unicode[STIX]{x1D6E5}|_{U_{0}}=\unicode[STIX]{x1D6E5}^{\text{hor}}|_{U_{0}}$
. According to the proof of Theorem 3.9, for any fiber
![]() $F\cong \mathbb{P}^{r}$
over
$F\cong \mathbb{P}^{r}$
over
![]() $C_{0}$
, we have
$C_{0}$
, we have
![]() $(\widetilde{p}^{\ast }K_{{\mathcal{F}}})|_{F}-K_{F}=0$
or
$(\widetilde{p}^{\ast }K_{{\mathcal{F}}})|_{F}-K_{F}=0$
or
![]() $H$
, where
$H$
, where
![]() $H\in |{\mathcal{O}}_{\mathbb{P}^{r}}(1)|$
. This shows that either
$H\in |{\mathcal{O}}_{\mathbb{P}^{r}}(1)|$
. This shows that either
![]() $\unicode[STIX]{x1D6E5}^{\text{hor}}$
is zero or
$\unicode[STIX]{x1D6E5}^{\text{hor}}$
is zero or
![]() $\unicode[STIX]{x1D6E5}^{\text{hor}}$
is a prime divisor such that
$\unicode[STIX]{x1D6E5}^{\text{hor}}$
is a prime divisor such that
![]() $\unicode[STIX]{x1D6E5}|_{U_{0}}=\unicode[STIX]{x1D6E5}^{\text{hor}}|_{U_{0}}\in |{\mathcal{O}}_{U_{0}}(1)|$
. In particular, the pair
$\unicode[STIX]{x1D6E5}|_{U_{0}}=\unicode[STIX]{x1D6E5}^{\text{hor}}|_{U_{0}}\in |{\mathcal{O}}_{U_{0}}(1)|$
. In particular, the pair
![]() $(U,\unicode[STIX]{x1D6E5}^{\text{hor}})$
is snc over
$(U,\unicode[STIX]{x1D6E5}^{\text{hor}})$
is snc over
![]() $U_{0}$
and
$U_{0}$
and
![]() $\unicode[STIX]{x1D6E5}^{\text{hor}}$
is reduced. Note that
$\unicode[STIX]{x1D6E5}^{\text{hor}}$
is reduced. Note that
![]() $\widetilde{p}:U\rightarrow \widetilde{p}(U)$
is a finite morphism, so the invertible sheaf
$\widetilde{p}:U\rightarrow \widetilde{p}(U)$
is a finite morphism, so the invertible sheaf
![]() $\widetilde{p}^{\ast }{\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample over
$\widetilde{p}^{\ast }{\mathcal{O}}_{X}(-K_{{\mathcal{F}}})$
is ample over
![]() $U^{\prime }=U\cap \widetilde{p}^{-1}(X^{\prime })$
. That is, the sheaf
$U^{\prime }=U\cap \widetilde{p}^{-1}(X^{\prime })$
. That is, the sheaf
![]() ${\mathcal{O}}_{U}(-K_{U/C}-\unicode[STIX]{x1D6E5})$
is ample over
${\mathcal{O}}_{U}(-K_{U/C}-\unicode[STIX]{x1D6E5})$
is ample over
![]() $U^{\prime }$
, which contradicts Theorem 4.1.☐
$U^{\prime }$
, which contradicts Theorem 4.1.☐
Now, our main result immediately follows.
Proof of Theorem 1.1.
Theorem 2.1 implies that there exist an open subset
![]() $X_{0}\subset X$
and a normal variety
$X_{0}\subset X$
and a normal variety
![]() $T_{0}$
such that
$T_{0}$
such that
![]() $X_{0}\rightarrow T_{0}$
is a
$X_{0}\rightarrow T_{0}$
is a
![]() $\mathbb{P}^{d+1}$
-bundle and
$\mathbb{P}^{d+1}$
-bundle and
![]() $d+1\geqslant r$
. Without loss of generality, we may assume that
$d+1\geqslant r$
. Without loss of generality, we may assume that
![]() $r<\dim (X)$
. By Theorem 3.9 followed by Proposition 4.3,
$r<\dim (X)$
. By Theorem 3.9 followed by Proposition 4.3,
![]() $\overline{{\mathcal{F}}}$
defines an algebraically integrable foliation over
$\overline{{\mathcal{F}}}$
defines an algebraically integrable foliation over
![]() $X$
such that there is a common point in the closure of general leaves of
$X$
such that there is a common point in the closure of general leaves of
![]() $\overline{{\mathcal{F}}}$
. However, this cannot happen if
$\overline{{\mathcal{F}}}$
. However, this cannot happen if
![]() $\dim (T_{0})\geqslant 1$
. Hence, we have
$\dim (T_{0})\geqslant 1$
. Hence, we have
![]() $\dim T_{0}=0$
and
$\dim T_{0}=0$
and
![]() $X\cong \mathbb{P}^{n}$
.☐
$X\cong \mathbb{P}^{n}$
.☐
5
 $\mathbb{P}^{r}$
-bundles as ample divisors
$\mathbb{P}^{r}$
-bundles as ample divisors
As an application of Theorem 1.1, we classify projective manifolds
![]() $X$
containing
$X$
containing
![]() $\mathbb{P}^{r}$
-bundles as ample divisors. This was originally conjectured by Beltrametti and Sommese (see [Reference Beltrametti and Sommese8, Conjecture 5.5.1]). In the remainder of this section, we follow the same notation and assumptions as in Theorem 1.3.
$\mathbb{P}^{r}$
-bundles as ample divisors. This was originally conjectured by Beltrametti and Sommese (see [Reference Beltrametti and Sommese8, Conjecture 5.5.1]). In the remainder of this section, we follow the same notation and assumptions as in Theorem 1.3.
The case
![]() $r\geqslant 2$
follows from Sommese’s extension theorem [Reference Sommese26, Proposition III] (see also [Reference Beltrametti and Sommese8, Theorem 5.5.2]). For
$r\geqslant 2$
follows from Sommese’s extension theorem [Reference Sommese26, Proposition III] (see also [Reference Beltrametti and Sommese8, Theorem 5.5.2]). For
![]() $r=1$
and
$r=1$
and
![]() $b=1$
, it is due to Bădescu [Reference Bădescu6, Theorem D] (see also [Reference Beltrametti and Sommese8, Theorem 5.5.3]). For
$b=1$
, it is due to Bădescu [Reference Bădescu6, Theorem D] (see also [Reference Beltrametti and Sommese8, Theorem 5.5.3]). For
![]() $r=1$
and
$r=1$
and
![]() $b=2$
, it is due to the work of several authors (see [Reference Beltrametti and Ionescu7, Theorem 7.4]). As mentioned in the introduction, Litt proved the following result, by which we can deduce Theorem 1.3 from Corollary 1.2.
$b=2$
, it is due to the work of several authors (see [Reference Beltrametti and Ionescu7, Theorem 7.4]). As mentioned in the introduction, Litt proved the following result, by which we can deduce Theorem 1.3 from Corollary 1.2.
Proposition 5.1. [Reference Litt23, Lemma 4]
Let
![]() $X$
be a projective manifold of dimension
$X$
be a projective manifold of dimension
![]() ${\geqslant}3$
, and let
${\geqslant}3$
, and let
![]() $A$
be an ample divisor. Assume that
$A$
be an ample divisor. Assume that
![]() $p:A\rightarrow B$
is a
$p:A\rightarrow B$
is a
![]() $\mathbb{P}^{1}$
-bundle, then either
$\mathbb{P}^{1}$
-bundle, then either
![]() $p$
extends to a morphism
$p$
extends to a morphism
![]() $\widehat{p}:X\rightarrow B$
, or there exists an ample vector bundle
$\widehat{p}:X\rightarrow B$
, or there exists an ample vector bundle
![]() $E$
on
$E$
on
![]() $B$
and a nonzero map
$B$
and a nonzero map
![]() $E\rightarrow T_{B}$
.
$E\rightarrow T_{B}$
.
For the reader’s convenience, we outline the argument of Litt that reduces Theorem 1.3 to Corollary 1.2.
Proof of Theorem 1.3.
Since the case
![]() $r\geqslant 2$
is already known, we can assume that
$r\geqslant 2$
is already known, we can assume that
![]() $r=1$
; that is,
$r=1$
; that is,
![]() $p:A\rightarrow B$
is a
$p:A\rightarrow B$
is a
![]() $\mathbb{P}^{1}$
-bundle.
$\mathbb{P}^{1}$
-bundle.
If
![]() $p$
extends to a morphism
$p$
extends to a morphism
![]() $\widehat{p}:X\rightarrow B$
, then the result follows from [Reference Beltrametti and Ionescu7, Theorem 5.5] and we are in case (i) of the theorem.
$\widehat{p}:X\rightarrow B$
, then the result follows from [Reference Beltrametti and Ionescu7, Theorem 5.5] and we are in case (i) of the theorem.
If
![]() $p$
does not extend to a morphism
$p$
does not extend to a morphism
![]() $X\rightarrow B$
, by Proposition 5.1, there exists an ample vector bundle
$X\rightarrow B$
, by Proposition 5.1, there exists an ample vector bundle
![]() $E$
over
$E$
over
![]() $B$
with a nonzero map
$B$
with a nonzero map
![]() $E\rightarrow T_{B}$
. Due to Corollary 1.2, we have
$E\rightarrow T_{B}$
. Due to Corollary 1.2, we have
![]() $B\cong \mathbb{P}^{b}$
. As the case
$B\cong \mathbb{P}^{b}$
. As the case
![]() $b\leqslant 2$
is also known, we may assume that
$b\leqslant 2$
is also known, we may assume that
![]() $b\geqslant 3$
. In this case, by [Reference Fania, Sato and Sommese13, Theorem 2.1], we conclude that
$b\geqslant 3$
. In this case, by [Reference Fania, Sato and Sommese13, Theorem 2.1], we conclude that
![]() $X$
is a
$X$
is a
![]() $\mathbb{P}^{n-1}$
-bundle over
$\mathbb{P}^{n-1}$
-bundle over
![]() $\mathbb{P}^{1}$
and we are in case (ii) of the theorem.☐
$\mathbb{P}^{1}$
and we are in case (ii) of the theorem.☐
Acknowledgments
I would like to express my deep gratitude to my advisor A. Höring for suggesting to me to work on this question and also for his many valuable discussions, guidance and help during the preparation of this paper. I would like to express my sincere thanks to S. Druel for his careful reading of the first draft of this paper and for kindly pointing out several mistakes. Special gratitude is due to M. Beltrametti, D. Litt and C. Mourougane for their interest and helpful comments.