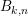1 Introduction
In this paper, we investigate the category ![]() $\text{CM}(B_{k,n})$ of Cohen–Macaulay modules of an algebra
$\text{CM}(B_{k,n})$ of Cohen–Macaulay modules of an algebra ![]() $B_{k,n}$, defined to categorify the cluster structure of the Grassmannian coordinate rings of
$B_{k,n}$, defined to categorify the cluster structure of the Grassmannian coordinate rings of ![]() $k$-planes in
$k$-planes in ![]() $n$-space
$n$-space ![]() $\mathbb{C}[G_{k,n}]$. We study parts of the Auslander–Reiten quiver of this category, mostly those Auslander–Reiten sequences and components containing rigid modules. Of particular interest are the indecomposable Cohen–Macaulay rigid modules with the same class in the Grothendieck group, that is, the modules with the same rank 1 modules appearing as composition factors in their filtrations.
$\mathbb{C}[G_{k,n}]$. We study parts of the Auslander–Reiten quiver of this category, mostly those Auslander–Reiten sequences and components containing rigid modules. Of particular interest are the indecomposable Cohen–Macaulay rigid modules with the same class in the Grothendieck group, that is, the modules with the same rank 1 modules appearing as composition factors in their filtrations.
It is known that rank 1 modules correspond to ![]() $k$-subsets of
$k$-subsets of ![]() $\mathbb{Z}_{n}:=\{1,2,\ldots ,n\}$ and that these in turn are in one-to-one correspondence with the Plücker coordinates in
$\mathbb{Z}_{n}:=\{1,2,\ldots ,n\}$ and that these in turn are in one-to-one correspondence with the Plücker coordinates in ![]() $\mathbb{C}[G_{k,n}]$. We write
$\mathbb{C}[G_{k,n}]$. We write ![]() $L_{I}$ for the rank 1 module associated to the
$L_{I}$ for the rank 1 module associated to the ![]() $k$-subset
$k$-subset ![]() $I$ (see Definition 2.2).
$I$ (see Definition 2.2).
Our first main result is a construction of canonical Auslander–Reiten sequences with rank 1 modules as end terms. A ![]() $k$-subset of
$k$-subset of ![]() $\mathbb{Z}_{n}$ is almost consecutive if it is a union of two intervals, one of them consisting of a single entry.
$\mathbb{Z}_{n}$ is almost consecutive if it is a union of two intervals, one of them consisting of a single entry.
Theorem 1. (Theorem 3.12)
Let ![]() $I$ be an almost consecutive
$I$ be an almost consecutive ![]() $k$-subset and
$k$-subset and ![]() $J$ be such that
$J$ be such that ![]() $L_{J}=\unicode[STIX]{x1D6FA}(L_{I})$. Then there is an AR-sequence
$L_{J}=\unicode[STIX]{x1D6FA}(L_{I})$. Then there is an AR-sequence
The middle term is a rigid rank ![]() $2$ module which is indecomposable if and only if
$2$ module which is indecomposable if and only if ![]() $X$ (and
$X$ (and ![]() $Y$) are almost consecutive.
$Y$) are almost consecutive.
So far, no explicit description of higher rank modules has been given. Our second main contribution is the definition of modules of arbitrary rank in Section 4. We prove in Proposition 4.7 that such modules are free over the center of ![]() $B_{k,n}$, hence they are Cohen–Macaulay.
$B_{k,n}$, hence they are Cohen–Macaulay.
When ![]() $\text{CM}(B_{k,n})$ is of finite representation type, there is a correspondence between indecomposable rank
$\text{CM}(B_{k,n})$ is of finite representation type, there is a correspondence between indecomposable rank ![]() $d$ modules and roots of degree
$d$ modules and roots of degree ![]() $d$ for an associated Kac–Moody algebra [Reference Jensen, King and Su15, Section 8]. We study this correspondence for rank 2 modules when
$d$ for an associated Kac–Moody algebra [Reference Jensen, King and Su15, Section 8]. We study this correspondence for rank 2 modules when ![]() $\text{CM}(B_{k,n})$ is of tame representation type. Our main tool for this is Auslander–Reiten quivers. We compute the tubular components of the Auslander–Reiten quiver containing rigid modules of rank 1 and rank 2 (see [Reference Ringel22, Chapter 3] for details on tubular components). We show that for each rigid indecomposable module of rank 2 we can cycle the filtration layers to obtain a new rigid indecomposable module. This yields the following important result.
$\text{CM}(B_{k,n})$ is of tame representation type. Our main tool for this is Auslander–Reiten quivers. We compute the tubular components of the Auslander–Reiten quiver containing rigid modules of rank 1 and rank 2 (see [Reference Ringel22, Chapter 3] for details on tubular components). We show that for each rigid indecomposable module of rank 2 we can cycle the filtration layers to obtain a new rigid indecomposable module. This yields the following important result.
Theorem 2. (Sections 6.1 and 7.1)
When ![]() $(k,n)=(3,9)$ or
$(k,n)=(3,9)$ or ![]() $(k,n)=(4,8)$, for every real root of degree
$(k,n)=(4,8)$, for every real root of degree ![]() $2$ there are two rigid indecomposable modules. Moreover, if
$2$ there are two rigid indecomposable modules. Moreover, if ![]() $M$ is such a rigid indecomposable rank
$M$ is such a rigid indecomposable rank ![]() $2$ module and if its filtration by rank
$2$ module and if its filtration by rank ![]() $1$ modules is
$1$ modules is ![]() $L_{I}|L_{J}$, then the rank
$L_{I}|L_{J}$, then the rank ![]() $2$ module with filtration
$2$ module with filtration ![]() $L_{J}|L_{I}$ is also rigid indecomposable.
$L_{J}|L_{I}$ is also rigid indecomposable.
Furthermore, in Conjecture 5.15, we give the number of rigid indecomposable rank 2 modules corresponding to real roots in the general case.
It is not hard to see, given the triangulated structure and the Auslander–Reiten translation of ![]() $\text{CM}(B_{k,n})$, that nonprojective rank 1 modules are
$\text{CM}(B_{k,n})$, that nonprojective rank 1 modules are ![]() $\unicode[STIX]{x1D70F}$ periodic (cf. [Reference Baur and Bogdanic4, Proposition 2.7]). We use results from Demonet–Luo [Reference Demonet and Luo7] to explain that this category is
$\unicode[STIX]{x1D70F}$ periodic (cf. [Reference Baur and Bogdanic4, Proposition 2.7]). We use results from Demonet–Luo [Reference Demonet and Luo7] to explain that this category is ![]() $\unicode[STIX]{x1D70F}$ periodic (see Section 3.3).
$\unicode[STIX]{x1D70F}$ periodic (see Section 3.3).
We refer to [Reference Happel14] and [Reference Assem, Simson and Skowroński2] for background on AR theory. For details about Cohen–Macaulay modules we recommend the textbook [Reference Yoshino27] by Yoshino and the work of Buchweitz [Reference Buchweitz6]. Details on the tame-wild dichotomy can be found in [Reference Simson and Skowroński26] or in [Reference Barot, Kussin and Lenzing3].
2 Background
In the following we recall the definition of ![]() $B_{k,n}$, the category of Cohen–Macaulay modules
$B_{k,n}$, the category of Cohen–Macaulay modules ![]() $\text{CM}(B_{k,n})$, and the relation between this category and root systems.
$\text{CM}(B_{k,n})$, and the relation between this category and root systems.
2.1 The category  $\text{CM}(B_{k,n})$
$\text{CM}(B_{k,n})$
We follow the exposition from [Reference Baur, King and Marsh5] in order to introduce notation. Let ![]() $n$ and
$n$ and ![]() $k$ be integers such that
$k$ be integers such that ![]() $1<k\leqslant n/2$. Let
$1<k\leqslant n/2$. Let ![]() $C$ be a circular graph with vertices
$C$ be a circular graph with vertices ![]() $C_{0}=\mathbb{Z}_{n}$ set clockwise around a circle, and with the set of edges,
$C_{0}=\mathbb{Z}_{n}$ set clockwise around a circle, and with the set of edges, ![]() $C_{1}$, also labeled by
$C_{1}$, also labeled by ![]() $\mathbb{Z}_{n}$, with edge
$\mathbb{Z}_{n}$, with edge ![]() $i$ joining vertices
$i$ joining vertices ![]() $i-1$ and
$i-1$ and ![]() $i$. For integers
$i$. For integers ![]() $a,b\in \{1,2,\ldots ,n\}$, we denote by
$a,b\in \{1,2,\ldots ,n\}$, we denote by ![]() $[a,b]$ the closed cyclic interval consisting of the elements of the set
$[a,b]$ the closed cyclic interval consisting of the elements of the set ![]() $\{a,a+1,\ldots ,b\}$ reduced modulo
$\{a,a+1,\ldots ,b\}$ reduced modulo ![]() $n$. Consider the quiver with vertices
$n$. Consider the quiver with vertices ![]() $C_{0}$ and, for each edge
$C_{0}$ and, for each edge ![]() $i\in C_{1}$, a pair of arrows
$i\in C_{1}$, a pair of arrows ![]() $x_{i}:i-1\rightarrow i$ and
$x_{i}:i-1\rightarrow i$ and ![]() $y_{i}:i\rightarrow i-1$. Then we consider the quotient of the path algebra over
$y_{i}:i\rightarrow i-1$. Then we consider the quotient of the path algebra over ![]() $\mathbb{C}$ of this quiver by the ideal generated by the
$\mathbb{C}$ of this quiver by the ideal generated by the ![]() $2n$ relations
$2n$ relations ![]() $xy=yx$ and
$xy=yx$ and ![]() $x^{k}=y^{n-k}$. Here, we interpret
$x^{k}=y^{n-k}$. Here, we interpret ![]() $x$ and
$x$ and ![]() $y$ as arrows of the form
$y$ as arrows of the form ![]() $x_{i},y_{i}$ appropriately, and starting at any vertex. For example, when
$x_{i},y_{i}$ appropriately, and starting at any vertex. For example, when ![]() $n=5$ we have the quiver
$n=5$ we have the quiver

The completion ![]() $B_{k,n}$ of this algebra coincides with the quotient of the completed path algebra of the graph
$B_{k,n}$ of this algebra coincides with the quotient of the completed path algebra of the graph ![]() $C$, that is, the doubled quiver as above, by the closure of the ideal generated by the relations above (we view the completed path algebra of the graph
$C$, that is, the doubled quiver as above, by the closure of the ideal generated by the relations above (we view the completed path algebra of the graph ![]() $C$ as a topological algebra via the
$C$ as a topological algebra via the ![]() $m$-adic topology, where
$m$-adic topology, where ![]() $m$ is the two-sided ideal generated by the arrows of the quiver, see [Reference Derksen, Weyman and Zelevinsky9, Section 1]). The algebra
$m$ is the two-sided ideal generated by the arrows of the quiver, see [Reference Derksen, Weyman and Zelevinsky9, Section 1]). The algebra ![]() $B_{k,n}$, that we will often denote by
$B_{k,n}$, that we will often denote by ![]() $B$ when there is no ambiguity, was introduced in [Reference Jensen, King and Su15], Section 3. Observe that
$B$ when there is no ambiguity, was introduced in [Reference Jensen, King and Su15], Section 3. Observe that ![]() $B_{k,n}$ is isomorphic to
$B_{k,n}$ is isomorphic to ![]() $\text{B}_{n-k,n}$, so we will always take
$\text{B}_{n-k,n}$, so we will always take ![]() $k\leqslant n/2$.
$k\leqslant n/2$.
The center ![]() $Z$ of
$Z$ of ![]() $B$ is the ring of formal power series
$B$ is the ring of formal power series ![]() $\mathbb{C}[[t]]$, where
$\mathbb{C}[[t]]$, where ![]() $t=\sum _{i=1}^{n}x_{i}y_{i}$. The (maximal) Cohen–Macaulay
$t=\sum _{i=1}^{n}x_{i}y_{i}$. The (maximal) Cohen–Macaulay ![]() $B$-modules are precisely those which are free as
$B$-modules are precisely those which are free as ![]() $Z$-modules. Indeed, such a module
$Z$-modules. Indeed, such a module ![]() $M$ is given by a representation
$M$ is given by a representation ![]() $\{M_{i}:i\in C_{0}\}$ of the quiver with each
$\{M_{i}:i\in C_{0}\}$ of the quiver with each ![]() $M_{i}$ a free
$M_{i}$ a free ![]() $Z$-module of the same rank (which is the rank of
$Z$-module of the same rank (which is the rank of ![]() $M$, cf. [Reference Jensen, King and Su15], Section 3).
$M$, cf. [Reference Jensen, King and Su15], Section 3).
Definition 2.1. ([Reference Jensen, King and Su15], Definition 3.5)
For any ![]() $B$-module
$B$-module ![]() $M$, if
$M$, if ![]() $K$ is the field of fractions of
$K$ is the field of fractions of ![]() $Z$, we define its rank
$Z$, we define its rank
Note that ![]() $B\otimes _{Z}K\cong M_{n}(K)$, which is a simple algebra. It is easy to check that the rank is additive on short exact sequences, that
$B\otimes _{Z}K\cong M_{n}(K)$, which is a simple algebra. It is easy to check that the rank is additive on short exact sequences, that ![]() $\operatorname{rk}(M)=0$ for any finite-dimensional
$\operatorname{rk}(M)=0$ for any finite-dimensional ![]() $B$-module (because these are torsion over
$B$-module (because these are torsion over ![]() $Z$) and that, for any Cohen–Macaulay
$Z$) and that, for any Cohen–Macaulay ![]() $B$-module
$B$-module ![]() $M$ and every idempotent
$M$ and every idempotent ![]() $e_{j}$,
$e_{j}$, ![]() $1\leqslant j\leqslant n$,
$1\leqslant j\leqslant n$, ![]() $\operatorname{rk}_{Z}(e_{j}M)=\operatorname{rk}(M)$, so that, in particular,
$\operatorname{rk}_{Z}(e_{j}M)=\operatorname{rk}(M)$, so that, in particular, ![]() $\operatorname{rk}_{Z}(M)=n\operatorname{rk}(M)$.
$\operatorname{rk}_{Z}(M)=n\operatorname{rk}(M)$.
Definition 2.2. [Reference Jensen, King and Su15, Definition 5.1]
For any ![]() $k$-subset
$k$-subset ![]() $I$ of
$I$ of ![]() $C_{1}$, we define a rank
$C_{1}$, we define a rank ![]() $1$
$1$![]() $B$-module
$B$-module
as follows. For each vertex ![]() $i\in C_{0}$, set
$i\in C_{0}$, set ![]() $U_{i}=\mathbb{C}[[t]]$ and, for each edge
$U_{i}=\mathbb{C}[[t]]$ and, for each edge ![]() $i\in C_{1}$, set
$i\in C_{1}$, set
 $x_{i}:U_{i-1}\rightarrow U_{i}$ to be multiplication by
$x_{i}:U_{i-1}\rightarrow U_{i}$ to be multiplication by  $1$ if
$1$ if  $i\in I$, and by
$i\in I$, and by  $t$ if
$t$ if  $i\not \in I$,
$i\not \in I$, $y_{i}:U_{i}\rightarrow U_{i-1}$ to be multiplication by
$y_{i}:U_{i}\rightarrow U_{i-1}$ to be multiplication by  $t$ if
$t$ if  $i\in I$, and by
$i\in I$, and by  $1$ if
$1$ if  $i\not \in I$.
$i\not \in I$.
The module ![]() $L_{I}$ can be represented by a lattice diagram
$L_{I}$ can be represented by a lattice diagram ![]() ${\mathcal{L}}_{I}$ in which
${\mathcal{L}}_{I}$ in which ![]() $U_{0},U_{1},U_{2},\ldots ,U_{n}$ are represented by columns from left to right (with
$U_{0},U_{1},U_{2},\ldots ,U_{n}$ are represented by columns from left to right (with ![]() $U_{0}$ and
$U_{0}$ and ![]() $U_{n}$ to be identified). The vertices in each column correspond to the natural monomial
$U_{n}$ to be identified). The vertices in each column correspond to the natural monomial ![]() $\mathbb{C}$-basis of
$\mathbb{C}$-basis of ![]() $\mathbb{C}[t]$. The column corresponding to
$\mathbb{C}[t]$. The column corresponding to ![]() $U_{i+1}$ is displaced half a step vertically downwards (respectively, upwards) in relation to
$U_{i+1}$ is displaced half a step vertically downwards (respectively, upwards) in relation to ![]() $U_{i}$ if
$U_{i}$ if ![]() $i+1\in I$ (respectively,
$i+1\in I$ (respectively, ![]() $i+1\not \in I$), and the actions of
$i+1\not \in I$), and the actions of ![]() $x_{i}$ and
$x_{i}$ and ![]() $y_{i}$ are shown as diagonal arrows. Note that the
$y_{i}$ are shown as diagonal arrows. Note that the ![]() $k$-subset
$k$-subset ![]() $I$ can then be read off as the set of labels on the arrows pointing down to the right which are exposed to the top of the diagram. For example, the lattice picture
$I$ can then be read off as the set of labels on the arrows pointing down to the right which are exposed to the top of the diagram. For example, the lattice picture ![]() ${\mathcal{L}}_{\{1,4,5\}}$ in the case
${\mathcal{L}}_{\{1,4,5\}}$ in the case ![]() $k=3$,
$k=3$, ![]() $n=8$, is shown in the following picture
$n=8$, is shown in the following picture

Figure 1. Lattice diagram of the module ![]() $L_{\{1,4,5\}}$.
$L_{\{1,4,5\}}$.
We see from Figure 1 that the module ![]() $L_{I}$ is determined by its upper boundary, denoted by the thick lines, which we refer to as the rim of the module
$L_{I}$ is determined by its upper boundary, denoted by the thick lines, which we refer to as the rim of the module ![]() $L_{I}$ (this is why we call the
$L_{I}$ (this is why we call the ![]() $k$-subset
$k$-subset ![]() $I$ as the rim of
$I$ as the rim of ![]() $L_{I}$). Throughout this paper we will identify a rank 1 module
$L_{I}$). Throughout this paper we will identify a rank 1 module ![]() $L_{I}$ with its rim. Moreover, most of the time we will omit the arrows in the rim of
$L_{I}$ with its rim. Moreover, most of the time we will omit the arrows in the rim of ![]() $L_{I}$ and represent it as an undirected graph.
$L_{I}$ and represent it as an undirected graph.
We say that ![]() $i$ is a peak of the rim
$i$ is a peak of the rim ![]() $I$ if
$I$ if ![]() $i\notin I$ and
$i\notin I$ and ![]() $i+1\in I$. In the above example, the peaks of
$i+1\in I$. In the above example, the peaks of ![]() $I=\{1,4,5\}$ are
$I=\{1,4,5\}$ are ![]() $3$ and
$3$ and ![]() $8$.
$8$.
Remark.
We identify the end points of a rim ![]() $I$. Unless specified otherwise, we will assume that the leftmost vertex is labeled by
$I$. Unless specified otherwise, we will assume that the leftmost vertex is labeled by ![]() $n$, and in this case, we may omit labels on the edges of the rim. Looking from left to right, the number of downward edges in the rim is
$n$, and in this case, we may omit labels on the edges of the rim. Looking from left to right, the number of downward edges in the rim is ![]() $k$ (these are the edges labeled by the elements of
$k$ (these are the edges labeled by the elements of ![]() $I$), and the number of upward edges is
$I$), and the number of upward edges is ![]() $n-k$ (these are the edges labeled by the elements of
$n-k$ (these are the edges labeled by the elements of ![]() $[1,n]\setminus I$).
$[1,n]\setminus I$).
Proposition 2.3. [Reference Jensen, King and Su15, Proposition 5.2]
Every rank ![]() $1$ Cohen–Macaulay
$1$ Cohen–Macaulay ![]() $B$-module is isomorphic to
$B$-module is isomorphic to ![]() $L_{I}$ for some unique
$L_{I}$ for some unique ![]() $k$-subset
$k$-subset ![]() $I$ of
$I$ of ![]() $C_{1}$.
$C_{1}$.
Every ![]() $B$-module has a canonical endomorphism given by multiplication by
$B$-module has a canonical endomorphism given by multiplication by ![]() $t\in Z$. For
$t\in Z$. For ![]() $L_{I}$ this corresponds to shifting
$L_{I}$ this corresponds to shifting ![]() ${\mathcal{L}}_{I}$ one step downwards. Since
${\mathcal{L}}_{I}$ one step downwards. Since ![]() $Z$ is central,
$Z$ is central, ![]() $\operatorname{Hom}_{B}(M,N)$ is a
$\operatorname{Hom}_{B}(M,N)$ is a ![]() $Z$-module for arbitrary
$Z$-module for arbitrary ![]() $B$-modules
$B$-modules ![]() $M$ and
$M$ and ![]() $N$.
$N$.
If ![]() $M,N$ are free
$M,N$ are free ![]() $Z$-modules, then so is
$Z$-modules, then so is ![]() $\operatorname{Hom}_{B}(M,N)$. In particular, for rank 1 Cohen–Macaulay
$\operatorname{Hom}_{B}(M,N)$. In particular, for rank 1 Cohen–Macaulay ![]() $B$-modules
$B$-modules ![]() $L_{I}$ and
$L_{I}$ and ![]() $L_{J}$,
$L_{J}$, ![]() $\operatorname{Hom}_{B}(L_{I},L_{J})$ is a free module of rank 1 over
$\operatorname{Hom}_{B}(L_{I},L_{J})$ is a free module of rank 1 over ![]() $Z=\mathbb{C}[[t]]$, generated by the canonical map given by placing the lattice of
$Z=\mathbb{C}[[t]]$, generated by the canonical map given by placing the lattice of ![]() $L_{I}$ inside the lattice of
$L_{I}$ inside the lattice of ![]() $L_{J}$ as far up as possible so that no part of the rim of
$L_{J}$ as far up as possible so that no part of the rim of ![]() $L_{I}$ is strictly above the rim of
$L_{I}$ is strictly above the rim of ![]() $L_{J}$ [Reference Baur, King and Marsh5, Section 6].
$L_{J}$ [Reference Baur, King and Marsh5, Section 6].
The algebra ![]() $B$ has
$B$ has ![]() $n$ indecomposable projective left modules
$n$ indecomposable projective left modules ![]() $P_{j}=Be_{j}$, corresponding to the vertex idempotents
$P_{j}=Be_{j}$, corresponding to the vertex idempotents ![]() $e_{j}\in B$, for
$e_{j}\in B$, for ![]() $j\in C_{0}$. Our convention is that representations of the quiver correspond to left
$j\in C_{0}$. Our convention is that representations of the quiver correspond to left ![]() $B$-modules. The projective indecomposable
$B$-modules. The projective indecomposable ![]() $B$-module
$B$-module ![]() $P_{j}$ is the rank 1 module
$P_{j}$ is the rank 1 module ![]() $L_{I}$, where
$L_{I}$, where ![]() $I=\{j+1,j+2,\ldots ,j+k\}$, so we represent projective indecomposable modules as in the following picture, where
$I=\{j+1,j+2,\ldots ,j+k\}$, so we represent projective indecomposable modules as in the following picture, where ![]() $P_{5}$ is pictured (
$P_{5}$ is pictured (![]() $n=5$,
$n=5$, ![]() $k=3$):
$k=3$):

Definition 2.4. A pair ![]() $I,J$ of
$I,J$ of ![]() $k$-subsets of
$k$-subsets of ![]() $C_{1}$ is said to be noncrossing (or weakly separated) if there are no elements
$C_{1}$ is said to be noncrossing (or weakly separated) if there are no elements ![]() $a,b,c,d$, cyclically ordered around
$a,b,c,d$, cyclically ordered around ![]() $C_{1}$, such that
$C_{1}$, such that ![]() $a,c\in I\setminus J$ and
$a,c\in I\setminus J$ and ![]() $b,d\in J\setminus I$.
$b,d\in J\setminus I$.
Definition 2.5. A ![]() $B$-module is rigid if
$B$-module is rigid if ![]() $\operatorname{Ext}_{B}^{1}(M,M)=0$.
$\operatorname{Ext}_{B}^{1}(M,M)=0$.
If ![]() $I$ and
$I$ and ![]() $J$ are noncrossing
$J$ are noncrossing ![]() $k$-subsets, then
$k$-subsets, then ![]() $\operatorname{Ext}_{B}^{1}(L_{I},L_{J})=0$, in particular, rank 1 modules are rigid (see [Reference Jensen, King and Su15, Proposition 5.6]).
$\operatorname{Ext}_{B}^{1}(L_{I},L_{J})=0$, in particular, rank 1 modules are rigid (see [Reference Jensen, King and Su15, Proposition 5.6]).
Notation 2.6. Every rigid indecomposable ![]() $M$ of rank
$M$ of rank ![]() $n$ in
$n$ in ![]() $\text{CM}(B)$ has a filtration having factors
$\text{CM}(B)$ has a filtration having factors ![]() $L_{I_{1}},L_{I_{2}},\ldots ,L_{I_{n}}$ of rank 1. This filtration is noted in its profile,
$L_{I_{1}},L_{I_{2}},\ldots ,L_{I_{n}}$ of rank 1. This filtration is noted in its profile, ![]() $\text{prf}(M)=I_{1}|I_{2}|\cdots |I_{n}$, [Reference Jensen, King and Su15, Corollary 6.7].
$\text{prf}(M)=I_{1}|I_{2}|\cdots |I_{n}$, [Reference Jensen, King and Su15, Corollary 6.7].
The category ![]() $\text{CM}(B)$ provides a categorification for the cluster structure of Grassmannian coordinate rings. As we will discuss later, the stable category
$\text{CM}(B)$ provides a categorification for the cluster structure of Grassmannian coordinate rings. As we will discuss later, the stable category ![]() $\text{}\underline{\text{CM}}(B)$ is 2-Calabi–Yau. Maximal noncrossing collections of
$\text{}\underline{\text{CM}}(B)$ is 2-Calabi–Yau. Maximal noncrossing collections of ![]() $k$-subsets give rise to cluster-tilting objects
$k$-subsets give rise to cluster-tilting objects ![]() $T$ as the corresponding rank 1 modules are pairwise ext-orthogonal. Given a maximal collection of noncrossing
$T$ as the corresponding rank 1 modules are pairwise ext-orthogonal. Given a maximal collection of noncrossing ![]() $k$-sets
$k$-sets ![]() ${\mathcal{I}}$ (including the projectives, i.e.,
${\mathcal{I}}$ (including the projectives, i.e., ![]() $k$-sets consisting of a single interval), the direct sum
$k$-sets consisting of a single interval), the direct sum ![]() $T=\bigoplus _{I\in {\mathcal{I}}}L_{I}$ corresponds to an alternating strand diagram [Reference Postnikov20] whose associated quiver is an example of a dimer model with boundary [Reference Baur, King and Marsh5, Section 3]. If we forget its frozen vertices (the vertices corresponding to projective indecomposables) we obtain a quiver with potential
$T=\bigoplus _{I\in {\mathcal{I}}}L_{I}$ corresponds to an alternating strand diagram [Reference Postnikov20] whose associated quiver is an example of a dimer model with boundary [Reference Baur, King and Marsh5, Section 3]. If we forget its frozen vertices (the vertices corresponding to projective indecomposables) we obtain a quiver with potential ![]() $(Q,P)$ encoding the endomorphism algebra
$(Q,P)$ encoding the endomorphism algebra ![]() $\operatorname{End}_{\text{}\underline{\text{CM}}}(T)$ as a finite-dimensional Jacobian algebra
$\operatorname{End}_{\text{}\underline{\text{CM}}}(T)$ as a finite-dimensional Jacobian algebra ![]() $J(Q,P)$ in the sense of [Reference Derksen, Weyman and Zelevinsky9].
$J(Q,P)$ in the sense of [Reference Derksen, Weyman and Zelevinsky9].
Remark 2.7. Any given ![]() $k$-subset
$k$-subset ![]() $I$ can be completed to a maximal noncrossing collection
$I$ can be completed to a maximal noncrossing collection ![]() ${\mathcal{I}}$. The arrows in the quiver
${\mathcal{I}}$. The arrows in the quiver ![]() $Q$ of
$Q$ of ![]() $\operatorname{End}_{\text{}\underline{\text{CM}}}(T)$ represent morphisms in
$\operatorname{End}_{\text{}\underline{\text{CM}}}(T)$ represent morphisms in ![]() $\operatorname{Hom}_{\text{}\underline{\text{CM}}}(L_{I},L_{J})$ that do not factor through
$\operatorname{Hom}_{\text{}\underline{\text{CM}}}(L_{I},L_{J})$ that do not factor through ![]() $L_{U}$ with
$L_{U}$ with ![]() $U\in {\mathcal{I}}$. Note that the quiver
$U\in {\mathcal{I}}$. Note that the quiver ![]() $Q$ has no loops.
$Q$ has no loops.
2.2 Root combinatorics
Here we recall the connection between indecomposable modules of the category ![]() $\text{CM}(B_{k,n})$ for
$\text{CM}(B_{k,n})$ for ![]() $k$ and
$k$ and ![]() $n$ as above and roots for an associated Kac–Moody algebra, as explained in [Reference Jensen, King and Su15]. For details about the connection between indecomposable modules and positive roots for Kac–Moody algebras, we refer to the book [Reference Derksen and Weyman8] by Derksen and Weyman.
$n$ as above and roots for an associated Kac–Moody algebra, as explained in [Reference Jensen, King and Su15]. For details about the connection between indecomposable modules and positive roots for Kac–Moody algebras, we refer to the book [Reference Derksen and Weyman8] by Derksen and Weyman.
For ![]() $(k,n)$ let
$(k,n)$ let ![]() $J_{k,n}$ be the tree obtained by drawing a Dynkin diagram of type
$J_{k,n}$ be the tree obtained by drawing a Dynkin diagram of type ![]() $A_{n-1}$, labeling the nodes
$A_{n-1}$, labeling the nodes ![]() $1,2,\ldots ,n-1$ and adding a node
$1,2,\ldots ,n-1$ and adding a node ![]() $n$ with an edge to node
$n$ with an edge to node ![]() $k$. We consider positive roots for the associated Kac–Moody algebra, denoting the simple root associated with node
$k$. We consider positive roots for the associated Kac–Moody algebra, denoting the simple root associated with node ![]() $i$ by
$i$ by ![]() $\unicode[STIX]{x1D6FC}_{i}$ for
$\unicode[STIX]{x1D6FC}_{i}$ for ![]() $i=1,\ldots ,n-1$ and the simple root associated with
$i=1,\ldots ,n-1$ and the simple root associated with ![]() $n$ by
$n$ by ![]() $\unicode[STIX]{x1D6FD}$. For
$\unicode[STIX]{x1D6FD}$. For ![]() $k=2$, the resulting diagram
$k=2$, the resulting diagram ![]() $J_{k,n}$ is a Dynkin diagram of type
$J_{k,n}$ is a Dynkin diagram of type ![]() $D_{n}$.
$D_{n}$.
For ![]() $n=6,7,8$ and
$n=6,7,8$ and ![]() $k=3$, we obtain
$k=3$, we obtain ![]() $E_{6}$,
$E_{6}$, ![]() $E_{7}$ and
$E_{7}$ and ![]() $E_{8}$, respectively.
$E_{8}$, respectively.
The diagrams ![]() $J_{4,8}$ and
$J_{4,8}$ and ![]() $J_{3,9}$ are
$J_{3,9}$ are ![]() $\widetilde{E}_{7}$ and
$\widetilde{E}_{7}$ and ![]() $\widetilde{E}_{8}$, respectively:
$\widetilde{E}_{8}$, respectively:
There is a grading on the roots of the corresponding Kac–Moody algebra, where the degree is given by the coefficient of the root at ![]() $\unicode[STIX]{x1D6FD}$, that is, at the
$\unicode[STIX]{x1D6FD}$, that is, at the ![]() $n$th node, the black node in the figures.
$n$th node, the black node in the figures.
Zelevinsky conjectured [Reference Zelevinsky28] that the number of degree ![]() $d$ cluster variables is equal to
$d$ cluster variables is equal to ![]() $d$ times the number of real roots for
$d$ times the number of real roots for ![]() $J_{k,n}$ of degree
$J_{k,n}$ of degree ![]() $d$. In the finite types, this is known to hold, [Reference Scott23, Theorems 6,7,8], whereas in the infinite cases it does not hold in this generality. It is expected that one needs to restrict to cluster variables which are associated to real roots. In this spirit, one can ask whether the number of rank
$d$. In the finite types, this is known to hold, [Reference Scott23, Theorems 6,7,8], whereas in the infinite cases it does not hold in this generality. It is expected that one needs to restrict to cluster variables which are associated to real roots. In this spirit, one can ask whether the number of rank ![]() $d$ rigid indecomposable modules of
$d$ rigid indecomposable modules of ![]() $\text{CM}(B_{k,n})$ is
$\text{CM}(B_{k,n})$ is ![]() $d$ times the number of real roots for
$d$ times the number of real roots for ![]() $J_{k,n}$ of degree
$J_{k,n}$ of degree ![]() $d$. Jensen et al. confirmed that this holds in the finite type cases [Reference Jensen, King and Su15, Observation 2.3], see also Example 2.8.
$d$. Jensen et al. confirmed that this holds in the finite type cases [Reference Jensen, King and Su15, Observation 2.3], see also Example 2.8.
We recall a map from indecomposable modules in ![]() $\text{CM}(B)$ to roots for
$\text{CM}(B)$ to roots for ![]() $J_{k,n}$ via a map from
$J_{k,n}$ via a map from ![]() $\operatorname{ind}\text{CM}(B)$ to
$\operatorname{ind}\text{CM}(B)$ to ![]() $\mathbb{Z}^{n}$ from [Reference Jensen, King and Su15, Section 8]: If
$\mathbb{Z}^{n}$ from [Reference Jensen, King and Su15, Section 8]: If ![]() $M=L_{1}|L_{2}|\cdots |L_{d}$ is indecomposable, let
$M=L_{1}|L_{2}|\cdots |L_{d}$ is indecomposable, let ![]() $\text{}\underline{a}=\text{}\underline{a}(M)=(a_{1},\ldots ,a_{n})$ be the vector where
$\text{}\underline{a}=\text{}\underline{a}(M)=(a_{1},\ldots ,a_{n})$ be the vector where ![]() $a_{i}$ is the multiplicity of
$a_{i}$ is the multiplicity of ![]() $i$ in
$i$ in ![]() $L_{1}\cup \cdots \cup L_{d}$, for
$L_{1}\cup \cdots \cup L_{d}$, for ![]() $i=1,\ldots ,n$. Let
$i=1,\ldots ,n$. Let ![]() $e_{1},\ldots ,e_{n}$ be the standard basis vectors for
$e_{1},\ldots ,e_{n}$ be the standard basis vectors for ![]() $\mathbb{Z}^{n}$. Then we can associate with
$\mathbb{Z}^{n}$. Then we can associate with ![]() $M$ a root
$M$ a root ![]() $\unicode[STIX]{x1D711}(M)$ for
$\unicode[STIX]{x1D711}(M)$ for ![]() $J_{k,n}$ via the correspondence
$J_{k,n}$ via the correspondence ![]() $\unicode[STIX]{x1D6FC}_{i}\longleftrightarrow -e_{i}+e_{i+1}$,
$\unicode[STIX]{x1D6FC}_{i}\longleftrightarrow -e_{i}+e_{i+1}$, ![]() $i=1,\ldots ,n-1,$ and
$i=1,\ldots ,n-1,$ and ![]() $\unicode[STIX]{x1D6FD}\longleftrightarrow e_{1}+e_{2}+\cdots +e_{k}$.
$\unicode[STIX]{x1D6FD}\longleftrightarrow e_{1}+e_{2}+\cdots +e_{k}$.
Note that the image of ![]() $M$ under
$M$ under ![]() $\text{}\underline{a}$ is in the sublattice
$\text{}\underline{a}$ is in the sublattice ![]() $\mathbb{Z}^{n}(k)=\{a\in \mathbb{Z}^{n}\mid k\text{ divides }\sum a_{i}\}$ and that
$\mathbb{Z}^{n}(k)=\{a\in \mathbb{Z}^{n}\mid k\text{ divides }\sum a_{i}\}$ and that ![]() $\unicode[STIX]{x1D711}(M)$ is a root of degree
$\unicode[STIX]{x1D711}(M)$ is a root of degree ![]() $d$. Via these correspondences, we can identify the lattice
$d$. Via these correspondences, we can identify the lattice ![]() $\mathbb{Z}^{n}(k)$ with the root lattice of the Kac–Moody algebra of
$\mathbb{Z}^{n}(k)$ with the root lattice of the Kac–Moody algebra of ![]() $J_{k,n}$ and we have the quadratic form
$J_{k,n}$ and we have the quadratic form
on ![]() $\mathbb{Z}^{n}(k)$ which characterizes roots for
$\mathbb{Z}^{n}(k)$ which characterizes roots for ![]() $J_{k,n}$ as the vectors with
$J_{k,n}$ as the vectors with ![]() $q(\text{}\underline{a})\leqslant 2$. Among them, the vectors with
$q(\text{}\underline{a})\leqslant 2$. Among them, the vectors with ![]() $q(\text{}\underline{a})=2$ correspond to real roots.
$q(\text{}\underline{a})=2$ correspond to real roots.
Conjecturally, rigid indecomposable modules correspond to roots and if a module belongs to a homogeneous tube, the associated root is imaginary. In the finite types, the correspondence between rigid indecomposable modules and (real) roots is confirmed. Here, we initiate the study of infinite representation types, and in particular, we study rank 2 indecomposable CM-modules. We show that, in the tame cases, for every real root of ![]() $J_{k,n}$ there exist two rigid indecomposable rank 2 modules (see Theorem 2). Note that for
$J_{k,n}$ there exist two rigid indecomposable rank 2 modules (see Theorem 2). Note that for ![]() $J_{4,8}$ there exist 8 rigid indecomposable rank 2 modules whose associated root is imaginary, see [Reference Jensen, King and Su15, Figure 13].
$J_{4,8}$ there exist 8 rigid indecomposable rank 2 modules whose associated root is imaginary, see [Reference Jensen, King and Su15, Figure 13].
Example 2.8. For ![]() $k=2$, there are no indecomposable modules of rank 2. The diagram
$k=2$, there are no indecomposable modules of rank 2. The diagram ![]() $J_{2,n}$ is a Dynkin diagram of type
$J_{2,n}$ is a Dynkin diagram of type ![]() $D_{n}$ for which there are no roots of degree 2.
$D_{n}$ for which there are no roots of degree 2.
Let ![]() $k=3$.
$k=3$.
(i) The diagram ![]() $J_{3,6}$ is a Dynkin diagram of type
$J_{3,6}$ is a Dynkin diagram of type ![]() $E_{6}$. The only root where node 6 has degree
$E_{6}$. The only root where node 6 has degree ![]() $2$ is the root
$2$ is the root ![]() $\unicode[STIX]{x1D6FC}_{1}+2\unicode[STIX]{x1D6FC}_{2}+3\unicode[STIX]{x1D6FC}_{3}+2\unicode[STIX]{x1D6FC}_{4}+\unicode[STIX]{x1D6FC}_{5}+2\unicode[STIX]{x1D6FD}$. It is known that there are exactly two degree
$\unicode[STIX]{x1D6FC}_{1}+2\unicode[STIX]{x1D6FC}_{2}+3\unicode[STIX]{x1D6FC}_{3}+2\unicode[STIX]{x1D6FC}_{4}+\unicode[STIX]{x1D6FC}_{5}+2\unicode[STIX]{x1D6FD}$. It is known that there are exactly two degree ![]() $2$ cluster variables, cf. [Reference Scott23, Theorem 6]. On the other hand, the only rank 2 (rigid) indecomposable modules in this case are
$2$ cluster variables, cf. [Reference Scott23, Theorem 6]. On the other hand, the only rank 2 (rigid) indecomposable modules in this case are ![]() $L_{135}|L_{246}$ and
$L_{135}|L_{246}$ and ![]() $L_{246}|L_{135}$, cf. [Reference Jensen, King and Su15, Figure 10].
$L_{246}|L_{135}$, cf. [Reference Jensen, King and Su15, Figure 10].
(ii) The diagram ![]() $J_{3,7}$ is a Dynkin diagram of type
$J_{3,7}$ is a Dynkin diagram of type ![]() $E_{7}$. The Lie algebra of type
$E_{7}$. The Lie algebra of type ![]() $E_{7}$ has 7 roots of degree 2. There are 14 cluster variables of degree 2 [Reference Scott23, Theorem 7] and, correspondingly, 14 rank 2 (rigid) indecomposable modules for
$E_{7}$ has 7 roots of degree 2. There are 14 cluster variables of degree 2 [Reference Scott23, Theorem 7] and, correspondingly, 14 rank 2 (rigid) indecomposable modules for ![]() $(3,7)$. These can be found in [Reference Jensen, King and Su15, Figure 11].
$(3,7)$. These can be found in [Reference Jensen, King and Su15, Figure 11].
(iii) The diagram ![]() $J_{3,8}$ is of type
$J_{3,8}$ is of type ![]() $E_{8}$, there are 28 roots of degree 2 in the corresponding root system. The number of cluster variables of degree 2, and the number of rank 2 (rigid) indecomposable modules is 56, cf. [Reference Jensen, King and Su15, Figure 12].
$E_{8}$, there are 28 roots of degree 2 in the corresponding root system. The number of cluster variables of degree 2, and the number of rank 2 (rigid) indecomposable modules is 56, cf. [Reference Jensen, King and Su15, Figure 12].
Remark 2.9. For ![]() $J_{3,9}$ there are 84 real roots of degree 2. For
$J_{3,9}$ there are 84 real roots of degree 2. For ![]() $J_{4,8}$ there are 56 real roots of degree 2. One can find all these roots considering the classical result [Reference Kac16, Theorem 5.6] and playing the so-called find the highest root game which is attributed to B. Kostant by Knutson [Reference Knutson19].
$J_{4,8}$ there are 56 real roots of degree 2. One can find all these roots considering the classical result [Reference Kac16, Theorem 5.6] and playing the so-called find the highest root game which is attributed to B. Kostant by Knutson [Reference Knutson19].
3 Homological properties
The algebra ![]() $B=B_{k,n}$ is Gorenstein, that is, it is left and right noetherian and of finite (left and right) injective dimension. Hence, the category
$B=B_{k,n}$ is Gorenstein, that is, it is left and right noetherian and of finite (left and right) injective dimension. Hence, the category ![]() $\text{CM}(B)$ is Frobenius and the projective–injective objects are the projective
$\text{CM}(B)$ is Frobenius and the projective–injective objects are the projective ![]() $B$-modules. The stable category
$B$-modules. The stable category ![]() $\text{}\underline{\text{CM}}(B)$ has a triangulated structure in which the suspension
$\text{}\underline{\text{CM}}(B)$ has a triangulated structure in which the suspension ![]() $[1]$ coincides with the formal inverse of
$[1]$ coincides with the formal inverse of ![]() $\unicode[STIX]{x1D6FA}$ [Reference Buchweitz6, Reference Happel14].
$\unicode[STIX]{x1D6FA}$ [Reference Buchweitz6, Reference Happel14].
Let ![]() $\unicode[STIX]{x1D6F1}_{k,n}$ be the quotient of the preprojective algebra of type
$\unicode[STIX]{x1D6F1}_{k,n}$ be the quotient of the preprojective algebra of type ![]() $\mathbb{A}_{n-1}$ over the ideal
$\mathbb{A}_{n-1}$ over the ideal ![]() $\langle x^{k},y^{n-k}\rangle$. This finite-dimensional
$\langle x^{k},y^{n-k}\rangle$. This finite-dimensional ![]() $\mathbb{C}$-algebra is Gorenstein of dimension 1. The category
$\mathbb{C}$-algebra is Gorenstein of dimension 1. The category ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ is equivalent to the exact subcategory
$\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ is equivalent to the exact subcategory ![]() $\text{Sub}Q_{k}$ defined in [Reference Geiss, Leclerc and Schröer13]. Analogously to
$\text{Sub}Q_{k}$ defined in [Reference Geiss, Leclerc and Schröer13]. Analogously to ![]() $\text{CM}(B)$,
$\text{CM}(B)$, ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ is Frobenius and the stable category
$\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ is Frobenius and the stable category ![]() $\text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$ has a triangulated structure in which
$\text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$ has a triangulated structure in which ![]() $[1]$ coincides with the formal inverse of
$[1]$ coincides with the formal inverse of ![]() $\unicode[STIX]{x1D6FA}$, denoted by
$\unicode[STIX]{x1D6FA}$, denoted by ![]() $(\unicode[STIX]{x1D6FA})^{-1}$. This formal inverse is not the co-syzygy
$(\unicode[STIX]{x1D6FA})^{-1}$. This formal inverse is not the co-syzygy ![]() $\unicode[STIX]{x1D6FA}^{-1}$ since the algebras
$\unicode[STIX]{x1D6FA}^{-1}$ since the algebras ![]() $B_{k,n}$ and
$B_{k,n}$ and ![]() $\unicode[STIX]{x1D6F1}_{k,n}$ are not self-injective, hence the slightly different notation.
$\unicode[STIX]{x1D6F1}_{k,n}$ are not self-injective, hence the slightly different notation.
By [Reference Jensen, King and Su15, Section 4], there is a (quotient) exact functor ![]() $\unicode[STIX]{x1D70B}:\text{CM}(B)\rightarrow \text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ setting a one-to-one correspondence between the indecomposable modules in
$\unicode[STIX]{x1D70B}:\text{CM}(B)\rightarrow \text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ setting a one-to-one correspondence between the indecomposable modules in ![]() $\text{CM}(B_{k,n})$ other than
$\text{CM}(B_{k,n})$ other than ![]() $P_{n}$ and the indecomposable modules in
$P_{n}$ and the indecomposable modules in ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$. This functor restricts to a triangle equivalence
$\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$. This functor restricts to a triangle equivalence ![]() $\text{}\underline{\unicode[STIX]{x1D70B}}:\text{}\underline{\text{CM}}(B)\rightarrow \text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$. By construction the standard triangles of
$\text{}\underline{\unicode[STIX]{x1D70B}}:\text{}\underline{\text{CM}}(B)\rightarrow \text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$. By construction the standard triangles of ![]() $\text{}\underline{\text{CM}}(B_{k,n})$, obtained via push-outs, are of the form
$\text{}\underline{\text{CM}}(B_{k,n})$, obtained via push-outs, are of the form
where ![]() $0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ is a short exact sequence in
$0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ is a short exact sequence in ![]() $\text{CM}(B)$. The functor
$\text{CM}(B)$. The functor ![]() $\unicode[STIX]{x1D70B}$ takes exact sequences to exact sequences. This implies that we can use the additivity of the dimension vector
$\unicode[STIX]{x1D70B}$ takes exact sequences to exact sequences. This implies that we can use the additivity of the dimension vector ![]() $\text{}\underline{\text{dim}}$ on
$\text{}\underline{\text{dim}}$ on ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ to reconstruct triangles, in particular, Auslander–Reiten triangles. We may refer to an Auslander–Reiten triangle
$\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ to reconstruct triangles, in particular, Auslander–Reiten triangles. We may refer to an Auslander–Reiten triangle
also as the associated short exact sequence ![]() $A{\hookrightarrow}B{\twoheadrightarrow}\unicode[STIX]{x1D70F}^{-1}A$.
$A{\hookrightarrow}B{\twoheadrightarrow}\unicode[STIX]{x1D70F}^{-1}A$.
The category ![]() $\text{}\underline{\text{Sub}}Q_{k}$ is triangulated and 2-Calabi–Yau [Reference Geiss, Leclerc and Schröer13, Proposition 3.4]. Denote by
$\text{}\underline{\text{Sub}}Q_{k}$ is triangulated and 2-Calabi–Yau [Reference Geiss, Leclerc and Schröer13, Proposition 3.4]. Denote by ![]() $[1]_{\text{Sub}}$ the shift in this category. Notice that
$[1]_{\text{Sub}}$ the shift in this category. Notice that ![]() $[1]_{\text{Sub}}$ can be interpreted as the formal inverse of the syzygy when we are in
$[1]_{\text{Sub}}$ can be interpreted as the formal inverse of the syzygy when we are in ![]() $\text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$, see [Reference Jensen, King and Su15, Remark 4.2]. By [Reference Reiten and Van den Bergh21],
$\text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$, see [Reference Jensen, King and Su15, Remark 4.2]. By [Reference Reiten and Van den Bergh21], ![]() $\unicode[STIX]{x1D70F}[1]_{\text{Sub}}\simeq S$, where
$\unicode[STIX]{x1D70F}[1]_{\text{Sub}}\simeq S$, where ![]() $S$ is the Serre functor. It also holds that
$S$ is the Serre functor. It also holds that ![]() $S=[2]_{\text{Sub}}$ from the 2-Calabi–Yau condition. Therefore,
$S=[2]_{\text{Sub}}$ from the 2-Calabi–Yau condition. Therefore, ![]() $\unicode[STIX]{x1D70F}=[1]_{\text{Sub}}$ over
$\unicode[STIX]{x1D70F}=[1]_{\text{Sub}}$ over ![]() $\text{}\underline{\text{Sub}}Q_{k}$, and this implies that
$\text{}\underline{\text{Sub}}Q_{k}$, and this implies that ![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D70F}^{-1}$ in the category
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D70F}^{-1}$ in the category ![]() $\text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$. Hence, by the equivalence
$\text{}\underline{\text{CM}}(\unicode[STIX]{x1D6F1}_{k,n})$. Hence, by the equivalence ![]() $\text{}\underline{\unicode[STIX]{x1D70B}}$, we have
$\text{}\underline{\unicode[STIX]{x1D70B}}$, we have ![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D70F}^{-1}$ in
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D70F}^{-1}$ in ![]() $\text{}\underline{\text{CM}}(B)$.
$\text{}\underline{\text{CM}}(B)$.

Figure 2. Lattice diagram of a module in ![]() $\text{CM}(B_{3,8})$ and its image in
$\text{CM}(B_{3,8})$ and its image in ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{3,8})$ under
$\text{CM}(\unicode[STIX]{x1D6F1}_{3,8})$ under ![]() $\unicode[STIX]{x1D70B}$, and the corresponding quotient poset
$\unicode[STIX]{x1D70B}$, and the corresponding quotient poset ![]() $(1^{3},2)$.
$(1^{3},2)$.
Example 3.1. Let ![]() $(k,n)=(3,8)$. Consider the rank 2 module
$(k,n)=(3,8)$. Consider the rank 2 module ![]() $M=L_{I}\mid L_{J}$ with
$M=L_{I}\mid L_{J}$ with ![]() $I=\{2,5,7\}$ and
$I=\{2,5,7\}$ and ![]() $J=\{1,3,6\}$. As for rank 1 modules, it is convenient to view higher rank modules as lattice diagrams. The lattice diagram of
$J=\{1,3,6\}$. As for rank 1 modules, it is convenient to view higher rank modules as lattice diagrams. The lattice diagram of ![]() $M$ is drawn on the left hand side in Figure 2. The image
$M$ is drawn on the left hand side in Figure 2. The image ![]() $\unicode[STIX]{x1D70B}(M)$ is obtained by taking the quotient of
$\unicode[STIX]{x1D70B}(M)$ is obtained by taking the quotient of ![]() $M$ by the projective
$M$ by the projective ![]() $P_{8}$. In particular, we can obtain the dimension vector of the
$P_{8}$. In particular, we can obtain the dimension vector of the ![]() $\unicode[STIX]{x1D6F1}_{k,n}$-module
$\unicode[STIX]{x1D6F1}_{k,n}$-module ![]() $\unicode[STIX]{x1D70B}(M)$ by cutting out the vertices corresponding to the lattice of
$\unicode[STIX]{x1D70B}(M)$ by cutting out the vertices corresponding to the lattice of ![]() $P_{8}$ from the lattice of
$P_{8}$ from the lattice of ![]() $L_{I}\mid L_{J}$ as in Figure 2 (center) and considering the multiplicities of the vertices 1 to
$L_{I}\mid L_{J}$ as in Figure 2 (center) and considering the multiplicities of the vertices 1 to ![]() $n-1$.
$n-1$.
There is a covering functor from the category of finitely generated complete poset representations for a poset ![]() $\unicode[STIX]{x1D6E4}$ [Reference Simson24, Chapter 13], see also [Reference Simson25], where
$\unicode[STIX]{x1D6E4}$ [Reference Simson24, Chapter 13], see also [Reference Simson25], where ![]() $\unicode[STIX]{x1D6E4}$ is a cylindrical covering of the circular quiver of
$\unicode[STIX]{x1D6E4}$ is a cylindrical covering of the circular quiver of ![]() $B$, to the category
$B$, to the category ![]() $\text{CM}(B_{k,n})$. The complete poset representations have a vector space at each vertex of
$\text{CM}(B_{k,n})$. The complete poset representations have a vector space at each vertex of ![]() $\unicode[STIX]{x1D6E4}$ and all arrows are subspace inclusions. If
$\unicode[STIX]{x1D6E4}$ and all arrows are subspace inclusions. If ![]() $\widetilde{M}$ is a complete poset representation for
$\widetilde{M}$ is a complete poset representation for ![]() $\unicode[STIX]{x1D6E4}$, it can be identified with a finite subspace configuration of a vector space, say
$\unicode[STIX]{x1D6E4}$, it can be identified with a finite subspace configuration of a vector space, say ![]() $M_{\ast }$, with
$M_{\ast }$, with ![]() $\dim M_{\ast }=\operatorname{rank}\widetilde{M}$.
$\dim M_{\ast }=\operatorname{rank}\widetilde{M}$.
It is important that ![]() $\widetilde{M}$, and therefore
$\widetilde{M}$, and therefore ![]() $M\in \text{CM}(B)$, can be identified with a pull-back from a finite quotient poset of
$M\in \text{CM}(B)$, can be identified with a pull-back from a finite quotient poset of ![]() $\unicode[STIX]{x1D6E4}$ and the indecomposability of
$\unicode[STIX]{x1D6E4}$ and the indecomposability of ![]() $M$ can be deduced from the indecomposability of
$M$ can be deduced from the indecomposability of ![]() $\widetilde{M}$. Moreover when
$\widetilde{M}$. Moreover when ![]() $M$ is rigid indecomposable,
$M$ is rigid indecomposable, ![]() $\widetilde{M}$ is unique up to a grade shift, [Reference Jensen, King and Su15, Lemma 6.2, Remark 6.3].
$\widetilde{M}$ is unique up to a grade shift, [Reference Jensen, King and Su15, Lemma 6.2, Remark 6.3].
Remark 3.2. Let ![]() $M$ be an indecomposable of rank 2 in
$M$ be an indecomposable of rank 2 in ![]() $\text{CM}(B)$. Then the corresponding finite quotient poset has to be of the form
$\text{CM}(B)$. Then the corresponding finite quotient poset has to be of the form ![]() $(1^{r},2)$ for some
$(1^{r},2)$ for some ![]() $r$. Since
$r$. Since ![]() $(1,2)$ and
$(1,2)$ and ![]() $(1^{2},2)$ are dimension vectors for the quivers
$(1^{2},2)$ are dimension vectors for the quivers ![]() $1\rightarrow 2$ and
$1\rightarrow 2$ and ![]() $1\rightarrow 2\leftarrow 3$, respectively, of Dynkin type
$1\rightarrow 2\leftarrow 3$, respectively, of Dynkin type ![]() $A_{2}$ and
$A_{2}$ and ![]() $A_{3}$, respectively, the corresponding representations cannot be indecomposable. Hence
$A_{3}$, respectively, the corresponding representations cannot be indecomposable. Hence ![]() $r\geqslant 3$. These posets are precisely the ones corresponding to indecomposable subspace configurations of rank 2.
$r\geqslant 3$. These posets are precisely the ones corresponding to indecomposable subspace configurations of rank 2.
Example 3.3. Let ![]() $M=L_{I}\mid L_{J}$ be a rank 2 module in
$M=L_{I}\mid L_{J}$ be a rank 2 module in ![]() $\text{CM}(B_{k,n})$ with
$\text{CM}(B_{k,n})$ with ![]() $I\neq J$. Then its poset is of the form
$I\neq J$. Then its poset is of the form ![]() $(1^{r},2)$ for
$(1^{r},2)$ for ![]() $0<r\leqslant k$. The modules
$0<r\leqslant k$. The modules ![]() $M=L_{I}\mid L_{J}$ with
$M=L_{I}\mid L_{J}$ with ![]() $I=\{2,5,7\}$ and
$I=\{2,5,7\}$ and ![]() $J=\{1,3,6\}$ from Example 3.1 and the first module in Figure 4 have poset
$J=\{1,3,6\}$ from Example 3.1 and the first module in Figure 4 have poset ![]() $(1^{3},2)$. Examples for the poset
$(1^{3},2)$. Examples for the poset ![]() $(1,2)$ are the modules in Figure 3 and the last module in Figure 4. An example for
$(1,2)$ are the modules in Figure 3 and the last module in Figure 4. An example for ![]() $(1^{2},2)$ is the second module in Figure 4.
$(1^{2},2)$ is the second module in Figure 4.

Figure 3. Rank 2 modules with submodule ![]() $L_{I}$ and quotient
$L_{I}$ and quotient ![]() $L_{J}$.
$L_{J}$.

Figure 4. Rank 2 modules with submodule ![]() $L_{I}$ and quotient
$L_{I}$ and quotient ![]() $L_{J}$, continued.
$L_{J}$, continued.
3.1 Extension spaces between rank 1 modules
Let ![]() $I$ be a rim, and let
$I$ be a rim, and let ![]() $d_{i}$ and
$d_{i}$ and ![]() $l_{i}$ respectively be the lengths of disjoint intervals of
$l_{i}$ respectively be the lengths of disjoint intervals of ![]() $I$ and the lengths of the corresponding intervals of the complement of
$I$ and the lengths of the corresponding intervals of the complement of ![]() $I$ in
$I$ in ![]() $\{1,2,\ldots ,n\}$. In other words, let
$\{1,2,\ldots ,n\}$. In other words, let ![]() $d_{i}$ and
$d_{i}$ and ![]() $l_{i}$ denote the lengths of downward and upward slopes, respectively, of
$l_{i}$ denote the lengths of downward and upward slopes, respectively, of ![]() $I$. Let
$I$. Let ![]() $m$ denote the minimum of the numbers
$m$ denote the minimum of the numbers ![]() $d_{i}$ and
$d_{i}$ and ![]() $l_{i}$.
$l_{i}$.
Proposition 3.4. Let ![]() $I$ be a rim with two peaks and let
$I$ be a rim with two peaks and let ![]() $J$ be any rim. If
$J$ be any rim. If ![]() $I$ and
$I$ and ![]() $J$ are crossing, then
$J$ are crossing, then
where ![]() $a$ is less or equal to the minimum
$a$ is less or equal to the minimum ![]() $m$ of the lengths of the slopes (both downward and upward) of
$m$ of the lengths of the slopes (both downward and upward) of ![]() $I$.
$I$.
Proof. Since there are only four slopes on the rim ![]() $I$, when
$I$, when ![]() $J$ is placed funderneath
$J$ is placed funderneath ![]() $I$ in the computation of
$I$ in the computation of ![]() $\operatorname{Ext}^{1}(L_{I},L_{J})$, as in [Reference Baur and Bogdanic4, Theorem 3.1], there are at most four trapezia appearing. Since we assumed that the rims are crossing, then there are exactly four trapezia with nontrivial lateral sides, and hence, there are exactly two boxes (each box consisting of two trapezia). Each of the lateral sides of the trapezia involved is of length at most equal to the length of the corresponding slope of the rim
$\operatorname{Ext}^{1}(L_{I},L_{J})$, as in [Reference Baur and Bogdanic4, Theorem 3.1], there are at most four trapezia appearing. Since we assumed that the rims are crossing, then there are exactly four trapezia with nontrivial lateral sides, and hence, there are exactly two boxes (each box consisting of two trapezia). Each of the lateral sides of the trapezia involved is of length at most equal to the length of the corresponding slope of the rim ![]() $I$. It follows that the matrix
$I$. It follows that the matrix ![]() $D^{\ast }$ is of the form
$D^{\ast }$ is of the form
where the numbers ![]() $m_{i}$ denote the lengths of the lateral sides of the trapezia used to compute the extension space
$m_{i}$ denote the lengths of the lateral sides of the trapezia used to compute the extension space ![]() $\operatorname{Ext}^{1}(L_{I},L_{J})$ [Reference Baur and Bogdanic4]. If we choose
$\operatorname{Ext}^{1}(L_{I},L_{J})$ [Reference Baur and Bogdanic4]. If we choose ![]() $a$ to be the minimal
$a$ to be the minimal ![]() $m_{i}$, then the proposition follows.◻
$m_{i}$, then the proposition follows.◻
Corollary 3.5. If ![]() $I$ and
$I$ and ![]() $J$ are crossing rims with two peaks each, then
$J$ are crossing rims with two peaks each, then
where ![]() $a$ is less or equal to the minimum of the lengths of all slopes of
$a$ is less or equal to the minimum of the lengths of all slopes of ![]() $I$ and
$I$ and ![]() $J$.
$J$.
Proof. It follows from ![]() $\operatorname{Ext}^{1}(L_{I},L_{J})\cong \operatorname{Ext}^{1}(L_{J},L_{I})$ (see [Reference Baur and Bogdanic4, Theorem 3.7]).◻
$\operatorname{Ext}^{1}(L_{I},L_{J})\cong \operatorname{Ext}^{1}(L_{J},L_{I})$ (see [Reference Baur and Bogdanic4, Theorem 3.7]).◻
Corollary 3.6. If ![]() $I$ and
$I$ and ![]() $J$ are crossing rims with
$J$ are crossing rims with ![]() $I$ having two peaks and one of the slopes of length
$I$ having two peaks and one of the slopes of length ![]() $1$, then
$1$, then
Proof. If ![]() $a$ is as in the previous proposition, then in this case
$a$ is as in the previous proposition, then in this case ![]() $a\leqslant 1$, and since
$a\leqslant 1$, and since ![]() $I$ and
$I$ and ![]() $J$ are crossing, we must have
$J$ are crossing, we must have ![]() $1\leqslant a$.◻
$1\leqslant a$.◻
We can use the previous corollary to construct part of the Auslander–Reiten quiver containing rank 1 modules whose rims have two peaks and a slope of length 1. For such a rim ![]() $I$, and
$I$, and ![]() $J$ such that
$J$ such that ![]() $\unicode[STIX]{x1D6FA}(L_{I})=L_{J}$, if we can find a nontrivial short exact sequence of the form
$\unicode[STIX]{x1D6FA}(L_{I})=L_{J}$, if we can find a nontrivial short exact sequence of the form
then this sequence must be an Auslander–Reiten sequence.
Example 3.7. If ![]() $I=\{1,2,\ldots ,k-1\}\cup \{m\}$, where
$I=\{1,2,\ldots ,k-1\}\cup \{m\}$, where ![]() $n>m>k$, then for any rim
$n>m>k$, then for any rim ![]() $J$ that is crossing with
$J$ that is crossing with ![]() $I$ we have
$I$ we have ![]() $\operatorname{Ext}^{1}(L_{I},L_{J})\cong \mathbb{C}$.
$\operatorname{Ext}^{1}(L_{I},L_{J})\cong \mathbb{C}$.
In the following proposition, we deal with a case where the upper bound from the previous proposition is achieved.
Proposition 3.8. Let ![]() $I$ be a rim with two peaks, and let
$I$ be a rim with two peaks, and let ![]() $m$ be as above, that is, the minimum of the lengths of the slopes of
$m$ be as above, that is, the minimum of the lengths of the slopes of ![]() $I$. Then
$I$. Then
Proof. Since the rim ![]() $I$ has two peaks, its first syzygy is also a rank 1 module. As in the proof of the previous proposition, from the proof of [Reference Baur and Bogdanic4, Theorem 3.1] we know that the matrix of the map
$I$ has two peaks, its first syzygy is also a rank 1 module. As in the proof of the previous proposition, from the proof of [Reference Baur and Bogdanic4, Theorem 3.1] we know that the matrix of the map ![]() $D^{\ast }$ from that proof is a
$D^{\ast }$ from that proof is a ![]() $2\times 2$ matrix of the form
$2\times 2$ matrix of the form
where the numbers ![]() $m_{1}$ and
$m_{1}$ and ![]() $m_{2}$ denote the lengths of the lateral sides of the trapezia used to compute the extension space (cf. [Reference Baur and Bogdanic4]), as in the following picture, and that
$m_{2}$ denote the lengths of the lateral sides of the trapezia used to compute the extension space (cf. [Reference Baur and Bogdanic4]), as in the following picture, and that ![]() $m=\min \{m_{1},m_{2}\}.$
$m=\min \{m_{1},m_{2}\}.$

We see from the picture that ![]() $m_{1}=\min \{d_{1},l_{2}\}$ and
$m_{1}=\min \{d_{1},l_{2}\}$ and ![]() $m_{2}=\min \{d_{2},l_{1}\}$. The proposition now follows.◻
$m_{2}=\min \{d_{2},l_{1}\}$. The proposition now follows.◻
Corollary 3.9. Let ![]() $I$ be a rim with two peaks and one of the slopes (either downward or upward) of length
$I$ be a rim with two peaks and one of the slopes (either downward or upward) of length ![]() $1$. Then
$1$. Then
3.2 Auslander–Reiten sequences.
The purpose of this subsection is to determine certain Auslander–Reiten sequences of the form ![]() $L_{I}\rightarrow M\rightarrow L_{J}$, where
$L_{I}\rightarrow M\rightarrow L_{J}$, where ![]() $L_{I}$ and
$L_{I}$ and ![]() $L_{J}$ are rank 1
$L_{J}$ are rank 1 ![]() $B_{k,n}$-modules. To do this we move back and forth from
$B_{k,n}$-modules. To do this we move back and forth from ![]() $\text{CM}(B_{k,n})$ to
$\text{CM}(B_{k,n})$ to ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ using the quotient functor
$\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ using the quotient functor ![]() $\unicode[STIX]{x1D70B}$.
$\unicode[STIX]{x1D70B}$.
Remark 3.10. Let ![]() $L_{I}$ and
$L_{I}$ and ![]() $L_{J}$ be two rank 1 modules such that
$L_{J}$ be two rank 1 modules such that ![]() $\dim \operatorname{Ext}^{1}(L_{J},L_{I})=1$. Using the quotient functor, the modules
$\dim \operatorname{Ext}^{1}(L_{J},L_{I})=1$. Using the quotient functor, the modules ![]() $\unicode[STIX]{x1D70B}(L_{I})$ and
$\unicode[STIX]{x1D70B}(L_{I})$ and ![]() $\unicode[STIX]{x1D70B}(L_{J})$ are rigid modules over
$\unicode[STIX]{x1D70B}(L_{J})$ are rigid modules over ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ (or one may consider them as modules in the subcategory
$\text{CM}(\unicode[STIX]{x1D6F1}_{k,n})$ (or one may consider them as modules in the subcategory ![]() $\text{Sub}Q_{k}$ of the preprojective algebra). Then, by [Reference Geiß, Leclerc and Schröer12, Proposition 5.7] the middle term
$\text{Sub}Q_{k}$ of the preprojective algebra). Then, by [Reference Geiß, Leclerc and Schröer12, Proposition 5.7] the middle term ![]() $\unicode[STIX]{x1D70B}(M)$ of the nontrivial extension is rigid. Thus, the middle term
$\unicode[STIX]{x1D70B}(M)$ of the nontrivial extension is rigid. Thus, the middle term ![]() $M$ is rigid.
$M$ is rigid.
Definition 3.11. Let ![]() $I$ be a
$I$ be a ![]() $k$-subset of
$k$-subset of ![]() $\mathbb{Z}_{n}$ consisting of two intervals where one of the intervals is a single element. We call such a
$\mathbb{Z}_{n}$ consisting of two intervals where one of the intervals is a single element. We call such a ![]() $k$-subset almost consecutive.
$k$-subset almost consecutive.
From [Reference Baur and Bogdanic4, Section 2], we know that if ![]() $I$ is almost consecutive, say
$I$ is almost consecutive, say ![]() $I=\{i,j,\ldots ,j+k-2\}$ for some
$I=\{i,j,\ldots ,j+k-2\}$ for some ![]() $j\in [i+2,\ldots ,n-k+i+1]$, then
$j\in [i+2,\ldots ,n-k+i+1]$, then ![]() $\unicode[STIX]{x1D6FA}(L_{I})=L_{J}$, where
$\unicode[STIX]{x1D6FA}(L_{I})=L_{J}$, where ![]() $J=\{i+1,\ldots ,i+k-1,j+k-1\}$ is also almost consecutive.
$J=\{i+1,\ldots ,i+k-1,j+k-1\}$ is also almost consecutive.
Theorem 3.12. Let ![]() $I=\{i,j,\ldots ,j+k-2\}$ be almost consecutive and
$I=\{i,j,\ldots ,j+k-2\}$ be almost consecutive and ![]() $J$ be such that
$J$ be such that ![]() $L_{J}=\unicode[STIX]{x1D6FA}(L_{I})$. Then the Auslander–Reiten sequence with
$L_{J}=\unicode[STIX]{x1D6FA}(L_{I})$. Then the Auslander–Reiten sequence with ![]() $L_{I}$ and
$L_{I}$ and ![]() $L_{J}$ as end term is as follows:
$L_{J}$ as end term is as follows:
with ![]() $X=\{i+1,j,j+1,\ldots ,j+k-3,j+k-1\}$ and
$X=\{i+1,j,j+1,\ldots ,j+k-3,j+k-1\}$ and ![]() $Y=(I\cup J)\setminus X$ and where
$Y=(I\cup J)\setminus X$ and where ![]() $L_{X}/L_{Y}$ is indecomposable if and only if
$L_{X}/L_{Y}$ is indecomposable if and only if ![]() $j\neq i+2$. In case
$j\neq i+2$. In case ![]() $j=i+2$,
$j=i+2$, ![]() $L_{X}/L_{Y}=P_{i}\oplus L_{U}$ for
$L_{X}/L_{Y}=P_{i}\oplus L_{U}$ for ![]() $U=\{i,i+2,i+3,\ldots ,k+i-1,k+i+1\}$.
$U=\{i,i+2,i+3,\ldots ,k+i-1,k+i+1\}$.
Furthermore, in both cases, the middle term is rigid.
Proof. We will prove the claims for ![]() $i=1$, the statement then follows from the symmetry of
$i=1$, the statement then follows from the symmetry of ![]() $B$. By Corollary 3.9, we have
$B$. By Corollary 3.9, we have ![]() $\dim \operatorname{Ext}^{1}(L_{J},L_{I})=1$, so the middle term
$\dim \operatorname{Ext}^{1}(L_{J},L_{I})=1$, so the middle term ![]() $M$ is rigid by Remark 3.10. Note that
$M$ is rigid by Remark 3.10. Note that ![]() $M$ is a rank 2 module, so it is either a direct sum of two rank 1 modules or indecomposable module of rank 2. The projective cover of
$M$ is a rank 2 module, so it is either a direct sum of two rank 1 modules or indecomposable module of rank 2. The projective cover of ![]() $M$ is a direct summand of the direct sum of the projective covers of
$M$ is a direct summand of the direct sum of the projective covers of ![]() $L_{I}$ and
$L_{I}$ and ![]() $L_{J}$, that is, a summand of
$L_{J}$, that is, a summand of ![]() $P_{0}\oplus P_{j-1}\oplus P_{1}\oplus P_{j+k-2}$.
$P_{0}\oplus P_{j-1}\oplus P_{1}\oplus P_{j+k-2}$.
Suppose that ![]() $M=L_{U}\oplus L_{V}$. By the above, the peaks of
$M=L_{U}\oplus L_{V}$. By the above, the peaks of ![]() $M$ belong to
$M$ belong to ![]() $\{0,1,j-1,j+k-2\}$.
$\{0,1,j-1,j+k-2\}$.
(i) If ![]() $M$ has a projective summand, say
$M$ has a projective summand, say ![]() $L_{V}=P_{a}$ for some
$L_{V}=P_{a}$ for some ![]() $a$, we have an irreducible monomorphism
$a$, we have an irreducible monomorphism ![]() $L_{I}{\hookrightarrow}P_{a}$, hence
$L_{I}{\hookrightarrow}P_{a}$, hence ![]() $L_{I}=\operatorname{rad}(P_{a})$. In that case,
$L_{I}=\operatorname{rad}(P_{a})$. In that case, ![]() $I=\{a,a+2,\ldots ,a+k\}$, that is,
$I=\{a,a+2,\ldots ,a+k\}$, that is, ![]() $a=1$,
$a=1$, ![]() $j=3$ and
$j=3$ and ![]() $L_{U}$ is as claimed in part (2) of the theorem.
$L_{U}$ is as claimed in part (2) of the theorem.
(ii) If none of the summands of ![]() $M$ are projective, they have two peaks each, so
$M$ are projective, they have two peaks each, so ![]() $U=A\cup B$ and
$U=A\cup B$ and ![]() $V=C\cup D$ are two-interval subsets of
$V=C\cup D$ are two-interval subsets of ![]() $C_{1}$.
$C_{1}$.
We first claim that if the vertices ![]() $1$ and
$1$ and ![]() $j+k-2$ are the two peaks of
$j+k-2$ are the two peaks of ![]() $L_{U}$, then
$L_{U}$, then ![]() $L_{U}\cong L_{J}$. To see this, let
$L_{U}\cong L_{J}$. To see this, let ![]() $U=A\cup B=\{2,\ldots \}\cup \{j+k-1,\ldots \}$. We use that
$U=A\cup B=\{2,\ldots \}\cup \{j+k-1,\ldots \}$. We use that ![]() $\unicode[STIX]{x1D70B}$ takes exact sequences to exact sequences. One checks that the dimension of
$\unicode[STIX]{x1D70B}$ takes exact sequences to exact sequences. One checks that the dimension of ![]() $\unicode[STIX]{x1D70B}(L_{I}\oplus L_{J})$ is zero at vertices
$\unicode[STIX]{x1D70B}(L_{I}\oplus L_{J})$ is zero at vertices ![]() $j+k-1$ and
$j+k-1$ and ![]() $j+k,\ldots ,n$ (see the following two figures).
$j+k,\ldots ,n$ (see the following two figures).

If ![]() $|B|>1$, then
$|B|>1$, then ![]() $\unicode[STIX]{x1D70B}(L_{U})$ has positive dimension at vertex
$\unicode[STIX]{x1D70B}(L_{U})$ has positive dimension at vertex ![]() $j+k-1$ (see the following figure).
$j+k-1$ (see the following figure).

Hence ![]() $|B|=1$, that is,
$|B|=1$, that is, ![]() $U=J$.
$U=J$.
Now we claim that the exact sequence ![]() $L_{I}\rightarrow L_{V}\oplus L_{J}\rightarrow L_{J}$ is not an Auslander–Reiten sequence. If
$L_{I}\rightarrow L_{V}\oplus L_{J}\rightarrow L_{J}$ is not an Auslander–Reiten sequence. If ![]() $L_{J}$ is a summand of a middle term of such Auslander–Reiten sequence, one can complete
$L_{J}$ is a summand of a middle term of such Auslander–Reiten sequence, one can complete ![]() $L_{J}$ to a cluster-tilting object
$L_{J}$ to a cluster-tilting object ![]() $T$ as in Remark 2.7. Then the quiver of the endomorphism algebra
$T$ as in Remark 2.7. Then the quiver of the endomorphism algebra ![]() $\operatorname{End}_{\text{}\underline{\text{CM}}(B)}(T)$ has a loop at the vertex
$\operatorname{End}_{\text{}\underline{\text{CM}}(B)}(T)$ has a loop at the vertex ![]() $L_{J}$ corresponding to the irreducible map
$L_{J}$ corresponding to the irreducible map ![]() $L_{J}\rightarrow L_{J}$, which is a contradiction.
$L_{J}\rightarrow L_{J}$, which is a contradiction.
So ![]() $U$ and
$U$ and ![]() $V$ both contain one peak of
$V$ both contain one peak of ![]() $I$ and one of
$I$ and one of ![]() $J$. Say
$J$. Say ![]() $U$ contains the peak at
$U$ contains the peak at ![]() $1$ and
$1$ and ![]() $V$ the peak at
$V$ the peak at ![]() $j+k-2$. Since
$j+k-2$. Since ![]() $0$ cannot be a peak of
$0$ cannot be a peak of ![]() $U$, we have
$U$, we have ![]() $U=\{2,\ldots \,\}\cup \{j,\ldots \,\}$ and
$U=\{2,\ldots \,\}\cup \{j,\ldots \,\}$ and ![]() $V=C\cup D=\{1,\ldots \,\}\cup \{j+k-1,\ldots \,\}$. By the same argument as above,
$V=C\cup D=\{1,\ldots \,\}\cup \{j+k-1,\ldots \,\}$. By the same argument as above, ![]() $|D|=1$. Applying
$|D|=1$. Applying ![]() $\unicode[STIX]{x1D70B}$ to our short exact sequence yields that the dimension at vertex 2 of
$\unicode[STIX]{x1D70B}$ to our short exact sequence yields that the dimension at vertex 2 of ![]() $\unicode[STIX]{x1D70B}(L_{U})$ is 1, whereas at vertex 2 of
$\unicode[STIX]{x1D70B}(L_{U})$ is 1, whereas at vertex 2 of ![]() $\unicode[STIX]{x1D70B}(L_{V})$ it is
$\unicode[STIX]{x1D70B}(L_{V})$ it is ![]() $0$. However,
$0$. However, ![]() $\unicode[STIX]{x1D70B}(L_{I}\oplus L_{J})$ has dimension 2 at vertex 2, which is a contradiction.
$\unicode[STIX]{x1D70B}(L_{I}\oplus L_{J})$ has dimension 2 at vertex 2, which is a contradiction.
We assume now that ![]() $M$ is indecomposable. By the discussion above (Remark 3.10)
$M$ is indecomposable. By the discussion above (Remark 3.10) ![]() $M$ is rigid so it is determined by its profile, and the profile provides a filtration by rank 1 modules,
$M$ is rigid so it is determined by its profile, and the profile provides a filtration by rank 1 modules, ![]() $M=L_{X}|L_{Y}$. There are infinitely many injective maps of
$M=L_{X}|L_{Y}$. There are infinitely many injective maps of ![]() $L_{I}$ into
$L_{I}$ into ![]() $M$. They differ by the relative positions of
$M$. They differ by the relative positions of ![]() $L_{I}$ and the quotient
$L_{I}$ and the quotient ![]() $L_{J}$ on the lattice diagram of
$L_{J}$ on the lattice diagram of ![]() $M$ covering the dimension vector of
$M$ covering the dimension vector of ![]() $M$. There are five distinct cases: the rim of
$M$. There are five distinct cases: the rim of ![]() $L_{I}$ can be strictly lower than the rim of
$L_{I}$ can be strictly lower than the rim of ![]() $L_{J}$, they can touch, intersect properly, or the rim of
$L_{J}$, they can touch, intersect properly, or the rim of ![]() $L_{J}$ can be below
$L_{J}$ can be below ![]() $L_{I}$, touching or being strictly lower, as in Figures 3 and 4.
$L_{I}$, touching or being strictly lower, as in Figures 3 and 4.
Note that all these representations have up to three disjoint regions with 1-dimensional vector spaces at finitely many vertices mapping to the infinite region with 2-dimensional vector spaces at every vertex. The only case providing a profile of an indecomposable module is the left one in Figure 4, yielding ![]() $X=\{2,j,\ldots ,j+k-3,j+k-1\}$ and
$X=\{2,j,\ldots ,j+k-3,j+k-1\}$ and ![]() $Y=\{2,4,\ldots ,k,j+k-2\}$.◻
$Y=\{2,4,\ldots ,k,j+k-2\}$.◻
Note that in the previous theorem, ![]() $X=I\cup \{i+1,j+k-1\}\setminus \{i,j+k-2\}$, whereas
$X=I\cup \{i+1,j+k-1\}\setminus \{i,j+k-2\}$, whereas ![]() $Y=J\cup \{i,i+k-2\}\setminus \{i+1,j+k-1\}$.
$Y=J\cup \{i,i+k-2\}\setminus \{i+1,j+k-1\}$.
Remark 3.13. In case ![]() $k=3$, Theorem 3.12 covers all possible Auslander–Reiten sequences where the start and end terms are of rank 1. By [Reference Baur and Bogdanic4, Section 2], the rank of
$k=3$, Theorem 3.12 covers all possible Auslander–Reiten sequences where the start and end terms are of rank 1. By [Reference Baur and Bogdanic4, Section 2], the rank of ![]() $\unicode[STIX]{x1D70F}^{-1}(L_{J})$ is one less than the number of peaks of
$\unicode[STIX]{x1D70F}^{-1}(L_{J})$ is one less than the number of peaks of ![]() $J$, so
$J$, so ![]() $\operatorname{rank}\unicode[STIX]{x1D70F}^{-1}(L_{J})=1$ if and only if
$\operatorname{rank}\unicode[STIX]{x1D70F}^{-1}(L_{J})=1$ if and only if ![]() $J$ is a 2-interval subset. Since
$J$ is a 2-interval subset. Since ![]() $k=3$, the 2-interval subsets are of the form
$k=3$, the 2-interval subsets are of the form ![]() $\{i,i+1,i+m\}$ with
$\{i,i+1,i+m\}$ with ![]() $2<m<n-1$.
$2<m<n-1$.
Assume ![]() $k=3$. If we are given a rank 2 module
$k=3$. If we are given a rank 2 module ![]() $M$ with profile
$M$ with profile ![]() $X|Y$, then how do we know if it is the middle term of an Auslander–Reiten sequence with rank 1 modules
$X|Y$, then how do we know if it is the middle term of an Auslander–Reiten sequence with rank 1 modules ![]() $L_{I}$ and
$L_{I}$ and ![]() $\unicode[STIX]{x1D6FA}(L_{I})$? From the previous theorem, and the diagram on the left hand side in the previous picture, in order for
$\unicode[STIX]{x1D6FA}(L_{I})$? From the previous theorem, and the diagram on the left hand side in the previous picture, in order for ![]() $M$ to be such a module,
$M$ to be such a module, ![]() $X$ and
$X$ and ![]() $Y$ must be
$Y$ must be ![]() $3$-interlacing (see the first definition in Section 5), and when drawn one above the other (as in the above picture), the diagram we obtain has to contain three consecutive diamonds, with no gaps between them and with the end two diamonds of lateral size 1. In order to recognize the rims of
$3$-interlacing (see the first definition in Section 5), and when drawn one above the other (as in the above picture), the diagram we obtain has to contain three consecutive diamonds, with no gaps between them and with the end two diamonds of lateral size 1. In order to recognize the rims of ![]() $L_{I}$ and
$L_{I}$ and ![]() $\unicode[STIX]{x1D6FA}(L_{I})$ from the profile
$\unicode[STIX]{x1D6FA}(L_{I})$ from the profile ![]() $X|Y$, the easiest thing to do is to identify the middle diamond if it happens to be of size greater than 1 (as in the above picture). If the middle diamond is of size 1, then we can identify the right hand side diamond, since it is followed by an upward “tail like” portion of the rim covered by both rim
$X|Y$, the easiest thing to do is to identify the middle diamond if it happens to be of size greater than 1 (as in the above picture). If the middle diamond is of size 1, then we can identify the right hand side diamond, since it is followed by an upward “tail like” portion of the rim covered by both rim ![]() $X$ and rim
$X$ and rim ![]() $Y$ in the above picture. If there is no tail, then we only have three diamonds of size 1, and then we deal with the module
$Y$ in the above picture. If there is no tail, then we only have three diamonds of size 1, and then we deal with the module ![]() $\{1,3,5\}|\{2,4,6\}$.
$\{1,3,5\}|\{2,4,6\}$.
Other rigid indecomposable rank 2 modules whose profile ![]() $X|Y$ does not satisfy these conditions do not appear as the middle term of an Auslander–Reiten sequence with rank 1 modules. In the tame cases, they either appear at the mouth of a tube, or they are meshes of the modules with at least one of them of rank greater than 1 as we will see later.
$X|Y$ does not satisfy these conditions do not appear as the middle term of an Auslander–Reiten sequence with rank 1 modules. In the tame cases, they either appear at the mouth of a tube, or they are meshes of the modules with at least one of them of rank greater than 1 as we will see later.
3.3 Periodicity
It follows from the direct computation in [Reference Baur and Bogdanic4, Proposition 2.7], that if ![]() $L_{I}$ is a rank
$L_{I}$ is a rank ![]() $1$ module, then
$1$ module, then ![]() $\unicode[STIX]{x1D6FA}^{2}(L_{I})=L_{I+k}$, where
$\unicode[STIX]{x1D6FA}^{2}(L_{I})=L_{I+k}$, where ![]() $(I_{1}\mid \ldots |I_{n})+m$ is the profile
$(I_{1}\mid \ldots |I_{n})+m$ is the profile ![]() $(I_{1}+m)|(I_{2}+m)|\cdots |(I_{n}+m)$ obtained by adding
$(I_{1}+m)|(I_{2}+m)|\cdots |(I_{n}+m)$ obtained by adding ![]() $m$ to each number in every
$m$ to each number in every ![]() $k$-subset appearing in the profile. Set
$k$-subset appearing in the profile. Set ![]() $v=\operatorname{lcm}(n,k)/k$. This leads to the next observation.
$v=\operatorname{lcm}(n,k)/k$. This leads to the next observation.
Remark 3.14. Let ![]() $L_{I}$ be a nonprojective rank
$L_{I}$ be a nonprojective rank ![]() $1$ module, and let
$1$ module, and let ![]() $M$ be a module in the
$M$ be a module in the ![]() $\unicode[STIX]{x1D70F}$-orbit of
$\unicode[STIX]{x1D70F}$-orbit of ![]() $L_{I}$. Then,
$L_{I}$. Then, ![]() $M$ is
$M$ is ![]() $\unicode[STIX]{x1D70F}$-periodic of period
$\unicode[STIX]{x1D70F}$-periodic of period ![]() $d$, for some factor
$d$, for some factor ![]() $d$ of
$d$ of ![]() $2v$.
$2v$.
It is not difficult to show that the same formula ![]() $\unicode[STIX]{x1D6FA}^{2}(L_{I}|L_{J})=L_{I}+k|L_{J}+k$ holds for the rigid rank 2 modules.
$\unicode[STIX]{x1D6FA}^{2}(L_{I}|L_{J})=L_{I}+k|L_{J}+k$ holds for the rigid rank 2 modules.
By graded Morita theory, ![]() $\text{CM}(B)$ is equivalent to
$\text{CM}(B)$ is equivalent to ![]() $\text{CM}^{\mathbb{Z}_{n}}(R_{k,n})$ where
$\text{CM}^{\mathbb{Z}_{n}}(R_{k,n})$ where ![]() $R_{k,n}=\mathbb{C}[x,y]/(x^{k}-y^{n-k})$ and where the
$R_{k,n}=\mathbb{C}[x,y]/(x^{k}-y^{n-k})$ and where the ![]() $\mathbb{Z}_{n}$-grading is given by
$\mathbb{Z}_{n}$-grading is given by ![]() $\deg x=1$ and
$\deg x=1$ and ![]() $\deg y=-1$, [Reference Demonet and Luo7, Theorem 3.16]. For the latter, Demonet–Luo show, [Reference Demonet and Luo7, Theorem 3.22], that there is an isomorphism of autoequivalences
$\deg y=-1$, [Reference Demonet and Luo7, Theorem 3.16]. For the latter, Demonet–Luo show, [Reference Demonet and Luo7, Theorem 3.22], that there is an isomorphism of autoequivalences ![]() $[2]\simeq (-k)$, where the notation
$[2]\simeq (-k)$, where the notation ![]() $(-1)$ refers to a shift in the
$(-1)$ refers to a shift in the ![]() $\mathbb{Z}_{n}$-grading. From that, we obtain:
$\mathbb{Z}_{n}$-grading. From that, we obtain:
Proposition 3.15. Every module in ![]() $\text{}\underline{\text{CM}}(B_{k,n})$ is
$\text{}\underline{\text{CM}}(B_{k,n})$ is ![]() $\unicode[STIX]{x1D70F}$-periodic with period a factor of
$\unicode[STIX]{x1D70F}$-periodic with period a factor of ![]() $2v$.
$2v$.
3.4 A different approach to periodicity
We now switch perspectives and use [Reference Baur, King and Marsh5] to follow an approach to periodicity by Keller, [Reference Keller17], which uses products of Dynkin types. This will allow us to identify the tame cases later.
The category ![]() $\text{}\underline{\text{CM}}(B_{k,n})$ has cluster-tilting objects whose endomorphism algebras have rectangular quivers built by
$\text{}\underline{\text{CM}}(B_{k,n})$ has cluster-tilting objects whose endomorphism algebras have rectangular quivers built by ![]() $(k-1)\times (n-k-1)$ lines of arrows, forming alternatingly oriented squares. These are exactly the quivers of the rectangular arrangements from [Reference Scott23, Section 4]. We will denote them by
$(k-1)\times (n-k-1)$ lines of arrows, forming alternatingly oriented squares. These are exactly the quivers of the rectangular arrangements from [Reference Scott23, Section 4]. We will denote them by ![]() $Q\Box Q^{\prime }$, where
$Q\Box Q^{\prime }$, where ![]() $Q$ is a Dynkin quiver of type
$Q$ is a Dynkin quiver of type ![]() $A_{k-1}$ and
$A_{k-1}$ and ![]() $Q^{\prime }$ of type
$Q^{\prime }$ of type ![]() $A_{n-k-1}$, with corresponding Coxeter numbers
$A_{n-k-1}$, with corresponding Coxeter numbers ![]() $h=k$ and
$h=k$ and ![]() $h^{\prime }=n-k$, as in [Reference Keller17]. These are quivers with a natural potential
$h^{\prime }=n-k$, as in [Reference Keller17]. These are quivers with a natural potential ![]() $P$, in the sense of [Reference Derksen, Weyman and Zelevinsky9], given by the sum of all clockwise cycles minus the sum of all anticlockwise cycles. We will write QP to abbreviate “quiver with potential.”
$P$, in the sense of [Reference Derksen, Weyman and Zelevinsky9], given by the sum of all clockwise cycles minus the sum of all anticlockwise cycles. We will write QP to abbreviate “quiver with potential.”
Example 3.16. For ![]() $(3,9)$ and for
$(3,9)$ and for ![]() $(4,8)$ the rectangles
$(4,8)$ the rectangles ![]() $Q\Box Q^{\prime }$ are as follows:
$Q\Box Q^{\prime }$ are as follows:

Such Jacobian algebras can also be obtained as 2-Calabi–Yau tilted algebras from certain (Hom-finite) generalized cluster categories ![]() ${\mathcal{C}}_{A}$ in the sense of [Reference Amiot1], since the corresponding QP are (QP-)mutation equivalent to
${\mathcal{C}}_{A}$ in the sense of [Reference Amiot1], since the corresponding QP are (QP-)mutation equivalent to ![]() $(Q\boxtimes Q^{\prime },\widetilde{P})$, following [Reference Keller17].
$(Q\boxtimes Q^{\prime },\widetilde{P})$, following [Reference Keller17].
In the cases ![]() $(3,9)$ and
$(3,9)$ and ![]() $(4,8)$, these QP are
$(4,8)$, these QP are

with potential the sum of all positive 3-cycles minus the sum of all negative 3-cycles (note that this agrees with the natural potential of the dimer model from [Reference Baur, King and Marsh5, Section 3]). By [Reference Keller and Reiten18, Section 2.1], there exists an equivalence of categories
where ![]() $(\unicode[STIX]{x1D6F4}T)$ is the ideal of morphisms that factor through
$(\unicode[STIX]{x1D6F4}T)$ is the ideal of morphisms that factor through ![]() $\text{add}\unicode[STIX]{x1D6F4}T$ for a cluster-tilting object
$\text{add}\unicode[STIX]{x1D6F4}T$ for a cluster-tilting object ![]() $T$ (respect.
$T$ (respect. ![]() $T^{\prime }$ and
$T^{\prime }$ and ![]() $(\unicode[STIX]{x1D6FA})^{-1}T^{\prime }$) over the 2-CY category. These categories are Krull–Schmidt, so by [Reference Keller and Reiten18, Section 3.5], the Auslander–Reiten quiver of
$(\unicode[STIX]{x1D6FA})^{-1}T^{\prime }$) over the 2-CY category. These categories are Krull–Schmidt, so by [Reference Keller and Reiten18, Section 3.5], the Auslander–Reiten quiver of ![]() $\text{mod}Jac(Q,P)$ is obtained from the Auslander–Reiten quiver of the 2-CY categories removing a finite number of vertices.
$\text{mod}Jac(Q,P)$ is obtained from the Auslander–Reiten quiver of the 2-CY categories removing a finite number of vertices.
Remark 3.17. If we denote ![]() $\unicode[STIX]{x1D6F4}$ by the shift functor,
$\unicode[STIX]{x1D6F4}$ by the shift functor, ![]() $S$ the Serre functor, and
$S$ the Serre functor, and ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{C}}}$ the Auslander–Reiten translation over
$\unicode[STIX]{x1D70F}_{{\mathcal{C}}}$ the Auslander–Reiten translation over ![]() ${\mathcal{C}}_{A}$, there is an isomorphism of functors
${\mathcal{C}}_{A}$, there is an isomorphism of functors ![]() $\unicode[STIX]{x1D6F4}^{2}=S$. On the other hand
$\unicode[STIX]{x1D6F4}^{2}=S$. On the other hand ![]() $S$ is
$S$ is ![]() $\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D70F}$ over
$\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D70F}$ over ![]() ${\mathcal{C}}_{A}$, so
${\mathcal{C}}_{A}$, so ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{C}}}=\unicode[STIX]{x1D6F4}$. Keller’s proof of the periodicity of the Zamolodchikov transformation
$\unicode[STIX]{x1D70F}_{{\mathcal{C}}}=\unicode[STIX]{x1D6F4}$. Keller’s proof of the periodicity of the Zamolodchikov transformation ![]() $(\unicode[STIX]{x1D70F}\otimes 1)$ [Reference Keller17, Theorem 8.3] indicates a way to prove
$(\unicode[STIX]{x1D70F}\otimes 1)$ [Reference Keller17, Theorem 8.3] indicates a way to prove ![]() $\unicode[STIX]{x1D70F}$-periodicity. In fact, one can show that
$\unicode[STIX]{x1D70F}$-periodicity. In fact, one can show that ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{C}}}$ is
$\unicode[STIX]{x1D70F}_{{\mathcal{C}}}$ is ![]() $2n$-periodic.
$2n$-periodic.
Keller shows that ![]() $(\unicode[STIX]{x1D70F}\otimes 1)^{h}=\unicode[STIX]{x1D6F4}^{-2}$ is an isomorphism of functors of
$(\unicode[STIX]{x1D70F}\otimes 1)^{h}=\unicode[STIX]{x1D6F4}^{-2}$ is an isomorphism of functors of ![]() ${\mathcal{C}}_{A}$ and with this that
${\mathcal{C}}_{A}$ and with this that ![]() $(\unicode[STIX]{x1D70F}\otimes 1)^{h+h^{\prime }}=\unicode[STIX]{x1D7D9}$ is isomorphism of functors of
$(\unicode[STIX]{x1D70F}\otimes 1)^{h+h^{\prime }}=\unicode[STIX]{x1D7D9}$ is isomorphism of functors of ![]() ${\mathcal{C}}_{A}$. We can do the following:
${\mathcal{C}}_{A}$. We can do the following:
In our case ![]() $2(h+h^{\prime })=2n$.
$2(h+h^{\prime })=2n$.
3.5 Tame cases
For ![]() $k=2$, such a quiver
$k=2$, such a quiver ![]() $Q\Box Q^{\prime }$ is of type
$Q\Box Q^{\prime }$ is of type ![]() $A_{n-3}$, for
$A_{n-3}$, for ![]() $(3,6)$ of (mutation) type
$(3,6)$ of (mutation) type ![]() $D_{4}$, for
$D_{4}$, for ![]() $(3,7)$ of type
$(3,7)$ of type ![]() $E_{6}$ and for
$E_{6}$ and for ![]() $(3,8)$ of type
$(3,8)$ of type ![]() $E_{8}$. The Dynkin types above are the only cases of finite representation type, whereas the two cases
$E_{8}$. The Dynkin types above are the only cases of finite representation type, whereas the two cases ![]() $(3,9)$ and
$(3,9)$ and ![]() $(4,8)$ in Example 3.16 are the first cases of infinite representation type. The quivers with potential give rise to path algebras with relations whose mutation class representation theory is studied in [Reference Geiß and González-Silva10]. They correspond to elliptic types
$(4,8)$ in Example 3.16 are the first cases of infinite representation type. The quivers with potential give rise to path algebras with relations whose mutation class representation theory is studied in [Reference Geiß and González-Silva10]. They correspond to elliptic types ![]() $E_{7,8}^{(1,1)}$, known to be tame [Reference Geiß, Labardini-Fragoso and Schröer11, Theorem 9.1]. Besides the cases
$E_{7,8}^{(1,1)}$, known to be tame [Reference Geiß, Labardini-Fragoso and Schröer11, Theorem 9.1]. Besides the cases ![]() $(3,9),(4,8)$ and the finite types, all other QP algebras obtained from rectangular arrangements are of wild type.
$(3,9),(4,8)$ and the finite types, all other QP algebras obtained from rectangular arrangements are of wild type.
In the cases ![]() $(3,9)$ and
$(3,9)$ and ![]() $(4,8)$ the QPs also arise from two cases of 2-Calabi–Yau categories
$(4,8)$ the QPs also arise from two cases of 2-Calabi–Yau categories ![]() ${\mathcal{C}}(A)$, called tubular cluster categories of types
${\mathcal{C}}(A)$, called tubular cluster categories of types ![]() $(6,3,2)$ and
$(6,3,2)$ and ![]() $(4,4,2)$, respectively. It is known that
$(4,4,2)$, respectively. It is known that ![]() ${\mathcal{C}}(A)$ is formed by a coproduct of tubular components
${\mathcal{C}}(A)$ is formed by a coproduct of tubular components ![]() $\coprod _{x\in \mathbb{X}}{\mathcal{T}}_{x}$ where almost all tubes
$\coprod _{x\in \mathbb{X}}{\mathcal{T}}_{x}$ where almost all tubes ![]() ${\mathcal{T}}_{x}$ are of rank 1, and there are finitely many tubes of ranks
${\mathcal{T}}_{x}$ are of rank 1, and there are finitely many tubes of ranks ![]() $6,3,2$ (resp.
$6,3,2$ (resp. ![]() $4,4,2$) [Reference Barot, Kussin and Lenzing3]. Therefore, the corresponding Auslander–Reiten quivers are formed by finitely many tubes of ranks
$4,4,2$) [Reference Barot, Kussin and Lenzing3]. Therefore, the corresponding Auslander–Reiten quivers are formed by finitely many tubes of ranks ![]() $6,3,2$ (resp.
$6,3,2$ (resp. ![]() $4,4,2$), and infinitely many homogeneous tubes.
$4,4,2$), and infinitely many homogeneous tubes.
4 Higher rank modules
In this section, we give a construction for higher rank modules in ![]() $\text{CM}(B_{k,n})$ in the spirit of the definition of rank 1 modules (Definition 2.2). Recall that the rank 1 modules in
$\text{CM}(B_{k,n})$ in the spirit of the definition of rank 1 modules (Definition 2.2). Recall that the rank 1 modules in ![]() $\text{CM}(B_{k,n})$ are in bijection with
$\text{CM}(B_{k,n})$ are in bijection with ![]() $k$-subsets of
$k$-subsets of ![]() $\mathbb{Z}_{n}$. Modules of higher rank can also be described combinatorially, as we will see here. For this, let
$\mathbb{Z}_{n}$. Modules of higher rank can also be described combinatorially, as we will see here. For this, let ![]() $\text{Id}_{s}$ be the
$\text{Id}_{s}$ be the ![]() $s\times s$-identity matrix, let
$s\times s$-identity matrix, let ![]() $E_{i,j}$ be the elementary
$E_{i,j}$ be the elementary ![]() $s\times s$-matrix with entry 1 at position
$s\times s$-matrix with entry 1 at position ![]() $(i,j)$ and 0 everywhere else. We set
$(i,j)$ and 0 everywhere else. We set ![]() $\unicode[STIX]{x1D70E}$ to be the following
$\unicode[STIX]{x1D70E}$ to be the following ![]() $s\times s$-matrix:
$s\times s$-matrix:
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}=\mathop{\sum }_{i=1}^{s-1}E_{i,i+1}+tE_{s,1}=\left(\begin{array}{@{}cccccc@{}}0 & 1 & 0 & & & \\ 0 & 0 & 1 & & \\ \vdots & & \ddots & & \\ 0 & & & 0 & 1\\ t & 0 & & & 0\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}=\mathop{\sum }_{i=1}^{s-1}E_{i,i+1}+tE_{s,1}=\left(\begin{array}{@{}cccccc@{}}0 & 1 & 0 & & & \\ 0 & 0 & 1 & & \\ \vdots & & \ddots & & \\ 0 & & & 0 & 1\\ t & 0 & & & 0\end{array}\right)\end{eqnarray}$$Lemma 4.1. For ![]() $j=0,\ldots ,s$ we have
$j=0,\ldots ,s$ we have
In particular, ![]() $\unicode[STIX]{x1D70E}^{s}=t\text{Id}_{s}$.
$\unicode[STIX]{x1D70E}^{s}=t\text{Id}_{s}$.
Proof. Straightforward. ◻
Let ![]() $I_{1},\ldots ,I_{s}$ be
$I_{1},\ldots ,I_{s}$ be ![]() $k$-subsets. We then construct a rank
$k$-subsets. We then construct a rank ![]() $s$
$s$![]() $B_{k,n}$-module
$B_{k,n}$-module ![]() $L(I_{1},\ldots ,I_{s})$. The maps
$L(I_{1},\ldots ,I_{s})$. The maps ![]() $x_{i}$ and
$x_{i}$ and ![]() $y_{i}$ depend on the number of
$y_{i}$ depend on the number of ![]() $k$-subsets among
$k$-subsets among ![]() $I_{1},\ldots ,I_{s}$ the index
$I_{1},\ldots ,I_{s}$ the index ![]() $i$ belongs to. For
$i$ belongs to. For ![]() $i\in [1,n]$ set
$i\in [1,n]$ set ![]() $r_{i}=|\{I_{j}\mid i\in I_{j}\}|$.
$r_{i}=|\{I_{j}\mid i\in I_{j}\}|$.
Definition 4.2. Let ![]() $I_{1},\ldots ,I_{s}$ be
$I_{1},\ldots ,I_{s}$ be ![]() $k$-subsets of
$k$-subsets of ![]() $[1,\ldots ,n]$. We define a module
$[1,\ldots ,n]$. We define a module ![]() $L(I_{1},\ldots ,I_{s})$ as follows.
$L(I_{1},\ldots ,I_{s})$ as follows.
For ![]() $i=1,\ldots ,n$ let
$i=1,\ldots ,n$ let ![]() $V_{i}:=e_{i}L(I_{1},\ldots ,I_{s})=\mathbb{C}[[t]]\oplus \mathbb{C}[[t]]\oplus \cdots \oplus \mathbb{C}[[t]]=Z^{s}$. Depending on the number of
$V_{i}:=e_{i}L(I_{1},\ldots ,I_{s})=\mathbb{C}[[t]]\oplus \mathbb{C}[[t]]\oplus \cdots \oplus \mathbb{C}[[t]]=Z^{s}$. Depending on the number of ![]() $k$-subsets
$k$-subsets ![]() $i$ belongs to, we define maps
$i$ belongs to, we define maps ![]() $x_{i},y_{i}:Z^{s}\rightarrow Z^{s}$ as follows:
$x_{i},y_{i}:Z^{s}\rightarrow Z^{s}$ as follows:
Remark 4.3. Note that we have ![]() $x_{i}y_{i}=y_{i+1}x_{i+1}=\unicode[STIX]{x1D70E}^{s}=t\text{Id}_{s}$ for all
$x_{i}y_{i}=y_{i+1}x_{i+1}=\unicode[STIX]{x1D70E}^{s}=t\text{Id}_{s}$ for all ![]() $i$ (Lemma 4.1). To see that
$i$ (Lemma 4.1). To see that ![]() $L(I_{1},\ldots ,I_{s})$ is a
$L(I_{1},\ldots ,I_{s})$ is a ![]() $B_{k,n}$-module, we need to check that the relations
$B_{k,n}$-module, we need to check that the relations ![]() $x^{k}=y^{n-k}$ hold.
$x^{k}=y^{n-k}$ hold.
Remark 4.4. The module ![]() $L(I_{1},\ldots ,I_{s})$ can be represented by a lattice diagram
$L(I_{1},\ldots ,I_{s})$ can be represented by a lattice diagram ![]() ${\mathcal{L}}_{I_{1},\ldots ,I_{s}}$ obtained by overlaying the lattice diagrams
${\mathcal{L}}_{I_{1},\ldots ,I_{s}}$ obtained by overlaying the lattice diagrams ![]() ${\mathcal{L}}_{I_{j}}$ such that
${\mathcal{L}}_{I_{j}}$ such that ![]() ${\mathcal{L}}_{I_{j}}$ is above
${\mathcal{L}}_{I_{j}}$ is above ![]() ${\mathcal{L}}_{I_{j+1}}$ for
${\mathcal{L}}_{I_{j+1}}$ for ![]() $j=1,\ldots ,s-1$, where the rims of
$j=1,\ldots ,s-1$, where the rims of ![]() ${\mathcal{L}}_{I_{j}}$ and of
${\mathcal{L}}_{I_{j}}$ and of ![]() ${\mathcal{L}}_{I_{j+1}}$ are meeting at at least one vertex and possibly share arrows but have no two-dimensional intersections. The vector spaces
${\mathcal{L}}_{I_{j+1}}$ are meeting at at least one vertex and possibly share arrows but have no two-dimensional intersections. The vector spaces ![]() $V_{0},V_{1},V_{2},\ldots ,V_{n}$ are represented by columns from left to right (with
$V_{0},V_{1},V_{2},\ldots ,V_{n}$ are represented by columns from left to right (with ![]() $V_{0}$ and
$V_{0}$ and ![]() $V_{n}$ to be identified). The vertices in each column correspond to some monomial
$V_{n}$ to be identified). The vertices in each column correspond to some monomial ![]() $\mathbb{C}$-basis of
$\mathbb{C}$-basis of ![]() $\mathbb{C}[t]\oplus \mathbb{C}[t]\oplus \cdots \oplus \mathbb{C}[t]$, depending on the sets
$\mathbb{C}[t]\oplus \mathbb{C}[t]\oplus \cdots \oplus \mathbb{C}[t]$, depending on the sets ![]() $I_{1},\ldots ,I_{s}$. Note that the
$I_{1},\ldots ,I_{s}$. Note that the ![]() $k$-subset
$k$-subset ![]() $I_{1}$ can then be read off as the set of labels on the arrows pointing down to the right which are exposed to the top of the diagram. Labels of successive
$I_{1}$ can then be read off as the set of labels on the arrows pointing down to the right which are exposed to the top of the diagram. Labels of successive ![]() $k$-subsets can be read off from successive levels in the diagrams. To illustrate this for
$k$-subsets can be read off from successive levels in the diagrams. To illustrate this for ![]() $s=2$, the lattice picture
$s=2$, the lattice picture ![]() ${\mathcal{L}}_{I,J}$ for
${\mathcal{L}}_{I,J}$ for ![]() $I=\{2,5,8,9\}$ and
$I=\{2,5,8,9\}$ and ![]() $J=\{1,3,7,8\}$,
$J=\{1,3,7,8\}$, ![]() $(k,n)=(4,9)$, is shown in Example 4.5.
$(k,n)=(4,9)$, is shown in Example 4.5.
Example 4.5. Let ![]() $(k,n)=(4,9)$. Consider the
$(k,n)=(4,9)$. Consider the ![]() $4$-subsets
$4$-subsets ![]() $I=\{2,5,8,9\}$ and
$I=\{2,5,8,9\}$ and ![]() $J=\{1,3,7,8\}$. The module
$J=\{1,3,7,8\}$. The module ![]() $L(I,J)$ is illustrated in Figure 5.
$L(I,J)$ is illustrated in Figure 5.

Figure 5. Lattice diagrams for ![]() $L(\{1,3,7,8\})$ and
$L(\{1,3,7,8\})$ and ![]() $L(\{2,5,7,8\},\{1,3,7,8\})$,
$L(\{2,5,7,8\},\{1,3,7,8\})$, ![]() $n=9.$
$n=9.$
Example 4.6. (1) Let ![]() $s=2$. Then
$s=2$. Then ![]() $\unicode[STIX]{x1D70E}=\left(\begin{array}{@{}cc@{}}0 & 1\\ t & 0\end{array}\right)$ and
$\unicode[STIX]{x1D70E}=\left(\begin{array}{@{}cc@{}}0 & 1\\ t & 0\end{array}\right)$ and ![]() $\unicode[STIX]{x1D70E}^{2}=\left(\begin{array}{@{}cc@{}}t & 0\\ 0 & t\end{array}\right)$. Here,
$\unicode[STIX]{x1D70E}^{2}=\left(\begin{array}{@{}cc@{}}t & 0\\ 0 & t\end{array}\right)$. Here, ![]() $x_{i}=y_{i}=\unicode[STIX]{x1D70E}$ for
$x_{i}=y_{i}=\unicode[STIX]{x1D70E}$ for ![]() $i\in (I_{1}\setminus I_{2})\cup (I_{2}\setminus I_{1})$,
$i\in (I_{1}\setminus I_{2})\cup (I_{2}\setminus I_{1})$, ![]() $x_{i}=\text{Id}_{2}$,
$x_{i}=\text{Id}_{2}$, ![]() $y_{i}=t\cdot \text{Id}_{2}$ for
$y_{i}=t\cdot \text{Id}_{2}$ for ![]() $i\in I_{1}\cap I_{2}$ and
$i\in I_{1}\cap I_{2}$ and ![]() $x_{i}=t\cdot \text{Id}_{2}$,
$x_{i}=t\cdot \text{Id}_{2}$, ![]() $y_{i}=\text{Id}_{2}$ for
$y_{i}=\text{Id}_{2}$ for ![]() $i\in I_{1}^{c}\cap I_{2}^{c}$.
$i\in I_{1}^{c}\cap I_{2}^{c}$.
(2) Let ![]() $s=3$. Then
$s=3$. Then  $\unicode[STIX]{x1D70E}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 1\\ t & 0 & 0\end{array}\right)$,
$\unicode[STIX]{x1D70E}=\left(\begin{array}{@{}ccc@{}}0 & 1 & 0\\ 0 & 0 & 1\\ t & 0 & 0\end{array}\right)$,  $\unicode[STIX]{x1D70E}^{2}=\left(\begin{array}{@{}ccc@{}}0 & 0 & 1\\ t & 0 & 0\\ 0 & t & 0\end{array}\right)$ and
$\unicode[STIX]{x1D70E}^{2}=\left(\begin{array}{@{}ccc@{}}0 & 0 & 1\\ t & 0 & 0\\ 0 & t & 0\end{array}\right)$ and  $\unicode[STIX]{x1D70E}^{3}=\left(\begin{array}{@{}ccc@{}}t & 0 & 0\\ 0 & t & 0\\ 0 & 0 & t\end{array}\right)$. An instance of this is in [Reference Jensen, King and Su15, Example 6.5] where
$\unicode[STIX]{x1D70E}^{3}=\left(\begin{array}{@{}ccc@{}}t & 0 & 0\\ 0 & t & 0\\ 0 & 0 & t\end{array}\right)$. An instance of this is in [Reference Jensen, King and Su15, Example 6.5] where ![]() $I_{1}=\{3,6,8\}$,
$I_{1}=\{3,6,8\}$, ![]() $I_{2}=\{2,5,8\}$ and
$I_{2}=\{2,5,8\}$ and ![]() $I_{3}=\{1,4,7\}$ for
$I_{3}=\{1,4,7\}$ for ![]() $(k,n)=(3,8)$.
$(k,n)=(3,8)$.
Proposition 4.7. ![]() $L(I_{1},\ldots ,I_{s})\in \text{CM}(B_{k,n})$.
$L(I_{1},\ldots ,I_{s})\in \text{CM}(B_{k,n})$.
Proof. We first check that ![]() $L(I_{1},\ldots ,I_{s})$ is a
$L(I_{1},\ldots ,I_{s})$ is a ![]() $B_{k,n}$-module. By Remark 4.3, it remains to show that the relations
$B_{k,n}$-module. By Remark 4.3, it remains to show that the relations ![]() $x^{k}=y^{n-k}$ hold. By construction, all the
$x^{k}=y^{n-k}$ hold. By construction, all the ![]() $x_{i}$ and all the
$x_{i}$ and all the ![]() $y_{i}$ commute. We have
$y_{i}$ commute. We have
 $$\begin{eqnarray}\begin{array}{@{}lcl@{}}x^{k} & = & x_{i+k-1}x_{i+k-2}\cdots x_{i+1}x_{i}=\unicode[STIX]{x1D70E}^{s-r_{i+k-1}}\cdots \unicode[STIX]{x1D70E}^{s-r_{i+1}}\unicode[STIX]{x1D70E}^{s-r_{i}}\\ & = & \unicode[STIX]{x1D70E}^{sk-(r_{i+k-1}+r_{i+k-2}+r_{i+1}+r_{i})}\\ y^{n-k} & = & y_{i+k}y_{i+k+1}\cdots y_{i-2}y_{i-1}=\unicode[STIX]{x1D70E}^{r_{i+k}}\unicode[STIX]{x1D70E}^{r_{i+k+1}}\cdots \unicode[STIX]{x1D70E}^{r_{i-2}}\unicode[STIX]{x1D70E}^{r_{i-1}}\\ & = & \unicode[STIX]{x1D70E}^{r_{i+k}+r_{i+k+1}+\cdots +r_{i-2}+r_{i-1}}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}lcl@{}}x^{k} & = & x_{i+k-1}x_{i+k-2}\cdots x_{i+1}x_{i}=\unicode[STIX]{x1D70E}^{s-r_{i+k-1}}\cdots \unicode[STIX]{x1D70E}^{s-r_{i+1}}\unicode[STIX]{x1D70E}^{s-r_{i}}\\ & = & \unicode[STIX]{x1D70E}^{sk-(r_{i+k-1}+r_{i+k-2}+r_{i+1}+r_{i})}\\ y^{n-k} & = & y_{i+k}y_{i+k+1}\cdots y_{i-2}y_{i-1}=\unicode[STIX]{x1D70E}^{r_{i+k}}\unicode[STIX]{x1D70E}^{r_{i+k+1}}\cdots \unicode[STIX]{x1D70E}^{r_{i-2}}\unicode[STIX]{x1D70E}^{r_{i-1}}\\ & = & \unicode[STIX]{x1D70E}^{r_{i+k}+r_{i+k+1}+\cdots +r_{i-2}+r_{i-1}}.\end{array}\end{eqnarray}$$ Now ![]() $r_{1}+r_{2}+\cdots +r_{n-1}+r_{n}=sk=|\bigcup _{j=1}^{s}I_{j}|$ and so:
$r_{1}+r_{2}+\cdots +r_{n-1}+r_{n}=sk=|\bigcup _{j=1}^{s}I_{j}|$ and so:
Since all the powers of ![]() $\unicode[STIX]{x1D70E}$ are invertible, we get
$\unicode[STIX]{x1D70E}$ are invertible, we get ![]() $x^{k}=y^{n-k}$.
$x^{k}=y^{n-k}$.
Consider ![]() $L(I_{1},\ldots ,I_{s})$ as a
$L(I_{1},\ldots ,I_{s})$ as a ![]() $Z$-module. It is a direct sum
$Z$-module. It is a direct sum ![]() $V_{1}\oplus V_{2}\oplus \cdots \oplus V_{n}$ where each of the
$V_{1}\oplus V_{2}\oplus \cdots \oplus V_{n}$ where each of the ![]() $V_{i}$ has a basis of size
$V_{i}$ has a basis of size ![]() $s$, hence
$s$, hence ![]() $L(I_{1},\ldots ,I_{s})$ is free over
$L(I_{1},\ldots ,I_{s})$ is free over ![]() $Z$.◻
$Z$.◻
5 Rank  $2$ modules and root combinatorics
$2$ modules and root combinatorics
In this section, we deal with rigid indecomposable rank 2 modules and relate them with roots for associated Kac–Moody algebras.
Definition 5.1. ( $r$-interlacing)
$r$-interlacing)
Let ![]() $I$ and
$I$ and ![]() $J$ be two
$J$ be two ![]() $k$-subsets of
$k$-subsets of ![]() $[1,n]$.
$[1,n]$. ![]() $I$ and
$I$ and ![]() $J$ are said to be
$J$ are said to be ![]() $r$-interlacing if there exist subsets
$r$-interlacing if there exist subsets ![]() $\{i_{1},i_{3},\ldots ,i_{2r-1}\}\subset I\setminus J$ and
$\{i_{1},i_{3},\ldots ,i_{2r-1}\}\subset I\setminus J$ and ![]() $\{i_{2},i_{4},\ldots ,i_{2r}\}\subset J\setminus I$ such that
$\{i_{2},i_{4},\ldots ,i_{2r}\}\subset J\setminus I$ such that ![]() $i_{1}<i_{2}<i_{3}<\cdots <i_{2r}<i_{1}$ (cyclically) and if there exist no larger subsets of
$i_{1}<i_{2}<i_{3}<\cdots <i_{2r}<i_{1}$ (cyclically) and if there exist no larger subsets of ![]() $I$ and of
$I$ and of ![]() $J$ with this property.
$J$ with this property.
If ![]() $I$ and
$I$ and ![]() $J$ are
$J$ are ![]() $r$-interlacing, then the poset of
$r$-interlacing, then the poset of ![]() $I\mid J$ is
$I\mid J$ is ![]() $(1^{r},2)$, see Figure 3.1 for
$(1^{r},2)$, see Figure 3.1 for ![]() $r=3$. The module in question is indecomposable for
$r=3$. The module in question is indecomposable for ![]() $r\geqslant 3$ (see Remark 3.2).
$r\geqslant 3$ (see Remark 3.2).
Proposition 5.2. Let ![]() $I$ and
$I$ and ![]() $J$ be
$J$ be ![]() $r$-interlacing. Then there exist
$r$-interlacing. Then there exist ![]() $0\leqslant a_{1}\leqslant a_{2}\leqslant \cdots \leqslant a_{r-1}$ such that, as
$0\leqslant a_{1}\leqslant a_{2}\leqslant \cdots \leqslant a_{r-1}$ such that, as ![]() $Z$-modules,
$Z$-modules,
Proof. We assume that we have drawn the rims ![]() $I$ and
$I$ and ![]() $J$ one above the other, say
$J$ one above the other, say ![]() $I$ above
$I$ above ![]() $J$, as in the proof of Theorem 3.1 in [Reference Baur and Bogdanic4, Section 3]. For every
$J$, as in the proof of Theorem 3.1 in [Reference Baur and Bogdanic4, Section 3]. For every ![]() $i_{2s}\in J\setminus I$ we have that rims
$i_{2s}\in J\setminus I$ we have that rims ![]() $I$ and
$I$ and ![]() $J$ are not parallel between points
$J$ are not parallel between points ![]() $i_{2s-1}$ and
$i_{2s-1}$ and ![]() $i_{2s}$, yielding a left trapezium. Similarly, for every
$i_{2s}$, yielding a left trapezium. Similarly, for every ![]() $i_{2s+1}\in I\setminus J$ we have that rims
$i_{2s+1}\in I\setminus J$ we have that rims ![]() $I$ and
$I$ and ![]() $J$ are not parallel between points
$J$ are not parallel between points ![]() $i_{2s}$ and
$i_{2s}$ and ![]() $i_{2s+1}$, yielding a right trapezium. Since
$i_{2s+1}$, yielding a right trapezium. Since ![]() $I$ and
$I$ and ![]() $J$ are
$J$ are ![]() $r$-interlacing, we have, in alternating order
$r$-interlacing, we have, in alternating order ![]() $r$-left and
$r$-left and ![]() $r$-right trapezia, giving us in total
$r$-right trapezia, giving us in total ![]() $r$ boxes. The statement now follows from the proof of Theorem 3.1 in [Reference Baur and Bogdanic4] which says that
$r$ boxes. The statement now follows from the proof of Theorem 3.1 in [Reference Baur and Bogdanic4] which says that ![]() $\text{Ext}^{1}(L_{I},L_{J})$ is a product of
$\text{Ext}^{1}(L_{I},L_{J})$ is a product of ![]() $r-1$ cyclic
$r-1$ cyclic ![]() $Z$-modules.◻
$Z$-modules.◻
Corollary 5.3. Let ![]() $k=3$ and
$k=3$ and ![]() $I$ and
$I$ and ![]() $J$ be rims. Then
$J$ be rims. Then ![]() $\text{Ext}^{1}(L_{I},L_{J})\cong \mathbb{C}\times \mathbb{C}$ if and only if
$\text{Ext}^{1}(L_{I},L_{J})\cong \mathbb{C}\times \mathbb{C}$ if and only if ![]() $I$ and
$I$ and ![]() $J$ are
$J$ are ![]() $3$-interlacing.
$3$-interlacing.
Proof. If ![]() $I$ and
$I$ and ![]() $J$ are
$J$ are ![]() $3$-interlacing, then they are both unions of three one-element sets. Hence, all the lateral sides in the boxes from the above proof are of length 1 and the statement follows since
$3$-interlacing, then they are both unions of three one-element sets. Hence, all the lateral sides in the boxes from the above proof are of length 1 and the statement follows since ![]() $a_{i}$ from the previous proposition are strictly positive, but at most equal to the lengths of the boxes involved.◻
$a_{i}$ from the previous proposition are strictly positive, but at most equal to the lengths of the boxes involved.◻
Corollary 5.4. Let ![]() $k=3$. If
$k=3$. If ![]() $I$ and
$I$ and ![]() $J$ are crossing but not
$J$ are crossing but not ![]() $3$-interlacing, then
$3$-interlacing, then ![]() $\text{Ext}^{1}(L_{I},L_{J})\cong \mathbb{C}$.
$\text{Ext}^{1}(L_{I},L_{J})\cong \mathbb{C}$.
Note that if in Corollary 5.4 we have ![]() $L_{J}=\unicode[STIX]{x1D70F}(L_{I})$, then we are in the situation of Theorem 3.12.
$L_{J}=\unicode[STIX]{x1D70F}(L_{I})$, then we are in the situation of Theorem 3.12.
Proposition 5.5. Assume that ![]() $(k,n)=(3,9)$ or
$(k,n)=(3,9)$ or ![]() $(k,n)=(4,8)$. Let
$(k,n)=(4,8)$. Let ![]() $M\in \text{CM}(B_{k,n})$ be a rigid indecomposable rank
$M\in \text{CM}(B_{k,n})$ be a rigid indecomposable rank ![]() $2$ module. Then
$2$ module. Then ![]() $M\cong L_{I}\mid L_{J}$ where
$M\cong L_{I}\mid L_{J}$ where ![]() $I$ and
$I$ and ![]() $J$ are
$J$ are ![]() $3$-interlacing.
$3$-interlacing.
Proof. Let ![]() $M=L_{I}\mid L_{J}$ be rigid indecomposable, with
$M=L_{I}\mid L_{J}$ be rigid indecomposable, with ![]() $I$ and
$I$ and ![]() $J$
$J$![]() $r$-interlacing. Since
$r$-interlacing. Since ![]() $M$ is indecomposable, we get
$M$ is indecomposable, we get ![]() $r\in \{3,4\}$. If
$r\in \{3,4\}$. If ![]() $r=4$, then we must have
$r=4$, then we must have ![]() $k=4$, and the only
$k=4$, and the only ![]() $4$-interlacing
$4$-interlacing ![]() $4$-subsets are
$4$-subsets are ![]() $I=\{1,3,5,7\}$ and
$I=\{1,3,5,7\}$ and ![]() $J=\{2,4,6,8\}$. Assume that
$J=\{2,4,6,8\}$. Assume that ![]() $M=L_{I}|L_{J}$ is rigid. Then it has a filtration given by its profile. Moreover, if any other module is rigid with the same profile it is isomorphic to
$M=L_{I}|L_{J}$ is rigid. Then it has a filtration given by its profile. Moreover, if any other module is rigid with the same profile it is isomorphic to ![]() $M$. On the other hand, if
$M$. On the other hand, if ![]() $M$ is rigid, then
$M$ is rigid, then ![]() $\unicode[STIX]{x1D70F}(M)$ is also rigid. If we compute
$\unicode[STIX]{x1D70F}(M)$ is also rigid. If we compute ![]() $\unicode[STIX]{x1D70F}^{-1}M=\unicode[STIX]{x1D6FA}(M)$ in
$\unicode[STIX]{x1D70F}^{-1}M=\unicode[STIX]{x1D6FA}(M)$ in ![]() $\text{CM}(\unicode[STIX]{x1D6F1}_{4,8})$, we obtain that they have the same filtration so
$\text{CM}(\unicode[STIX]{x1D6F1}_{4,8})$, we obtain that they have the same filtration so ![]() $\unicode[STIX]{x1D70F}^{-1}M=M$. So
$\unicode[STIX]{x1D70F}^{-1}M=M$. So ![]() $M$ and
$M$ and ![]() $\unicode[STIX]{x1D70F}^{-1}(M)$ are the end terms of an Auslander–Reiten sequence and
$\unicode[STIX]{x1D70F}^{-1}(M)$ are the end terms of an Auslander–Reiten sequence and ![]() $M$ is not rigid, a contradiction. Then
$M$ is not rigid, a contradiction. Then ![]() $I$ and
$I$ and ![]() $J$ must be
$J$ must be ![]() $3$-interlacing.◻
$3$-interlacing.◻
Corollary 5.6. Let ![]() $M\in \text{CM}(B_{3,9})$ be a rigid indecomposable rank
$M\in \text{CM}(B_{3,9})$ be a rigid indecomposable rank ![]() $2$ module. Then
$2$ module. Then ![]() $\unicode[STIX]{x1D711}(M)$ is a real root for
$\unicode[STIX]{x1D711}(M)$ is a real root for ![]() $J_{3,9}$ of degree
$J_{3,9}$ of degree ![]() $2$.
$2$.
Proof. By Proposition 5.5, ![]() $M\cong L_{I}\mid L_{J}$ with
$M\cong L_{I}\mid L_{J}$ with ![]() $I$ and
$I$ and ![]() $J$ 3-interlacing, so
$J$ 3-interlacing, so ![]() $I\cup J$ consists of six distinct elements of
$I\cup J$ consists of six distinct elements of ![]() $\{1,2,\ldots ,n\}$. But then in
$\{1,2,\ldots ,n\}$. But then in ![]() $\text{}\underline{a}(M)=(a_{1},\ldots ,a_{9})$ there are six entries equal to
$\text{}\underline{a}(M)=(a_{1},\ldots ,a_{9})$ there are six entries equal to ![]() $1$ and three entries equal to 0. Recalling the quadratic form
$1$ and three entries equal to 0. Recalling the quadratic form ![]() $q(\text{}\underline{a})$ of equation (2.1), we have
$q(\text{}\underline{a})$ of equation (2.1), we have ![]() $q(\text{}\underline{a})=\sum a_{i}^{2}-\frac{1}{9}(\sum a_{i})^{2}=6-4=2.$ ◻
$q(\text{}\underline{a})=\sum a_{i}^{2}-\frac{1}{9}(\sum a_{i})^{2}=6-4=2.$ ◻
We observe that there exist rigid rank 2 modules corresponding to imaginary roots, an example is ![]() $L_{2568}\mid L_{1347}$ [Reference Jensen, King and Su15, Figure 13]. We expect that if we impose that the modules correspond to real roots, we get a counterpart to Proposition 5.5.
$L_{2568}\mid L_{1347}$ [Reference Jensen, King and Su15, Figure 13]. We expect that if we impose that the modules correspond to real roots, we get a counterpart to Proposition 5.5.
Proposition 5.7. Let ![]() $M$ be a rank
$M$ be a rank ![]() $2$ indecomposable module with profile
$2$ indecomposable module with profile ![]() $I|J$. If
$I|J$. If ![]() $M$ corresponds to a real root of
$M$ corresponds to a real root of ![]() $J_{k,n}$, then
$J_{k,n}$, then ![]() $|I\cap J|=k-3.$
$|I\cap J|=k-3.$
Proof. Assume that ![]() $|I\cap J|=k-3-m$ for some
$|I\cap J|=k-3-m$ for some ![]() $m\geqslant 0$. Note that
$m\geqslant 0$. Note that ![]() $|I\cap J|$ cannot be greater than
$|I\cap J|$ cannot be greater than ![]() $k-3$, because in this case, the corresponding poset would be either
$k-3$, because in this case, the corresponding poset would be either ![]() $(1^{2},2)$ or
$(1^{2},2)$ or ![]() $(1,2)$, which do not correspond to an indecomposable module. If there are
$(1,2)$, which do not correspond to an indecomposable module. If there are ![]() $k-3-m$ common elements in
$k-3-m$ common elements in ![]() $I$ and
$I$ and ![]() $J$, then the corresponding vector, say
$J$, then the corresponding vector, say ![]() $\text{}\underline{a}$, has
$\text{}\underline{a}$, has ![]() $k-3-m$ coordinates equal to 2,
$k-3-m$ coordinates equal to 2, ![]() $2(m+3)$ coordinates equal to 1, and the rest are equal to 0. If we apply our quadratic form
$2(m+3)$ coordinates equal to 1, and the rest are equal to 0. If we apply our quadratic form ![]() $q$ to this vector
$q$ to this vector ![]() $\text{}\underline{a}$, then we get that
$\text{}\underline{a}$, then we get that ![]() $q(\text{}\underline{a})=2-2m$. In order for
$q(\text{}\underline{a})=2-2m$. In order for ![]() $\text{}\underline{a}$ to be real, it has to be that
$\text{}\underline{a}$ to be real, it has to be that ![]() $m=0$.◻
$m=0$.◻
Example 5.8. Assume ![]() $(k,n)=(3,9)$ and
$(k,n)=(3,9)$ and ![]() $M$ is a rank
$M$ is a rank ![]() $2$ indecomposable module with profile
$2$ indecomposable module with profile ![]() $I|J$. The conditions on
$I|J$. The conditions on ![]() $I$ and
$I$ and ![]() $J$ imply that the form
$J$ imply that the form ![]() $q$ of such a module evaluates to 2, as in that case,
$q$ of such a module evaluates to 2, as in that case, ![]() $\text{}\underline{a}=(1,1,1,1,1,1,0,0,0)$, up to permuting the entries.
$\text{}\underline{a}=(1,1,1,1,1,1,0,0,0)$, up to permuting the entries.
Corollary 5.9. Let ![]() $M$ be a rank
$M$ be a rank ![]() $2$ indecomposable module corresponding to a real root. Then the poset of
$2$ indecomposable module corresponding to a real root. Then the poset of ![]() $M$ is
$M$ is ![]() $(1^{3},2)$.
$(1^{3},2)$.
Proof. If the poset is of the form ![]() $(1^{r},2)$, where
$(1^{r},2)$, where ![]() $r\geqslant 4$, then
$r\geqslant 4$, then ![]() $|I\cap J|<k-3$. If
$|I\cap J|<k-3$. If ![]() $r\leqslant 2$, then the module in question is not indecomposable.◻
$r\leqslant 2$, then the module in question is not indecomposable.◻
It follows that necessary conditions for a rank 2 indecomposable module ![]() $M$ with profile
$M$ with profile ![]() $I|J$ to be rigid are
$I|J$ to be rigid are ![]() $|I\cap J|=k-3$ and that the poset of
$|I\cap J|=k-3$ and that the poset of ![]() $M$ is
$M$ is ![]() $(1^{3},2)$. Unfortunately, we do not know if these conditions are sufficient in the general case. We will show that these conditions are sufficient in the tame cases, and we conjecture that it holds in general.
$(1^{3},2)$. Unfortunately, we do not know if these conditions are sufficient in the general case. We will show that these conditions are sufficient in the tame cases, and we conjecture that it holds in general.
Notation 5.10. Let ![]() $I$ and
$I$ and ![]() $J$ be
$J$ be ![]() $3$-interlacing
$3$-interlacing ![]() $k$-subsets. We say that
$k$-subsets. We say that ![]() $I$ and
$I$ and ![]() $J$ are tightly
$J$ are tightly ![]() $3$-interlacing if
$3$-interlacing if ![]() $|I\cap J|=k-3$.
$|I\cap J|=k-3$.
Lemma 5.11. Let ![]() $M\in \text{CM}(B_{k,n})$ be a module with
$M\in \text{CM}(B_{k,n})$ be a module with ![]() $M\cong L_{I}\mid L_{J}$ where
$M\cong L_{I}\mid L_{J}$ where ![]() $I$ and
$I$ and ![]() $J$ are tightly
$J$ are tightly ![]() $3$-interlacing. Then
$3$-interlacing. Then ![]() $M$ is indecomposable and
$M$ is indecomposable and ![]() $q(M)$ is a real root for
$q(M)$ is a real root for ![]() $J_{k,n}$.
$J_{k,n}$.
Proof. The poset of ![]() $M$ is
$M$ is ![]() $(1^{3},2)$, thus
$(1^{3},2)$, thus ![]() $M$ is indecomposable. Since
$M$ is indecomposable. Since ![]() $|I\cap J|=k-3$, up to permuting the entries,
$|I\cap J|=k-3$, up to permuting the entries, ![]() $\text{}\underline{a}(M)=(\underbrace{2,\ldots ,2}_{k-3},\underbrace{1,\ldots ,1}_{6},0,\ldots ,0)$, yielding
$\text{}\underline{a}(M)=(\underbrace{2,\ldots ,2}_{k-3},\underbrace{1,\ldots ,1}_{6},0,\ldots ,0)$, yielding ![]() $q(M)=q(a)=2$.◻
$q(M)=q(a)=2$.◻
Lemma 5.12. ![]() $(1)$ Let
$(1)$ Let ![]() $I$ and
$I$ and ![]() $J$ be
$J$ be ![]() $r$-interlacing, for
$r$-interlacing, for ![]() $r\geqslant 3$. Then
$r\geqslant 3$. Then ![]() $L(I,J)$ is a rank
$L(I,J)$ is a rank ![]() $2$ module in
$2$ module in ![]() $\text{CM}(B_{k,n})$ with filtration
$\text{CM}(B_{k,n})$ with filtration ![]() $L_{I}\mid L_{J}$.
$L_{I}\mid L_{J}$.
![]() $(2)$ If
$(2)$ If ![]() $I$ and
$I$ and ![]() $J$ are tightly
$J$ are tightly ![]() $3$-interlacing, then
$3$-interlacing, then ![]() $L(I,J)$ and
$L(I,J)$ and ![]() $L(J,I)$ are indecomposable.
$L(J,I)$ are indecomposable.
Note that Lemma 5.12(2) provides modules with cyclically reordered filtration, as discussed in [Reference Jensen, King and Su15, Observation 8.2].
Proof. (1) The module ![]() $L_{J}$ embeds in
$L_{J}$ embeds in ![]() $L(I,J)$ diagonally via the map
$L(I,J)$ diagonally via the map ![]() $a\mapsto (a,a)$ lattice point wise, as in Figure 5 of Example 4.5, sending column
$a\mapsto (a,a)$ lattice point wise, as in Figure 5 of Example 4.5, sending column ![]() $U_{i}$ to column
$U_{i}$ to column ![]() $V_{i}$ in a way to get an image of
$V_{i}$ in a way to get an image of ![]() $L_{J}$ as high up as possible. This yields an exact sequence
$L_{J}$ as high up as possible. This yields an exact sequence ![]() $0\rightarrow L_{J}\rightarrow L(I,J)\rightarrow L_{I}\rightarrow 0$, giving the claimed filtration.
$0\rightarrow L_{J}\rightarrow L(I,J)\rightarrow L_{I}\rightarrow 0$, giving the claimed filtration.
(2) The indecomposability follows from the fact that for tightly 3-interlacing ![]() $k$-subsets both modules have poset
$k$-subsets both modules have poset ![]() $(1^{3},2)$.◻
$(1^{3},2)$.◻
We expect that tightly 3-interlacing subsets always yield rigid modules. Combined with the preceding statements, this would give us:
Conjecture 5.13. Fix ![]() $(k,n)$ with
$(k,n)$ with ![]() $k\geqslant 3$. Let
$k\geqslant 3$. Let ![]() $I$ and
$I$ and ![]() $J$ be tightly
$J$ be tightly ![]() $3$-interlacing. Then
$3$-interlacing. Then ![]() $L(I,J)$ is a rigid indecomposable rank
$L(I,J)$ is a rigid indecomposable rank ![]() $2$ module.
$2$ module.
Theorem 3.12 provides further evidence for Conjecture 5.13 for arbitrary ![]() $(k,n)$: We can use part 1 to find many examples of rigid indecomposable rank 2 modules
$(k,n)$: We can use part 1 to find many examples of rigid indecomposable rank 2 modules ![]() $L(X,Y)=L_{X}\mid L_{Y}$, where
$L(X,Y)=L_{X}\mid L_{Y}$, where ![]() $X$ and
$X$ and ![]() $Y$ are tightly 3-interlacing
$Y$ are tightly 3-interlacing ![]() $k$-subsets satisfying
$k$-subsets satisfying ![]() $|X\cap Y|=k-3$ by choosing
$|X\cap Y|=k-3$ by choosing ![]() $j=i+3$ in the theorem.
$j=i+3$ in the theorem.
Conjecture 5.14. Let ![]() $M$ be a rank
$M$ be a rank ![]() $2$ module with poset
$2$ module with poset ![]() $(1^{r},2)$, for
$(1^{r},2)$, for ![]() $r\geqslant 4$. Then
$r\geqslant 4$. Then ![]() $M$ is not rigid.
$M$ is not rigid.
We recall that in the finite cases with ![]() $k=3$, the numbers of (rigid) indecomposable rank
$k=3$, the numbers of (rigid) indecomposable rank ![]() $2$ modules are 2 (for
$2$ modules are 2 (for ![]() $n=6$), 14 (for
$n=6$), 14 (for ![]() $n=7$) and 56 (for
$n=7$) and 56 (for ![]() $n=8$). All these correspond to real roots for the associated Kac–Moody algebra
$n=8$). All these correspond to real roots for the associated Kac–Moody algebra ![]() $J_{k,n}$.
$J_{k,n}$.
In the tame cases ![]() $(3,9)$ and
$(3,9)$ and ![]() $(4,8)$, we will show that there are, respectively, 168 and 120 rigid indecomposable modules of rank 2. This follows from Proposition 5.5 and the fact that in these cases, the real root in question has to correspond to a
$(4,8)$, we will show that there are, respectively, 168 and 120 rigid indecomposable modules of rank 2. This follows from Proposition 5.5 and the fact that in these cases, the real root in question has to correspond to a ![]() $9$-tuple
$9$-tuple ![]() $(a_{1},\ldots ,a_{9})$ with six entries equal to 1 and zeros elsewhere, or to an
$(a_{1},\ldots ,a_{9})$ with six entries equal to 1 and zeros elsewhere, or to an ![]() $8$-tuple
$8$-tuple ![]() $(a_{1},\ldots ,a_{8})$ with one entry equal to 2, six entries equal to 1 and one 0, respectively. We will confirm the above numbers explicitly in the next two sections by computing all tubes that contain rank 2 modules in the Auslander–Reiten quiver.
$(a_{1},\ldots ,a_{8})$ with one entry equal to 2, six entries equal to 1 and one 0, respectively. We will confirm the above numbers explicitly in the next two sections by computing all tubes that contain rank 2 modules in the Auslander–Reiten quiver.
This leads us to a conjectured formula for the number of rigid indecomposable rank 2 modules which correspond to real roots. The 3-interlacing property (Proposition 5.5) yields the factor ![]() $\binom{n}{6}$, a choice of 6 elements from
$\binom{n}{6}$, a choice of 6 elements from ![]() $[1,n]$, say
$[1,n]$, say ![]() $\{1\leqslant i_{1}<j_{1}<i_{2}<j_{2}<i_{3}<j_{3}\leqslant n\}$, with
$\{1\leqslant i_{1}<j_{1}<i_{2}<j_{2}<i_{3}<j_{3}\leqslant n\}$, with ![]() $\{i_{1},i_{2},i_{3}\}\subset I$ and
$\{i_{1},i_{2},i_{3}\}\subset I$ and ![]() $\{j_{1},j_{2},j_{3}\}\subset J$. If Conjecture 5.13 is true, each pair
$\{j_{1},j_{2},j_{3}\}\subset J$. If Conjecture 5.13 is true, each pair ![]() $I$ and
$I$ and ![]() $J$ of 3-interlacing subsets where the remaining
$J$ of 3-interlacing subsets where the remaining ![]() $k-3$ labels are common to
$k-3$ labels are common to ![]() $I$ and
$I$ and ![]() $J$ yields two rigid indecomposable rank 2 modules. Using the map from indecomposable modules to roots for
$J$ yields two rigid indecomposable rank 2 modules. Using the map from indecomposable modules to roots for ![]() $J_{k,n}$ (see Section 2.2) we see that these give rise to real roots. So there is a choice of
$J_{k,n}$ (see Section 2.2) we see that these give rise to real roots. So there is a choice of ![]() $k-3$ elements from the remaining
$k-3$ elements from the remaining ![]() $n-6$ elements of
$n-6$ elements of ![]() $[1,n]$, yielding a factor
$[1,n]$, yielding a factor ![]() $\binom{n-6}{k-3}$. Finally, there is a factor 2 which arises from the choice of which of these subsets is
$\binom{n-6}{k-3}$. Finally, there is a factor 2 which arises from the choice of which of these subsets is ![]() $I$ and which is
$I$ and which is ![]() $J$. The above arguments give an upper bound for the number of rigid indecomposable rank
$J$. The above arguments give an upper bound for the number of rigid indecomposable rank ![]() $2$ modules corresponding to real roots.
$2$ modules corresponding to real roots.
Conjecture 5.15. Let ![]() $3\leqslant k\leqslant n/2$. For every real root
$3\leqslant k\leqslant n/2$. For every real root ![]() $\unicode[STIX]{x1D6FC}$ of degree
$\unicode[STIX]{x1D6FC}$ of degree ![]() $2$ there are exactly two nonisomorphic rigid indecomposable rank
$2$ there are exactly two nonisomorphic rigid indecomposable rank ![]() $2$ modules
$2$ modules ![]() $M_{1}$ and
$M_{1}$ and ![]() $M_{2}$ such that
$M_{2}$ such that ![]() $\unicode[STIX]{x1D711}(M_{1})=\unicode[STIX]{x1D711}(M_{2})=\unicode[STIX]{x1D6FC}$. Thus, there are
$\unicode[STIX]{x1D711}(M_{1})=\unicode[STIX]{x1D711}(M_{2})=\unicode[STIX]{x1D6FC}$. Thus, there are ![]() $2\binom{n}{6}\binom{n-6}{k-3}$ rigid indecomposable rank
$2\binom{n}{6}\binom{n-6}{k-3}$ rigid indecomposable rank ![]() $2$ modules corresponding to real roots.
$2$ modules corresponding to real roots.
Remark.
Note that we have proved (Proposition 5.7, Corollary 5.9) that the number ![]() $2\binom{n}{6}\binom{n-6}{k-3}$ is the number of indecomposable rank 2 modules corresponding to real roots. Combinatorially, indecomposable rank 2 modules corresponding to real roots are determined by the conditions
$2\binom{n}{6}\binom{n-6}{k-3}$ is the number of indecomposable rank 2 modules corresponding to real roots. Combinatorially, indecomposable rank 2 modules corresponding to real roots are determined by the conditions ![]() $|I\cap J|=k-3$ (which follows from the quadratic form) and the poset of the module is
$|I\cap J|=k-3$ (which follows from the quadratic form) and the poset of the module is ![]() $(1^{3},2)$ (which follows from the indecomposability requirement).
$(1^{3},2)$ (which follows from the indecomposability requirement).
6 The tame case  $(k,n)=(3,9)$
$(k,n)=(3,9)$
Here we will describe all the tubes of ![]() $\text{CM}(B_{3,9})$ which contain rank 1 and rank 2 modules. Recall that every exceptional tube of rank
$\text{CM}(B_{3,9})$ which contain rank 1 and rank 2 modules. Recall that every exceptional tube of rank ![]() $s$ contains
$s$ contains ![]() $s-1$
$s-1$![]() $\,$
$\,$![]() $\unicode[STIX]{x1D70F}$-orbits of rigid modules. We will write down the
$\unicode[STIX]{x1D70F}$-orbits of rigid modules. We will write down the ![]() $\unicode[STIX]{x1D70F}$-orbits where we can give explicit filtrations. In the end, we use this to find the number of rigid indecomposable rank 2 modules in
$\unicode[STIX]{x1D70F}$-orbits where we can give explicit filtrations. In the end, we use this to find the number of rigid indecomposable rank 2 modules in ![]() $\text{CM}(B_{3,9})$. We start by describing all such tubes of rank 6 in Figure 6. For example, Figure 6(A) shows one of the three tubes containing projective–injective modules, Figure 6(B) shows one of the three tubes with modules of the form
$\text{CM}(B_{3,9})$. We start by describing all such tubes of rank 6 in Figure 6. For example, Figure 6(A) shows one of the three tubes containing projective–injective modules, Figure 6(B) shows one of the three tubes with modules of the form ![]() $L_{i,i+1,i+6}$.
$L_{i,i+1,i+6}$.

Figure 6. Rank 6 tubes for ![]() $\text{CM}(B_{3,9})$.
$\text{CM}(B_{3,9})$.
Next we give the rank 3 tubes containing rigid modules in Figure 7. There are two such types (three tubes of this form).

Figure 7. Rank 3 tubes for ![]() $\text{CM}(B_{3,9})$.
$\text{CM}(B_{3,9})$.
Furthermore, there are two types of tubes of rank 2, described in Figure 8. The modules in the second ![]() $\unicode[STIX]{x1D70F}$-orbit are not rigid. To indicate this, they are written in gray.
$\unicode[STIX]{x1D70F}$-orbit are not rigid. To indicate this, they are written in gray.

Figure 8. Rank 2 tubes for ![]() $\text{CM}(B_{3,9})$.
$\text{CM}(B_{3,9})$.
6.1 Counting rigid indecomposables for  $Gr(3,9)$
$Gr(3,9)$
By Proposition 5.5 there are at most 168 rigid indecomposable rank 2 modules in ![]() $\text{CM}(B_{3,9})$, because there are 84 3-interlacing pairs
$\text{CM}(B_{3,9})$, because there are 84 3-interlacing pairs ![]() $(I,J)$ in that case. The tubes with rank 1 modules contain 84 rigid rank 2 modules. The remaining 84 rank 2 modules are at the mouths of further tubes of rank 2, 3, and 6. To sum up, the number of rigid indecomposable modules of rank 1, 2, and 3 in the above tubes, listed by rank is:
$(I,J)$ in that case. The tubes with rank 1 modules contain 84 rigid rank 2 modules. The remaining 84 rank 2 modules are at the mouths of further tubes of rank 2, 3, and 6. To sum up, the number of rigid indecomposable modules of rank 1, 2, and 3 in the above tubes, listed by rank is:
We have collected all rank 1 and rank 2 rigid indecomposable modules. Since there are 168 rigid indecomposable modules whose roots are real, and 84 real roots of ![]() $J_{3,9}$ of degree 2, we have proved that for every real root of degree 2 there are two rigid indecomposable modules
$J_{3,9}$ of degree 2, we have proved that for every real root of degree 2 there are two rigid indecomposable modules ![]() $L_{J}|L_{I}$ and
$L_{J}|L_{I}$ and ![]() $L_{I}|L_{J}$. Moreover in this case the number of rigid indecomposables of rank 2 is exactly twice the number of real roots of degree 2.
$L_{I}|L_{J}$. Moreover in this case the number of rigid indecomposables of rank 2 is exactly twice the number of real roots of degree 2.
Therefore, both Theorem 2 and Conjecture 5.15 hold in this case.
7 The tame case  $(k,n)=(4,8)$
$(k,n)=(4,8)$
Here we will describe all the tubes of ![]() $\text{CM}(B_{4,8})$ which contain rank 1 and rank 2 modules, as in the previous section for
$\text{CM}(B_{4,8})$ which contain rank 1 and rank 2 modules, as in the previous section for ![]() $(k,n)=(3,9)$. We use this to find the number of rigid indecomposable rank 2 modules in this case. We start by describing all such tubes of rank 4 in Figure 9. For example, Figure 9(A) shows one of the four tubes containing projective–injective modules, Figure 9(B) shows one of the four tubes with rank 1 modules for
$(k,n)=(3,9)$. We use this to find the number of rigid indecomposable rank 2 modules in this case. We start by describing all such tubes of rank 4 in Figure 9. For example, Figure 9(A) shows one of the four tubes containing projective–injective modules, Figure 9(B) shows one of the four tubes with rank 1 modules for ![]() $4$-subsets of the form
$4$-subsets of the form ![]() $I=\{i,i+1,i+2,i+5\}$.
$I=\{i,i+1,i+2,i+5\}$.

Figure 9. Rank 4 tubes for ![]() $\text{CM}(B_{4,8})$.
$\text{CM}(B_{4,8})$.
In addition to these, there are two types of rank 2 tubes in ![]() $\text{CM}(B_{4,8})$. They are described in Figure 10. As before, gray indicates nonrigid modules.
$\text{CM}(B_{4,8})$. They are described in Figure 10. As before, gray indicates nonrigid modules.

Figure 10. Rank 2 tubes for ![]() $\text{CM}(B_{4,8})$.
$\text{CM}(B_{4,8})$.
7.1 Summing up
To sum up, the number of rigid indecomposable modules of rank 1, 2, and 3 in all these tubes is:
Since there are 70 rank 1 modules for ![]() $(4,8)$, we have covered all tubes containing such modules. Overall, there are 120 rank 2 rigid indecomposable modules. Among these, there are eight modules that do not correspond to the real roots. These are the modules with profile of the form
$(4,8)$, we have covered all tubes containing such modules. Overall, there are 120 rank 2 rigid indecomposable modules. Among these, there are eight modules that do not correspond to the real roots. These are the modules with profile of the form ![]() $1246|3578$. So there are 112 rigid indecomposable modules of rank 2 that correspond to real roots of
$1246|3578$. So there are 112 rigid indecomposable modules of rank 2 that correspond to real roots of ![]() $J_{4,8}$. Since there are 56 roots of degree 2, we have shown that the number of rigid indecomposable rank 2 modules corresponding to real roots is twice the number of real roots of degree 2 for
$J_{4,8}$. Since there are 56 roots of degree 2, we have shown that the number of rigid indecomposable rank 2 modules corresponding to real roots is twice the number of real roots of degree 2 for ![]() $J_{4,8}$. Also, for every rank 2 rigid indecomposable module whose root is real, and whose filtration is
$J_{4,8}$. Also, for every rank 2 rigid indecomposable module whose root is real, and whose filtration is ![]() $L_{I}|L_{J}$, there exists a rigid indecomposable module with filtration
$L_{I}|L_{J}$, there exists a rigid indecomposable module with filtration ![]() $L_{J}|L_{I}$. Therefore, both Theorem 2 and Conjecture 5.15 hold in this case.
$L_{J}|L_{I}$. Therefore, both Theorem 2 and Conjecture 5.15 hold in this case.
Acknowledgments
We thank Osamu Iyama, Bernhard Keller and Alastair King for very useful discussions. In particular, we thank Matthew Pressland for many discussions and for very helpful comments on a first version of this work. We thank the referee for helpful comments.