1 Introduction
Let
![]() $\mathsf{C}$
be a triangulated category with suspension
$\mathsf{C}$
be a triangulated category with suspension
![]() ${\rm\Sigma}:\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{C}$
. Given a cohomological functor
${\rm\Sigma}:\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{C}$
. Given a cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Mod}\,k$
into the category of modules over some (not necessarily commutative) ring
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Mod}\,k$
into the category of modules over some (not necessarily commutative) ring
![]() $k$
such that
$k$
such that
![]() $H(C)$
has finite length for each object
$H(C)$
has finite length for each object
![]() $C$
, we consider the function
$C$
, we consider the function
and ask the following questions.
- –
-
What are the characteristic properties of such a function
 $\mathsf{Ob}\,\mathsf{C}\longrightarrow \mathbb{N}$
?
$\mathsf{Ob}\,\mathsf{C}\longrightarrow \mathbb{N}$
? - –
-
Can we recover
 $H$
from
$H$
from
 ${\it\chi}$
?
${\it\chi}$
?
Somewhat surprisingly, we can offer fairly complete answers to both questions.
It should be noted that similar questions arise in Boij–Söderberg theory when cohomology tables are studied; recent progress [Reference Eisenbud and Ermann8, Reference Eisenbud and Schreyer9] provides some motivation for our work. Further motivation comes from the quest (initiated by Paul Balmer, for instance) for points in the context of triangulated categories.
Typical examples of cohomological functors are the representable functors of the form
![]() $\mathsf{Hom}(-,X)$
for some object
$\mathsf{Hom}(-,X)$
for some object
![]() $X$
in
$X$
in
![]() $\mathsf{C}$
. We begin with a result that takes care of this case; its proof is based on a theorem of Bongartz [Reference Bongartz4].
$\mathsf{C}$
. We begin with a result that takes care of this case; its proof is based on a theorem of Bongartz [Reference Bongartz4].
Theorem 1.1. (Jensen–Su–Zimmerman [Reference Jensen, Su and Zimmermann19])
Let
![]() $k$
be a commutative ring, and let
$k$
be a commutative ring, and let
![]() $\mathsf{C}$
be a
$\mathsf{C}$
be a
![]() $k$
-linear triangulated category such that each morphism set in
$k$
-linear triangulated category such that each morphism set in
![]() $\mathsf{C}$
has finite length as a
$\mathsf{C}$
has finite length as a
![]() $k$
-module. Suppose also for each pair of objects
$k$
-module. Suppose also for each pair of objects
![]() $X,Y$
that
$X,Y$
that
![]() $\mathsf{Hom}(X,{\rm\Sigma}^{n}Y)=0$
for some
$\mathsf{Hom}(X,{\rm\Sigma}^{n}Y)=0$
for some
![]() $n\in \mathbb{Z}$
. Then, two objects
$n\in \mathbb{Z}$
. Then, two objects
![]() $X$
and
$X$
and
![]() $Y$
are isomorphic if and only if the lengths of
$Y$
are isomorphic if and only if the lengths of
![]() $\mathsf{Hom}(C,X)$
and
$\mathsf{Hom}(C,X)$
and
![]() $\mathsf{Hom}(C,Y)$
coincide for all
$\mathsf{Hom}(C,Y)$
coincide for all
![]() $C$
in
$C$
in
![]() $\mathsf{C}$
.◻
$\mathsf{C}$
.◻
Examples of triangulated categories satisfying the assumptions in this theorem arise from bounded derived categories. To be precise, if
![]() $\mathsf{A}$
is a
$\mathsf{A}$
is a
![]() $k$
-linear exact category such that each extension group in
$k$
-linear exact category such that each extension group in
![]() $\mathsf{A}$
has finite length as a
$\mathsf{A}$
has finite length as a
![]() $k$
-module, then its bounded derived category
$k$
-module, then its bounded derived category
![]() $\mathsf{D}^{b}(\mathsf{A})$
satisfies the above assumptions, since for all objects
$\mathsf{D}^{b}(\mathsf{A})$
satisfies the above assumptions, since for all objects
![]() $X,Y$
in
$X,Y$
in
![]() $\mathsf{A}$
(viewed as complexes concentrated in degree zero)
$\mathsf{A}$
(viewed as complexes concentrated in degree zero)
On the other hand, Auslander and Reiten provided in [Reference Auslander and Reiten2, Section 4.4] simple examples of triangulated categories that do not have the property that objects are determined by the lengths of their morphism spaces (see also [Reference Benson and Parker3]).
Now, let
![]() $\mathsf{C}$
be an essentially small triangulated category. Thus, the isomorphism classes of objects in
$\mathsf{C}$
be an essentially small triangulated category. Thus, the isomorphism classes of objects in
![]() $\mathsf{C}$
form a set. Given any additive functor
$\mathsf{C}$
form a set. Given any additive functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
into the category of abelian groups, we denote by
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
into the category of abelian groups, we denote by
![]() $\mathsf{End}(H)$
the endomorphism ring formed by all natural transformations
$\mathsf{End}(H)$
the endomorphism ring formed by all natural transformations
![]() $H\rightarrow H$
. It should be noted that
$H\rightarrow H$
. It should be noted that
![]() $\mathsf{End}(H)$
acts on
$\mathsf{End}(H)$
acts on
![]() $H(C)$
for all objects
$H(C)$
for all objects
![]() $C$
. Moreover, if a ring
$C$
. Moreover, if a ring
![]() $k$
acts on
$k$
acts on
![]() $H(C)$
for all objects
$H(C)$
for all objects
![]() $C$
in a way that commutes with all morphisms in
$C$
in a way that commutes with all morphisms in
![]() $\mathsf{C}$
, then this action factors through that of
$\mathsf{C}$
, then this action factors through that of
![]() $\mathsf{End}(H)$
via a ring homomorphism
$\mathsf{End}(H)$
via a ring homomorphism
![]() $k\rightarrow \mathsf{End}(H)$
. In particular, when
$k\rightarrow \mathsf{End}(H)$
. In particular, when
![]() $H(C)$
has finite length over
$H(C)$
has finite length over
![]() $k$
, then it also has finite length over
$k$
, then it also has finite length over
![]() $\mathsf{End}(H)$
. This observation motivates the following definition.
$\mathsf{End}(H)$
. This observation motivates the following definition.
Definition 1.2. A cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is called endofinite
Footnote
1
provided that for each object
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is called endofinite
Footnote
1
provided that for each object
![]() $C$
$C$
-
(1)
 $H(C)$
has finite length as a module over the ring
$H(C)$
has finite length as a module over the ring
 $\mathsf{End}(H)$
, and
$\mathsf{End}(H)$
, and -
(2)
 $H({\rm\Sigma}^{n}C)=0$
for some
$H({\rm\Sigma}^{n}C)=0$
for some
 $n\in \mathbb{Z}$
.
$n\in \mathbb{Z}$
.
If
![]() $(H_{i})_{i\in I}$
are cohomological functors, then the direct sum
$(H_{i})_{i\in I}$
are cohomological functors, then the direct sum
![]() $\bigoplus _{i\in I}H_{i}$
is cohomological. A non-zero cohomological functor
$\bigoplus _{i\in I}H_{i}$
is cohomological. A non-zero cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is indecomposable if it cannot be written as a direct sum of two non-zero cohomological functors.
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is indecomposable if it cannot be written as a direct sum of two non-zero cohomological functors.
An endofinite cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
gives rise to a function
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
gives rise to a function
which is cohomological in the following sense (see Lemma 2.4).
Definition 1.3. A function
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
is called cohomological provided that
${\it\chi}:\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
is called cohomological provided that
-
(1)
 ${\it\chi}(C\oplus C^{\prime })={\it\chi}(C)+{\it\chi}(C^{\prime })$
for each pair of objects
${\it\chi}(C\oplus C^{\prime })={\it\chi}(C)+{\it\chi}(C^{\prime })$
for each pair of objects
 $C$
and
$C$
and
 $C^{\prime }$
,
$C^{\prime }$
, -
(2) for each object
 $C$
there is some
$C$
there is some
 $n\in \mathbb{Z}$
such that
$n\in \mathbb{Z}$
such that
 ${\it\chi}({\rm\Sigma}^{n}C)=0$
, and
${\it\chi}({\rm\Sigma}^{n}C)=0$
, and -
(3) for each exact triangle
 $A\rightarrow B\rightarrow C\rightarrow$
in
$A\rightarrow B\rightarrow C\rightarrow$
in
 $\mathsf{C}$
and each labeling of the induced sequence
$\mathsf{C}$
and each labeling of the induced sequence $$\begin{eqnarray}\cdots \rightarrow X_{-2}\rightarrow X_{-1}\rightarrow X_{0}\rightarrow X_{1}\rightarrow X_{2}\rightarrow \cdots\end{eqnarray}$$
with
$$\begin{eqnarray}\cdots \rightarrow X_{-2}\rightarrow X_{-1}\rightarrow X_{0}\rightarrow X_{1}\rightarrow X_{2}\rightarrow \cdots\end{eqnarray}$$
with $$\begin{eqnarray}\cdots \rightarrow {\rm\Sigma}^{-1}B\rightarrow {\rm\Sigma}^{-1}C\rightarrow A\rightarrow B\rightarrow C\rightarrow {\rm\Sigma}A\rightarrow {\rm\Sigma}B\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow {\rm\Sigma}^{-1}B\rightarrow {\rm\Sigma}^{-1}C\rightarrow A\rightarrow B\rightarrow C\rightarrow {\rm\Sigma}A\rightarrow {\rm\Sigma}B\rightarrow \cdots\end{eqnarray}$$
 ${\it\chi}(X_{0})=0$
we have and equality holds when
${\it\chi}(X_{0})=0$
we have and equality holds when $$\begin{eqnarray}\mathop{\sum }_{i=0}^{n}(-1)^{i+n}{\it\chi}(X_{i})\geqslant 0\quad \text{for all }n\in \mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=0}^{n}(-1)^{i+n}{\it\chi}(X_{i})\geqslant 0\quad \text{for all }n\in \mathbb{Z},\end{eqnarray}$$
 ${\it\chi}(X_{n})=0$
.
${\it\chi}(X_{n})=0$
.
If
![]() $({\it\chi}_{i})_{i\in I}$
are cohomological functions, and for any
$({\it\chi}_{i})_{i\in I}$
are cohomological functions, and for any
![]() $C$
in
$C$
in
![]() $\mathsf{C}$
the set
$\mathsf{C}$
the set
![]() $\{i\in I\mid {\it\chi}_{i}(C)\neq 0\}$
is finite, then we can define the locally finite sum
$\{i\in I\mid {\it\chi}_{i}(C)\neq 0\}$
is finite, then we can define the locally finite sum
![]() $\sum _{i\in I}{\it\chi}_{i}$
. A non-zero cohomological function is irreducible if it cannot be written as a sum of two non-zero cohomological functions.
$\sum _{i\in I}{\it\chi}_{i}$
. A non-zero cohomological function is irreducible if it cannot be written as a sum of two non-zero cohomological functions.
The following theorem is the main result of this paper; it is proved in Section 2 and builds on work of Crawley-Boevey on finite endolength objects (see [Reference Crawley-Boevey6, Reference Crawley-Boevey7]).
Theorem 1.4. Let
![]() $\mathsf{C}$
be an essentially small triangulated category.
$\mathsf{C}$
be an essentially small triangulated category.
-
(1) Every endofinite cohomological functor
 $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
decomposes essentially uniquely into a direct sum of indecomposable endofinite cohomological functors with local endomorphism rings.
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
decomposes essentially uniquely into a direct sum of indecomposable endofinite cohomological functors with local endomorphism rings. -
(2) Every cohomological function
 $\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
can be written uniquely as a locally finite sum of irreducible cohomological functions.
$\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
can be written uniquely as a locally finite sum of irreducible cohomological functions. -
(3) The assignment
 $H\mapsto {\it\chi}_{H}$
induces a bijection between the isomorphism classes of indecomposable endofinite cohomological functors
$H\mapsto {\it\chi}_{H}$
induces a bijection between the isomorphism classes of indecomposable endofinite cohomological functors
 $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
and the irreducible cohomological functions
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
and the irreducible cohomological functions
 $\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
.
$\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
.
Examples of endofinite cohomological functors arise from representable functors of the form
![]() $\mathsf{Hom}(-,X)$
when
$\mathsf{Hom}(-,X)$
when
![]() $\mathsf{C}$
is a Hom-finite
$\mathsf{C}$
is a Hom-finite
![]() $k$
-linear category. Thus, Theorem 1.1 can be deduced from Theorem 1.4. The following remark shows that in some appropriate setting each endofinite cohomological functor is representable.
$k$
-linear category. Thus, Theorem 1.1 can be deduced from Theorem 1.4. The following remark shows that in some appropriate setting each endofinite cohomological functor is representable.
Remark 1.5. Let
![]() $\mathsf{T}$
be a compactly generated triangulated category, and let
$\mathsf{T}$
be a compactly generated triangulated category, and let
![]() $\mathsf{C}$
be the full subcategory formed by all compact objects. Then, each endofinite cohomological functor
$\mathsf{C}$
be the full subcategory formed by all compact objects. Then, each endofinite cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is isomorphic to
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is isomorphic to
![]() $\mathsf{Hom}(-,X)|_{\mathsf{C}}$
for some object
$\mathsf{Hom}(-,X)|_{\mathsf{C}}$
for some object
![]() $X$
in
$X$
in
![]() $\mathsf{T}$
, which is unique up to an isomorphism and represents the functorFootnote
2
$\mathsf{T}$
, which is unique up to an isomorphism and represents the functorFootnote
2
Thus, cohomological functions are “represented” by objects in this setting. For specific examples, see [Reference Krause and Reichenbach25].
Next, we consider the set of irreducible cohomological functions
![]() $\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
and endow it with the Ziegler topology (see Proposition B.5). The quotient
$\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
and endow it with the Ziegler topology (see Proposition B.5). The quotient
with respect to the action of the suspension is by definition the space of cohomological functions on
![]() $\mathsf{C}$
. Thus, the points of
$\mathsf{C}$
. Thus, the points of
![]() $\mathsf{Sp}\,\mathsf{C}$
are equivalence classes of the form
$\mathsf{Sp}\,\mathsf{C}$
are equivalence classes of the form
![]() $[{\it\chi}]=\{{\it\chi}\circ {\rm\Sigma}^{n}\mid n\in \mathbb{Z}\}$
.
$[{\it\chi}]=\{{\it\chi}\circ {\rm\Sigma}^{n}\mid n\in \mathbb{Z}\}$
.
Take as an example the category of perfect complexes
![]() $\mathsf{D}^{b}(\mathsf{proj}\,A)$
over a commutative ring
$\mathsf{D}^{b}(\mathsf{proj}\,A)$
over a commutative ring
![]() $A$
. A prime ideal
$A$
. A prime ideal
![]() $\mathfrak{p}\in \mathsf{Spec}\,A$
with residue field
$\mathfrak{p}\in \mathsf{Spec}\,A$
with residue field
![]() $k(\mathfrak{p})$
yields an irreducible cohomological function
$k(\mathfrak{p})$
yields an irreducible cohomological function
where
![]() $k(\mathfrak{p})$
is viewed as a complex concentrated in degree zero.
$k(\mathfrak{p})$
is viewed as a complex concentrated in degree zero.
Theorem 1.6. The map
![]() $\mathsf{Spec}\,A\rightarrow \mathsf{Sp}\,\mathsf{D}^{b}(\mathsf{proj}\,A)$
sending
$\mathsf{Spec}\,A\rightarrow \mathsf{Sp}\,\mathsf{D}^{b}(\mathsf{proj}\,A)$
sending
![]() $\mathfrak{p}$
to
$\mathfrak{p}$
to
![]() $[{\it\chi}_{k(\mathfrak{p})}]$
is injective and closed with respect to the Hochster dual of the Zariski topology on
$[{\it\chi}_{k(\mathfrak{p})}]$
is injective and closed with respect to the Hochster dual of the Zariski topology on
![]() $\mathsf{Spec}\,A$
.
$\mathsf{Spec}\,A$
.
We prove this result in Section 4 by analyzing the Ziegler spectrum [Reference Krause24, Reference Ziegler34] of the category of perfect complexes. A general method for computing the space
![]() $\mathsf{Sp}\,\mathsf{C}$
of cohomological functions is to compute the Krull–Gabriel filtration [Reference Gabriel11, Reference Gruson and Jensen15] of the abelianization
$\mathsf{Sp}\,\mathsf{C}$
of cohomological functions is to compute the Krull–Gabriel filtration [Reference Gabriel11, Reference Gruson and Jensen15] of the abelianization
![]() $\mathsf{Ab}\,\mathsf{C}$
(see [Reference Freyd10, Reference Verdier31] or Section 2).
$\mathsf{Ab}\,\mathsf{C}$
(see [Reference Freyd10, Reference Verdier31] or Section 2).
A specific example is the algebra
![]() $k[{\it\varepsilon}]$
of dual numbers over a field
$k[{\it\varepsilon}]$
of dual numbers over a field
![]() $k$
. Each complex
$k$
. Each complex
of length
![]() $n$
corresponds to an isolated point in
$n$
corresponds to an isolated point in
![]() $\mathsf{Sp}\,\mathsf{D}^{b}(\mathsf{proj}\,k[{\it\varepsilon}])$
, and their closure yields exactly one extra point corresponding to the residue field. Thus,
$\mathsf{Sp}\,\mathsf{D}^{b}(\mathsf{proj}\,k[{\it\varepsilon}])$
, and their closure yields exactly one extra point corresponding to the residue field. Thus,
This example is of particular interest because the derived category
![]() $\mathsf{D}^{b}(\mathsf{proj}\,k[{\it\varepsilon}])$
is discrete in the sense of Vossieck [Reference Vossieck32]; that is, there are no continuous families of indecomposable objects. On the other hand, there are infinitely many indecomposable objects, even up to shift. The Krull–Gabriel dimension explains this behavior because it measures how far an abelian category is away from being a length category. For instance, a triangulated category
$\mathsf{D}^{b}(\mathsf{proj}\,k[{\it\varepsilon}])$
is discrete in the sense of Vossieck [Reference Vossieck32]; that is, there are no continuous families of indecomposable objects. On the other hand, there are infinitely many indecomposable objects, even up to shift. The Krull–Gabriel dimension explains this behavior because it measures how far an abelian category is away from being a length category. For instance, a triangulated category
![]() $\mathsf{C}$
is locally finite (see [Reference Krause26] or Section 4) if and only if the Krull–Gabriel dimension of
$\mathsf{C}$
is locally finite (see [Reference Krause26] or Section 4) if and only if the Krull–Gabriel dimension of
![]() $\mathsf{Ab}\,\mathsf{C}$
equals at most
$\mathsf{Ab}\,\mathsf{C}$
equals at most
![]() $0$
.
$0$
.
Proposition 1.7. The abelianization
![]() $\mathsf{Ab}\,\mathsf{D}^{b}(\mathsf{proj}\,k[{\it\varepsilon}])$
has Krull–Gabriel dimension equal to
$\mathsf{Ab}\,\mathsf{D}^{b}(\mathsf{proj}\,k[{\it\varepsilon}])$
has Krull–Gabriel dimension equal to
![]() $1$
.
$1$
.
It should be noted that the Krull–Gabriel dimension of the free abelian category
![]() $\mathsf{Ab}\,A$
over an Artin algebra
$\mathsf{Ab}\,A$
over an Artin algebra
![]() $A$
[Reference Gruson14] behaves differently; it equals
$A$
[Reference Gruson14] behaves differently; it equals
![]() $0$
if and only if
$0$
if and only if
![]() $A$
is of finite representation type by a result of Auslander [Reference Auslander1], and is greater than
$A$
is of finite representation type by a result of Auslander [Reference Auslander1], and is greater than
![]() $1$
otherwise (see [Reference Herzog17, Reference Krause21]).
$1$
otherwise (see [Reference Herzog17, Reference Krause21]).
As a final example, let us describe the cohomological functions for the category
![]() $\mathsf{coh}\,\mathbb{P}_{k}^{1}$
of coherent sheaves on the projective line over a field
$\mathsf{coh}\,\mathbb{P}_{k}^{1}$
of coherent sheaves on the projective line over a field
![]() $k$
.
$k$
.
Proposition 1.8. The abelianization
![]() $\mathsf{Ab}\,\mathsf{D}^{b}(\mathsf{coh}\,\mathbb{P}_{k}^{1})$
has Krull–Gabriel dimension equal to
$\mathsf{Ab}\,\mathsf{D}^{b}(\mathsf{coh}\,\mathbb{P}_{k}^{1})$
has Krull–Gabriel dimension equal to
![]() $2$
, and
$2$
, and
These examples illustrate in the triangulated context the following representation theoretic paradigm:
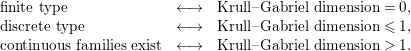 $$\begin{eqnarray}\displaystyle \begin{array}{@{}lcr@{}}\text{finite type} & \leftrightarrow & \text{Krull}{-}\text{Gabriel dimension}=0,\\ \text{discrete type} & \leftrightarrow & \text{Krull}{-}\text{Gabriel dimension}\leqslant 1,\\ \text{continuous families exist} & \leftrightarrow & \text{Krull}{-}\text{Gabriel dimension}>1.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}lcr@{}}\text{finite type} & \leftrightarrow & \text{Krull}{-}\text{Gabriel dimension}=0,\\ \text{discrete type} & \leftrightarrow & \text{Krull}{-}\text{Gabriel dimension}\leqslant 1,\\ \text{continuous families exist} & \leftrightarrow & \text{Krull}{-}\text{Gabriel dimension}>1.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
2 Cohomological functors and functions
In this section, Theorem 1.4 is proved. We deduce it from work of Crawley-Boevey on endofinite objects in locally finitely presented abelian categories (see [Reference Crawley-Boevey6, Reference Crawley-Boevey7]). We begin with some preparations.
Let
![]() $\mathsf{C}$
be an essentially small triangulated category.
$\mathsf{C}$
be an essentially small triangulated category.
The abelianization. Following Freyd [Reference Freyd10, Section 3] and Verdier [Reference Verdier31, II.3], we consider the abelianization
![]() $\mathsf{Ab}\,\mathsf{C}$
of
$\mathsf{Ab}\,\mathsf{C}$
of
![]() $\mathsf{C}$
, which is the abelian category of additive functors
$\mathsf{C}$
, which is the abelian category of additive functors
![]() $F:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
into the category
$F:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
into the category
![]() $\mathsf{Ab}$
of abelian groups that admit a copresentation
$\mathsf{Ab}$
of abelian groups that admit a copresentation
The suspension
![]() ${\rm\Sigma}:\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{C}$
extends to an equivalence
${\rm\Sigma}:\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{C}$
extends to an equivalence
![]() $\mathsf{Ab}\,\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{Ab}\,\mathsf{C}$
sending
$\mathsf{Ab}\,\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{Ab}\,\mathsf{C}$
sending
![]() $F$
to
$F$
to
![]() ${\rm\Sigma}F:=F\circ {\rm\Sigma}^{-1}$
.
${\rm\Sigma}F:=F\circ {\rm\Sigma}^{-1}$
.
In addition, we work in the category
![]() $\mathsf{Mod}\,\mathsf{C}$
of additive functors
$\mathsf{Mod}\,\mathsf{C}$
of additive functors
![]() $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
. This is a locally finitely presented abelian category, and the abelianization
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
. This is a locally finitely presented abelian category, and the abelianization
![]() $\mathsf{Ab}\,\mathsf{C}$
identifies with the full subcategory of finitely presented objects of
$\mathsf{Ab}\,\mathsf{C}$
identifies with the full subcategory of finitely presented objects of
![]() $\mathsf{Mod}\,\mathsf{C}$
(see [Reference Crawley-Boevey6] for details).
$\mathsf{Mod}\,\mathsf{C}$
(see [Reference Crawley-Boevey6] for details).
Additive functions. Let us introduce the analogue of a cohomological function for the abelianization of
![]() $\mathsf{C}$
.
$\mathsf{C}$
.
Definition 2.1. A function
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
is called additive
Footnote
3
provided that
${\it\chi}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
is called additive
Footnote
3
provided that
-
(1)
 ${\it\chi}(F)={\it\chi}(F^{\prime })+{\it\chi}(F^{\prime \prime })$
if
${\it\chi}(F)={\it\chi}(F^{\prime })+{\it\chi}(F^{\prime \prime })$
if
 $0\rightarrow F^{\prime }\rightarrow F\rightarrow F^{\prime \prime }\rightarrow 0$
is an exact sequence, and
$0\rightarrow F^{\prime }\rightarrow F\rightarrow F^{\prime \prime }\rightarrow 0$
is an exact sequence, and -
(2) for each object
 $F$
there is some
$F$
there is some
 $n\in \mathbb{Z}$
such that
$n\in \mathbb{Z}$
such that
 ${\it\chi}({\rm\Sigma}^{n}F)=0$
.
${\it\chi}({\rm\Sigma}^{n}F)=0$
.
We show that additive and cohomological functions are closely related.
Lemma 2.2. Restricting a function
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
to
${\it\chi}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
to
![]() $\mathsf{Ob}\,\mathsf{C}$
by setting
$\mathsf{Ob}\,\mathsf{C}$
by setting
![]() ${\it\chi}(C)={\it\chi}(\mathsf{Hom}(-,C))$
gives a natural bijection between
${\it\chi}(C)={\it\chi}(\mathsf{Hom}(-,C))$
gives a natural bijection between
- –
-
the additive functions
 $\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
and
$\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
and - –
-
the cohomological functions
 $\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
.
$\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
.
Proof. Let
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
be an additive function. An exact triangle
${\it\chi}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
be an additive function. An exact triangle
![]() $A\rightarrow B\rightarrow C\rightarrow$
in
$A\rightarrow B\rightarrow C\rightarrow$
in
![]() $\mathsf{C}$
yields in
$\mathsf{C}$
yields in
![]() $\mathsf{Ab}\,\mathsf{C}$
an exact sequence
$\mathsf{Ab}\,\mathsf{C}$
an exact sequence
Using this sequence, it is easily checked that the restriction of
![]() ${\it\chi}$
to
${\it\chi}$
to
![]() $\mathsf{C}$
is a cohomological function.
$\mathsf{C}$
is a cohomological function.
Conversely, given a cohomological function
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
, we extend it to a function
${\it\chi}:\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
, we extend it to a function
![]() $\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
, which again we denote by
$\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
, which again we denote by
![]() ${\it\chi}$
. We fix
${\it\chi}$
. We fix
![]() $F$
in
$F$
in
![]() $\mathsf{Ab}\,\mathsf{C}$
with copresentation as above induced by an exact triangle
$\mathsf{Ab}\,\mathsf{C}$
with copresentation as above induced by an exact triangle
![]() $A\rightarrow B\rightarrow C\rightarrow$
in
$A\rightarrow B\rightarrow C\rightarrow$
in
![]() $\mathsf{C}$
, and choose
$\mathsf{C}$
, and choose
![]() $n\in \mathbb{Z}$
such that
$n\in \mathbb{Z}$
such that
![]() ${\it\chi}({\rm\Sigma}^{n}(A\oplus B\oplus C))=0$
. Then, we define
${\it\chi}({\rm\Sigma}^{n}(A\oplus B\oplus C))=0$
. Then, we define
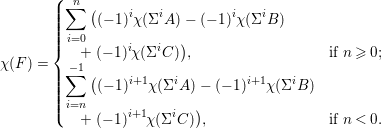 $$\begin{eqnarray}{\it\chi}(F)=\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{i=0}^{n}\big((-1)^{i}{\it\chi}({\rm\Sigma}^{i}A)-(-1)^{i}{\it\chi}({\rm\Sigma}^{i}B) & \\ \displaystyle \quad +\,(-1)^{i}{\it\chi}({\rm\Sigma}^{i}C)\big), & \text{if }n\geqslant 0;\\ \displaystyle \mathop{\sum }_{i=n}^{-1}\big((-1)^{i+1}{\it\chi}({\rm\Sigma}^{i}A)-(-1)^{i+1}{\it\chi}({\rm\Sigma}^{i}B) & \\ \displaystyle \quad +\,(-1)^{i+1}{\it\chi}({\rm\Sigma}^{i}C)\big), & \text{if }n<0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}(F)=\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{i=0}^{n}\big((-1)^{i}{\it\chi}({\rm\Sigma}^{i}A)-(-1)^{i}{\it\chi}({\rm\Sigma}^{i}B) & \\ \displaystyle \quad +\,(-1)^{i}{\it\chi}({\rm\Sigma}^{i}C)\big), & \text{if }n\geqslant 0;\\ \displaystyle \mathop{\sum }_{i=n}^{-1}\big((-1)^{i+1}{\it\chi}({\rm\Sigma}^{i}A)-(-1)^{i+1}{\it\chi}({\rm\Sigma}^{i}B) & \\ \displaystyle \quad +\,(-1)^{i+1}{\it\chi}({\rm\Sigma}^{i}C)\big), & \text{if }n<0.\end{array}\right.\end{eqnarray}$$
This gives a non-negative integer, and does not depend on
![]() $n$
since
$n$
since
![]() ${\it\chi}$
is a cohomological function. Moreover,
${\it\chi}$
is a cohomological function. Moreover,
![]() ${\it\chi}(F)$
does not depend on the choice of the exact triangle that presents
${\it\chi}(F)$
does not depend on the choice of the exact triangle that presents
![]() $F$
by a variant of Schanuel’s lemma (see Lemma A.1). It should be noted that
$F$
by a variant of Schanuel’s lemma (see Lemma A.1). It should be noted that
![]() ${\it\chi}(\mathsf{Hom}(-,C))={\it\chi}(C)$
for each
${\it\chi}(\mathsf{Hom}(-,C))={\it\chi}(C)$
for each
![]() $C$
in
$C$
in
![]() $\mathsf{C}$
. Standard arguments involving resolutions in
$\mathsf{C}$
. Standard arguments involving resolutions in
![]() $\mathsf{Ab}\,\mathsf{C}$
show that
$\mathsf{Ab}\,\mathsf{C}$
show that
![]() ${\it\chi}$
is additive.
${\it\chi}$
is additive.
Clearly, restricting from
![]() $\mathsf{Ab}\,\mathsf{C}$
to
$\mathsf{Ab}\,\mathsf{C}$
to
![]() $\mathsf{C}$
and extending from
$\mathsf{C}$
and extending from
![]() $\mathsf{C}$
to
$\mathsf{C}$
to
![]() $\mathsf{Ab}\,\mathsf{C}$
are mutually inverse operations.◻
$\mathsf{Ab}\,\mathsf{C}$
are mutually inverse operations.◻
There is a parallel between functions and functors. The analogue of Lemma 2.2 for functors is due to Freyd.
Lemma 2.3. (Freyd [Reference Freyd10])
Restricting a functor
![]() $F:(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
to
$F:(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
to
![]() $\mathsf{C}$
by setting
$\mathsf{C}$
by setting
![]() $F(C)=F(\mathsf{Hom}(-,C))$
gives a natural bijection between
$F(C)=F(\mathsf{Hom}(-,C))$
gives a natural bijection between
- –
-
the exact functors
 $(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
and
$(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
and - –
-
the cohomological functors
 $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
.
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
.
Proof. The inverse map sends a cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
to the exact functor
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
to the exact functor
![]() $\mathsf{Hom}(-,H):(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
.◻
$\mathsf{Hom}(-,H):(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
.◻
An endofinite cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
induces two functions:
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
induces two functions:
Lemma 2.4. The function
![]() ${\it\chi}_{H}$
is cohomological, and
${\it\chi}_{H}$
is cohomological, and
![]() $\hat{{\it\chi}}_{H}$
is additive.
$\hat{{\it\chi}}_{H}$
is additive.
Proof. The functor
![]() $\mathsf{Hom}(-,H):(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
is exact since
$\mathsf{Hom}(-,H):(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
is exact since
![]() $H$
is cohomological. It follows that
$H$
is cohomological. It follows that
![]() $\hat{{\it\chi}}_{H}$
is additive. The restriction of
$\hat{{\it\chi}}_{H}$
is additive. The restriction of
![]() $\hat{{\it\chi}}_{H}$
to
$\hat{{\it\chi}}_{H}$
to
![]() $\mathsf{C}$
equals
$\mathsf{C}$
equals
![]() ${\it\chi}_{H}$
. Thus,
${\it\chi}_{H}$
. Thus,
![]() ${\it\chi}_{H}$
is cohomological by Lemma 2.2.◻
${\it\chi}_{H}$
is cohomological by Lemma 2.2.◻
Proof of the main theorem. The proof of our main result is based on work of Crawley-Boevey, but we provide some complementary material in Appendix B.
Proof of Theorem 1.4.
An endofinite cohomological functor
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is a finite endolength injective object in
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
is a finite endolength injective object in
![]() $\mathsf{Mod}\,\mathsf{C}$
, as defined in [Reference Crawley-Boevey6]. The term “finite endolength” refers to the fact that
$\mathsf{Mod}\,\mathsf{C}$
, as defined in [Reference Crawley-Boevey6]. The term “finite endolength” refers to the fact that
![]() $\mathsf{Hom}(F,H)$
has finite length as
$\mathsf{Hom}(F,H)$
has finite length as
![]() $\mathsf{End}(H)$
-module for each
$\mathsf{End}(H)$
-module for each
![]() $F$
in
$F$
in
![]() $\mathsf{Ab}\,\mathsf{C}$
(see Lemma 2.4). The injectivity follows from the proof of [Reference Krause23, Theorem 1.2], using that
$\mathsf{Ab}\,\mathsf{C}$
(see Lemma 2.4). The injectivity follows from the proof of [Reference Krause23, Theorem 1.2], using that
![]() $\mathsf{Ext}^{1}(-,H)$
vanishes on
$\mathsf{Ext}^{1}(-,H)$
vanishes on
![]() $\mathsf{Ab}\,\mathsf{C}$
for any cohomological functor
$\mathsf{Ab}\,\mathsf{C}$
for any cohomological functor
![]() $H$
.
$H$
.
In [Reference Crawley-Boevey6, Theorem 3.5.2], it is shown that each finite endolength object decomposes into a direct sum of indecomposable objects with local endomorphism rings. (See [Reference Krause23, Theorem 1.2] for an alternative proof.) This yields part (1).
In [Reference Crawley-Boevey7], additive functions on locally finitely presented abelian categories are studied. In particular, there it is shown that every additive function on
![]() $\mathsf{Ab}\,\mathsf{C}$
can be written uniquely as a locally finite sum of irreducible additive functions. This proves part (2), in view of Lemma 2.2. For an alternative proof, see Proposition B.1.
$\mathsf{Ab}\,\mathsf{C}$
can be written uniquely as a locally finite sum of irreducible additive functions. This proves part (2), in view of Lemma 2.2. For an alternative proof, see Proposition B.1.
Finally, part (3) follows from the main theorem in [Reference Crawley-Boevey7], which establishes the bijection between isomorphism classes of indecomposable finite endolength injective objects in
![]() $\mathsf{Mod}\,\mathsf{C}$
and irreducible additive functions
$\mathsf{Mod}\,\mathsf{C}$
and irreducible additive functions
![]() $\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
. For an alternative proof, see Proposition B.2, using the bijection between cohomological and exact functors from Lemma 2.3.◻
$\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
. For an alternative proof, see Proposition B.2, using the bijection between cohomological and exact functors from Lemma 2.3.◻
3 Properties of cohomological functions
The correspondence between functors and functions. The assignment
![]() $H\mapsto {\it\chi}_{H}$
between endofinite cohomological functors and cohomological functions satisfies some weighted additivity. For instance,
$H\mapsto {\it\chi}_{H}$
between endofinite cohomological functors and cohomological functions satisfies some weighted additivity. For instance,
![]() ${\it\chi}_{H\oplus H^{\prime }}={\it\chi}_{H}+{\it\chi}_{H^{\prime }}$
provided that
${\it\chi}_{H\oplus H^{\prime }}={\it\chi}_{H}+{\it\chi}_{H^{\prime }}$
provided that
![]() $H$
and
$H$
and
![]() $H^{\prime }$
have no common indecomposable summand, but
$H^{\prime }$
have no common indecomposable summand, but
![]() ${\it\chi}_{H\oplus H}={\it\chi}_{H}$
. We have the following concise formula.
${\it\chi}_{H\oplus H}={\it\chi}_{H}$
. We have the following concise formula.
Proposition 3.1. Let
![]() $H=\bigoplus _{i\in I}H_{i}$
be the decomposition of an endofinite cohomological functor
$H=\bigoplus _{i\in I}H_{i}$
be the decomposition of an endofinite cohomological functor
![]() $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
into indecomposables. If
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
into indecomposables. If
![]() $J\subseteq I$
is a subset such that
$J\subseteq I$
is a subset such that
![]() $(H_{i})_{i\in J}$
contains each isomorphism class from
$(H_{i})_{i\in J}$
contains each isomorphism class from
![]() $(H_{i})_{i\in I}$
exactly once, then
$(H_{i})_{i\in I}$
exactly once, then
![]() ${\it\chi}_{H}=\sum _{i\in J}{\it\chi}_{H_{i}}$
.
${\it\chi}_{H}=\sum _{i\in J}{\it\chi}_{H_{i}}$
.
Proof. We adapt the proofs of [Reference Krause and Reichenbach25, Propositions 4.5 and 4.6]. Alternatively, we use Remark B.4. ◻
Remark 3.2. Let
![]() $\mathsf{C}$
be a
$\mathsf{C}$
be a
![]() $k$
-linear category such that each morphism set in
$k$
-linear category such that each morphism set in
![]() $\mathsf{C}$
has finite length as a
$\mathsf{C}$
has finite length as a
![]() $k$
-module. Then, we have two maps
$k$
-module. Then, we have two maps
![]() $\mathsf{Ob}\,\mathsf{C}\times \mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
, taking
$\mathsf{Ob}\,\mathsf{C}\times \mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
, taking
![]() $(X,Y)$
either to
$(X,Y)$
either to
![]() $\mathsf{length}_{k}\,\mathsf{Hom}(X,Y)$
or to
$\mathsf{length}_{k}\,\mathsf{Hom}(X,Y)$
or to
![]() $\mathsf{length}_{\mathsf{End}(Y)}\,\mathsf{Hom}(X,Y)$
. While the first map preserves sums in both arguments, the second one does not in the second argument, but it satisfies the above “weighted additivity”.
$\mathsf{length}_{\mathsf{End}(Y)}\,\mathsf{Hom}(X,Y)$
. While the first map preserves sums in both arguments, the second one does not in the second argument, but it satisfies the above “weighted additivity”.
Duality. The correspondence in Theorem 1.4 yields a remarkable duality between cohomological functors
![]() $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
and cohomological functors
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
and cohomological functors
![]() $\mathsf{C}\rightarrow \mathsf{Ab}$
. This follows from the fact that the definition of a cohomological function
$\mathsf{C}\rightarrow \mathsf{Ab}$
. This follows from the fact that the definition of a cohomological function
![]() $\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
is self-dual; it is an analogue of the elementary duality between left and right modules over a ring studied by Herzog [Reference Herzog16].
$\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
is self-dual; it is an analogue of the elementary duality between left and right modules over a ring studied by Herzog [Reference Herzog16].
The duality links indecomposable endofinite cohomological functors
![]() $H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
and
$H:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
and
![]() $H^{\prime }:\mathsf{C}\rightarrow \mathsf{Ab}$
when
$H^{\prime }:\mathsf{C}\rightarrow \mathsf{Ab}$
when
![]() ${\it\chi}_{H}={\it\chi}_{H^{\prime }}$
. In that case,
${\it\chi}_{H}={\it\chi}_{H^{\prime }}$
. In that case,
where
![]() $\mathsf{rad}\,A$
denotes the Jacobson radical of a ring
$\mathsf{rad}\,A$
denotes the Jacobson radical of a ring
![]() $A$
. This follows from Remark B.3.
$A$
. This follows from Remark B.3.
The duality specializes to Serre duality when
![]() $\mathsf{C}$
is a Hom-finite
$\mathsf{C}$
is a Hom-finite
![]() $k$
-linear category with
$k$
-linear category with
![]() $k$
a field. More precisely, if
$k$
a field. More precisely, if
![]() $F:\mathsf{C}\rightarrow \mathsf{C}$
is a Serre functor [Reference Reiten and Van den Bergh29] and
$F:\mathsf{C}\rightarrow \mathsf{C}$
is a Serre functor [Reference Reiten and Van den Bergh29] and
![]() $D=\mathsf{Hom}(-,k)$
, then
$D=\mathsf{Hom}(-,k)$
, then
for each object
![]() $X$
, and therefore
$X$
, and therefore
![]() ${\it\chi}_{\mathsf{Hom}(-,FX)}={\it\chi}_{\mathsf{Hom}(X,-)}$
.
${\it\chi}_{\mathsf{Hom}(-,FX)}={\it\chi}_{\mathsf{Hom}(X,-)}$
.
The space of cohomological functions. Consider the set of irreducible cohomological functions
![]() $\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
, and identify this via Lemma 2.2 with a subspace of
$\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
, and identify this via Lemma 2.2 with a subspace of
![]() $\mathsf{Sp}\,\mathsf{Ab}\,\mathsf{C}$
, endowed with the Ziegler topology, as explained in Proposition B.5. The quotient
$\mathsf{Sp}\,\mathsf{Ab}\,\mathsf{C}$
, endowed with the Ziegler topology, as explained in Proposition B.5. The quotient
with respect to the action of the suspension is by definition the space of cohomological functions on
![]() $\mathsf{C}$
. Thus, the points of
$\mathsf{C}$
. Thus, the points of
![]() $\mathsf{Sp}\,\mathsf{C}$
are equivalence classes of the form
$\mathsf{Sp}\,\mathsf{C}$
are equivalence classes of the form
![]() $[{\it\chi}]=\{{\it\chi}\circ {\rm\Sigma}^{n}\mid n\in \mathbb{Z}\}$
.
$[{\it\chi}]=\{{\it\chi}\circ {\rm\Sigma}^{n}\mid n\in \mathbb{Z}\}$
.
The construction of this space is functorial with respect to certain functors. Let
![]() $f:\mathsf{C}\rightarrow \mathsf{D}$
be an exact functor between triangulated categories. Given
$f:\mathsf{C}\rightarrow \mathsf{D}$
be an exact functor between triangulated categories. Given
![]() $[{\it\chi}]$
in
$[{\it\chi}]$
in
![]() $\mathsf{Sp}\,\mathsf{D}$
, the composite
$\mathsf{Sp}\,\mathsf{D}$
, the composite
![]() ${\it\chi}\circ f$
is cohomological but need not be irreducible. Thus,
${\it\chi}\circ f$
is cohomological but need not be irreducible. Thus,
![]() $f$
induces a continuous map
$f$
induces a continuous map
![]() $\mathsf{Sp}\,\mathsf{D}\rightarrow \mathsf{Sp}\,\mathsf{C}$
provided that irreducibility is preserved. For instance, a quotient functor
$\mathsf{Sp}\,\mathsf{D}\rightarrow \mathsf{Sp}\,\mathsf{C}$
provided that irreducibility is preserved. For instance, a quotient functor
![]() $\mathsf{C}\rightarrow \mathsf{C}/\mathsf{B}$
with respect to a triangulated subcategory
$\mathsf{C}\rightarrow \mathsf{C}/\mathsf{B}$
with respect to a triangulated subcategory
![]() $\mathsf{B}\subseteq \mathsf{C}$
has this property; it induces a homeomorphism
$\mathsf{B}\subseteq \mathsf{C}$
has this property; it induces a homeomorphism
Before we discuss specific examples, let us give one general result. Let
![]() $k$
be a field, and let
$k$
be a field, and let
![]() $\mathsf{C}$
be a
$\mathsf{C}$
be a
![]() $k$
-linear triangulated category such that for each pair of objects
$k$
-linear triangulated category such that for each pair of objects
![]() $X,Y$
we have
$X,Y$
we have
![]() $\mathsf{Hom}(X,{\rm\Sigma}^{n}Y)=0$
for some
$\mathsf{Hom}(X,{\rm\Sigma}^{n}Y)=0$
for some
![]() $n\in \mathbb{Z}$
. Suppose that all morphism spaces are finite dimensional, and that
$n\in \mathbb{Z}$
. Suppose that all morphism spaces are finite dimensional, and that
![]() $\mathsf{C}$
is idempotent complete. Suppose also that
$\mathsf{C}$
is idempotent complete. Suppose also that
![]() $\mathsf{C}$
admits a Serre functor [Reference Reiten and Van den Bergh29]. Denote for each object
$\mathsf{C}$
admits a Serre functor [Reference Reiten and Van den Bergh29]. Denote for each object
![]() $X$
by
$X$
by
![]() ${\it\chi}_{X}$
the cohomological function corresponding to
${\it\chi}_{X}$
the cohomological function corresponding to
![]() $\mathsf{Hom}(-,X)$
.
$\mathsf{Hom}(-,X)$
.
Proposition 3.3. A point in
![]() $\mathsf{Sp}\,\mathsf{C}$
is isolated if and only if it equals
$\mathsf{Sp}\,\mathsf{C}$
is isolated if and only if it equals
![]() $[{\it\chi}_{X}]$
for some indecomposable object
$[{\it\chi}_{X}]$
for some indecomposable object
![]() $X$
. Moreover, the isolated points form a dense subset of
$X$
. Moreover, the isolated points form a dense subset of
![]() $\mathsf{Sp}\,\mathsf{C}$
.
$\mathsf{Sp}\,\mathsf{C}$
.
Proof. Each indecomposable object
![]() $X$
fits into an Auslander–Reiten triangle
$X$
fits into an Auslander–Reiten triangle
![]() $X\rightarrow Y\rightarrow Z\rightarrow$
in
$X\rightarrow Y\rightarrow Z\rightarrow$
in
![]() $\mathsf{C}$
, by [Reference Reiten and Van den Bergh29, Theorem I.2.4]. Such a triangle provides in
$\mathsf{C}$
, by [Reference Reiten and Van den Bergh29, Theorem I.2.4]. Such a triangle provides in
![]() $\mathsf{Ab}\,\mathsf{C}$
the following copresentation of a simple object
$\mathsf{Ab}\,\mathsf{C}$
the following copresentation of a simple object
![]() $S_{X}$
:
$S_{X}$
:
Thus,
![]() $(S_{X})=\{{\it\chi}_{X}\}$
is a basic open set for each indecomposable object
$(S_{X})=\{{\it\chi}_{X}\}$
is a basic open set for each indecomposable object
![]() $X$
.
$X$
.
Now, let
![]() $(F)$
be a non-empty basic open set with
$(F)$
be a non-empty basic open set with
![]() $F\in \mathsf{Ab}\,\mathsf{C}$
. The functor
$F\in \mathsf{Ab}\,\mathsf{C}$
. The functor
![]() $F$
admits a copresentation
$F$
admits a copresentation
with an indecomposable direct summand
![]() $X^{\prime }\subseteq X$
such that
$X^{\prime }\subseteq X$
such that
Thus,
![]() ${\it\chi}_{X^{\prime }}$
belongs to
${\it\chi}_{X^{\prime }}$
belongs to
![]() $(F)$
. It follows that each non-empty open subset of
$(F)$
. It follows that each non-empty open subset of
![]() $\mathsf{Sp}\,\mathsf{C}$
contains a point of the form
$\mathsf{Sp}\,\mathsf{C}$
contains a point of the form
![]() $[{\it\chi}_{X}]$
.◻
$[{\it\chi}_{X}]$
.◻
The space of cohomological functions may be empty, as the following example shows.
Example 3.4. Let
![]() $A$
be a ring without invariant basis number, for example the endomorphism ring of an infinite dimensional vector space. Then, there is no non-zero endofinite cohomological functor
$A$
be a ring without invariant basis number, for example the endomorphism ring of an infinite dimensional vector space. Then, there is no non-zero endofinite cohomological functor
![]() $H:\mathsf{D}^{b}(\mathsf{proj}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
. To see this, observe that
$H:\mathsf{D}^{b}(\mathsf{proj}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
. To see this, observe that
![]() $H({\rm\Sigma}^{n}A)$
is a finite endolength
$H({\rm\Sigma}^{n}A)$
is a finite endolength
![]() $A$
-module for all
$A$
-module for all
![]() $n\in \mathbb{Z}$
, and therefore the zero module (see [Reference Crawley-Boevey5, Section 4.7]).
$n\in \mathbb{Z}$
, and therefore the zero module (see [Reference Crawley-Boevey5, Section 4.7]).
4 Examples: perfect complexes
We compute the space
![]() $\mathsf{Sp}\,\mathsf{C}$
of cohomological functions in some examples, for instance when
$\mathsf{Sp}\,\mathsf{C}$
of cohomological functions in some examples, for instance when
![]() $\mathsf{C}$
is the triangulated category of perfect complexes over some ring. It is convenient to view
$\mathsf{C}$
is the triangulated category of perfect complexes over some ring. It is convenient to view
![]() $\mathsf{Sp}\,\mathsf{C}$
as a subspace of the spectrum
$\mathsf{Sp}\,\mathsf{C}$
as a subspace of the spectrum
![]() $\mathsf{Zsp}\,\mathsf{C}$
, as defined in Appendix C.
$\mathsf{Zsp}\,\mathsf{C}$
, as defined in Appendix C.
The problem of computing the space of cohomological functions is reduced to the study of the Krull–Gabriel filtration of the abelianization
![]() $\mathsf{Ab}\,\mathsf{C}$
. This filtration yields a dimension. For an abelian category
$\mathsf{Ab}\,\mathsf{C}$
. This filtration yields a dimension. For an abelian category
![]() $\mathsf{A}$
, the Krull–Gabriel dimension
$\mathsf{A}$
, the Krull–Gabriel dimension
![]() $\mathsf{KGdim}\,\mathsf{A}$
is an invariant, which measures how far
$\mathsf{KGdim}\,\mathsf{A}$
is an invariant, which measures how far
![]() $\mathsf{A}$
is away from being a length category (see Appendix C).
$\mathsf{A}$
is away from being a length category (see Appendix C).
Modules. Let
![]() $A$
be a ring. We write
$A$
be a ring. We write
![]() $\mathsf{Mod}\,A$
for the category of
$\mathsf{Mod}\,A$
for the category of
![]() $A$
-modules,
$A$
-modules,
![]() $\mathsf{mod}\,A$
for the full subcategory of finitely presented ones, and
$\mathsf{mod}\,A$
for the full subcategory of finitely presented ones, and
![]() $\mathsf{proj}\,A$
for the full subcategory of finitely generated projectives.
$\mathsf{proj}\,A$
for the full subcategory of finitely generated projectives.
Following [Reference Gruson14], we consider the free abelian category
Footnote
4
over
![]() $A$
, and denote it by
$A$
, and denote it by
![]() $\mathsf{Ab}\,A$
. Thus, the category of
$\mathsf{Ab}\,A$
. Thus, the category of
![]() $A$
-modules identifies with the category of exact functors
$A$
-modules identifies with the category of exact functors
![]() $(\mathsf{Ab}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
.
$(\mathsf{Ab}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
.
We consider the derived category
![]() $\mathsf{D}(\mathsf{Mod}\,A)$
, and write
$\mathsf{D}(\mathsf{Mod}\,A)$
, and write
![]() $\mathsf{per}\,A$
for the full subcategory
$\mathsf{per}\,A$
for the full subcategory
![]() $\mathsf{D}^{b}(\mathsf{proj}\,A)$
of perfect complexes.
$\mathsf{D}^{b}(\mathsf{proj}\,A)$
of perfect complexes.
The Ziegler spectrum
![]() $\mathsf{Zsp}\,A$
of
$\mathsf{Zsp}\,A$
of
![]() $A$
is by definition the set of isomorphism classes of indecomposable pure-injective
$A$
is by definition the set of isomorphism classes of indecomposable pure-injective
![]() $A$
-modules with the topology introduced by Ziegler [Reference Prest28, Reference Ziegler34]. We identify
$A$
-modules with the topology introduced by Ziegler [Reference Prest28, Reference Ziegler34]. We identify
![]() $\mathsf{Zsp}\,A$
with the spectrum
$\mathsf{Zsp}\,A$
with the spectrum
![]() $\mathsf{Zsp}\,\mathsf{Ab}\,A$
of the abelian category
$\mathsf{Zsp}\,\mathsf{Ab}\,A$
of the abelian category
![]() $\mathsf{Ab}\,A$
(see Appendix C).
$\mathsf{Ab}\,A$
(see Appendix C).
It should be noted that the spectrum
![]() $\mathsf{Zsp}\,\mathsf{per}\,A$
identifies with a quotient of the Ziegler spectrum of the compactly generated triangulated category
$\mathsf{Zsp}\,\mathsf{per}\,A$
identifies with a quotient of the Ziegler spectrum of the compactly generated triangulated category
![]() $\mathsf{D}(\mathsf{Mod}\,A)$
introduced in [Reference Krause24] and further investigated in [Reference Garkusha and Prest12]. The identification takes an object
$\mathsf{D}(\mathsf{Mod}\,A)$
introduced in [Reference Krause24] and further investigated in [Reference Garkusha and Prest12]. The identification takes an object
![]() $X$
in
$X$
in
![]() $\mathsf{D}(\mathsf{Mod}\,A)$
to
$\mathsf{D}(\mathsf{Mod}\,A)$
to
![]() $\mathsf{Hom}(-,X)|_{\mathsf{per}\,A}$
.
$\mathsf{Hom}(-,X)|_{\mathsf{per}\,A}$
.
Let us compare
![]() $\mathsf{Zsp}\,A$
and
$\mathsf{Zsp}\,A$
and
![]() $\mathsf{Zsp}\,\mathsf{per}\,A$
. We consider the natural inclusion
$\mathsf{Zsp}\,\mathsf{per}\,A$
. We consider the natural inclusion
![]() $i:A\rightarrow \mathsf{per}\,A$
, which extends to an exact functor
$i:A\rightarrow \mathsf{per}\,A$
, which extends to an exact functor
![]() $i^{\ast }:\mathsf{Ab}\,A\rightarrow \mathsf{Ab}\,\mathsf{per}\,A$
by the universal property of
$i^{\ast }:\mathsf{Ab}\,A\rightarrow \mathsf{Ab}\,\mathsf{per}\,A$
by the universal property of
![]() $\mathsf{Ab}\,A$
.
$\mathsf{Ab}\,A$
.
Lemma 4.1. Let
![]() $\mathsf{S}_{0}\subseteq \mathsf{Ab}\,\mathsf{per}\,A$
be the Serre subcategory generated by the representable functors
$\mathsf{S}_{0}\subseteq \mathsf{Ab}\,\mathsf{per}\,A$
be the Serre subcategory generated by the representable functors
![]() $\mathsf{Hom}(-,{\rm\Sigma}^{n}A)$
with
$\mathsf{Hom}(-,{\rm\Sigma}^{n}A)$
with
![]() $n\neq 0$
. Then, the composite
$n\neq 0$
. Then, the composite
is an equivalence.
Proof. The cohomological functors
![]() $H:(\mathsf{per}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
annihilating
$H:(\mathsf{per}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
annihilating
![]() ${\rm\Sigma}^{n}A$
for all
${\rm\Sigma}^{n}A$
for all
![]() $n\neq 0$
identify with
$n\neq 0$
identify with
![]() $\mathsf{Mod}\,A$
, by taking
$\mathsf{Mod}\,A$
, by taking
![]() $H$
to
$H$
to
![]() $H(A)$
. Thus, the exact functors
$H(A)$
. Thus, the exact functors
![]() $(\mathsf{Ab}\,\mathsf{per}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
annihilating
$(\mathsf{Ab}\,\mathsf{per}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
annihilating
![]() $\mathsf{S}_{0}$
identify with
$\mathsf{S}_{0}$
identify with
![]() $\mathsf{Mod}\,A$
, by Lemma 2.3. It remains to observe that an exact functor
$\mathsf{Mod}\,A$
, by Lemma 2.3. It remains to observe that an exact functor
![]() $f:\mathsf{C}\rightarrow \mathsf{D}$
between abelian categories is an equivalence if precomposition with
$f:\mathsf{C}\rightarrow \mathsf{D}$
between abelian categories is an equivalence if precomposition with
![]() $f$
induces an equivalence between the categories of exact functors
$f$
induces an equivalence between the categories of exact functors
![]() $\mathsf{D}^{\text{op}}\rightarrow \mathsf{Ab}$
and
$\mathsf{D}^{\text{op}}\rightarrow \mathsf{Ab}$
and
![]() $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
.◻
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
.◻
We view an
![]() $A$
-module
$A$
-module
![]() $X$
as a complex concentrated in degree zero, and denote by
$X$
as a complex concentrated in degree zero, and denote by
![]() $H_{X}$
the corresponding cohomological functor
$H_{X}$
the corresponding cohomological functor
![]() $\mathsf{Hom}(-,X):(\mathsf{per}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
. It is convenient to identify
$\mathsf{Hom}(-,X):(\mathsf{per}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
. It is convenient to identify
![]() $H_{X}$
with the exact functor
$H_{X}$
with the exact functor
Proposition 4.2. The assignment
![]() $X\mapsto [H_{X}]$
induces an injective and continuous map
$X\mapsto [H_{X}]$
induces an injective and continuous map
![]() ${\it\phi}:\mathsf{Zsp}\,A\rightarrow \mathsf{Zsp}\,\mathsf{per}\,A$
; its image is a closed subset.
${\it\phi}:\mathsf{Zsp}\,A\rightarrow \mathsf{Zsp}\,\mathsf{per}\,A$
; its image is a closed subset.
Proof. We apply Lemma 4.1. The composite
identifies
![]() $\mathsf{Zsp}\,A$
with a closed subset of
$\mathsf{Zsp}\,A$
with a closed subset of
![]() $\mathsf{Zsp}\,\mathsf{Ab}\,\mathsf{per}\,A$
, which we denote by
$\mathsf{Zsp}\,\mathsf{Ab}\,\mathsf{per}\,A$
, which we denote by
![]() $\mathsf{U}$
. Viewing an
$\mathsf{U}$
. Viewing an
![]() $A$
-module
$A$
-module
![]() $X$
as an exact functor
$X$
as an exact functor
![]() $(\mathsf{Ab}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
, we have
$(\mathsf{Ab}\,A)^{\text{op}}\rightarrow \mathsf{Ab}$
, we have
![]() $X\circ f=H_{X}$
. It should be noted that the subsets
$X\circ f=H_{X}$
. It should be noted that the subsets
![]() ${\rm\Sigma}^{n}\mathsf{U}$
,
${\rm\Sigma}^{n}\mathsf{U}$
,
![]() $n\in \mathbb{Z}$
, are pairwise disjoint. It follows that
$n\in \mathbb{Z}$
, are pairwise disjoint. It follows that
![]() ${\it\phi}$
is injective.
${\it\phi}$
is injective.
Next, we observe that
where
![]() $(r,s)$
runs through all pairs of integers
$(r,s)$
runs through all pairs of integers
![]() $r\neq s$
, and
$r\neq s$
, and
Thus, the image of
![]() ${\it\phi}$
is closed.
${\it\phi}$
is closed.
Now, let
![]() $\mathsf{V}\subseteq \mathsf{Zsp}\,\mathsf{per}\,A$
be a closed subset, which corresponds to a Serre subcategory
$\mathsf{V}\subseteq \mathsf{Zsp}\,\mathsf{per}\,A$
be a closed subset, which corresponds to a Serre subcategory
![]() $\mathsf{S}\subseteq \mathsf{Ab}\,\mathsf{per}\,A$
(see Lemma C.1). Thus,
$\mathsf{S}\subseteq \mathsf{Ab}\,\mathsf{per}\,A$
(see Lemma C.1). Thus,
![]() $\mathsf{V}$
consists of all functors in
$\mathsf{V}$
consists of all functors in
![]() $\mathsf{Zsp}\,\mathsf{per}\,A$
that vanish on
$\mathsf{Zsp}\,\mathsf{per}\,A$
that vanish on
![]() $\mathsf{S}$
. Then,
$\mathsf{S}$
. Then,
![]() ${\it\phi}^{-1}(\mathsf{V})$
consists of all functors vanishing on
${\it\phi}^{-1}(\mathsf{V})$
consists of all functors vanishing on
![]() $f(\mathsf{S})$
. It follows that
$f(\mathsf{S})$
. It follows that
![]() ${\it\phi}$
is continuous.◻
${\it\phi}$
is continuous.◻
Hereditary rings. A complex of
![]() $A$
-modules can be written as a direct sum of stalk complexes when
$A$
-modules can be written as a direct sum of stalk complexes when
![]() $A$
is hereditary. This has some useful consequences, which are collected in the following proposition.
$A$
is hereditary. This has some useful consequences, which are collected in the following proposition.
Proposition 4.3. For a hereditary ring
![]() $A$
, the following holds.
$A$
, the following holds.
-
(1) The map
 ${\it\phi}:\mathsf{Zsp}\,A\rightarrow \mathsf{Zsp}\,\mathsf{per}\,A$
taking
${\it\phi}:\mathsf{Zsp}\,A\rightarrow \mathsf{Zsp}\,\mathsf{per}\,A$
taking
 $X$
to
$X$
to
 $[H_{X}]$
is a homeomorphism.
$[H_{X}]$
is a homeomorphism. -
(2)
 $\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{per}\,A=\mathsf{KGdim}\,\mathsf{Ab}\,A$
.
$\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{per}\,A=\mathsf{KGdim}\,\mathsf{Ab}\,A$
.
Proof. (1) We apply Proposition 4.2. Each indecomposable complex of
![]() $A$
-modules is concentrated in a single degree since
$A$
-modules is concentrated in a single degree since
![]() $A$
is hereditary. This observation yields a disjoint union
$A$
is hereditary. This observation yields a disjoint union
and each
![]() $\mathsf{U}_{n}$
is homeomorphic to
$\mathsf{U}_{n}$
is homeomorphic to
![]() $\mathsf{Zsp}\,A$
. An open subset
$\mathsf{Zsp}\,A$
. An open subset
![]() $\mathsf{V}\subseteq \mathsf{Zsp}\,A$
identifies with an open subset
$\mathsf{V}\subseteq \mathsf{Zsp}\,A$
identifies with an open subset
![]() $\mathsf{V}_{n}\subseteq \mathsf{U}_{n}$
, and therefore with an open subset of
$\mathsf{V}_{n}\subseteq \mathsf{U}_{n}$
, and therefore with an open subset of
![]() $\mathsf{Zsp}\,\mathsf{per}\,A$
via
$\mathsf{Zsp}\,\mathsf{per}\,A$
via
![]() ${\it\phi}$
. It follows that
${\it\phi}$
. It follows that
![]() ${\it\phi}$
is open and therefore a homeomorphism by Proposition 4.2.
${\it\phi}$
is open and therefore a homeomorphism by Proposition 4.2.
(2) We apply Lemma C.4 and use the family of quotient functors
from Lemma 4.1, where
![]() $\mathsf{S}_{n}$
is by definition the Serre subcategory generated by the representable functors
$\mathsf{S}_{n}$
is by definition the Serre subcategory generated by the representable functors
![]() $\mathsf{Hom}(-,{\rm\Sigma}^{p}A)$
with
$\mathsf{Hom}(-,{\rm\Sigma}^{p}A)$
with
![]() $p\neq n$
.◻
$p\neq n$
.◻
Commutative rings. Let
![]() $A$
be a commutative ring, and let
$A$
be a commutative ring, and let
![]() $\mathsf{Spec}\,A$
be the set of prime ideals. We endow
$\mathsf{Spec}\,A$
be the set of prime ideals. We endow
![]() $\mathsf{Spec}\,A$
with the dual of the Zariski topology in the sense of Hochster [Reference Hochster18]. A prime ideal
$\mathsf{Spec}\,A$
with the dual of the Zariski topology in the sense of Hochster [Reference Hochster18]. A prime ideal
![]() $\mathfrak{p}$
with residue field
$\mathfrak{p}$
with residue field
![]() $k(\mathfrak{p})$
yields an irreducible cohomological function
$k(\mathfrak{p})$
yields an irreducible cohomological function
As before, we identify
![]() ${\it\chi}_{k(\mathfrak{p})}$
with
${\it\chi}_{k(\mathfrak{p})}$
with
![]() $k(\mathfrak{p})$
. In particular,
$k(\mathfrak{p})$
. In particular,
![]() ${\it\chi}_{k(\mathfrak{p})}$
is irreducible since
${\it\chi}_{k(\mathfrak{p})}$
is irreducible since
![]() $k(\mathfrak{p})$
is indecomposable.
$k(\mathfrak{p})$
is indecomposable.
Theorem 4.4. The map
![]() ${\it\rho}:\mathsf{Spec}\,A\rightarrow \mathsf{Sp}\,\mathsf{per}\,A$
sending
${\it\rho}:\mathsf{Spec}\,A\rightarrow \mathsf{Sp}\,\mathsf{per}\,A$
sending
![]() $\mathfrak{p}$
to
$\mathfrak{p}$
to
![]() $[{\it\chi}_{k(\mathfrak{p})}]$
is injective and closed with respect to the Hochster dual of the Zariski topology on
$[{\it\chi}_{k(\mathfrak{p})}]$
is injective and closed with respect to the Hochster dual of the Zariski topology on
![]() $\mathsf{Spec}\,A$
.
$\mathsf{Spec}\,A$
.
Proof. The injectivity is clear since different primes
![]() $\mathfrak{p},\mathfrak{q}$
yield non-isomorphic functors
$\mathfrak{p},\mathfrak{q}$
yield non-isomorphic functors
![]() $\mathsf{Hom}(-,k(\mathfrak{p}))$
and
$\mathsf{Hom}(-,k(\mathfrak{p}))$
and
![]() $\mathsf{Hom}(-,k(\mathfrak{q}))$
.
$\mathsf{Hom}(-,k(\mathfrak{q}))$
.
To show that the image
![]() $\mathsf{Im}\,{\it\rho}$
is closed, observe first that
$\mathsf{Im}\,{\it\rho}$
is closed, observe first that
is closed by Proposition 4.2. Moreover,
is closed by Lemma B.6. The indecomposable
![]() $A$
-modules
$A$
-modules
![]() $X$
with
$X$
with
![]() $\mathsf{length}_{\mathsf{End}(X)}\,X\leqslant 1$
are precisely the residue fields
$\mathsf{length}_{\mathsf{End}(X)}\,X\leqslant 1$
are precisely the residue fields
![]() $k(\mathfrak{p})$
(see [Reference Crawley-Boevey5, Section 4.7]). Thus,
$k(\mathfrak{p})$
(see [Reference Crawley-Boevey5, Section 4.7]). Thus,
![]() $\mathsf{Im}\,{\it\rho}=\mathsf{U}\cap \mathsf{U}_{1}$
is closed.
$\mathsf{Im}\,{\it\rho}=\mathsf{U}\cap \mathsf{U}_{1}$
is closed.
Given a closed subset
![]() $\mathsf{V}\subseteq \mathsf{Spec}\,A$
, we need to show that
$\mathsf{V}\subseteq \mathsf{Spec}\,A$
, we need to show that
![]() ${\it\rho}(\mathsf{V})$
is closed. It follows from Thomason’s classification of thick subcategories [Reference Thomason30, Theorem 3.15] that there is a thick subcategory
${\it\rho}(\mathsf{V})$
is closed. It follows from Thomason’s classification of thick subcategories [Reference Thomason30, Theorem 3.15] that there is a thick subcategory
![]() $\mathsf{C}$
of
$\mathsf{C}$
of
![]() $\mathsf{per}\,A$
with
$\mathsf{per}\,A$
with
![]() $\mathfrak{p}\in \mathsf{V}$
if and only if
$\mathfrak{p}\in \mathsf{V}$
if and only if
![]() $\mathsf{Hom}(X,k(\mathfrak{p}))=0$
for all
$\mathsf{Hom}(X,k(\mathfrak{p}))=0$
for all
![]() $X\in \mathsf{C}$
. Here, one uses that
$X\in \mathsf{C}$
. Here, one uses that
![]() $X^{\ast }\otimes _{A}^{\mathbf{L}}k(\mathfrak{p})\cong \mathsf{RHom}_{A}(X,k(\mathfrak{p}))$
when
$X^{\ast }\otimes _{A}^{\mathbf{L}}k(\mathfrak{p})\cong \mathsf{RHom}_{A}(X,k(\mathfrak{p}))$
when
![]() $X$
is perfect.
$X$
is perfect.
The latter condition means that
![]() ${\it\chi}_{k(\mathfrak{p})}(X)=0$
for all
${\it\chi}_{k(\mathfrak{p})}(X)=0$
for all
![]() $X\in \mathsf{C}$
. Thus,
$X\in \mathsf{C}$
. Thus,
![]() $\{[{\it\chi}_{k(\mathfrak{p})}]\mid \mathfrak{p}\in \mathsf{V}\}$
is Ziegler closed.◻
$\{[{\it\chi}_{k(\mathfrak{p})}]\mid \mathfrak{p}\in \mathsf{V}\}$
is Ziegler closed.◻
Remark 4.5. This result generalizes to schemes that are quasi-compact and quasi-separated.
Krull–Gabriel dimension zero. Following [Reference Krause26], a triangulated category
![]() $\mathsf{C}$
is locally finite if its abelianization
$\mathsf{C}$
is locally finite if its abelianization
![]() $\mathsf{Ab}\,\mathsf{C}$
is a length category, which means that
$\mathsf{Ab}\,\mathsf{C}$
is a length category, which means that
![]() $\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{C}\leqslant 0$
. We set
$\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{C}\leqslant 0$
. We set
![]() ${\it\chi}_{X}={\it\chi}_{\mathsf{Hom}(-,X)}$
for
${\it\chi}_{X}={\it\chi}_{\mathsf{Hom}(-,X)}$
for
![]() $X\in \mathsf{C}$
when
$X\in \mathsf{C}$
when
![]() $\mathsf{Hom}(-,X)$
is endofinite.
$\mathsf{Hom}(-,X)$
is endofinite.
Proposition 4.6. Let
![]() $\mathsf{C}$
be a locally finite and idempotent complete triangulated category. Suppose for each pair of objects
$\mathsf{C}$
be a locally finite and idempotent complete triangulated category. Suppose for each pair of objects
![]() $X,Y$
that
$X,Y$
that
![]() $\mathsf{Hom}(X,{\rm\Sigma}^{n}Y)=0$
for some
$\mathsf{Hom}(X,{\rm\Sigma}^{n}Y)=0$
for some
![]() $n\in \mathbb{Z}$
. Then,
$n\in \mathbb{Z}$
. Then,
Proof. Let
![]() $X$
be an object in
$X$
be an object in
![]() $\mathsf{C}$
. Then, we have for each object
$\mathsf{C}$
. Then, we have for each object
![]() $C$
$C$
by [Reference Auslander1, Theorem 2.12] (see also Remark B.4). Thus,
![]() $\mathsf{Hom}(-,X)$
is endofinite.
$\mathsf{Hom}(-,X)$
is endofinite.
Let
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
be an irreducible cohomological function, and let
${\it\chi}:\mathsf{Ob}\,\mathsf{C}\rightarrow \mathbb{N}$
be an irreducible cohomological function, and let
![]() $\hat{{\it\chi}}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
be its extension to
$\hat{{\it\chi}}:\mathsf{Ob}\,\mathsf{Ab}\,\mathsf{C}\rightarrow \mathbb{N}$
be its extension to
![]() $\mathsf{Ab}\,\mathsf{C}$
. Then,
$\mathsf{Ab}\,\mathsf{C}$
. Then,
![]() $\hat{{\it\chi}}(S)\neq 0$
for some simple object
$\hat{{\it\chi}}(S)\neq 0$
for some simple object
![]() $S$
. There is an indecomposable object
$S$
. There is an indecomposable object
![]() $X$
in
$X$
in
![]() $\mathsf{C}$
with
$\mathsf{C}$
with
![]() $\mathsf{Hom}(S,\mathsf{Hom}(-,X))\neq 0$
, and it follows that
$\mathsf{Hom}(S,\mathsf{Hom}(-,X))\neq 0$
, and it follows that
![]() $\mathsf{Hom}(-,X)$
is an injective envelope. Thus,
$\mathsf{Hom}(-,X)$
is an injective envelope. Thus,
![]() ${\it\chi}={\it\chi}_{X}$
.◻
${\it\chi}={\it\chi}_{X}$
.◻
Example 4.7. Let
![]() $k$
be a field, and let
$k$
be a field, and let
![]() ${\rm\Gamma}$
be a quiver with underlying diagram of Dynkin type. Denote by
${\rm\Gamma}$
be a quiver with underlying diagram of Dynkin type. Denote by
![]() $\mathsf{rep}({\rm\Gamma},k)$
the category of finite dimensional
$\mathsf{rep}({\rm\Gamma},k)$
the category of finite dimensional
![]() $k$
-linear representations of
$k$
-linear representations of
![]() ${\rm\Gamma}$
. The indecomposable endofinite cohomological functors
${\rm\Gamma}$
. The indecomposable endofinite cohomological functors
![]() $\mathsf{D}^{b}(\mathsf{rep}({\rm\Gamma},k))^{\text{op}}\rightarrow \mathsf{Ab}$
are precisely (up to isomorphism) the representable functors
$\mathsf{D}^{b}(\mathsf{rep}({\rm\Gamma},k))^{\text{op}}\rightarrow \mathsf{Ab}$
are precisely (up to isomorphism) the representable functors
![]() $\mathsf{Hom}(-,{\rm\Sigma}^{n}X)$
, with
$\mathsf{Hom}(-,{\rm\Sigma}^{n}X)$
, with
![]() $X$
an indecomposable object in
$X$
an indecomposable object in
![]() $\mathsf{rep}({\rm\Gamma},k)$
(viewed as complex concentrated in degree zero) and
$\mathsf{rep}({\rm\Gamma},k)$
(viewed as complex concentrated in degree zero) and
![]() $n\in \mathbb{Z}$
.
$n\in \mathbb{Z}$
.
Examples of triangulated categories
![]() $\mathsf{C}$
with
$\mathsf{C}$
with
![]() $\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{C}=1$
show that the description of
$\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{C}=1$
show that the description of
![]() $\mathsf{Sp}\,\mathsf{C}$
in Proposition 4.6 does not hold more generally.
$\mathsf{Sp}\,\mathsf{C}$
in Proposition 4.6 does not hold more generally.
Krull–Gabriel dimension one. Let
![]() $k$
be a field. We give an example of a finite dimensional
$k$
be a field. We give an example of a finite dimensional
![]() $k$
-algebra
$k$
-algebra
![]() $A$
such that the Krull–Gabriel dimension of
$A$
such that the Krull–Gabriel dimension of
![]() $\mathsf{Ab}\,\mathsf{per}\,A$
equals
$\mathsf{Ab}\,\mathsf{per}\,A$
equals
![]() $1$
. This gives some evidence for the following conjecture.
$1$
. This gives some evidence for the following conjecture.
Conjecture 4.8. Let
![]() $A$
be a finite dimensional
$A$
be a finite dimensional
![]() $k$
-algebra. Then, the Krull–Gabriel dimension of
$k$
-algebra. Then, the Krull–Gabriel dimension of
![]() $\mathsf{Ab}\,\mathsf{per}\,A$
equals
$\mathsf{Ab}\,\mathsf{per}\,A$
equals
![]() $0$
or
$0$
or
![]() $1$
if and only if
$1$
if and only if
![]() $\mathsf{per}\,A$
is a discrete derived category in the sense of [Reference Vossieck32].
$\mathsf{per}\,A$
is a discrete derived category in the sense of [Reference Vossieck32].
Proposition 4.9. Let
![]() $k[{\it\varepsilon}]$
be the algebra of dual numbers. Then,
$k[{\it\varepsilon}]$
be the algebra of dual numbers. Then,
Proof. Set
![]() $\mathsf{C}=\mathsf{per}\,k[{\it\varepsilon}]$
, and write
$\mathsf{C}=\mathsf{per}\,k[{\it\varepsilon}]$
, and write
![]() $H_{X}=\mathsf{Hom}(-,X)$
for each
$H_{X}=\mathsf{Hom}(-,X)$
for each
![]() $X$
in
$X$
in
![]() $\mathsf{C}$
. The indecomposable objects are the complexes
$\mathsf{C}$
. The indecomposable objects are the complexes
concentrated in degrees
![]() $n,n+1,\cdots \,,n+r$
and parametrized by pairs
$n,n+1,\cdots \,,n+r$
and parametrized by pairs
![]() $(n,r)$
in
$(n,r)$
in
![]() $\mathbb{Z}\times \mathbb{N}$
. We denote by
$\mathbb{Z}\times \mathbb{N}$
. We denote by
![]() $\tilde{{\it\varepsilon}}:X_{n,r}\rightarrow X_{n,r}$
the endomorphism given by
$\tilde{{\it\varepsilon}}:X_{n,r}\rightarrow X_{n,r}$
the endomorphism given by
![]() $k[{\it\varepsilon}]\xrightarrow[]{{\it\varepsilon}}k[{\it\varepsilon}]$
in degree
$k[{\it\varepsilon}]\xrightarrow[]{{\it\varepsilon}}k[{\it\varepsilon}]$
in degree
![]() $n$
, and zero in all other degrees. The Auslander–Reiten triangles are of the form
$n$
, and zero in all other degrees. The Auslander–Reiten triangles are of the form
with
![]() $X_{n,-1}=0$
. Such a triangle induces in
$X_{n,-1}=0$
. Such a triangle induces in
![]() $\mathsf{Ab}\,\mathsf{C}$
an exact sequence
$\mathsf{Ab}\,\mathsf{C}$
an exact sequence
with simple end terms.
We fix
![]() $n\in \mathbb{Z}$
. We claim that the Hasse diagram of the lattice of subobjects of
$n\in \mathbb{Z}$
. We claim that the Hasse diagram of the lattice of subobjects of
![]() $H_{X_{n,0}}$
has the following form:
$H_{X_{n,0}}$
has the following form:
![]()
To prove this, consider the sequence of morphisms
given by the Auslander–Reiten triangles. For each
![]() $t\geqslant 0$
, the composite
$t\geqslant 0$
, the composite
![]() ${\it\phi}_{n,t}:X_{n,t}\rightarrow X_{n,0}$
induces a morphism
${\it\phi}_{n,t}:X_{n,t}\rightarrow X_{n,0}$
induces a morphism
![]() $H_{{\it\phi}_{n,t}}$
in
$H_{{\it\phi}_{n,t}}$
in
![]() $\mathsf{Ab}\,\mathsf{C}$
, and its image is the unique subobject
$\mathsf{Ab}\,\mathsf{C}$
, and its image is the unique subobject
![]() $U\subseteq H_{X_{n,0}}$
such that
$U\subseteq H_{X_{n,0}}$
such that
![]() $H_{X_{n,0}}/U$
has length
$H_{X_{n,0}}/U$
has length
![]() $t$
. This explains the upper half of the Hasse diagram. The form of the lower half then follows by Serre duality. More precisely, Serre duality yields an equivalence
$t$
. This explains the upper half of the Hasse diagram. The form of the lower half then follows by Serre duality. More precisely, Serre duality yields an equivalence
![]() $\mathsf{C}^{\text{op}}\xrightarrow[]{{\sim}}\mathsf{C}$
, which is the identity on objects. It extends to an equivalence
$\mathsf{C}^{\text{op}}\xrightarrow[]{{\sim}}\mathsf{C}$
, which is the identity on objects. It extends to an equivalence
![]() $(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\xrightarrow[]{{\sim}}\mathsf{Ab}(\mathsf{C}^{\text{op}})\xrightarrow[]{{\sim}}\mathsf{Ab}\,\mathsf{C}$
, which induces a bijection between subobjects and quotient objects of
$(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\xrightarrow[]{{\sim}}\mathsf{Ab}(\mathsf{C}^{\text{op}})\xrightarrow[]{{\sim}}\mathsf{Ab}\,\mathsf{C}$
, which induces a bijection between subobjects and quotient objects of
![]() $H_{X_{n,0}}$
. It remains to show that
$H_{X_{n,0}}$
. It remains to show that
![]() $H_{X_{n,0}}$
has no further subobjects. To see this, let
$H_{X_{n,0}}$
has no further subobjects. To see this, let
![]() $V\subseteq H_{X_{n,0}}$
be a subobject; it is the image of some morphism
$V\subseteq H_{X_{n,0}}$
be a subobject; it is the image of some morphism
![]() $H_{{\it\phi}}:H_{X}\rightarrow H_{X_{n,0}}$
. We may assume that
$H_{{\it\phi}}:H_{X}\rightarrow H_{X_{n,0}}$
. We may assume that
![]() ${\it\phi}\neq 0$
, and that
${\it\phi}\neq 0$
, and that
![]() $X$
is indecomposable. The property of the Auslander–Reiten triangle for
$X$
is indecomposable. The property of the Auslander–Reiten triangle for
![]() $X_{n,0}$
implies that the endomorphism
$X_{n,0}$
implies that the endomorphism
![]() $\tilde{{\it\varepsilon}}:X_{n,0}\rightarrow X_{n,0}$
factors through
$\tilde{{\it\varepsilon}}:X_{n,0}\rightarrow X_{n,0}$
factors through
![]() ${\it\phi}$
via a morphism
${\it\phi}$
via a morphism
![]() ${\it\phi}^{\prime }:X_{n,0}\rightarrow X$
, since
${\it\phi}^{\prime }:X_{n,0}\rightarrow X$
, since
![]() $X_{n,0}\rightarrow \mathsf{cone}\,{\it\phi}$
factors through the left almost split morphism
$X_{n,0}\rightarrow \mathsf{cone}\,{\it\phi}$
factors through the left almost split morphism
![]() $X_{n,0}\rightarrow X_{n,1}$
. Thus,
$X_{n,0}\rightarrow X_{n,1}$
. Thus,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() ${\it\phi}^{\prime }$
yield in degree
${\it\phi}^{\prime }$
yield in degree
![]() $n$
endomorphisms of
$n$
endomorphisms of
![]() $k[{\it\varepsilon}]$
, and exactly one of them is an isomorphism. If
$k[{\it\varepsilon}]$
, and exactly one of them is an isomorphism. If
![]() ${\it\phi}^{n}$
is an isomorphism, then
${\it\phi}^{n}$
is an isomorphism, then
![]() $H_{X_{n,0}}/V$
has finite length; otherwise
$H_{X_{n,0}}/V$
has finite length; otherwise
![]() $V$
is of finite length.
$V$
is of finite length.
The form of the lattice of subobjects implies that
![]() $H_{X_{n,0}}$
is a simple object in
$H_{X_{n,0}}$
is a simple object in
![]() $(\mathsf{Ab}\,\mathsf{C})/(\mathsf{Ab}\,\mathsf{C})_{0}$
. Using induction on
$(\mathsf{Ab}\,\mathsf{C})/(\mathsf{Ab}\,\mathsf{C})_{0}$
. Using induction on
![]() $r$
, the sequence (4.1) shows that
$r$
, the sequence (4.1) shows that
![]() $H_{X_{n,r}}$
has length
$H_{X_{n,r}}$
has length
![]() $r+1$
. Thus,
$r+1$
. Thus,
![]() $(\mathsf{Ab}\,\mathsf{C})_{1}=\mathsf{Ab}\,\mathsf{C}$
.◻
$(\mathsf{Ab}\,\mathsf{C})_{1}=\mathsf{Ab}\,\mathsf{C}$
.◻
Corollary 4.10. We have
![]() $\mathsf{Sp}\,\mathsf{per}\,k[{\it\varepsilon}]=\{[{\it\chi}_{X_{0,r}}]\mid r\in \mathbb{N}\}\cup \{[{\it\chi}_{k}]\}$
.
$\mathsf{Sp}\,\mathsf{per}\,k[{\it\varepsilon}]=\{[{\it\chi}_{X_{0,r}}]\mid r\in \mathbb{N}\}\cup \{[{\it\chi}_{k}]\}$
.
Proof. Set
![]() $\mathsf{C}=\mathsf{per}\,k[{\it\varepsilon}]$
. The Krull–Gabriel filtration of
$\mathsf{C}=\mathsf{per}\,k[{\it\varepsilon}]$
. The Krull–Gabriel filtration of
![]() $\mathsf{Ab}\,\mathsf{C}$
yields a filtration of
$\mathsf{Ab}\,\mathsf{C}$
yields a filtration of
![]() $\mathsf{Zsp}\,\mathsf{C}$
by Proposition C.2. Thus, the points of
$\mathsf{Zsp}\,\mathsf{C}$
by Proposition C.2. Thus, the points of
![]() $\mathsf{Zsp}\,\mathsf{C}$
correspond to the simple objects in
$\mathsf{Zsp}\,\mathsf{C}$
correspond to the simple objects in
![]() $\mathsf{Ab}\,\mathsf{C}$
and
$\mathsf{Ab}\,\mathsf{C}$
and
![]() $(\mathsf{Ab}\,\mathsf{C})/(\mathsf{Ab}\,\mathsf{C})_{0}$
. These simple objects are described in the proof of Proposition 4.9. The simples in
$(\mathsf{Ab}\,\mathsf{C})/(\mathsf{Ab}\,\mathsf{C})_{0}$
. These simple objects are described in the proof of Proposition 4.9. The simples in
![]() $\mathsf{Ab}\,\mathsf{C}$
correspond to the indecomposable objects in
$\mathsf{Ab}\,\mathsf{C}$
correspond to the indecomposable objects in
![]() $\mathsf{C}$
, and yield isolated points (see also Proposition 3.3 and its proof). The simples in
$\mathsf{C}$
, and yield isolated points (see also Proposition 3.3 and its proof). The simples in
![]() $(\mathsf{Ab}\,\mathsf{C})/(\mathsf{Ab}\,\mathsf{C})_{0}$
correspond to the complexes with
$(\mathsf{Ab}\,\mathsf{C})/(\mathsf{Ab}\,\mathsf{C})_{0}$
correspond to the complexes with
![]() $k$
concentrated in a single degree. Thus, all points in
$k$
concentrated in a single degree. Thus, all points in
![]() $\mathsf{Zsp}\,\mathsf{C}$
are endofinite, and this yields the description of
$\mathsf{Zsp}\,\mathsf{C}$
are endofinite, and this yields the description of
![]() $\mathsf{Sp}\,\mathsf{C}$
.◻
$\mathsf{Sp}\,\mathsf{C}$
.◻
Remark 4.11. It should be noted that
![]() $\mathsf{KGdim}\,\mathsf{Ab}\,A\neq 1$
for any Artin algebra
$\mathsf{KGdim}\,\mathsf{Ab}\,A\neq 1$
for any Artin algebra
![]() $A$
(see [Reference Herzog17, Reference Krause21]).
$A$
(see [Reference Herzog17, Reference Krause21]).
Krull–Gabriel dimension two. Let
![]() $k$
be a field, and consider the Kronecker algebra
$k$
be a field, and consider the Kronecker algebra
![]() $A=\left[\!\begin{smallmatrix}k & k^{2}\\ 0 & k\end{smallmatrix}\!\right]$
. Work of Geigle [Reference Geigle13] shows that the Krull–Gabriel dimension of
$A=\left[\!\begin{smallmatrix}k & k^{2}\\ 0 & k\end{smallmatrix}\!\right]$
. Work of Geigle [Reference Geigle13] shows that the Krull–Gabriel dimension of
![]() $\mathsf{Ab}\,A$
equals
$\mathsf{Ab}\,A$
equals
![]() $2$
. Thus,
$2$
. Thus,
![]() $\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{per}\,A=2$
by Proposition 4.3, since
$\mathsf{KGdim}\,\mathsf{Ab}\,\mathsf{per}\,A=2$
by Proposition 4.3, since
![]() $A$
is hereditary.
$A$
is hereditary.
Now, let
![]() $\mathsf{coh}\,\mathbb{P}_{k}^{1}$
be the category of coherent sheaves on the projective line over
$\mathsf{coh}\,\mathbb{P}_{k}^{1}$
be the category of coherent sheaves on the projective line over
![]() $k$
. There is a well-known derived equivalence
$k$
. There is a well-known derived equivalence
given by
![]() $T={\mathcal{O}}(0)\oplus {\mathcal{O}}(1)$
, and we use this to establish the description of the cohomological functions on
$T={\mathcal{O}}(0)\oplus {\mathcal{O}}(1)$
, and we use this to establish the description of the cohomological functions on
![]() $\mathsf{coh}\,\mathbb{P}_{k}^{1}$
stated in the introduction.
$\mathsf{coh}\,\mathbb{P}_{k}^{1}$
stated in the introduction.
Proof of Proposition 1.8.
We have
by Proposition 4.3 and [Reference Geigle13, Theorem 4.3]. This yields an explicit description of the points in
![]() $\mathsf{Zsp}\,\mathsf{D}^{b}(\mathsf{coh}\,\mathbb{P}_{k}^{1})$
, which is parallel to that given in Corollary 4.10. More explicitly, the indecomposable endofinite cohomological functors
$\mathsf{Zsp}\,\mathsf{D}^{b}(\mathsf{coh}\,\mathbb{P}_{k}^{1})$
, which is parallel to that given in Corollary 4.10. More explicitly, the indecomposable endofinite cohomological functors
![]() $\mathsf{D}^{b}(\mathsf{coh}\,\mathbb{P}_{k}^{1})^{\text{op}}\rightarrow \mathsf{Ab}$
are precisely the representable functors
$\mathsf{D}^{b}(\mathsf{coh}\,\mathbb{P}_{k}^{1})^{\text{op}}\rightarrow \mathsf{Ab}$
are precisely the representable functors
![]() $\mathsf{Hom}(-,{\rm\Sigma}^{n}X)$
, with
$\mathsf{Hom}(-,{\rm\Sigma}^{n}X)$
, with
![]() $X$
an indecomposable object in
$X$
an indecomposable object in
![]() $\mathsf{coh}\,\mathbb{P}_{k}^{1}$
or
$\mathsf{coh}\,\mathbb{P}_{k}^{1}$
or
![]() $X=k(t)$
the function field, and
$X=k(t)$
the function field, and
![]() $n\in \mathbb{Z}$
.◻
$n\in \mathbb{Z}$
.◻
Added in proof. Further material on Conjecture 4.8 can be found in the following subsequent publication: G. Bobiski and H. Krause, The Krull-Gabriel dimension of discrete derived categories, Bull. Sci. Math. 139 (2015), 269–282.
Acknowledgments
This work was inspired by lectures of David Eisenbud (Guanajuato, May 2012) and Peter Webb (Seattle, August 2012) (see also [Reference Webb33]). I wish to thank Peter Webb for various helpful comments. Moreover, I am grateful to two anonymous referees for suggesting improvements to the presentation.
Appendix A. Schanuel’s lemma for triangulated categories
Let
![]() $\mathsf{C}$
be a triangulated category. An exact triangle
$\mathsf{C}$
be a triangulated category. An exact triangle
![]() $A\rightarrow B\rightarrow C\rightarrow$
induces a presentation of a functor
$A\rightarrow B\rightarrow C\rightarrow$
induces a presentation of a functor
![]() $F:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
provided that there exists an exact sequence
$F:\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
provided that there exists an exact sequence
Two exact triangles are called homotopy equivalent Footnote 5 if they induce presentations of the same functor.
Lemma A.1. Let
![]() $A\rightarrow B\rightarrow C\rightarrow$
and
$A\rightarrow B\rightarrow C\rightarrow$
and
![]() $A^{\prime }\rightarrow B^{\prime }\rightarrow C^{\prime }\rightarrow$
be two homotopy equivalent exact triangles. Then,
$A^{\prime }\rightarrow B^{\prime }\rightarrow C^{\prime }\rightarrow$
be two homotopy equivalent exact triangles. Then,
![]() $A\oplus B^{\prime }\oplus C\cong A^{\prime }\oplus B\oplus C^{\prime }$
.
$A\oplus B^{\prime }\oplus C\cong A^{\prime }\oplus B\oplus C^{\prime }$
.
Proof. The triangles induce exact sequences
and
which represent the same class in
![]() $\mathsf{Ext}^{3}(F,{\rm\Sigma}^{-1}F)$
, since the presentations induce a morphism between the two triangles. Now, we apply the variant of Schanuel’s lemma, which is given below.◻
$\mathsf{Ext}^{3}(F,{\rm\Sigma}^{-1}F)$
, since the presentations induce a morphism between the two triangles. Now, we apply the variant of Schanuel’s lemma, which is given below.◻
Lemma A.2. Let
and
be exact sequences in some abelian category, which represent the same class in
![]() $\mathsf{Ext}^{r+1}(N,M)$
. If all
$\mathsf{Ext}^{r+1}(N,M)$
. If all
![]() $P_{i}$
and
$P_{i}$
and
![]() $Q_{i}$
are projective, then
$Q_{i}$
are projective, then
Proof. We use induction on
![]() $r$
. The case
$r$
. The case
![]() $r=0$
is clear, and we suppose that
$r=0$
is clear, and we suppose that
![]() $r>0$
. The pullback of
$r>0$
. The pullback of
![]() ${\it\eta}:P_{0}\rightarrow N$
and
${\it\eta}:P_{0}\rightarrow N$
and
![]() ${\it\theta}:Q_{0}\rightarrow N$
induces an exact sequence
${\it\theta}:Q_{0}\rightarrow N$
induces an exact sequence
with
![]() $Q_{0}\oplus \mathsf{Ker}\,{\it\eta}\cong K\cong P_{0}\oplus \mathsf{Ker}\,{\it\theta}$
, by Schanuel’s lemma. Adding complexes of the form
$Q_{0}\oplus \mathsf{Ker}\,{\it\eta}\cong K\cong P_{0}\oplus \mathsf{Ker}\,{\it\theta}$
, by Schanuel’s lemma. Adding complexes of the form
![]() $Q_{0}\xrightarrow[]{\operatorname{id}}Q_{0}$
and
$Q_{0}\xrightarrow[]{\operatorname{id}}Q_{0}$
and
![]() $P_{0}\xrightarrow[]{\operatorname{id}}P_{0}$
yields two exact sequences
$P_{0}\xrightarrow[]{\operatorname{id}}P_{0}$
yields two exact sequences
and
which represent the same class in
![]() $\mathsf{Ext}^{r}(K,M)$
, since multiplication with the class corresponding to
$\mathsf{Ext}^{r}(K,M)$
, since multiplication with the class corresponding to
![]() ${\it\varepsilon}$
induces an isomorphism
${\it\varepsilon}$
induces an isomorphism
![]() $\mathsf{Ext}^{r}(K,M)\xrightarrow[]{{\sim}}\mathsf{Ext}^{r+1}(N,M)$
. Now, the assertion follows from the induction hypothesis.◻
$\mathsf{Ext}^{r}(K,M)\xrightarrow[]{{\sim}}\mathsf{Ext}^{r+1}(N,M)$
. Now, the assertion follows from the induction hypothesis.◻
Appendix B. Additive functions
Let
![]() $\mathsf{A}$
be an abelian category. A function
$\mathsf{A}$
be an abelian category. A function
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
is called additive if
${\it\chi}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
is called additive if
![]() ${\it\chi}(X)={\it\chi}(X^{\prime })+{\it\chi}(X^{\prime \prime })$
for each exact sequence
${\it\chi}(X)={\it\chi}(X^{\prime })+{\it\chi}(X^{\prime \prime })$
for each exact sequence
![]() $0\rightarrow X^{\prime }\rightarrow X\rightarrow X^{\prime \prime }\rightarrow 0$
.
$0\rightarrow X^{\prime }\rightarrow X\rightarrow X^{\prime \prime }\rightarrow 0$
.
We give a quick proof of the following result using the localization theory for abelian categories [Reference Gabriel11].
Proposition B.1. (Crawley-Boevey [Reference Crawley-Boevey7])
Every additive function
![]() $\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
can be written uniquely as a locally finite sum of irreducible additive functions.
$\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
can be written uniquely as a locally finite sum of irreducible additive functions.
Proof. Fix an additive function
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
. The objects
${\it\chi}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
. The objects
![]() $X$
satisfying
$X$
satisfying
![]() ${\it\chi}(X)=0$
form a Serre subcategory of
${\it\chi}(X)=0$
form a Serre subcategory of
![]() $\mathsf{A}$
, which we denote by
$\mathsf{A}$
, which we denote by
![]() $\mathsf{S}_{{\it\chi}}$
. The quotient category
$\mathsf{S}_{{\it\chi}}$
. The quotient category
![]() $\mathsf{A}/\mathsf{S}_{{\it\chi}}$
is an abelian length category since the length of each object
$\mathsf{A}/\mathsf{S}_{{\it\chi}}$
is an abelian length category since the length of each object
![]() $X$
is bounded by
$X$
is bounded by
![]() ${\it\chi}(X)$
. Let
${\it\chi}(X)$
. Let
![]() $\mathsf{Sp}\,{\it\chi}$
(the spectrum of
$\mathsf{Sp}\,{\it\chi}$
(the spectrum of
![]() ${\it\chi}$
) denote a representative set of simple objects in
${\it\chi}$
) denote a representative set of simple objects in
![]() $\mathsf{A}/\mathsf{S}_{{\it\chi}}$
. For each
$\mathsf{A}/\mathsf{S}_{{\it\chi}}$
. For each
![]() $S$
in
$S$
in
![]() $\mathsf{Sp}\,{\it\chi}$
, let
$\mathsf{Sp}\,{\it\chi}$
, let
![]() $\mathsf{S}_{S}$
denote the Serre subcategory of
$\mathsf{S}_{S}$
denote the Serre subcategory of
![]() $\mathsf{A}$
formed by all objects
$\mathsf{A}$
formed by all objects
![]() $X$
such that a composition series of
$X$
such that a composition series of
![]() $X$
in
$X$
in
![]() $\mathsf{A}/\mathsf{S}_{{\it\chi}}$
has no factor isomorphic to
$\mathsf{A}/\mathsf{S}_{{\it\chi}}$
has no factor isomorphic to
![]() $S$
. Define
$S$
. Define
![]() ${\it\chi}_{S}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
by sending
${\it\chi}_{S}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
by sending
![]() $X$
to the length of
$X$
to the length of
![]() $X$
in
$X$
in
![]() $\mathsf{A}/\mathsf{S}_{S}$
. From the construction, it follows that
$\mathsf{A}/\mathsf{S}_{S}$
. From the construction, it follows that
We claim that each
![]() ${\it\chi}_{S}$
is irreducible, and that the above expression is unique. To see this, we write
${\it\chi}_{S}$
is irreducible, and that the above expression is unique. To see this, we write
![]() ${\it\chi}={\it\chi}^{\prime }+{\it\chi}^{\prime \prime }$
as a sum of two additive functions. This implies that
${\it\chi}={\it\chi}^{\prime }+{\it\chi}^{\prime \prime }$
as a sum of two additive functions. This implies that
![]() $\mathsf{S}_{{\it\chi}}\subseteq \mathsf{S}_{{\it\chi}^{\prime }}$
, and if
$\mathsf{S}_{{\it\chi}}\subseteq \mathsf{S}_{{\it\chi}^{\prime }}$
, and if
![]() ${\it\chi}^{\prime }\neq 0$
, then for some
${\it\chi}^{\prime }\neq 0$
, then for some
![]() $S\in \mathsf{Sp}\,{\it\chi}$
the object
$S\in \mathsf{Sp}\,{\it\chi}$
the object
![]() $S$
is non-zero in
$S$
is non-zero in
![]() $\mathsf{A}/\mathsf{S}_{{\it\chi}^{\prime }}$
. In that case,
$\mathsf{A}/\mathsf{S}_{{\it\chi}^{\prime }}$
. In that case,
![]() ${\it\chi}_{S}$
arises as a summand of
${\it\chi}_{S}$
arises as a summand of
![]() ${\it\chi}^{\prime }$
with multiplicity
${\it\chi}^{\prime }$
with multiplicity
![]() ${\it\chi}^{\prime }(S)$
.◻
${\it\chi}^{\prime }(S)$
.◻
Now, suppose that
![]() $\mathsf{A}$
is essentially small. Thus, the isomorphism classes of objects in
$\mathsf{A}$
is essentially small. Thus, the isomorphism classes of objects in
![]() $\mathsf{A}$
form a set. An exact functor
$\mathsf{A}$
form a set. An exact functor
![]() $F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
is called endofinite if
$F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
is called endofinite if
![]() $F(X)$
has finite length as
$F(X)$
has finite length as
![]() $\mathsf{End}(F)$
-module for each object
$\mathsf{End}(F)$
-module for each object
![]() $X$
. An endofinite exact functor
$X$
. An endofinite exact functor
![]() $F$
induces an additive function
$F$
induces an additive function
Proposition B.2. The assignment
![]() $F\mapsto {\it\chi}_{F}$
induces a bijection between the isomorphism classes of indecomposable endofinite exact functors
$F\mapsto {\it\chi}_{F}$
induces a bijection between the isomorphism classes of indecomposable endofinite exact functors
![]() $\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
and the irreducible additive functions
$\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
and the irreducible additive functions
![]() $\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
.
$\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
.
Proof. We construct the inverse map. Let
![]() ${\it\chi}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
be an irreducible additive function. Following the proof of Proposition B.1, we consider the Serre subcategory
${\it\chi}:\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
be an irreducible additive function. Following the proof of Proposition B.1, we consider the Serre subcategory
![]() $\mathsf{S}_{{\it\chi}}$
of
$\mathsf{S}_{{\it\chi}}$
of
![]() $\mathsf{A}$
consisting of the objects
$\mathsf{A}$
consisting of the objects
![]() $X$
satisfying
$X$
satisfying
![]() ${\it\chi}(X)=0$
. The quotient category
${\it\chi}(X)=0$
. The quotient category
![]() $\mathsf{B}=\mathsf{A}/\mathsf{S}_{{\it\chi}}$
is an abelian length category, and
$\mathsf{B}=\mathsf{A}/\mathsf{S}_{{\it\chi}}$
is an abelian length category, and
![]() ${\it\chi}(X)$
equals the length of
${\it\chi}(X)$
equals the length of
![]() $X$
in
$X$
in
![]() $\mathsf{B}$
for each object
$\mathsf{B}$
for each object
![]() $X$
, since
$X$
, since
![]() ${\it\chi}$
is irreducible. Now, consider the abelian category
${\it\chi}$
is irreducible. Now, consider the abelian category
![]() $\mathsf{Lex}(\mathsf{B}^{\text{op}},\mathsf{Ab})$
of left exact functors
$\mathsf{Lex}(\mathsf{B}^{\text{op}},\mathsf{Ab})$
of left exact functors
![]() $\mathsf{B}^{\text{op}}\rightarrow \mathsf{Ab}$
(see [Reference Gabriel11] for details). The Yoneda functor
$\mathsf{B}^{\text{op}}\rightarrow \mathsf{Ab}$
(see [Reference Gabriel11] for details). The Yoneda functor
identifies
![]() $\mathsf{B}$
with the full subcategory of finite length objects. There is a unique simple object in
$\mathsf{B}$
with the full subcategory of finite length objects. There is a unique simple object in
![]() $\mathsf{Lex}(\mathsf{B}^{\text{op}},\mathsf{Ab})$
since
$\mathsf{Lex}(\mathsf{B}^{\text{op}},\mathsf{Ab})$
since
![]() ${\it\chi}$
is irreducible, and we denote by
${\it\chi}$
is irreducible, and we denote by
![]() $F$
its injective envelope. It follows that
$F$
its injective envelope. It follows that
![]() $F$
is indecomposable, and the injectivity implies that
$F$
is indecomposable, and the injectivity implies that
![]() $F$
is exact. For each
$F$
is exact. For each
![]() $X$
in
$X$
in
![]() $\mathsf{B}$
we have
$\mathsf{B}$
we have
since each finitely generated
![]() $\mathsf{End}(F)$
-submodule of
$\mathsf{End}(F)$
-submodule of
![]() $\mathsf{Hom}(H_{X},F)$
is of the form
$\mathsf{Hom}(H_{X},F)$
is of the form
![]() $\mathsf{Hom}(H_{X}/H_{X^{\prime }},F)$
for some subobject
$\mathsf{Hom}(H_{X}/H_{X^{\prime }},F)$
for some subobject
![]() $X^{\prime }\subseteq X$
. Let
$X^{\prime }\subseteq X$
. Let
![]() $F^{\prime }:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
be the composite of
$F^{\prime }:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
be the composite of
![]() $F$
with the quotient functor
$F$
with the quotient functor
![]() $\mathsf{A}\rightarrow \mathsf{B}$
, and observe that
$\mathsf{A}\rightarrow \mathsf{B}$
, and observe that
![]() $\mathsf{End}(F^{\prime })\cong \mathsf{End}(F)$
. Then
$\mathsf{End}(F^{\prime })\cong \mathsf{End}(F)$
. Then
![]() $F^{\prime }$
has the desired properties: it is indecomposable endofinite exact, and
$F^{\prime }$
has the desired properties: it is indecomposable endofinite exact, and
![]() ${\it\chi}_{F^{\prime }}={\it\chi}$
.
${\it\chi}_{F^{\prime }}={\it\chi}$
.
It remains to show for an indecomposable endofinite exact functor
![]() $F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
that the function
$F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
that the function
![]() ${\it\chi}_{F}$
is irreducible. Set
${\it\chi}_{F}$
is irreducible. Set
![]() $\mathsf{B}=\mathsf{A}/\mathsf{S}_{{\it\chi}_{F}}$
, and view
$\mathsf{B}=\mathsf{A}/\mathsf{S}_{{\it\chi}_{F}}$
, and view
![]() $F$
as an exact functor
$F$
as an exact functor
![]() $\mathsf{B}^{\text{op}}\rightarrow \mathsf{Ab}$
. It should be noted that
$\mathsf{B}^{\text{op}}\rightarrow \mathsf{Ab}$
. It should be noted that
![]() $\mathsf{Hom}(H_{S},F)=F(S)\neq 0$
for each simple object
$\mathsf{Hom}(H_{S},F)=F(S)\neq 0$
for each simple object
![]() $S$
in
$S$
in
![]() $\mathsf{B}$
. The indecomposability of
$\mathsf{B}$
. The indecomposability of
![]() $F$
implies that all simple objects in
$F$
implies that all simple objects in
![]() $\mathsf{B}$
are isomorphic, and the equation (B.1) then implies that
$\mathsf{B}$
are isomorphic, and the equation (B.1) then implies that
![]() ${\it\chi}$
is irreducible, since for each simple object
${\it\chi}$
is irreducible, since for each simple object
![]() $S$
$S$
Remark B.3. Let
![]() $F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
be an indecomposable endofinite exact functor, and let
$F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
be an indecomposable endofinite exact functor, and let
![]() $S$
be the corresponding simple object in
$S$
be the corresponding simple object in
![]() $\mathsf{A}/\mathsf{S}_{{\it\chi}_{F}}$
. Then, the endomorphism ring
$\mathsf{A}/\mathsf{S}_{{\it\chi}_{F}}$
. Then, the endomorphism ring
![]() $\mathsf{End}(F)$
is local, and
$\mathsf{End}(F)$
is local, and
since
![]() $F$
identifies with an injective envelope of
$F$
identifies with an injective envelope of
![]() $S$
. Here,
$S$
. Here,
![]() $\mathsf{rad}\,A$
denotes the Jacobson radical of a ring
$\mathsf{rad}\,A$
denotes the Jacobson radical of a ring
![]() $A$
.
$A$
.
Remark B.4. Let
![]() $F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
be an exact functor, and let
$F:\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
be an exact functor, and let
![]() $\mathsf{B}=\mathsf{A}/\mathsf{S}_{F}$
, where
$\mathsf{B}=\mathsf{A}/\mathsf{S}_{F}$
, where
![]() $\mathsf{S}_{F}$
denotes the Serre subcategory of objects
$\mathsf{S}_{F}$
denotes the Serre subcategory of objects
![]() $X$
satisfying
$X$
satisfying
![]() $F(X)=0$
. For each object
$F(X)=0$
. For each object
![]() $X$
in
$X$
in
![]() $\mathsf{A}$
, we have
$\mathsf{A}$
, we have
and this can be used to compute
![]() $\sum _{i}{\it\chi}_{F_{i}}$
for any decomposition
$\sum _{i}{\it\chi}_{F_{i}}$
for any decomposition
![]() $F=\bigoplus _{i}F_{i}$
into exact functors.
$F=\bigoplus _{i}F_{i}$
into exact functors.
Let
![]() $\mathsf{Sp}\,\mathsf{A}$
denote the set of irreducible additive functions
$\mathsf{Sp}\,\mathsf{A}$
denote the set of irreducible additive functions
![]() $\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
. Following [Reference Krause20, Section 4], we define on
$\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
. Following [Reference Krause20, Section 4], we define on
![]() $\mathsf{Sp}\,\mathsf{A}$
the Ziegler topology. The basic open sets are of the form
$\mathsf{Sp}\,\mathsf{A}$
the Ziegler topology. The basic open sets are of the form
Proposition B.5. The set
![]() $\mathsf{Sp}\,\mathsf{A}$
of irreducible additive functions
$\mathsf{Sp}\,\mathsf{A}$
of irreducible additive functions
![]() $\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
forms a topological space which satisfies the
$\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
forms a topological space which satisfies the
![]() $T_{1}$
-axiom; that is,
$T_{1}$
-axiom; that is,
![]() $\{{\it\chi}\}$
is closed for each
$\{{\it\chi}\}$
is closed for each
![]() ${\it\chi}\in \mathsf{Sp}\,\mathsf{A}$
.
${\it\chi}\in \mathsf{Sp}\,\mathsf{A}$
.
Proof. We identify each irreducible additive function
![]() $\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
with an indecomposable injective object in
$\mathsf{Ob}\,\mathsf{A}\rightarrow \mathbb{N}$
with an indecomposable injective object in
![]() $\mathsf{Lex}(\mathsf{A}^{\text{op}},\mathsf{Ab}),$
as in Proposition B.2 and its proof. Thus, [Reference Krause20, Lemma 4.1] applies, and the argument given there shows that for two objects
$\mathsf{Lex}(\mathsf{A}^{\text{op}},\mathsf{Ab}),$
as in Proposition B.2 and its proof. Thus, [Reference Krause20, Lemma 4.1] applies, and the argument given there shows that for two objects
![]() $X_{1},X_{2}$
in
$X_{1},X_{2}$
in
![]() $\mathsf{A}$
, the set
$\mathsf{A}$
, the set
![]() $(X_{1})\cap (X_{2})$
can be written as a union of basic open sets.
$(X_{1})\cap (X_{2})$
can be written as a union of basic open sets.
A singleton
![]() $\{{\it\chi}\}$
is closed since
$\{{\it\chi}\}$
is closed since
![]() ${\it\chi}$
is the only irreducible function satisfying
${\it\chi}$
is the only irreducible function satisfying
![]() ${\it\chi}(X)=0$
for all
${\it\chi}(X)=0$
for all
![]() $X\in \mathsf{S}_{{\it\chi}}$
.◻
$X\in \mathsf{S}_{{\it\chi}}$
.◻
The space
![]() $\mathsf{Sp}\,\mathsf{A}$
of additive functions identifies via Proposition B.2 with a subspace of
$\mathsf{Sp}\,\mathsf{A}$
of additive functions identifies via Proposition B.2 with a subspace of
![]() $\mathsf{Zsp}\,\mathsf{A}$
, which is discussed in the subsequent Appendix C.
$\mathsf{Zsp}\,\mathsf{A}$
, which is discussed in the subsequent Appendix C.
Lemma B.6. Let
![]() $X$
be an object in
$X$
be an object in
![]() $\mathsf{A}$
, and let
$\mathsf{A}$
, and let
![]() $n\geqslant 0$
. Then,
$n\geqslant 0$
. Then,
is a closed subset of
![]() $\mathsf{Sp}\,\mathsf{A}$
.
$\mathsf{Sp}\,\mathsf{A}$
.
Proof. For a chain of subobjects
set
and let
![]() $\mathsf{U}=\bigcap _{{\it\phi}}\mathsf{U}_{{\it\phi}}$
, where
$\mathsf{U}=\bigcap _{{\it\phi}}\mathsf{U}_{{\it\phi}}$
, where
![]() ${\it\phi}=(X_{i})_{0\leqslant i\leqslant n+1}$
runs through all such chains. This set is closed by construction, and it follows from Remark B.4 that
${\it\phi}=(X_{i})_{0\leqslant i\leqslant n+1}$
runs through all such chains. This set is closed by construction, and it follows from Remark B.4 that
![]() $\mathsf{U}=\mathsf{U}_{X,n}$
.◻
$\mathsf{U}=\mathsf{U}_{X,n}$
.◻
Appendix C. The spectrum of an abelian category
Let
![]() $\mathsf{A}$
be an essentially small abelian category. We consider the category of exact functors
$\mathsf{A}$
be an essentially small abelian category. We consider the category of exact functors
![]() $\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
. This category inherits an exact structure from
$\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
. This category inherits an exact structure from
![]() $\mathsf{Ab}$
, and we denote by
$\mathsf{Ab}$
, and we denote by
![]() $\mathsf{Zsp}\,\mathsf{A}$
the set of isomorphism classes of indecomposable injective objects. It should be noted that
$\mathsf{Zsp}\,\mathsf{A}$
the set of isomorphism classes of indecomposable injective objects. It should be noted that
![]() $\mathsf{Zsp}\,\mathsf{A}$
equals the spectrum of the Grothendieck abelian category
$\mathsf{Zsp}\,\mathsf{A}$
equals the spectrum of the Grothendieck abelian category
![]() $\mathsf{Lex}(\mathsf{A}^{\text{op}},\mathsf{Ab})$
of left exact functors
$\mathsf{Lex}(\mathsf{A}^{\text{op}},\mathsf{Ab})$
of left exact functors
![]() $\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
in the sense of [Reference Gabriel11, Chapter IV]. Following [Reference Krause20, Section 4], we define on
$\mathsf{A}^{\text{op}}\rightarrow \mathsf{Ab}$
in the sense of [Reference Gabriel11, Chapter IV]. Following [Reference Krause20, Section 4], we define on
![]() $\mathsf{Zsp}\,\mathsf{A}$
the Ziegler topology. The basic open sets are of the form
$\mathsf{Zsp}\,\mathsf{A}$
the Ziegler topology. The basic open sets are of the form
Lemma C.1. The assignment
induces an inclusion reversing bijection between the closed subsets of
![]() $\mathsf{Zsp}\,\mathsf{A}$
and the Serre subcategories of
$\mathsf{Zsp}\,\mathsf{A}$
and the Serre subcategories of
![]() $\mathsf{A}$
. In particular,
$\mathsf{A}$
. In particular,
![]() $\mathsf{Zsp}\,\mathsf{A}$
is quasi-compact if and only if
$\mathsf{Zsp}\,\mathsf{A}$
is quasi-compact if and only if
![]() $\mathsf{A}$
admits a generator; that is, an object not contained in any proper Serre subcategory of
$\mathsf{A}$
admits a generator; that is, an object not contained in any proper Serre subcategory of
![]() $\mathsf{A}$
.
$\mathsf{A}$
.
Proof. See [Reference Krause20, Theorem 4.2 and Corollary 4.5]. ◻
The construction of this space is functorial with respect to certain functors. Let
![]() $f:\mathsf{A}\rightarrow \mathsf{B}$
be an exact functor between abelian categories. Given
$f:\mathsf{A}\rightarrow \mathsf{B}$
be an exact functor between abelian categories. Given
![]() $F$
in
$F$
in
![]() $\mathsf{Zsp}\,\mathsf{B}$
, the composite
$\mathsf{Zsp}\,\mathsf{B}$
, the composite
![]() $F\circ f$
is injective, since the left adjoint of restriction along
$F\circ f$
is injective, since the left adjoint of restriction along
![]() $f$
is exact, and a right adjoint of an exact functor preserves injectivity. However,
$f$
is exact, and a right adjoint of an exact functor preserves injectivity. However,
![]() $F\circ f$
need not be indecomposable. Thus,
$F\circ f$
need not be indecomposable. Thus,
![]() $f$
induces a continuous map
$f$
induces a continuous map
![]() $\mathsf{Zsp}\,\mathsf{B}\rightarrow \mathsf{Zsp}\,\mathsf{A}$
provided that indecomposability is preserved. For instance, a quotient functor
$\mathsf{Zsp}\,\mathsf{B}\rightarrow \mathsf{Zsp}\,\mathsf{A}$
provided that indecomposability is preserved. For instance, a quotient functor
![]() $\mathsf{A}\rightarrow \mathsf{A}/\mathsf{C}$
with respect to a Serre subcategory
$\mathsf{A}\rightarrow \mathsf{A}/\mathsf{C}$
with respect to a Serre subcategory
![]() $\mathsf{C}\subseteq \mathsf{A}$
has this property; it induces a homeomorphism
$\mathsf{C}\subseteq \mathsf{A}$
has this property; it induces a homeomorphism
The Krull–Gabriel filtration. Following [Reference Gabriel11, Chapter IV] and [Reference Gruson and Jensen15, Section 6], we define a filtration of
![]() $\mathsf{A}$
recursively as follows.
$\mathsf{A}$
recursively as follows.
- –
-
 $\mathsf{A}_{-1}$
is the full subcategory containing only the zero object.
$\mathsf{A}_{-1}$
is the full subcategory containing only the zero object. - –
-
 $\mathsf{A}_{{\it\alpha}}$
is the full subcategory of objects of finite length in
$\mathsf{A}_{{\it\alpha}}$
is the full subcategory of objects of finite length in
 $\mathsf{A}/\mathsf{A}_{{\it\beta}}$
, if
$\mathsf{A}/\mathsf{A}_{{\it\beta}}$
, if
 ${\it\alpha}={\it\beta}+1$
.
${\it\alpha}={\it\beta}+1$
. - –
-
 $\mathsf{A}_{{\it\alpha}}=\bigcup _{{\it\gamma}<{\it\alpha}}\mathsf{A}_{{\it\gamma}}$
, if
$\mathsf{A}_{{\it\alpha}}=\bigcup _{{\it\gamma}<{\it\alpha}}\mathsf{A}_{{\it\gamma}}$
, if
 ${\it\alpha}$
is a limit ordinal.
${\it\alpha}$
is a limit ordinal.
If
![]() $\mathsf{A}=\bigcup _{{\it\alpha}}\mathsf{A}_{{\it\alpha}}$
, then the smallest ordinal
$\mathsf{A}=\bigcup _{{\it\alpha}}\mathsf{A}_{{\it\alpha}}$
, then the smallest ordinal
![]() ${\it\alpha}$
such that
${\it\alpha}$
such that
![]() $\mathsf{A}=\mathsf{A}_{{\it\alpha}}$
is called the Krull–Gabriel dimension, and is denoted
$\mathsf{A}=\mathsf{A}_{{\it\alpha}}$
is called the Krull–Gabriel dimension, and is denoted
![]() $\mathsf{KGdim}\,\mathsf{A}$
. In that case, we say that
$\mathsf{KGdim}\,\mathsf{A}$
. In that case, we say that
![]() $\mathsf{KGdim}\,\mathsf{A}$
exists.
$\mathsf{KGdim}\,\mathsf{A}$
exists.
For each ordinal
![]() ${\it\alpha}$
, let
${\it\alpha}$
, let
![]() $\mathsf{Zsp}_{{\it\alpha}}\,\mathsf{A}$
denote the set of functors
$\mathsf{Zsp}_{{\it\alpha}}\,\mathsf{A}$
denote the set of functors
![]() $F\in \mathsf{Zsp}\,\mathsf{A}$
such that
$F\in \mathsf{Zsp}\,\mathsf{A}$
such that
![]() $F(\mathsf{A}_{{\it\alpha}})=0$
and
$F(\mathsf{A}_{{\it\alpha}})=0$
and
![]() $F(X)\neq 0$
for some object
$F(X)\neq 0$
for some object
![]() $X$
that is simple in
$X$
that is simple in
![]() $\mathsf{A}/\mathsf{A}_{{\it\alpha}}$
. This yields a bijection between the isomorphism classes of simple objects in
$\mathsf{A}/\mathsf{A}_{{\it\alpha}}$
. This yields a bijection between the isomorphism classes of simple objects in
![]() $\mathsf{A}/\mathsf{A}_{{\it\alpha}}$
and the elements in
$\mathsf{A}/\mathsf{A}_{{\it\alpha}}$
and the elements in
![]() $\mathsf{Zsp}_{{\it\alpha}}\,\mathsf{A}$
.
$\mathsf{Zsp}_{{\it\alpha}}\,\mathsf{A}$
.
Proposition C.2. Suppose that
![]() $\mathsf{KGdim}\,\mathsf{A}={\it\alpha}$
. Then,
$\mathsf{KGdim}\,\mathsf{A}={\it\alpha}$
. Then,
![]() $\mathsf{Zsp}\,\mathsf{A}$
equals the disjoint union
$\mathsf{Zsp}\,\mathsf{A}$
equals the disjoint union
![]() $\bigcup _{{\it\beta}<{\it\alpha}}\mathsf{Zsp}_{{\it\beta}}\,\mathsf{A}$
.
$\bigcup _{{\it\beta}<{\it\alpha}}\mathsf{Zsp}_{{\it\beta}}\,\mathsf{A}$
.
Proof. See [Reference Krause22, Theorem 12.7]. ◻
Removing successively from
![]() $\mathsf{Zsp}\,\mathsf{A}$
the points in
$\mathsf{Zsp}\,\mathsf{A}$
the points in
![]() $\mathsf{Zsp}_{{\it\beta}}\,\mathsf{A}$
for
$\mathsf{Zsp}_{{\it\beta}}\,\mathsf{A}$
for
![]() ${\it\beta}=-1,0,1,\ldots$
yields the Cantor–Bendixson filtration of
${\it\beta}=-1,0,1,\ldots$
yields the Cantor–Bendixson filtration of
![]() $\mathsf{Zsp}\,\mathsf{A}$
, provided that
$\mathsf{Zsp}\,\mathsf{A}$
, provided that
![]() $\mathsf{KGdim}\,\mathsf{A}$
exists. This follows from the next lemma.
$\mathsf{KGdim}\,\mathsf{A}$
exists. This follows from the next lemma.
Lemma C.3. Let
![]() $F\in \mathsf{Zsp}\,\mathsf{A}$
. If
$F\in \mathsf{Zsp}\,\mathsf{A}$
. If
![]() $F(X)\neq 0$
for some finite length object
$F(X)\neq 0$
for some finite length object
![]() $X$
, then
$X$
, then
![]() $F$
is isolated; that is,
$F$
is isolated; that is,
![]() $\{F\}$
is open. The converse holds when
$\{F\}$
is open. The converse holds when
![]() $\mathsf{KGdim}\,\mathsf{A}$
exists.
$\mathsf{KGdim}\,\mathsf{A}$
exists.
Proof. If
![]() $F(X)\neq 0$
for some finite length object
$F(X)\neq 0$
for some finite length object
![]() $X$
, then we may assume that
$X$
, then we may assume that
![]() $X$
is simple. Thus,
$X$
is simple. Thus,
![]() $\{F\}=(X)$
, since
$\{F\}=(X)$
, since
![]() $F$
is an injective envelope of
$F$
is an injective envelope of
![]() $\mathsf{Hom}(-,X)$
in
$\mathsf{Hom}(-,X)$
in
![]() $\mathsf{Lex}(\mathsf{A}^{\text{op}},\mathsf{Ab})$
. For the converse, see [Reference Krause22, Lemma 12.11].◻
$\mathsf{Lex}(\mathsf{A}^{\text{op}},\mathsf{Ab})$
. For the converse, see [Reference Krause22, Lemma 12.11].◻
Lemma C.4. Let
![]() $(f_{i}:\mathsf{A}\rightarrow \mathsf{A}_{i})_{i\in I}$
be a family of quotient functors, and set
$(f_{i}:\mathsf{A}\rightarrow \mathsf{A}_{i})_{i\in I}$
be a family of quotient functors, and set
![]() $\mathsf{U}_{i}=\{F\in \mathsf{Zsp}\,\mathsf{A}\mid F\text{ factors through }f_{i}\}$
for each
$\mathsf{U}_{i}=\{F\in \mathsf{Zsp}\,\mathsf{A}\mid F\text{ factors through }f_{i}\}$
for each
![]() $i$
. Suppose that
$i$
. Suppose that
![]() $\mathsf{Zsp}\,\mathsf{A}=\bigcup _{i}\mathsf{U}_{i}$
, and that each
$\mathsf{Zsp}\,\mathsf{A}=\bigcup _{i}\mathsf{U}_{i}$
, and that each
![]() $\mathsf{U}_{i}$
is an open subset. If
$\mathsf{U}_{i}$
is an open subset. If
![]() $\mathsf{KGdim}\,\mathsf{A}$
exists, then
$\mathsf{KGdim}\,\mathsf{A}$
exists, then
![]() $\mathsf{KGdim}\,\mathsf{A}=\mathsf{sup}_{i}\,\mathsf{KGdim}\,\mathsf{A}_{i}$
.
$\mathsf{KGdim}\,\mathsf{A}=\mathsf{sup}_{i}\,\mathsf{KGdim}\,\mathsf{A}_{i}$
.
Proof. The assumption on each
![]() $\mathsf{U}_{i}$
to be open implies that
$\mathsf{U}_{i}$
to be open implies that
![]() $f_{i}(\mathsf{A}_{{\it\alpha}})=(\mathsf{A}_{i})_{{\it\alpha}}$
for all
$f_{i}(\mathsf{A}_{{\it\alpha}})=(\mathsf{A}_{i})_{{\it\alpha}}$
for all
![]() $i$
and each ordinal
$i$
and each ordinal
![]() ${\it\alpha}$
, by Lemma C.3. On the other hand,
${\it\alpha}$
, by Lemma C.3. On the other hand,
![]() $(\mathsf{A}_{i})_{{\it\alpha}}=\mathsf{A}_{i}$
for all
$(\mathsf{A}_{i})_{{\it\alpha}}=\mathsf{A}_{i}$
for all
![]() $i$
implies
$i$
implies
![]() $\mathsf{A}_{{\it\alpha}}=\mathsf{A}$
, since
$\mathsf{A}_{{\it\alpha}}=\mathsf{A}$
, since
![]() $\mathsf{Zsp}\,\mathsf{A}=\bigcup _{i}\mathsf{U}_{i}$
. From this the assertion follows.◻
$\mathsf{Zsp}\,\mathsf{A}=\bigcup _{i}\mathsf{U}_{i}$
. From this the assertion follows.◻
Triangulated categories. Let
![]() $G$
be a group of automorphisms acting on
$G$
be a group of automorphisms acting on
![]() $\mathsf{A}$
. Then, we denote by
$\mathsf{A}$
. Then, we denote by
![]() $\mathsf{Zsp}\,\mathsf{A}/G$
the corresponding orbit space of
$\mathsf{Zsp}\,\mathsf{A}/G$
the corresponding orbit space of
![]() $\mathsf{Zsp}\,\mathsf{A}$
. Thus, the points in
$\mathsf{Zsp}\,\mathsf{A}$
. Thus, the points in
![]() $\mathsf{Zsp}\,\mathsf{A}/G$
are the equivalence classes of the form
$\mathsf{Zsp}\,\mathsf{A}/G$
are the equivalence classes of the form
![]() $[F]=\{F\circ {\it\gamma}\mid {\it\gamma}\in G\}$
. The closed subsets correspond to Serre subcategories of
$[F]=\{F\circ {\it\gamma}\mid {\it\gamma}\in G\}$
. The closed subsets correspond to Serre subcategories of
![]() $\mathsf{A}$
that are
$\mathsf{A}$
that are
![]() $G$
-invariant.
$G$
-invariant.
Let
![]() $\mathsf{C}$
be an essentially small triangulated category with suspension
$\mathsf{C}$
be an essentially small triangulated category with suspension
![]() ${\rm\Sigma}:\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{C}$
. We identify cohomological functors
${\rm\Sigma}:\mathsf{C}\xrightarrow[]{{\sim}}\mathsf{C}$
. We identify cohomological functors
![]() $\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
with exact functors
$\mathsf{C}^{\text{op}}\rightarrow \mathsf{Ab}$
with exact functors
![]() $(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
via Lemma 2.3, and denote by
$(\mathsf{Ab}\,\mathsf{C})^{\text{op}}\rightarrow \mathsf{Ab}$
via Lemma 2.3, and denote by
![]() $\mathsf{Zsp}\,\mathsf{C}$
the orbit space
$\mathsf{Zsp}\,\mathsf{C}$
the orbit space
![]() $(\mathsf{Zsp}\,\mathsf{Ab}\,\mathsf{C})/{\rm\Sigma}$
with respect to the action of
$(\mathsf{Zsp}\,\mathsf{Ab}\,\mathsf{C})/{\rm\Sigma}$
with respect to the action of
![]() ${\rm\Sigma}$
.
${\rm\Sigma}$
.
Lemma C.5. The space
![]() $\mathsf{Zsp}\,\mathsf{C}$
is quasi-compact if and only if
$\mathsf{Zsp}\,\mathsf{C}$
is quasi-compact if and only if
![]() $\mathsf{C}$
admits a generator; that is, an object not contained in any proper thick subcategory of
$\mathsf{C}$
admits a generator; that is, an object not contained in any proper thick subcategory of
![]() $\mathsf{C}$
.
$\mathsf{C}$
.
Proof. Suppose first that
![]() $\mathsf{C}$
has a generator, say
$\mathsf{C}$
has a generator, say
![]() $X$
. Then, any
$X$
. Then, any
![]() ${\rm\Sigma}$
-invariant Serre subcategory of
${\rm\Sigma}$
-invariant Serre subcategory of
![]() $\mathsf{Ab}\,\mathsf{C}$
containing
$\mathsf{Ab}\,\mathsf{C}$
containing
![]() $\mathsf{Hom}(-,X)$
equals
$\mathsf{Hom}(-,X)$
equals
![]() $\mathsf{Ab}\,\mathsf{C}$
. Thus,
$\mathsf{Ab}\,\mathsf{C}$
. Thus,
![]() $\mathsf{Zsp}\,\mathsf{C}$
is quasi-compact by Lemma C.1. To show the converse, consider for each
$\mathsf{Zsp}\,\mathsf{C}$
is quasi-compact by Lemma C.1. To show the converse, consider for each
![]() $X\in \mathsf{C}$
the closed subset
$X\in \mathsf{C}$
the closed subset
Then,
![]() $\bigcap _{X\in \mathsf{C}}\mathsf{U}_{X}=\varnothing$
. If
$\bigcap _{X\in \mathsf{C}}\mathsf{U}_{X}=\varnothing$
. If
![]() $\mathsf{Zsp}\,\mathsf{C}$
is quasi-compact, then there are finitely many objects such that
$\mathsf{Zsp}\,\mathsf{C}$
is quasi-compact, then there are finitely many objects such that
![]() $\mathsf{U}_{X_{1}}\cap \cdots \cap \mathsf{U}_{X_{r}}=\varnothing$
. This implies
$\mathsf{U}_{X_{1}}\cap \cdots \cap \mathsf{U}_{X_{r}}=\varnothing$
. This implies
![]() $\mathsf{C}=\mathsf{Thick}(X_{1},\ldots ,X_{r})$
.◻
$\mathsf{C}=\mathsf{Thick}(X_{1},\ldots ,X_{r})$
.◻

