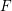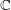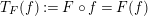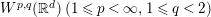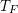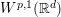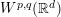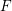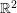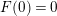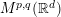1 Introduction
Let ![]() $X$ and
$X$ and ![]() $Y$ be normed spaces of complex functions on
$Y$ be normed spaces of complex functions on ![]() $\mathbb{R}^{d}$. For a given function
$\mathbb{R}^{d}$. For a given function ![]() $F:\mathbb{R}^{2}(=\mathbb{C})\rightarrow \mathbb{C}$, we associate it, with the composition operator
$F:\mathbb{R}^{2}(=\mathbb{C})\rightarrow \mathbb{C}$, we associate it, with the composition operator ![]() $T_{F}:f\mapsto F(f)$, where
$T_{F}:f\mapsto F(f)$, where ![]() $F(f)=F\circ f$ is the composition of functions
$F(f)=F\circ f$ is the composition of functions ![]() $F$ and
$F$ and ![]() $f:\mathbb{R}^{d}\rightarrow \mathbb{C}$. If
$f:\mathbb{R}^{d}\rightarrow \mathbb{C}$. If ![]() $T_{F}(X)\subset Y$, we say the composition operator
$T_{F}(X)\subset Y$, we say the composition operator ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $X$ to
$X$ to ![]() $Y$. In particular, if
$Y$. In particular, if ![]() $T_{F}(X)\subset X$, we say the composition operator
$T_{F}(X)\subset X$, we say the composition operator ![]() $T_{F}$ acts on
$T_{F}$ acts on ![]() $X$. Which functions
$X$. Which functions ![]() $F$ have the property that
$F$ have the property that ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $X$ to
$X$ to ![]() $Y$? Of course, the properties of the operator
$Y$? Of course, the properties of the operator ![]() $T_{F}$ strongly depend on
$T_{F}$ strongly depend on ![]() $X$ and
$X$ and ![]() $Y$. The aim of this paper is to take a small step toward the answer in the case of modulation and Wiener amalgam spaces (see Section 2.2 for precise definitions).
$Y$. The aim of this paper is to take a small step toward the answer in the case of modulation and Wiener amalgam spaces (see Section 2.2 for precise definitions).
In the last decade, modulation and Wiener amalgam spaces have turned out to be very fruitful within pure and applied mathematics. In fact, these spaces are nowadays present in investigations that concern problems on pseudodifferential/Fourier integral operators, Strichartz estimates, and so on (we refer the reader to recent survey [Reference Ruzhansky, Sugimoto and Wang24] and the reference therein). For instance, the unimodular Fourier multiplier operator ![]() $e^{i|D|^{\unicode[STIX]{x1D6FC}}}$ is not bounded on most of the Lebesgue spaces
$e^{i|D|^{\unicode[STIX]{x1D6FC}}}$ is not bounded on most of the Lebesgue spaces ![]() $L^{p}(\mathbb{R}^{d})\;(p\neq 2)$, in contrast it is bounded on
$L^{p}(\mathbb{R}^{d})\;(p\neq 2)$, in contrast it is bounded on ![]() $W^{p,q}(\mathbb{R}^{d})(1\leqslant p,q\leqslant \infty )$ for
$W^{p,q}(\mathbb{R}^{d})(1\leqslant p,q\leqslant \infty )$ for ![]() $\unicode[STIX]{x1D6FC}\in [0,1]$, and on
$\unicode[STIX]{x1D6FC}\in [0,1]$, and on ![]() $M^{p,q}(\mathbb{R}^{d})(1\leqslant p,q\leqslant \infty )$ for
$M^{p,q}(\mathbb{R}^{d})(1\leqslant p,q\leqslant \infty )$ for ![]() $\unicode[STIX]{x1D6FC}\in [0,2]$ (cf. [Reference Bényi, Gröchenig, Okoudjou and Rogers1, Reference Bényi and Okoudjou3, Reference Cunanan and Sugimoto9]). The cases
$\unicode[STIX]{x1D6FC}\in [0,2]$ (cf. [Reference Bényi, Gröchenig, Okoudjou and Rogers1, Reference Bényi and Okoudjou3, Reference Cunanan and Sugimoto9]). The cases ![]() $\unicode[STIX]{x1D6FC}=1,2$ are of particular interest because they occur in the time evolution of wave and Schrödinger equations, respectively.
$\unicode[STIX]{x1D6FC}=1,2$ are of particular interest because they occur in the time evolution of wave and Schrödinger equations, respectively.
Mathematicians [Reference Bényi, Gröchenig, Okoudjou and Rogers1, Reference Bényi and Okoudjou3, Reference Bhimani5, Reference Cordero and Nicola8, Reference Ruzhansky, Sugimoto and Wang24, Reference Wang, Lifeng and Boling26, Reference Wang, Zhaohui, Chengchun and Zihua27] have been using these spaces as a regularity class of initial data of the Cauchy problem for nonlinear dispersive equations. But one of the underneath issues of the nonlinear dispersive equations in the realm of modulation and Wiener amalgam spaces is to determine, which is the most general nonlinearity one can take, which is not yet completely clear. Composition operators are simple examples of nonlinear mappings. And when we try to study local and global well-posedness results for nonlinear dispersive equations (Schrödinger/wave/Klein–Gordon etc.) in modulation and Wiener amalgam spaces, it is indispensable to study nonlinear mappings on it. Taking these considerations into our account, we are motivated to study composition operators on these spaces. Specifically, we prove the following theorem.
Theorem 1.1. Let ![]() $1\leqslant p\leqslant \infty ,1\leqslant q<2$, and let
$1\leqslant p\leqslant \infty ,1\leqslant q<2$, and let
Suppose that ![]() $T_{F}$ is the composition operator associated to a complex function
$T_{F}$ is the composition operator associated to a complex function ![]() $F$ on
$F$ on ![]() $\mathbb{C}$. Then
$\mathbb{C}$. Then
(1) If
 $T_{F}$ maps
$T_{F}$ maps  $X$ to
$X$ to  $Y$, then
$Y$, then  $F$ must be real analytic on
$F$ must be real analytic on  $\mathbb{R}^{2}$. Moreover,
$\mathbb{R}^{2}$. Moreover,  $F(0)=0$ if
$F(0)=0$ if  $p<\infty$.
$p<\infty$.(2) If
 $F$ is real analytic on
$F$ is real analytic on  $\mathbb{R}^{2}$ which takes origin to itself, and
$\mathbb{R}^{2}$ which takes origin to itself, and  $p<\infty$, then
$p<\infty$, then  $T_{F}$ acts on
$T_{F}$ acts on  $X$.
$X$.
Corollary 1.2. Let ![]() $1\leqslant p<\infty ,1\leqslant q<2$, and let
$1\leqslant p<\infty ,1\leqslant q<2$, and let
Then ![]() $F$ is real analytic on
$F$ is real analytic on ![]() $\mathbb{R}^{2}$ and
$\mathbb{R}^{2}$ and ![]() $F(0)=0$ if and only if
$F(0)=0$ if and only if ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $X$ to
$X$ to ![]() $Y$. In particular,
$Y$. In particular, ![]() $F$ is real analytic on
$F$ is real analytic on ![]() $\mathbb{R}^{2}$ and
$\mathbb{R}^{2}$ and ![]() $F(0)=0$ if and only if
$F(0)=0$ if and only if ![]() $T_{F}$ acts on
$T_{F}$ acts on ![]() $X$.
$X$.
Corollary 1.3. ![]() $(1)$ There exists
$(1)$ There exists ![]() $f\in W^{p,1}(\mathbb{R}^{d})$ such that
$f\in W^{p,1}(\mathbb{R}^{d})$ such that ![]() $f|f|^{\unicode[STIX]{x1D6FC}}\notin W^{p,q}(\mathbb{R}^{d})\;(1\leqslant p\leqslant \infty ,1\leqslant q<2)$ for any
$f|f|^{\unicode[STIX]{x1D6FC}}\notin W^{p,q}(\mathbb{R}^{d})\;(1\leqslant p\leqslant \infty ,1\leqslant q<2)$ for any ![]() $\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N}$.
$\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N}$. ![]() $(2)$ There exists
$(2)$ There exists ![]() $f\in M^{p,1}(\mathbb{R}^{d})$ such that
$f\in M^{p,1}(\mathbb{R}^{d})$ such that ![]() $f|f|^{\unicode[STIX]{x1D6FC}}\notin M^{p,q}(\mathbb{R}^{d})\;(1\leqslant p\leqslant \infty ,1\leqslant q<2)$ for any
$f|f|^{\unicode[STIX]{x1D6FC}}\notin M^{p,q}(\mathbb{R}^{d})\;(1\leqslant p\leqslant \infty ,1\leqslant q<2)$ for any ![]() $\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N}$.
$\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N}$.
We note that recently Bhimani–Ratnakumar [Reference Bhimani and Ratnakumar6, Theorem 3.9] have proved if ![]() $F:\mathbb{R}^{2}\rightarrow \mathbb{C}$ is real analytic and
$F:\mathbb{R}^{2}\rightarrow \mathbb{C}$ is real analytic and ![]() $F(0)=0$, then
$F(0)=0$, then ![]() $T_{F}$ acts on
$T_{F}$ acts on![]() $X=M^{1,1}(\mathbb{R}^{d}),d\geqslant 1$. And this result is generalized by Kobayashi–Sato [Reference Kobayshi and Sato15, Theorem 1.1] for
$X=M^{1,1}(\mathbb{R}^{d}),d\geqslant 1$. And this result is generalized by Kobayashi–Sato [Reference Kobayshi and Sato15, Theorem 1.1] for ![]() $X=M^{p,1}(\mathbb{R})$ or
$X=M^{p,1}(\mathbb{R})$ or ![]() $W^{p,1}(\mathbb{R})$ for
$W^{p,1}(\mathbb{R})$ for ![]() $1<p<\infty$, although it is restricted to the case when
$1<p<\infty$, although it is restricted to the case when ![]() $d=1$. Thus we remark that our Theorem 1.1(2) settles the case when
$d=1$. Thus we remark that our Theorem 1.1(2) settles the case when ![]() $d>1$, and gives an affirmative answer to the open question proposed in [Reference Bhimani and Ratnakumar6, p. 646]. It is also worth noting the following.
$d>1$, and gives an affirmative answer to the open question proposed in [Reference Bhimani and Ratnakumar6, p. 646]. It is also worth noting the following.
(1) In Theorem 1.1(1), conditions on the range of
 $q\in [1,2)$ are sharp in the sense that if we take
$q\in [1,2)$ are sharp in the sense that if we take  $q=2$ then the same conclusion may not hold. (Since
$q=2$ then the same conclusion may not hold. (Since  $W^{2,2}(\mathbb{R}^{d})=L^{2}(\mathbb{R}^{d})$, if
$W^{2,2}(\mathbb{R}^{d})=L^{2}(\mathbb{R}^{d})$, if  $T_{F}:W^{p,1}(\mathbb{R}^{d})\rightarrow W^{p,2}(\mathbb{R}^{d})$, then
$T_{F}:W^{p,1}(\mathbb{R}^{d})\rightarrow W^{p,2}(\mathbb{R}^{d})$, then  $F$ may not be real analytic on
$F$ may not be real analytic on  $\mathbb{R}^{2}$.)
$\mathbb{R}^{2}$.)(2) Bhimani–Ratnakumar [Reference Bhimani and Ratnakumar6, Theorem 3.2] is a particular case of Theorem 1.2(1) as
 $M^{p,1}(\mathbb{R}^{d})$ is a proper subclass of
$M^{p,1}(\mathbb{R}^{d})$ is a proper subclass of  $M^{p,q}(\mathbb{R}^{d})(1<q<2)$.
$M^{p,q}(\mathbb{R}^{d})(1<q<2)$.(3) In view of Corollary 1.3, we can point out that the standard method for evolving nonlinear dispersive equations, with the nonlinearity
 $f|f|^{\unicode[STIX]{x1D6FC}}\;(\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N})$, which is of importance in applications, is ruled out.
$f|f|^{\unicode[STIX]{x1D6FC}}\;(\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N})$, which is of importance in applications, is ruled out.
The sequel contains required notations and preliminary in Section 2, proof for the necessary condition of Theorem 1.1(1) in Section 3, proof for the sufficient condition of Theorem 1.1(2) in Section 4, and concluding remarks in Section 5.
2 Notations and preliminaries
2.1 Notations
The notation ![]() $A\lesssim B$ means
$A\lesssim B$ means ![]() $A\leqslant cB$ for some constant
$A\leqslant cB$ for some constant ![]() $c>0$, whereas
$c>0$, whereas ![]() $A\asymp B$ means
$A\asymp B$ means ![]() $c^{-1}A\leqslant B\leqslant cA$ for some
$c^{-1}A\leqslant B\leqslant cA$ for some ![]() $c\geqslant 1$. The symbol
$c\geqslant 1$. The symbol ![]() $A_{1}{\hookrightarrow}A_{2}$ denotes the continuous embedding of the topological linear space
$A_{1}{\hookrightarrow}A_{2}$ denotes the continuous embedding of the topological linear space ![]() $A_{1}$ into
$A_{1}$ into ![]() $A_{2}$. The mixed
$A_{2}$. The mixed ![]() $L^{p,q}(\mathbb{R}^{d}\times \mathbb{R}^{d})$ norm is denoted by
$L^{p,q}(\mathbb{R}^{d}\times \mathbb{R}^{d})$ norm is denoted by
 $$\begin{eqnarray}\Vert f\Vert _{L^{p,q}}=\left(\int _{\mathbb{R}^{d}}\left(\int _{\mathbb{R}^{d}}|f(x,w)|^{p}\,dx\right)^{q/p}\,dw\right)^{1/q}\quad (1\leqslant p,q<\infty ),\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{L^{p,q}}=\left(\int _{\mathbb{R}^{d}}\left(\int _{\mathbb{R}^{d}}|f(x,w)|^{p}\,dx\right)^{q/p}\,dw\right)^{1/q}\quad (1\leqslant p,q<\infty ),\end{eqnarray}$$ the ![]() $L^{\infty }(\mathbb{R}^{d})$ norm is
$L^{\infty }(\mathbb{R}^{d})$ norm is ![]() $\Vert f\Vert _{L^{\infty }}=\text{ess.sup}_{x\in \mathbb{R}^{d}}|f(x)|$, the
$\Vert f\Vert _{L^{\infty }}=\text{ess.sup}_{x\in \mathbb{R}^{d}}|f(x)|$, the ![]() $\ell ^{q}(\mathbb{Z}^{d})$ norm is
$\ell ^{q}(\mathbb{Z}^{d})$ norm is ![]() $\Vert a_{n}\Vert _{\ell ^{q}}=(\sum _{n\in \mathbb{Z}^{d}}|a_{n}|^{q})^{1/q}$. We denote
$\Vert a_{n}\Vert _{\ell ^{q}}=(\sum _{n\in \mathbb{Z}^{d}}|a_{n}|^{q})^{1/q}$. We denote ![]() $d$-dimensional torus by
$d$-dimensional torus by ![]() $\mathbb{T}^{d}\equiv [\!0,2\unicode[STIX]{x1D70B}\!)^{d}$, and
$\mathbb{T}^{d}\equiv [\!0,2\unicode[STIX]{x1D70B}\!)^{d}$, and ![]() $L^{p}(\mathbb{T}^{d})$-norm is denoted by
$L^{p}(\mathbb{T}^{d})$-norm is denoted by
 $$\begin{eqnarray}\Vert f\Vert _{L^{p}(\mathbb{T}^{d})}=\left(\int _{[\!0,2\unicode[STIX]{x1D70B}\! )^{d}}|f(t)|^{p}\,dt\right)^{1/p}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{L^{p}(\mathbb{T}^{d})}=\left(\int _{[\!0,2\unicode[STIX]{x1D70B}\! )^{d}}|f(t)|^{p}\,dt\right)^{1/p}.\end{eqnarray}$$ The space of smooth functions on ![]() $\mathbb{R}^{d}$ with compact support is denoted by
$\mathbb{R}^{d}$ with compact support is denoted by ![]() $C_{c}^{\infty }(\mathbb{R}^{d})$, the Schwartz class is
$C_{c}^{\infty }(\mathbb{R}^{d})$, the Schwartz class is ![]() ${\mathcal{S}}(\mathbb{R}^{d})$ (with its usual topology), the space of tempered distributions is
${\mathcal{S}}(\mathbb{R}^{d})$ (with its usual topology), the space of tempered distributions is ![]() ${\mathcal{S}}^{\prime }(\mathbb{R}^{d})$. For
${\mathcal{S}}^{\prime }(\mathbb{R}^{d})$. For ![]() $x=(x_{1},\ldots ,x_{d}),y=(y_{1},\ldots ,y_{d})\in \mathbb{R}^{d}$, we put
$x=(x_{1},\ldots ,x_{d}),y=(y_{1},\ldots ,y_{d})\in \mathbb{R}^{d}$, we put ![]() $x\cdot y=\sum _{i=1}^{d}x_{i}y_{i}$. Let
$x\cdot y=\sum _{i=1}^{d}x_{i}y_{i}$. Let ![]() ${\mathcal{F}}:{\mathcal{S}}(\mathbb{R}^{d})\rightarrow {\mathcal{S}}(\mathbb{R}^{d})$ be the Fourier transform defined by
${\mathcal{F}}:{\mathcal{S}}(\mathbb{R}^{d})\rightarrow {\mathcal{S}}(\mathbb{R}^{d})$ be the Fourier transform defined by
Then ![]() ${\mathcal{F}}$ is a bijection and the inverse Fourier transform is given by
${\mathcal{F}}$ is a bijection and the inverse Fourier transform is given by
and this Fourier transform can be uniquely extended to ![]() ${\mathcal{F}}:{\mathcal{S}}^{\prime }(\mathbb{R}^{d})\rightarrow {\mathcal{S}}^{\prime }(\mathbb{R}^{d})$. For
${\mathcal{F}}:{\mathcal{S}}^{\prime }(\mathbb{R}^{d})\rightarrow {\mathcal{S}}^{\prime }(\mathbb{R}^{d})$. For ![]() $s\in \mathbb{R},w\in \mathbb{R}^{d}$, we put
$s\in \mathbb{R},w\in \mathbb{R}^{d}$, we put ![]() $\langle w\rangle ^{s}=(1+|w|^{2})^{s/2}$.
$\langle w\rangle ^{s}=(1+|w|^{2})^{s/2}$.
2.2 Modulation and Wiener amalgam spaces
Let ![]() $g\in {\mathcal{S}}(\mathbb{R}^{d})$ be a nonzero window function. The short-time Fourier transform (STFT) of a function (tempered distribution)
$g\in {\mathcal{S}}(\mathbb{R}^{d})$ be a nonzero window function. The short-time Fourier transform (STFT) of a function (tempered distribution) ![]() $f$ with respect to a window
$f$ with respect to a window ![]() $g$ is
$g$ is
whenever the integral exists.
In 1983, Feichtinger [Reference Feichtinger10] introduced a class of Banach spaces, which allow a measurement of the space variable and the Fourier transform variable of a function or distribution ![]() $f$ on
$f$ on ![]() $\mathbb{R}^{d}$ simultaneously using the STFT, the so-called modulation spaces.
$\mathbb{R}^{d}$ simultaneously using the STFT, the so-called modulation spaces.
Definition 2.1. (Modulation spaces)
For ![]() $1\leqslant p,q\leqslant \infty$, and for given a nonzero smooth rapidly decreasing function
$1\leqslant p,q\leqslant \infty$, and for given a nonzero smooth rapidly decreasing function ![]() $g\in {\mathcal{S}}(\mathbb{R}^{d})$, the weighted modulation space
$g\in {\mathcal{S}}(\mathbb{R}^{d})$, the weighted modulation space ![]() $M_{s}^{p,q}(\mathbb{R}^{d})$ consists of all tempered distributions
$M_{s}^{p,q}(\mathbb{R}^{d})$ consists of all tempered distributions ![]() $f\in {\mathcal{S}}^{\prime }(\mathbb{R}^{d})$ for which, the following norm
$f\in {\mathcal{S}}^{\prime }(\mathbb{R}^{d})$ for which, the following norm
 $$\begin{eqnarray}\Vert f\Vert _{M_{s}^{p,q}}=\left(\int _{\mathbb{R}^{d}}\left(\int _{\mathbb{R}^{d}}|V_{g}f(x,w)|^{p}\,dx\right)^{q/p}\langle w\rangle ^{sq}\,dw\right)^{1/q}\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{M_{s}^{p,q}}=\left(\int _{\mathbb{R}^{d}}\left(\int _{\mathbb{R}^{d}}|V_{g}f(x,w)|^{p}\,dx\right)^{q/p}\langle w\rangle ^{sq}\,dw\right)^{1/q}\end{eqnarray}$$ is finite, with the usual modification if ![]() $p$ or
$p$ or ![]() $q$ are infinite.
$q$ are infinite.
This definition is independent of the choice of the window, in the sense that different window functions yield equivalent modulation space norms (cf. [Reference Gröchenig12, Proposition 11.3.2(c), p. 233]). When ![]() $s=0$, we simply write
$s=0$, we simply write ![]() $M_{0}^{p,q}(\mathbb{R}^{d})=M^{p,q}(\mathbb{R}^{d})$.
$M_{0}^{p,q}(\mathbb{R}^{d})=M^{p,q}(\mathbb{R}^{d})$.
By reversing the order of integration we define the another family of spaces, so-called Wiener amalgam spaces.
Definition 2.2. (Wiener amalgam spaces)
For ![]() $1\leqslant p,q\leqslant \infty ,s\in \mathbb{R}$ and
$1\leqslant p,q\leqslant \infty ,s\in \mathbb{R}$ and ![]() $0\neq g\in {\mathcal{S}}(\mathbb{R}^{d})$, the weighted Wiener amalgam space
$0\neq g\in {\mathcal{S}}(\mathbb{R}^{d})$, the weighted Wiener amalgam space ![]() $W_{s}^{p,q}(\mathbb{R}^{d})$ consists of all tempered distributions
$W_{s}^{p,q}(\mathbb{R}^{d})$ consists of all tempered distributions ![]() $f\in {\mathcal{S}}^{\prime }(\mathbb{R}^{d})$ such that the norm
$f\in {\mathcal{S}}^{\prime }(\mathbb{R}^{d})$ such that the norm
 $$\begin{eqnarray}\Vert f\Vert _{W_{s}^{p,q}}=\left(\int _{\mathbb{R}^{d}}\left(\int _{\mathbb{R}^{d}}|V_{g}f(x,w)|^{q}\langle w\rangle ^{sq}\,dw\right)^{p/q}\,dx\right)^{1/p}\end{eqnarray}$$
$$\begin{eqnarray}\Vert f\Vert _{W_{s}^{p,q}}=\left(\int _{\mathbb{R}^{d}}\left(\int _{\mathbb{R}^{d}}|V_{g}f(x,w)|^{q}\langle w\rangle ^{sq}\,dw\right)^{p/q}\,dx\right)^{1/p}\end{eqnarray}$$ is finite, with usual modifications if ![]() $p$ or
$p$ or ![]() $q=\infty$.
$q=\infty$.
This definition is independent of the choice of the window ![]() $g$, in the sense that different window functions yield equivalent Wiener amalgam space norms. When
$g$, in the sense that different window functions yield equivalent Wiener amalgam space norms. When ![]() $s=0$, we simply write
$s=0$, we simply write ![]() $W_{0}^{p,q}(\mathbb{R}^{d})=W^{p,q}(\mathbb{R}^{d})$.
$W_{0}^{p,q}(\mathbb{R}^{d})=W^{p,q}(\mathbb{R}^{d})$.
We note that there is another characterization [Reference Triebel25] of Wiener amalgam and modulation spaces: let ![]() $\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{R}^{d})$ such that
and
Then we have the equivalence
and
where ![]() $\unicode[STIX]{x1D719}(D-k)f={\mathcal{F}}^{-1}(\widehat{f}\cdot T_{k}\unicode[STIX]{x1D719})$.
$\unicode[STIX]{x1D719}(D-k)f={\mathcal{F}}^{-1}(\widehat{f}\cdot T_{k}\unicode[STIX]{x1D719})$.
2.3 Properties of modulation and Wiener amalgam spaces
We gather some basic properties of Wiener amalgam and modulation spaces which will be frequently used in the sequel.
Lemma 2.3. Let ![]() $p,q,p_{i},q_{i}\in [1,\infty ]\;(i=1,2)$.
$p,q,p_{i},q_{i}\in [1,\infty ]\;(i=1,2)$.
(1)
 $W^{p,q_{1}}(\mathbb{R}^{d}){\hookrightarrow}L^{p}(\mathbb{R}^{d}){\hookrightarrow}W^{p,q_{2}}(\mathbb{R}^{d})$ and
$W^{p,q_{1}}(\mathbb{R}^{d}){\hookrightarrow}L^{p}(\mathbb{R}^{d}){\hookrightarrow}W^{p,q_{2}}(\mathbb{R}^{d})$ and  $M^{p,q_{1}}(\mathbb{R}^{d}){\hookrightarrow}L^{p}(\mathbb{R}^{d}){\hookrightarrow}M^{p,q_{2}}(\mathbb{R}^{d})$ hold for
$M^{p,q_{1}}(\mathbb{R}^{d}){\hookrightarrow}L^{p}(\mathbb{R}^{d}){\hookrightarrow}M^{p,q_{2}}(\mathbb{R}^{d})$ hold for  $q_{1}\leqslant \min \{p,p^{\prime }\}$ and
$q_{1}\leqslant \min \{p,p^{\prime }\}$ and  $q_{2}\geqslant \max \{p,p^{\prime }\}$ with
$q_{2}\geqslant \max \{p,p^{\prime }\}$ with  $1/p+1/p^{\prime }=1$.
$1/p+1/p^{\prime }=1$.(2) If
 $q_{1}\leqslant q_{2}$ and
$q_{1}\leqslant q_{2}$ and  $p_{1}\leqslant p_{2}$, then
$p_{1}\leqslant p_{2}$, then  $W^{p_{1},q_{1}}(\mathbb{R}^{d}){\hookrightarrow}W^{p_{2},q_{2}}(\mathbb{R}^{d})$ and
$W^{p_{1},q_{1}}(\mathbb{R}^{d}){\hookrightarrow}W^{p_{2},q_{2}}(\mathbb{R}^{d})$ and  $M^{p_{1},q_{1}}(\mathbb{R}^{d}){\hookrightarrow}M^{p_{2},q_{2}}(\mathbb{R}^{d})$.
$M^{p_{1},q_{1}}(\mathbb{R}^{d}){\hookrightarrow}M^{p_{2},q_{2}}(\mathbb{R}^{d})$.(3)
 $M^{p,q}(\mathbb{R}^{d}){\hookrightarrow}W^{p,q}(\mathbb{R}^{d})$ when
$M^{p,q}(\mathbb{R}^{d}){\hookrightarrow}W^{p,q}(\mathbb{R}^{d})$ when  $q\leqslant p$ and
$q\leqslant p$ and  $W^{p,q}(\mathbb{R}^{d}){\hookrightarrow}M^{p,q}(\mathbb{R}^{d})$ when
$W^{p,q}(\mathbb{R}^{d}){\hookrightarrow}M^{p,q}(\mathbb{R}^{d})$ when  $p\leqslant q$.
$p\leqslant q$.(4) The space
 $W^{p,p}(\mathbb{R}^{d})=M^{p,p}(\mathbb{R}^{d})(1\leqslant p<\infty )$ is invariant under Fourier transform.
$W^{p,p}(\mathbb{R}^{d})=M^{p,p}(\mathbb{R}^{d})(1\leqslant p<\infty )$ is invariant under Fourier transform.(5) The spaces
 $W^{p,q}(\mathbb{R}^{d})$ and
$W^{p,q}(\mathbb{R}^{d})$ and  $M^{p,q}(\mathbb{R}^{d})$ are Banach spaces.
$M^{p,q}(\mathbb{R}^{d})$ are Banach spaces.(6) The spaces
 $W^{p,q}(\mathbb{R}^{d})$ and
$W^{p,q}(\mathbb{R}^{d})$ and  $M^{p,q}(\mathbb{R}^{d})$ are invariant under complex conjugation.
$M^{p,q}(\mathbb{R}^{d})$ are invariant under complex conjugation.(7)
 ${\mathcal{S}}(\mathbb{R}^{d})$ is dense in
${\mathcal{S}}(\mathbb{R}^{d})$ is dense in  $M^{p,q}(\mathbb{R}^{d})$ and
$M^{p,q}(\mathbb{R}^{d})$ and  $W^{p,q}(\mathbb{R}^{d})$ for
$W^{p,q}(\mathbb{R}^{d})$ for  $p,q\in [1,\infty )$.
$p,q\in [1,\infty )$.(8) Let
 $0<\unicode[STIX]{x1D706}\leqslant 1$, and put
$0<\unicode[STIX]{x1D706}\leqslant 1$, and put  $f_{\unicode[STIX]{x1D706}}(x)=f(\unicode[STIX]{x1D706}x)$. There exist constants
$f_{\unicode[STIX]{x1D706}}(x)=f(\unicode[STIX]{x1D706}x)$. There exist constants  $C$ and
$C$ and  $C^{\prime }$ such that
$C^{\prime }$ such that  $\Vert f_{\unicode[STIX]{x1D706}}\Vert _{M^{\infty ,1}}\leqslant C\Vert f\Vert _{M^{\infty ,1}}$ for
$\Vert f_{\unicode[STIX]{x1D706}}\Vert _{M^{\infty ,1}}\leqslant C\Vert f\Vert _{M^{\infty ,1}}$ for  $f\in M^{\infty ,1}(\mathbb{R}^{d})$.
$f\in M^{\infty ,1}(\mathbb{R}^{d})$.
Proof. The proof of statements (1) and (2) can be found in [Reference Sugimoto, Tomita and Wang23] and [Reference Ruzhansky, Sugimoto, Toft and Tomita21], respectively. For the proof of statement (8), see [Reference Sugimoto and Tomita22]. For the proof of statements (2), (5), and (7), see [Reference Gröchenig12]. We only give the arguments for the statement (6) because it provides the reader with some insight about the fundamental identity of time–frequency analysis: in fact, easy computation gives the fundamental identity
but this immediately gives a proof of (6). ◻
Proposition 2.4. (Algebra property)
Let ![]() $p,q,p_{i},q_{i}\in [1,\infty ]\;(i=0,1,2)$ satisfy
$p,q,p_{i},q_{i}\in [1,\infty ]\;(i=0,1,2)$ satisfy ![]() $1/p_{1}+1/p_{2}=1/p_{0}$ and
$1/p_{1}+1/p_{2}=1/p_{0}$ and ![]() $1/q_{1}+1/q_{2}=1+1/q_{0}$. Then
$1/q_{1}+1/q_{2}=1+1/q_{0}$. Then
(1)
 $M^{p_{1},q_{1}}(\mathbb{R}^{d})\cdot M^{p_{2},q_{2}}(\mathbb{R}^{d}){\hookrightarrow}M^{p_{0},q_{0}}(\mathbb{R}^{d})$ with norm inequality In particular,
$M^{p_{1},q_{1}}(\mathbb{R}^{d})\cdot M^{p_{2},q_{2}}(\mathbb{R}^{d}){\hookrightarrow}M^{p_{0},q_{0}}(\mathbb{R}^{d})$ with norm inequality In particular, $$\begin{eqnarray}\Vert fg\Vert _{M^{p_{0},q_{0}}}\lesssim \Vert f\Vert _{M^{p_{1},q_{1}}}\Vert g\Vert _{M^{p_{2},q_{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert fg\Vert _{M^{p_{0},q_{0}}}\lesssim \Vert f\Vert _{M^{p_{1},q_{1}}}\Vert g\Vert _{M^{p_{2},q_{2}}}.\end{eqnarray}$$ $M^{p,1}(\mathbb{R}^{d})$ is an algebra under pointwise multiplication with norm inequality
$M^{p,1}(\mathbb{R}^{d})$ is an algebra under pointwise multiplication with norm inequality  $$\begin{eqnarray}\Vert fg\Vert _{M^{p,1}}\lesssim \Vert f\Vert _{M^{p,1}}\Vert g\Vert _{M^{p,1}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert fg\Vert _{M^{p,1}}\lesssim \Vert f\Vert _{M^{p,1}}\Vert g\Vert _{M^{p,1}}.\end{eqnarray}$$(2)
 $W^{p_{1},q_{1}}(\mathbb{R}^{d})\cdot W^{p_{2},q_{2}}(\mathbb{R}^{d}){\hookrightarrow}W^{p_{0},q_{0}}(\mathbb{R}^{d})$ with norm inequality In particular,
$W^{p_{1},q_{1}}(\mathbb{R}^{d})\cdot W^{p_{2},q_{2}}(\mathbb{R}^{d}){\hookrightarrow}W^{p_{0},q_{0}}(\mathbb{R}^{d})$ with norm inequality In particular, $$\begin{eqnarray}\Vert fg\Vert _{W^{p_{0},q_{0}}}\lesssim \Vert f\Vert _{W^{p_{1},q_{1}}}\Vert g\Vert _{W^{p_{2},q_{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert fg\Vert _{W^{p_{0},q_{0}}}\lesssim \Vert f\Vert _{W^{p_{1},q_{1}}}\Vert g\Vert _{W^{p_{2},q_{2}}}.\end{eqnarray}$$ $W^{p,1}(\mathbb{R}^{d})$ is an algebra under pointwise multiplication with norm inequality
$W^{p,1}(\mathbb{R}^{d})$ is an algebra under pointwise multiplication with norm inequality  $$\begin{eqnarray}\Vert fg\Vert _{W^{p,1}}\lesssim \Vert f\Vert _{W^{p,1}}\Vert g\Vert _{W^{p,1}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert fg\Vert _{W^{p,1}}\lesssim \Vert f\Vert _{W^{p,1}}\Vert g\Vert _{W^{p,1}}.\end{eqnarray}$$
Proof. Cf. [Reference Wang, Lifeng and Boling26], [Reference Bényi and Okoudjou3, Corollary 2.7], and [Reference Cordero and Nicola8, Lemma 2.2]. ◻
We refer to [Reference Gröchenig12] for a classical foundation of these spaces and [Reference Wang, Zhaohui, Chengchun and Zihua27] for some recent developments in nonlinear dispersive equations and connections to these spaces and the references therein.
3 Necessary condition
In this section, we prove Theorem 1.1(1): if the composition operator ![]() $T_{F}$ maps Wiener amalgam spaces
$T_{F}$ maps Wiener amalgam spaces ![]() $W^{p,1}(\mathbb{R}^{d})$ to
$W^{p,1}(\mathbb{R}^{d})$ to ![]() $W^{p,q}(\mathbb{R}^{d})$, then, necessarily,
$W^{p,q}(\mathbb{R}^{d})$, then, necessarily, ![]() $F$ is real analytic on
$F$ is real analytic on ![]() $\mathbb{R}^{2}$. And also a similar necessity condition for modulation spaces. We start with the following.
$\mathbb{R}^{2}$. And also a similar necessity condition for modulation spaces. We start with the following.
Definition 3.1. A complex valued function ![]() $F$, defined on an open set
$F$, defined on an open set ![]() $E$ in the plane
$E$ in the plane ![]() $\mathbb{R}^{2}$, is said to be real analytic on
$\mathbb{R}^{2}$, is said to be real analytic on ![]() $E$, if to every point
$E$, if to every point ![]() $(s_{0},t_{0})\in E$, there exists an expansion of the form
$(s_{0},t_{0})\in E$, there exists an expansion of the form
which converges absolutely for all ![]() $(s,t)$ in some neighborhood of
$(s,t)$ in some neighborhood of ![]() $(s_{0},t_{0})$. If
$(s_{0},t_{0})$. If ![]() $E=\mathbb{R}^{2}$ and the above series converges absolutely for all
$E=\mathbb{R}^{2}$ and the above series converges absolutely for all ![]() $(s,t)\in \mathbb{R}^{2}$, then
$(s,t)\in \mathbb{R}^{2}$, then ![]() $F$ is called real entire.
$F$ is called real entire.
We let ![]() $A^{q}(\mathbb{T}^{d})$ be the class of all complex functions
$A^{q}(\mathbb{T}^{d})$ be the class of all complex functions ![]() $f$ on the
$f$ on the ![]() $d-$torus
$d-$torus ![]() $\mathbb{T}^{d}$ whose Fourier coefficients
$\mathbb{T}^{d}$ whose Fourier coefficients
satisfy the condition
We recall, the classical theorem of Katznelson [Reference Helson, Kahane, Katznelson and Rudin13, p. 156], see also, [Reference Rudin20, Theorem 6.9.2] for ![]() $A^{1}(\mathbb{T})$ which have been proved in 1959, and later generalized by Rudin [Reference Rudin19] in 1962 for
$A^{1}(\mathbb{T})$ which have been proved in 1959, and later generalized by Rudin [Reference Rudin19] in 1962 for ![]() $A^{q}(G)$, where
$A^{q}(G)$, where ![]() $G$ is infinite compact abelian group and
$G$ is infinite compact abelian group and ![]() $1<q<2$. We just rephrased it here by combining both of them as required in our context.
$1<q<2$. We just rephrased it here by combining both of them as required in our context.
Theorem 3.2. (Katznelson–Rudin)
Suppose that ![]() $T_{F}$ is the composition operator associated to a complex function
$T_{F}$ is the composition operator associated to a complex function ![]() $F$ on
$F$ on ![]() $\mathbb{C}$, and
$\mathbb{C}$, and ![]() $1\leqslant q<2$. If
$1\leqslant q<2$. If ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $A^{1}(\mathbb{T}^{d})$ to
$A^{1}(\mathbb{T}^{d})$ to ![]() $A^{q}(\mathbb{T}^{d})$, then
$A^{q}(\mathbb{T}^{d})$, then ![]() $F$ is real analytic on
$F$ is real analytic on ![]() $\mathbb{R}^{2}$.
$\mathbb{R}^{2}$.
Now we introduce periodic Wiener amalgam and modulation spaces, and for this reason, first we recall some definitions, and introduce temporary notations. We are starting by noting that there is a one-to-one correspondence between functions on ![]() $\mathbb{R}^{d}$ that are 1-periodic in each of the coordinate directions and functions on torus
$\mathbb{R}^{d}$ that are 1-periodic in each of the coordinate directions and functions on torus ![]() $\mathbb{T}^{d}$, and we may identify
$\mathbb{T}^{d}$, and we may identify ![]() $\mathbb{T}^{d}=\mathbb{R}^{d}/\mathbb{Z}^{d}$ with
$\mathbb{T}^{d}=\mathbb{R}^{d}/\mathbb{Z}^{d}$ with ![]() $[\!0,1\!)^{d}$. Let
$[\!0,1\!)^{d}$. Let ![]() ${\mathcal{D}}(\mathbb{T}^{d})$ be the vector space
${\mathcal{D}}(\mathbb{T}^{d})$ be the vector space ![]() $C^{\infty }(\mathbb{T}^{d})$ endowed with the usual test function topology, and let
$C^{\infty }(\mathbb{T}^{d})$ endowed with the usual test function topology, and let ![]() ${\mathcal{D}}^{\prime }(\mathbb{T}^{d})$ be its dual, the space of distributions on
${\mathcal{D}}^{\prime }(\mathbb{T}^{d})$ be its dual, the space of distributions on ![]() $\mathbb{T}^{d}$. Let
$\mathbb{T}^{d}$. Let ![]() ${\mathcal{S}}(\mathbb{Z}^{d})$ denote the space of rapidly decaying functions
${\mathcal{S}}(\mathbb{Z}^{d})$ denote the space of rapidly decaying functions ![]() $\mathbb{Z}^{d}\rightarrow \mathbb{C}$. Let
$\mathbb{Z}^{d}\rightarrow \mathbb{C}$. Let ![]() ${\mathcal{F}}_{T}:{\mathcal{D}}(\mathbb{T}^{d})\rightarrow {\mathcal{S}}(\mathbb{Z}^{d})$ be the toroidal Fourier transform (hence the subscript
${\mathcal{F}}_{T}:{\mathcal{D}}(\mathbb{T}^{d})\rightarrow {\mathcal{S}}(\mathbb{Z}^{d})$ be the toroidal Fourier transform (hence the subscript ![]() $T$) defined by
$T$) defined by
Then ![]() ${\mathcal{F}}_{T}$ is a bijection and the inverse Fourier transform is given by
${\mathcal{F}}_{T}$ is a bijection and the inverse Fourier transform is given by
and this Fourier transform is extended uniquely to ![]() ${\mathcal{F}}_{T}:{\mathcal{D}}^{\prime }(\mathbb{T}^{d})\rightarrow {\mathcal{S}}^{\prime }(\mathbb{Z}^{d})$.
${\mathcal{F}}_{T}:{\mathcal{D}}^{\prime }(\mathbb{T}^{d})\rightarrow {\mathcal{S}}^{\prime }(\mathbb{Z}^{d})$.
The Wiener amalgam spaces ![]() $W^{p,q}(\mathbb{T}^{d})$ consist of all
$W^{p,q}(\mathbb{T}^{d})$ consist of all ![]() $f\in {\mathcal{D}}^{\prime }(\mathbb{T}^{d})$ such that
$f\in {\mathcal{D}}^{\prime }(\mathbb{T}^{d})$ such that
and modulation spaces ![]() $M^{p,q}(\mathbb{T}^{d})$ consist of all
$M^{p,q}(\mathbb{T}^{d})$ consist of all ![]() $f\in {\mathcal{D}}^{\prime }(\mathbb{T}^{d})$ such that
$f\in {\mathcal{D}}^{\prime }(\mathbb{T}^{d})$ such that
for some ![]() $\unicode[STIX]{x1D719}$ with compact support in the discrete topology of
$\unicode[STIX]{x1D719}$ with compact support in the discrete topology of ![]() $\mathbb{Z}^{d}$, where
$\mathbb{Z}^{d}$, where ![]() $\unicode[STIX]{x1D719}(D_{T}-k)f={\mathcal{F}}_{T}^{-1}(T_{k}\unicode[STIX]{x1D719}\cdot {\mathcal{F}}_{T}f)$.
$\unicode[STIX]{x1D719}(D_{T}-k)f={\mathcal{F}}_{T}^{-1}(T_{k}\unicode[STIX]{x1D719}\cdot {\mathcal{F}}_{T}f)$.
The next result ensures that Wiener amalgam and modulation spaces coincide with the classical Fourier algebra. Specifically, we have the following proposition.
Proposition 3.3. Let ![]() $1\leqslant p,q\leqslant \infty$. Then, we have
$1\leqslant p,q\leqslant \infty$. Then, we have
with norm inequality
Proof. For the proof we refer to [Reference Ruzhansky, Sugimoto, Toft and Tomita21, Section 5] and [Reference Okoudjou17, Lemma 1]. ◻
We now define the local-in-time versions of the Wiener amalgam and modulation spaces in the following way. Given an interval ![]() $I= [\!0,1\!)^{d}$, we let
$I= [\!0,1\!)^{d}$, we let ![]() $W^{p,q}(I)$ be the restriction of
$W^{p,q}(I)$ be the restriction of ![]() $W^{p,q}(\mathbb{R}^{d})$ onto
$W^{p,q}(\mathbb{R}^{d})$ onto ![]() $I$ via
$I$ via
and ![]() $M^{p,q}(I)$ the restriction of
$M^{p,q}(I)$ the restriction of ![]() $M^{p,q}(\mathbb{R}^{d})$ onto
$M^{p,q}(\mathbb{R}^{d})$ onto ![]() $I$ via
$I$ via
We note that Bényi–Oh has proved the “equivalence” of the periodic function spaces (![]() $M^{p,q}(\mathbb{T}^{d})$ and
$M^{p,q}(\mathbb{T}^{d})$ and ![]() $W^{p,q}(\mathbb{T}^{d})$) and their local-in-time versions (defined on a bounded interval
$W^{p,q}(\mathbb{T}^{d})$) and their local-in-time versions (defined on a bounded interval ![]() $I= [\!0,1\!)^{d}$, that is
$I= [\!0,1\!)^{d}$, that is ![]() $M^{p,q}(I)$ and
$M^{p,q}(I)$ and ![]() $W^{p,q}(I)$) in [Reference Bényi and Oh2, Appendix B] (see also [Reference Bényi and Oh2, Remark 3.3]) via establishing the equivalence of norms:
$W^{p,q}(I)$) in [Reference Bényi and Oh2, Appendix B] (see also [Reference Bényi and Oh2, Remark 3.3]) via establishing the equivalence of norms:
where ![]() $1\leqslant p$,
$1\leqslant p$, ![]() $q\leqslant \infty$.
$q\leqslant \infty$.
Proposition 3.4. Suppose that ![]() $T_{F}$ is the composition operator associated to a complex function
$T_{F}$ is the composition operator associated to a complex function ![]() $F$ on
$F$ on ![]() $\mathbb{C}$, and
$\mathbb{C}$, and ![]() $1\leqslant q<2$. If
$1\leqslant q<2$. If ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $W^{p,1}(\mathbb{R}^{d})$ to
$W^{p,1}(\mathbb{R}^{d})$ to ![]() $W^{p,q}(\mathbb{R}^{d})$, then
$W^{p,q}(\mathbb{R}^{d})$, then ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $A^{1}(\mathbb{T}^{d})$ to
$A^{1}(\mathbb{T}^{d})$ to ![]() $A^{q}(\mathbb{T}^{d})$.
$A^{q}(\mathbb{T}^{d})$.
Proof. Let ![]() $f\in A^{1}(\mathbb{T}^{d})$. Then
$f\in A^{1}(\mathbb{T}^{d})$. Then ![]() $f^{\ast }(x)=f(e^{2\unicode[STIX]{x1D70B}ix_{1}},\ldots ,e^{2\unicode[STIX]{x1D70B}ix_{d}})$ is a periodic function on
$f^{\ast }(x)=f(e^{2\unicode[STIX]{x1D70B}ix_{1}},\ldots ,e^{2\unicode[STIX]{x1D70B}ix_{d}})$ is a periodic function on ![]() $\mathbb{R}^{d}$ with absolutely convergent Fourier series
$\mathbb{R}^{d}$ with absolutely convergent Fourier series
Choose ![]() $g\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$g\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that ![]() $g\equiv 1$ on
$g\equiv 1$ on ![]() $Q_{d}= [\!0,1\!)^{d}$. Then we claim that
$Q_{d}= [\!0,1\!)^{d}$. Then we claim that ![]() $gf^{\ast }\in W^{1,1}(\mathbb{R}^{d})\subset W^{p,1}(\mathbb{R}^{d})$. Once the claim is assumed, by hypothesis, we have
$gf^{\ast }\in W^{1,1}(\mathbb{R}^{d})\subset W^{p,1}(\mathbb{R}^{d})$. Once the claim is assumed, by hypothesis, we have
Note that if ![]() $z\in \mathbb{T}^{d}$, then
$z\in \mathbb{T}^{d}$, then ![]() $z=(e^{2\unicode[STIX]{x1D70B}ix_{1}},\ldots ,e^{2\unicode[STIX]{x1D70B}ix_{d}})$ with some unique
$z=(e^{2\unicode[STIX]{x1D70B}ix_{1}},\ldots ,e^{2\unicode[STIX]{x1D70B}ix_{d}})$ with some unique ![]() $x=(x_{1},\ldots ,x_{d})\in Q_{d}$, hence
$x=(x_{1},\ldots ,x_{d})\in Q_{d}$, hence
Now if ![]() $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{T}^{d})$, then
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{T}^{d})$, then ![]() $g\unicode[STIX]{x1D719}^{\ast }$ is a compactly supported smooth function on
$g\unicode[STIX]{x1D719}^{\ast }$ is a compactly supported smooth function on ![]() $\mathbb{R}^{d}$. Also
$\mathbb{R}^{d}$. Also ![]() $\unicode[STIX]{x1D719}(z)=g(x)\unicode[STIX]{x1D719}^{\ast }(x)$ for every
$\unicode[STIX]{x1D719}(z)=g(x)\unicode[STIX]{x1D719}^{\ast }(x)$ for every ![]() $x\in Q_{d}$, as per the notation above and hence
$x\in Q_{d}$, as per the notation above and hence
for some ![]() $x\in Q_{d}$.
$x\in Q_{d}$.
By (9), Proposition 3.3, (6), (4), and Proposition 2.4(2), we obtain
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D719}F(f)\Vert _{A^{q}(\mathbb{T}^{d})} & = & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{A^{q}(\mathbb{T}^{d})}\nonumber\\ \displaystyle & \asymp & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{W^{p,q}(\mathbb{T}^{d})}\nonumber\\ \displaystyle & \asymp & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{W^{p,q}(Q_{d})}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{W^{p,q}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }\Vert _{W^{\infty ,1}}\Vert F(gf^{\ast })\Vert _{W^{p,q}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D719}F(f)\Vert _{A^{q}(\mathbb{T}^{d})} & = & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{A^{q}(\mathbb{T}^{d})}\nonumber\\ \displaystyle & \asymp & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{W^{p,q}(\mathbb{T}^{d})}\nonumber\\ \displaystyle & \asymp & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{W^{p,q}(Q_{d})}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }F(gf^{\ast })\Vert _{W^{p,q}}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \Vert g\unicode[STIX]{x1D719}^{\ast }\Vert _{W^{\infty ,1}}\Vert F(gf^{\ast })\Vert _{W^{p,q}},\nonumber\end{eqnarray}$$ which is finite for every smooth cutoff function ![]() $\unicode[STIX]{x1D719}$ supported on
$\unicode[STIX]{x1D719}$ supported on ![]() $Q_{d}$ in view of Lemma 2.3(1), and (7). Now by compactness of
$Q_{d}$ in view of Lemma 2.3(1), and (7). Now by compactness of ![]() $\mathbb{T}^{d}$, a partition of unity argument shows that
$\mathbb{T}^{d}$, a partition of unity argument shows that ![]() $F(f)\in A^{q}(\mathbb{T}^{d})$.
$F(f)\in A^{q}(\mathbb{T}^{d})$.
To complete the proof, we need to prove the claim. By Lemma 2.3(4), it is enough to show that ![]() $\widehat{gf^{\ast }}=\widehat{g}\ast \widehat{f^{\ast }}\in W^{1,1}(\mathbb{R}^{d})$. We put,
$\widehat{gf^{\ast }}=\widehat{g}\ast \widehat{f^{\ast }}\in W^{1,1}(\mathbb{R}^{d})$. We put, ![]() $\unicode[STIX]{x1D707}=\sum _{k\in \mathbb{Z}^{d}}c_{k}\unicode[STIX]{x1D6FF}_{k}$, where
$\unicode[STIX]{x1D707}=\sum _{k\in \mathbb{Z}^{d}}c_{k}\unicode[STIX]{x1D6FF}_{k}$, where ![]() $c_{k}=\widehat{f}(k)$ and
$c_{k}=\widehat{f}(k)$ and ![]() $\unicode[STIX]{x1D6FF}_{k}$ is the unit Dirac mass at
$\unicode[STIX]{x1D6FF}_{k}$ is the unit Dirac mass at ![]() $k$. We note that,
$k$. We note that, ![]() $\unicode[STIX]{x1D707}$ is a complex Borel measure on
$\unicode[STIX]{x1D707}$ is a complex Borel measure on ![]() $\mathbb{R}^{d}$, and the total variation of
$\mathbb{R}^{d}$, and the total variation of ![]() $\unicode[STIX]{x1D707},$ that is,
$\unicode[STIX]{x1D707},$ that is, ![]() $\Vert \unicode[STIX]{x1D707}\Vert =|\unicode[STIX]{x1D707}|(\mathbb{R}^{d})=\sum _{k\in \mathbb{Z}^{n}}|c_{k}|$ is finite. We compute the Fourier–Stieltjes transform of
$\Vert \unicode[STIX]{x1D707}\Vert =|\unicode[STIX]{x1D707}|(\mathbb{R}^{d})=\sum _{k\in \mathbb{Z}^{n}}|c_{k}|$ is finite. We compute the Fourier–Stieltjes transform of ![]() $\unicode[STIX]{x1D707}$:
$\unicode[STIX]{x1D707}$:
 $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(y) & = & \displaystyle \int _{\mathbb{R}^{d}}e^{-2\unicode[STIX]{x1D70B}ix\cdot y}d\unicode[STIX]{x1D707}(x)\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbb{R}^{d}}e^{-2\unicode[STIX]{x1D70B}ix\cdot y}\left(\mathop{\sum }_{k\in \mathbb{Z}^{d}}c_{k}d\unicode[STIX]{x1D6FF}_{k}(x)\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k\in \mathbb{Z}^{d}}c_{k}\int _{\mathbb{R}^{d}}e^{-2\unicode[STIX]{x1D70B}ix\cdot y}d\unicode[STIX]{x1D6FF}_{k}(x)\nonumber\\ \displaystyle & = & \displaystyle f^{\ast }(-y).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D707}}(y) & = & \displaystyle \int _{\mathbb{R}^{d}}e^{-2\unicode[STIX]{x1D70B}ix\cdot y}d\unicode[STIX]{x1D707}(x)\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbb{R}^{d}}e^{-2\unicode[STIX]{x1D70B}ix\cdot y}\left(\mathop{\sum }_{k\in \mathbb{Z}^{d}}c_{k}d\unicode[STIX]{x1D6FF}_{k}(x)\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k\in \mathbb{Z}^{d}}c_{k}\int _{\mathbb{R}^{d}}e^{-2\unicode[STIX]{x1D70B}ix\cdot y}d\unicode[STIX]{x1D6FF}_{k}(x)\nonumber\\ \displaystyle & = & \displaystyle f^{\ast }(-y).\nonumber\end{eqnarray}$$So,
It follows that
Since the translation operator ![]() $T_{m}$ is an isometry on
$T_{m}$ is an isometry on ![]() $W^{1,1}(\mathbb{R}^{d})$, it follows that the above series is absolutely convergent in
$W^{1,1}(\mathbb{R}^{d})$, it follows that the above series is absolutely convergent in ![]() $W^{1,1}(\mathbb{R}^{d})$, and hence
$W^{1,1}(\mathbb{R}^{d})$, and hence ![]() $\widehat{gf^{\ast }}\in W^{1,1}(\mathbb{R}^{d})$ as claimed.◻
$\widehat{gf^{\ast }}\in W^{1,1}(\mathbb{R}^{d})$ as claimed.◻
Proof of Theorem 1.1(1).
If ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $W^{p,1}(\mathbb{R}^{d})$ to
$W^{p,1}(\mathbb{R}^{d})$ to ![]() $W^{p,q}(\mathbb{R}^{d})$, then
$W^{p,q}(\mathbb{R}^{d})$, then ![]() $T_{F}$ maps
$T_{F}$ maps ![]() $A^{1}(\mathbb{T}^{d})$ to
$A^{1}(\mathbb{T}^{d})$ to ![]() $A^{q}(\mathbb{T}^{d})$ by Proposition 3.4. Hence the analyticity follows from Theorem 3.2.
$A^{q}(\mathbb{T}^{d})$ by Proposition 3.4. Hence the analyticity follows from Theorem 3.2.
The necessity of ![]() $F(0)=0$ is obvious if
$F(0)=0$ is obvious if ![]() $p<\infty$ and can be obtained by taking Lemma 2.3(1) into our account and testing
$p<\infty$ and can be obtained by taking Lemma 2.3(1) into our account and testing ![]() $T_{F}$ for zero function. In fact, we can compute (see [Reference Bényi, Gröchenig, Okoudjou and Rogers1, Proof of Theorem 14]) the STFT of a constant function (say 1) with respect to the windowed function
$T_{F}$ for zero function. In fact, we can compute (see [Reference Bényi, Gröchenig, Okoudjou and Rogers1, Proof of Theorem 14]) the STFT of a constant function (say 1) with respect to the windowed function ![]() $g(\unicode[STIX]{x1D709})=e^{-\unicode[STIX]{x1D70B}|\unicode[STIX]{x1D709}|^{2}}$, which can be given by
$g(\unicode[STIX]{x1D709})=e^{-\unicode[STIX]{x1D70B}|\unicode[STIX]{x1D709}|^{2}}$, which can be given by
From this it is clear that nonzero constant functions cannot be in ![]() $W^{p,q}(\mathbb{R}^{d})$ if
$W^{p,q}(\mathbb{R}^{d})$ if ![]() $p<\infty$. This completes the proof of Theorem 1.1(1) for the pair
$p<\infty$. This completes the proof of Theorem 1.1(1) for the pair ![]() $(X,Y)=(W^{p,1}(\mathbb{R}^{d}),W^{p,q}(\mathbb{R}^{d}))$. Taking Proposition 3.3 into account and exploiting the method as before, the proof of Theorem 1.1(1) can be obtained for the pair
$(X,Y)=(W^{p,1}(\mathbb{R}^{d}),W^{p,q}(\mathbb{R}^{d}))$. Taking Proposition 3.3 into account and exploiting the method as before, the proof of Theorem 1.1(1) can be obtained for the pair ![]() $(X,Y)=(M^{p,1}(\mathbb{R}^{d}),M^{p,q}(\mathbb{R}^{d}))$.◻
$(X,Y)=(M^{p,1}(\mathbb{R}^{d}),M^{p,q}(\mathbb{R}^{d}))$.◻
Proof of Corollary 1.3.
The nonlinear mapping ![]() $F:\mathbb{C}\rightarrow \mathbb{C}:z\mapsto z|z|^{\unicode[STIX]{x1D6FC}}$ is not real analytic on
$F:\mathbb{C}\rightarrow \mathbb{C}:z\mapsto z|z|^{\unicode[STIX]{x1D6FC}}$ is not real analytic on ![]() $\mathbb{R}^{2}$ for
$\mathbb{R}^{2}$ for ![]() $\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N}$.◻
$\unicode[STIX]{x1D6FC}\in (0,\infty )\setminus 2\mathbb{N}$.◻
4 Sufficient conditions
We recall that in 1932 Wiener proved that if ![]() $F(z)=1/z$, then
$F(z)=1/z$, then ![]() $T_{F}$ acts on
$T_{F}$ acts on ![]() $A^{1}(\mathbb{T})\setminus \{0\}$, and in 1935 Lévy generalizes this result: if
$A^{1}(\mathbb{T})\setminus \{0\}$, and in 1935 Lévy generalizes this result: if ![]() $F$ is real analytic on
$F$ is real analytic on ![]() $\mathbb{R}^{2}$, then
$\mathbb{R}^{2}$, then ![]() $T_{F}$ acts on
$T_{F}$ acts on ![]() $A^{1}(\mathbb{T})$. This is called Wiener–Lévy [Reference Lévy16, Reference Wiener28] theorem. Now in this section, we shall prove Theorem 1.1(2), and we note that our approach to the proof is inspired by the Wiener–Lévy theorem.
$A^{1}(\mathbb{T})$. This is called Wiener–Lévy [Reference Lévy16, Reference Wiener28] theorem. Now in this section, we shall prove Theorem 1.1(2), and we note that our approach to the proof is inspired by the Wiener–Lévy theorem.
Unless explicitly mentioned, throughout this section we assume that ![]() $X=M^{p,1}(\mathbb{R}^{d})$ or
$X=M^{p,1}(\mathbb{R}^{d})$ or ![]() $W^{p,1}(\mathbb{R}^{d})$ with
$W^{p,1}(\mathbb{R}^{d})$ with ![]() $1\leqslant p<\infty$. First, we collect some technical results which should be regarded as the tool to proving Theorem 1.1(2). We start with the following.
$1\leqslant p<\infty$. First, we collect some technical results which should be regarded as the tool to proving Theorem 1.1(2). We start with the following.
Definition 4.1. Let ![]() $\unicode[STIX]{x1D719}$ be a function defined on
$\unicode[STIX]{x1D719}$ be a function defined on ![]() $\mathbb{R}^{d}$.
$\mathbb{R}^{d}$.
(1) We say that
 $\unicode[STIX]{x1D719}$ belongs to
$\unicode[STIX]{x1D719}$ belongs to  $X$ locally at point
$X$ locally at point  $\unicode[STIX]{x1D6FE}_{0}\in \mathbb{R}^{d}$ if there is a neighborhood
$\unicode[STIX]{x1D6FE}_{0}\in \mathbb{R}^{d}$ if there is a neighborhood  $V$ of
$V$ of  $\unicode[STIX]{x1D6FE}_{0}$ and a function
$\unicode[STIX]{x1D6FE}_{0}$ and a function  $h\in X$ such that
$h\in X$ such that  $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})=h(\unicode[STIX]{x1D6FE})$ for every
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})=h(\unicode[STIX]{x1D6FE})$ for every  $\unicode[STIX]{x1D6FE}\in V$.
$\unicode[STIX]{x1D6FE}\in V$.(2) We say that
 $\unicode[STIX]{x1D719}$ belongs to
$\unicode[STIX]{x1D719}$ belongs to  $X$ locally at
$X$ locally at  $\infty$ if there is a compact set
$\infty$ if there is a compact set  $K\subset \mathbb{R}^{d}$ and a function
$K\subset \mathbb{R}^{d}$ and a function  $h\in X$ such that
$h\in X$ such that  $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})=h(\unicode[STIX]{x1D6FE})$ in the complement of
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE})=h(\unicode[STIX]{x1D6FE})$ in the complement of  $K$.
$K$.
The next lemma gives the useful criterion for functions to be in ![]() $X$.
$X$.
Lemma 4.2. If ![]() $\unicode[STIX]{x1D719}$ belongs to
$\unicode[STIX]{x1D719}$ belongs to ![]() $X$ locally at every point of
$X$ locally at every point of ![]() $\mathbb{R}^{d}\cup \{\infty \}$, then
$\mathbb{R}^{d}\cup \{\infty \}$, then ![]() $\unicode[STIX]{x1D719}\in X$.
$\unicode[STIX]{x1D719}\in X$.
To prove Lemma 4.2 and for the sake of the convenience of the reader, first we recall the following two lemmas.
Lemma 4.3. (The  $C^{\infty }$ Urysohn Lemma)
$C^{\infty }$ Urysohn Lemma)
If ![]() $K\subset \mathbb{R}^{d}$ is compact and
$K\subset \mathbb{R}^{d}$ is compact and ![]() $U$ is an open set containing
$U$ is an open set containing ![]() $K$, there exists
$K$, there exists ![]() $f\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$f\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that ![]() $0\leqslant f\leqslant 1,f=1$ on
$0\leqslant f\leqslant 1,f=1$ on ![]() $K$, and
$K$, and ![]() $\text{supp}(f)\subset U$. (For the proof, see [Reference Folland11, p. 245]).
$\text{supp}(f)\subset U$. (For the proof, see [Reference Folland11, p. 245]).
Lemma 4.4. Suppose ![]() $K\subset \mathbb{R}^{d}$ is compact and let
$K\subset \mathbb{R}^{d}$ is compact and let ![]() $V_{1},\ldots ,V_{n}$ be open sets with
$V_{1},\ldots ,V_{n}$ be open sets with ![]() $K\subset \bigcup _{j=1}^{n}V_{j}$. Then there exist open sets
$K\subset \bigcup _{j=1}^{n}V_{j}$. Then there exist open sets ![]() $W_{1},W_{2},\ldots ,W_{n}$ with
$W_{1},W_{2},\ldots ,W_{n}$ with ![]() $\overline{W_{j}}\subset V_{j}$ and
$\overline{W_{j}}\subset V_{j}$ and ![]() $K\subset \bigcup _{j=1}^{n}W_{j}$.
$K\subset \bigcup _{j=1}^{n}W_{j}$.
Proof. For each ![]() $\unicode[STIX]{x1D716}>0$ let
$\unicode[STIX]{x1D716}>0$ let ![]() $V_{j}^{\unicode[STIX]{x1D716}}$ be the set of points in
$V_{j}^{\unicode[STIX]{x1D716}}$ be the set of points in ![]() $V_{j}$ whose distance from
$V_{j}$ whose distance from ![]() $\mathbb{R}^{d}\setminus V_{j}$ is greater than
$\mathbb{R}^{d}\setminus V_{j}$ is greater than ![]() $\unicode[STIX]{x1D716}$. Clearly
$\unicode[STIX]{x1D716}$. Clearly ![]() $V_{j}^{\unicode[STIX]{x1D716}}$ is open and
$V_{j}^{\unicode[STIX]{x1D716}}$ is open and ![]() $\overline{V_{j}^{\unicode[STIX]{x1D716}}}\subset V_{j}$. It follows that
$\overline{V_{j}^{\unicode[STIX]{x1D716}}}\subset V_{j}$. It follows that ![]() $K\subset \bigcup _{1}^{n}V_{j}^{\unicode[STIX]{x1D716}}$ if
$K\subset \bigcup _{1}^{n}V_{j}^{\unicode[STIX]{x1D716}}$ if ![]() $\unicode[STIX]{x1D716}$ is sufficiently small.◻
$\unicode[STIX]{x1D716}$ is sufficiently small.◻
Proof of Lemma 4.2.
Suppose first that ![]() $\unicode[STIX]{x1D719}$ has a compact support
$\unicode[STIX]{x1D719}$ has a compact support ![]() $K$. By hypothesis, it follows that, for any
$K$. By hypothesis, it follows that, for any ![]() $\unicode[STIX]{x1D6FE}\in K$, there is a neighborhood of
$\unicode[STIX]{x1D6FE}\in K$, there is a neighborhood of ![]() $\unicode[STIX]{x1D6FE}$, say
$\unicode[STIX]{x1D6FE}$, say ![]() $V_{\unicode[STIX]{x1D6FE}}$, and
$V_{\unicode[STIX]{x1D6FE}}$, and ![]() $h_{\unicode[STIX]{x1D6FE}}\in W^{p,1}(\mathbb{R}^{d})$ such that,
$h_{\unicode[STIX]{x1D6FE}}\in W^{p,1}(\mathbb{R}^{d})$ such that, ![]() $\unicode[STIX]{x1D719}(x)=h_{\unicode[STIX]{x1D6FE}}(x)$ for all
$\unicode[STIX]{x1D719}(x)=h_{\unicode[STIX]{x1D6FE}}(x)$ for all ![]() $x\in V_{\unicode[STIX]{x1D6FE}}$. Next, we observe that,
$x\in V_{\unicode[STIX]{x1D6FE}}$. Next, we observe that, ![]() $\{V_{\unicode[STIX]{x1D6FE}}:\unicode[STIX]{x1D6FE}\in K\}$ forms an open cover of
$\{V_{\unicode[STIX]{x1D6FE}}:\unicode[STIX]{x1D6FE}\in K\}$ forms an open cover of ![]() $K$, since
$K$, since ![]() $K$ is compact, there exist open sets
$K$ is compact, there exist open sets ![]() $V_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,V_{\unicode[STIX]{x1D6FE}_{n}}$ and functions
$V_{\unicode[STIX]{x1D6FE}_{1}},\ldots ,V_{\unicode[STIX]{x1D6FE}_{n}}$ and functions ![]() $h_{1},\ldots ,h_{n}\in W^{p,1}(\mathbb{R}^{d})$ such that
$h_{1},\ldots ,h_{n}\in W^{p,1}(\mathbb{R}^{d})$ such that ![]() $\unicode[STIX]{x1D719}=h_{i}$ in
$\unicode[STIX]{x1D719}=h_{i}$ in ![]() $V_{\unicode[STIX]{x1D6FE}_{i}}$ and
$V_{\unicode[STIX]{x1D6FE}_{i}}$ and ![]() $V_{\unicode[STIX]{x1D6FE}_{1}}\cup V_{\unicode[STIX]{x1D6FE}_{2}}\cup \cdots \cup V_{\unicode[STIX]{x1D6FE}_{n}}$ covers
$V_{\unicode[STIX]{x1D6FE}_{1}}\cup V_{\unicode[STIX]{x1D6FE}_{2}}\cup \cdots \cup V_{\unicode[STIX]{x1D6FE}_{n}}$ covers ![]() $K$, that is,
$K$, that is, ![]() $K\subset \bigcup _{j=1}^{n}V_{\unicode[STIX]{x1D6FE}_{j}}$. Then by Lemma 4.4, we have
$K\subset \bigcup _{j=1}^{n}V_{\unicode[STIX]{x1D6FE}_{j}}$. Then by Lemma 4.4, we have
(i) open sets
 $W_{1},\ldots ,W_{n}$ with compact closures
$W_{1},\ldots ,W_{n}$ with compact closures  $\overline{W_{j}}\subset V_{\unicode[STIX]{x1D6FE}_{j}}$ such that
$\overline{W_{j}}\subset V_{\unicode[STIX]{x1D6FE}_{j}}$ such that  $W_{1}\cup \cdots \cup W_{n}$ covers
$W_{1}\cup \cdots \cup W_{n}$ covers  $K$, that is,
$K$, that is,  $K\subset \bigcup _{j=1}^{n}W_{j};$ and by Lemma 4.3, we get
$K\subset \bigcup _{j=1}^{n}W_{j};$ and by Lemma 4.3, we get(ii) functions
 $k_{j}\in W^{p,1}(\mathbb{R}^{d})$ such that
$k_{j}\in W^{p,1}(\mathbb{R}^{d})$ such that  $k_{j}=1$ on
$k_{j}=1$ on  $\overline{W_{j}}$ and
$\overline{W_{j}}$ and  $k_{j}=0$ outside
$k_{j}=0$ outside  $V_{\unicode[STIX]{x1D6FE}_{j}}$.
$V_{\unicode[STIX]{x1D6FE}_{j}}$.
Now, by using (i) and (ii), we have, ![]() $\unicode[STIX]{x1D719}(x)k_{j}(x)=h_{j}(x)k_{j}(x)$, for all
$\unicode[STIX]{x1D719}(x)k_{j}(x)=h_{j}(x)k_{j}(x)$, for all ![]() $x\in \mathbb{R}^{d}$ and by Proposition 2.4, we get,
$x\in \mathbb{R}^{d}$ and by Proposition 2.4, we get, ![]() $h_{j}k_{j}\in W^{p,1}(\mathbb{R}^{d})$, and so
$h_{j}k_{j}\in W^{p,1}(\mathbb{R}^{d})$, and so ![]() $\unicode[STIX]{x1D719}k_{j}\in W^{p,1}(\mathbb{R}^{d})$, for
$\unicode[STIX]{x1D719}k_{j}\in W^{p,1}(\mathbb{R}^{d})$, for ![]() $1\leqslant j\leqslant n$. Therefore, if we put
$1\leqslant j\leqslant n$. Therefore, if we put
it follows that ![]() $\unicode[STIX]{x1D713}\in W^{p,1}(\mathbb{R}^{d})$.
$\unicode[STIX]{x1D713}\in W^{p,1}(\mathbb{R}^{d})$.
The multiplier of ![]() $\unicode[STIX]{x1D713}$ in (10) is 1 whenever one of
$\unicode[STIX]{x1D713}$ in (10) is 1 whenever one of ![]() $k_{i}$ is 1, and this happens at every point of
$k_{i}$ is 1, and this happens at every point of ![]() $K;$ outside
$K;$ outside ![]() $K$,
$K$, ![]() $\unicode[STIX]{x1D719}=0$; hence
$\unicode[STIX]{x1D719}=0$; hence ![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}$, and thus
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}$, and thus ![]() $\unicode[STIX]{x1D719}\in W^{p,1}(\mathbb{R}^{d})$.
$\unicode[STIX]{x1D719}\in W^{p,1}(\mathbb{R}^{d})$.
In the general case, ![]() $\unicode[STIX]{x1D719}$ belongs to
$\unicode[STIX]{x1D719}$ belongs to ![]() $W^{p,1}(\mathbb{R}^{d})$ locally at
$W^{p,1}(\mathbb{R}^{d})$ locally at ![]() $\infty$, so that there is a function
$\infty$, so that there is a function ![]() $g\in W^{p,1}(\mathbb{R}^{d})$ which coincides with
$g\in W^{p,1}(\mathbb{R}^{d})$ which coincides with ![]() $\unicode[STIX]{x1D719}$ outside some compact subset of
$\unicode[STIX]{x1D719}$ outside some compact subset of ![]() $\mathbb{R}^{d}$. Then
$\mathbb{R}^{d}$. Then ![]() $\unicode[STIX]{x1D719}-g$ has compact support and belongs to
$\unicode[STIX]{x1D719}-g$ has compact support and belongs to ![]() $W^{p,1}(\mathbb{R}^{d})$ locally at every point of
$W^{p,1}(\mathbb{R}^{d})$ locally at every point of ![]() $\mathbb{R}^{d};$ by the first case,
$\mathbb{R}^{d};$ by the first case, ![]() $\unicode[STIX]{x1D719}-g\in W^{p,1}(\mathbb{R}^{d})$, and so
$\unicode[STIX]{x1D719}-g\in W^{p,1}(\mathbb{R}^{d})$, and so ![]() $\unicode[STIX]{x1D719}\in W^{p,1}(\mathbb{R}^{d})$. This completes the proof if
$\unicode[STIX]{x1D719}\in W^{p,1}(\mathbb{R}^{d})$. This completes the proof if ![]() $X=W^{p,1}(\mathbb{R}^{d})$. The case
$X=W^{p,1}(\mathbb{R}^{d})$. The case ![]() $X=M^{p,1}(\mathbb{R}^{d})$ can be obtained similarly.◻
$X=M^{p,1}(\mathbb{R}^{d})$ can be obtained similarly.◻
We denote by ![]() $X_{\text{loc}}$ the space functions that are locally in
$X_{\text{loc}}$ the space functions that are locally in ![]() $X$ at each
$X$ at each ![]() $\unicode[STIX]{x1D6FE}_{0}\in \mathbb{R}^{d}$.
$\unicode[STIX]{x1D6FE}_{0}\in \mathbb{R}^{d}$.
Lemma 4.5. [Reference Bhimani and Ratnakumar6, p. 634]
Let ![]() $f$ be a function defined on
$f$ be a function defined on ![]() $\mathbb{R}^{d}$.
$\mathbb{R}^{d}$.
(1)
 $f\in X_{\text{loc}}$ if and only if
$f\in X_{\text{loc}}$ if and only if  $\unicode[STIX]{x1D719}f\in X$ for all
$\unicode[STIX]{x1D719}f\in X$ for all  $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$.
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$.(2)
 $f$ belongs to
$f$ belongs to  $X$ locally at
$X$ locally at  $\infty$ if and only if there exists
$\infty$ if and only if there exists  $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that  $(1-\unicode[STIX]{x1D719})f\in X$.
$(1-\unicode[STIX]{x1D719})f\in X$.
Proposition 4.6. [Reference Bhimani and Ratnakumar6, Proposition 3.14]
Let ![]() $f\in M^{1,1}(\mathbb{R}^{d})$,
$f\in M^{1,1}(\mathbb{R}^{d})$, ![]() $x_{0}\in \mathbb{R}^{d}$ and
$x_{0}\in \mathbb{R}^{d}$ and ![]() $\unicode[STIX]{x1D716}>0$. Then there exists a
$\unicode[STIX]{x1D716}>0$. Then there exists a ![]() $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that ![]() $\Vert \unicode[STIX]{x1D719}\left[f-f(x_{0})\right]\Vert _{M^{1,1}}<\unicode[STIX]{x1D716}$. The function
$\Vert \unicode[STIX]{x1D719}\left[f-f(x_{0})\right]\Vert _{M^{1,1}}<\unicode[STIX]{x1D716}$. The function ![]() $\unicode[STIX]{x1D719}$ can be chosen so that
$\unicode[STIX]{x1D719}$ can be chosen so that ![]() $\unicode[STIX]{x1D719}\equiv 1$ in some neighborhood of
$\unicode[STIX]{x1D719}\equiv 1$ in some neighborhood of ![]() $x_{0}$.
$x_{0}$.
Proposition 4.7. Let ![]() $f\in X,x_{0}\in \mathbb{R}^{d}$ and
$f\in X,x_{0}\in \mathbb{R}^{d}$ and ![]() $\unicode[STIX]{x1D716}>0$. Then there exists a
$\unicode[STIX]{x1D716}>0$. Then there exists a ![]() $\unicode[STIX]{x1D6F7}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D6F7}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that ![]() $\Vert \unicode[STIX]{x1D6F7}[f-f(x_{0})]\Vert _{X}<\unicode[STIX]{x1D716}$. The function
$\Vert \unicode[STIX]{x1D6F7}[f-f(x_{0})]\Vert _{X}<\unicode[STIX]{x1D716}$. The function ![]() $\unicode[STIX]{x1D719}$ can be chosen so that
$\unicode[STIX]{x1D719}$ can be chosen so that ![]() $\unicode[STIX]{x1D6F7}\equiv 1$ in some neighborhood of
$\unicode[STIX]{x1D6F7}\equiv 1$ in some neighborhood of ![]() $x_{0}$.
$x_{0}$.
Proof. Let ![]() $f\in X$. Choose
$f\in X$. Choose ![]() $\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that ![]() $\unicode[STIX]{x1D713}\equiv 1$ in some neighborhood of
$\unicode[STIX]{x1D713}\equiv 1$ in some neighborhood of ![]() $x_{0}$. In view of
$x_{0}$. In view of ![]() $M^{1,1}(\mathbb{R}^{d})=W^{1,1}(\mathbb{R}^{d})$ and Proposition 2.4, we have
$M^{1,1}(\mathbb{R}^{d})=W^{1,1}(\mathbb{R}^{d})$ and Proposition 2.4, we have
where ![]() $Y=M^{\infty ,1}$ if
$Y=M^{\infty ,1}$ if ![]() $X=M^{p,1}$ and
$X=M^{p,1}$ and ![]() $Y=W^{\infty ,1}$ if
$Y=W^{\infty ,1}$ if ![]() $X=W^{p,1}$. Thus
$X=W^{p,1}$. Thus ![]() $h:=\unicode[STIX]{x1D713}f\in M^{1,1}(\mathbb{R}^{d})$. We can now apply Proposition 4.6 for
$h:=\unicode[STIX]{x1D713}f\in M^{1,1}(\mathbb{R}^{d})$. We can now apply Proposition 4.6 for ![]() $h\in M^{1,1}(\mathbb{R}^{d}):$ given
$h\in M^{1,1}(\mathbb{R}^{d}):$ given ![]() $\unicode[STIX]{x1D716}^{\prime }>0$, there exists
$\unicode[STIX]{x1D716}^{\prime }>0$, there exists ![]() $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
and ![]() $\unicode[STIX]{x1D719}\equiv 1$ on the support of
$\unicode[STIX]{x1D719}\equiv 1$ on the support of ![]() $\unicode[STIX]{x1D713}$. Now define
$\unicode[STIX]{x1D713}$. Now define ![]() $\unicode[STIX]{x1D6F7}(x)=\unicode[STIX]{x1D713}(x)\unicode[STIX]{x1D719}(x)$ for all
$\unicode[STIX]{x1D6F7}(x)=\unicode[STIX]{x1D713}(x)\unicode[STIX]{x1D719}(x)$ for all ![]() $x\in \mathbb{R}^{d}$. Note that
$x\in \mathbb{R}^{d}$. Note that ![]() $\unicode[STIX]{x1D6F7}\in C_{c}^{\infty }(\mathbb{R}^{d})$ and
$\unicode[STIX]{x1D6F7}\in C_{c}^{\infty }(\mathbb{R}^{d})$ and ![]() $\unicode[STIX]{x1D6F7}\equiv 1$ on some neighborhood of
$\unicode[STIX]{x1D6F7}\equiv 1$ on some neighborhood of ![]() $x_{0}$. By definition of
$x_{0}$. By definition of ![]() $\unicode[STIX]{x1D6F7}$ and Lemma 2.3, we have
$\unicode[STIX]{x1D6F7}$ and Lemma 2.3, we have
Taking ![]() $\unicode[STIX]{x1D716}^{\prime }=\unicode[STIX]{x1D716}/C,$ we get
$\unicode[STIX]{x1D716}^{\prime }=\unicode[STIX]{x1D716}/C,$ we get ![]() $\Vert \unicode[STIX]{x1D6F7}(f-f(x_{0}))\Vert _{X}<\unicode[STIX]{x1D716}$. This completes the proof.◻
$\Vert \unicode[STIX]{x1D6F7}(f-f(x_{0}))\Vert _{X}<\unicode[STIX]{x1D716}$. This completes the proof.◻
Proposition 4.8. Let ![]() $f\in X$, and
$f\in X$, and ![]() $\unicode[STIX]{x1D716}>0$. There also exists a
$\unicode[STIX]{x1D716}>0$. There also exists a ![]() $\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that ![]() $\Vert (1-\unicode[STIX]{x1D713})f\Vert _{X}<\unicode[STIX]{x1D716}$.
$\Vert (1-\unicode[STIX]{x1D713})f\Vert _{X}<\unicode[STIX]{x1D716}$.
Proof. Let ![]() $f\in X$, and
$f\in X$, and ![]() $\unicode[STIX]{x1D716}^{\prime }>0$. By Lemma 2.3(7), there exists
$\unicode[STIX]{x1D716}^{\prime }>0$. By Lemma 2.3(7), there exists ![]() $g\in {\mathcal{S}}(\mathbb{R}^{d})$ such that
$g\in {\mathcal{S}}(\mathbb{R}^{d})$ such that
We recall the fact that for any ![]() $g\in {\mathcal{S}}(\mathbb{R}^{d})$, there exists
$g\in {\mathcal{S}}(\mathbb{R}^{d})$, there exists ![]() $\unicode[STIX]{x1D706}_{0}\in (0,1)$ such that
$\unicode[STIX]{x1D706}_{0}\in (0,1)$ such that
for any ![]() $\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$, where
$\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$, where ![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}(x)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)\in C_{c}^{\infty }(\mathbb{R}^{d})$, (see for instance the proof of [Reference Bhimani and Ratnakumar6, Proposition 3.14]). We define
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}(x)=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)\in C_{c}^{\infty }(\mathbb{R}^{d})$, (see for instance the proof of [Reference Bhimani and Ratnakumar6, Proposition 3.14]). We define ![]() $\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that
$\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$ such that ![]() $\unicode[STIX]{x1D713}(x):=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)$ where
$\unicode[STIX]{x1D713}(x):=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D706}x)$ where ![]() $\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$. By Lemma 2.3 and (12), we have
$\unicode[STIX]{x1D706}\in (0,\unicode[STIX]{x1D706}_{0})$. By Lemma 2.3 and (12), we have
 $$\begin{eqnarray}\displaystyle \Vert (1-\unicode[STIX]{x1D713})f\Vert _{X} & {\leqslant} & \displaystyle \Vert (1-\unicode[STIX]{x1D713})(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D713})g\Vert _{X}\nonumber\\ \displaystyle & = & \displaystyle \Vert f-g-\unicode[STIX]{x1D713}(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{X}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert f-g\Vert _{X}+C\Vert \unicode[STIX]{x1D713}\Vert _{Y}\Vert f-g\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{M^{1,1}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (1+C\Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{Y})\Vert f-g\Vert _{X}+\frac{\unicode[STIX]{x1D716}}{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert (1-\unicode[STIX]{x1D713})f\Vert _{X} & {\leqslant} & \displaystyle \Vert (1-\unicode[STIX]{x1D713})(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D713})g\Vert _{X}\nonumber\\ \displaystyle & = & \displaystyle \Vert f-g-\unicode[STIX]{x1D713}(f-g)\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{X}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert f-g\Vert _{X}+C\Vert \unicode[STIX]{x1D713}\Vert _{Y}\Vert f-g\Vert _{X}+\Vert (1-\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}})g\Vert _{M^{1,1}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (1+C\Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{Y})\Vert f-g\Vert _{X}+\frac{\unicode[STIX]{x1D716}}{2},\nonumber\end{eqnarray}$$ where ![]() $Y=M^{\infty ,1}$ if
$Y=M^{\infty ,1}$ if ![]() $X=M^{p,1}$ and
$X=M^{p,1}$ and ![]() $Y=W^{\infty ,1}$ if
$Y=W^{\infty ,1}$ if ![]() $X=M^{p,1}$. By Lemma 2.3(3) and 2.3(8), we have
$X=M^{p,1}$. By Lemma 2.3(3) and 2.3(8), we have ![]() $\Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{Y}\lesssim \Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{M^{\infty ,1}}\lesssim \Vert \unicode[STIX]{x1D719}\Vert _{M^{\infty ,1}}$. Using this, we have
$\Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{Y}\lesssim \Vert \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D706}}\Vert _{M^{\infty ,1}}\lesssim \Vert \unicode[STIX]{x1D719}\Vert _{M^{\infty ,1}}$. Using this, we have
Taking ![]() $\unicode[STIX]{x1D716}^{\prime }=\unicode[STIX]{x1D716}/2(1+C^{\prime }\Vert \unicode[STIX]{x1D719}\Vert _{M^{\infty ,1}})$, and using (11) and (12), we obtain that
$\unicode[STIX]{x1D716}^{\prime }=\unicode[STIX]{x1D716}/2(1+C^{\prime }\Vert \unicode[STIX]{x1D719}\Vert _{M^{\infty ,1}})$, and using (11) and (12), we obtain that ![]() $\Vert (1-\unicode[STIX]{x1D713})f\Vert _{X}<\unicode[STIX]{x1D716}$.◻
$\Vert (1-\unicode[STIX]{x1D713})f\Vert _{X}<\unicode[STIX]{x1D716}$.◻
Proof of Theorem 1.1(2).
Write ![]() $f=f_{1}+if_{2}\in X$, where
$f=f_{1}+if_{2}\in X$, where ![]() $f_{1}$ and
$f_{1}$ and ![]() $f_{2}$ are real functions, and with an abuse of notation, we write
$f_{2}$ are real functions, and with an abuse of notation, we write ![]() $F(f)=F(f_{1},f_{2})$. To show that
$F(f)=F(f_{1},f_{2})$. To show that ![]() $F(f)$ is in
$F(f)$ is in ![]() $X$, enough to show, in view of Lemma 4.2 that
$X$, enough to show, in view of Lemma 4.2 that ![]() $F(f)\in X_{\text{loc}}$ and
$F(f)\in X_{\text{loc}}$ and ![]() $F(f)$ belongs to
$F(f)$ belongs to ![]() $X$ locally at
$X$ locally at ![]() $\infty$. First we show that
$\infty$. First we show that ![]() $F(f)\in X_{\text{loc}}$. Fix
$F(f)\in X_{\text{loc}}$. Fix ![]() $x_{0}\in \mathbb{R}^{d}$ and put
$x_{0}\in \mathbb{R}^{d}$ and put ![]() $f(x_{0})=s_{0}+it_{0}$. Since
$f(x_{0})=s_{0}+it_{0}$. Since ![]() $F$ is real analytic at
$F$ is real analytic at ![]() $(s_{0},t_{0})$, there exists
$(s_{0},t_{0})$, there exists ![]() $\unicode[STIX]{x1D6FF}>0$ such that
$\unicode[STIX]{x1D6FF}>0$ such that ![]() $F$ has the power series expansion
$F$ has the power series expansion
which converges absolutely for ![]() $|s-s_{0}|\leqslant \unicode[STIX]{x1D6FF},|t-t_{0}|\leqslant \unicode[STIX]{x1D6FF}$. Then
$|s-s_{0}|\leqslant \unicode[STIX]{x1D6FF},|t-t_{0}|\leqslant \unicode[STIX]{x1D6FF}$. Then
 $$\begin{eqnarray}\displaystyle F(f_{1}(x),f_{2}(x)) & = & \displaystyle F(s_{0},t_{0})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{(m,n)\neq (0,0)}a_{mn}[f_{1}(x)-f_{1}(x_{0})]^{m}[f_{2}(x)-f_{2}(x_{0})]^{n}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(f_{1}(x),f_{2}(x)) & = & \displaystyle F(s_{0},t_{0})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{(m,n)\neq (0,0)}a_{mn}[f_{1}(x)-f_{1}(x_{0})]^{m}[f_{2}(x)-f_{2}(x_{0})]^{n}\end{eqnarray}$$whenever the series converges.
Note that both ![]() $f_{1}$ and
$f_{1}$ and ![]() $f_{2}$ are in
$f_{2}$ are in ![]() $X$, being the real and imaginary parts of
$X$, being the real and imaginary parts of ![]() $f$. Hence in view of Proposition 4.6, we can find
$f$. Hence in view of Proposition 4.6, we can find ![]() $\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$, such that
$\unicode[STIX]{x1D719}\in C_{c}^{\infty }(\mathbb{R}^{d})$, such that ![]() $\unicode[STIX]{x1D719}\equiv 1$ near
$\unicode[STIX]{x1D719}\equiv 1$ near ![]() $x_{0}$ and
$x_{0}$ and ![]() $\Vert \unicode[STIX]{x1D719}[f_{i}-f_{i}(x_{0})]\Vert _{X}<\unicode[STIX]{x1D6FF}$, for
$\Vert \unicode[STIX]{x1D719}[f_{i}-f_{i}(x_{0})]\Vert _{X}<\unicode[STIX]{x1D6FF}$, for ![]() $i=1,2$. Now consider the function
$i=1,2$. Now consider the function ![]() $G$ on
$G$ on ![]() $\mathbb{R}^{d}$ defined by
$\mathbb{R}^{d}$ defined by
 $$\begin{eqnarray}\displaystyle G(x) & = & \displaystyle \unicode[STIX]{x1D719}(x)F(s_{0},t_{0})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{(m,n)\neq (0,0)}a_{mn}(\unicode[STIX]{x1D719}(x)[f_{1}(x)-f_{1}(x_{0})])^{m}(\unicode[STIX]{x1D719}(x)[f_{2}(x)-f_{2}(x_{0})])^{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G(x) & = & \displaystyle \unicode[STIX]{x1D719}(x)F(s_{0},t_{0})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{(m,n)\neq (0,0)}a_{mn}(\unicode[STIX]{x1D719}(x)[f_{1}(x)-f_{1}(x_{0})])^{m}(\unicode[STIX]{x1D719}(x)[f_{2}(x)-f_{2}(x_{0})])^{n}.\nonumber\end{eqnarray}$$ Since ![]() $\Vert \unicode[STIX]{x1D719}[f_{i}-f_{i}(x_{0})]\Vert _{X}<\unicode[STIX]{x1D6FF}$, for
$\Vert \unicode[STIX]{x1D719}[f_{i}-f_{i}(x_{0})]\Vert _{X}<\unicode[STIX]{x1D6FF}$, for ![]() $i=1,2$ and in view of Proposition 2.4, we see that the above series is absolutely convergent in
$i=1,2$ and in view of Proposition 2.4, we see that the above series is absolutely convergent in ![]() $X$. Also since
$X$. Also since ![]() $\unicode[STIX]{x1D719}\equiv 1$ in some neighborhood of
$\unicode[STIX]{x1D719}\equiv 1$ in some neighborhood of ![]() $x_{0}$, it follows that
$x_{0}$, it follows that ![]() $G\equiv F(f)$ in some neighborhood of
$G\equiv F(f)$ in some neighborhood of ![]() $x_{0}$. Since
$x_{0}$. Since ![]() $x_{0}$ is arbitrary, this shows that
$x_{0}$ is arbitrary, this shows that ![]() $F(f)\in X_{\text{loc}}$.
$F(f)\in X_{\text{loc}}$.
To show that ![]() $F(f)\in X$ locally at infinity, we take
$F(f)\in X$ locally at infinity, we take ![]() $(s_{0},t_{0})=(0,0)$ in equation (14). Since
$(s_{0},t_{0})=(0,0)$ in equation (14). Since ![]() $F(0)=0$, the expansion (15) now becomes
$F(0)=0$, the expansion (15) now becomes
whenever the series converges.
By Proposition 4.8, we have ![]() $\Vert (1-\unicode[STIX]{x1D713})f_{i}\Vert _{X}<\unicode[STIX]{x1D6FF}$, for
$\Vert (1-\unicode[STIX]{x1D713})f_{i}\Vert _{X}<\unicode[STIX]{x1D6FF}$, for ![]() $i=1,2$ for some
$i=1,2$ for some ![]() $\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$. Now consider the function
$\unicode[STIX]{x1D713}\in C_{c}^{\infty }(\mathbb{R}^{d})$. Now consider the function ![]() $H$ defined by
$H$ defined by
The above series is absolutely convergent in ![]() $X$, in view of the above norm estimates, hence
$X$, in view of the above norm estimates, hence ![]() $H\in X$. Also since
$H\in X$. Also since ![]() $\unicode[STIX]{x1D713}$ is compactly supported,
$\unicode[STIX]{x1D713}$ is compactly supported, ![]() $1-\unicode[STIX]{x1D713}\equiv 1$ in the complement of a large ball centered at the origin, hence
$1-\unicode[STIX]{x1D713}\equiv 1$ in the complement of a large ball centered at the origin, hence ![]() $H=F(f)$ in the compliment of a compact set. This shows that
$H=F(f)$ in the compliment of a compact set. This shows that ![]() $F(f)$ belongs to
$F(f)$ belongs to ![]() $X$ locally at infinity. This completes the proof of Theorem 1.1(2).◻
$X$ locally at infinity. This completes the proof of Theorem 1.1(2).◻
Theorem 4.9. Suppose that ![]() $T_{F}$ is the composition operator associated to a complex function
$T_{F}$ is the composition operator associated to a complex function ![]() $F$ on
$F$ on ![]() $\mathbb{C}$, and
$\mathbb{C}$, and ![]() $1\leqslant p\leqslant \infty$. If
$1\leqslant p\leqslant \infty$. If ![]() $F$ is a real entire given by
$F$ is a real entire given by ![]() $F(s,t)=\sum _{m,n=0}^{\infty }a_{mn}s^{m}t^{n}$ with
$F(s,t)=\sum _{m,n=0}^{\infty }a_{mn}s^{m}t^{n}$ with ![]() $F(0)=0$, then
$F(0)=0$, then ![]() $T_{F}$ acts on
$T_{F}$ acts on ![]() $W^{p,1}(\mathbb{R}^{d})$. In particular, we have
$W^{p,1}(\mathbb{R}^{d})$. In particular, we have
Proof. Let ![]() $f\in W^{p,1}(\mathbb{R}^{d})$ with
$f\in W^{p,1}(\mathbb{R}^{d})$ with ![]() $f_{1}=(f+\bar{f})/2$ and
$f_{1}=(f+\bar{f})/2$ and ![]() $f_{2}=(f-\bar{f})/2i$. Then
$f_{2}=(f-\bar{f})/2i$. Then ![]() $f_{1},f_{2}\in W^{p,1}(\mathbb{R}^{d})$ and so
$f_{1},f_{2}\in W^{p,1}(\mathbb{R}^{d})$ and so ![]() $f_{1}^{m},f_{2}^{n}\in W^{p,1}(\mathbb{R}^{d})$ by Proposition 2.4. Since the series
$f_{1}^{m},f_{2}^{n}\in W^{p,1}(\mathbb{R}^{d})$ by Proposition 2.4. Since the series ![]() $\sum _{m,n=0}^{\infty }a_{mn}s^{m}t^{n}$ converges absolutely for all
$\sum _{m,n=0}^{\infty }a_{mn}s^{m}t^{n}$ converges absolutely for all ![]() $(s,t)$, the series
$(s,t)$, the series ![]() $\sum _{n,m=0}^{\infty }a_{mn}f_{1}^{m}f_{2}^{n}$ converges in the norm of
$\sum _{n,m=0}^{\infty }a_{mn}f_{1}^{m}f_{2}^{n}$ converges in the norm of ![]() $W^{p,1}(\mathbb{R}^{d})$; and its sum is
$W^{p,1}(\mathbb{R}^{d})$; and its sum is ![]() $F(f)=\sum _{n,m=0}^{\infty }a_{mn}f_{1}^{m}f_{2}^{m}$.◻
$F(f)=\sum _{n,m=0}^{\infty }a_{mn}f_{1}^{m}f_{2}^{m}$.◻
5 Concluding remarks
By the frequency-uniform localization (see [Reference Wang, Zhaohui, Chengchun and Zihua27, Chapter 6]) techniques, the modulation and Wiener amalgam spaces can be viewed as a Besov/Lizorkin–Triebel type space associated with a uniform decomposition (see [Reference Triebel25, Reference Wang, Lifeng and Boling26]). We note that in the last two decades, composition operators have been studied (by Bourdaud, Sickel et al.) extensively on Besov and Lizorkin–Triebel spaces. We refer to the enlightening survey article [Reference Bourdaud and Sickel7] by Bourdaud–Sickel and the references therein for more details. Recently [Reference Bhimani4, Reference Kato, Sugimoto and Tomita14, Reference Kobayshi and Sato15, Reference Reich, Reissig and Sickel18, Reference Sugimoto, Tomita and Wang23] some progress has been made for a composition operator on weighted modulation spaces. But we believe, yet we have very little information for composition operators on modulation and Wiener amalgam spaces. Specifically, we note:
(1) Feichtinger [Reference Feichtinger10] has established the basic properties of Wiener amalgam spaces and modulation spaces on locally compact groups. It would be interesting to investigate the analogue of Theorem 1.1 for locally compact groups.
(2) We have answered the problem stated in introductory paragraph in a few specific cases (Theorem 1.1). What about the remaining cases?
(3) It would be interesting to find necessary and sufficient conditions on
 $F:\mathbb{C}\rightarrow \mathbb{C}$ such that the composition operator is bounded on modulation/Wiener amalgam spaces, that is,
$F:\mathbb{C}\rightarrow \mathbb{C}$ such that the composition operator is bounded on modulation/Wiener amalgam spaces, that is,  $\Vert F\circ f\Vert _{X}\lesssim \Vert f\Vert _{X}$ for
$\Vert F\circ f\Vert _{X}\lesssim \Vert f\Vert _{X}$ for  $X=M^{p,q}(\mathbb{R}^{d})$ or
$X=M^{p,q}(\mathbb{R}^{d})$ or  $W^{p,q}(\mathbb{R}^{d})$ (
$W^{p,q}(\mathbb{R}^{d})$ ( $p=q\neq 2$).
$p=q\neq 2$).
Acknowledgments
The author wishes to thank Professor P. K. Ratnakumar for suggesting to look at this problem and for the encouragement on the subject of this paper. The author is grateful to IUSTF and Indo-US SERB and DST-INSPIRE, and TIFR CAM for the support. The author is very grateful to Professor Kasso Okoudjou for his hospitality and arranging excellent research facilities at the University of Maryland. The author is also grateful to his friend Jay Mehta for his help on TeX file type setting. The author wishes to thank the anonymous referee for meticulous reading of the manuscript and his thoughtful comments.