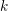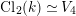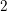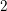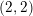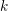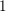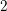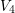1 Introduction
Let
![]() $k$
be an imaginary quadratic field. We denote by
$k$
be an imaginary quadratic field. We denote by
![]() $\operatorname{Cl}_{2}(k)$
the Sylow
$\operatorname{Cl}_{2}(k)$
the Sylow
![]() $2$
-subgroup of the class group of
$2$
-subgroup of the class group of
![]() $k$
, and by
$k$
, and by
![]() $G_{2}(k)$
the Galois group of the maximal unramified
$G_{2}(k)$
the Galois group of the maximal unramified
![]() $2$
-extension of
$2$
-extension of
![]() $k$
.
$k$
.
Consider the
![]() $2$
-class field tower
$2$
-class field tower
where
![]() $k^{i+1}$
is the Hilbert
$k^{i+1}$
is the Hilbert
![]() $2$
-class field of
$2$
-class field of
![]() $k^{i}$
. It is easily seen that, for
$k^{i}$
. It is easily seen that, for
![]() $i<j$
,
$i<j$
,
![]() $k^{j}/k^{i}$
is Galois and
$k^{j}/k^{i}$
is Galois and
![]() $\operatorname{Gal}(k^{j}/k^{i+1})$
is the derived subgroup of
$\operatorname{Gal}(k^{j}/k^{i+1})$
is the derived subgroup of
![]() $\operatorname{Gal}(k^{j}/k^{i})$
.
$\operatorname{Gal}(k^{j}/k^{i})$
.
We shall consider the case of
![]() $\operatorname{Cl}_{2}(k)\simeq \operatorname{Gal}(k^{1}/k)\simeq V_{4}$
, the Klein four group. It is well-known [Reference Furtwängler4, Reference Taussky17] in the group theory that all the finite
$\operatorname{Cl}_{2}(k)\simeq \operatorname{Gal}(k^{1}/k)\simeq V_{4}$
, the Klein four group. It is well-known [Reference Furtwängler4, Reference Taussky17] in the group theory that all the finite
![]() $2$
-groups whose abelianization is isomorphic to
$2$
-groups whose abelianization is isomorphic to
![]() $V_{4}$
are:
$V_{4}$
are:
(i)
 $V_{4}$
itself;
$V_{4}$
itself;(ii)
 $Q_{2^{n}}~(n\geqslant 3)$
, the (generalized) quaternion group of order
$Q_{2^{n}}~(n\geqslant 3)$
, the (generalized) quaternion group of order
 $2^{n}$
;
$2^{n}$
;(iii)
 $D_{2^{n}}~(n\geqslant 3)$
, the dihedral group of order
$D_{2^{n}}~(n\geqslant 3)$
, the dihedral group of order
 $2^{n}$
;
$2^{n}$
;(iv)
 $\mathit{SD}_{2^{n}}~(n\geqslant 4)$
, the semidihedral group of order
$\mathit{SD}_{2^{n}}~(n\geqslant 4)$
, the semidihedral group of order
 $2^{n}$
.
$2^{n}$
.
Moreover, the derived subgroups of these groups are cyclic. Hence, we find that
![]() $\operatorname{Gal}(k^{2}/k)$
is isomorphic to one of these groups and
$\operatorname{Gal}(k^{2}/k)$
is isomorphic to one of these groups and
![]() $\operatorname{Gal}(k^{2}/k^{1})$
is cyclic. In addition, it is known that a group with cyclic abelianization is itself cyclic, so that
$\operatorname{Gal}(k^{2}/k^{1})$
is cyclic. In addition, it is known that a group with cyclic abelianization is itself cyclic, so that
![]() $k^{2}=k^{3}=\cdots \,$
. This means
$k^{2}=k^{3}=\cdots \,$
. This means
![]() $G_{2}(k)=\operatorname{Gal}(k^{2}/k)$
, and it is isomorphic to
$G_{2}(k)=\operatorname{Gal}(k^{2}/k)$
, and it is isomorphic to
![]() $V_{4},Q_{2^{n}},D_{2^{n}}$
, or
$V_{4},Q_{2^{n}},D_{2^{n}}$
, or
![]() $\mathit{SD}_{2^{n}}$
.
$\mathit{SD}_{2^{n}}$
.
We want to know the distribution of
![]() $k$
with
$k$
with
![]() $G_{2}(k)$
isomorphic to each group.
$G_{2}(k)$
isomorphic to each group.
Definition.
Let
![]() $A,B$
be subsets of
$A,B$
be subsets of
![]() $\mathbb{N}$
. Here
$\mathbb{N}$
. Here
![]() $0\notin \mathbb{N}$
. If the limit
$0\notin \mathbb{N}$
. If the limit
exists, we call it the relative density of
![]() $A$
with respect to
$A$
with respect to
![]() $B$
, and denote it by
$B$
, and denote it by
![]() $\unicode[STIX]{x1D6FF}(A/B)$
.
$\unicode[STIX]{x1D6FF}(A/B)$
.
Let
and we consider the densities
![]() $\unicode[STIX]{x1D6FF}(A(G)/B)$
for
$\unicode[STIX]{x1D6FF}(A(G)/B)$
for
![]() $G=V_{4},Q_{2^{n}},D_{2^{n}}$
, and
$G=V_{4},Q_{2^{n}},D_{2^{n}}$
, and
![]() $\mathit{SD}_{2^{n}}$
with appropriate set
$\mathit{SD}_{2^{n}}$
with appropriate set
![]() $B$
. Here we take
$B$
. Here we take
The density of
![]() $k$
such that the
$k$
such that the
![]() $2$
-class field tower terminates at
$2$
-class field tower terminates at
![]() $k^{1}$
is known by Gerth [Reference Gerth6]:
$k^{1}$
is known by Gerth [Reference Gerth6]:
Theorem 1. (Gerth)
In Section 3, we shall extend this theorem for
![]() $Q_{2^{n}},D_{2^{n}}$
, and
$Q_{2^{n}},D_{2^{n}}$
, and
![]() $\mathit{SD}_{2^{n}}$
. For this purpose, we need to extend the Chebotarev density theorem for products of prime numbers. Accordingly, we shall produce a “multivariable” version of the Chebotarev density theorem as our main theorem. We shall prove this theorem by assuming the generalized Riemann hypothesis and using the effective version of the Chebotarev density theorem.
$\mathit{SD}_{2^{n}}$
. For this purpose, we need to extend the Chebotarev density theorem for products of prime numbers. Accordingly, we shall produce a “multivariable” version of the Chebotarev density theorem as our main theorem. We shall prove this theorem by assuming the generalized Riemann hypothesis and using the effective version of the Chebotarev density theorem.
We shall use following notations:
(i)
 $\operatorname{Cl}_{2}(k)$
is the Sylow
$\operatorname{Cl}_{2}(k)$
is the Sylow
 $2$
-subgroup of the class group of
$2$
-subgroup of the class group of
 $k$
, and
$k$
, and
 $\operatorname{Cl}_{2}^{+}(k)$
is that of the narrow class group of
$\operatorname{Cl}_{2}^{+}(k)$
is that of the narrow class group of
 $k$
;
$k$
;(ii)
 $h_{2}(k)$
and
$h_{2}(k)$
and
 $h_{2}^{+}(k)$
are the orders of
$h_{2}^{+}(k)$
are the orders of
 $\operatorname{Cl}_{2}(k)$
and
$\operatorname{Cl}_{2}(k)$
and
 $\operatorname{Cl}_{2}^{+}(k)$
, respectively;
$\operatorname{Cl}_{2}^{+}(k)$
, respectively;(iii)
 $d_{k}$
is the discriminant of
$d_{k}$
is the discriminant of
 $k$
;
$k$
;(iv)
 $(\cdot /\cdot )$
is the Kronecker symbol,
$(\cdot /\cdot )$
is the Kronecker symbol,
 $(\cdot /\cdot )_{4}$
is the quartic residue symbol, and
$(\cdot /\cdot )_{4}$
is the quartic residue symbol, and
 $(\cdot ,\cdot /\cdot )$
is the Hilbert symbol.
$(\cdot ,\cdot /\cdot )$
is the Hilbert symbol.
2 Conditions for
 $G_{2}(k)\simeq G$
$G_{2}(k)\simeq G$
At first we have to know when
![]() $G_{2}(k)\simeq Q_{2^{n}},D_{2^{n}}$
, or
$G_{2}(k)\simeq Q_{2^{n}},D_{2^{n}}$
, or
![]() $\mathit{SD}_{2^{n}}$
. Moreover, the conditions should be able to be written by splitting of primes in a number field because we use the Chebotarev density theorem. The conditions are known by several authors and gathered (together with other groups) in the table in [Reference Benjamin, Lemmermeyer and Snyder1]. In this section, we outline the conditions and prove them partially.
$\mathit{SD}_{2^{n}}$
. Moreover, the conditions should be able to be written by splitting of primes in a number field because we use the Chebotarev density theorem. The conditions are known by several authors and gathered (together with other groups) in the table in [Reference Benjamin, Lemmermeyer and Snyder1]. In this section, we outline the conditions and prove them partially.
The
![]() $2$
-rank of the narrow class group of a quadratic field is obtained by the genus theory:
$2$
-rank of the narrow class group of a quadratic field is obtained by the genus theory:
Proposition 1. Let
![]() $F$
be a quadratic field and let
$F$
be a quadratic field and let
![]() $t$
be the number of distinct prime divisors of
$t$
be the number of distinct prime divisors of
![]() $d_{F}$
. Then the
$d_{F}$
. Then the
![]() $2$
-rank
$2$
-rank
![]() $\dim _{\mathbb{F}_{2}}\operatorname{Cl}_{2}^{+}(F)$
of
$\dim _{\mathbb{F}_{2}}\operatorname{Cl}_{2}^{+}(F)$
of
![]() $\operatorname{Cl}_{2}^{+}(F)$
equals to
$\operatorname{Cl}_{2}^{+}(F)$
equals to
![]() $t-1$
.
$t-1$
.
The
![]() $4$
-rank can also be calculated by using the Rédei–Reichardt criterion [Reference Rédei and Reichardt14]:
$4$
-rank can also be calculated by using the Rédei–Reichardt criterion [Reference Rédei and Reichardt14]:
Proposition 2. Let
![]() $F$
be a quadratic field and
$F$
be a quadratic field and
![]() $l_{1},\ldots ,l_{t}$
be all the distinct prime divisors of
$l_{1},\ldots ,l_{t}$
be all the distinct prime divisors of
![]() $d_{F}$
. We define the Rédei matrix:
$d_{F}$
. We define the Rédei matrix:
where
![]() $[l_{i},d_{F}/l_{j}]\in \mathbb{F}_{2}$
is defined as
$[l_{i},d_{F}/l_{j}]\in \mathbb{F}_{2}$
is defined as
Then the
![]() $4$
-rank
$4$
-rank
![]() $\dim _{\mathbb{F}_{2}}(\operatorname{Cl}_{2}^{+}(F)^{2}/\operatorname{Cl}_{2}^{+}(F)^{4})$
of
$\dim _{\mathbb{F}_{2}}(\operatorname{Cl}_{2}^{+}(F)^{2}/\operatorname{Cl}_{2}^{+}(F)^{4})$
of
![]() $\operatorname{Cl}_{2}^{+}(F)$
equals to
$\operatorname{Cl}_{2}^{+}(F)$
equals to
![]() $t-1-\operatorname{rank}R_{F}$
.
$t-1-\operatorname{rank}R_{F}$
.
From Propositions 1 and 2, one can show
Proposition 3. Let
![]() $k$
be an imaginary quadratic field with odd discriminant. Then,
$k$
be an imaginary quadratic field with odd discriminant. Then,
![]() $\operatorname{Cl}_{2}(k)\simeq V_{4}$
if and only if
$\operatorname{Cl}_{2}(k)\simeq V_{4}$
if and only if
![]() $k=\mathbb{Q}(\sqrt{-pqr})$
for some distinct primes
$k=\mathbb{Q}(\sqrt{-pqr})$
for some distinct primes
![]() $p,q,r$
such that:
$p,q,r$
such that:
(i)
 $p\equiv q\equiv r\equiv -1~(4)$
and
$p\equiv q\equiv r\equiv -1~(4)$
and
 $(p/q)=(q/r)=(r/p)$
; or
$(p/q)=(q/r)=(r/p)$
; or(ii)
 $-p\equiv q\equiv r\equiv 1~(4)$
and at least two of
$-p\equiv q\equiv r\equiv 1~(4)$
and at least two of
 $(p/q),(p/r),(q/r)$
equal to
$(p/q),(p/r),(q/r)$
equal to
 $-1$
.
$-1$
.
The following conditions are shown by several authors, see [Reference Benjamin, Lemmermeyer and Snyder1]:
Proposition 4.
(1) Let
 $k=\mathbb{Q}(\sqrt{-pqr})$
where
$k=\mathbb{Q}(\sqrt{-pqr})$
where
 $p,q$
, and
$p,q$
, and
 $r$
are distinct primes with
$r$
are distinct primes with
 $p\equiv q\equiv r\equiv -1~(4)$
. Then
$p\equiv q\equiv r\equiv -1~(4)$
. Then
 $G_{2}(k)$
is abelian.
$G_{2}(k)$
is abelian.(2) Let
 $k=\mathbb{Q}(\sqrt{-pqr})$
where
$k=\mathbb{Q}(\sqrt{-pqr})$
where
 $p,q$
, and
$p,q$
, and
 $r$
are distinct primes with
$r$
are distinct primes with
 $-p\equiv q\equiv r\equiv 1~(4)$
. Then:
$-p\equiv q\equiv r\equiv 1~(4)$
. Then:(a)
 $G_{2}(k)\simeq Q_{8}$
if and only if
$G_{2}(k)\simeq Q_{8}$
if and only if
(b)
 $G_{2}(k)\simeq Q_{2^{n}}~(n\geqslant 4)$
if and only if
$G_{2}(k)\simeq Q_{2^{n}}~(n\geqslant 4)$
if and only if
(c)
 $G_{2}(k)\simeq D_{2^{n}}~(n\geqslant 3)$
if and only if
$G_{2}(k)\simeq D_{2^{n}}~(n\geqslant 3)$
if and only if
(d)
 $G_{2}(k)\simeq \mathit{SD}_{2^{n}}~(n\geqslant 4)$
if and only if, by swapping
$G_{2}(k)\simeq \mathit{SD}_{2^{n}}~(n\geqslant 4)$
if and only if, by swapping
 $q$
and
$q$
and
 $r$
if necessary,
$r$
if necessary,
Here
![]() $\mathbf{N}$
is the absolute norm and
$\mathbf{N}$
is the absolute norm and
![]() $h_{2}(m)=h_{2}(\mathbb{Q}(\sqrt{m}))$
for
$h_{2}(m)=h_{2}(\mathbb{Q}(\sqrt{m}))$
for
![]() $m\in \mathbb{Z}$
.
$m\in \mathbb{Z}$
.
This proposition is shown by Kisilevsky [Reference Kisilevsky8] except for the conditions
![]() $2^{n}=4h_{2}(qr)$
and
$2^{n}=4h_{2}(qr)$
and
![]() $2^{n}=4h_{2}(-pq)$
in (2b), (2c), and (2d). We give a proof of the conditions
$2^{n}=4h_{2}(-pq)$
in (2b), (2c), and (2d). We give a proof of the conditions
![]() $2^{n}=4h_{2}(qr)$
and
$2^{n}=4h_{2}(qr)$
and
![]() $2^{n}=4h_{2}(-pq)$
in (2b), (2c), and (2d) because no proof is given in [Reference Benjamin, Lemmermeyer and Snyder1].
$2^{n}=4h_{2}(-pq)$
in (2b), (2c), and (2d) because no proof is given in [Reference Benjamin, Lemmermeyer and Snyder1].
Let
![]() $k=\mathbb{Q}(\sqrt{-pqr})$
where
$k=\mathbb{Q}(\sqrt{-pqr})$
where
![]() $p,q,r$
are distinct primes with
$p,q,r$
are distinct primes with
![]() $-p\equiv q\equiv r\equiv 1~(4)$
, and assume
$-p\equiv q\equiv r\equiv 1~(4)$
, and assume
![]() $h_{2}(k)=4$
. Then the Hilbert
$h_{2}(k)=4$
. Then the Hilbert
![]() $2$
-class field
$2$
-class field
![]() $k^{1}$
is
$k^{1}$
is
![]() $\mathbb{Q}(\sqrt{-p},\sqrt{q},\sqrt{r})$
. Let
$\mathbb{Q}(\sqrt{-p},\sqrt{q},\sqrt{r})$
. Let
![]() $K$
be the maximal real subfield of
$K$
be the maximal real subfield of
![]() $k^{1}$
, that is,
$k^{1}$
, that is,
![]() $K=\mathbb{Q}(\sqrt{q},\sqrt{r})$
.
$K=\mathbb{Q}(\sqrt{q},\sqrt{r})$
.
Lemma 1.
where
![]() $h_{2}(m)=h_{2}(\mathbb{Q}(\sqrt{m}))$
for
$h_{2}(m)=h_{2}(\mathbb{Q}(\sqrt{m}))$
for
![]() $m\in \mathbb{Z}$
.
$m\in \mathbb{Z}$
.
Proof. From the relative class number formula [Reference Washington18, Chapter 4], one has
 $$\begin{eqnarray}h(k^{1})/h(K)=wQ\mathop{\prod }_{\unicode[STIX]{x1D712}:\text{odd}}\biggl(-\frac{1}{2f_{\unicode[STIX]{x1D712}}}\mathop{\sum }_{a=1}^{f_{\unicode[STIX]{x1D712}}}\unicode[STIX]{x1D712}(a)a\biggr)\end{eqnarray}$$
$$\begin{eqnarray}h(k^{1})/h(K)=wQ\mathop{\prod }_{\unicode[STIX]{x1D712}:\text{odd}}\biggl(-\frac{1}{2f_{\unicode[STIX]{x1D712}}}\mathop{\sum }_{a=1}^{f_{\unicode[STIX]{x1D712}}}\unicode[STIX]{x1D712}(a)a\biggr)\end{eqnarray}$$
where the product runs over the odd Dirichlet characters of
![]() $k^{1}$
and
$k^{1}$
and
(i)
 $h$
is the class number;
$h$
is the class number;(ii)
 $w$
is the number of the roots of unity in
$w$
is the number of the roots of unity in
 $k^{1}$
;
$k^{1}$
;(iii)
 $Q=[U:\unicode[STIX]{x1D707}U_{K}]$
, where
$Q=[U:\unicode[STIX]{x1D707}U_{K}]$
, where
 $U$
and
$U$
and
 $U_{K}$
are the unit groups of
$U_{K}$
are the unit groups of
 $k^{1}$
and
$k^{1}$
and
 $K$
, respectively, and
$K$
, respectively, and
 $\unicode[STIX]{x1D707}$
is the group of the roots of unity in
$\unicode[STIX]{x1D707}$
is the group of the roots of unity in
 $k^{1}$
;
$k^{1}$
;(iv)
 $f_{\unicode[STIX]{x1D712}}$
is the conductor of
$f_{\unicode[STIX]{x1D712}}$
is the conductor of
 $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
Note that one can easily show
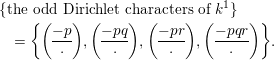
Similarly we have
for
![]() $m=-p,-pq,-pr,-pqr$
, where
$m=-p,-pq,-pr,-pqr$
, where
![]() $h(m)=h(\mathbb{Q}(\sqrt{m})),\,w_{m}=w_{\mathbb{Q}(\sqrt{m})}$
, and
$h(m)=h(\mathbb{Q}(\sqrt{m})),\,w_{m}=w_{\mathbb{Q}(\sqrt{m})}$
, and
![]() $d_{m}=d_{\mathbb{Q}(\sqrt{m})}$
. Putting these formulas together we obtain
$d_{m}=d_{\mathbb{Q}(\sqrt{m})}$
. Putting these formulas together we obtain
Now
![]() $h(-p)$
is odd by Proposition 1 and
$h(-p)$
is odd by Proposition 1 and
![]() $h_{2}(k)=4$
. Also we know that the
$h_{2}(k)=4$
. Also we know that the
![]() $2$
-parts of
$2$
-parts of
![]() $w,w_{p},w_{pq},w_{pr}$
, and
$w,w_{p},w_{pq},w_{pr}$
, and
![]() $w_{k}$
are
$w_{k}$
are
![]() $2$
since
$2$
since
![]() $k^{1}/\mathbb{Q}$
is unramified at
$k^{1}/\mathbb{Q}$
is unramified at
![]() $2$
.
$2$
.
Hence it suffices to show
![]() $Q=1$
. By [Reference Washington18, Theorem 4.12],
$Q=1$
. By [Reference Washington18, Theorem 4.12],
![]() $Q=1$
if and only if
$Q=1$
if and only if
![]() $\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}\in \unicode[STIX]{x1D707}^{2}$
for any
$\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}\in \unicode[STIX]{x1D707}^{2}$
for any
![]() $\unicode[STIX]{x1D700}\in U$
, where
$\unicode[STIX]{x1D700}\in U$
, where
![]() $\overline{\unicode[STIX]{x1D700}}$
means the conjugate of
$\overline{\unicode[STIX]{x1D700}}$
means the conjugate of
![]() $\unicode[STIX]{x1D700}$
over
$\unicode[STIX]{x1D700}$
over
![]() $K$
. Suppose
$K$
. Suppose
![]() $\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}\notin \unicode[STIX]{x1D707}^{2}$
for some
$\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}\notin \unicode[STIX]{x1D707}^{2}$
for some
![]() $\unicode[STIX]{x1D700}\in U$
. It can be easily shown that
$\unicode[STIX]{x1D700}\in U$
. It can be easily shown that
![]() $w=2$
or
$w=2$
or
![]() $6$
. Hence,
$6$
. Hence,
![]() $\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}=-1$
or
$\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}=-1$
or
![]() $(1\pm \sqrt{-3})/2$
. We let
$(1\pm \sqrt{-3})/2$
. We let
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D700}\sqrt{-p}\quad & \displaystyle \text{if }\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}=-1,\\ \displaystyle \unicode[STIX]{x1D700}\biggl(\frac{3\mp \sqrt{-3}}{2}\biggr)\quad & \displaystyle \text{if }\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}=\frac{1\pm \sqrt{-3}}{2}\quad (p=3).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D700}\sqrt{-p}\quad & \displaystyle \text{if }\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}=-1,\\ \displaystyle \unicode[STIX]{x1D700}\biggl(\frac{3\mp \sqrt{-3}}{2}\biggr)\quad & \displaystyle \text{if }\unicode[STIX]{x1D700}/\overline{\unicode[STIX]{x1D700}}=\frac{1\pm \sqrt{-3}}{2}\quad (p=3).\end{array}\right.\end{eqnarray}$$
We can check
![]() $\unicode[STIX]{x1D6FC}=\overline{\unicode[STIX]{x1D6FC}}$
so that
$\unicode[STIX]{x1D6FC}=\overline{\unicode[STIX]{x1D6FC}}$
so that
![]() $\unicode[STIX]{x1D6FC}\in K$
. Hence,
$\unicode[STIX]{x1D6FC}\in K$
. Hence,
Since
![]() $N_{k^{1}/K}(\unicode[STIX]{x1D700})\in U_{K}$
, this implies that
$N_{k^{1}/K}(\unicode[STIX]{x1D700})\in U_{K}$
, this implies that
![]() $p$
ramifies in
$p$
ramifies in
![]() $K/\mathbb{Q}$
, which is absurd.◻
$K/\mathbb{Q}$
, which is absurd.◻
Lemma 2. The Hilbert
![]() $2$
-class fields of
$2$
-class fields of
![]() $K$
and of
$K$
and of
![]() $\mathbb{Q}(\sqrt{qr})$
coincide.
$\mathbb{Q}(\sqrt{qr})$
coincide.
Proof. Let
![]() $K^{1}$
and
$K^{1}$
and
![]() $\mathbb{Q}(\sqrt{qr})^{1}$
be the Hilbert
$\mathbb{Q}(\sqrt{qr})^{1}$
be the Hilbert
![]() $2$
-class fields of
$2$
-class fields of
![]() $K$
and
$K$
and
![]() $\mathbb{Q}(\sqrt{qr})$
, respectively. It can be shown that
$\mathbb{Q}(\sqrt{qr})$
, respectively. It can be shown that
![]() $K^{1}/\mathbb{Q}(\sqrt{qr})$
is Galois and
$K^{1}/\mathbb{Q}(\sqrt{qr})$
is Galois and
![]() $K^{1}\supseteq \mathbb{Q}(\sqrt{qr})^{1}$
. Since
$K^{1}\supseteq \mathbb{Q}(\sqrt{qr})^{1}$
. Since
![]() $K/\mathbb{Q}(\sqrt{qr})$
is unramified, so is
$K/\mathbb{Q}(\sqrt{qr})$
is unramified, so is
![]() $K^{1}/\mathbb{Q}(\sqrt{qr})$
. Hence
$K^{1}/\mathbb{Q}(\sqrt{qr})$
. Hence
![]() $\mathbb{Q}(\sqrt{qr})^{1}$
is the maximal abelian subextension of
$\mathbb{Q}(\sqrt{qr})^{1}$
is the maximal abelian subextension of
![]() $K^{1}/\mathbb{Q}(\sqrt{qr})$
, and the abelianization of
$K^{1}/\mathbb{Q}(\sqrt{qr})$
, and the abelianization of
![]() $\operatorname{Gal}(K^{1}/\mathbb{Q}(\sqrt{qr}))$
is
$\operatorname{Gal}(K^{1}/\mathbb{Q}(\sqrt{qr}))$
is
![]() $\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{qr}))$
. On the other hand,
$\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{qr}))$
. On the other hand,
![]() $\operatorname{Cl}_{2}^{+}(\mathbb{Q}(\sqrt{qr}))$
is cyclic by Proposition 1; therefore
$\operatorname{Cl}_{2}^{+}(\mathbb{Q}(\sqrt{qr}))$
is cyclic by Proposition 1; therefore
![]() $\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{qr}))$
is also cyclic. Hence,
$\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{qr}))$
is also cyclic. Hence,
![]() $\operatorname{Gal}(K^{1}/\mathbb{Q}(\sqrt{qr}))$
is cyclic and
$\operatorname{Gal}(K^{1}/\mathbb{Q}(\sqrt{qr}))$
is cyclic and
![]() $K^{1}=\mathbb{Q}(\sqrt{qr})^{1}$
.◻
$K^{1}=\mathbb{Q}(\sqrt{qr})^{1}$
.◻
Proof of Proposition 4.
Now we determine
![]() $n$
. We know that
$n$
. We know that
From Lemma 2 we have
![]() $h_{2}(qr)=2h_{2}(K)$
. Hence from Lemma 1,
$h_{2}(qr)=2h_{2}(K)$
. Hence from Lemma 1,
Since
![]() $(p/q)=(p/r)=-1$
, we get
$(p/q)=(p/r)=-1$
, we get
![]() $h_{2}(-pq)=h_{2}(-pr)=2$
from Proposition 1 (see Proposition 5 below). Hence
$h_{2}(-pq)=h_{2}(-pr)=2$
from Proposition 1 (see Proposition 5 below). Hence
![]() $2^{n}=4h_{2}(k^{1})=4h_{2}(qr)$
.
$2^{n}=4h_{2}(k^{1})=4h_{2}(qr)$
.
(2d)
Similarly, we get
![]() $h_{2}(-pr)=2$
. Since
$h_{2}(-pr)=2$
. Since
![]() $(q/r)=-1$
, we get
$(q/r)=-1$
, we get
![]() $h_{2}^{+}(qr)=2$
from Proposition 1. Since
$h_{2}^{+}(qr)=2$
from Proposition 1. Since
![]() $h_{2}(qr)=2h_{2}(K)$
is even, we have
$h_{2}(qr)=2h_{2}(K)$
is even, we have
![]() $h_{2}(qr)=2$
. Hence
$h_{2}(qr)=2$
. Hence
![]() $2^{n}=4h_{2}(k^{1})=4h_{2}(-pq)$
.◻
$2^{n}=4h_{2}(k^{1})=4h_{2}(-pq)$
.◻
Also the following conditions are known, see [Reference Yamamoto19]:
Proposition 5. Let
![]() $p,q$
, and
$p,q$
, and
![]() $r$
be distinct primes with
$r$
be distinct primes with
![]() $-p\equiv q\equiv r\equiv 1~(4)$
. Then:
$-p\equiv q\equiv r\equiv 1~(4)$
. Then:
(1)
 $h_{2}(qr)=2$
and
$h_{2}(qr)=2$
and
 $\mathbf{N}\unicode[STIX]{x1D700}_{qr}=-1$
if and only if
$\mathbf{N}\unicode[STIX]{x1D700}_{qr}=-1$
if and only if
 $(q/r)=-1$
;
$(q/r)=-1$
;(2)
 $h_{2}(qr)=2$
and
$h_{2}(qr)=2$
and
 $\mathbf{N}\unicode[STIX]{x1D700}_{qr}=1$
if and only if
$\mathbf{N}\unicode[STIX]{x1D700}_{qr}=1$
if and only if
 $(q/r)=1$
and
$(q/r)=1$
and
 $(q/r)_{4}(r/q)_{4}=-1$
;
$(q/r)_{4}(r/q)_{4}=-1$
;(3)
 $h_{2}(qr)=4$
and
$h_{2}(qr)=4$
and
 $\mathbf{N}\unicode[STIX]{x1D700}_{qr}=-1$
if and only if
$\mathbf{N}\unicode[STIX]{x1D700}_{qr}=-1$
if and only if
 $(q/r)=1$
and
$(q/r)=1$
and
 $(q/r)_{4}=(r/q)_{4}=-1$
;
$(q/r)_{4}=(r/q)_{4}=-1$
;(4)
 $h_{2}(-pq)=2$
if and only if
$h_{2}(-pq)=2$
if and only if
 $(p/q)=-1$
;
$(p/q)=-1$
;(5)
 $h_{2}(-pq)=4$
if and only if
$h_{2}(-pq)=4$
if and only if
 $(p/q)=1$
and
$(p/q)=1$
and
 $(-p/q)_{4}=-1$
.
$(-p/q)_{4}=-1$
.
3 Densities for
 $Q_{8},Q_{16},D_{8}$
, and
$Q_{8},Q_{16},D_{8}$
, and
 $\mathit{SD}_{16}$
$\mathit{SD}_{16}$
We want to find the densities of quadratic fields which have maximal unramified
![]() $2$
-extensions with Galois groups isomorphic to
$2$
-extensions with Galois groups isomorphic to
![]() $Q_{2^{n}},D_{2^{n}}$
, or
$Q_{2^{n}},D_{2^{n}}$
, or
![]() $\mathit{SD}_{2^{n}}$
. In other words, we want to calculate the densities,
$\mathit{SD}_{2^{n}}$
. In other words, we want to calculate the densities,
![]() $\unicode[STIX]{x1D6FF}(A(G)/B(V_{4}))$
for
$\unicode[STIX]{x1D6FF}(A(G)/B(V_{4}))$
for
![]() $G=Q_{2^{n}},D_{2^{n}},\mathit{SD}_{2^{n}}$
. For this purpose, we produce a multivariable version of the Chebotarev density theorem.
$G=Q_{2^{n}},D_{2^{n}},\mathit{SD}_{2^{n}}$
. For this purpose, we produce a multivariable version of the Chebotarev density theorem.
For an integer
![]() $n\geqslant 0$
, we let
$n\geqslant 0$
, we let
At first we calculate
![]() $\unicode[STIX]{x1D6FF}(A(G)/P_{3})$
. Note that in our definition of
$\unicode[STIX]{x1D6FF}(A(G)/P_{3})$
. Note that in our definition of
![]() $\unicode[STIX]{x1D6FF}(A/B)$
, we do not assume
$\unicode[STIX]{x1D6FF}(A/B)$
, we do not assume
![]() $A\subseteq B$
. It is known [Reference Hardy and Wright7, Theorem 437] that for
$A\subseteq B$
. It is known [Reference Hardy and Wright7, Theorem 437] that for
![]() $n\geqslant 1$
$n\geqslant 1$
Suppose that
![]() $F_{a}$
and
$F_{a}$
and
![]() ${\mathcal{C}}_{a}$
are given for each square-free positive integer
${\mathcal{C}}_{a}$
are given for each square-free positive integer
![]() $a$
, where
$a$
, where
![]() $F_{a}$
is a number field which is Galois over
$F_{a}$
is a number field which is Galois over
![]() $\mathbb{Q}$
, and
$\mathbb{Q}$
, and
![]() ${\mathcal{C}}_{a}$
is a conjugacy class in
${\mathcal{C}}_{a}$
is a conjugacy class in
![]() ${\mathcal{G}}_{a}=\operatorname{Gal}(F_{a}/\mathbb{Q})$
. For a prime number
${\mathcal{G}}_{a}=\operatorname{Gal}(F_{a}/\mathbb{Q})$
. For a prime number
![]() $p$
, we let
$p$
, we let
![]() $\unicode[STIX]{x1D711}_{a}(p)=1$
when
$\unicode[STIX]{x1D711}_{a}(p)=1$
when
![]() $p$
does not ramify in
$p$
does not ramify in
![]() $F_{a}$
and
$F_{a}$
and
and
![]() $\unicode[STIX]{x1D711}_{a}(p)=0$
otherwise. We denote for
$\unicode[STIX]{x1D711}_{a}(p)=0$
otherwise. We denote for
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
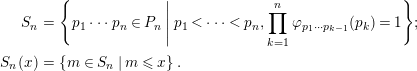 $$\begin{eqnarray}\displaystyle S_{n} & = & \displaystyle \left\{\hspace{2.22198pt}p_{1}\cdots p_{n}\in P_{n}\;|\;p_{1}<\cdots <p_{n},\mathop{\prod }_{k=1}^{n}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})=1\hspace{2.22198pt}\right\}\!;\nonumber\\ \displaystyle S_{n}(x) & = & \displaystyle \{\,m\in S_{n}\mid m\leqslant x\,\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{n} & = & \displaystyle \left\{\hspace{2.22198pt}p_{1}\cdots p_{n}\in P_{n}\;|\;p_{1}<\cdots <p_{n},\mathop{\prod }_{k=1}^{n}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})=1\hspace{2.22198pt}\right\}\!;\nonumber\\ \displaystyle S_{n}(x) & = & \displaystyle \{\,m\in S_{n}\mid m\leqslant x\,\}.\nonumber\end{eqnarray}$$
Note that the empty product means
![]() $1$
and
$1$
and
![]() $P_{0}=S_{0}=\{1\}$
.
$P_{0}=S_{0}=\{1\}$
.
Now we state our main theorem:
Theorem 2. Let
![]() $n$
be a positive integer. Assume that:
$n$
be a positive integer. Assume that:
(i) the Generalized Riemann Hypothesis (GRH) holds for the Dedekind zeta function of
 $F_{a}$
for all
$F_{a}$
for all
 $a\in S_{0}\cup \cdots \cup S_{n-1}$
;
$a\in S_{0}\cup \cdots \cup S_{n-1}$
;(ii) there are positive constants
 $c_{0}$
and
$c_{0}$
and
 $\unicode[STIX]{x1D700}$
depending only on
$\unicode[STIX]{x1D700}$
depending only on
 $n$
, such that for
$n$
, such that for
 $1\leqslant k\leqslant n-1$
and
$1\leqslant k\leqslant n-1$
and
 $a=p_{1}\cdots p_{k}\in S_{k}~(p_{1}<\cdots <p_{k})$
,
$a=p_{1}\cdots p_{k}\in S_{k}~(p_{1}<\cdots <p_{k})$
,  $$\begin{eqnarray}\log |d_{F_{a}}|\leqslant \frac{c_{0}\sqrt{p_{k}}}{(\log p_{k})^{1+\unicode[STIX]{x1D700}}}\qquad \text{and}\qquad [F_{a}:\mathbb{Q}]\leqslant \frac{c_{0}\sqrt{p_{k}}}{(\log p_{k})^{2+\unicode[STIX]{x1D700}}};\end{eqnarray}$$
$$\begin{eqnarray}\log |d_{F_{a}}|\leqslant \frac{c_{0}\sqrt{p_{k}}}{(\log p_{k})^{1+\unicode[STIX]{x1D700}}}\qquad \text{and}\qquad [F_{a}:\mathbb{Q}]\leqslant \frac{c_{0}\sqrt{p_{k}}}{(\log p_{k})^{2+\unicode[STIX]{x1D700}}};\end{eqnarray}$$
(iii) for
 $1\leqslant k\leqslant n$
, there is a rational number
$1\leqslant k\leqslant n$
, there is a rational number
 $\unicode[STIX]{x1D6FF}_{k}$
such that for any
$\unicode[STIX]{x1D6FF}_{k}$
such that for any
 $a\in S_{k-1}$
,
$a\in S_{k-1}$
,  $$\begin{eqnarray}\frac{\#{\mathcal{C}}_{a}}{\#{\mathcal{G}}_{a}}=\unicode[STIX]{x1D6FF}_{k}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\#{\mathcal{C}}_{a}}{\#{\mathcal{G}}_{a}}=\unicode[STIX]{x1D6FF}_{k}.\end{eqnarray}$$
Then
The proof of this theorem is given in the next section.
Now we shall calculate
![]() $\unicode[STIX]{x1D6FF}(A(G)/B(V_{4}))$
by using the theorem. Here we only calculate
$\unicode[STIX]{x1D6FF}(A(G)/B(V_{4}))$
by using the theorem. Here we only calculate
![]() $\unicode[STIX]{x1D6FF}(A(D_{8})/B(V_{4}))$
. From Propositions 4 and 5, we know that
$\unicode[STIX]{x1D6FF}(A(D_{8})/B(V_{4}))$
. From Propositions 4 and 5, we know that
![]() $\mathbb{Q}(\sqrt{-m})$
has odd discriminant and
$\mathbb{Q}(\sqrt{-m})$
has odd discriminant and
![]() $m\in A(D_{8})$
, if and only if,
$m\in A(D_{8})$
, if and only if,
![]() $m=pqr$
such that
$m=pqr$
such that
![]() $p,q$
, and
$p,q$
, and
![]() $r$
are distinct primes with
$r$
are distinct primes with
![]() $-p\equiv q\equiv r\equiv 1~(4)$
and
$-p\equiv q\equiv r\equiv 1~(4)$
and
Let
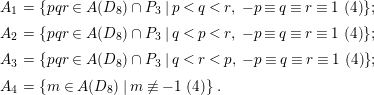 $$\begin{eqnarray}\displaystyle A_{1} & = & \displaystyle \{\,pqr\in A(D_{8})\cap P_{3}\mid p<q<r,\,-p\equiv q\equiv r\equiv 1~(4)\,\}\!;\nonumber\\ \displaystyle A_{2} & = & \displaystyle \{\,pqr\in A(D_{8})\cap P_{3}\mid q<p<r,\,-p\equiv q\equiv r\equiv 1~(4)\,\}\!;\nonumber\\ \displaystyle A_{3} & = & \displaystyle \{\,pqr\in A(D_{8})\cap P_{3}\mid q<r<p,\,-p\equiv q\equiv r\equiv 1~(4)\,\}\!;\nonumber\\ \displaystyle A_{4} & = & \displaystyle \{\,m\in A(D_{8})\mid m\not \equiv -1~(4)\,\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{1} & = & \displaystyle \{\,pqr\in A(D_{8})\cap P_{3}\mid p<q<r,\,-p\equiv q\equiv r\equiv 1~(4)\,\}\!;\nonumber\\ \displaystyle A_{2} & = & \displaystyle \{\,pqr\in A(D_{8})\cap P_{3}\mid q<p<r,\,-p\equiv q\equiv r\equiv 1~(4)\,\}\!;\nonumber\\ \displaystyle A_{3} & = & \displaystyle \{\,pqr\in A(D_{8})\cap P_{3}\mid q<r<p,\,-p\equiv q\equiv r\equiv 1~(4)\,\}\!;\nonumber\\ \displaystyle A_{4} & = & \displaystyle \{\,m\in A(D_{8})\mid m\not \equiv -1~(4)\,\}.\nonumber\end{eqnarray}$$
Then clearly these are disjoint, and we know
from Propositions 1 and 4. Note that if
![]() $m\in A_{4}$
then
$m\in A_{4}$
then
![]() $\mathbb{Q}(\sqrt{-m})$
has even discriminant; therefore from Proposition 1, we can easily show that
$\mathbb{Q}(\sqrt{-m})$
has even discriminant; therefore from Proposition 1, we can easily show that
![]() $m\in P_{2}$
or
$m\in P_{2}$
or
![]() $m/2\in P_{2}$
. But we know
$m/2\in P_{2}$
. But we know
![]() $\unicode[STIX]{x1D6FF}(P_{2}/P_{3})=0$
from (1), which yields
$\unicode[STIX]{x1D6FF}(P_{2}/P_{3})=0$
from (1), which yields
![]() $\unicode[STIX]{x1D6FF}(A_{4}/P_{3})=0$
. Hence,
$\unicode[STIX]{x1D6FF}(A_{4}/P_{3})=0$
. Hence,
Now we see
![]() $\unicode[STIX]{x1D6FF}(A_{1}/P_{3})$
. We put:
$\unicode[STIX]{x1D6FF}(A_{1}/P_{3})$
. We put:
(i)
 $F_{1}=\mathbb{Q}(\sqrt{-1}),{\mathcal{C}}_{1}=\{j\},\unicode[STIX]{x1D6FF}_{1}=\frac{1}{2}$
where
$F_{1}=\mathbb{Q}(\sqrt{-1}),{\mathcal{C}}_{1}=\{j\},\unicode[STIX]{x1D6FF}_{1}=\frac{1}{2}$
where  corresponds to
corresponds to
 $\mathbb{Q}$
;
$\mathbb{Q}$
;(ii)
 $F_{p}=\mathbb{Q}(\sqrt{-1},\sqrt{p}),{\mathcal{C}}_{p}=\{\unicode[STIX]{x1D70E}\},\unicode[STIX]{x1D6FF}_{2}=\frac{1}{4}$
for primes
$F_{p}=\mathbb{Q}(\sqrt{-1},\sqrt{p}),{\mathcal{C}}_{p}=\{\unicode[STIX]{x1D70E}\},\unicode[STIX]{x1D6FF}_{2}=\frac{1}{4}$
for primes
 $p\equiv -1~(4)$
, where
$p\equiv -1~(4)$
, where  corresponds to
corresponds to
 $\mathbb{Q}(\sqrt{-1})$
;
$\mathbb{Q}(\sqrt{-1})$
;(iii)
 $F_{pq}=\mathbb{Q}(\sqrt{-1},\sqrt{p},\sqrt{q},\sqrt{\unicode[STIX]{x1D700}_{q}}),{\mathcal{C}}_{pq}=\{\unicode[STIX]{x1D70F}\},\unicode[STIX]{x1D6FF}_{3}=\frac{1}{16}$
for primes
$F_{pq}=\mathbb{Q}(\sqrt{-1},\sqrt{p},\sqrt{q},\sqrt{\unicode[STIX]{x1D700}_{q}}),{\mathcal{C}}_{pq}=\{\unicode[STIX]{x1D70F}\},\unicode[STIX]{x1D6FF}_{3}=\frac{1}{16}$
for primes
 $p<q,\,-p\equiv q\equiv 1~(4)$
, where
$p<q,\,-p\equiv q\equiv 1~(4)$
, where
 $\unicode[STIX]{x1D700}_{q}$
is the fundamental unit of
$\unicode[STIX]{x1D700}_{q}$
is the fundamental unit of
 $\mathbb{Q}(\sqrt{q})$
, and
$\mathbb{Q}(\sqrt{q})$
, and  corresponds to
corresponds to
 $\mathbb{Q}(\sqrt{-1},\sqrt{q},\sqrt{p\unicode[STIX]{x1D700}_{q}})$
.
$\mathbb{Q}(\sqrt{-1},\sqrt{q},\sqrt{p\unicode[STIX]{x1D700}_{q}})$
.
Assume that GRH holds for these fields.
![]() $F_{a}$
and
$F_{a}$
and
![]() ${\mathcal{C}}_{a}$
are unused for the other integers
${\mathcal{C}}_{a}$
are unused for the other integers
![]() $a$
, so we may let them be anything.
$a$
, so we may let them be anything.
Then we show
![]() $S_{3}=A_{1}$
. As is well-known that
$S_{3}=A_{1}$
. As is well-known that
Now we consider
![]() $F_{pq}$
. Assume
$F_{pq}$
. Assume
![]() $p<q$
and
$p<q$
and
![]() $-p\equiv q\equiv 1~(4)$
. By Scholz’s reciprocity law [Reference Lemmermeyer12, Proposition 5.8], if
$-p\equiv q\equiv 1~(4)$
. By Scholz’s reciprocity law [Reference Lemmermeyer12, Proposition 5.8], if
![]() $q\equiv r\equiv 1~(4)$
and
$q\equiv r\equiv 1~(4)$
and
![]() $(q/r)=1$
,
$(q/r)=1$
,
We know that
 $$\begin{eqnarray}\displaystyle (p/r)=-1 & \;\Longleftrightarrow \; & \displaystyle r\text{ is inert in }\mathbb{Q}(\sqrt{p})/\mathbb{Q};\nonumber\\ \displaystyle (q/r)=+1 & \;\Longleftrightarrow \; & \displaystyle r\text{ splits in }\mathbb{Q}(\sqrt{q})/\mathbb{Q};\nonumber\\ \displaystyle (\unicode[STIX]{x1D700}_{q}/r)=-1 & \;\Longleftrightarrow \; & \displaystyle \text{the primes above }r\text{ are inert in }\mathbb{Q}(\sqrt{q},\sqrt{\unicode[STIX]{x1D700}_{q}})/\mathbb{Q}(\sqrt{q}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (p/r)=-1 & \;\Longleftrightarrow \; & \displaystyle r\text{ is inert in }\mathbb{Q}(\sqrt{p})/\mathbb{Q};\nonumber\\ \displaystyle (q/r)=+1 & \;\Longleftrightarrow \; & \displaystyle r\text{ splits in }\mathbb{Q}(\sqrt{q})/\mathbb{Q};\nonumber\\ \displaystyle (\unicode[STIX]{x1D700}_{q}/r)=-1 & \;\Longleftrightarrow \; & \displaystyle \text{the primes above }r\text{ are inert in }\mathbb{Q}(\sqrt{q},\sqrt{\unicode[STIX]{x1D700}_{q}})/\mathbb{Q}(\sqrt{q}).\nonumber\end{eqnarray}$$
![]() $F_{pq}$
includes these fields. It is straightforward to show that
$F_{pq}$
includes these fields. It is straightforward to show that
![]() $-(p/r)=(q/r)=-(\unicode[STIX]{x1D700}_{q}/r)=1$
if and only if the decomposition group of any prime ideal of
$-(p/r)=(q/r)=-(\unicode[STIX]{x1D700}_{q}/r)=1$
if and only if the decomposition group of any prime ideal of
![]() $F_{pq}$
above
$F_{pq}$
above
![]() $r$
is
$r$
is
![]() $\mathbb{Q}(\sqrt{-1},\sqrt{q},\sqrt{p\unicode[STIX]{x1D700}_{q}})$
. Hence, we have
$\mathbb{Q}(\sqrt{-1},\sqrt{q},\sqrt{p\unicode[STIX]{x1D700}_{q}})$
. Hence, we have
Therefore, for any primes
![]() $p<q<r$
we get
$p<q<r$
we get
This means
![]() $S_{3}=A_{1}$
by definition.
$S_{3}=A_{1}$
by definition.
Finally, we estimate the discriminant of
![]() $F_{a}$
. Clearly
$F_{a}$
. Clearly
![]() $|d_{F_{1}}|=4$
. Now
$|d_{F_{1}}|=4$
. Now
![]() $\mathbb{Q}(\sqrt{-1})$
and
$\mathbb{Q}(\sqrt{-1})$
and
![]() $\mathbb{Q}(\sqrt{-p})$
are linearly disjoint over
$\mathbb{Q}(\sqrt{-p})$
are linearly disjoint over
![]() $\mathbb{Q}$
, and their discriminants are coprime. This yields [Reference Lang11, Chapter III, Proposition 17]
$\mathbb{Q}$
, and their discriminants are coprime. This yields [Reference Lang11, Chapter III, Proposition 17]
For
![]() $F_{pq}$
, we first let
$F_{pq}$
, we first let
![]() $L=\mathbb{Q}(\sqrt{-1},\sqrt{-p},\sqrt{q})$
and we deduce as above
$L=\mathbb{Q}(\sqrt{-1},\sqrt{-p},\sqrt{q})$
and we deduce as above
Then we use the formula:
where
![]() $\mathfrak{d}_{F_{pq}/L}$
is the relative discriminant. Also we use the fact that
$\mathfrak{d}_{F_{pq}/L}$
is the relative discriminant. Also we use the fact that
![]() $\mathfrak{d}_{F_{pq}/L}$
divides the discriminant of the minimal polynomial of
$\mathfrak{d}_{F_{pq}/L}$
divides the discriminant of the minimal polynomial of
![]() $\sqrt{\unicode[STIX]{x1D700}_{q}}$
over
$\sqrt{\unicode[STIX]{x1D700}_{q}}$
over
![]() $L$
in
$L$
in
![]() ${\mathcal{O}}_{L}$
, the ring of integers in
${\mathcal{O}}_{L}$
, the ring of integers in
![]() $L$
. Hence, we have
$L$
. Hence, we have
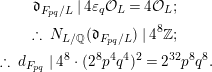 $$\begin{eqnarray}\displaystyle & \displaystyle \mathfrak{d}_{F_{pq}/L}\mid 4\unicode[STIX]{x1D700}_{q}{\mathcal{O}}_{L}=4{\mathcal{O}}_{L}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \therefore ~N_{L/\mathbb{Q}}(\mathfrak{d}_{F_{pq}/L})\mid 4^{8}\mathbb{Z}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \therefore ~d_{F_{pq}}\mid 4^{8}\cdot (2^{8}p^{4}q^{4})^{2}=2^{32}p^{8}q^{8}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathfrak{d}_{F_{pq}/L}\mid 4\unicode[STIX]{x1D700}_{q}{\mathcal{O}}_{L}=4{\mathcal{O}}_{L}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \therefore ~N_{L/\mathbb{Q}}(\mathfrak{d}_{F_{pq}/L})\mid 4^{8}\mathbb{Z}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \therefore ~d_{F_{pq}}\mid 4^{8}\cdot (2^{8}p^{4}q^{4})^{2}=2^{32}p^{8}q^{8}. & \displaystyle \nonumber\end{eqnarray}$$
In any cases,
![]() $F_{a}$
satisfies the discriminant condition of Theorem 2. For the facts about discriminants used above, see [Reference Fröhlich and Taylor3, Section III.2].
$F_{a}$
satisfies the discriminant condition of Theorem 2. For the facts about discriminants used above, see [Reference Fröhlich and Taylor3, Section III.2].
At this time we can apply Theorem 2, which yields
Similarly as above, we can also deduce
![]() $\unicode[STIX]{x1D6FF}(A_{2}/P_{3})=1/128$
by using
$\unicode[STIX]{x1D6FF}(A_{2}/P_{3})=1/128$
by using
and
![]() $\unicode[STIX]{x1D6FF}(A_{3}/P_{3})=1/128$
by using
$\unicode[STIX]{x1D6FF}(A_{3}/P_{3})=1/128$
by using
Therefore, we have
It is known in [Reference Gerth6] that
![]() $\unicode[STIX]{x1D6FF}(B(V_{4})/P_{3})=7/32$
; hence, we conclude
$\unicode[STIX]{x1D6FF}(B(V_{4})/P_{3})=7/32$
; hence, we conclude
Also we can calculate densities for
![]() $Q_{8},Q_{16}$
, and
$Q_{8},Q_{16}$
, and
![]() $\mathit{SD}_{16}$
in the same way. One can easily find the appropriate
$\mathit{SD}_{16}$
in the same way. One can easily find the appropriate
![]() $F_{a}$
and
$F_{a}$
and
![]() ${\mathcal{C}}_{a}$
by using the following fact: If
${\mathcal{C}}_{a}$
by using the following fact: If
![]() $q,r$
are odd primes with
$q,r$
are odd primes with
![]() $r\equiv 1~(4)$
and
$r\equiv 1~(4)$
and
![]() $(q/r)=1$
then
$(q/r)=1$
then
where
![]() $\mathbb{Q}(\unicode[STIX]{x1D701}_{r})_{4}$
is the quartic subfield of the
$\mathbb{Q}(\unicode[STIX]{x1D701}_{r})_{4}$
is the quartic subfield of the
![]() $r$
th cyclotomic field.
$r$
th cyclotomic field.
Theorem 3. The results in Table 1 hold.
Table 1. Densities.

Note that if the condition for
![]() $m\in A(G)$
can be written by using only quadratic residue symbols, we do not need GRH since we can use the same way as Gerth.
$m\in A(G)$
can be written by using only quadratic residue symbols, we do not need GRH since we can use the same way as Gerth.
4 Proof of Theorem 2
The following argument is basically from Gerth [Reference Gerth5]. However, we cannot use the same way to estimate error terms because the quartic residue symbol
![]() $(p/\cdot )_{4}$
cannot be considered as Dirichlet characters. Hence, we shall use the effective Chebotarev density theorem.
$(p/\cdot )_{4}$
cannot be considered as Dirichlet characters. Hence, we shall use the effective Chebotarev density theorem.
In what follows, we use the following notations:
(i)
 $\sum _{a<p\leqslant b}$
means a single summation on
$\sum _{a<p\leqslant b}$
means a single summation on
 $p$
only over primes.
$p$
only over primes.(ii) For a multivariable function
 $f$
,
$f$
,
 $O(f)$
means a term whose absolute value is always at most
$O(f)$
means a term whose absolute value is always at most
 $c|f|$
for some constant
$c|f|$
for some constant
 $c$
depending only on
$c$
depending only on
 $n$
and
$n$
and
 $\unicode[STIX]{x1D700}$
.
$\unicode[STIX]{x1D700}$
.
We shall use the following formulas [Reference Koch.9, Section 27.1], [Reference Hardy and Wright7, Chapter XXII]:
We may assume
![]() $n\geqslant 2$
. It suffices to show
$n\geqslant 2$
. It suffices to show
As in [Reference Gerth5], we write
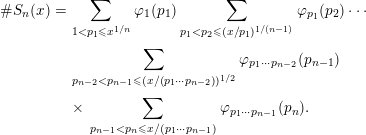 $$\begin{eqnarray}\displaystyle \#S_{n}(x) & = & \displaystyle \mathop{\sum }_{1<p_{1}\leqslant x^{1/n}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{1}<p_{2}\leqslant (x/p_{1})^{1/(n-1)}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \nonumber\\ \displaystyle & & \displaystyle \mathop{\sum }_{p_{n-2}<p_{n-1}\leqslant (x/(p_{1}\cdots p_{n-2}))^{1/2}}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-2}}(p_{n-1})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{p_{n-1}<p_{n}\leqslant x/(p_{1}\cdots p_{n-1})}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#S_{n}(x) & = & \displaystyle \mathop{\sum }_{1<p_{1}\leqslant x^{1/n}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{1}<p_{2}\leqslant (x/p_{1})^{1/(n-1)}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \nonumber\\ \displaystyle & & \displaystyle \mathop{\sum }_{p_{n-2}<p_{n-1}\leqslant (x/(p_{1}\cdots p_{n-2}))^{1/2}}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-2}}(p_{n-1})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{p_{n-1}<p_{n}\leqslant x/(p_{1}\cdots p_{n-1})}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n}).\nonumber\end{eqnarray}$$
Note that if
![]() $p_{1},\ldots ,p_{k}$
are in each interval, one has
$p_{1},\ldots ,p_{k}$
are in each interval, one has
In particular,
An elementary calculation shows
 $$\begin{eqnarray}\displaystyle \#S_{n}(x) & = & \displaystyle \mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p_{1}}\unicode[STIX]{x1D6FF}_{1}\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D6FF}_{2}\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D6FF}_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{p_{1}}(\unicode[STIX]{x1D711}_{1}(p_{1})-\unicode[STIX]{x1D6FF}_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D6FF}_{2}\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D6FF}_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}(\unicode[STIX]{x1D711}_{p_{1}}(p_{2})-\unicode[STIX]{x1D6FF}_{2})\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D6FF}_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\cdots \nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \mathop{\sum }_{p_{n}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#S_{n}(x) & = & \displaystyle \mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p_{1}}\unicode[STIX]{x1D6FF}_{1}\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D6FF}_{2}\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D6FF}_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{p_{1}}(\unicode[STIX]{x1D711}_{1}(p_{1})-\unicode[STIX]{x1D6FF}_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D6FF}_{2}\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D6FF}_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}(\unicode[STIX]{x1D711}_{p_{1}}(p_{2})-\unicode[STIX]{x1D6FF}_{2})\cdots \mathop{\sum }_{p_{n}}\unicode[STIX]{x1D6FF}_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\cdots \nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \mathop{\sum }_{p_{n}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n}).\end{eqnarray}$$
The first term in the right-hand side of (6) equals to
![]() $\unicode[STIX]{x1D6FF}_{1}\cdots \unicode[STIX]{x1D6FF}_{n}\#P_{n}(x)$
. So we have to estimate the remaining terms.
$\unicode[STIX]{x1D6FF}_{1}\cdots \unicode[STIX]{x1D6FF}_{n}\#P_{n}(x)$
. So we have to estimate the remaining terms.
We need the following estimation:
Lemma 3. Let
![]() $1\leqslant k\leqslant n$
and
$1\leqslant k\leqslant n$
and
![]() $a=p_{1}\cdots p_{k-1}\in P_{k-1}~(p_{1}<\cdots <p_{k-1})$
. Then for
$a=p_{1}\cdots p_{k-1}\in P_{k-1}~(p_{1}<\cdots <p_{k-1})$
. Then for
![]() $y\geqslant p_{k-1}$
,
$y\geqslant p_{k-1}$
,
Proof. From the definition of
![]() $\unicode[STIX]{x1D711}_{a}$
, we know
$\unicode[STIX]{x1D711}_{a}$
, we know

Also we note that
![]() $\unicode[STIX]{x1D70B}(y)=\sum _{p\leqslant y}1$
is the usual prime-counting function and
$\unicode[STIX]{x1D70B}(y)=\sum _{p\leqslant y}1$
is the usual prime-counting function and
![]() $\unicode[STIX]{x1D6FF}_{k}=\#{\mathcal{C}}_{a}/\#{\mathcal{G}}_{a}$
.
$\unicode[STIX]{x1D6FF}_{k}=\#{\mathcal{C}}_{a}/\#{\mathcal{G}}_{a}$
.
From the effective version of the Chebotarev density theorem [Reference Lagarias and Odlyzko10, Reference Serre15], we have
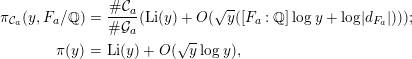 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{{\mathcal{C}}_{a}}(y,F_{a}/\mathbb{Q}) & = & \displaystyle \frac{\#{\mathcal{C}}_{a}}{\#{\mathcal{G}}_{a}}(\operatorname{Li}(y)+O(\sqrt{y}([F_{a}:\mathbb{Q}]\log y+\log |d_{F_{a}}|)));\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}(y) & = & \displaystyle \operatorname{Li}(y)+O(\sqrt{y}\log y),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{{\mathcal{C}}_{a}}(y,F_{a}/\mathbb{Q}) & = & \displaystyle \frac{\#{\mathcal{C}}_{a}}{\#{\mathcal{G}}_{a}}(\operatorname{Li}(y)+O(\sqrt{y}([F_{a}:\mathbb{Q}]\log y+\log |d_{F_{a}}|)));\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}(y) & = & \displaystyle \operatorname{Li}(y)+O(\sqrt{y}\log y),\nonumber\end{eqnarray}$$
where
Note that GRH for the Dedekind zeta function of
![]() $F_{a}$
implies the usual Riemann hypothesis. Our claim follows from these equations and our assumptions for
$F_{a}$
implies the usual Riemann hypothesis. Our claim follows from these equations and our assumptions for
![]() $|d_{F_{a}}|$
and
$|d_{F_{a}}|$
and
![]() $[F_{a}:\mathbb{Q}]$
.◻
$[F_{a}:\mathbb{Q}]$
.◻
We consider the last term of (6). Since
![]() $x/p_{1}\cdots p_{n-1}\geqslant p_{n-1}$
, we get
$x/p_{1}\cdots p_{n-1}\geqslant p_{n-1}$
, we get
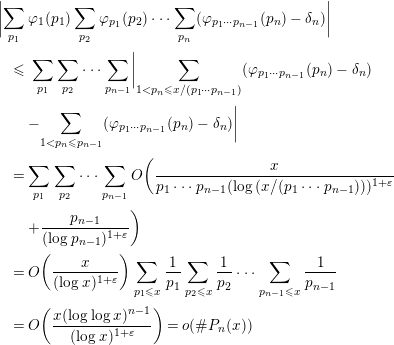 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \mathop{\sum }_{p_{n}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n})\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,\mathop{\sum }_{p_{1}}\mathop{\sum }_{p_{2}}\cdots \mathop{\sum }_{p_{n-1}}\biggl|\mathop{\sum }_{1<p_{n}\leqslant x/(p_{1}\cdots p_{n-1})}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n})\nonumber\\ \displaystyle & & \displaystyle \qquad -\mathop{\sum }_{1<p_{n}\leqslant p_{n-1}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n})\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p_{1}}\mathop{\sum }_{p_{2}}\cdots \mathop{\sum }_{p_{n-1}}O\biggl(\frac{x}{p_{1}\cdots p_{n-1}(\log (x/(p_{1}\cdots p_{n-1})))^{1+\unicode[STIX]{x1D700}}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\frac{p_{n-1}}{(\log p_{n-1})^{1+\unicode[STIX]{x1D700}}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x}{(\log x)^{1+\unicode[STIX]{x1D700}}}\biggr)\mathop{\sum }_{p_{1}\leqslant x}\frac{1}{p_{1}}\mathop{\sum }_{p_{2}\leqslant x}\frac{1}{p_{2}}\cdots \mathop{\sum }_{p_{n-1}\leqslant x}\frac{1}{p_{n-1}}\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x(\log \log x)^{n-1}}{(\log x)^{1+\unicode[STIX]{x1D700}}}\biggr)=o(\#P_{n}(x))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\mathop{\sum }_{p_{2}}\unicode[STIX]{x1D711}_{p_{1}}(p_{2})\cdots \mathop{\sum }_{p_{n}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n})\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,\mathop{\sum }_{p_{1}}\mathop{\sum }_{p_{2}}\cdots \mathop{\sum }_{p_{n-1}}\biggl|\mathop{\sum }_{1<p_{n}\leqslant x/(p_{1}\cdots p_{n-1})}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n})\nonumber\\ \displaystyle & & \displaystyle \qquad -\mathop{\sum }_{1<p_{n}\leqslant p_{n-1}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{n-1}}(p_{n})-\unicode[STIX]{x1D6FF}_{n})\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p_{1}}\mathop{\sum }_{p_{2}}\cdots \mathop{\sum }_{p_{n-1}}O\biggl(\frac{x}{p_{1}\cdots p_{n-1}(\log (x/(p_{1}\cdots p_{n-1})))^{1+\unicode[STIX]{x1D700}}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\frac{p_{n-1}}{(\log p_{n-1})^{1+\unicode[STIX]{x1D700}}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x}{(\log x)^{1+\unicode[STIX]{x1D700}}}\biggr)\mathop{\sum }_{p_{1}\leqslant x}\frac{1}{p_{1}}\mathop{\sum }_{p_{2}\leqslant x}\frac{1}{p_{2}}\cdots \mathop{\sum }_{p_{n-1}\leqslant x}\frac{1}{p_{n-1}}\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x(\log \log x)^{n-1}}{(\log x)^{1+\unicode[STIX]{x1D700}}}\biggr)=o(\#P_{n}(x))\nonumber\end{eqnarray}$$
Next we see the middle terms in the right-hand side of (6). We first claim
In fact, from (2) we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{1<p_{n}\leqslant (x/(p_{1}\cdots p_{n-1}))}1=\frac{x}{p_{1}\cdots p_{n-1}\log (x/(p_{1}\cdots p_{n-1}))}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\biggl(\frac{x}{p_{1}\cdots p_{n-1}(\log (x/(p_{1}\cdots p_{n-1})))^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x}{p_{1}\cdots p_{n-1}\log x}+\frac{x\log (p_{1}\cdots p_{n-1})}{p_{1}\cdots p_{n-1}\log (x/(p_{1}\cdots p_{n-1}))\log x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\biggl(\frac{x}{p_{1}\cdots p_{n-1}(\log x)^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x}{p_{1}\cdots p_{n-1}\log x}+O\biggl(\frac{x\log p_{n-1}}{p_{1}\cdots p_{n-1}(\log x)^{2}}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{1<p_{n}\leqslant (x/(p_{1}\cdots p_{n-1}))}1=\frac{x}{p_{1}\cdots p_{n-1}\log (x/(p_{1}\cdots p_{n-1}))}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\biggl(\frac{x}{p_{1}\cdots p_{n-1}(\log (x/(p_{1}\cdots p_{n-1})))^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x}{p_{1}\cdots p_{n-1}\log x}+\frac{x\log (p_{1}\cdots p_{n-1})}{p_{1}\cdots p_{n-1}\log (x/(p_{1}\cdots p_{n-1}))\log x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\biggl(\frac{x}{p_{1}\cdots p_{n-1}(\log x)^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{x}{p_{1}\cdots p_{n-1}\log x}+O\biggl(\frac{x\log p_{n-1}}{p_{1}\cdots p_{n-1}(\log x)^{2}}\biggr),\nonumber\end{eqnarray}$$
and from
we have
Hence, (7) follows. Then we can ignore the error term of (7) since
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p_{1}}\mathop{\sum }_{p_{2}}\cdots \mathop{\sum }_{p_{n-1}}O\biggl(\frac{x\log p_{n-1}}{p_{1}\cdots p_{n-1}(\log x)^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x}{(\log x)^{2}}\biggr)\mathop{\sum }_{p_{1}\leqslant x}\frac{1}{p_{1}}\mathop{\sum }_{p_{2}\leqslant x}\frac{1}{p_{2}}\cdots \mathop{\sum }_{p_{n-1}\leqslant x}\frac{\log p_{n-1}}{p_{n-1}}\nonumber\\ \displaystyle & = & \displaystyle O\biggl(\frac{x(\log \log x)^{n-2}}{\log x}\biggr)=o(\#P_{n}(x))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p_{1}}\mathop{\sum }_{p_{2}}\cdots \mathop{\sum }_{p_{n-1}}O\biggl(\frac{x\log p_{n-1}}{p_{1}\cdots p_{n-1}(\log x)^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x}{(\log x)^{2}}\biggr)\mathop{\sum }_{p_{1}\leqslant x}\frac{1}{p_{1}}\mathop{\sum }_{p_{2}\leqslant x}\frac{1}{p_{2}}\cdots \mathop{\sum }_{p_{n-1}\leqslant x}\frac{\log p_{n-1}}{p_{n-1}}\nonumber\\ \displaystyle & = & \displaystyle O\biggl(\frac{x(\log \log x)^{n-2}}{\log x}\biggr)=o(\#P_{n}(x))\nonumber\end{eqnarray}$$
from (3) and (4). Thus, we have to estimate
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\cdots \mathop{\sum }_{p_{k}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k})\mathop{\sum }_{p_{k+1}}\unicode[STIX]{x1D6FF}_{k+1}\cdots \nonumber\\ \displaystyle & & \displaystyle \quad \mathop{\sum }_{p_{n-1}}\unicode[STIX]{x1D6FF}_{n-1}\frac{\unicode[STIX]{x1D6FF}_{n}x}{p_{1}\cdots p_{n-1}\log x}\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x}{\log x}\biggr)\mathop{\sum }_{p_{1}}\frac{1}{p_{1}}\cdots \mathop{\sum }_{p_{k_{1}}}\frac{1}{p_{k-1}}\nonumber\\ \displaystyle & & \displaystyle \quad \biggl|\mathop{\sum }_{p_{k}}\frac{\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k}}{p_{k}}\mathop{\sum }_{p_{k+1}}\frac{1}{p_{k+1}}\cdots \mathop{\sum }_{p_{n-1}}\frac{1}{p_{n-1}}\biggr|\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p_{1}}\unicode[STIX]{x1D711}_{1}(p_{1})\cdots \mathop{\sum }_{p_{k}}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k})\mathop{\sum }_{p_{k+1}}\unicode[STIX]{x1D6FF}_{k+1}\cdots \nonumber\\ \displaystyle & & \displaystyle \quad \mathop{\sum }_{p_{n-1}}\unicode[STIX]{x1D6FF}_{n-1}\frac{\unicode[STIX]{x1D6FF}_{n}x}{p_{1}\cdots p_{n-1}\log x}\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x}{\log x}\biggr)\mathop{\sum }_{p_{1}}\frac{1}{p_{1}}\cdots \mathop{\sum }_{p_{k_{1}}}\frac{1}{p_{k-1}}\nonumber\\ \displaystyle & & \displaystyle \quad \biggl|\mathop{\sum }_{p_{k}}\frac{\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k}}{p_{k}}\mathop{\sum }_{p_{k+1}}\frac{1}{p_{k+1}}\cdots \mathop{\sum }_{p_{n-1}}\frac{1}{p_{n-1}}\biggr|\end{eqnarray}$$
for
![]() $1\leqslant k\leqslant n-1$
.We write
$1\leqslant k\leqslant n-1$
.We write
for
![]() $1\leqslant k\leqslant n-2$
and
$1\leqslant k\leqslant n-2$
and
![]() $s_{n-1}=1$
. Then we prove
$s_{n-1}=1$
. Then we prove
for
![]() $1\leqslant k\leqslant n-1$
. If
$1\leqslant k\leqslant n-1$
. If
![]() $k=n-1$
it is obvious, and if
$k=n-1$
it is obvious, and if
![]() $k=n-2$
it follows from (3) and (5). Suppose
$k=n-2$
it follows from (3) and (5). Suppose
![]() $2\leqslant k\leqslant n-2$
. Put
$2\leqslant k\leqslant n-2$
. Put
Suppose now
![]() $s_{k}=f_{1}(p_{k})+O((\log \log x)^{n-k-2})$
. Let
$s_{k}=f_{1}(p_{k})+O((\log \log x)^{n-k-2})$
. Let
then from (5),
Let
![]() $C_{1}(t)=\sum _{p\leqslant t}1/p$
. Then from (3)
$C_{1}(t)=\sum _{p\leqslant t}1/p$
. Then from (3)
Next we quote Abel’s summation formula [Reference Hardy and Wright7, Theorem 421]:
Proposition 6. Let
![]() $\{{c_{m}\}}_{m\in \mathbb{N}}$
be a sequence of numbers. Put
$\{{c_{m}\}}_{m\in \mathbb{N}}$
be a sequence of numbers. Put
Let
![]() $f(t)$
be a function which is continuously differentiable for
$f(t)$
be a function which is continuously differentiable for
![]() $t\geqslant 1$
. Then
$t\geqslant 1$
. Then
Using this proposition we have
 $$\begin{eqnarray}\displaystyle s_{k-1} & = & \displaystyle \mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{s_{k}}{p_{k}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{1}{p_{k}}f_{1}(p_{k})+O((\log \log x)^{n-k-2})\mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{1}{p_{k}}\nonumber\\ \displaystyle & = & \displaystyle C_{1}(y)f_{1}(y)-C_{1}(p_{k-1})f_{1}(p_{k-1})\nonumber\\ \displaystyle & & \displaystyle -\,\int _{p_{k-1}}^{y}C_{1}(t)f_{1}^{\prime }(t)\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle (\log \log x+O(1))O(1)-(\log \log p_{k-1}+O(1))f_{1}(p_{k-1})\nonumber\\ \displaystyle & & \displaystyle +\,\int _{p_{k-1}}^{y}(\log \log t+O(1))|f_{1}^{\prime }(t)|\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}+(\log \log x+O(1))\int _{p_{k-1}}^{y}|f_{1}^{\prime }(t)|\,dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{p_{k-1}}^{y}(\log \log x-\log \log t)|f_{1}^{\prime }(t)|\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}-(\log \log x+O(1))\int _{p_{k-1}}^{y}f_{1}^{\prime }(t)\,dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{p_{k-1}}^{y}\frac{(\log \log x-\log \log t)^{n-k-1}}{(n-k-2)!\,t\log t}\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}-(\log \log x+O(1))[f_{1}(t)]_{p_{k-1}}^{y}\nonumber\\ \displaystyle & & \displaystyle -\,\biggl[-\frac{(\log \log x-\log \log t)^{n-k}}{(n-k-2)!(n-k)}\biggr]_{p_{k-1}}^{y}+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}+f_{1}(p_{k-1})\log \log x\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(\log \log x-\log \log p_{k-1})^{n-k}}{(n-k-2)!(n-k)}+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{(\log \log x-\log \log p_{k-1})^{n-k}}{(n-k-2)!}\biggl(\frac{1}{n-k-1}-\frac{1}{n-k}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{(\log \log x-\log \log p_{k-1})^{n-k}}{(n-k)!}+O((\log \log x)^{n-k-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{k-1} & = & \displaystyle \mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{s_{k}}{p_{k}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{1}{p_{k}}f_{1}(p_{k})+O((\log \log x)^{n-k-2})\mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{1}{p_{k}}\nonumber\\ \displaystyle & = & \displaystyle C_{1}(y)f_{1}(y)-C_{1}(p_{k-1})f_{1}(p_{k-1})\nonumber\\ \displaystyle & & \displaystyle -\,\int _{p_{k-1}}^{y}C_{1}(t)f_{1}^{\prime }(t)\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle (\log \log x+O(1))O(1)-(\log \log p_{k-1}+O(1))f_{1}(p_{k-1})\nonumber\\ \displaystyle & & \displaystyle +\,\int _{p_{k-1}}^{y}(\log \log t+O(1))|f_{1}^{\prime }(t)|\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}+(\log \log x+O(1))\int _{p_{k-1}}^{y}|f_{1}^{\prime }(t)|\,dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{p_{k-1}}^{y}(\log \log x-\log \log t)|f_{1}^{\prime }(t)|\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}-(\log \log x+O(1))\int _{p_{k-1}}^{y}f_{1}^{\prime }(t)\,dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{p_{k-1}}^{y}\frac{(\log \log x-\log \log t)^{n-k-1}}{(n-k-2)!\,t\log t}\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}-(\log \log x+O(1))[f_{1}(t)]_{p_{k-1}}^{y}\nonumber\\ \displaystyle & & \displaystyle -\,\biggl[-\frac{(\log \log x-\log \log t)^{n-k}}{(n-k-2)!(n-k)}\biggr]_{p_{k-1}}^{y}+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle -f_{1}(p_{k-1})\log \log p_{k-1}+f_{1}(p_{k-1})\log \log x\nonumber\\ \displaystyle & & \displaystyle -\,\frac{(\log \log x-\log \log p_{k-1})^{n-k}}{(n-k-2)!(n-k)}+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{(\log \log x-\log \log p_{k-1})^{n-k}}{(n-k-2)!}\biggl(\frac{1}{n-k-1}-\frac{1}{n-k}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & = & \displaystyle \frac{(\log \log x-\log \log p_{k-1})^{n-k}}{(n-k)!}+O((\log \log x)^{n-k-1}).\nonumber\end{eqnarray}$$
Hence we have proved (9) by induction.
Next we claim
for
![]() $1\leqslant k\leqslant n-1$
. In fact, let
$1\leqslant k\leqslant n-1$
. In fact, let
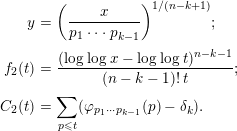 $$\begin{eqnarray}\displaystyle y & = & \displaystyle \biggl(\frac{x}{p_{1}\cdots p_{k-1}}\biggr)^{1/(n-k+1)};\nonumber\\ \displaystyle f_{2}(t) & = & \displaystyle \frac{(\log \log x-\log \log t)^{n-k-1}}{(n-k-1)!\,t};\nonumber\\ \displaystyle C_{2}(t) & = & \displaystyle \mathop{\sum }_{p\leqslant t}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p)-\unicode[STIX]{x1D6FF}_{k}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y & = & \displaystyle \biggl(\frac{x}{p_{1}\cdots p_{k-1}}\biggr)^{1/(n-k+1)};\nonumber\\ \displaystyle f_{2}(t) & = & \displaystyle \frac{(\log \log x-\log \log t)^{n-k-1}}{(n-k-1)!\,t};\nonumber\\ \displaystyle C_{2}(t) & = & \displaystyle \mathop{\sum }_{p\leqslant t}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p)-\unicode[STIX]{x1D6FF}_{k}).\nonumber\end{eqnarray}$$
Then from (9) we have
and from Lemma 3,
for
![]() $t\geqslant p_{k-1}$
. Similarly as before, by Proposition 6,
$t\geqslant p_{k-1}$
. Similarly as before, by Proposition 6,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k}}{p_{k}}s_{k}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k})f_{2}(p_{k})+O((\log \log x)^{n-k-2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{1}{p_{k}}=C_{2}(y)f_{2}(y)-C_{2}(p_{k-1})f_{2}(p_{k-1})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{p_{k-1}}^{y}C_{2}(t)f_{2}^{\prime }(t)\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{y}{(\log y)^{1+\unicode[STIX]{x1D700}}}\biggr)O\biggl(\frac{1}{y}\biggr)+O\biggl(\frac{p_{k-1}}{(\log p_{k-1})^{1+\unicode[STIX]{x1D700}}}\biggr)O\biggl(\frac{(\log \log x)^{n-k-1}}{p_{k-1}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{p_{k-1}}^{y}O\biggl(\frac{t}{(\log t)^{1+\unicode[STIX]{x1D700}}}\biggr)|f_{2}^{\prime }(t)|\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{p_{k-1}}^{y}O\biggl(\frac{t}{(\log t)^{1+\unicode[STIX]{x1D700}}}\biggr)O\biggl(\frac{(\log \log x)^{n-k-1}}{t^{2}}\biggr)\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O((\log \log x)^{n-k-1})\int _{p_{k-1}}^{y}\frac{1}{t(\log t)^{1+\unicode[STIX]{x1D700}}}\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O((\log \log x)^{n-k-1})\biggl[-\frac{1}{(\log t)^{\unicode[STIX]{x1D700}}}\biggr]_{p_{k-1}}^{y}+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O((\log \log x)^{n-k-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k}}{p_{k}}s_{k}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}(\unicode[STIX]{x1D711}_{p_{1}\cdots p_{k-1}}(p_{k})-\unicode[STIX]{x1D6FF}_{k})f_{2}(p_{k})+O((\log \log x)^{n-k-2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{p_{k-1}<p_{k}\leqslant y}\frac{1}{p_{k}}=C_{2}(y)f_{2}(y)-C_{2}(p_{k-1})f_{2}(p_{k-1})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{p_{k-1}}^{y}C_{2}(t)f_{2}^{\prime }(t)\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{y}{(\log y)^{1+\unicode[STIX]{x1D700}}}\biggr)O\biggl(\frac{1}{y}\biggr)+O\biggl(\frac{p_{k-1}}{(\log p_{k-1})^{1+\unicode[STIX]{x1D700}}}\biggr)O\biggl(\frac{(\log \log x)^{n-k-1}}{p_{k-1}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{p_{k-1}}^{y}O\biggl(\frac{t}{(\log t)^{1+\unicode[STIX]{x1D700}}}\biggr)|f_{2}^{\prime }(t)|\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{p_{k-1}}^{y}O\biggl(\frac{t}{(\log t)^{1+\unicode[STIX]{x1D700}}}\biggr)O\biggl(\frac{(\log \log x)^{n-k-1}}{t^{2}}\biggr)\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O((\log \log x)^{n-k-1})\int _{p_{k-1}}^{y}\frac{1}{t(\log t)^{1+\unicode[STIX]{x1D700}}}\,dt+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O((\log \log x)^{n-k-1})\biggl[-\frac{1}{(\log t)^{\unicode[STIX]{x1D700}}}\biggr]_{p_{k-1}}^{y}+O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O((\log \log x)^{n-k-1}).\nonumber\end{eqnarray}$$
Thus (10) follows.
Therefore, (8) becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle O\biggl(\frac{x}{\log x}\biggr)\mathop{\sum }_{p_{1}}\frac{1}{p_{1}}\cdots \mathop{\sum }_{p_{k-1}}\frac{1}{p_{k-1}}O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x(\log \log x)^{n-2}}{\log x}\biggr)=o(\#P_{n}(x)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle O\biggl(\frac{x}{\log x}\biggr)\mathop{\sum }_{p_{1}}\frac{1}{p_{1}}\cdots \mathop{\sum }_{p_{k-1}}\frac{1}{p_{k-1}}O((\log \log x)^{n-k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =O\biggl(\frac{x(\log \log x)^{n-2}}{\log x}\biggr)=o(\#P_{n}(x)).\nonumber\end{eqnarray}$$
Hence we have completed the proof.
5 Densities for the remaining groups
We cannot get the densities for the remaining groups because we do not know any conditions for them in which Theorem 2 can be applied. We want to know about the conditions
![]() $h_{2}(-pq)=2^{n},h_{2}(qr)=2^{n}$
or
$h_{2}(-pq)=2^{n},h_{2}(qr)=2^{n}$
or
![]() $\mathbf{N}\unicode[STIX]{x1D700}_{qr}=1$
in detail.
$\mathbf{N}\unicode[STIX]{x1D700}_{qr}=1$
in detail.
Cohn and Lagarias [Reference Cohn and Lagarias2] considered
![]() $\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{dp}))$
as
$\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{dp}))$
as
![]() $p$
varies where
$p$
varies where
![]() $d\not \equiv 2~(4)$
is an integer. They conjectured that the splitting of primes in a number field determines the structure of
$d\not \equiv 2~(4)$
is an integer. They conjectured that the splitting of primes in a number field determines the structure of
![]() $\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{dp}))$
, and they also considered numerically. Here we consider
$\operatorname{Cl}_{2}(\mathbb{Q}(\sqrt{dp}))$
, and they also considered numerically. Here we consider
![]() $h_{2}(dp)$
and
$h_{2}(dp)$
and
![]() $h_{2}^{+}(dp)$
where
$h_{2}^{+}(dp)$
where
![]() $d$
is an odd prime discriminant.
$d$
is an odd prime discriminant.
We suggest the following conjecture:
Conjecture 1.
(1) For a prime
 $p\equiv -1~(4)$
and an integer
$p\equiv -1~(4)$
and an integer
 $n\geqslant 1$
, there are
$n\geqslant 1$
, there are
 $F_{p}^{(n)}$
and
$F_{p}^{(n)}$
and
 ${\mathcal{C}}_{p}^{(n)}$
as in Section 3 such that for a prime
${\mathcal{C}}_{p}^{(n)}$
as in Section 3 such that for a prime
 $q\equiv 1~(4)$
which does not ramify in
$q\equiv 1~(4)$
which does not ramify in
 $F_{p}^{(n)}$
,In addition,
$F_{p}^{(n)}$
,In addition,
 $\#{\mathcal{C}}_{p}^{(n)}/[F_{p}^{(n)}:\mathbb{Q}]=1/2^{n}$
. And the similar one holds for
$\#{\mathcal{C}}_{p}^{(n)}/[F_{p}^{(n)}:\mathbb{Q}]=1/2^{n}$
. And the similar one holds for
 $p\equiv 1~(4)$
and
$p\equiv 1~(4)$
and
 $q\equiv -1~(4)$
.
$q\equiv -1~(4)$
.(2) For a prime
 $p\equiv 1~(4)$
and integers
$p\equiv 1~(4)$
and integers
 $m,n$
with
$m,n$
with
 $1\leqslant m\leqslant n\leqslant m+1$
, there are
$1\leqslant m\leqslant n\leqslant m+1$
, there are
 $F_{p}^{(m,n)}$
and
$F_{p}^{(m,n)}$
and
 ${\mathcal{C}}_{p}^{(m,n)}$
as in Section 3 such that for a prime
${\mathcal{C}}_{p}^{(m,n)}$
as in Section 3 such that for a prime
 $q\equiv 1~(4)$
which does not ramify in
$q\equiv 1~(4)$
which does not ramify in
 $F_{p}^{(m,n)}\!$
,In addition,
$F_{p}^{(m,n)}\!$
,In addition,
 $\#{\mathcal{C}}_{p}^{(m,n)}/[F_{p}^{(m,n)}:\mathbb{Q}]=1/2^{m+n-1}$
.
$\#{\mathcal{C}}_{p}^{(m,n)}/[F_{p}^{(m,n)}:\mathbb{Q}]=1/2^{m+n-1}$
.
Note that
![]() $h_{2}(pq)=h_{2}^{+}(pq)$
if and only if
$h_{2}(pq)=h_{2}^{+}(pq)$
if and only if
![]() $\mathbf{N}\unicode[STIX]{x1D700}_{pq}=-1$
.
$\mathbf{N}\unicode[STIX]{x1D700}_{pq}=-1$
.
Stevenhagen [Reference Stevenhagen16] showed that the narrow
![]() $8$
-ranks of quadratic fields are determined by number fields. Hence the cases
$8$
-ranks of quadratic fields are determined by number fields. Hence the cases
![]() $n\leqslant 2$
in both 1 and 2 of Conjecture 1 are known to be true. Unfortunately however, Milovic [Reference Milovic13] gives some evidence against Conjecture 1 for
$n\leqslant 2$
in both 1 and 2 of Conjecture 1 are known to be true. Unfortunately however, Milovic [Reference Milovic13] gives some evidence against Conjecture 1 for
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
We calculated the numbers of
![]() $pq<10^{7}$
(
$pq<10^{7}$
(
![]() $p,q:$
primes) with
$p,q:$
primes) with
![]() $-p\equiv q\equiv 1~(4),h_{2}(-pq)=2^{n}$
; and also with
$-p\equiv q\equiv 1~(4),h_{2}(-pq)=2^{n}$
; and also with
![]() $p\equiv q\equiv 1~(4)$
and
$p\equiv q\equiv 1~(4)$
and
![]() $h_{2}(pq)h_{2}^{+}(pq)/2=2^{n}$
for each
$h_{2}(pq)h_{2}^{+}(pq)/2=2^{n}$
for each
![]() $n\in \mathbb{N}$
(using SageMath 6.10); see Table 2. Note that both
$n\in \mathbb{N}$
(using SageMath 6.10); see Table 2. Note that both
![]() $p$
and
$p$
and
![]() $q$
vary.
$q$
vary.
Table 2. Numbers of
![]() $pq<10^{7}$
with
$pq<10^{7}$
with
![]() $h_{2}(-pq)=2^{n}$
and with
$h_{2}(-pq)=2^{n}$
and with
![]() $h_{2}(pq)h_{2}^{+}(pq)/2=2^{n}$
.
$h_{2}(pq)h_{2}^{+}(pq)/2=2^{n}$
.

Table 3. Conjectured densities.

This conjecture yields the densities for the remaining groups:
Theorem 4. Assume that Conjecture 1 holds. In addition, we assume that each
![]() $F_{p}$
in Conjecture 1 satisfies
$F_{p}$
in Conjecture 1 satisfies
Moreover we assume GRH.
Then the results in Table 3 hold.
Proof. From our assumptions, we can apply Theorem 2. We omit the details.
Note that
![]() $\unicode[STIX]{x1D6FF}(\cdot /B(V_{4}))$
is not countably additive in general. In this case, however, we can calculate the densities of
$\unicode[STIX]{x1D6FF}(\cdot /B(V_{4}))$
is not countably additive in general. In this case, however, we can calculate the densities of
![]() $A_{Q}=\bigcup _{n=3}^{\infty }A(Q_{2^{n}})$
and
$A_{Q}=\bigcup _{n=3}^{\infty }A(Q_{2^{n}})$
and
![]() $A_{D}=\bigcup _{n=3}^{\infty }A(D_{2^{n}})$
. In fact, for
$A_{D}=\bigcup _{n=3}^{\infty }A(D_{2^{n}})$
. In fact, for
![]() $N,x\in \mathbb{N}$
$N,x\in \mathbb{N}$
where
![]() $A(x)=\{\,m\in A\,|\,m\leqslant x\,\}$
for
$A(x)=\{\,m\in A\,|\,m\leqslant x\,\}$
for
![]() $A\subseteq \mathbb{N}$
. Hence,
$A\subseteq \mathbb{N}$
. Hence,
for
![]() $N\in \mathbb{N}$
. Hence,
$N\in \mathbb{N}$
. Hence,
Similarly,
On the other hand, since
we have
 $$\begin{eqnarray}\displaystyle \limsup _{x\rightarrow \infty }\frac{\#A_{Q}(x)}{\#B(V_{4})(x)} & = & \displaystyle \limsup _{x\rightarrow \infty }\biggl(\frac{\#(A_{Q}(x)\cup A_{D}(x))}{\#B(V_{4})(x)}-\frac{\#A_{D}(x)}{\#B(V_{4})(x)}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \lim _{x\rightarrow \infty }\frac{\#(A_{Q}(x)\cup A_{D}(x))}{\#B(V_{4})(x)}-\liminf _{x\rightarrow \infty }\frac{\#A_{D}(x)}{\#B(V_{4})(x)}\leqslant \frac{2}{7}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \limsup _{x\rightarrow \infty }\frac{\#A_{Q}(x)}{\#B(V_{4})(x)} & = & \displaystyle \limsup _{x\rightarrow \infty }\biggl(\frac{\#(A_{Q}(x)\cup A_{D}(x))}{\#B(V_{4})(x)}-\frac{\#A_{D}(x)}{\#B(V_{4})(x)}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \lim _{x\rightarrow \infty }\frac{\#(A_{Q}(x)\cup A_{D}(x))}{\#B(V_{4})(x)}-\liminf _{x\rightarrow \infty }\frac{\#A_{D}(x)}{\#B(V_{4})(x)}\leqslant \frac{2}{7}.\nonumber\end{eqnarray}$$
Putting these together, we obtain that all these inequalities are equalities and
![]() $\liminf =\limsup$
. It is similar for
$\liminf =\limsup$
. It is similar for
![]() $A_{D}$
.◻
$A_{D}$
.◻