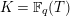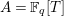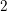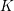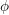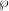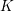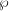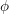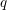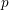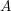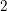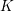1 Introduction
It is well known that there is a close analogy between the arithmetic of Drinfeld
![]() $A$
-modules of rank
$A$
-modules of rank
![]() $2$
over
$2$
over
![]() $K=\mathbb{F}_{q}(T)$
(where
$K=\mathbb{F}_{q}(T)$
(where
![]() $A=\mathbb{F}_{q}[T]$
and
$A=\mathbb{F}_{q}[T]$
and
![]() $\mathbb{F}_{q}$
is a finite field of order
$\mathbb{F}_{q}$
is a finite field of order
![]() $q$
), and elliptic curves over
$q$
), and elliptic curves over
![]() $\mathbb{Q}$
, and that considering arithmetical problems from both perspectives enhances our understanding of the intrinsic difficulty of the problems in question. In this paper, we investigate the problem of obtaining explicit large image results for the fields generated by torsion points of Drinfeld modules.
$\mathbb{Q}$
, and that considering arithmetical problems from both perspectives enhances our understanding of the intrinsic difficulty of the problems in question. In this paper, we investigate the problem of obtaining explicit large image results for the fields generated by torsion points of Drinfeld modules.
Serre proved in [Reference Serre24] that if
![]() $E$
is an elliptic curve over a number field
$E$
is an elliptic curve over a number field
![]() $K$
without complex multiplication, then there is a constant
$K$
without complex multiplication, then there is a constant
![]() $c_{K,E}$
dependent only on
$c_{K,E}$
dependent only on
![]() $K$
and
$K$
and
![]() $E$
such that the Galois representation
$E$
such that the Galois representation
![]() $\unicode[STIX]{x1D70C}_{E,p}$
on the
$\unicode[STIX]{x1D70C}_{E,p}$
on the
![]() $p$
-torsion points of
$p$
-torsion points of
![]() $E$
is surjective for any prime number
$E$
is surjective for any prime number
![]() $p>c_{K,E}$
. There has been some work on obtaining explicit values for the constants
$p>c_{K,E}$
. There has been some work on obtaining explicit values for the constants
![]() $c_{K,E}$
when
$c_{K,E}$
when
![]() $K=\mathbb{Q}$
(Serre [Reference Serre26], Kraus [Reference Kraus14], Cojocaru–Hall [Reference Cojocaru and Hall4], Lombardo [Reference Lombardo16]). The assumption of the generalized Riemann hypothesis allows one to considerably improve these bounds [Reference Serre26].
$K=\mathbb{Q}$
(Serre [Reference Serre26], Kraus [Reference Kraus14], Cojocaru–Hall [Reference Cojocaru and Hall4], Lombardo [Reference Lombardo16]). The assumption of the generalized Riemann hypothesis allows one to considerably improve these bounds [Reference Serre26].
In the case
![]() $K=\mathbb{Q}$
, the analysis normally proceeds by dividing the argument into which type of maximal proper subgroup contains the image of
$K=\mathbb{Q}$
, the analysis normally proceeds by dividing the argument into which type of maximal proper subgroup contains the image of
![]() $\unicode[STIX]{x1D70C}_{E,p}$
. The most difficult case is when the image of
$\unicode[STIX]{x1D70C}_{E,p}$
. The most difficult case is when the image of
![]() $\unicode[STIX]{x1D70C}_{E,p}$
lies in the normalizer of a Cartan subgroup of
$\unicode[STIX]{x1D70C}_{E,p}$
lies in the normalizer of a Cartan subgroup of
![]() $\operatorname{GL}_{2}(\mathbb{Z}/p\mathbb{Z})$
. In all other cases, one in fact has a uniform bound on
$\operatorname{GL}_{2}(\mathbb{Z}/p\mathbb{Z})$
. In all other cases, one in fact has a uniform bound on
![]() $c_{K,E}$
which is independent of the elliptic curve
$c_{K,E}$
which is independent of the elliptic curve
![]() $E$
without complex multiplication, by work of Mazur [Reference Mazur17] on rational points on modular curves.
$E$
without complex multiplication, by work of Mazur [Reference Mazur17] on rational points on modular curves.
The analogue of Serre’s result [Reference Serre24] for Drinfeld
![]() $A$
-modules of rank
$A$
-modules of rank
![]() $2$
was proved by Gardeyn [Reference Gardeyn11], using the earlier work of Pink on the Mumford–Tate conjecture for Drinfeld modules [Reference Pink20]. In detail, if
$2$
was proved by Gardeyn [Reference Gardeyn11], using the earlier work of Pink on the Mumford–Tate conjecture for Drinfeld modules [Reference Pink20]. In detail, if
![]() $\unicode[STIX]{x1D719}$
is a Drinfeld module of rank
$\unicode[STIX]{x1D719}$
is a Drinfeld module of rank
![]() $2$
without complex multiplication over a fixed finite extension of
$2$
without complex multiplication over a fixed finite extension of
![]() $K$
, then there are only finitely many primes
$K$
, then there are only finitely many primes
![]() ${\wp}$
such that the image of the Galois representation
${\wp}$
such that the image of the Galois representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
on the
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
on the
![]() ${\wp}$
-torsion points of
${\wp}$
-torsion points of
![]() $\unicode[STIX]{x1D719}$
is not surjective. The case of general rank was recently proven in [Reference Pink and Rütsche21].
$\unicode[STIX]{x1D719}$
is not surjective. The case of general rank was recently proven in [Reference Pink and Rütsche21].
In this paper, we obtain an explicit upper bound on the degree of primes
![]() ${\wp}$
of
${\wp}$
of
![]() $K$
such that
$K$
such that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective, for any Drinfeld
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective, for any Drinfeld
![]() $A$
-module
$A$
-module
![]() $\unicode[STIX]{x1D719}$
of rank
$\unicode[STIX]{x1D719}$
of rank
![]() $2$
over
$2$
over
![]() $K=\mathbb{F}_{q}(T)$
without complex multiplication, in the case when
$K=\mathbb{F}_{q}(T)$
without complex multiplication, in the case when
![]() $q$
is odd.
$q$
is odd.
The proof is modeled on the strategy of [Reference Serre24] and [Reference Serre26], some parts of which were made effective, though not explicit in [Reference Gardeyn12].
New difficulties arise however in carrying out the strategy of [Reference Serre24, Reference Serre26] in the setting of Drinfeld modules. One of these is obtaining an explicit bound on the degree of the different divisor of division fields of
![]() $\unicode[STIX]{x1D719}$
, which in the function field case does not follow immediately from algebraic considerations. For this, we rely heavily on the results in [Reference Chen and Lee2, Reference Chen and Lee3] to make explicit the bounds on the different divisor and constant field extensions of torsion fields of Drinfeld
$\unicode[STIX]{x1D719}$
, which in the function field case does not follow immediately from algebraic considerations. For this, we rely heavily on the results in [Reference Chen and Lee2, Reference Chen and Lee3] to make explicit the bounds on the different divisor and constant field extensions of torsion fields of Drinfeld
![]() $A$
-modules over
$A$
-modules over
![]() $K$
.
$K$
.
On the other hand, the generalized Riemann hypothesis holds for function fields, so we are entitled to use better effective Chebotarev density theorems, which makes the final results unconditional and stronger when compared to the number field setting. In the Drinfeld module setting, we do not have uniform bounds in the Borel case because Mazur’s method has not yet been successfully adapted to work with Drinfeld modular curves in general. However, there are some partial results in this direction [Reference Armana1, Reference Pál19].
As part of the proof of the Cartan case, we also derive an explicit isogeny theorem for Drinfeld modules of rank
![]() $2$
over
$2$
over
![]() $K$
which uses the explicit bounds on the different divisor and constant field extensions obtained in [Reference Chen and Lee2]. A partially explicit isogeny theorem valid for general rank
$K$
which uses the explicit bounds on the different divisor and constant field extensions obtained in [Reference Chen and Lee2]. A partially explicit isogeny theorem valid for general rank
![]() $r$
and
$r$
and
![]() $K$
is proven in [Reference Chen and Lee3].
$K$
is proven in [Reference Chen and Lee3].
2 Main result
Let
![]() $\mathbb{F}_{q}$
be a finite field of order
$\mathbb{F}_{q}$
be a finite field of order
![]() $q$
,
$q$
,
![]() $A=\mathbb{F}_{q}[T]$
, and
$A=\mathbb{F}_{q}[T]$
, and
![]() $K=\mathbb{F}_{q}(T)$
. Throughout the paper, for the sake of simplicity,
$K=\mathbb{F}_{q}(T)$
. Throughout the paper, for the sake of simplicity,
![]() $:=$
is denoted to mean “is defined to be”.
$:=$
is denoted to mean “is defined to be”.
Let
![]() $L$
be a finite extension of
$L$
be a finite extension of
![]() $K$
,
$K$
,
![]() ${\mathcal{O}}_{L}$
be the maximal order of
${\mathcal{O}}_{L}$
be the maximal order of
![]() $L$
, that is, the integral closure of
$L$
, that is, the integral closure of
![]() $A$
in
$A$
in
![]() $L$
, and
$L$
, and
![]() $\mathbb{F}_{L}$
be the constant field of
$\mathbb{F}_{L}$
be the constant field of
![]() $L$
. For a prime ideal
$L$
. For a prime ideal
![]() $\mathfrak{B}$
of
$\mathfrak{B}$
of
![]() ${\mathcal{O}}_{L}$
, we let
${\mathcal{O}}_{L}$
, we let
![]() $\deg _{L}\mathfrak{B}$
be the
$\deg _{L}\mathfrak{B}$
be the
![]() $\mathbb{F}_{L}$
-dimension of the residue class field
$\mathbb{F}_{L}$
-dimension of the residue class field
![]() $\mathbb{F}_{L,\mathfrak{B}}:={\mathcal{O}}_{L}/\mathfrak{B}$
of
$\mathbb{F}_{L,\mathfrak{B}}:={\mathcal{O}}_{L}/\mathfrak{B}$
of
![]() $\mathfrak{B}$
, extending this to a general ideal
$\mathfrak{B}$
, extending this to a general ideal
![]() $I$
of
$I$
of
![]() ${\mathcal{O}}_{L}$
by additivity on products. For
${\mathcal{O}}_{L}$
by additivity on products. For
![]() $a$
in
$a$
in
![]() ${\mathcal{O}}_{L}$
, we define the degree of
${\mathcal{O}}_{L}$
, we define the degree of
![]() $a$
by
$a$
by
![]() $\deg _{L}a:=\deg _{L}(a)$
, where
$\deg _{L}a:=\deg _{L}(a)$
, where
![]() $(a)$
is the principal ideal of
$(a)$
is the principal ideal of
![]() ${\mathcal{O}}_{L}$
generated by
${\mathcal{O}}_{L}$
generated by
![]() $a$
.
$a$
.
By a prime
![]() ${\wp}$
(or place) of
${\wp}$
(or place) of
![]() $K$
, we mean a discrete valuation ring with field of fractions
$K$
, we mean a discrete valuation ring with field of fractions
![]() $K$
and maximal ideal
$K$
and maximal ideal
![]() ${\wp}$
, and
${\wp}$
, and
![]() $v$
denotes the discrete valuation associated to a prime
$v$
denotes the discrete valuation associated to a prime
![]() ${\wp}$
of
${\wp}$
of
![]() $K$
. Let
$K$
. Let
![]() $\infty$
be the infinite prime of
$\infty$
be the infinite prime of
![]() $K$
with corresponding discrete valuation
$K$
with corresponding discrete valuation
![]() $v_{\infty }(f/g)=\deg _{K}g-\deg _{K}f,$
where
$v_{\infty }(f/g)=\deg _{K}g-\deg _{K}f,$
where
![]() $f,g\in A$
.
$f,g\in A$
.
Let
![]() $\unicode[STIX]{x1D70F}$
be the map which raises an element to its
$\unicode[STIX]{x1D70F}$
be the map which raises an element to its
![]() $q$
th power. A Drinfeld
$q$
th power. A Drinfeld
![]() $A$
-module
$A$
-module
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $K$
is given by an
$K$
is given by an
![]() $\mathbb{F}_{q}$
-algebra homomorphism
$\mathbb{F}_{q}$
-algebra homomorphism
such that
![]() $\unicode[STIX]{x1D719}(a)$
has constant term
$\unicode[STIX]{x1D719}(a)$
has constant term
![]() $a$
for any
$a$
for any
![]() $a\in A$
, and the image of
$a\in A$
, and the image of
![]() $\unicode[STIX]{x1D719}$
is not contained in
$\unicode[STIX]{x1D719}$
is not contained in
![]() $K$
.
$K$
.
A Drinfeld
![]() $A$
-module
$A$
-module
![]() $\unicode[STIX]{x1D719}$
of rank
$\unicode[STIX]{x1D719}$
of rank
![]() $r$
over
$r$
over
![]() $K$
is completely determined by
$K$
is completely determined by
where
![]() $a_{j}(\unicode[STIX]{x1D719})\in K$
for
$a_{j}(\unicode[STIX]{x1D719})\in K$
for
![]() $j=1,2,\ldots ,r$
and
$j=1,2,\ldots ,r$
and
![]() $a_{r}(\unicode[STIX]{x1D719})$
is nonzero. For any monic
$a_{r}(\unicode[STIX]{x1D719})$
is nonzero. For any monic
![]() $a\in \mathbb{F}_{q}[T]$
, we then have
$a\in \mathbb{F}_{q}[T]$
, we then have
for some
![]() $a_{j}(\unicode[STIX]{x1D719},a)\in K$
, where
$a_{j}(\unicode[STIX]{x1D719},a)\in K$
, where
![]() $M=r\deg _{K}a$
and
$M=r\deg _{K}a$
and
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D719}):=a_{r}(\unicode[STIX]{x1D719})$
.
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D719}):=a_{r}(\unicode[STIX]{x1D719})$
.
For any nonzero
![]() $a\in A$
, we define the
$a\in A$
, we define the
![]() $A$
-module of
$A$
-module of
![]() $a$
-torsion points as
$a$
-torsion points as
where
![]() $\unicode[STIX]{x1D719}_{a}$
denotes
$\unicode[STIX]{x1D719}_{a}$
denotes
![]() $\unicode[STIX]{x1D719}(a)$
and
$\unicode[STIX]{x1D719}(a)$
and
![]() $\overline{K}$
is a fixed separable algebraic closure of
$\overline{K}$
is a fixed separable algebraic closure of
![]() $K$
. We have that
$K$
. We have that
![]() $\unicode[STIX]{x1D719}[a]\simeq (A/aA)^{r}$
(see for instance, [Reference Rosen23, Proposition 12.4]). If
$\unicode[STIX]{x1D719}[a]\simeq (A/aA)^{r}$
(see for instance, [Reference Rosen23, Proposition 12.4]). If
![]() $I$
is a nonzero ideal of
$I$
is a nonzero ideal of
![]() $A$
, we similarly define the
$A$
, we similarly define the
![]() $A$
-module of
$A$
-module of
![]() $I$
-torsion points
$I$
-torsion points
Let
![]() $K(\unicode[STIX]{x1D719}[a])$
be the field obtained by adjoining
$K(\unicode[STIX]{x1D719}[a])$
be the field obtained by adjoining
![]() $a$
-torsion points of
$a$
-torsion points of
![]() $\unicode[STIX]{x1D719}$
to
$\unicode[STIX]{x1D719}$
to
![]() $K$
, and let
$K$
, and let
![]() $K_{\unicode[STIX]{x1D719},I}:=K(\unicode[STIX]{x1D719}[I])$
.
$K_{\unicode[STIX]{x1D719},I}:=K(\unicode[STIX]{x1D719}[I])$
.
Let
![]() $\mathfrak{L}$
be a finite prime of
$\mathfrak{L}$
be a finite prime of
![]() $K$
. The
$K$
. The
![]() $\mathfrak{L}$
-torsion points of
$\mathfrak{L}$
-torsion points of
![]() $\unicode[STIX]{x1D719}$
in
$\unicode[STIX]{x1D719}$
in
![]() $\overline{K}$
give rise to a representation
$\overline{K}$
give rise to a representation
where
![]() $G_{K}$
is the absolute Galois group of
$G_{K}$
is the absolute Galois group of
![]() $K$
. For a prime
$K$
. For a prime
![]() ${\wp}$
of
${\wp}$
of
![]() $K$
, if
$K$
, if
![]() $\unicode[STIX]{x1D719}$
has good reduction at
$\unicode[STIX]{x1D719}$
has good reduction at
![]() ${\wp}$
, then
${\wp}$
, then
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},\mathfrak{L}}$
is unramified at
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},\mathfrak{L}}$
is unramified at
![]() ${\wp}$
if
${\wp}$
if
![]() ${\wp}\neq \mathfrak{L}$
.
${\wp}\neq \mathfrak{L}$
.
If
![]() $\unicode[STIX]{x1D719}$
is a Drinfeld
$\unicode[STIX]{x1D719}$
is a Drinfeld
![]() $A$
-module defined over
$A$
-module defined over
![]() $K$
, and all its defining coefficients
$K$
, and all its defining coefficients
![]() $a_{i}(\unicode[STIX]{x1D719})$
lie in
$a_{i}(\unicode[STIX]{x1D719})$
lie in
![]() $A$
, then we say that
$A$
, then we say that
![]() $\unicode[STIX]{x1D719}$
is integral over
$\unicode[STIX]{x1D719}$
is integral over
![]() $A$
. If
$A$
. If
![]() $\unicode[STIX]{x1D719}$
is integral over
$\unicode[STIX]{x1D719}$
is integral over
![]() $A$
, then it has good reduction outside any set of primes
$A$
, then it has good reduction outside any set of primes
![]() $S$
of
$S$
of
![]() $K$
which includes the prime at
$K$
which includes the prime at
![]() $\infty$
and the primes dividing the discriminant
$\infty$
and the primes dividing the discriminant
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D719})$
of
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D719})$
of
![]() $\unicode[STIX]{x1D719}$
. In particular, the
$\unicode[STIX]{x1D719}$
. In particular, the
![]() $G_{K}$
-modules
$G_{K}$
-modules
![]() $\unicode[STIX]{x1D719}[\mathfrak{L}^{\infty }]:=\bigcup _{m\geqslant 1}\unicode[STIX]{x1D719}[\mathfrak{L}^{m}]$
and
$\unicode[STIX]{x1D719}[\mathfrak{L}^{\infty }]:=\bigcup _{m\geqslant 1}\unicode[STIX]{x1D719}[\mathfrak{L}^{m}]$
and
![]() $\unicode[STIX]{x1D719}[\mathfrak{L}]$
are unramified outside
$\unicode[STIX]{x1D719}[\mathfrak{L}]$
are unramified outside
![]() $S\cup \{\mathfrak{L}\}$
.
$S\cup \{\mathfrak{L}\}$
.
For a prime
![]() ${\wp}$
of
${\wp}$
of
![]() $K$
, let
$K$
, let
![]() $\operatorname{Frob}_{{\wp}}\in G_{K}$
denote a Frobenius conjugacy class at
$\operatorname{Frob}_{{\wp}}\in G_{K}$
denote a Frobenius conjugacy class at
![]() ${\wp}$
, and let
${\wp}$
, and let
![]() $T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
be the
$T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
be the
![]() $\mathfrak{L}$
-adic Tate module of
$\mathfrak{L}$
-adic Tate module of
![]() $\unicode[STIX]{x1D719}$
, which is defined as an inverse limit of the
$\unicode[STIX]{x1D719}$
, which is defined as an inverse limit of the
![]() $\unicode[STIX]{x1D719}[\mathfrak{L}^{n}]$
, that is,
$\unicode[STIX]{x1D719}[\mathfrak{L}^{n}]$
, that is,
![]() $\underset{\longleftarrow _{n}}{\lim }\unicode[STIX]{x1D719}[\mathfrak{L}^{n}]$
.
$\underset{\longleftarrow _{n}}{\lim }\unicode[STIX]{x1D719}[\mathfrak{L}^{n}]$
.
Let
![]() $a_{{\wp}}(\unicode[STIX]{x1D719})$
denote the trace of
$a_{{\wp}}(\unicode[STIX]{x1D719})$
denote the trace of
![]() $\operatorname{Frob}_{{\wp}}$
on the
$\operatorname{Frob}_{{\wp}}$
on the
![]() $T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
and
$T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
and
![]() $P_{{\wp}}(\unicode[STIX]{x1D719})(X)$
the characteristic polynomial of
$P_{{\wp}}(\unicode[STIX]{x1D719})(X)$
the characteristic polynomial of
![]() $\operatorname{Frob}_{{\wp}}$
on the
$\operatorname{Frob}_{{\wp}}$
on the
![]() $T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
(when the Frobenius conjugacy class is unramified in the relevant extensions). It is known that
$T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
(when the Frobenius conjugacy class is unramified in the relevant extensions). It is known that
![]() $a_{{\wp}}(\unicode[STIX]{x1D719})$
and
$a_{{\wp}}(\unicode[STIX]{x1D719})$
and
![]() $P_{{\wp}}(\unicode[STIX]{x1D719})(X)$
are independent of
$P_{{\wp}}(\unicode[STIX]{x1D719})(X)$
are independent of
![]() $\mathfrak{L}$
[Reference Goss9, Theorem 4.12.12].
$\mathfrak{L}$
[Reference Goss9, Theorem 4.12.12].
The ring of
![]() $K$
-isogenies of
$K$
-isogenies of
![]() $\unicode[STIX]{x1D719}$
is denoted by
$\unicode[STIX]{x1D719}$
is denoted by
![]() $\operatorname{End}_{K}(\unicode[STIX]{x1D719})$
, and the ring of
$\operatorname{End}_{K}(\unicode[STIX]{x1D719})$
, and the ring of
![]() $\overline{K}$
-isogenies is denoted by
$\overline{K}$
-isogenies is denoted by
![]() $\operatorname{End}(\unicode[STIX]{x1D719})$
. We have that
$\operatorname{End}(\unicode[STIX]{x1D719})$
. We have that
![]() $\unicode[STIX]{x1D719}(A)\subseteq \operatorname{End}_{K}(\unicode[STIX]{x1D719})$
. When
$\unicode[STIX]{x1D719}(A)\subseteq \operatorname{End}_{K}(\unicode[STIX]{x1D719})$
. When
![]() $\unicode[STIX]{x1D719}$
is a Drinfeld
$\unicode[STIX]{x1D719}$
is a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
,
$K$
,
![]() $\operatorname{End}(\unicode[STIX]{x1D719})$
is either
$\operatorname{End}(\unicode[STIX]{x1D719})$
is either
![]() $\unicode[STIX]{x1D719}(A)$
or an order
$\unicode[STIX]{x1D719}(A)$
or an order
![]() ${\mathcal{O}}$
in some quadratic imaginary extension over
${\mathcal{O}}$
in some quadratic imaginary extension over
![]() $K$
. In the latter case, we say that
$K$
. In the latter case, we say that
![]() $\unicode[STIX]{x1D719}$
has complex multiplication (by
$\unicode[STIX]{x1D719}$
has complex multiplication (by
![]() ${\mathcal{O}}$
).
${\mathcal{O}}$
).
We use the following notation for Theorem 2.1 and throughout the paper.
Notation 1:
![]() $\ln x=$
the natural logarithm of
$\ln x=$
the natural logarithm of
![]() $x$
,
$x$
,
![]() $\log _{q}x$
= the logarithm of
$\log _{q}x$
= the logarithm of
![]() $x$
to base
$x$
to base
![]() $q$
,
$q$
,
![]() $\log _{q}^{\ast }x=\log _{q}\max \left\{x,1\right\}$
,
$\log _{q}^{\ast }x=\log _{q}\max \left\{x,1\right\}$
,
![]() $c_{0}=9+\log _{q}{\displaystyle \frac{64}{3}}$
,
$c_{0}=9+\log _{q}{\displaystyle \frac{64}{3}}$
,
![]() $s_{q}={\displaystyle \frac{9\ln (qc_{0})}{\ln (qc_{0})-1}}$
,
$s_{q}={\displaystyle \frac{9\ln (qc_{0})}{\ln (qc_{0})-1}}$
,
![]() $C_{q}=c_{0}+9\log _{q}c_{0}+s_{q}\left(\log _{q}4+\log _{q}(1+\log _{q}c_{0})\right)$
,
$C_{q}=c_{0}+9\log _{q}c_{0}+s_{q}\left(\log _{q}4+\log _{q}(1+\log _{q}c_{0})\right)$
,
![]() $\unicode[STIX]{x1D719}$
is a Drinfeld
$\unicode[STIX]{x1D719}$
is a Drinfeld
![]() $A$
-module over
$A$
-module over
![]() $K$
,
$K$
,
![]() $S_{\unicode[STIX]{x1D719}}$
is the set of primes of bad reduction of
$S_{\unicode[STIX]{x1D719}}$
is the set of primes of bad reduction of
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $K$
,
$K$
,
![]() $j(\unicode[STIX]{x1D719})={\displaystyle \frac{{a_{1}(\unicode[STIX]{x1D719})}^{q+1}}{a_{2}(\unicode[STIX]{x1D719})}}$
,
$j(\unicode[STIX]{x1D719})={\displaystyle \frac{{a_{1}(\unicode[STIX]{x1D719})}^{q+1}}{a_{2}(\unicode[STIX]{x1D719})}}$
,
![]() $m=$
the least positive integer such that
$m=$
the least positive integer such that
![]() $-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q^{m+1}$
,
$-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q^{m+1}$
,
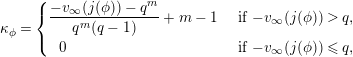 $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{-v_{\infty }(j(\unicode[STIX]{x1D719}))-q^{m}}{q^{m}(q-1)}}+m-1\quad & \text{ if }-v_{\infty }(j(\unicode[STIX]{x1D719}))>q,\\ ~~0~\quad & \text{ if }-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q,\end{array}\right.$
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{-v_{\infty }(j(\unicode[STIX]{x1D719}))-q^{m}}{q^{m}(q-1)}}+m-1\quad & \text{ if }-v_{\infty }(j(\unicode[STIX]{x1D719}))>q,\\ ~~0~\quad & \text{ if }-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q,\end{array}\right.$
![]() $s_{1}(\unicode[STIX]{x1D719})={\displaystyle \frac{v_{\infty }(a_{1}(\unicode[STIX]{x1D719}))+q}{q-1}},$
$s_{1}(\unicode[STIX]{x1D719})={\displaystyle \frac{v_{\infty }(a_{1}(\unicode[STIX]{x1D719}))+q}{q-1}},$
![]() $\tilde{s}_{1}(\unicode[STIX]{x1D719})={\displaystyle \frac{v_{\infty }(a_{2}(\unicode[STIX]{x1D719}))+q^{2}}{q^{2}-1}},$
$\tilde{s}_{1}(\unicode[STIX]{x1D719})={\displaystyle \frac{v_{\infty }(a_{2}(\unicode[STIX]{x1D719}))+q^{2}}{q^{2}-1}},$
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}=$
the (monic) denominator of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}=$
the (monic) denominator of
![]() $j(\unicode[STIX]{x1D719})$
as represented by a fraction in reduced form,
$j(\unicode[STIX]{x1D719})$
as represented by a fraction in reduced form,
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}=$
the product of finite primes
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}=$
the product of finite primes
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $K$
such that
$K$
such that
![]() $\unicode[STIX]{x1D719}$
has bad reduction over
$\unicode[STIX]{x1D719}$
has bad reduction over
![]() $K_{\mathfrak{p}}$
, where
$K_{\mathfrak{p}}$
, where
![]() $K_{\mathfrak{p}}$
is the completion at
$K_{\mathfrak{p}}$
is the completion at
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $K$
.
$K$
.
We state the main result of this paper as follows.
Theorem 2.1. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
without complex multiplication with
$K$
without complex multiplication with
![]() $\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
, and let
$\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
, and let
![]() $q$
be odd. Let
$q$
be odd. Let
![]() $S_{\unicode[STIX]{x1D719}}$
be the set of primes of bad reduction of
$S_{\unicode[STIX]{x1D719}}$
be the set of primes of bad reduction of
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $K$
. Let
$K$
. Let
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
be the Galois representation on the
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
be the Galois representation on the
![]() ${\wp}$
-torsion points of
${\wp}$
-torsion points of
![]() $\unicode[STIX]{x1D719}$
, where
$\unicode[STIX]{x1D719}$
, where
![]() ${\wp}$
is a finite prime of
${\wp}$
is a finite prime of
![]() $K$
. Let
$K$
. Let
![]() $q_{{\wp}}$
be the cardinality of the residue field
$q_{{\wp}}$
be the cardinality of the residue field
![]() $A/{\wp}$
. We use notation given in Notation 1.
$A/{\wp}$
. We use notation given in Notation 1.
If
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective, then either:
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective, then either:
(1)
 $q_{{\wp}}\leqslant 5$
or
$q_{{\wp}}\leqslant 5$
or
 ${\wp}\in S_{\unicode[STIX]{x1D719}}$
,
${\wp}\in S_{\unicode[STIX]{x1D719}}$
,(2) or, the image of
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer of a Cartan subgroup of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer of a Cartan subgroup of
 $\operatorname{GL}_{2}(A/{\wp})$
but not in the Cartan subgroup and where
$\operatorname{GL}_{2}(A/{\wp})$
but not in the Cartan subgroup and where $$\begin{eqnarray}\deg _{K}{\wp}\leqslant 2(C_{q}+\widetilde{W}+s_{q}\log _{q}(c_{0}+\widetilde{W})),\end{eqnarray}$$
$$\begin{eqnarray}\deg _{K}{\wp}\leqslant 2(C_{q}+\widetilde{W}+s_{q}\log _{q}(c_{0}+\widetilde{W})),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \widetilde{W} & := & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)^{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{W} & := & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)^{2},\nonumber\end{eqnarray}$$
(3) or, the image of
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
 $\operatorname{GL}_{2}(A/{\wp})$
and where
$\operatorname{GL}_{2}(A/{\wp})$
and where $$\begin{eqnarray}\deg _{K}{\wp}\leqslant \unicode[STIX]{x1D711}((q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}})\deg _{K}P,\end{eqnarray}$$
$$\begin{eqnarray}\deg _{K}{\wp}\leqslant \unicode[STIX]{x1D711}((q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}})\deg _{K}P,\end{eqnarray}$$
 $\unicode[STIX]{x1D711}$
denotes the Euler-phi function,
$\unicode[STIX]{x1D711}$
denotes the Euler-phi function,
 $P$
is the least degree prime of
$P$
is the least degree prime of
 $K$
at which
$K$
at which
 $\unicode[STIX]{x1D719}$
has good reduction, and
$\unicode[STIX]{x1D719}$
has good reduction, and
 $n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer.
$n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer.
This paper is organized as follows. We establish an explicit isogeny theorem for Drinfeld modules of rank
![]() $2$
in Section 3 which is used in the Cartan case. Some ingredients needed to set up the proof of the main theorem are discussed in Sections 4 and 5. Section 6 (Section 7, respectively) deals with the Cartan case (the Borel case, respectively). The proof of Theorem 2.1 is then given in Section 8.
$2$
in Section 3 which is used in the Cartan case. Some ingredients needed to set up the proof of the main theorem are discussed in Sections 4 and 5. Section 6 (Section 7, respectively) deals with the Cartan case (the Borel case, respectively). The proof of Theorem 2.1 is then given in Section 8.
3 An explicit isogeny theorem for rank
 $2$
$2$
Let
![]() $L/K$
be a finite extension. Writing divisors in terms of places instead of primes, the different divisor
$L/K$
be a finite extension. Writing divisors in terms of places instead of primes, the different divisor
![]() $\mathfrak{D}(L/K)$
of
$\mathfrak{D}(L/K)$
of
![]() $L/K$
is defined as
$L/K$
is defined as
and its degree is given by
where
![]() $w$
ranges through all normalized places of
$w$
ranges through all normalized places of
![]() $L$
, and
$L$
, and
![]() $D(L_{w}/K_{v})$
is the different ideal of
$D(L_{w}/K_{v})$
is the different ideal of
![]() $L_{w}/K_{v}$
. For convenience, we define the degree with respect to
$L_{w}/K_{v}$
. For convenience, we define the degree with respect to
![]() $K$
of
$K$
of
![]() $\mathfrak{D}(L/K)$
as
$\mathfrak{D}(L/K)$
as
where
![]() $v$
ranges through all normalized places of
$v$
ranges through all normalized places of
![]() $K$
.
$K$
.
The following theorem presents an upper bound on the degree of the different divisor
![]() $\mathfrak{D}(K(\unicode[STIX]{x1D719}[a])/K)$
of
$\mathfrak{D}(K(\unicode[STIX]{x1D719}[a])/K)$
of
![]() $K(\unicode[STIX]{x1D719}[a])$
over
$K(\unicode[STIX]{x1D719}[a])$
over
![]() $K$
based on work from [Reference Chen and Lee2, Reference Chen and Lee3].
$K$
based on work from [Reference Chen and Lee2, Reference Chen and Lee3].
Theorem 3.1. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
with
$K$
with
![]() $\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
and
$\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
and
![]() $a$
be nonzero in
$a$
be nonzero in
![]() $A$
. Let
$A$
. Let
![]() $j(\unicode[STIX]{x1D719})$
,
$j(\unicode[STIX]{x1D719})$
,
![]() $m$
,
$m$
,
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
,
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
,
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}$
and
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}$
be the same as given in Notation 1. Let
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}$
be the same as given in Notation 1. Let
![]() $\mathfrak{D}(K(\unicode[STIX]{x1D719}[a])/K)$
be the different divisor of the torsion field
$\mathfrak{D}(K(\unicode[STIX]{x1D719}[a])/K)$
be the different divisor of the torsion field
![]() $K(\unicode[STIX]{x1D719}[a])$
over
$K(\unicode[STIX]{x1D719}[a])$
over
![]() $K$
. Then
$K$
. Then
 $$\begin{eqnarray}\displaystyle \deg _{K}\mathfrak{D}(K(\unicode[STIX]{x1D719}[a])/K) & {\leqslant} & \displaystyle 2\deg _{K}a+\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\nonumber\\ \displaystyle & & \displaystyle \times \deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \deg _{K}\mathfrak{D}(K(\unicode[STIX]{x1D719}[a])/K) & {\leqslant} & \displaystyle 2\deg _{K}a+\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\nonumber\\ \displaystyle & & \displaystyle \times \deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1).\end{eqnarray}$$
Proof. See [Reference Chen and Lee2, Reference Chen and Lee3]. ◻
We have an upper bound on the extension degree of the constant field of
![]() $K(\unicode[STIX]{x1D719}[a])$
over
$K(\unicode[STIX]{x1D719}[a])$
over
![]() $\mathbb{F}_{q}$
as follows.
$\mathbb{F}_{q}$
as follows.
Theorem 3.2. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
with
$K$
with
![]() $\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
and
$\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
and
![]() $a$
be nonzero in
$a$
be nonzero in
![]() $A$
. Let
$A$
. Let
![]() $j(\unicode[STIX]{x1D719})$
,
$j(\unicode[STIX]{x1D719})$
,
![]() $m$
and
$m$
and
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
be the same as given in Notation 1. Let
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
be the same as given in Notation 1. Let
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719},a}:=[\mathbb{F}_{K(\unicode[STIX]{x1D719}[a])}:\mathbb{F}_{q}]$
, where
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719},a}:=[\mathbb{F}_{K(\unicode[STIX]{x1D719}[a])}:\mathbb{F}_{q}]$
, where
![]() $\mathbb{F}_{K(\unicode[STIX]{x1D719}[a])}$
denotes the algebraic closure of
$\mathbb{F}_{K(\unicode[STIX]{x1D719}[a])}$
denotes the algebraic closure of
![]() $\mathbb{F}_{q}$
in
$\mathbb{F}_{q}$
in
![]() $K(\unicode[STIX]{x1D719}[a])$
(that is,
$K(\unicode[STIX]{x1D719}[a])$
(that is,
![]() $\mathbb{F}_{K(\unicode[STIX]{x1D719}[a])}$
is the constant field of
$\mathbb{F}_{K(\unicode[STIX]{x1D719}[a])}$
is the constant field of
![]() $K(\unicode[STIX]{x1D719}[a])$
). Then we have
$K(\unicode[STIX]{x1D719}[a])$
). Then we have
where
![]() $s_{1}(\unicode[STIX]{x1D719})=(v_{\infty }(a_{1}(\unicode[STIX]{x1D719}))+q)/(q-1)$
.
$s_{1}(\unicode[STIX]{x1D719})=(v_{\infty }(a_{1}(\unicode[STIX]{x1D719}))+q)/(q-1)$
.
Proof. Let
![]() $g_{\unicode[STIX]{x1D719},\infty }=[K_{\infty }(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty }):K_{\infty }]$
, where
$g_{\unicode[STIX]{x1D719},\infty }=[K_{\infty }(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty }):K_{\infty }]$
, where
![]() $K_{\infty }$
denotes the completion at
$K_{\infty }$
denotes the completion at
![]() $\infty$
of
$\infty$
of
![]() $K$
,
$K$
,
![]() $C_{\infty }$
denotes the completion of an algebraic closure of
$C_{\infty }$
denotes the completion of an algebraic closure of
![]() $K_{\infty }$
and
$K_{\infty }$
and
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty }$
is the lattice associated to the uniformization of
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty }$
is the lattice associated to the uniformization of
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $C_{\infty }$
. As
$C_{\infty }$
. As
![]() $K_{\infty }(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty })$
contains
$K_{\infty }(\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty })$
contains
![]() $\unicode[STIX]{x1D719}[a]$
and
$\unicode[STIX]{x1D719}[a]$
and
![]() $\mathbb{F}_{K_{\infty }}=\mathbb{F}_{K}$
, we have that
$\mathbb{F}_{K_{\infty }}=\mathbb{F}_{K}$
, we have that
Hence,
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719},a}\leqslant g_{\unicode[STIX]{x1D719},\infty }$
.
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719},a}\leqslant g_{\unicode[STIX]{x1D719},\infty }$
.
One can bound
![]() $g_{\unicode[STIX]{x1D719},\infty }$
using knowledge of the successive minima of the lattice
$g_{\unicode[STIX]{x1D719},\infty }$
using knowledge of the successive minima of the lattice
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty }$
associated to
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D719},\infty }$
associated to
![]() $\unicode[STIX]{x1D719}$
[Reference Gardeyn12, Proposition 4(i)]. Concerning the term
$\unicode[STIX]{x1D719}$
[Reference Gardeyn12, Proposition 4(i)]. Concerning the term
![]() $g_{\unicode[STIX]{x1D719},\infty }$
, we have from [Reference Gardeyn12] that
$g_{\unicode[STIX]{x1D719},\infty }$
, we have from [Reference Gardeyn12] that
where
![]() $\unicode[STIX]{x1D708}_{i,\infty }(\unicode[STIX]{x1D719})$
is the ith successive minima of
$\unicode[STIX]{x1D708}_{i,\infty }(\unicode[STIX]{x1D719})$
is the ith successive minima of
![]() $\unicode[STIX]{x1D719}$
associated to its uniformization over
$\unicode[STIX]{x1D719}$
associated to its uniformization over
![]() $C_{\infty }$
. From [Reference Chen and Lee2], an explicit bound for these successive minima
$C_{\infty }$
. From [Reference Chen and Lee2], an explicit bound for these successive minima
![]() $\unicode[STIX]{x1D708}_{i,\infty }(\unicode[STIX]{x1D719})$
is determined as follows:
$\unicode[STIX]{x1D708}_{i,\infty }(\unicode[STIX]{x1D719})$
is determined as follows:
Case
![]() $1$
: If
$1$
: If
![]() $-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q$
, then
$-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q$
, then
![]() $\unicode[STIX]{x1D708}_{1,\infty }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D708}_{2,\infty }(\unicode[STIX]{x1D719})=-\tilde{s}_{1}(\unicode[STIX]{x1D719})$
,
$\unicode[STIX]{x1D708}_{1,\infty }(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D708}_{2,\infty }(\unicode[STIX]{x1D719})=-\tilde{s}_{1}(\unicode[STIX]{x1D719})$
,
Case
![]() $2$
: If
$2$
: If
![]() $q<-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q^{m+1}$
, then
$q<-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q^{m+1}$
, then
![]() $\unicode[STIX]{x1D708}_{1,\infty }(\unicode[STIX]{x1D719})=-s_{1}(\unicode[STIX]{x1D719})$
and
$\unicode[STIX]{x1D708}_{1,\infty }(\unicode[STIX]{x1D719})=-s_{1}(\unicode[STIX]{x1D719})$
and
![]() $\unicode[STIX]{x1D708}_{2,\infty }(\unicode[STIX]{x1D719})=-s_{1}(\unicode[STIX]{x1D719})-\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
, where notations for
$\unicode[STIX]{x1D708}_{2,\infty }(\unicode[STIX]{x1D719})=-s_{1}(\unicode[STIX]{x1D719})-\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
, where notations for
![]() $s_{1}(\unicode[STIX]{x1D719})$
and
$s_{1}(\unicode[STIX]{x1D719})$
and
![]() $\tilde{s}_{1}(\unicode[STIX]{x1D719})$
are given in Notation 1.
$\tilde{s}_{1}(\unicode[STIX]{x1D719})$
are given in Notation 1.
Combining all these yields the result. ◻
Remark 3.3. Under the assumptions of Theorem 3.2, if
![]() $-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q$
, then
$-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q$
, then
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)$
, and if
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)$
, and if
![]() $q<-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q^{m+1}$
, then we see that
$q<-v_{\infty }(j(\unicode[STIX]{x1D719}))\leqslant q^{m+1}$
, then we see that
Recall the isogeny theorem for Drinfeld
![]() $A$
-modules, proven in [Reference Taguchi27, Proposition 3.1].
$A$
-modules, proven in [Reference Taguchi27, Proposition 3.1].
Theorem 3.4. Let
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
be rank
$\unicode[STIX]{x1D719}^{\prime }$
be rank
![]() $r$
Drinfeld
$r$
Drinfeld
![]() $A$
-modules over
$A$
-modules over
![]() $K$
. Then
$K$
. Then
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
are
$\unicode[STIX]{x1D719}^{\prime }$
are
![]() $K$
-isogenous if and only if
$K$
-isogenous if and only if
![]() $P_{{\wp}}(\unicode[STIX]{x1D719})(X)=P_{{\wp}}(\unicode[STIX]{x1D719}^{\prime })(X)$
for all but finitely many primes
$P_{{\wp}}(\unicode[STIX]{x1D719})(X)=P_{{\wp}}(\unicode[STIX]{x1D719}^{\prime })(X)$
for all but finitely many primes
![]() ${\wp}$
of
${\wp}$
of
![]() $K$
.
$K$
.
The following theorem is an explicit and effective version of the isogeny theorem for rank 2 Drinfeld
![]() $A$
-modules over
$A$
-modules over
![]() $K$
. The proof of Theorem 3.5 is similar to that of [Reference Chen and Lee3, Theorem 1.2], except that it uses more refined and explicit bound on the different divisor and the degree of constant field extensions given in Theorems 3.1 and 3.2. For completeness, we summarize the proof to explain and justify all the new constants, for example,
$K$
. The proof of Theorem 3.5 is similar to that of [Reference Chen and Lee3, Theorem 1.2], except that it uses more refined and explicit bound on the different divisor and the degree of constant field extensions given in Theorems 3.1 and 3.2. For completeness, we summarize the proof to explain and justify all the new constants, for example,
![]() $c_{0},s_{q},C_{q}$
,
$c_{0},s_{q},C_{q}$
,
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{i}},s_{1}(\unicode[STIX]{x1D719}_{i}),\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{i}}$
, which arise.
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{i}},s_{1}(\unicode[STIX]{x1D719}_{i}),\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{i}}$
, which arise.
Theorem 3.5. Let
![]() $\unicode[STIX]{x1D719}_{1}$
and
$\unicode[STIX]{x1D719}_{1}$
and
![]() $\unicode[STIX]{x1D719}_{2}$
be Drinfeld
$\unicode[STIX]{x1D719}_{2}$
be Drinfeld
![]() $A$
-modules of rank
$A$
-modules of rank
![]() $2$
over
$2$
over
![]() $K$
which are not
$K$
which are not
![]() $K$
-isogenous with
$K$
-isogenous with
![]() $\unicode[STIX]{x1D719}_{i}(T)=T+a_{1}(\unicode[STIX]{x1D719}_{i})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719}_{i})\unicode[STIX]{x1D70F}^{2}$
for
$\unicode[STIX]{x1D719}_{i}(T)=T+a_{1}(\unicode[STIX]{x1D719}_{i})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719}_{i})\unicode[STIX]{x1D70F}^{2}$
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $j(\unicode[STIX]{x1D719}_{i})={a_{1}(\unicode[STIX]{x1D719}_{i})}^{q+1}/a_{2}(\unicode[STIX]{x1D719}_{i})$
and
$j(\unicode[STIX]{x1D719}_{i})={a_{1}(\unicode[STIX]{x1D719}_{i})}^{q+1}/a_{2}(\unicode[STIX]{x1D719}_{i})$
and
![]() $m_{i}$
be the least positive integer such that
$m_{i}$
be the least positive integer such that
![]() $-v_{\infty }(j(\unicode[STIX]{x1D719}_{i}))\leqslant q^{m_{i}+1}$
for
$-v_{\infty }(j(\unicode[STIX]{x1D719}_{i}))\leqslant q^{m_{i}+1}$
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $S=S_{\unicode[STIX]{x1D719}_{1}}\cup S_{\unicode[STIX]{x1D719}_{2}}\cup \{\infty \}$
be the set of primes of bad reduction of
$S=S_{\unicode[STIX]{x1D719}_{1}}\cup S_{\unicode[STIX]{x1D719}_{2}}\cup \{\infty \}$
be the set of primes of bad reduction of
![]() $\unicode[STIX]{x1D719}_{1}$
or
$\unicode[STIX]{x1D719}_{1}$
or
![]() $\unicode[STIX]{x1D719}_{2}$
over
$\unicode[STIX]{x1D719}_{2}$
over
![]() $K$
together with the infinite prime
$K$
together with the infinite prime
![]() $\infty$
of
$\infty$
of
![]() $K$
.
$K$
.
Assume that
![]() ${\wp}\not \in S$
is a prime of
${\wp}\not \in S$
is a prime of
![]() $K$
of least degree such that
$K$
of least degree such that
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{1})\neq P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
. Then we have
$P_{{\wp}}(\unicode[STIX]{x1D719}_{1})\neq P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
. Then we have
where we let
![]() $c_{0},s_{q},C_{q}$
,
$c_{0},s_{q},C_{q}$
,
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{i}},s_{1}(\unicode[STIX]{x1D719}_{i}),\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{i}}$
and
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{i}},s_{1}(\unicode[STIX]{x1D719}_{i}),\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{i}}$
and
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{i}}$
for each
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{i}}$
for each
![]() $\unicode[STIX]{x1D719}_{i}$
,
$\unicode[STIX]{x1D719}_{i}$
,
![]() $i=1,2$
be the same as given in Notation 1, and
$i=1,2$
be the same as given in Notation 1, and
 $$\begin{eqnarray}\displaystyle W & = & \displaystyle \log _{q}^{\ast }\bigg(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}\nonumber\\ \displaystyle & & \displaystyle +\,2+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}+1}-1\right)+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}+1}-1\right)\bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}}{s_{1}(\unicode[STIX]{x1D719}_{1})}\right)\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}}{s_{1}(\unicode[STIX]{x1D719}_{2})}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W & = & \displaystyle \log _{q}^{\ast }\bigg(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}\nonumber\\ \displaystyle & & \displaystyle +\,2+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}+1}-1\right)+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}+1}-1\right)\bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}}{s_{1}(\unicode[STIX]{x1D719}_{1})}\right)\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}}{s_{1}(\unicode[STIX]{x1D719}_{2})}\right).\nonumber\end{eqnarray}$$
Proof. Let
![]() ${\wp}\not \in S$
be a prime of
${\wp}\not \in S$
be a prime of
![]() $K$
with least degree such that
$K$
with least degree such that
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{1})\not =P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
(which exists from the hypotheses and Theorem 3.4). Let
$P_{{\wp}}(\unicode[STIX]{x1D719}_{1})\not =P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
(which exists from the hypotheses and Theorem 3.4). Let
![]() $\unicode[STIX]{x1D6FC}_{0}$
be a nonzero coefficient of
$\unicode[STIX]{x1D6FC}_{0}$
be a nonzero coefficient of
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{1})-P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
. It is known that a root
$P_{{\wp}}(\unicode[STIX]{x1D719}_{1})-P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
. It is known that a root
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{1})$
or
$P_{{\wp}}(\unicode[STIX]{x1D719}_{1})$
or
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
satisfies
$P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
satisfies
(cf. [Reference Goss and Goss10, Theorem 3.2.3(c)(d)], [Reference Gardeyn12, Proposition 9]). This implies that each coefficient
![]() $\unicode[STIX]{x1D6FD}$
of
$\unicode[STIX]{x1D6FD}$
of
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{1})$
and
$P_{{\wp}}(\unicode[STIX]{x1D719}_{1})$
and
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
satisfies
$P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
satisfies
![]() $\deg _{K}\unicode[STIX]{x1D6FD}\leqslant \deg _{K}{\wp}$
, and hence each coefficient
$\deg _{K}\unicode[STIX]{x1D6FD}\leqslant \deg _{K}{\wp}$
, and hence each coefficient
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $P_{{\wp}}(\unicode[STIX]{x1D719}_{1})-P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
also satisfies
$P_{{\wp}}(\unicode[STIX]{x1D719}_{1})-P_{{\wp}}(\unicode[STIX]{x1D719}_{2})$
also satisfies
![]() $\deg _{K}\unicode[STIX]{x1D6FC}\leqslant \deg _{K}{\wp}$
, in particular
$\deg _{K}\unicode[STIX]{x1D6FC}\leqslant \deg _{K}{\wp}$
, in particular
![]() $\deg _{K}\unicode[STIX]{x1D6FC}_{0}\leqslant \deg _{K}{\wp}$
.
$\deg _{K}\unicode[STIX]{x1D6FC}_{0}\leqslant \deg _{K}{\wp}$
.
We choose a finite prime
![]() $\mathfrak{L}$
of
$\mathfrak{L}$
of
![]() $K$
by [Reference Chen and Lee3, Lemma 5.2] such that
$K$
by [Reference Chen and Lee3, Lemma 5.2] such that
and write
![]() $\mathfrak{L}=(a)$
, where
$\mathfrak{L}=(a)$
, where
![]() $a$
is monic in
$a$
is monic in
![]() $A$
. Note that either
$A$
. Note that either
![]() $\deg _{K}{\wp}\leqslant 2$
or
$\deg _{K}{\wp}\leqslant 2$
or
![]() $\mathfrak{L}\neq {\wp}$
by the above inequality.
$\mathfrak{L}\neq {\wp}$
by the above inequality.
Suppose we are now in the latter case where
![]() $\mathfrak{L}\neq {\wp}$
. Consider the representation
$\mathfrak{L}\neq {\wp}$
. Consider the representation
where
![]() $\unicode[STIX]{x1D713}_{\mathfrak{L}}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}_{1},\mathfrak{L}}\times \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}_{2},\mathfrak{L}}$
. Let
$\unicode[STIX]{x1D713}_{\mathfrak{L}}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}_{1},\mathfrak{L}}\times \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}_{2},\mathfrak{L}}$
. Let
![]() $G_{\mathfrak{L}}$
be the image of this homomorphism. Let
$G_{\mathfrak{L}}$
be the image of this homomorphism. Let
![]() $C_{\mathfrak{L}}$
be the subset of
$C_{\mathfrak{L}}$
be the subset of
![]() $G_{\mathfrak{L}}$
consisting of pairs
$G_{\mathfrak{L}}$
consisting of pairs
![]() $(\mathfrak{a},\mathfrak{b})$
such that the characteristic polynomials of
$(\mathfrak{a},\mathfrak{b})$
such that the characteristic polynomials of
![]() $\mathfrak{a}$
and
$\mathfrak{a}$
and
![]() $\mathfrak{b}$
are not equal. Note that
$\mathfrak{b}$
are not equal. Note that
![]() $C_{\mathfrak{L}}$
is invariant under conjugation, so it is a union of conjugacy classes in
$C_{\mathfrak{L}}$
is invariant under conjugation, so it is a union of conjugacy classes in
![]() $G_{\mathfrak{L}}$
. Since
$G_{\mathfrak{L}}$
. Since
![]() $\mathfrak{L}\neq {\wp}$
, we have that
$\mathfrak{L}\neq {\wp}$
, we have that
![]() $C_{\mathfrak{L}}\not =\emptyset$
, and in particular, there is some conjugacy class
$C_{\mathfrak{L}}\not =\emptyset$
, and in particular, there is some conjugacy class
![]() ${\mathcal{C}}\subseteq C_{\mathfrak{L}}$
in
${\mathcal{C}}\subseteq C_{\mathfrak{L}}$
in
![]() $G_{\mathfrak{L}}$
with
$G_{\mathfrak{L}}$
with
![]() ${\mathcal{C}}\not =\emptyset$
.
${\mathcal{C}}\not =\emptyset$
.
Let
![]() $S_{\mathfrak{L}}=S\cup \left\{\mathfrak{L}\right\}$
. Then the Galois representation
$S_{\mathfrak{L}}=S\cup \left\{\mathfrak{L}\right\}$
. Then the Galois representation
![]() $\unicode[STIX]{x1D713}_{\mathfrak{L}}$
is unramified outside
$\unicode[STIX]{x1D713}_{\mathfrak{L}}$
is unramified outside
![]() $S_{\mathfrak{L}}$
. We have that
$S_{\mathfrak{L}}$
. We have that
![]() $A/\mathfrak{L}\cong \mathbb{F}_{\ell }$
where
$A/\mathfrak{L}\cong \mathbb{F}_{\ell }$
where
![]() $\ell =q^{\deg _{K}\mathfrak{L}}$
. Let
$\ell =q^{\deg _{K}\mathfrak{L}}$
. Let
![]() $\widetilde{K}/K$
be the field extension associated to
$\widetilde{K}/K$
be the field extension associated to
![]() $\unicode[STIX]{x1D713}_{\mathfrak{L}}$
, and let
$\unicode[STIX]{x1D713}_{\mathfrak{L}}$
, and let
![]() $n$
(resp.
$n$
(resp.
![]() $n^{\prime }$
) be its extension degree (resp. geometric extension degree). By an explicit Chebotarev argument as in [Reference Chen and Lee3, Theorem 1.2], we deduce that there is a prime
$n^{\prime }$
) be its extension degree (resp. geometric extension degree). By an explicit Chebotarev argument as in [Reference Chen and Lee3, Theorem 1.2], we deduce that there is a prime
![]() $P\not \in S_{\mathfrak{L}}$
such that
$P\not \in S_{\mathfrak{L}}$
such that
![]() $\operatorname{Frob}_{P}={\mathcal{C}}\subseteq C_{\mathfrak{L}}$
and
$\operatorname{Frob}_{P}={\mathcal{C}}\subseteq C_{\mathfrak{L}}$
and
where
 $$\begin{eqnarray}\displaystyle & & \unicode[STIX]{x1D6F4}^{\prime }:=\;\mathop{\sum }_{\mathfrak{p}\in S_{\mathfrak{L}}}\mathfrak{p}\geqslant \unicode[STIX]{x1D6F4}:=\;\mathop{\sum }_{\mathfrak{p}\in S}\mathfrak{p},\quad m=[\mathbb{F}_{\widetilde{K}}:\mathbb{F}_{K}],\\ & & \deg _{K}\unicode[STIX]{x1D6F4}^{\prime }\leqslant \deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\deg _{K}\mathfrak{L}+1,\\ & & \mathfrak{D}=\mathfrak{D}(\widetilde{K}/K)\text{ is the different divisor }of\widetilde{K}/K,\\ & & B=\max \left\{\deg _{K}\unicode[STIX]{x1D6F4}^{\prime },\deg _{\widetilde{K}}\mathfrak{D},2\right\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \unicode[STIX]{x1D6F4}^{\prime }:=\;\mathop{\sum }_{\mathfrak{p}\in S_{\mathfrak{L}}}\mathfrak{p}\geqslant \unicode[STIX]{x1D6F4}:=\;\mathop{\sum }_{\mathfrak{p}\in S}\mathfrak{p},\quad m=[\mathbb{F}_{\widetilde{K}}:\mathbb{F}_{K}],\\ & & \deg _{K}\unicode[STIX]{x1D6F4}^{\prime }\leqslant \deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\deg _{K}\mathfrak{L}+1,\\ & & \mathfrak{D}=\mathfrak{D}(\widetilde{K}/K)\text{ is the different divisor }of\widetilde{K}/K,\\ & & B=\max \left\{\deg _{K}\unicode[STIX]{x1D6F4}^{\prime },\deg _{\widetilde{K}}\mathfrak{D},2\right\}. & & \displaystyle\end{eqnarray}$$
By using the explicit bound on the different divisor
![]() $\mathfrak{D}$
in Theorem 3.1, we obtain
$\mathfrak{D}$
in Theorem 3.1, we obtain
 $$\begin{eqnarray}\displaystyle & & \quad \deg _{\widetilde{K}}\mathfrak{D}\leqslant n^{\prime }\left(4\deg _{K}a+\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\right),\\ & & \quad \quad \text{where}\quad \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}:=2+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}+1}-1\right)+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}+1}-1\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \quad \deg _{\widetilde{K}}\mathfrak{D}\leqslant n^{\prime }\left(4\deg _{K}a+\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\right),\\ & & \quad \quad \text{where}\quad \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}:=2+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{1}}+1}-1\right)+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}_{2}}+1}-1\right). & & \displaystyle\end{eqnarray}$$
Then from (6) and (7), we note that
![]() $B$
is bounded above by the upper bound of
$B$
is bounded above by the upper bound of
![]() $\deg _{\widetilde{K}}\mathfrak{D}$
in (8); thus we have that
$\deg _{\widetilde{K}}\mathfrak{D}$
in (8); thus we have that
 $$\begin{eqnarray}\displaystyle \log _{q}\frac{4}{3}B & {\leqslant} & \displaystyle \log _{q}n^{\prime }+\log _{q}\frac{16}{3}+\log _{q}(\log _{q}\ell )+\log _{q}^{\ast }\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \log _{q}\frac{4}{3}B & {\leqslant} & \displaystyle \log _{q}n^{\prime }+\log _{q}\frac{16}{3}+\log _{q}(\log _{q}\ell )+\log _{q}^{\ast }\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\right).\nonumber\end{eqnarray}$$
(We use the inequality
![]() $\log _{q}(x+y)\leqslant \log _{q}x+\log _{q}y$
for
$\log _{q}(x+y)\leqslant \log _{q}x+\log _{q}y$
for
![]() $x,y\geqslant 2$
; in more detail, in (8), both
$x,y\geqslant 2$
; in more detail, in (8), both
![]() $4\deg _{K}a$
and the other terms,
$4\deg _{K}a$
and the other terms,
![]() $\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+(2/(q-1))\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}$
, are greater than 2 since
$\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+(2/(q-1))\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}$
, are greater than 2 since
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}>2$
.)
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}>2$
.)
We note that
![]() $n^{\prime }\leqslant n=\left|G_{\mathfrak{L}}\right|<\ell ^{8}$
, so
$n^{\prime }\leqslant n=\left|G_{\mathfrak{L}}\right|<\ell ^{8}$
, so
![]() $\log _{q}n^{\prime }<8\log _{q}\ell$
. Returning to (6), we obtain
$\log _{q}n^{\prime }<8\log _{q}\ell$
. Returning to (6), we obtain
 $$\begin{eqnarray}\displaystyle \deg _{K}P & & \displaystyle \leqslant 4\bigg(\log _{q}\frac{64}{3}+\log _{q}(\log _{q}\ell )+8\log _{q}\ell \nonumber\\ \displaystyle & & \displaystyle +\,\log _{q}^{\ast }\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\right)\bigg)+m\nonumber\\ \displaystyle & & \displaystyle \leqslant 4\bigg(\log _{q}\frac{64}{3}+9\log _{q}\ell +\log _{q}^{\ast }\bigg(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\bigg)\bigg)+m.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \deg _{K}P & & \displaystyle \leqslant 4\bigg(\log _{q}\frac{64}{3}+\log _{q}(\log _{q}\ell )+8\log _{q}\ell \nonumber\\ \displaystyle & & \displaystyle +\,\log _{q}^{\ast }\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\right)\bigg)+m\nonumber\\ \displaystyle & & \displaystyle \leqslant 4\bigg(\log _{q}\frac{64}{3}+9\log _{q}\ell +\log _{q}^{\ast }\bigg(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\bigg)\bigg)+m.\nonumber\end{eqnarray}$$
By construction of
![]() $C_{\mathfrak{L}}$
, we have that
$C_{\mathfrak{L}}$
, we have that
![]() $P_{P}(\unicode[STIX]{x1D719}_{1})\not \equiv P_{P}(\unicode[STIX]{x1D719}_{2})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{L})$
. Thus, we have
$P_{P}(\unicode[STIX]{x1D719}_{1})\not \equiv P_{P}(\unicode[STIX]{x1D719}_{2})\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{L})$
. Thus, we have
![]() $\deg _{K}{\wp}\leqslant \deg _{K}P$
, and from (5), it follows that
$\deg _{K}{\wp}\leqslant \deg _{K}P$
, and from (5), it follows that
 $$\begin{eqnarray}\displaystyle \deg _{K}{\wp} & {\leqslant} & \displaystyle 4\bigg(\log _{q}\frac{64}{3}+9(1+\log _{q}\deg _{K}{\wp})+\log _{q}^{\ast }\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\bigg)+\frac{m}{4}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \deg _{K}{\wp} & {\leqslant} & \displaystyle 4\bigg(\log _{q}\frac{64}{3}+9(1+\log _{q}\deg _{K}{\wp})+\log _{q}^{\ast }\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}}\bigg)+\frac{m}{4}\bigg).\end{eqnarray}$$
As
![]() $1+\log _{q}y\geqslant 1$
and
$1+\log _{q}y\geqslant 1$
and
![]() $(\log _{q}y)/y\leqslant 1$
, we have that
$(\log _{q}y)/y\leqslant 1$
, we have that
where
![]() $c_{0}:=9+\log _{q}(64/3)$
and
$c_{0}:=9+\log _{q}(64/3)$
and
![]() $W_{0}:=\log _{q}^{\ast }(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+(2/(q-1))\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}})+m/4$
.
$W_{0}:=\log _{q}^{\ast }(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}_{2}}+(2/(q-1))\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}_{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}})+m/4$
.
Thus, (9) can be written as follows:
Let
![]() $t^{\ast }=(\ln (qc_{0})-1)/\ln (qc_{0})$
and
$t^{\ast }=(\ln (qc_{0})-1)/\ln (qc_{0})$
and
![]() $s^{\ast }=1/t^{\ast }=\ln (qc_{0})/(\ln (qc_{0})-1)$
. If
$s^{\ast }=1/t^{\ast }=\ln (qc_{0})/(\ln (qc_{0})-1)$
. If
![]() $x:=\deg _{K}{\wp}\geqslant c_{0}$
, then using [Reference Chen and Lee3, Lemma 5.3 and the calculation in (32)] with
$x:=\deg _{K}{\wp}\geqslant c_{0}$
, then using [Reference Chen and Lee3, Lemma 5.3 and the calculation in (32)] with
![]() $c^{\ast }=c_{0}$
, we see that
$c^{\ast }=c_{0}$
, we see that
 $$\begin{eqnarray}\displaystyle \log _{q}\deg _{K}{\wp}=\log _{q}x & {\leqslant} & \displaystyle \frac{1}{t^{\ast }}\log _{q}\left(4(c_{0}+W_{0})\frac{1+\log _{q}c_{0}}{c_{0}^{1/\ln (qc_{0})}}\right)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle s^{\ast }\left(\log _{q}4+\log _{q}(c_{0}+W_{0})+\log _{q}(1+\log _{q}c_{0})\right)\nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{1}{1-\ln (qc_{0})}\right)\log _{q}c_{0}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle s^{\ast }\left(\log _{q}4+\log _{q}(c_{0}+W_{0})+\log _{q}(1+\log _{q}c_{0})\right)\nonumber\\ \displaystyle & & \displaystyle +\,\log _{q}c_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \log _{q}\deg _{K}{\wp}=\log _{q}x & {\leqslant} & \displaystyle \frac{1}{t^{\ast }}\log _{q}\left(4(c_{0}+W_{0})\frac{1+\log _{q}c_{0}}{c_{0}^{1/\ln (qc_{0})}}\right)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle s^{\ast }\left(\log _{q}4+\log _{q}(c_{0}+W_{0})+\log _{q}(1+\log _{q}c_{0})\right)\nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{1}{1-\ln (qc_{0})}\right)\log _{q}c_{0}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle s^{\ast }\left(\log _{q}4+\log _{q}(c_{0}+W_{0})+\log _{q}(1+\log _{q}c_{0})\right)\nonumber\\ \displaystyle & & \displaystyle +\,\log _{q}c_{0}.\end{eqnarray}$$
Substitution of (11) into (10) yields
where
![]() $C_{q}:=c_{0}+9\log _{q}c_{0}+9s^{\ast }\left(\log _{q}4+\log _{q}(1+\log _{q}c_{0})\right).$
$C_{q}:=c_{0}+9\log _{q}c_{0}+9s^{\ast }\left(\log _{q}4+\log _{q}(1+\log _{q}c_{0})\right).$
Finally, from Theorem 3.2, it follows that
![]() $m\leqslant \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}_{2}}$
and
$m\leqslant \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}_{1}}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}_{2}}$
and
Therefore, we either have the above upper bound (12) on
![]() $\deg _{K}{\wp}$
or
$\deg _{K}{\wp}$
or
![]() $\deg _{K}{\wp}\leqslant c_{0}\leqslant C_{q}$
; so in the end, we get
$\deg _{K}{\wp}\leqslant c_{0}\leqslant C_{q}$
; so in the end, we get
where
![]() $s_{q}=9s^{\ast }$
. The result thus follows as desired.◻
$s_{q}=9s^{\ast }$
. The result thus follows as desired.◻
4 Twists of Drinfeld modules
Let
![]() $L/K$
be an extension where
$L/K$
be an extension where
![]() $K=\mathbb{F}_{q}(T)$
. Suppose that
$K=\mathbb{F}_{q}(T)$
. Suppose that
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
are rank
$\unicode[STIX]{x1D719}^{\prime }$
are rank
![]() $r$
Drinfeld
$r$
Drinfeld
![]() $A$
-modules over
$A$
-modules over
![]() $K$
given by
$K$
given by
Then
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
are isomorphic over
$\unicode[STIX]{x1D719}^{\prime }$
are isomorphic over
![]() $L$
if and only if there is a
$L$
if and only if there is a
![]() $c\in L^{\ast }$
such that
$c\in L^{\ast }$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D719}^{\prime }(T)c=\left(\mathop{\sum }_{i=0}^{r}a_{j}^{\prime }\unicode[STIX]{x1D70F}^{j}\right)c=c\left(\mathop{\sum }_{j=0}^{r}c^{q^{j}-1}a_{j}^{\prime }\unicode[STIX]{x1D70F}^{j}\right)=c\unicode[STIX]{x1D719}(T).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}^{\prime }(T)c=\left(\mathop{\sum }_{i=0}^{r}a_{j}^{\prime }\unicode[STIX]{x1D70F}^{j}\right)c=c\left(\mathop{\sum }_{j=0}^{r}c^{q^{j}-1}a_{j}^{\prime }\unicode[STIX]{x1D70F}^{j}\right)=c\unicode[STIX]{x1D719}(T).\end{eqnarray}$$
Explicitly, this implies that
![]() $a_{j}^{\prime }=a_{j}/c^{q^{j}-1}$
for any
$a_{j}^{\prime }=a_{j}/c^{q^{j}-1}$
for any
![]() $j=0,1,\ldots ,r$
. Here
$j=0,1,\ldots ,r$
. Here
![]() $c\in L^{\ast }$
is regarded as an element of
$c\in L^{\ast }$
is regarded as an element of
![]() $\operatorname{Hom}_{L}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime })$
and induces a map
$\operatorname{Hom}_{L}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime })$
and induces a map
![]() $L\rightarrow L$
as Drinfeld
$L\rightarrow L$
as Drinfeld
![]() $A$
-modules by
$A$
-modules by
![]() $x\mapsto cx$
, where the first
$x\mapsto cx$
, where the first
![]() $L$
is an
$L$
is an
![]() $A$
-module under
$A$
-module under
![]() $\unicode[STIX]{x1D719}$
and the second under
$\unicode[STIX]{x1D719}$
and the second under
![]() $\unicode[STIX]{x1D719}^{\prime }$
.
$\unicode[STIX]{x1D719}^{\prime }$
.
Lemma 4.1. Let
![]() $K=\mathbb{F}_{q}(T)$
and
$K=\mathbb{F}_{q}(T)$
and
![]() $q$
be odd. For Drinfeld
$q$
be odd. For Drinfeld
![]() $A$
-modules
$A$
-modules
![]() $\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }$
of rank
$\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }$
of rank
![]() $r$
over
$r$
over
![]() $K$
, suppose there is an isomorphism
$K$
, suppose there is an isomorphism
![]() $f(x)=cx$
from
$f(x)=cx$
from
![]() $\unicode[STIX]{x1D719}$
to
$\unicode[STIX]{x1D719}$
to
![]() $\unicode[STIX]{x1D719}^{\prime }$
given by
$\unicode[STIX]{x1D719}^{\prime }$
given by
![]() $c\unicode[STIX]{x1D719}_{a}=\unicode[STIX]{x1D719}_{a}^{\prime }c$
, where
$c\unicode[STIX]{x1D719}_{a}=\unicode[STIX]{x1D719}_{a}^{\prime }c$
, where
![]() $c=\unicode[STIX]{x1D6FF}^{1/(q-1)}$
for some
$c=\unicode[STIX]{x1D6FF}^{1/(q-1)}$
for some
![]() $\unicode[STIX]{x1D6FF}\in K^{\ast }$
. Let
$\unicode[STIX]{x1D6FF}\in K^{\ast }$
. Let
![]() $\unicode[STIX]{x1D716}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
denote the Galois character such that
$\unicode[STIX]{x1D716}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
denote the Galois character such that
![]() $\unicode[STIX]{x1D70E}(c)=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})c$
for
$\unicode[STIX]{x1D70E}(c)=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})c$
for
![]() $\unicode[STIX]{x1D70E}\in G_{K}$
. Let
$\unicode[STIX]{x1D70E}\in G_{K}$
. Let
![]() $\unicode[STIX]{x1D719}[a]$
and
$\unicode[STIX]{x1D719}[a]$
and
![]() $\unicode[STIX]{x1D719}^{\prime }[a]$
be the
$\unicode[STIX]{x1D719}^{\prime }[a]$
be the
![]() $A$
-modules of
$A$
-modules of
![]() $a$
-torsion points of
$a$
-torsion points of
![]() $\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }$
with
$\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }$
with
![]() $a\in A$
nonzero and let
$a\in A$
nonzero and let
be their associated mod
![]() $a$
representations. Then
$a$
representations. Then
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },a}\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},a}\otimes \unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },a}\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},a}\otimes \unicode[STIX]{x1D716}$
.
Proof. Let
![]() $\unicode[STIX]{x1D713}:\unicode[STIX]{x1D719}[a]\rightarrow \unicode[STIX]{x1D719}^{\prime }[a]$
be the isomorphism induced by
$\unicode[STIX]{x1D713}:\unicode[STIX]{x1D719}[a]\rightarrow \unicode[STIX]{x1D719}^{\prime }[a]$
be the isomorphism induced by
![]() $f$
, namely
$f$
, namely
![]() $P\mapsto cP$
, where
$P\mapsto cP$
, where
![]() $P\in \unicode[STIX]{x1D719}[a]$
. For
$P\in \unicode[STIX]{x1D719}[a]$
. For
![]() $P\in \unicode[STIX]{x1D719}[a]$
, we then have that
$P\in \unicode[STIX]{x1D719}[a]$
, we then have that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },a}(\unicode[STIX]{x1D70E})(\unicode[STIX]{x1D713}(P))=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },a}(\unicode[STIX]{x1D70E})cP=\unicode[STIX]{x1D70E}(cP)=\unicode[STIX]{x1D70E}(c)\unicode[STIX]{x1D70E}(P)=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})c\unicode[STIX]{x1D70E}(P)=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},a}(\unicode[STIX]{x1D70E})(P))$
, hence the result follows.◻
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },a}(\unicode[STIX]{x1D70E})(\unicode[STIX]{x1D713}(P))=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },a}(\unicode[STIX]{x1D70E})cP=\unicode[STIX]{x1D70E}(cP)=\unicode[STIX]{x1D70E}(c)\unicode[STIX]{x1D70E}(P)=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})c\unicode[STIX]{x1D70E}(P)=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},a}(\unicode[STIX]{x1D70E})(P))$
, hence the result follows.◻
In the above lemma, we call the resulting
![]() $\unicode[STIX]{x1D719}^{\prime }$
the twist of
$\unicode[STIX]{x1D719}^{\prime }$
the twist of
![]() $\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}$
by
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
Lemma 4.2. Let
![]() $\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }$
be Drinfeld
$\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime }$
be Drinfeld
![]() $A$
-modules of rank
$A$
-modules of rank
![]() $r$
over
$r$
over
![]() $K=\mathbb{F}_{q}(T)$
, and suppose that
$K=\mathbb{F}_{q}(T)$
, and suppose that
![]() $\unicode[STIX]{x1D719}^{\prime }$
is the twist of
$\unicode[STIX]{x1D719}^{\prime }$
is the twist of
![]() $\unicode[STIX]{x1D719}$
by a nontrivial character
$\unicode[STIX]{x1D719}$
by a nontrivial character
![]() $\unicode[STIX]{x1D716}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
. Assume that
$\unicode[STIX]{x1D716}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
. Assume that
![]() $\operatorname{End}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}(A)$
(that is,
$\operatorname{End}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}(A)$
(that is,
![]() $\unicode[STIX]{x1D719}$
has no complex multiplication). Then
$\unicode[STIX]{x1D719}$
has no complex multiplication). Then
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
are not
$\unicode[STIX]{x1D719}^{\prime }$
are not
![]() $K$
-isogenous.
$K$
-isogenous.
Proof. We note that there is an isomorphism
![]() $\unicode[STIX]{x1D713}:\unicode[STIX]{x1D719}^{\prime }\rightarrow \unicode[STIX]{x1D719}$
defined over
$\unicode[STIX]{x1D713}:\unicode[STIX]{x1D719}^{\prime }\rightarrow \unicode[STIX]{x1D719}$
defined over
![]() $\overline{K}$
but not over
$\overline{K}$
but not over
![]() $K$
. Explicitly, it is given by the element
$K$
. Explicitly, it is given by the element
![]() $c\in \overline{K}^{\ast }$
but not in
$c\in \overline{K}^{\ast }$
but not in
![]() $K^{\ast }$
such that
$K^{\ast }$
such that
![]() $c\unicode[STIX]{x1D719}^{\prime }(a)=\unicode[STIX]{x1D719}(a)c$
for all
$c\unicode[STIX]{x1D719}^{\prime }(a)=\unicode[STIX]{x1D719}(a)c$
for all
![]() $a\in A$
.
$a\in A$
.
Suppose there is a
![]() $K$
-isogeny
$K$
-isogeny
![]() $\unicode[STIX]{x1D706}:\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}^{\prime }$
. Explicitly, there is a
$\unicode[STIX]{x1D706}:\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}^{\prime }$
. Explicitly, there is a
![]() $g\in K\left\{\unicode[STIX]{x1D70F}\right\}$
such that
$g\in K\left\{\unicode[STIX]{x1D70F}\right\}$
such that
![]() $g\unicode[STIX]{x1D719}(a)=\unicode[STIX]{x1D719}^{\prime }(a)g$
for all
$g\unicode[STIX]{x1D719}(a)=\unicode[STIX]{x1D719}^{\prime }(a)g$
for all
![]() $a\in A$
. Hence,
$a\in A$
. Hence,
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D706}:\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}$
is given by
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D706}:\unicode[STIX]{x1D719}\rightarrow \unicode[STIX]{x1D719}$
is given by
![]() $cg$
so that
$cg$
so that
![]() $(cg)\unicode[STIX]{x1D719}(a)=\unicode[STIX]{x1D719}(a)(cg)$
for all
$(cg)\unicode[STIX]{x1D719}(a)=\unicode[STIX]{x1D719}(a)(cg)$
for all
![]() $a\in A$
. We may assume now that
$a\in A$
. We may assume now that
![]() $cg\in \unicode[STIX]{x1D719}(A)$
or else
$cg\in \unicode[STIX]{x1D719}(A)$
or else
![]() $\operatorname{End}(\unicode[STIX]{x1D719})$
is strictly bigger than
$\operatorname{End}(\unicode[STIX]{x1D719})$
is strictly bigger than
![]() $\unicode[STIX]{x1D719}(A)$
. Hence,
$\unicode[STIX]{x1D719}(A)$
. Hence,
![]() $cg=\unicode[STIX]{x1D719}(m)$
for some
$cg=\unicode[STIX]{x1D719}(m)$
for some
![]() $m\in A$
. But this means that
$m\in A$
. But this means that
![]() $c\in K\left\{\unicode[STIX]{x1D70F}\right\}$
, contradicting the fact that
$c\in K\left\{\unicode[STIX]{x1D70F}\right\}$
, contradicting the fact that
![]() $c\in \overline{K}^{\ast }$
but not in
$c\in \overline{K}^{\ast }$
but not in
![]() $K^{\ast }$
.◻
$K^{\ast }$
.◻
Lemma 4.3. Let
![]() $\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$
be Drinfeld
$\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2}$
be Drinfeld
![]() $A$
-modules of rank
$A$
-modules of rank
![]() $2$
over
$2$
over
![]() $K=\mathbb{F}_{q}(T)$
, and suppose
$K=\mathbb{F}_{q}(T)$
, and suppose
![]() $\unicode[STIX]{x1D719}_{2}$
is the twist of
$\unicode[STIX]{x1D719}_{2}$
is the twist of
![]() $\unicode[STIX]{x1D719}_{1}$
by a nontrivial character
$\unicode[STIX]{x1D719}_{1}$
by a nontrivial character
![]() $\unicode[STIX]{x1D716}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
which is ramified on a subset of the set of primes of bad reduction of
$\unicode[STIX]{x1D716}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
which is ramified on a subset of the set of primes of bad reduction of
![]() $\unicode[STIX]{x1D719}_{1}$
. Then the bound on the different divisor for
$\unicode[STIX]{x1D719}_{1}$
. Then the bound on the different divisor for
![]() $K(\unicode[STIX]{x1D719}_{2}[a])/K$
from Theorem 3.1 can be taken to be the bound on the different divisor for
$K(\unicode[STIX]{x1D719}_{2}[a])/K$
from Theorem 3.1 can be taken to be the bound on the different divisor for
![]() $K(\unicode[STIX]{x1D719}_{1}[a])/K$
from Theorem 3.1.
$K(\unicode[STIX]{x1D719}_{1}[a])/K$
from Theorem 3.1.
Proof. This follows from the fact that the dependence of the bounds from Theorem 3.1 on
![]() $\unicode[STIX]{x1D719}$
is only through the
$\unicode[STIX]{x1D719}$
is only through the
![]() $j$
-invariant of
$j$
-invariant of
![]() $\unicode[STIX]{x1D719}$
and the set of primes of bad reduction of
$\unicode[STIX]{x1D719}$
and the set of primes of bad reduction of
![]() $\unicode[STIX]{x1D719}$
.◻
$\unicode[STIX]{x1D719}$
.◻
5 Semi-stable reduction in rank
 $2$
and Weil pairings
$2$
and Weil pairings
Let
![]() $P$
be a finite prime of
$P$
be a finite prime of
![]() $K$
,
$K$
,
![]() $K_{P}$
be the completion at
$K_{P}$
be the completion at
![]() $P$
of
$P$
of
![]() $K$
and
$K$
and
![]() ${\mathcal{O}}_{P}\subseteq K_{P}$
be the valuation ring of
${\mathcal{O}}_{P}\subseteq K_{P}$
be the valuation ring of
![]() $P$
. We say that a Drinfeld
$P$
. We say that a Drinfeld
![]() $A$
-module
$A$
-module
![]() $\unicode[STIX]{x1D719}$
of rank 2 over
$\unicode[STIX]{x1D719}$
of rank 2 over
![]() $K$
has stable reduction at
$K$
has stable reduction at
![]() $P$
if there exists a Drinfeld module
$P$
if there exists a Drinfeld module
![]() $\unicode[STIX]{x1D719}^{\prime }$
over
$\unicode[STIX]{x1D719}^{\prime }$
over
![]() $K_{P}$
which is integral over
$K_{P}$
which is integral over
![]() ${\mathcal{O}}_{P}$
such that its reduction modulo
${\mathcal{O}}_{P}$
such that its reduction modulo
![]() $P$
defines a Drinfeld module over
$P$
defines a Drinfeld module over
![]() ${\mathcal{O}}_{P}/P$
and
${\mathcal{O}}_{P}/P$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
is isomorphic to
$\unicode[STIX]{x1D719}^{\prime }$
is isomorphic to
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $K_{P}$
. Furthermore, we say that
$K_{P}$
. Furthermore, we say that
![]() $\unicode[STIX]{x1D719}$
has good reduction at
$\unicode[STIX]{x1D719}$
has good reduction at
![]() $P$
if
$P$
if
![]() $\unicode[STIX]{x1D719}$
has stable reduction at
$\unicode[STIX]{x1D719}$
has stable reduction at
![]() $P$
such that
$P$
such that
![]() $P\nmid a_{2}(\unicode[STIX]{x1D719})$
, otherwise we say that
$P\nmid a_{2}(\unicode[STIX]{x1D719})$
, otherwise we say that
![]() $\unicode[STIX]{x1D719}$
has bad reduction at
$\unicode[STIX]{x1D719}$
has bad reduction at
![]() $P$
. If
$P$
. If
![]() $\unicode[STIX]{x1D719}$
has bad reduction at
$\unicode[STIX]{x1D719}$
has bad reduction at
![]() $P$
, but has stable reduction over
$P$
, but has stable reduction over
![]() ${\mathcal{O}}_{P}$
such that
${\mathcal{O}}_{P}$
such that
![]() $P\nmid a_{1}(\unicode[STIX]{x1D719})$
, we say that
$P\nmid a_{1}(\unicode[STIX]{x1D719})$
, we say that
![]() $\unicode[STIX]{x1D719}$
has bad Tate reduction at
$\unicode[STIX]{x1D719}$
has bad Tate reduction at
![]() $P$
. If
$P$
. If
![]() $\unicode[STIX]{x1D719}$
has good reduction, or bad Tate reduction at
$\unicode[STIX]{x1D719}$
has good reduction, or bad Tate reduction at
![]() $P$
, we say that
$P$
, we say that
![]() $\unicode[STIX]{x1D719}$
is semi-stable reduction at
$\unicode[STIX]{x1D719}$
is semi-stable reduction at
![]() $P$
.
$P$
.
Lemma 5.1. Let
![]() $P$
be a finite prime of
$P$
be a finite prime of
![]() $K$
and
$K$
and
![]() ${\mathcal{O}}_{P}\subseteq K_{P}$
be the valuation ring of
${\mathcal{O}}_{P}\subseteq K_{P}$
be the valuation ring of
![]() $P$
. Let
$P$
. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
, with
$K$
, with
![]() $\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
, and
$\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
, and
![]() $a_{1}(\unicode[STIX]{x1D719}),a_{2}(\unicode[STIX]{x1D719})\in {\mathcal{O}}_{P}$
. Then there is a finite tamely ramified extension
$a_{1}(\unicode[STIX]{x1D719}),a_{2}(\unicode[STIX]{x1D719})\in {\mathcal{O}}_{P}$
. Then there is a finite tamely ramified extension
![]() $K^{\prime }/K_{P}$
such that
$K^{\prime }/K_{P}$
such that
![]() $\unicode[STIX]{x1D719}$
attains semi-stable reduction over
$\unicode[STIX]{x1D719}$
attains semi-stable reduction over
![]() $K^{\prime }$
and the degree of
$K^{\prime }$
and the degree of
![]() $K_{P}^{\text{nr}}\cdot K^{\prime }/K_{P}^{\text{nr}}$
divides
$K_{P}^{\text{nr}}\cdot K^{\prime }/K_{P}^{\text{nr}}$
divides
![]() $q^{2}-1$
, where
$q^{2}-1$
, where
![]() $K_{P}^{\text{nr}}$
is the maximal unramified extension of
$K_{P}^{\text{nr}}$
is the maximal unramified extension of
![]() $K_{P}$
.
$K_{P}$
.
Proof. A twist
![]() $\unicode[STIX]{x1D719}^{\prime }$
of
$\unicode[STIX]{x1D719}^{\prime }$
of
![]() $\unicode[STIX]{x1D719}$
has the form:
$\unicode[STIX]{x1D719}$
has the form:
Let
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{P}$
be a uniformizer, and let
$\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{P}$
be a uniformizer, and let
![]() $v$
be the corresponding valuation at
$v$
be the corresponding valuation at
![]() $P$
of
$P$
of
![]() $K$
which we extend to
$K$
which we extend to
![]() $\overline{K}$
.
$\overline{K}$
.
Recall
![]() $j(\unicode[STIX]{x1D719})=a_{1}(\unicode[STIX]{x1D719})^{q+1}/a_{2}(\unicode[STIX]{x1D719})$
.
$j(\unicode[STIX]{x1D719})=a_{1}(\unicode[STIX]{x1D719})^{q+1}/a_{2}(\unicode[STIX]{x1D719})$
.
Case
![]() $v(j(\unicode[STIX]{x1D719}))\geqslant 0$
: Let
$v(j(\unicode[STIX]{x1D719}))\geqslant 0$
: Let
![]() $c=1/\unicode[STIX]{x1D70B}^{v(a_{2}(\unicode[STIX]{x1D719}))/(q^{2}-1)}$
. The corresponding twist
$c=1/\unicode[STIX]{x1D70B}^{v(a_{2}(\unicode[STIX]{x1D719}))/(q^{2}-1)}$
. The corresponding twist
![]() $\unicode[STIX]{x1D719}^{\prime }$
over
$\unicode[STIX]{x1D719}^{\prime }$
over
![]() $K^{\prime }$
then has
$K^{\prime }$
then has
![]() $v(a_{1}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{1}(\unicode[STIX]{x1D719})c^{q-1})\geqslant 0$
and
$v(a_{1}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{1}(\unicode[STIX]{x1D719})c^{q-1})\geqslant 0$
and
![]() $v(a_{2}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{2}(\unicode[STIX]{x1D719})c^{q^{2}-1})=0$
, where
$v(a_{2}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{2}(\unicode[STIX]{x1D719})c^{q^{2}-1})=0$
, where
![]() $K^{\prime }=K_{P}(\unicode[STIX]{x1D70B}^{v(a_{2}(\unicode[STIX]{x1D719}))/(q^{2}-1)})$
. Hence,
$K^{\prime }=K_{P}(\unicode[STIX]{x1D70B}^{v(a_{2}(\unicode[STIX]{x1D719}))/(q^{2}-1)})$
. Hence,
![]() $\unicode[STIX]{x1D719}^{\prime }$
has good reduction over
$\unicode[STIX]{x1D719}^{\prime }$
has good reduction over
![]() $K^{\prime }$
.
$K^{\prime }$
.
Case
![]() $v(j(\unicode[STIX]{x1D719}))<0$
: Let
$v(j(\unicode[STIX]{x1D719}))<0$
: Let
![]() $c=1/\unicode[STIX]{x1D70B}^{v(a_{1}(\unicode[STIX]{x1D719}))/(q-1)}$
. The corresponding twist
$c=1/\unicode[STIX]{x1D70B}^{v(a_{1}(\unicode[STIX]{x1D719}))/(q-1)}$
. The corresponding twist
![]() $\unicode[STIX]{x1D719}^{\prime }$
then has
$\unicode[STIX]{x1D719}^{\prime }$
then has
![]() $v(a_{1}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{1}(\unicode[STIX]{x1D719})c^{q-1})=0$
and
$v(a_{1}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{1}(\unicode[STIX]{x1D719})c^{q-1})=0$
and
![]() $v(a_{2}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{2}(\unicode[STIX]{x1D719})c^{q^{2}-1})>0$
, where
$v(a_{2}(\unicode[STIX]{x1D719}^{\prime }))=v(a_{2}(\unicode[STIX]{x1D719})c^{q^{2}-1})>0$
, where
![]() $K^{\prime }=K_{P}(\unicode[STIX]{x1D70B}^{v(a_{1}(\unicode[STIX]{x1D719}))/(q-1)})$
. Hence,
$K^{\prime }=K_{P}(\unicode[STIX]{x1D70B}^{v(a_{1}(\unicode[STIX]{x1D719}))/(q-1)})$
. Hence,
![]() $\unicode[STIX]{x1D719}^{\prime }$
has bad Tate reduction over
$\unicode[STIX]{x1D719}^{\prime }$
has bad Tate reduction over
![]() $K^{\prime }$
.
$K^{\prime }$
.
In both cases,
![]() $K^{\prime }/K_{P}$
is tamely ramified and the degree of
$K^{\prime }/K_{P}$
is tamely ramified and the degree of
![]() $K_{P}^{\text{nr}}\cdot K^{\prime }/K_{P}^{\text{nr}}$
divides
$K_{P}^{\text{nr}}\cdot K^{\prime }/K_{P}^{\text{nr}}$
divides
![]() $q^{2}-1$
.◻
$q^{2}-1$
.◻
Theorem 5.2. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module over
$A$
-module over
![]() $K$
of rank
$K$
of rank
![]() $2$
with
$2$
with
![]() $\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
,
$\unicode[STIX]{x1D719}(T)=i(T)+a_{1}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}+a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}^{2}$
,
![]() $q$
be odd, and let
$q$
be odd, and let
![]() $\unicode[STIX]{x1D713}$
be the Drinfeld
$\unicode[STIX]{x1D713}$
be the Drinfeld
![]() $A$
-module over
$A$
-module over
![]() $K$
of rank
$K$
of rank
![]() $1$
defined by
$1$
defined by
![]() $\unicode[STIX]{x1D713}(T)=T-a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}$
. If
$\unicode[STIX]{x1D713}(T)=T-a_{2}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D70F}$
. If
![]() ${\wp}$
is a finite prime of
${\wp}$
is a finite prime of
![]() $K$
, then we have that
$K$
, then we have that
Proof. This follows by combining the second part of [Reference van der Heiden31, Theorem 5.3] and [Reference van der Heiden31, Proposition 7.4], under the assumption that
![]() $\unicode[STIX]{x1D719}$
has rank
$\unicode[STIX]{x1D719}$
has rank
![]() $2$
and
$2$
and
![]() $A=\mathbb{F}_{q}[T]$
. It can also be deduced by showing that
$A=\mathbb{F}_{q}[T]$
. It can also be deduced by showing that
![]() $\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
and
$\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
and
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}$
coincide on Frobenius elements using [Reference Gekeler8, Theorem 2.11], again under the assumption that
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}$
coincide on Frobenius elements using [Reference Gekeler8, Theorem 2.11], again under the assumption that
![]() $\unicode[STIX]{x1D719}$
has rank
$\unicode[STIX]{x1D719}$
has rank
![]() $2$
and
$2$
and
![]() $A=\mathbb{F}_{q}[T]$
, so by the Chebotarev density theorem, the two Galois characters are the same.◻
$A=\mathbb{F}_{q}[T]$
, so by the Chebotarev density theorem, the two Galois characters are the same.◻
For a definition of the Weil pairing between a Drinfeld
![]() $A$
-module and its dual, see [Reference Poonen22].
$A$
-module and its dual, see [Reference Poonen22].
We use the convention
![]() $\unicode[STIX]{x1D712}(P):=\unicode[STIX]{x1D712}(\operatorname{Frob}_{P})$
for a Galois character
$\unicode[STIX]{x1D712}(P):=\unicode[STIX]{x1D712}(\operatorname{Frob}_{P})$
for a Galois character
![]() $\unicode[STIX]{x1D712}:G_{K}\rightarrow (A/{\wp})^{\times }$
.
$\unicode[STIX]{x1D712}:G_{K}\rightarrow (A/{\wp})^{\times }$
.
Proposition 5.3. Under the hypothesis of Theorem 5.2, we have that
for all
![]() $P$
not in
$P$
not in
![]() $S_{\unicode[STIX]{x1D719}}$
and
$S_{\unicode[STIX]{x1D719}}$
and
![]() $P\neq {\wp},\infty$
, where
$P\neq {\wp},\infty$
, where
![]() $\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }\subseteq (A/{\wp})^{\times }$
is a Galois character.
$\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }\subseteq (A/{\wp})^{\times }$
is a Galois character.
Proof. Note that
![]() $\unicode[STIX]{x1D713}$
is isomorphic to the Carlitz module
$\unicode[STIX]{x1D713}$
is isomorphic to the Carlitz module
![]() $C(T)=T+\unicode[STIX]{x1D70F}$
over
$C(T)=T+\unicode[STIX]{x1D70F}$
over
![]() $K(c)$
, where
$K(c)$
, where
![]() $c=(-a_{2}(\unicode[STIX]{x1D719}))^{1/(q-1)}$
, that is,
$c=(-a_{2}(\unicode[STIX]{x1D719}))^{1/(q-1)}$
, that is,
![]() $C\circ f=f\circ \unicode[STIX]{x1D713}$
where
$C\circ f=f\circ \unicode[STIX]{x1D713}$
where
![]() $f(z)=cz$
. Thus, we have that
$f(z)=cz$
. Thus, we have that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}=\unicode[STIX]{x1D70C}_{C,{\wp}}\otimes \unicode[STIX]{x1D716}_{0}$
, where
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}=\unicode[STIX]{x1D70C}_{C,{\wp}}\otimes \unicode[STIX]{x1D716}_{0}$
, where
![]() $\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
giving the action of
$\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
giving the action of
![]() $G_{K}$
on
$G_{K}$
on
![]() $c$
.
$c$
.
Now,
![]() $C[P]\cong A/P$
and the elements of
$C[P]\cong A/P$
and the elements of
![]() $(A/P)^{\times }$
correspond to the roots of
$(A/P)^{\times }$
correspond to the roots of
![]() $C(P)(X)/X$
.
$C(P)(X)/X$
.
Furthermore, from [Reference Rosen23, Theorem 12.10], we have that
![]() $C(P)(X)/X\in A[X]$
is an Eisenstein polynomial for the prime
$C(P)(X)/X\in A[X]$
is an Eisenstein polynomial for the prime
![]() $P$
. Hence,
$P$
. Hence,
![]() $C(P)(X)\equiv X^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}P)$
, where
$C(P)(X)\equiv X^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}P)$
, where
![]() $\left|P\right|=q^{\deg _{K}P}$
.
$\left|P\right|=q^{\deg _{K}P}$
.
Let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $K(C[{\wp}])$
lying above
$K(C[{\wp}])$
lying above
![]() $P$
. We then have that
$P$
. We then have that
![]() $C(P)(X)\equiv X^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{P})$
.
$C(P)(X)\equiv X^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{P})$
.
Let
![]() $\unicode[STIX]{x1D706}$
be a generator for
$\unicode[STIX]{x1D706}$
be a generator for
![]() $C[{\wp}]$
. Since
$C[{\wp}]$
. Since
![]() $\operatorname{Frob}_{P}(\unicode[STIX]{x1D706})\equiv \unicode[STIX]{x1D706}^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{P})$
and
$\operatorname{Frob}_{P}(\unicode[STIX]{x1D706})\equiv \unicode[STIX]{x1D706}^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{P})$
and
![]() $C(P)(\unicode[STIX]{x1D706})\equiv \unicode[STIX]{x1D706}^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{P})$
, we have that
$C(P)(\unicode[STIX]{x1D706})\equiv \unicode[STIX]{x1D706}^{\left|P\right|}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{P})$
, we have that
![]() $\unicode[STIX]{x1D70C}_{C,{\wp}}(\operatorname{Frob}_{P})\equiv P\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
.
$\unicode[STIX]{x1D70C}_{C,{\wp}}(\operatorname{Frob}_{P})\equiv P\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
.
Thus, we get that
![]() $\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{P})=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}(\operatorname{Frob}_{P})=\unicode[STIX]{x1D70C}_{C,{\wp}}\otimes \unicode[STIX]{x1D716}_{0}(\operatorname{Frob}_{P})\equiv \unicode[STIX]{x1D716}_{0}(P)P\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
.◻
$\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{P})=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}(\operatorname{Frob}_{P})=\unicode[STIX]{x1D70C}_{C,{\wp}}\otimes \unicode[STIX]{x1D716}_{0}(\operatorname{Frob}_{P})\equiv \unicode[STIX]{x1D716}_{0}(P)P\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
.◻
6 The Cartan case
In this section, we assume throughout that
![]() $q$
is odd.
$q$
is odd.
Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
without complex multiplication, and let
$K$
without complex multiplication, and let
![]() ${\wp}$
be a finite prime of
${\wp}$
be a finite prime of
![]() $K$
. In this section, we suppose throughout that the image of
$K$
. In this section, we suppose throughout that the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer
![]() ${\mathcal{N}}$
of a Cartan subgroup
${\mathcal{N}}$
of a Cartan subgroup
![]() ${\mathcal{C}}$
of
${\mathcal{C}}$
of
![]() $\operatorname{GL}_{2}(A/{\wp})$
but not in
$\operatorname{GL}_{2}(A/{\wp})$
but not in
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Consider the associated character
![]() $\unicode[STIX]{x1D716}_{{\wp}}:G_{K}\rightarrow \left\{\pm 1\right\}$
obtained by applying
$\unicode[STIX]{x1D716}_{{\wp}}:G_{K}\rightarrow \left\{\pm 1\right\}$
obtained by applying
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
and then the quotient map
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
and then the quotient map
![]() ${\mathcal{N}}/{\mathcal{C}}\cong \left\{\pm 1\right\}$
. Let
${\mathcal{N}}/{\mathcal{C}}\cong \left\{\pm 1\right\}$
. Let
![]() $K^{\prime }/K$
be the quadratic extension associated to
$K^{\prime }/K$
be the quadratic extension associated to
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
.
$\unicode[STIX]{x1D716}_{{\wp}}$
.
Gardeyn studies the image of the inertia group
![]() $I_{K_{{\wp}}}$
of
$I_{K_{{\wp}}}$
of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
at the finite prime
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
at the finite prime
![]() ${\wp}$
of
${\wp}$
of
![]() $K$
[Reference Gardeyn11, Theorem 2.23, Corollary 2.24]. He shows the following theorem, where we do not need the assumption that the image of
$K$
[Reference Gardeyn11, Theorem 2.23, Corollary 2.24]. He shows the following theorem, where we do not need the assumption that the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer
![]() ${\mathcal{N}}$
of a Cartan subgroup
${\mathcal{N}}$
of a Cartan subgroup
![]() ${\mathcal{C}}$
of
${\mathcal{C}}$
of
![]() $\operatorname{GL}_{2}(A/{\wp})$
but not in
$\operatorname{GL}_{2}(A/{\wp})$
but not in
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Theorem 6.1. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
with good reduction at
$K$
with good reduction at
![]() ${\wp}$
and
${\wp}$
and
![]() $I_{K_{{\wp}}}$
be the inertia group at
$I_{K_{{\wp}}}$
be the inertia group at
![]() ${\wp}$
of
${\wp}$
of
![]() $K$
. Then
$K$
. Then
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is
(1) a nonsplit Cartan subgroup of order
 $q_{{\wp}}^{2}-1$
(if
$q_{{\wp}}^{2}-1$
(if
 $\unicode[STIX]{x1D719}$
has good reduction at
$\unicode[STIX]{x1D719}$
has good reduction at
 ${\wp}$
of height
${\wp}$
of height
 $2$
);
$2$
);(2) a semisplit Cartan or semisplit Borel subgroup of order divisible by
 $q_{{\wp}}-1$
(if
$q_{{\wp}}-1$
(if
 $\unicode[STIX]{x1D719}$
has good reduction at
$\unicode[STIX]{x1D719}$
has good reduction at
 ${\wp}$
of height 1),
${\wp}$
of height 1),
where
![]() $q_{{\wp}}$
is the size of the residue field
$q_{{\wp}}$
is the size of the residue field
![]() $A/{\wp}$
.
$A/{\wp}$
.
Proof. See [Reference Pink and Rütsche21, Proposition 2.7], [Reference Gardeyn11, Theorem 2.23, Corollary 2.24], [Reference Serre24, Proposition 11, 12, 13]. ◻
Remark 6.2. The elliptic curve analogue of the above theorem is described in [Reference Serre24, Proposition 11, 12, 13]. The reader may be curious about the situation of bad Tate reduction at
![]() ${\wp}$
. For elliptic curves, one knows by [Reference Serre24, Proposition 13], that
${\wp}$
. For elliptic curves, one knows by [Reference Serre24, Proposition 13], that
![]() $\unicode[STIX]{x1D70C}_{E,p}(I_{p})$
lies in a semisplit Borel subgroup if
$\unicode[STIX]{x1D70C}_{E,p}(I_{p})$
lies in a semisplit Borel subgroup if
![]() $E$
has bad multiplicative reduction at
$E$
has bad multiplicative reduction at
![]() $p$
. However, for Drinfeld modules, we only have that
$p$
. However, for Drinfeld modules, we only have that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{{\wp}})$
lies in a Borel subgroup, for reasons that we explain below.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{{\wp}})$
lies in a Borel subgroup, for reasons that we explain below.
If
![]() $\unicode[STIX]{x1D719}$
has bad Tate reduction at
$\unicode[STIX]{x1D719}$
has bad Tate reduction at
![]() ${\wp}$
, then over
${\wp}$
, then over
![]() $C_{{\wp}}$
, where
$C_{{\wp}}$
, where
![]() $C_{{\wp}}$
is the completion of an algebraic closure of
$C_{{\wp}}$
is the completion of an algebraic closure of
![]() $K_{{\wp}}$
, we have a uniformization [Reference Drinfeld6] given by a surjective analytic map
$K_{{\wp}}$
, we have a uniformization [Reference Drinfeld6] given by a surjective analytic map
![]() $e_{{\wp}}:C_{{\wp}}\rightarrow C_{{\wp}}$
which relates
$e_{{\wp}}:C_{{\wp}}\rightarrow C_{{\wp}}$
which relates
![]() $\unicode[STIX]{x1D719}$
to a Drinfeld
$\unicode[STIX]{x1D719}$
to a Drinfeld
![]() $A$
-module
$A$
-module
![]() $\unicode[STIX]{x1D713}$
of rank
$\unicode[STIX]{x1D713}$
of rank
![]() $1$
with good reduction at
$1$
with good reduction at
![]() ${\wp}$
via the relation
${\wp}$
via the relation
![]() $\unicode[STIX]{x1D713}_{a}\circ e_{{\wp}}=e_{{\wp}}\circ \unicode[STIX]{x1D719}_{a}$
. Let
$\unicode[STIX]{x1D713}_{a}\circ e_{{\wp}}=e_{{\wp}}\circ \unicode[STIX]{x1D719}_{a}$
. Let
![]() $\unicode[STIX]{x1D6EC}_{{\wp}}$
be the set of zeros of
$\unicode[STIX]{x1D6EC}_{{\wp}}$
be the set of zeros of
![]() $e_{{\wp}}$
. Then by [Reference Drinfeld6],
$e_{{\wp}}$
. Then by [Reference Drinfeld6],
![]() $\unicode[STIX]{x1D6EC}_{{\wp}}=A\cdot \unicode[STIX]{x1D706}_{1}$
is an
$\unicode[STIX]{x1D6EC}_{{\wp}}=A\cdot \unicode[STIX]{x1D706}_{1}$
is an
![]() $A$
-lattice in
$A$
-lattice in
![]() $C_{{\wp}}$
of rank
$C_{{\wp}}$
of rank
![]() $1$
, where the
$1$
, where the
![]() $A$
-module structure on
$A$
-module structure on
![]() $C_{{\wp}}$
is given by
$C_{{\wp}}$
is given by
![]() $\unicode[STIX]{x1D6FC}\cdot x:=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(x)$
.
$\unicode[STIX]{x1D6FC}\cdot x:=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(x)$
.
Write
![]() ${\wp}=(a)$
. The analytic map
${\wp}=(a)$
. The analytic map
![]() $e_{{\wp}}$
is
$e_{{\wp}}$
is
![]() $G_{K_{{\wp}}}$
-equivariant and induces an isomorphism
$G_{K_{{\wp}}}$
-equivariant and induces an isomorphism
![]() $\unicode[STIX]{x1D713}_{{\wp}}^{-1}(\unicode[STIX]{x1D6EC}_{{\wp}})/\unicode[STIX]{x1D6EC}_{{\wp}}\cong \unicode[STIX]{x1D719}[{\wp}]$
. We also have an exact sequence
$\unicode[STIX]{x1D713}_{{\wp}}^{-1}(\unicode[STIX]{x1D6EC}_{{\wp}})/\unicode[STIX]{x1D6EC}_{{\wp}}\cong \unicode[STIX]{x1D719}[{\wp}]$
. We also have an exact sequence
Thus,
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
has the form
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
has the form
where
![]() $\unicode[STIX]{x1D712}^{\prime }\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}$
. Since
$\unicode[STIX]{x1D712}^{\prime }\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}$
. Since
![]() $\unicode[STIX]{x1D713}$
is of rank
$\unicode[STIX]{x1D713}$
is of rank
![]() $1$
and has good reduction at
$1$
and has good reduction at
![]() ${\wp}$
, by application of [Reference Pink and Rütsche21, Proposition 2.7], we see that
${\wp}$
, by application of [Reference Pink and Rütsche21, Proposition 2.7], we see that
![]() $\unicode[STIX]{x1D712}_{\mid I_{{\wp}}}^{\prime }$
has image
$\unicode[STIX]{x1D712}_{\mid I_{{\wp}}}^{\prime }$
has image
![]() $\mathbb{F}_{{\wp}}^{\times }=(A/{\wp})^{\times }$
.
$\mathbb{F}_{{\wp}}^{\times }=(A/{\wp})^{\times }$
.
Since
![]() $\unicode[STIX]{x1D6EC}_{{\wp}}$
is
$\unicode[STIX]{x1D6EC}_{{\wp}}$
is
![]() $G_{K_{{\wp}}}$
-invariant, we have that
$G_{K_{{\wp}}}$
-invariant, we have that
where
![]() $\unicode[STIX]{x1D70E}\in G_{K,{\wp}}$
and
$\unicode[STIX]{x1D70E}\in G_{K,{\wp}}$
and
![]() $\unicode[STIX]{x1D712}^{\prime \prime }(\unicode[STIX]{x1D70E})\in A^{\times }=\mathbb{F}_{q}^{\times }$
. This implies that
$\unicode[STIX]{x1D712}^{\prime \prime }(\unicode[STIX]{x1D70E})\in A^{\times }=\mathbb{F}_{q}^{\times }$
. This implies that
![]() $\unicode[STIX]{x1D706}_{1}^{q-1}=c\in K_{{\wp}}^{\ast }$
. Now,
$\unicode[STIX]{x1D706}_{1}^{q-1}=c\in K_{{\wp}}^{\ast }$
. Now,
![]() $\unicode[STIX]{x1D712}^{\prime \prime }$
is unramified at
$\unicode[STIX]{x1D712}^{\prime \prime }$
is unramified at
![]() ${\wp}$
if and only if
${\wp}$
if and only if
![]() $v_{{\wp}}(c)\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}q-1)$
:
$v_{{\wp}}(c)\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}q-1)$
:
Write
![]() $c=u\unicode[STIX]{x1D70B}^{(q-1)k+r}$
, where
$c=u\unicode[STIX]{x1D70B}^{(q-1)k+r}$
, where
![]() $0\leqslant r<q-1$
,
$0\leqslant r<q-1$
,
![]() $\unicode[STIX]{x1D70B}$
is a uniformizer for
$\unicode[STIX]{x1D70B}$
is a uniformizer for
![]() $K_{{\wp}}$
, and
$K_{{\wp}}$
, and
![]() $u$
is a unit in
$u$
is a unit in
![]() $K_{{\wp}}$
. Then
$K_{{\wp}}$
. Then
![]() $\unicode[STIX]{x1D706}_{1}=u^{1/(q-1)}\unicode[STIX]{x1D70B}^{k}\unicode[STIX]{x1D70B}^{r/(q-1)}$
, which lies in
$\unicode[STIX]{x1D706}_{1}=u^{1/(q-1)}\unicode[STIX]{x1D70B}^{k}\unicode[STIX]{x1D70B}^{r/(q-1)}$
, which lies in
![]() $K_{{\wp}}^{\text{nr}}$
or
$K_{{\wp}}^{\text{nr}}$
or
![]() $K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D70B}^{r/(q-1)})=K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D70B}^{1/(q-1)})$
accordingly as
$K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D70B}^{r/(q-1)})=K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D70B}^{1/(q-1)})$
accordingly as
![]() $r=0$
or
$r=0$
or
![]() $r\not =0$
. In the former case,
$r\not =0$
. In the former case,
![]() $K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D706}_{1})=K_{{\wp}}^{\text{nr}}$
is unramified, and in the latter case,
$K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D706}_{1})=K_{{\wp}}^{\text{nr}}$
is unramified, and in the latter case,
![]() $K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D706}_{1})=K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D70B}^{1/(q-1)})$
is tamely ramified.
$K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D706}_{1})=K_{{\wp}}^{\text{nr}}(\unicode[STIX]{x1D70B}^{1/(q-1)})$
is tamely ramified.
Thus, in general both
![]() $\unicode[STIX]{x1D712}^{\prime }$
and
$\unicode[STIX]{x1D712}^{\prime }$
and
![]() $\unicode[STIX]{x1D712}^{\prime \prime }$
are ramified at
$\unicode[STIX]{x1D712}^{\prime \prime }$
are ramified at
![]() ${\wp}$
.
${\wp}$
.
Lemma 6.3. Suppose
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
and
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
and
![]() $q_{{\wp}}\geqslant 5$
. Then the character
$q_{{\wp}}\geqslant 5$
. Then the character
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
is unramified at
$\unicode[STIX]{x1D716}_{{\wp}}$
is unramified at
![]() ${\wp}$
.
${\wp}$
.
Proof. Using Theorem 6.1,
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is a nonsplit Cartan subgroup, semisplit Cartan subgroup, or semisplit Borel subgroup. In the first case, we obtain that
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is a nonsplit Cartan subgroup, semisplit Cartan subgroup, or semisplit Borel subgroup. In the first case, we obtain that
![]() $\unicode[STIX]{x1D716}_{{\wp}}(I_{K_{{\wp}}})=1$
by definition of
$\unicode[STIX]{x1D716}_{{\wp}}(I_{K_{{\wp}}})=1$
by definition of
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
.
$\unicode[STIX]{x1D716}_{{\wp}}$
.
Recall we are under the running assumption that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
has image contained in the normalizer of a Cartan subgroup
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
has image contained in the normalizer of a Cartan subgroup
![]() ${\mathcal{N}}$
. Hence, the last case does not occur as no semisplit Borel subgroup can be contained in
${\mathcal{N}}$
. Hence, the last case does not occur as no semisplit Borel subgroup can be contained in
![]() ${\mathcal{N}}$
.
${\mathcal{N}}$
.
In the second case,
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is a semisplit Cartan subgroup contained in
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is a semisplit Cartan subgroup contained in
![]() ${\mathcal{N}}$
. As
${\mathcal{N}}$
. As
![]() $q_{{\wp}}\geqslant 5$
, it follows that
$q_{{\wp}}\geqslant 5$
, it follows that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is the unique such semisplit Cartan subgroup in
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is the unique such semisplit Cartan subgroup in
![]() ${\mathcal{N}}$
(the proof in [Reference Serre24, Proposition 14] works for general finite fields). Since this semisplit Cartan subgroup is contained in
${\mathcal{N}}$
(the proof in [Reference Serre24, Proposition 14] works for general finite fields). Since this semisplit Cartan subgroup is contained in
![]() ${\mathcal{C}}$
, we have that
${\mathcal{C}}$
, we have that
![]() $\unicode[STIX]{x1D716}_{{\wp}}(I_{K_{{\wp}}})=1$
.◻
$\unicode[STIX]{x1D716}_{{\wp}}(I_{K_{{\wp}}})=1$
.◻
Corollary 6.4. Assume the notation and hypotheses of Lemma 6.3. Let
![]() $\unicode[STIX]{x1D719}^{\prime }$
be the twist of
$\unicode[STIX]{x1D719}^{\prime }$
be the twist of
![]() $\unicode[STIX]{x1D719}$
by the character
$\unicode[STIX]{x1D719}$
by the character
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
. Then
$\unicode[STIX]{x1D716}_{{\wp}}$
. Then
and in fact,
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}$
.
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}$
.
Proof. The character
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
is unramified outside the set of primes containing
$\unicode[STIX]{x1D716}_{{\wp}}$
is unramified outside the set of primes containing
![]() $\infty$
and the primes which divide
$\infty$
and the primes which divide
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}$
. Thus,
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}$
. Thus,
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}\mid \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}$
from Lemma 4.1. On the other hand,
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}\mid \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}$
from Lemma 4.1. On the other hand,
![]() $\unicode[STIX]{x1D719}$
is the twist of
$\unicode[STIX]{x1D719}$
is the twist of
![]() $\unicode[STIX]{x1D719}^{\prime }$
by
$\unicode[STIX]{x1D719}^{\prime }$
by
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
as well, so we obtain
$\unicode[STIX]{x1D716}_{{\wp}}$
as well, so we obtain
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}\mid \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}$
.◻
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}\mid \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}$
.◻
Let
![]() $\unicode[STIX]{x1D719}^{\prime }$
be the twist of
$\unicode[STIX]{x1D719}^{\prime }$
be the twist of
![]() $\unicode[STIX]{x1D719}$
by the character
$\unicode[STIX]{x1D719}$
by the character
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
, and let
$\unicode[STIX]{x1D716}_{{\wp}}$
, and let
![]() $S$
denote a set of primes outside of which both
$S$
denote a set of primes outside of which both
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
have good reduction. We have that
$\unicode[STIX]{x1D719}^{\prime }$
have good reduction. We have that
by Lemma 4.1 as
![]() $\unicode[STIX]{x1D719}^{\prime }$
is the twist of
$\unicode[STIX]{x1D719}^{\prime }$
is the twist of
![]() $\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}$
by
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
. Thus,
$\unicode[STIX]{x1D716}_{{\wp}}$
. Thus,
![]() $a_{P}(\unicode[STIX]{x1D719}^{\prime })=a_{P}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{P})$
, where
$a_{P}(\unicode[STIX]{x1D719}^{\prime })=a_{P}(\unicode[STIX]{x1D719})\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{P})$
, where
![]() $a_{{\wp}}(\unicode[STIX]{x1D719})$
denotes the trace of a Frobenius conjugacy class
$a_{{\wp}}(\unicode[STIX]{x1D719})$
denotes the trace of a Frobenius conjugacy class
![]() $\operatorname{Frob}_{{\wp}}$
at
$\operatorname{Frob}_{{\wp}}$
at
![]() ${\wp}$
on the Tate module
${\wp}$
on the Tate module
![]() $T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
, and similarly for
$T_{\mathfrak{L}}(\unicode[STIX]{x1D719})$
, and similarly for
![]() $a_{P}(\unicode[STIX]{x1D719}^{\prime })$
. Also,
$a_{P}(\unicode[STIX]{x1D719}^{\prime })$
. Also,
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}\mid _{G_{K^{\prime }}}\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}\mid _{G_{K^{\prime }}}\cong \unicode[STIX]{x1D70E}$
for a
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}\mid _{G_{K^{\prime }}}\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}\mid _{G_{K^{\prime }}}\cong \unicode[STIX]{x1D70E}$
for a
![]() $1$
-dimensional representation
$1$
-dimensional representation
![]() $\unicode[STIX]{x1D70E}:G_{K^{\prime }}\rightarrow \overline{\mathbb{F}}_{q}^{\times }$
, so we have
$\unicode[STIX]{x1D70E}:G_{K^{\prime }}\rightarrow \overline{\mathbb{F}}_{q}^{\times }$
, so we have
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}\cong \operatorname{Ind}_{G_{K^{\prime }}}^{G_{K}}\unicode[STIX]{x1D70E}\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
. Hence, we have
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}\cong \operatorname{Ind}_{G_{K^{\prime }}}^{G_{K}}\unicode[STIX]{x1D70E}\cong \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
. Hence, we have
![]() $a_{P}(\unicode[STIX]{x1D719}^{\prime })\equiv a_{P}(\unicode[STIX]{x1D719})\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
for all primes
$a_{P}(\unicode[STIX]{x1D719}^{\prime })\equiv a_{P}(\unicode[STIX]{x1D719})\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
for all primes
![]() $P\not \in S$
. Now, if
$P\not \in S$
. Now, if
![]() $\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{P})=-1$
, we get that
$\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{P})=-1$
, we get that
by the relationship between
![]() $a_{P}(\unicode[STIX]{x1D719}^{^{\prime }})$
and
$a_{P}(\unicode[STIX]{x1D719}^{^{\prime }})$
and
![]() $a_{P}(\unicode[STIX]{x1D719})$
following (14). Since
$a_{P}(\unicode[STIX]{x1D719})$
following (14). Since
![]() $\unicode[STIX]{x1D719}$
does not have complex multiplication and
$\unicode[STIX]{x1D719}$
does not have complex multiplication and
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
is nontrivial, by Lemma 4.2 we have that
$\unicode[STIX]{x1D716}_{{\wp}}$
is nontrivial, by Lemma 4.2 we have that
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
are not
$\unicode[STIX]{x1D719}^{\prime }$
are not
![]() $K$
-isogenous. Hence, by the isogeny theorem [Reference Taguchi27, Proposition 3.1], there are only finitely many
$K$
-isogenous. Hence, by the isogeny theorem [Reference Taguchi27, Proposition 3.1], there are only finitely many
![]() $P\not \in S$
such that
$P\not \in S$
such that
![]() $\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{P})=-1$
and
$\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{P})=-1$
and
![]() $a_{P}(\unicode[STIX]{x1D719})=0$
.
$a_{P}(\unicode[STIX]{x1D719})=0$
.
We now use Theorem 3.5 with
![]() $\unicode[STIX]{x1D719}^{\prime }$
being the twist of
$\unicode[STIX]{x1D719}^{\prime }$
being the twist of
![]() $\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}$
by
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
to obtain the following result.
$\unicode[STIX]{x1D716}_{{\wp}}$
to obtain the following result.
Theorem 6.5. Assume that
![]() $q$
is odd,
$q$
is odd,
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
, and
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
, and
![]() $q_{{\wp}}\geqslant 5$
. Let
$q_{{\wp}}\geqslant 5$
. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
without complex multiplication, and let
$K$
without complex multiplication, and let
![]() ${\wp}$
be a finite prime of
${\wp}$
be a finite prime of
![]() $K$
. Suppose that the image of
$K$
. Suppose that the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer of a Cartan subgroup of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer of a Cartan subgroup of
![]() $\operatorname{GL}_{2}(A/{\wp})$
but not in the Cartan subgroup. Let
$\operatorname{GL}_{2}(A/{\wp})$
but not in the Cartan subgroup. Let
![]() $\unicode[STIX]{x1D716}_{{\wp}}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
be the associated Galois character as before.
$\unicode[STIX]{x1D716}_{{\wp}}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
be the associated Galois character as before.
Let
![]() $\mathfrak{p}\not \in S=S_{\unicode[STIX]{x1D719}}\cup \{\infty \}$
be a prime of least degree such that
$\mathfrak{p}\not \in S=S_{\unicode[STIX]{x1D719}}\cup \{\infty \}$
be a prime of least degree such that
![]() $\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=-1$
and
$\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=-1$
and
![]() $a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\neq 0$
; such a prime exists since
$a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\neq 0$
; such a prime exists since
![]() $\unicode[STIX]{x1D719}$
has no complex multiplication. Then
$\unicode[STIX]{x1D719}$
has no complex multiplication. Then
where
 $$\begin{eqnarray}\displaystyle \widetilde{W} & := & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{W} & := & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)^{2},\end{eqnarray}$$
and the notation is taken from Notation 1.
Proof. Let
![]() $\unicode[STIX]{x1D719}^{\prime }$
be the twist of
$\unicode[STIX]{x1D719}^{\prime }$
be the twist of
![]() $\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}$
by
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
over
$\unicode[STIX]{x1D716}_{{\wp}}$
over
![]() $K$
given explicitly by
$K$
given explicitly by
![]() $c\unicode[STIX]{x1D719}_{a}=\unicode[STIX]{x1D719}_{a}^{\prime }c$
, where
$c\unicode[STIX]{x1D719}_{a}=\unicode[STIX]{x1D719}_{a}^{\prime }c$
, where
![]() $c=\sqrt{\unicode[STIX]{x1D6FF}}$
for some
$c=\sqrt{\unicode[STIX]{x1D6FF}}$
for some
![]() $\unicode[STIX]{x1D6FF}\in K^{\ast }$
with
$\unicode[STIX]{x1D6FF}\in K^{\ast }$
with
![]() $v_{\infty }(\unicode[STIX]{x1D6FF})\leqslant 0$
.
$v_{\infty }(\unicode[STIX]{x1D6FF})\leqslant 0$
.
We note that if
![]() $\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=1$
then
$\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=1$
then
![]() $a_{\mathfrak{p}}(\unicode[STIX]{x1D719})=a_{\mathfrak{p}}(\unicode[STIX]{x1D719}^{\prime })$
. Therefore, if
$a_{\mathfrak{p}}(\unicode[STIX]{x1D719})=a_{\mathfrak{p}}(\unicode[STIX]{x1D719}^{\prime })$
. Therefore, if
![]() $a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\not =a_{\mathfrak{p}}(\unicode[STIX]{x1D719}^{\prime })$
, we have that
$a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\not =a_{\mathfrak{p}}(\unicode[STIX]{x1D719}^{\prime })$
, we have that
![]() $\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=-1$
and
$\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=-1$
and
![]() $a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\neq 0$
.
$a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\neq 0$
.
Since
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
and
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
and
![]() $q_{{\wp}}\geqslant 5$
, by Corollary 6.4, we have that
$q_{{\wp}}\geqslant 5$
, by Corollary 6.4, we have that
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}$
. Furthermore, as
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}^{\prime }}$
. Furthermore, as
![]() $j(\unicode[STIX]{x1D719})=j(\unicode[STIX]{x1D719}^{\prime })$
, we have that
$j(\unicode[STIX]{x1D719})=j(\unicode[STIX]{x1D719}^{\prime })$
, we have that
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}^{\prime }}$
. We thus have
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}^{\prime }}$
. We thus have
![]() $s_{1}(\unicode[STIX]{x1D719}^{\prime })=s_{1}(\unicode[STIX]{x1D719})-\frac{1}{2}v_{\infty }(\unicode[STIX]{x1D6FF})$
since
$s_{1}(\unicode[STIX]{x1D719}^{\prime })=s_{1}(\unicode[STIX]{x1D719})-\frac{1}{2}v_{\infty }(\unicode[STIX]{x1D6FF})$
since
![]() $a_{1}(\unicode[STIX]{x1D719}^{\prime })=a_{1}(\unicode[STIX]{x1D719})/c^{q-1}$
.
$a_{1}(\unicode[STIX]{x1D719}^{\prime })=a_{1}(\unicode[STIX]{x1D719})/c^{q-1}$
.
By taking
![]() $\unicode[STIX]{x1D719}_{2}=\unicode[STIX]{x1D719}^{\prime }$
to be the twist of
$\unicode[STIX]{x1D719}_{2}=\unicode[STIX]{x1D719}^{\prime }$
to be the twist of
![]() $\unicode[STIX]{x1D719}_{1}=\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}_{1}=\unicode[STIX]{x1D719}$
by
![]() $\unicode[STIX]{x1D716}_{{\wp}}$
and
$\unicode[STIX]{x1D716}_{{\wp}}$
and
![]() $S_{\unicode[STIX]{x1D719}}\cup S_{\unicode[STIX]{x1D719}^{\prime }}\cup \{\infty \}=S_{\unicode[STIX]{x1D719}}\cup \{\infty \}=S$
, we deduce from Theorem 3.5 that
$S_{\unicode[STIX]{x1D719}}\cup S_{\unicode[STIX]{x1D719}^{\prime }}\cup \{\infty \}=S_{\unicode[STIX]{x1D719}}\cup \{\infty \}=S$
, we deduce from Theorem 3.5 that
where
 $$\begin{eqnarray}\displaystyle W & = & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})-\frac{1}{2}v_{\infty }(\unicode[STIX]{x1D6FF})}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W & = & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})-\frac{1}{2}v_{\infty }(\unicode[STIX]{x1D6FF})}\right).\nonumber\end{eqnarray}$$
Since
![]() $1/(s_{1}(\unicode[STIX]{x1D719})-\frac{1}{2}v_{\infty }(\unicode[STIX]{x1D6FF}))\leqslant 1/s_{1}(\unicode[STIX]{x1D719})$
, the result follows.◻
$1/(s_{1}(\unicode[STIX]{x1D719})-\frac{1}{2}v_{\infty }(\unicode[STIX]{x1D6FF}))\leqslant 1/s_{1}(\unicode[STIX]{x1D719})$
, the result follows.◻
The above theorem implies the following bound on the degree of
![]() ${\wp}$
in the Cartan case:
${\wp}$
in the Cartan case:
Theorem 6.6. Assume that
![]() $q$
is odd. Let
$q$
is odd. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
without complex multiplication, and let
$K$
without complex multiplication, and let
![]() ${\wp}$
be a finite prime of
${\wp}$
be a finite prime of
![]() $K$
. Suppose that the image of
$K$
. Suppose that the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer of a Cartan subgroup of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in the normalizer of a Cartan subgroup of
![]() $\operatorname{GL}_{2}(A/{\wp})$
but not in the Cartan subgroup.
$\operatorname{GL}_{2}(A/{\wp})$
but not in the Cartan subgroup.
Then either
![]() ${\wp}\in S_{\unicode[STIX]{x1D719}}$
, or
${\wp}\in S_{\unicode[STIX]{x1D719}}$
, or
where
 $$\begin{eqnarray}\displaystyle \widetilde{W} & := & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{W} & := & \displaystyle \log _{q}^{\ast }2\left(\deg _{K}\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D719}}+\frac{2}{q-1}\deg _{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D719}}+1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}\left(q^{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}+1}-1\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{4}((q^{2}-1)(q^{2}-q))^{2}\left(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})}\right)^{2},\end{eqnarray}$$
and the quantities in the above formula are as given in Notation 1.
Proof. Note that if
![]() $q_{{\wp}}<5$
, then the conclusion follows as the bounds on
$q_{{\wp}}<5$
, then the conclusion follows as the bounds on
![]() ${\wp}$
are larger than
${\wp}$
are larger than
![]() $1$
, so we may assume without generality from now on that
$1$
, so we may assume without generality from now on that
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
and
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
and
![]() $q_{{\wp}}\geqslant 5$
.
$q_{{\wp}}\geqslant 5$
.
As
![]() $\unicode[STIX]{x1D719}$
has no complex multiplication, there exists a prime
$\unicode[STIX]{x1D719}$
has no complex multiplication, there exists a prime
![]() $\mathfrak{p}\not \in S_{\unicode[STIX]{x1D719}}\cup \{\infty \}$
of least degree such that
$\mathfrak{p}\not \in S_{\unicode[STIX]{x1D719}}\cup \{\infty \}$
of least degree such that
![]() $\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=-1$
and
$\unicode[STIX]{x1D716}_{{\wp}}(\operatorname{Frob}_{\mathfrak{p}})=-1$
and
![]() $a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\not =0$
. Then applying Theorem 6.5, it follows that
$a_{\mathfrak{p}}(\unicode[STIX]{x1D719})\not =0$
. Then applying Theorem 6.5, it follows that
where the quantities in the above formula are as given in Notation 1.
Then
![]() ${\wp}\mid 2a_{\mathfrak{p}}(\unicode[STIX]{x1D719})$
by (15). Since the analogue of Hasse’s Theorem [Reference Gekeler7] gives
${\wp}\mid 2a_{\mathfrak{p}}(\unicode[STIX]{x1D719})$
by (15). Since the analogue of Hasse’s Theorem [Reference Gekeler7] gives
we obtain
Hence, the assertion follows. ◻
7 The Borel case
The arguments in this section are Drinfeld module analogues of the arguments in [Reference Serre24, Section 5.6] for elliptic curves.
In this section, let
![]() $K=\mathbb{F}_{q}(T)$
. Let
$K=\mathbb{F}_{q}(T)$
. Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
without complex multiplication, and let
$K$
without complex multiplication, and let
![]() ${\wp}$
be a finite prime of
${\wp}$
be a finite prime of
![]() $K$
such that
$K$
such that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective.
We also suppose that the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
![]() $\operatorname{GL}_{2}(A/{\wp})$
.
$\operatorname{GL}_{2}(A/{\wp})$
.
Let
![]() $\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D712}^{\prime \prime }:G_{K}\rightarrow (A/{\wp})^{\times }$
be the characters of
$\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D712}^{\prime \prime }:G_{K}\rightarrow (A/{\wp})^{\times }$
be the characters of
![]() $G_{K}$
such that
$G_{K}$
such that
We use the convention
![]() $\unicode[STIX]{x1D712}(P):=\unicode[STIX]{x1D712}(\operatorname{Frob}_{P})$
for a Galois character
$\unicode[STIX]{x1D712}(P):=\unicode[STIX]{x1D712}(\operatorname{Frob}_{P})$
for a Galois character
![]() $\unicode[STIX]{x1D712}:G_{K}\rightarrow (A/{\wp})^{\times }$
.
$\unicode[STIX]{x1D712}:G_{K}\rightarrow (A/{\wp})^{\times }$
.
We fix
![]() $\overline{K}\subseteq \overline{K}_{P}$
for each prime
$\overline{K}\subseteq \overline{K}_{P}$
for each prime
![]() $P$
of
$P$
of
![]() $K$
.
$K$
.
Recall we let
![]() $S_{\unicode[STIX]{x1D719}}$
be the set of primes of bad reduction of
$S_{\unicode[STIX]{x1D719}}$
be the set of primes of bad reduction of
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $K$
. Let
$K$
. Let
![]() $S_{\unicode[STIX]{x1D719}}^{\prime }$
be the subset of
$S_{\unicode[STIX]{x1D719}}^{\prime }$
be the subset of
![]() $S_{\unicode[STIX]{x1D719}}$
of primes where
$S_{\unicode[STIX]{x1D719}}$
of primes where
![]() $\unicode[STIX]{x1D719}$
does not have bad Tate reduction.
$\unicode[STIX]{x1D719}$
does not have bad Tate reduction.
Proposition 7.1. We assume that the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
![]() $\operatorname{GL}_{2}(A/{\wp})$
.
$\operatorname{GL}_{2}(A/{\wp})$
.
(1) The characters
 $\unicode[STIX]{x1D712}^{\prime }$
and
$\unicode[STIX]{x1D712}^{\prime }$
and
 $\unicode[STIX]{x1D712}^{\prime \prime }$
are unramified outside
$\unicode[STIX]{x1D712}^{\prime \prime }$
are unramified outside
 $S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
.
$S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
.(2) For all primes
 $P\notin S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
, we have that where
$P\notin S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
, we have that where $$\begin{eqnarray}\displaystyle a_{P}(\unicode[STIX]{x1D719})\equiv \unicode[STIX]{x1D712}^{\prime }(P)+\unicode[STIX]{x1D712}^{\prime \prime }(P) & & \displaystyle \hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})\;\;\text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D716}_{0}(P)P\equiv \unicode[STIX]{x1D712}^{\prime }(P)\unicode[STIX]{x1D712}^{\prime \prime }(P) & & \displaystyle \hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{P}(\unicode[STIX]{x1D719})\equiv \unicode[STIX]{x1D712}^{\prime }(P)+\unicode[STIX]{x1D712}^{\prime \prime }(P) & & \displaystyle \hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})\;\;\text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D716}_{0}(P)P\equiv \unicode[STIX]{x1D712}^{\prime }(P)\unicode[STIX]{x1D712}^{\prime \prime }(P) & & \displaystyle \hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp}),\nonumber\end{eqnarray}$$
 $a_{P}(\unicode[STIX]{x1D719})$
is the trace of
$a_{P}(\unicode[STIX]{x1D719})$
is the trace of
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{P})$
and
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{P})$
and
 $\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow (A/{\wp})^{\times }$
is some character.
$\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow (A/{\wp})^{\times }$
is some character.(3) Suppose
 ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. Then one of
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. Then one of
 $\unicode[STIX]{x1D712}^{\prime }$
or
$\unicode[STIX]{x1D712}^{\prime }$
or
 $\unicode[STIX]{x1D712}^{\prime \prime }$
is unramified at
$\unicode[STIX]{x1D712}^{\prime \prime }$
is unramified at
 ${\wp}$
. Denoting this by
${\wp}$
. Denoting this by
 $\unicode[STIX]{x1D6FC}_{{\wp}}$
, we have that for all primes
$\unicode[STIX]{x1D6FC}_{{\wp}}$
, we have that for all primes $$\begin{eqnarray}a_{P}(\unicode[STIX]{x1D719})\equiv \unicode[STIX]{x1D6FC}_{{\wp}}(P)+\unicode[STIX]{x1D716}_{0}(P)P\unicode[STIX]{x1D6FC}_{{\wp}}(P)^{-1}\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp}),\end{eqnarray}$$
$$\begin{eqnarray}a_{P}(\unicode[STIX]{x1D719})\equiv \unicode[STIX]{x1D6FC}_{{\wp}}(P)+\unicode[STIX]{x1D716}_{0}(P)P\unicode[STIX]{x1D6FC}_{{\wp}}(P)^{-1}\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp}),\end{eqnarray}$$
 $P\notin S_{\unicode[STIX]{x1D719}}\cup \{\infty \}$
.
$P\notin S_{\unicode[STIX]{x1D719}}\cup \{\infty \}$
.(4) Suppose
 ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. Then we have that
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. Then we have that
 $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}}=1,$
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}}=1,$
where
![]() $n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer, and
$n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer, and
![]() $s_{1}(\unicode[STIX]{x1D719})$
and
$s_{1}(\unicode[STIX]{x1D719})$
and
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
are the same as given in Notation 1.
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
are the same as given in Notation 1.
Proof. Since
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},P}$
is unramified for
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},P}$
is unramified for
![]() $P\notin S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
, the same is true for
$P\notin S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
, the same is true for
![]() $\unicode[STIX]{x1D712}^{\prime }$
and
$\unicode[STIX]{x1D712}^{\prime }$
and
![]() $\unicode[STIX]{x1D712}^{\prime \prime }$
; hence, the part (1) follows.
$\unicode[STIX]{x1D712}^{\prime \prime }$
; hence, the part (1) follows.
If
![]() $P\not \in S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
, then from Proposition 5.3, we obtain that
$P\not \in S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
, then from Proposition 5.3, we obtain that
![]() $\unicode[STIX]{x1D716}_{0}(P)P\equiv \unicode[STIX]{x1D712}^{\prime }(P)\unicode[STIX]{x1D712}^{\prime \prime }(P)\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
, and hence
$\unicode[STIX]{x1D716}_{0}(P)P\equiv \unicode[STIX]{x1D712}^{\prime }(P)\unicode[STIX]{x1D712}^{\prime \prime }(P)\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
, and hence
Suppose
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. Then
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. Then
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is a semisplit Cartan or semisplit Borel subgroup from Theorem 6.1 (the image of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{{\wp}}})$
is a semisplit Cartan or semisplit Borel subgroup from Theorem 6.1 (the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is assumed to lie in a Borel subgroup, which does not contain any nonsplit Cartan subgroup, so the case of a nonsplit Cartan subgroup in Theorem 6.1 does not occur under the hypotheses of this proposition). From Theorem 6.1, we also know that
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is assumed to lie in a Borel subgroup, which does not contain any nonsplit Cartan subgroup, so the case of a nonsplit Cartan subgroup in Theorem 6.1 does not occur under the hypotheses of this proposition). From Theorem 6.1, we also know that
![]() $\unicode[STIX]{x1D712}^{\prime }$
can be assumed to be unramified at
$\unicode[STIX]{x1D712}^{\prime }$
can be assumed to be unramified at
![]() ${\wp}$
, which we now denote by
${\wp}$
, which we now denote by
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}$
. Thus, we have
$\unicode[STIX]{x1D6FC}_{{\wp}}$
. Thus, we have
for all
![]() $P\notin S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
.
$P\notin S_{\unicode[STIX]{x1D719}}\cup \{{\wp},\infty \}$
.
Now, if
![]() $P={\wp}$
, then we still have
$P={\wp}$
, then we still have
by the following argument. Note that we now define
![]() $a_{{\wp}}(\unicode[STIX]{x1D719})$
as the trace of
$a_{{\wp}}(\unicode[STIX]{x1D719})$
as the trace of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{{\wp}})$
on inertial invariants. The inertial invariants under
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{{\wp}})$
on inertial invariants. The inertial invariants under
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
are spanned by the vector
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
are spanned by the vector
![]() $\text{}^{T}(1,0)$
. Then we have that
$\text{}^{T}(1,0)$
. Then we have that
![]() $\operatorname{Frob}_{{\wp}}$
acts on the vector
$\operatorname{Frob}_{{\wp}}$
acts on the vector
![]() $\text{}^{T}(1,0)$
via
$\text{}^{T}(1,0)$
via
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}$
, hence
$\unicode[STIX]{x1D6FC}_{{\wp}}$
, hence
![]() $a_{{\wp}}(\unicode[STIX]{x1D719})\equiv \unicode[STIX]{x1D6FC}_{{\wp}}({\wp})\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
.
$a_{{\wp}}(\unicode[STIX]{x1D719})\equiv \unicode[STIX]{x1D6FC}_{{\wp}}({\wp})\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
.
Thus, parts (2) and (3) follow.
For the part (4), suppose that
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
, so as before
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
, so as before
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}$
is unramified at
$\unicode[STIX]{x1D6FC}_{{\wp}}$
is unramified at
![]() ${\wp}$
.
${\wp}$
.
We show that
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified at every prime
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified at every prime
![]() $P\not ={\wp}$
. This will be done according to each of the following cases:
$P\not ={\wp}$
. This will be done according to each of the following cases:
(i)
 $P\in S_{\unicode[STIX]{x1D719}}\setminus S_{\unicode[STIX]{x1D719}}^{\prime }$
with
$P\in S_{\unicode[STIX]{x1D719}}\setminus S_{\unicode[STIX]{x1D719}}^{\prime }$
with
 $P\neq {\wp}$
,
$P\neq {\wp}$
,(ii)
 $P\in S_{\unicode[STIX]{x1D719}}^{\prime }$
.
$P\in S_{\unicode[STIX]{x1D719}}^{\prime }$
.
In the case (i),
![]() $P$
is a prime of bad Tate reduction of
$P$
is a prime of bad Tate reduction of
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $K$
and
$K$
and
![]() $P\not ={\wp}$
. Then over
$P\not ={\wp}$
. Then over
![]() $C_{P}$
, where
$C_{P}$
, where
![]() $C_{P}$
is the completion of an algebraic closure of
$C_{P}$
is the completion of an algebraic closure of
![]() $K_{P}$
, we have a uniformization [Reference Drinfeld6] given by a surjective analytic map
$K_{P}$
, we have a uniformization [Reference Drinfeld6] given by a surjective analytic map
![]() $e_{P}:C_{P}\rightarrow C_{P}$
which relates
$e_{P}:C_{P}\rightarrow C_{P}$
which relates
![]() $\unicode[STIX]{x1D719}$
to a Drinfeld
$\unicode[STIX]{x1D719}$
to a Drinfeld
![]() $A$
-module
$A$
-module
![]() $\unicode[STIX]{x1D713}$
of rank
$\unicode[STIX]{x1D713}$
of rank
![]() $1$
via the relation
$1$
via the relation
![]() $\unicode[STIX]{x1D713}_{a}\circ e_{P}=e_{P}\circ \unicode[STIX]{x1D719}_{a}$
. Let
$\unicode[STIX]{x1D713}_{a}\circ e_{P}=e_{P}\circ \unicode[STIX]{x1D719}_{a}$
. Let
![]() $\unicode[STIX]{x1D6EC}_{P}$
be the set of zeros of
$\unicode[STIX]{x1D6EC}_{P}$
be the set of zeros of
![]() $e_{P}$
. Then by [Reference Drinfeld6],
$e_{P}$
. Then by [Reference Drinfeld6],
![]() $\unicode[STIX]{x1D6EC}_{P}=A\cdot \unicode[STIX]{x1D706}_{1}$
is an
$\unicode[STIX]{x1D6EC}_{P}=A\cdot \unicode[STIX]{x1D706}_{1}$
is an
![]() $A$
-lattice in
$A$
-lattice in
![]() $C_{P}$
of rank
$C_{P}$
of rank
![]() $1$
, where the
$1$
, where the
![]() $A$
-module structure on
$A$
-module structure on
![]() $C_{P}$
is given by
$C_{P}$
is given by
![]() $\unicode[STIX]{x1D6FC}\cdot x:=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(x)$
.
$\unicode[STIX]{x1D6FC}\cdot x:=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(x)$
.
Let
![]() $K_{P}^{0}=K_{P}(\unicode[STIX]{x1D6EC}_{P},\unicode[STIX]{x1D713}[{\wp}])$
. Then Gardeyn [Reference Gardeyn12, pp. 247–248] shows that:
$K_{P}^{0}=K_{P}(\unicode[STIX]{x1D6EC}_{P},\unicode[STIX]{x1D713}[{\wp}])$
. Then Gardeyn [Reference Gardeyn12, pp. 247–248] shows that:
(1)
 $K_{P}(\unicode[STIX]{x1D719}[{\wp}])\subseteq K_{P}^{0}(\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P}))=K_{P}^{0}(s_{1})$
, where
$K_{P}(\unicode[STIX]{x1D719}[{\wp}])\subseteq K_{P}^{0}(\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P}))=K_{P}^{0}(s_{1})$
, where
 $s_{1}\in \unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D706}_{1})$
;
$s_{1}\in \unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D706}_{1})$
;(2) the conjugates of
 $s_{1}$
over
$s_{1}$
over
 $K_{P}^{0}$
lie in
$K_{P}^{0}$
lie in
 $s_{1}+\unicode[STIX]{x1D713}[{\wp}]$
.
$s_{1}+\unicode[STIX]{x1D713}[{\wp}]$
.
The equality
![]() $K_{P}^{0}(\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P}))=K_{P}^{0}(s_{1})$
can be seen as follows. Pick a
$K_{P}^{0}(\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P}))=K_{P}^{0}(s_{1})$
can be seen as follows. Pick a
![]() $s_{1}\in C_{P}$
such that
$s_{1}\in C_{P}$
such that
![]() $\unicode[STIX]{x1D713}_{P}(s_{1})=\unicode[STIX]{x1D706}_{1}$
. Then if
$\unicode[STIX]{x1D713}_{P}(s_{1})=\unicode[STIX]{x1D706}_{1}$
. Then if
![]() $\unicode[STIX]{x1D6FC}\in A$
,
$\unicode[STIX]{x1D6FC}\in A$
,
![]() $\unicode[STIX]{x1D6FC}\cdot s_{1}:=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(s_{1})$
so that
$\unicode[STIX]{x1D6FC}\cdot s_{1}:=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(s_{1})$
so that
![]() $\unicode[STIX]{x1D713}_{P}(\unicode[STIX]{x1D6FC}\cdot s_{1})=\unicode[STIX]{x1D713}_{P}\circ \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(s_{1})=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D713}_{P}(s_{1})=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D706}_{1})=\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D706}_{1}$
. Hence,
$\unicode[STIX]{x1D713}_{P}(\unicode[STIX]{x1D6FC}\cdot s_{1})=\unicode[STIX]{x1D713}_{P}\circ \unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(s_{1})=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}\circ \unicode[STIX]{x1D713}_{P}(s_{1})=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D706}_{1})=\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D706}_{1}$
. Hence,
![]() $\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P})\supseteq A\cdot s_{1}$
. If
$\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P})\supseteq A\cdot s_{1}$
. If
![]() $x\in \unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P})$
, then
$x\in \unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P})$
, then
![]() $\unicode[STIX]{x1D713}_{P}(x)=\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D713}_{P}(\unicode[STIX]{x1D6FC}\cdot s_{1})$
for some
$\unicode[STIX]{x1D713}_{P}(x)=\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D713}_{P}(\unicode[STIX]{x1D6FC}\cdot s_{1})$
for some
![]() $\unicode[STIX]{x1D6FC}\in A$
. Hence,
$\unicode[STIX]{x1D6FC}\in A$
. Hence,
![]() $x\in A\cdot s_{1}+\unicode[STIX]{x1D6EC}_{P}$
. Since
$x\in A\cdot s_{1}+\unicode[STIX]{x1D6EC}_{P}$
. Since
![]() $K_{P}^{0}\supseteq \unicode[STIX]{x1D6EC}_{P}$
, we have
$K_{P}^{0}\supseteq \unicode[STIX]{x1D6EC}_{P}$
, we have
![]() $K_{P}^{0}(\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P}))=K_{P}^{0}(s_{1})$
.
$K_{P}^{0}(\unicode[STIX]{x1D713}_{P}^{-1}(\unicode[STIX]{x1D6EC}_{P}))=K_{P}^{0}(s_{1})$
.
The above properties yield a representation
![]() $\unicode[STIX]{x1D70C}:\operatorname{Gal}(K_{P}^{0}(s_{1})/K_{P}^{0})\rightarrow \unicode[STIX]{x1D713}[{\wp}]$
from the formula
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(K_{P}^{0}(s_{1})/K_{P}^{0})\rightarrow \unicode[STIX]{x1D713}[{\wp}]$
from the formula
![]() $\unicode[STIX]{x1D70E}(s_{1})=s_{1}+\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})$
. Hence, the image of
$\unicode[STIX]{x1D70E}(s_{1})=s_{1}+\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})$
. Hence, the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
consists only of elements of order a power of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
consists only of elements of order a power of
![]() $p$
when
$p$
when
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is restricted to
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is restricted to
![]() $G_{K_{P}^{0}}$
.
$G_{K_{P}^{0}}$
.
Finally, since
![]() $P\neq {\wp}$
, we have that
$P\neq {\wp}$
, we have that
![]() $K_{P}^{0}/K_{P}(\unicode[STIX]{x1D6EC}_{P})$
is unramified, so the inertia subgroup
$K_{P}^{0}/K_{P}(\unicode[STIX]{x1D6EC}_{P})$
is unramified, so the inertia subgroup
![]() $I_{K_{P}(\unicode[STIX]{x1D6EC}_{P})}$
of
$I_{K_{P}(\unicode[STIX]{x1D6EC}_{P})}$
of
![]() $K_{P}(\unicode[STIX]{x1D6EC}_{P})$
is contained in
$K_{P}(\unicode[STIX]{x1D6EC}_{P})$
is contained in
![]() $G_{K_{P}^{0}}$
. Hence, the image
$G_{K_{P}^{0}}$
. Hence, the image
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{P}(\unicode[STIX]{x1D6EC}_{P})})$
consists only of elements of order a power of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(I_{K_{P}(\unicode[STIX]{x1D6EC}_{P})})$
consists only of elements of order a power of
![]() $p$
. It follows that
$p$
. It follows that
![]() $\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D712}^{\prime \prime }$
are unramified when restricted to
$\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D712}^{\prime \prime }$
are unramified when restricted to
![]() $G_{K_{P}(\unicode[STIX]{x1D6EC}_{P})}$
.
$G_{K_{P}(\unicode[STIX]{x1D6EC}_{P})}$
.
Since
![]() $\unicode[STIX]{x1D719}$
has bad Tate reduction at the finite prime
$\unicode[STIX]{x1D719}$
has bad Tate reduction at the finite prime
![]() $P$
, by [Reference Gardeyn12, Proposition 4(i)], we have that
$P$
, by [Reference Gardeyn12, Proposition 4(i)], we have that
![]() $[K_{P}(\unicode[STIX]{x1D6EC}_{P}):K_{P}]$
is bounded above by
$[K_{P}(\unicode[STIX]{x1D6EC}_{P}):K_{P}]$
is bounded above by
![]() $g_{P}=\#\operatorname{GL}(1,\mathbb{F}_{q})=q-1$
. In fact, the proof in [Reference Gardeyn12, Proposition 4(i)] shows that
$g_{P}=\#\operatorname{GL}(1,\mathbb{F}_{q})=q-1$
. In fact, the proof in [Reference Gardeyn12, Proposition 4(i)] shows that
![]() $[K_{P}(\unicode[STIX]{x1D6EC}_{P}):K_{P}]\mid q-1$
. Thus,
$[K_{P}(\unicode[STIX]{x1D6EC}_{P}):K_{P}]\mid q-1$
. Thus,
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{q-1}$
is unramified when restricted to
$\unicode[STIX]{x1D6FC}_{{\wp}}^{q-1}$
is unramified when restricted to
![]() $G_{K_{P}}$
.
$G_{K_{P}}$
.
In the case (ii),
![]() $P\in S_{\unicode[STIX]{x1D719}}$
(we then have that
$P\in S_{\unicode[STIX]{x1D719}}$
(we then have that
![]() $P\not ={\wp}$
because
$P\not ={\wp}$
because
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}\supseteq S_{\unicode[STIX]{x1D719}}^{\prime }$
). We know that there exists an extension
${\wp}\notin S_{\unicode[STIX]{x1D719}}\supseteq S_{\unicode[STIX]{x1D719}}^{\prime }$
). We know that there exists an extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $K_{P}$
such that
$K_{P}$
such that
![]() $\unicode[STIX]{x1D719}$
attains semi-stable reduction over
$\unicode[STIX]{x1D719}$
attains semi-stable reduction over
![]() $K^{\prime }$
by Lemma 5.1, and the extension degree [
$K^{\prime }$
by Lemma 5.1, and the extension degree [
![]() $K_{P}^{\text{nr}}\cdot K^{\prime }:K_{P}^{\text{nr}}$
] divides
$K_{P}^{\text{nr}}\cdot K^{\prime }:K_{P}^{\text{nr}}$
] divides
![]() $q^{2}-1$
.
$q^{2}-1$
.
Let
![]() $P^{\prime }$
denote the prime of
$P^{\prime }$
denote the prime of
![]() $K^{\prime }$
above the prime
$K^{\prime }$
above the prime
![]() $P$
. If
$P$
. If
![]() $P^{\prime }$
is a bad Tate reduction prime of
$P^{\prime }$
is a bad Tate reduction prime of
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
![]() $K^{\prime }$
, we thus have
$K^{\prime }$
, we thus have
![]() $P^{\prime }\neq {\wp}^{\prime }$
, where
$P^{\prime }\neq {\wp}^{\prime }$
, where
![]() ${\wp}^{\prime }$
is a prime of
${\wp}^{\prime }$
is a prime of
![]() $K^{\prime }$
lying above
$K^{\prime }$
lying above
![]() ${\wp}$
, so the same argument as above shows (by replacing
${\wp}$
, so the same argument as above shows (by replacing
![]() $K$
by
$K$
by
![]() $K^{\prime }$
,
$K^{\prime }$
,
![]() $P$
by
$P$
by
![]() $P^{\prime }$
) that
$P^{\prime }$
) that
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{q-1}$
is unramified when restricted to
$\unicode[STIX]{x1D6FC}_{{\wp}}^{q-1}$
is unramified when restricted to
![]() $G_{K_{P^{\prime }}^{\prime }}$
(the results from [Reference Gardeyn12] used above apply equally well over the extension
$G_{K_{P^{\prime }}^{\prime }}$
(the results from [Reference Gardeyn12] used above apply equally well over the extension
![]() $K_{P^{\prime }}^{\prime }$
).
$K_{P^{\prime }}^{\prime }$
).
Now
![]() $K_{P}^{\text{nr}}\cdot K^{\prime }$
is Galois over
$K_{P}^{\text{nr}}\cdot K^{\prime }$
is Galois over
![]() $K_{P}^{\text{nr}}$
of degree dividing
$K_{P}^{\text{nr}}$
of degree dividing
![]() $q^{2}-1$
, where
$q^{2}-1$
, where
![]() $K_{P}^{\text{nr}}$
is the maximal unramified extension of
$K_{P}^{\text{nr}}$
is the maximal unramified extension of
![]() $K_{P}$
. Also,
$K_{P}$
. Also,
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified when restricted to
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified when restricted to
![]() $G_{K_{P}}$
if and only if
$G_{K_{P}}$
if and only if
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified when restricted to
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified when restricted to
![]() $G_{K_{P}^{\text{nr}}}$
, which is the case.
$G_{K_{P}^{\text{nr}}}$
, which is the case.
Finally,
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified at every finite prime of
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
is unramified at every finite prime of
![]() $K$
.
$K$
.
Furthermore, we claim that as a character of
![]() $G_{K}$
, we have that
$G_{K}$
, we have that
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}}=1$
, where
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}}=1$
, where
![]() $n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})})$
is a positive integer.
$n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\frac{\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}}{s_{1}(\unicode[STIX]{x1D719})})$
is a positive integer.
Let
![]() $L$
be a finite, separable, tamely ramified, and geometric extension of
$L$
be a finite, separable, tamely ramified, and geometric extension of
![]() $K$
(recall
$K$
(recall
![]() $L$
is a geometric extension of
$L$
is a geometric extension of
![]() $K$
if and only if the algebraic closure of
$K$
if and only if the algebraic closure of
![]() $\mathbb{F}_{K}$
in
$\mathbb{F}_{K}$
in
![]() $L$
is
$L$
is
![]() $\mathbb{F}_{K}$
itself). Suppose that
$\mathbb{F}_{K}$
itself). Suppose that
![]() $M$
is a field with
$M$
is a field with
![]() $K\subset M\subset L$
and
$K\subset M\subset L$
and
![]() $L/M$
is unramified except possibly at the primes
$L/M$
is unramified except possibly at the primes
![]() $\infty _{i}$
lying above a prime
$\infty _{i}$
lying above a prime
![]() $\infty$
of
$\infty$
of
![]() $M$
. From Riemann–Hurwitz, since
$M$
. From Riemann–Hurwitz, since
![]() $L/K$
is tamely ramified, we have the following equality:
$L/K$
is tamely ramified, we have the following equality:
where
![]() $m:=[L:K]$
,
$m:=[L:K]$
,
![]() $g_{L}$
(resp.
$g_{L}$
(resp.
![]() $g_{M}$
) is the genus of
$g_{M}$
) is the genus of
![]() $L$
(resp.
$L$
(resp.
![]() $M$
), and
$M$
), and
![]() $e_{i}$
(resp.
$e_{i}$
(resp.
![]() $f_{i}$
) denotes the ramification index (resp. the inertial degree) of
$f_{i}$
) denotes the ramification index (resp. the inertial degree) of
![]() $\infty _{i}$
over
$\infty _{i}$
over
![]() $\infty$
. This implies that
$\infty$
. This implies that
![]() $2g_{L}=2-m-\sum _{i=1}^{t}f_{i}$
since
$2g_{L}=2-m-\sum _{i=1}^{t}f_{i}$
since
![]() $g_{M}=0$
and
$g_{M}=0$
and
![]() $\sum _{i=1}^{t}e_{i}f_{i}=m$
. Thus, we have
$\sum _{i=1}^{t}e_{i}f_{i}=m$
. Thus, we have
![]() $m\leqslant 2-\sum _{i=1}^{t}f_{i}\leqslant 1$
as
$m\leqslant 2-\sum _{i=1}^{t}f_{i}\leqslant 1$
as
![]() $g_{L}\geqslant 0$
, and hence
$g_{L}\geqslant 0$
, and hence
![]() $m=1$
, that is,
$m=1$
, that is,
![]() $L=M$
.
$L=M$
.
Suppose that a Galois character
![]() $\unicode[STIX]{x1D713}:G_{K}\rightarrow \mathbb{F}_{{\wp}}^{\times }$
is unramified at every finite prime of
$\unicode[STIX]{x1D713}:G_{K}\rightarrow \mathbb{F}_{{\wp}}^{\times }$
is unramified at every finite prime of
![]() $K$
. Let
$K$
. Let
![]() $L$
be the field cut out by
$L$
be the field cut out by
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $M=\mathbb{F}_{L}\cdot K=\mathbb{F}_{q^{n}}\cdot K$
(where
$M=\mathbb{F}_{L}\cdot K=\mathbb{F}_{q^{n}}\cdot K$
(where
![]() $\mathbb{F}_{L}=\mathbb{F}_{q^{n}}$
is the algebraic closure of
$\mathbb{F}_{L}=\mathbb{F}_{q^{n}}$
is the algebraic closure of
![]() $\mathbb{F}_{K}=\mathbb{F}_{q}$
in
$\mathbb{F}_{K}=\mathbb{F}_{q}$
in
![]() $L$
) so
$L$
) so
![]() $L/M$
is a geometric extension. Applying the previous paragraph, we deduce that
$L/M$
is a geometric extension. Applying the previous paragraph, we deduce that
![]() $L=M$
. It thus follows that a Galois character
$L=M$
. It thus follows that a Galois character
![]() $\unicode[STIX]{x1D713}:G_{K}\rightarrow \mathbb{F}_{{\wp}}^{\times }$
which is unramified at every finite prime of
$\unicode[STIX]{x1D713}:G_{K}\rightarrow \mathbb{F}_{{\wp}}^{\times }$
which is unramified at every finite prime of
![]() $K$
must factor through the Galois group of a finite constant field extension
$K$
must factor through the Galois group of a finite constant field extension
![]() $\mathbb{F}_{q^{n}}K/K$
for some positive integer
$\mathbb{F}_{q^{n}}K/K$
for some positive integer
![]() $n$
, where
$n$
, where
![]() $n=[\mathbb{F}_{L}:\mathbb{F}_{K}]$
.
$n=[\mathbb{F}_{L}:\mathbb{F}_{K}]$
.
Applying the above to the character
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
(which is unramified at every finite prime of
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)}$
(which is unramified at every finite prime of
![]() $K$
) and using Theorem 3.2, we get
$K$
) and using Theorem 3.2, we get
![]() $\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}}=1$
, where
$\unicode[STIX]{x1D6FC}_{{\wp}}^{(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}}=1$
, where
![]() $n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer as claimed. ◻
$n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer as claimed. ◻
Theorem 7.2. Let
![]() $K=\mathbb{F}_{q}(T)$
and
$K=\mathbb{F}_{q}(T)$
and
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K$
without complex multiplication and
$K$
without complex multiplication and
![]() ${\wp}$
be a finite prime of
${\wp}$
be a finite prime of
![]() $K$
. Let
$K$
. Let
![]() $P$
be the least degree prime of
$P$
be the least degree prime of
![]() $K$
where
$K$
where
![]() $\unicode[STIX]{x1D719}$
has good reduction.
$\unicode[STIX]{x1D719}$
has good reduction.
Suppose that the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
lies in a Borel subgroup of
![]() $\operatorname{GL}_{2}(A/{\wp})$
.
$\operatorname{GL}_{2}(A/{\wp})$
.
Then either
where
![]() $\unicode[STIX]{x1D711}$
is the Euler-phi function,
$\unicode[STIX]{x1D711}$
is the Euler-phi function,
![]() $s_{1}(\unicode[STIX]{x1D719})$
and
$s_{1}(\unicode[STIX]{x1D719})$
and
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
are the same as given in Notation 1, and
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}$
are the same as given in Notation 1, and
![]() $n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer.
$n_{\unicode[STIX]{x1D719}}\leqslant (q^{2}-1)(q^{2}-q)(1+\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D719}}/s_{1}(\unicode[STIX]{x1D719}))$
is a positive integer.
Proof. Suppose
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. From Proposition 7.1, we have that
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
. From Proposition 7.1, we have that
where
![]() $z$
is a
$z$
is a
![]() $(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}$
th root of unity in
$(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}$
th root of unity in
![]() $A/{\wp}$
.
$A/{\wp}$
.
Let
![]() $d$
be the order of
$d$
be the order of
![]() $z$
,
$z$
,
![]() $S_{d}(X)$
the
$S_{d}(X)$
the
![]() $d$
th cyclotomic polynomial, and
$d$
th cyclotomic polynomial, and
![]() $F_{P}(X)=X^{2}-a_{P}(\unicode[STIX]{x1D719})X+\unicode[STIX]{x1D716}_{0}(P)P$
.
$F_{P}(X)=X^{2}-a_{P}(\unicode[STIX]{x1D719})X+\unicode[STIX]{x1D716}_{0}(P)P$
.
The congruence in (22) implies that
![]() $S_{d}$
and
$S_{d}$
and
![]() $F_{P}$
have a common root mod
$F_{P}$
have a common root mod
![]() ${\wp}$
, hence their resultant
${\wp}$
, hence their resultant
![]() $R\in A$
is divisible by
$R\in A$
is divisible by
![]() ${\wp}$
. The resultant
${\wp}$
. The resultant
![]() $R$
is given by
$R$
is given by
where
![]() $x$
and
$x$
and
![]() $x^{\prime }$
are the two roots of
$x^{\prime }$
are the two roots of
![]() $F_{P}(X)$
and
$F_{P}(X)$
and
![]() $\unicode[STIX]{x1D701}$
runs through the set of primitive
$\unicode[STIX]{x1D701}$
runs through the set of primitive
![]() $d$
th roots of unity.
$d$
th roots of unity.
Let
![]() $\left|x\right|=q^{-v_{\infty }(x)}$
denote the absolute value of
$\left|x\right|=q^{-v_{\infty }(x)}$
denote the absolute value of
![]() $x$
associated to the prime
$x$
associated to the prime
![]() $\infty$
. Then we have that
$\infty$
. Then we have that
Hence, we have that
where
![]() $n=\deg S_{d}(X)=\unicode[STIX]{x1D711}(d)$
. Since
$n=\deg S_{d}(X)=\unicode[STIX]{x1D711}(d)$
. Since
![]() $d$
divides
$d$
divides
![]() $(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}$
, we have that
$(q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}}$
, we have that
![]() $n\leqslant \unicode[STIX]{x1D711}((q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}})$
.
$n\leqslant \unicode[STIX]{x1D711}((q-1)(q^{2}-1)n_{\unicode[STIX]{x1D719}})$
.
Now,
![]() ${\wp}$
divides
${\wp}$
divides
![]() $R$
, so we get that
$R$
, so we get that
The result thus follows. ◻
8 Proof of Theorem 2.1
Let
![]() $\unicode[STIX]{x1D719}$
be a Drinfeld
$\unicode[STIX]{x1D719}$
be a Drinfeld
![]() $A$
-module of rank
$A$
-module of rank
![]() $2$
over
$2$
over
![]() $K=\mathbb{F}_{q}(T)$
without complex multiplication, and
$K=\mathbb{F}_{q}(T)$
without complex multiplication, and
![]() ${\wp}$
be a finite prime of
${\wp}$
be a finite prime of
![]() $K$
such that
$K$
such that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is not surjective.
We first recall a classification of the proper maximal subgroups of
![]() $\operatorname{PGL}_{2}(k)$
, where
$\operatorname{PGL}_{2}(k)$
, where
![]() $k$
is a finite field of characteristic
$k$
is a finite field of characteristic
![]() $p$
.
$p$
.
Theorem 8.1. The maximal proper subgroups of
![]() $\operatorname{PGL}_{2}(k)$
, where
$\operatorname{PGL}_{2}(k)$
, where
![]() $k$
is a finite field of characteristic
$k$
is a finite field of characteristic
![]() $p$
, are:
$p$
, are:
(i) the projective image of a Borel subgroup of
 $\operatorname{GL}_{2}(k)$
;
$\operatorname{GL}_{2}(k)$
;(ii) the projective image of the normalizer of a Cartan subgroup of
 $\operatorname{GL}_{2}(k)$
;
$\operatorname{GL}_{2}(k)$
;(iii)
 $\operatorname{PSL}_{2}(k)$
;
$\operatorname{PSL}_{2}(k)$
;(iv) isomorphic to the subgroup
 $\operatorname{PGL}_{2}(k^{\prime })$
for some proper subfield
$\operatorname{PGL}_{2}(k^{\prime })$
for some proper subfield
 $k^{\prime }$
of
$k^{\prime }$
of
 $k$
;
$k$
;(v) isomorphic to one of the groups
 $A_{4}$
,
$A_{4}$
,
 $S_{4}$
, or
$S_{4}$
, or
 $A_{5}$
.
$A_{5}$
.
Proof. This result is stated in [Reference Gardeyn11, Proposition 3.12] as being deduced from the version of Dickson’s classification of the subgroups of
![]() $\operatorname{PSL}_{2}(k)$
proven in [Reference Huppert13, Theorem 8.27, Chapter II]. For completeness, we explain how to deduce the above classification. In order to shorten the arguments, we also rely on [Reference Serre24, Proposition 16] (or [Reference Lang15, Chapter XI, §2, Theorem 2.3]).
$\operatorname{PSL}_{2}(k)$
proven in [Reference Huppert13, Theorem 8.27, Chapter II]. For completeness, we explain how to deduce the above classification. In order to shorten the arguments, we also rely on [Reference Serre24, Proposition 16] (or [Reference Lang15, Chapter XI, §2, Theorem 2.3]).
Let
![]() $K$
be a finite field of order
$K$
be a finite field of order
![]() $p^{f}$
. From [Reference Huppert13, Theorem 8.27], a subgroup of
$p^{f}$
. From [Reference Huppert13, Theorem 8.27], a subgroup of
![]() $\operatorname{PSL}_{2}(K)$
is one of:
$\operatorname{PSL}_{2}(K)$
is one of:
(1) an elementary abelian
 $p$
-group;
$p$
-group;(2) a cyclic group of order
 $n\mid (p^{f}\pm 1)/w$
where
$n\mid (p^{f}\pm 1)/w$
where
 $w=(p^{f}-1,2)$
;
$w=(p^{f}-1,2)$
;(3) a dihedral group of order
 $2n$
with
$2n$
with
 $n$
as in (2);
$n$
as in (2);(4) isomorphic to
 $A_{4}$
;
$A_{4}$
;(5) isomorphic to
 $S_{4}$
;
$S_{4}$
;(6) isomorphic to
 $A_{5}$
;
$A_{5}$
;(7) a semidirect product of an elementary abelian
 $p$
-group of order
$p$
-group of order
 $p^{m}$
with a cyclic subgroup of order
$p^{m}$
with a cyclic subgroup of order
 $t$
with
$t$
with
 $t\mid (p^{m}-1,p^{f}-1)$
;
$t\mid (p^{m}-1,p^{f}-1)$
;(8) isomorphic to
 $\operatorname{PSL}_{2}(K^{\prime })$
, where
$\operatorname{PSL}_{2}(K^{\prime })$
, where
 $K^{\prime }$
is a subfield of
$K^{\prime }$
is a subfield of
 $K$
, or
$K$
, or
 $\operatorname{PGL}_{2}(K^{\prime })$
, where a quadratic extension of
$\operatorname{PGL}_{2}(K^{\prime })$
, where a quadratic extension of
 $K^{\prime }$
is a subfield of
$K^{\prime }$
is a subfield of
 $K$
.
$K$
.
We note that the proof of [Reference Huppert13, Theorem 8.27] shows that the subgroups in the case (8) are in fact
![]() $\operatorname{PGL}_{2}(K)$
-conjugate to
$\operatorname{PGL}_{2}(K)$
-conjugate to
![]() $\operatorname{PSL}_{2}(K^{\prime })$
or
$\operatorname{PSL}_{2}(K^{\prime })$
or
![]() $\operatorname{PGL}_{2}(K^{\prime })$
. However, since we do not need this additional information for the proof of our results, we omit further discussion of this point.
$\operatorname{PGL}_{2}(K^{\prime })$
. However, since we do not need this additional information for the proof of our results, we omit further discussion of this point.
Let
![]() $\bar{H}$
be a maximal proper subgroup of
$\bar{H}$
be a maximal proper subgroup of
![]() $\operatorname{PGL}_{2}(k)$
. If
$\operatorname{PGL}_{2}(k)$
. If
![]() $p\nmid \left|\bar{H}\right|$
, then we have that
$p\nmid \left|\bar{H}\right|$
, then we have that
![]() $\bar{H}$
is
$\bar{H}$
is
(1) the projective image of the normalizer of a Cartan subgroup of
 $\operatorname{GL}_{2}(k)$
;
$\operatorname{GL}_{2}(k)$
;(2) isomorphic to
 $A_{4}$
,
$A_{4}$
,
 $S_{4}$
, or
$S_{4}$
, or
 $A_{5}$
$A_{5}$
by [Reference Serre24, Proposition 16]. Thus, let us now assume that we are in the case
![]() $p\mid \left|\bar{H}\right|$
.
$p\mid \left|\bar{H}\right|$
.
If
![]() $p=2$
, then
$p=2$
, then
![]() $\operatorname{PGL}_{2}(k)=\operatorname{PSL}_{2}(k)$
. If
$\operatorname{PGL}_{2}(k)=\operatorname{PSL}_{2}(k)$
. If
![]() $p$
is odd, then
$p$
is odd, then
![]() $\operatorname{PGL}_{2}(k)$
is a subgroup of
$\operatorname{PGL}_{2}(k)$
is a subgroup of
![]() $\operatorname{PSL}_{2}(K)$
where
$\operatorname{PSL}_{2}(K)$
where
![]() $[K:k]=2$
. Hence, applying [Reference Huppert13, Theorem 8.27] to
$[K:k]=2$
. Hence, applying [Reference Huppert13, Theorem 8.27] to
![]() $\operatorname{PSL}_{2}(K)$
,
$\operatorname{PSL}_{2}(K)$
,
![]() $\bar{H}$
is isomorphic to one of the eight types of subgroups listed above.
$\bar{H}$
is isomorphic to one of the eight types of subgroups listed above.
Cases (2) and (3): The condition
![]() $p\mid \left|\bar{H}\right|$
implies that we are not in the case (2). If
$p\mid \left|\bar{H}\right|$
implies that we are not in the case (2). If
![]() $\bar{H}$
is in the case (3), then
$\bar{H}$
is in the case (3), then
![]() $p=2$
. Consider the cyclic subgroup
$p=2$
. Consider the cyclic subgroup
![]() $\bar{Z}$
of order
$\bar{Z}$
of order
![]() $n$
of
$n$
of
![]() $\bar{H}$
. If
$\bar{H}$
. If
![]() $n=1$
, then
$n=1$
, then
![]() $\bar{H}$
is generated by a unipotent element of order
$\bar{H}$
is generated by a unipotent element of order
![]() $2$
and hence lies in a Borel subgroup of
$2$
and hence lies in a Borel subgroup of
![]() $\operatorname{GL}_{2}(k)$
.
$\operatorname{GL}_{2}(k)$
.
Assume now that
![]() $n>1$
. Since
$n>1$
. Since
![]() $p\nmid n$
, we have that
$p\nmid n$
, we have that
![]() $\bar{Z}$
is contained in the projective image of a Cartan subgroup
$\bar{Z}$
is contained in the projective image of a Cartan subgroup
![]() $\bar{C}$
of
$\bar{C}$
of
![]() $\operatorname{GL}_{2}(k)$
by [Reference Serre24, Proposition 16]. An element of
$\operatorname{GL}_{2}(k)$
by [Reference Serre24, Proposition 16]. An element of
![]() $\operatorname{GL}_{2}(k)$
which conjugates a nontrivial element of
$\operatorname{GL}_{2}(k)$
which conjugates a nontrivial element of
![]() $\bar{C}$
to another nontrivial element of
$\bar{C}$
to another nontrivial element of
![]() $\bar{C}$
must in fact normalize all of
$\bar{C}$
must in fact normalize all of
![]() $\bar{C}$
. Hence
$\bar{C}$
. Hence
![]() $\bar{H}$
is contained in the projective image of the normalizer of a Cartan subgroup of
$\bar{H}$
is contained in the projective image of the normalizer of a Cartan subgroup of
![]() $\operatorname{GL}_{2}(k)$
.
$\operatorname{GL}_{2}(k)$
.
Cases (1) and (7): We show here that
![]() $\bar{H}$
is contained in the projective image of a Borel subgroup of
$\bar{H}$
is contained in the projective image of a Borel subgroup of
![]() $\operatorname{GL}_{2}(k)$
. Let
$\operatorname{GL}_{2}(k)$
. Let
![]() $\bar{E}$
be the elementary abelian
$\bar{E}$
be the elementary abelian
![]() $p$
-subgroup of the case (1) or the case (7). Let
$p$
-subgroup of the case (1) or the case (7). Let
![]() $E$
be the inverse image of
$E$
be the inverse image of
![]() $\bar{E}$
under the homomorphism
$\bar{E}$
under the homomorphism
![]() $\unicode[STIX]{x1D70B}:\operatorname{SL}_{2}(K)\rightarrow \operatorname{PSL}_{2}(K)$
. Note that
$\unicode[STIX]{x1D70B}:\operatorname{SL}_{2}(K)\rightarrow \operatorname{PSL}_{2}(K)$
. Note that
![]() $E$
is abelian and
$E$
is abelian and
![]() $E=E_{0}\times E^{\prime }$
for a unique elementary abelian
$E=E_{0}\times E^{\prime }$
for a unique elementary abelian
![]() $p$
-group
$p$
-group
![]() $E_{0}$
which is isomorphic to
$E_{0}$
which is isomorphic to
![]() $\bar{E}$
under
$\bar{E}$
under
![]() $\unicode[STIX]{x1D70B}$
and an abelian group
$\unicode[STIX]{x1D70B}$
and an abelian group
![]() $E^{\prime }$
of order coprime to
$E^{\prime }$
of order coprime to
![]() $p$
. Since every element in
$p$
. Since every element in
![]() $E_{0}$
has order dividing
$E_{0}$
has order dividing
![]() $p$
and
$p$
and
![]() $E_{0}$
is abelian, it follows that
$E_{0}$
is abelian, it follows that
![]() $E_{0}$
up to conjugation is contained in the subgroup
$E_{0}$
up to conjugation is contained in the subgroup
of
![]() $\operatorname{SL}_{2}(K)$
which has order
$\operatorname{SL}_{2}(K)$
which has order
![]() $p^{f}$
.
$p^{f}$
.
An element of
![]() $\operatorname{SL}_{2}(K)$
which conjugates a nontrivial element of
$\operatorname{SL}_{2}(K)$
which conjugates a nontrivial element of
![]() $U$
to another nontrivial element of
$U$
to another nontrivial element of
![]() $U$
must in fact normalize
$U$
must in fact normalize
![]() $U$
. Let
$U$
. Let
![]() $H$
be the inverse image of
$H$
be the inverse image of
![]() $\bar{H}$
under
$\bar{H}$
under
![]() $\unicode[STIX]{x1D70B}$
. Then
$\unicode[STIX]{x1D70B}$
. Then
![]() $H$
is contained in the normalizer of
$H$
is contained in the normalizer of
![]() $U$
in
$U$
in
![]() $\operatorname{SL}_{2}(K)$
which is given by
$\operatorname{SL}_{2}(K)$
which is given by
It follows that the line that is fixed by
![]() $E$
is also fixed by all of
$E$
is also fixed by all of
![]() $H$
. Hence,
$H$
. Hence,
![]() $\bar{H}$
is contained in the projective image of a Borel subgroup of
$\bar{H}$
is contained in the projective image of a Borel subgroup of
![]() $\operatorname{GL}_{2}(k)$
.
$\operatorname{GL}_{2}(k)$
.
Case (8): Here,
![]() $\bar{H}$
is isomorphic to
$\bar{H}$
is isomorphic to
![]() $\operatorname{PGL}_{2}(k^{\prime })$
for some proper subfield
$\operatorname{PGL}_{2}(k^{\prime })$
for some proper subfield
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
, or
$k$
, or
![]() $\operatorname{PSL}_{2}(k)$
.◻
$\operatorname{PSL}_{2}(k)$
.◻
Assume that
![]() $q_{{\wp}}>5$
. Suppose also that
$q_{{\wp}}>5$
. Suppose also that
![]() ${\wp}\notin S_{\unicode[STIX]{x1D719}}$
, so that
${\wp}\notin S_{\unicode[STIX]{x1D719}}$
, so that
![]() $\unicode[STIX]{x1D70C}_{{\wp}}(I_{K_{{\wp}}})$
contains a nonsplit Cartan subgroup or a semisplit Cartan subgroup by Theorem 6.1. The projective image of a nonsplit Cartan subgroup and of a semisplit Cartan subgroup has a cyclic subgroup of order at least
$\unicode[STIX]{x1D70C}_{{\wp}}(I_{K_{{\wp}}})$
contains a nonsplit Cartan subgroup or a semisplit Cartan subgroup by Theorem 6.1. The projective image of a nonsplit Cartan subgroup and of a semisplit Cartan subgroup has a cyclic subgroup of order at least
![]() $q_{{\wp}}\pm 1>5$
, which rules out the case
$q_{{\wp}}\pm 1>5$
, which rules out the case
![]() $(v)$
. On the other hand, the order of the projective image of a nonsplit Cartan subgroup or of a semisplit Cartan subgroup does not divide the order of
$(v)$
. On the other hand, the order of the projective image of a nonsplit Cartan subgroup or of a semisplit Cartan subgroup does not divide the order of
![]() $\operatorname{PGL}_{2}(k^{\prime })$
for a proper subfield
$\operatorname{PGL}_{2}(k^{\prime })$
for a proper subfield
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
, ruling out the case (iv). Since the image of the determinant map on a nonsplit Cartan and semisplit Cartan subgroup is
$k$
, ruling out the case (iv). Since the image of the determinant map on a nonsplit Cartan and semisplit Cartan subgroup is
![]() $(A/{\wp})^{\times }$
, the case (iii) is ruled out.
$(A/{\wp})^{\times }$
, the case (iii) is ruled out.
Thus, we are in one of the following cases:
(1) Image of
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is contained in the normalizer
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is contained in the normalizer
 ${\mathcal{N}}$
of a Cartan subgroup
${\mathcal{N}}$
of a Cartan subgroup
 ${\mathcal{C}}$
, but not in
${\mathcal{C}}$
, but not in
 ${\mathcal{C}}$
;
${\mathcal{C}}$
;(2) Image of
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is contained in a Borel subgroup;
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is contained in a Borel subgroup;(3) Image of
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is contained in a nonsplit Cartan subgroup.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
is contained in a nonsplit Cartan subgroup.
Proposition 8.2. Assume
![]() $q$
is odd. The representation
$q$
is odd. The representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
cannot have image contained in a nonsplit Cartan subgroup.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
cannot have image contained in a nonsplit Cartan subgroup.
Proof. Let
![]() $\bar{c}$
be an element of
$\bar{c}$
be an element of
![]() $G(K(C[{\wp}])/K)\cong (A/{\wp})^{\times }$
of order
$G(K(C[{\wp}])/K)\cong (A/{\wp})^{\times }$
of order
![]() $q_{{\wp}}-1$
, where
$q_{{\wp}}-1$
, where
![]() $q_{{\wp}}=q^{\deg _{K}{\wp}}$
and
$q_{{\wp}}=q^{\deg _{K}{\wp}}$
and
![]() $C$
is the Carlitz module as in Proposition 5.3. Extend
$C$
is the Carlitz module as in Proposition 5.3. Extend
![]() $\bar{c}$
to an element
$\bar{c}$
to an element
![]() $c\in G_{K}$
of order
$c\in G_{K}$
of order
![]() $q_{{\wp}}-1$
.
$q_{{\wp}}-1$
.
From Proposition 5.3, there is a Galois character
![]() $\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
and a rank
$\unicode[STIX]{x1D716}_{0}:G_{K}\rightarrow \mathbb{F}_{q}^{\times }$
and a rank
![]() $1$
Drinfeld
$1$
Drinfeld
![]() $A$
-module
$A$
-module
![]() $\unicode[STIX]{x1D713}$
such that
$\unicode[STIX]{x1D713}$
such that
![]() $\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{P})=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}(\operatorname{Frob}_{P})\equiv \unicode[STIX]{x1D716}_{0}(P)P\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
for all primes
$\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}(\operatorname{Frob}_{P})=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},{\wp}}(\operatorname{Frob}_{P})\equiv \unicode[STIX]{x1D716}_{0}(P)P\hspace{0.6em}({\rm mod}\hspace{0.2em}{\wp})$
for all primes
![]() $P$
of
$P$
of
![]() $K$
such that
$K$
such that
![]() $P\notin S_{\unicode[STIX]{x1D719}}$
and
$P\notin S_{\unicode[STIX]{x1D719}}$
and
![]() $P\not ={\wp},\infty$
.
$P\not ={\wp},\infty$
.
Let
![]() $\unicode[STIX]{x1D719}^{\prime }$
be the twist of
$\unicode[STIX]{x1D719}^{\prime }$
be the twist of
![]() $\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}$
by
![]() $\unicode[STIX]{x1D716}_{0}^{-1}$
. From the proof of Proposition 5.3, we have that
$\unicode[STIX]{x1D716}_{0}^{-1}$
. From the proof of Proposition 5.3, we have that
![]() $\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}=\unicode[STIX]{x1D70C}_{C,{\wp}}$
. If
$\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}=\unicode[STIX]{x1D70C}_{C,{\wp}}$
. If
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
has image lying in a nonsplit Cartan subgroup, then
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719},{\wp}}$
has image lying in a nonsplit Cartan subgroup, then
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}$
also has image in a nonsplit Cartan subgroup. Therefore,
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}$
also has image in a nonsplit Cartan subgroup. Therefore,
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)$
is contained in the scalars, and hence
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)$
is contained in the scalars, and hence
![]() $\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)$
is a square; thus, the order of
$\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)$
is a square; thus, the order of
![]() $\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)$
divides
$\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)$
divides
![]() $(q_{{\wp}}-1)/2$
. But
$(q_{{\wp}}-1)/2$
. But
![]() $\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)=\unicode[STIX]{x1D70C}_{C,{\wp}}(c)=\bar{c}$
has order
$\det \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D719}^{\prime },{\wp}}(c)=\unicode[STIX]{x1D70C}_{C,{\wp}}(c)=\bar{c}$
has order
![]() $q_{{\wp}}-1$
, yielding a contradiction.◻
$q_{{\wp}}-1$
, yielding a contradiction.◻
Thus, Case (3) is ruled out. We dealt with Case (1) in Section 6, and with Case (2) in Section 7. Combining all the results together, we obtain Theorem 2.1.
Acknowledgments
We would like to thank C. David and A. Cojocaru for useful initial discussions pertaining to the subject of this paper. We also thank the referee for a careful reading, which improved this paper greatly.