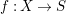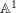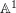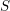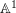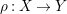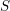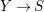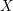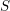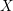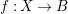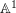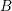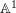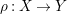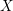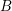Introduction
The general structure of smooth noncomplete surfaces
![]() $X$
with negative (logarithmic) Kodaira dimension is not fully understood yet. For say smooth quasi-projective surfaces over an algebraically closed field of characteristic zero, it was established by Keel and McKernan [Reference Keel and McKernan10] that the negativity of the Kodaira dimension is equivalent to the fact that
$X$
with negative (logarithmic) Kodaira dimension is not fully understood yet. For say smooth quasi-projective surfaces over an algebraically closed field of characteristic zero, it was established by Keel and McKernan [Reference Keel and McKernan10] that the negativity of the Kodaira dimension is equivalent to the fact that
![]() $X$
is generically covered by images of the affine line
$X$
is generically covered by images of the affine line
![]() $\mathbb{A}^{1}$
in the sense that the set of points
$\mathbb{A}^{1}$
in the sense that the set of points
![]() $x\in X$
with the property that there exists a nonconstant morphism
$x\in X$
with the property that there exists a nonconstant morphism
![]() $f:\mathbb{A}^{1}\rightarrow X$
such that
$f:\mathbb{A}^{1}\rightarrow X$
such that
![]() $x\in f(\mathbb{A}^{1})$
is dense in
$x\in f(\mathbb{A}^{1})$
is dense in
![]() $X$
with respect to the Zariski topology. This property, called
$X$
with respect to the Zariski topology. This property, called
![]() $\mathbb{A}^{1}$
-uniruledness is equivalent to the existence of an open embedding
$\mathbb{A}^{1}$
-uniruledness is equivalent to the existence of an open embedding
![]() $X{\hookrightarrow}(\overline{X},B)$
into a complete variety
$X{\hookrightarrow}(\overline{X},B)$
into a complete variety
![]() $\overline{X}$
covered by proper rational curves meeting the boundary
$\overline{X}$
covered by proper rational curves meeting the boundary
![]() $B=\overline{X}\setminus X$
in at most one point. In the case where
$B=\overline{X}\setminus X$
in at most one point. In the case where
![]() $X$
is smooth and affine, an earlier deep result of Miyanishi–Sugie and Fujita [Reference Miyanishi and Sugie14] asserts the stronger property that
$X$
is smooth and affine, an earlier deep result of Miyanishi–Sugie and Fujita [Reference Miyanishi and Sugie14] asserts the stronger property that
![]() $X$
is
$X$
is
![]() $\mathbb{A}^{1}$
-ruled: there exists a Zariski dense open subset
$\mathbb{A}^{1}$
-ruled: there exists a Zariski dense open subset
![]() $U\subset X$
of the form
$U\subset X$
of the form
![]() $U\simeq Z\times \mathbb{A}^{1}$
for a suitable smooth curve
$U\simeq Z\times \mathbb{A}^{1}$
for a suitable smooth curve
![]() $Z$
. Equivalently,
$Z$
. Equivalently,
![]() $X$
admits a surjective flat morphism
$X$
admits a surjective flat morphism
![]() $\unicode[STIX]{x1D70C}:X\rightarrow C$
to an open subset
$\unicode[STIX]{x1D70C}:X\rightarrow C$
to an open subset
![]() $C$
of a smooth projective model
$C$
of a smooth projective model
![]() $\overline{Z}$
of
$\overline{Z}$
of
![]() $Z$
, whose generic fiber is isomorphic to the affine line over the function field of
$Z$
, whose generic fiber is isomorphic to the affine line over the function field of
![]() $C$
. Such a morphism
$C$
. Such a morphism
![]() $\unicode[STIX]{x1D70C}:X\rightarrow C$
is called an
$\unicode[STIX]{x1D70C}:X\rightarrow C$
is called an
![]() $\mathbb{A}^{1}$
-fibration, and
$\mathbb{A}^{1}$
-fibration, and
![]() $\unicode[STIX]{x1D70C}$
is said to be of affine type or complete type when the base curve
$\unicode[STIX]{x1D70C}$
is said to be of affine type or complete type when the base curve
![]() $C$
is affine or complete, respectively.
$C$
is affine or complete, respectively.
Smooth
![]() $\mathbb{A}^{1}$
-uniruled but not
$\mathbb{A}^{1}$
-uniruled but not
![]() $\mathbb{A}^{1}$
-ruled affine varieties are known to exist in every dimension
$\mathbb{A}^{1}$
-ruled affine varieties are known to exist in every dimension
![]() ${\geqslant}3$
[Reference Dubouloz and Kishimoto1]. Many examples of
${\geqslant}3$
[Reference Dubouloz and Kishimoto1]. Many examples of
![]() $\mathbb{A}^{1}$
-uniruled affine threefolds can be constructed in the form of flat families
$\mathbb{A}^{1}$
-uniruled affine threefolds can be constructed in the form of flat families
![]() $f:X\rightarrow B$
of smooth
$f:X\rightarrow B$
of smooth
![]() $\mathbb{A}^{1}$
-ruled affine surfaces parametrized by a smooth base curve
$\mathbb{A}^{1}$
-ruled affine surfaces parametrized by a smooth base curve
![]() $B$
. For instance, the complement
$B$
. For instance, the complement
![]() $X$
of a smooth cubic surface
$X$
of a smooth cubic surface
![]() $S\subset \mathbb{P}_{\mathbb{C}}^{3}$
is the total space of a family
$S\subset \mathbb{P}_{\mathbb{C}}^{3}$
is the total space of a family
![]() $f:X\rightarrow \mathbb{A}^{1}=\text{Spec}(\mathbb{C}[t])$
of
$f:X\rightarrow \mathbb{A}^{1}=\text{Spec}(\mathbb{C}[t])$
of
![]() $\mathbb{A}^{1}$
-ruled surfaces induced by the restriction of a pencil
$\mathbb{A}^{1}$
-ruled surfaces induced by the restriction of a pencil
![]() $\overline{f}:\mathbb{P}^{3}{\dashrightarrow}\mathbb{P}^{1}$
on
$\overline{f}:\mathbb{P}^{3}{\dashrightarrow}\mathbb{P}^{1}$
on
![]() $\mathbb{P}^{3}$
generated by
$\mathbb{P}^{3}$
generated by
![]() $S$
and three times a tangent hyperplane
$S$
and three times a tangent hyperplane
![]() $H$
to
$H$
to
![]() $S$
whose intersection with
$S$
whose intersection with
![]() $S$
consists of a cuspidal cubic curve. The general fibers of
$S$
consists of a cuspidal cubic curve. The general fibers of
![]() $f$
have negative Kodaira dimension, carrying
$f$
have negative Kodaira dimension, carrying
![]() $\mathbb{A}^{1}$
-fibrations of complete type only, and the failure of
$\mathbb{A}^{1}$
-fibrations of complete type only, and the failure of
![]() $\mathbb{A}^{1}$
-ruledness is intimately related to the fact that the generic fiber
$\mathbb{A}^{1}$
-ruledness is intimately related to the fact that the generic fiber
![]() $X_{\unicode[STIX]{x1D702}}$
of
$X_{\unicode[STIX]{x1D702}}$
of
![]() $f$
, which is a surface defined over the field
$f$
, which is a surface defined over the field
![]() $K=\mathbb{C}(t)$
, does not admit any
$K=\mathbb{C}(t)$
, does not admit any
![]() $\mathbb{A}^{1}$
-fibration defined over
$\mathbb{A}^{1}$
-fibration defined over
![]() $\mathbb{C}(t)$
. Nevertheless, it was noticed in [Reference Gurjar, Masuda and Miyanishi3, Theorem 6.1] that one can infer straight from the construction of
$\mathbb{C}(t)$
. Nevertheless, it was noticed in [Reference Gurjar, Masuda and Miyanishi3, Theorem 6.1] that one can infer straight from the construction of
![]() $f:X\rightarrow \mathbb{A}^{1}$
the existence of a finite base extension
$f:X\rightarrow \mathbb{A}^{1}$
the existence of a finite base extension
![]() $\text{Spec}(L)\rightarrow \text{Spec}(K)$
for which the surface
$\text{Spec}(L)\rightarrow \text{Spec}(K)$
for which the surface
![]() $X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)$
carries an
$X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)$
carries an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)\rightarrow \mathbb{P}_{L}^{1}$
defined over the field
$\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)\rightarrow \mathbb{P}_{L}^{1}$
defined over the field
![]() $L$
.
$L$
.
A natural question is then to decide whether this phenomenon holds in general for families
![]() $f:X\rightarrow B$
of
$f:X\rightarrow B$
of
![]() $\mathbb{A}^{1}$
-ruled affine surfaces parameterized by a smooth base curve
$\mathbb{A}^{1}$
-ruled affine surfaces parameterized by a smooth base curve
![]() $B$
, namely, does the existence of
$B$
, namely, does the existence of
![]() $\mathbb{A}^{1}$
-fibrations on the general fibers of
$\mathbb{A}^{1}$
-fibrations on the general fibers of
![]() $f$
imply the existence of one on the generic fiber of
$f$
imply the existence of one on the generic fiber of
![]() $f$
, possibly after a finite extension of the base
$f$
, possibly after a finite extension of the base
![]() $B$
? A partial positive answer is given by Gurjar et al. [Reference Gurjar, Masuda and Miyanishi3, Theorem 3.8] under the additional assumption that the general fibers of
$B$
? A partial positive answer is given by Gurjar et al. [Reference Gurjar, Masuda and Miyanishi3, Theorem 3.8] under the additional assumption that the general fibers of
![]() $f$
carry
$f$
carry
![]() $\mathbb{A}^{1}$
-fibrations of affine type. The main result in Gurjar et al. [Reference Gurjar, Masuda and Miyanishi3, Theorem 3.8] is derived from the study of log-deformations of suitable relative normal projective models
$\mathbb{A}^{1}$
-fibrations of affine type. The main result in Gurjar et al. [Reference Gurjar, Masuda and Miyanishi3, Theorem 3.8] is derived from the study of log-deformations of suitable relative normal projective models
![]() $\overline{f}:(\overline{X},D)\rightarrow B$
of
$\overline{f}:(\overline{X},D)\rightarrow B$
of
![]() $X$
over
$X$
over
![]() $B$
with appropriate boundaries
$B$
with appropriate boundaries
![]() $D$
. It is established in particular that the structure of the boundary divisor of a well-chosen smooth projective completion of a general closed fiber
$D$
. It is established in particular that the structure of the boundary divisor of a well-chosen smooth projective completion of a general closed fiber
![]() $X_{s}$
is stable under small deformations, a property which implies in turn, possibly after a finite extension of the base
$X_{s}$
is stable under small deformations, a property which implies in turn, possibly after a finite extension of the base
![]() $B$
, the existence of an
$B$
, the existence of an
![]() $\mathbb{A}^{1}$
-fibration of affine type on the generic fiber of
$\mathbb{A}^{1}$
-fibration of affine type on the generic fiber of
![]() $f$
. This log-deformation theoretic approach is also central in the related recent work of Flenner et al. [Reference Flenner, Kaliman and Zaidenberg2] on the classification of normal affine surfaces with
$f$
. This log-deformation theoretic approach is also central in the related recent work of Flenner et al. [Reference Flenner, Kaliman and Zaidenberg2] on the classification of normal affine surfaces with
![]() $\mathbb{A}^{1}$
-fibrations of affine type up to a certain notion of deformation equivalence, defined for families which admit suitable relative projective models satisfying Kamawata’s axioms of logarithmic deformations of pairs [Reference Kawamata8]. The fact that the
$\mathbb{A}^{1}$
-fibrations of affine type up to a certain notion of deformation equivalence, defined for families which admit suitable relative projective models satisfying Kamawata’s axioms of logarithmic deformations of pairs [Reference Kawamata8]. The fact that the
![]() $\mathbb{A}^{1}$
-fibrations under consideration are of affine type plays again a crucial role and, in contrast with the situation considered in [Reference Gurjar, Masuda and Miyanishi3], the restrictions imposed on the families imply the existence of
$\mathbb{A}^{1}$
-fibrations under consideration are of affine type plays again a crucial role and, in contrast with the situation considered in [Reference Gurjar, Masuda and Miyanishi3], the restrictions imposed on the families imply the existence of
![]() $\mathbb{A}^{1}$
-fibrations of affine type on their generic fibers.
$\mathbb{A}^{1}$
-fibrations of affine type on their generic fibers.
Our main result (Theorem 7) consists of a generalization of the results in [Reference Gurjar, Masuda and Miyanishi3] to families
![]() $f:X\rightarrow S$
of
$f:X\rightarrow S$
of
![]() $\mathbb{A}^{1}$
-ruled surfaces over an arbitrary normal base
$\mathbb{A}^{1}$
-ruled surfaces over an arbitrary normal base
![]() $S$
, which also includes the case where a general closed fiber
$S$
, which also includes the case where a general closed fiber
![]() $X_{s}$
of
$X_{s}$
of
![]() $f$
admits
$f$
admits
![]() $\mathbb{A}^{1}$
-fibrations of complete type only. In particular, we obtain the following positive answer to [Reference Gurjar, Masuda and Miyanishi3, Conjecture 6.2]:
$\mathbb{A}^{1}$
-fibrations of complete type only. In particular, we obtain the following positive answer to [Reference Gurjar, Masuda and Miyanishi3, Conjecture 6.2]:
Theorem.
Let
![]() $f:X\rightarrow S$
be a dominant morphism between normal complex algebraic varieties whose general fibers are smooth
$f:X\rightarrow S$
be a dominant morphism between normal complex algebraic varieties whose general fibers are smooth
![]() $\mathbb{A}^{1}$
-ruled affine surfaces. Then there exist a dense open subset
$\mathbb{A}^{1}$
-ruled affine surfaces. Then there exist a dense open subset
![]() $S_{\ast }\subset S$
, a finite étale morphism
$S_{\ast }\subset S$
, a finite étale morphism
![]() $T\rightarrow S_{\ast }$
and a normal
$T\rightarrow S_{\ast }$
and a normal
![]() $T$
-scheme
$T$
-scheme
![]() $h:Y\rightarrow T$
such that the induced morphism
$h:Y\rightarrow T$
such that the induced morphism
![]() $f_{T}=\text{p}r_{T}:X_{T}=X\times _{S_{\ast }}T\rightarrow T$
factors as
$f_{T}=\text{p}r_{T}:X_{T}=X\times _{S_{\ast }}T\rightarrow T$
factors as
where
![]() $\unicode[STIX]{x1D70C}:X_{T}\rightarrow Y$
is an
$\unicode[STIX]{x1D70C}:X_{T}\rightarrow Y$
is an
![]() $\mathbb{A}^{1}$
-fibration.
$\mathbb{A}^{1}$
-fibration.
In contrast with the log-deformation theoretic strategy used in [Reference Gurjar, Masuda and Miyanishi3], which involves the study of certain Hilbert schemes of rational curves on well-chosen relative normal projective models
![]() $\overline{f}:(\overline{X},B)\rightarrow S$
of
$\overline{f}:(\overline{X},B)\rightarrow S$
of
![]() $X$
over
$X$
over
![]() $S$
, our approach is more elementary, based on the notion of Kodaira dimension [Reference Iitaka7] adapted to the case of geometrically connected varieties defined over arbitrary base fields of characteristic zero. Indeed, the hypothesis means equivalently that the general fibers of
$S$
, our approach is more elementary, based on the notion of Kodaira dimension [Reference Iitaka7] adapted to the case of geometrically connected varieties defined over arbitrary base fields of characteristic zero. Indeed, the hypothesis means equivalently that the general fibers of
![]() $f$
have negative Kodaira dimension. This property is in turn inherited by the generic fiber of
$f$
have negative Kodaira dimension. This property is in turn inherited by the generic fiber of
![]() $f$
, which is a smooth affine surface defined over the function field of
$f$
, which is a smooth affine surface defined over the function field of
![]() $S$
, thanks to a standard Lefschetz principle argument. Then we are left with checking that a smooth affine surface
$S$
, thanks to a standard Lefschetz principle argument. Then we are left with checking that a smooth affine surface
![]() $X$
defined over an arbitrary base field
$X$
defined over an arbitrary base field
![]() $k$
of characteristic zero and with negative Kodaira dimension admits an
$k$
of characteristic zero and with negative Kodaira dimension admits an
![]() $\mathbb{A}^{1}$
-fibration, possibly after a suitable finite base extension
$\mathbb{A}^{1}$
-fibration, possibly after a suitable finite base extension
![]() $\text{Spec}(k_{0})\rightarrow \text{Spec}(k)$
, a fact which ultimately follows from finite type hypotheses and the aforementioned characterization of Miyanishi and Sugie [Reference Miyanishi and Sugie14].
$\text{Spec}(k_{0})\rightarrow \text{Spec}(k)$
, a fact which ultimately follows from finite type hypotheses and the aforementioned characterization of Miyanishi and Sugie [Reference Miyanishi and Sugie14].
The article is organized as follows. The first section contains a review of the structure of smooth affine surfaces of negative Kodaira dimension over arbitrary base fields
![]() $k$
of characteristic zero. We show in particular that every such surface
$k$
of characteristic zero. We show in particular that every such surface
![]() $X$
admits an
$X$
admits an
![]() $\mathbb{A}^{1}$
-fibration after a finite extension of the base field
$\mathbb{A}^{1}$
-fibration after a finite extension of the base field
![]() $k$
, and we give criteria for the existence of
$k$
, and we give criteria for the existence of
![]() $\mathbb{A}^{1}$
-fibrations defined over
$\mathbb{A}^{1}$
-fibrations defined over
![]() $k$
. These results are then applied in the second section to the study of deformations
$k$
. These results are then applied in the second section to the study of deformations
![]() $f:X\rightarrow S$
of smooth
$f:X\rightarrow S$
of smooth
![]() $\mathbb{A}^{1}$
-ruled affine surfaces: after giving the proof of the main result, Theorem 7, we consider in more detail the particular situation where the general fibers of
$\mathbb{A}^{1}$
-ruled affine surfaces: after giving the proof of the main result, Theorem 7, we consider in more detail the particular situation where the general fibers of
![]() $f:X\rightarrow S$
are irrational. In this case, after shrinking
$f:X\rightarrow S$
are irrational. In this case, after shrinking
![]() $S$
if necessary, we show that the morphism
$S$
if necessary, we show that the morphism
![]() $f$
actually factors through an
$f$
actually factors through an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
over an
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
over an
![]() $S$
-scheme
$S$
-scheme
![]() $h:Y\rightarrow S$
which coincides, up to birational equivalence, with the maximally rationally connected quotient of a relative smooth projective model
$h:Y\rightarrow S$
which coincides, up to birational equivalence, with the maximally rationally connected quotient of a relative smooth projective model
![]() $\overline{f}:\overline{X}\rightarrow S$
of
$\overline{f}:\overline{X}\rightarrow S$
of
![]() $X$
over
$X$
over
![]() $S$
. The last section is devoted to the case of affine threefolds equipped with a fibration
$S$
. The last section is devoted to the case of affine threefolds equipped with a fibration
![]() $f:X\rightarrow B$
by irrational
$f:X\rightarrow B$
by irrational
![]() $\mathbb{A}^{1}$
-ruled surfaces over a smooth base curve
$\mathbb{A}^{1}$
-ruled surfaces over a smooth base curve
![]() $B$
: we explain in particular how to construct an
$B$
: we explain in particular how to construct an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
factoring
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
factoring
![]() $f$
by means of a relative minimal model program applied to a smooth projective model
$f$
by means of a relative minimal model program applied to a smooth projective model
![]() $\overline{f}:\overline{X}\rightarrow B$
of
$\overline{f}:\overline{X}\rightarrow B$
of
![]() $X$
over
$X$
over
![]() $B$
.
$B$
.
1
 $\mathbb{A}^{1}$
-ruledness of affine surfaces over nonclosed field
$\mathbb{A}^{1}$
-ruledness of affine surfaces over nonclosed field
In what follows, the term
![]() $k$
-variety refers to a geometrically integral scheme of finite type over a base field
$k$
-variety refers to a geometrically integral scheme of finite type over a base field
![]() $k$
of characteristic zero. A
$k$
of characteristic zero. A
![]() $k$
-variety
$k$
-variety
![]() $X$
is said to be
$X$
is said to be
![]() $k$
-rational if it is birationally isomorphic over
$k$
-rational if it is birationally isomorphic over
![]() $k$
to the projective space
$k$
to the projective space
![]() $\mathbb{P}_{k}^{n}$
, where
$\mathbb{P}_{k}^{n}$
, where
![]() $n=\dim _{k}X$
. When no particular base field is indicated, we use simply the term rational to refer to a geometrically rational variety. We call a variety irrational if it is not rational in the previous sense.
$n=\dim _{k}X$
. When no particular base field is indicated, we use simply the term rational to refer to a geometrically rational variety. We call a variety irrational if it is not rational in the previous sense.
1.1 Logarithmic Kodaira dimension
1.1.1. Let
![]() $X$
be a smooth algebraic variety defined over a field
$X$
be a smooth algebraic variety defined over a field
![]() $k$
of characteristic zero. By virtue of Nagata compactification [Reference Nagata15] and Hironaka desingularization [Reference Hironaka5] theorems, there exists an open immersion
$k$
of characteristic zero. By virtue of Nagata compactification [Reference Nagata15] and Hironaka desingularization [Reference Hironaka5] theorems, there exists an open immersion
![]() $X{\hookrightarrow}(\overline{X},B)$
into a smooth complete algebraic variety
$X{\hookrightarrow}(\overline{X},B)$
into a smooth complete algebraic variety
![]() $\overline{X}$
with reduced SNC boundary divisor
$\overline{X}$
with reduced SNC boundary divisor
![]() $B=\overline{X}\setminus X$
. The (logarithmic) Kodaira dimension
$B=\overline{X}\setminus X$
. The (logarithmic) Kodaira dimension
![]() $\unicode[STIX]{x1D705}(X)$
of
$\unicode[STIX]{x1D705}(X)$
of
![]() $X$
is then defined as the Iitaka dimension [Reference Iitaka6] of the pair
$X$
is then defined as the Iitaka dimension [Reference Iitaka6] of the pair
![]() $(\overline{X};\unicode[STIX]{x1D714}_{\overline{X}}(\log B))$
, where
$(\overline{X};\unicode[STIX]{x1D714}_{\overline{X}}(\log B))$
, where
![]() $\unicode[STIX]{x1D714}_{\overline{X}}(\log B)=(\det \unicode[STIX]{x1D6FA}_{\overline{X}/k}^{1})\otimes {\mathcal{O}}_{\overline{X}}(B)$
. So letting
$\unicode[STIX]{x1D714}_{\overline{X}}(\log B)=(\det \unicode[STIX]{x1D6FA}_{\overline{X}/k}^{1})\otimes {\mathcal{O}}_{\overline{X}}(B)$
. So letting
we have
![]() $\unicode[STIX]{x1D705}(X)=\text{tr}.\deg _{k}{\mathcal{R}}(\overline{X},B)-1$
if
$\unicode[STIX]{x1D705}(X)=\text{tr}.\deg _{k}{\mathcal{R}}(\overline{X},B)-1$
if
![]() $H^{0}(\overline{X},\unicode[STIX]{x1D714}_{\overline{X}}(\log B)^{\otimes m})\neq 0$
for sufficiently large
$H^{0}(\overline{X},\unicode[STIX]{x1D714}_{\overline{X}}(\log B)^{\otimes m})\neq 0$
for sufficiently large
![]() $m$
. Otherwise, if
$m$
. Otherwise, if
![]() $H^{0}(\overline{X},\unicode[STIX]{x1D714}_{\overline{X}}(\log B)^{\otimes m})=0$
for every
$H^{0}(\overline{X},\unicode[STIX]{x1D714}_{\overline{X}}(\log B)^{\otimes m})=0$
for every
![]() $m\geqslant 1$
, we set by convention
$m\geqslant 1$
, we set by convention
![]() $\unicode[STIX]{x1D705}(X)=-\infty$
and we say that
$\unicode[STIX]{x1D705}(X)=-\infty$
and we say that
![]() $\unicode[STIX]{x1D705}(X)$
is negative. The so-defined element
$\unicode[STIX]{x1D705}(X)$
is negative. The so-defined element
![]() $\unicode[STIX]{x1D705}(X)\in \{-\infty \}\cup \left\{0,\ldots ,\text{dim}_{k}X\right\}$
is independent of the choice of a smooth complete model
$\unicode[STIX]{x1D705}(X)\in \{-\infty \}\cup \left\{0,\ldots ,\text{dim}_{k}X\right\}$
is independent of the choice of a smooth complete model
![]() $(\overline{X},B)$
[Reference Iitaka7].
$(\overline{X},B)$
[Reference Iitaka7].
Furthermore, the Kodaira dimension of
![]() $X$
is invariant under arbitrary extensions of the base field
$X$
is invariant under arbitrary extensions of the base field
![]() $k$
. Indeed, given an extension
$k$
. Indeed, given an extension
![]() $k\subset k^{\prime }$
, the pair
$k\subset k^{\prime }$
, the pair
![]() $(\overline{X}_{k^{\prime }},B_{k^{\prime }})$
obtained by the base change
$(\overline{X}_{k^{\prime }},B_{k^{\prime }})$
obtained by the base change
![]() $\text{Spec}(k^{\prime })\rightarrow \text{Spec}(k)$
is a smooth complete model of
$\text{Spec}(k^{\prime })\rightarrow \text{Spec}(k)$
is a smooth complete model of
![]() $X_{k^{\prime }}=X\times _{\text{Spec}(k)}\text{Spec}(k^{\prime })$
with reduced SNC boundary
$X_{k^{\prime }}=X\times _{\text{Spec}(k)}\text{Spec}(k^{\prime })$
with reduced SNC boundary
![]() $B_{k^{\prime }}$
. Furthermore letting
$B_{k^{\prime }}$
. Furthermore letting
![]() $\unicode[STIX]{x1D70B}:\overline{X}_{k^{\prime }}\rightarrow \overline{X}$
be the corresponding faithfully flat morphism, we have
$\unicode[STIX]{x1D70B}:\overline{X}_{k^{\prime }}\rightarrow \overline{X}$
be the corresponding faithfully flat morphism, we have
![]() $\unicode[STIX]{x1D714}_{\overline{X}_{k^{\prime }}}(\log B_{k^{\prime }})\simeq \unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{X}(\log B)$
and so
$\unicode[STIX]{x1D714}_{\overline{X}_{k^{\prime }}}(\log B_{k^{\prime }})\simeq \unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{X}(\log B)$
and so
![]() ${\mathcal{R}}(X_{k^{\prime }})\simeq {\mathcal{R}}(X)\otimes _{k}k^{\prime }$
by the flat base change theorem [Reference Hartshorne4, Proposition III.9.3]. Thus
${\mathcal{R}}(X_{k^{\prime }})\simeq {\mathcal{R}}(X)\otimes _{k}k^{\prime }$
by the flat base change theorem [Reference Hartshorne4, Proposition III.9.3]. Thus
![]() $\unicode[STIX]{x1D705}(X)=\unicode[STIX]{x1D705}(X_{k^{\prime }})$
.
$\unicode[STIX]{x1D705}(X)=\unicode[STIX]{x1D705}(X_{k^{\prime }})$
.
Example 1. The affine line
![]() $\mathbb{A}_{k}^{1}$
is the only smooth geometrically connected noncomplete curve
$\mathbb{A}_{k}^{1}$
is the only smooth geometrically connected noncomplete curve
![]() $C$
with negative Kodaira dimension. Indeed, let
$C$
with negative Kodaira dimension. Indeed, let
![]() $\overline{C}$
be a smooth projective model of
$\overline{C}$
be a smooth projective model of
![]() $C$
and let
$C$
and let
![]() $\overline{C}_{\overline{k}}$
be the curve obtained by the base change to an algebraic closure
$\overline{C}_{\overline{k}}$
be the curve obtained by the base change to an algebraic closure
![]() $\overline{k}$
of
$\overline{k}$
of
![]() $k$
. Since
$k$
. Since
![]() $C$
is noncomplete,
$C$
is noncomplete,
![]() $B=\overline{C}_{\overline{k}}\setminus C_{\overline{k}}$
consists of a finite collection of closed points
$B=\overline{C}_{\overline{k}}\setminus C_{\overline{k}}$
consists of a finite collection of closed points
![]() $p_{1},\ldots ,p_{s}$
,
$p_{1},\ldots ,p_{s}$
,
![]() $s\geqslant 1$
, on which the Galois group
$s\geqslant 1$
, on which the Galois group
![]() $\text{Gal}(\overline{k}/k)$
acts by
$\text{Gal}(\overline{k}/k)$
acts by
![]() $k$
-automorphisms of
$k$
-automorphisms of
![]() $\overline{C}_{\overline{k}}$
. Clearly,
$\overline{C}_{\overline{k}}$
. Clearly,
![]() $H^{0}(\overline{C}_{\overline{k}},\unicode[STIX]{x1D714}_{\bar{C}_{\overline{k}}}(\log B)^{\otimes m})\neq 0$
unless
$H^{0}(\overline{C}_{\overline{k}},\unicode[STIX]{x1D714}_{\bar{C}_{\overline{k}}}(\log B)^{\otimes m})\neq 0$
unless
![]() $\overline{C}_{\overline{k}}\simeq \mathbb{P}_{\overline{k}}^{1}$
and
$\overline{C}_{\overline{k}}\simeq \mathbb{P}_{\overline{k}}^{1}$
and
![]() $s=1$
. Since
$s=1$
. Since
![]() $p_{1}$
is then necessarily
$p_{1}$
is then necessarily
![]() $\text{Gal}(\overline{k}/k)$
-invariant,
$\text{Gal}(\overline{k}/k)$
-invariant,
![]() $\overline{C}\setminus C$
consists of unique
$\overline{C}\setminus C$
consists of unique
![]() $k$
-rational point, showing that
$k$
-rational point, showing that
![]() $\overline{C}\simeq \mathbb{P}_{k}^{1}$
and
$\overline{C}\simeq \mathbb{P}_{k}^{1}$
and
![]() $C\simeq \mathbb{A}_{k}^{1}$
.
$C\simeq \mathbb{A}_{k}^{1}$
.
1.2 Smooth affine surfaces with negative Kodaira dimension
Recall that by virtue of [Reference Miyanishi and Sugie14], a smooth affine surface
![]() $X$
defined over an algebraically closed field of characteristic zero has negative Kodaira dimension if and only if it is
$X$
defined over an algebraically closed field of characteristic zero has negative Kodaira dimension if and only if it is
![]() $\mathbb{A}^{1}$
-ruled: there exists a Zariski dense open subset
$\mathbb{A}^{1}$
-ruled: there exists a Zariski dense open subset
![]() $U\subset X$
of the form
$U\subset X$
of the form
![]() $U\simeq Z\times \mathbb{A}^{1}$
for a suitable smooth curve
$U\simeq Z\times \mathbb{A}^{1}$
for a suitable smooth curve
![]() $Z$
. In fact, the projection
$Z$
. In fact, the projection
![]() $\text{pr}_{Z}:U\simeq Z\times \mathbb{A}^{1}\rightarrow Z$
always extends to an
$\text{pr}_{Z}:U\simeq Z\times \mathbb{A}^{1}\rightarrow Z$
always extends to an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow C$
over an open subset
$\unicode[STIX]{x1D70C}:X\rightarrow C$
over an open subset
![]() $C$
of a smooth projective model
$C$
of a smooth projective model
![]() $\overline{Z}$
of
$\overline{Z}$
of
![]() $Z$
. This characterization admits the following straightforward generalization to arbitrary base fields of characteristic zero:
$Z$
. This characterization admits the following straightforward generalization to arbitrary base fields of characteristic zero:
Theorem 2. Let
![]() $X$
be a smooth geometrically connected affine surface defined over a field
$X$
be a smooth geometrically connected affine surface defined over a field
![]() $k$
of characteristic zero. Then the following are equivalent:
$k$
of characteristic zero. Then the following are equivalent:
-
(a) The Kodaira dimension
 $\unicode[STIX]{x1D705}(X)$
of
$\unicode[STIX]{x1D705}(X)$
of
 $X$
is negative.
$X$
is negative. -
(b) For some finite extension
 $k_{0}$
of
$k_{0}$
of
 $k$
, the surface
$k$
, the surface
 $X_{k_{0}}$
contains an open subset
$X_{k_{0}}$
contains an open subset
 $U\simeq Z\times \mathbb{A}_{k_{0}}^{1}$
for some smooth curve
$U\simeq Z\times \mathbb{A}_{k_{0}}^{1}$
for some smooth curve
 $Z$
defined over
$Z$
defined over
 $k_{0}$
.
$k_{0}$
. -
(c) There exist a finite extension
 $k_{0}$
of
$k_{0}$
of
 $k$
and an
$k$
and an
 $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
 $\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow C_{0}$
over a smooth curve
$\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow C_{0}$
over a smooth curve
 $C_{0}$
defined over
$C_{0}$
defined over
 $k_{0}$
.
$k_{0}$
.
Proof. Clearly (c) implies (b) and (b) implies (a). To show that (a) implies (c), we observe that letting
![]() $\overline{k}$
be an algebraic closure of
$\overline{k}$
be an algebraic closure of
![]() $k$
, we have
$k$
, we have
![]() $\unicode[STIX]{x1D705}(X_{\overline{k}})=\unicode[STIX]{x1D705}(X)<0$
. It then follows from the aforementioned result of Miyanishi and Sugie [Reference Miyanishi and Sugie14] that
$\unicode[STIX]{x1D705}(X_{\overline{k}})=\unicode[STIX]{x1D705}(X)<0$
. It then follows from the aforementioned result of Miyanishi and Sugie [Reference Miyanishi and Sugie14] that
![]() $X_{\overline{k}}$
admits an
$X_{\overline{k}}$
admits an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $q:X_{\overline{k}}\rightarrow C$
over a smooth curve
$q:X_{\overline{k}}\rightarrow C$
over a smooth curve
![]() $C$
, with smooth projective model
$C$
, with smooth projective model
![]() $\overline{C}$
. Since
$\overline{C}$
. Since
![]() $X_{\overline{k}}$
and
$X_{\overline{k}}$
and
![]() $\overline{C}$
are of finite type over
$\overline{C}$
are of finite type over
![]() $\overline{k}$
, there exists a finite extension
$\overline{k}$
, there exists a finite extension
![]() $k\subset k_{0}$
such that
$k\subset k_{0}$
such that
![]() $q:X_{\overline{k}}\rightarrow \overline{C}$
is obtained from a morphism
$q:X_{\overline{k}}\rightarrow \overline{C}$
is obtained from a morphism
![]() $\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow \overline{C}_{0}$
to a smooth projective curve
$\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow \overline{C}_{0}$
to a smooth projective curve
![]() $\overline{C}_{0}$
defined over
$\overline{C}_{0}$
defined over
![]() $k_{0}$
by the base extension
$k_{0}$
by the base extension
![]() $\text{Spec}(\overline{k})\rightarrow \text{Spec}(k_{0})$
. By virtue of Example 1,
$\text{Spec}(\overline{k})\rightarrow \text{Spec}(k_{0})$
. By virtue of Example 1,
![]() $\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow \overline{C}_{0}$
is an
$\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow \overline{C}_{0}$
is an
![]() $\mathbb{A}^{1}$
-fibration.◻
$\mathbb{A}^{1}$
-fibration.◻
Examples of smooth affine surfaces
![]() $X$
of negative Kodaira dimension without any
$X$
of negative Kodaira dimension without any
![]() $\mathbb{A}^{1}$
-fibration defined over the base field but admitting
$\mathbb{A}^{1}$
-fibration defined over the base field but admitting
![]() $\mathbb{A}^{1}$
-fibrations of complete type after a finite base extension were already constructed in [Reference Dubouloz and Kishimoto1]. The following example illustrates the fact that a similar phenomenon occurs for
$\mathbb{A}^{1}$
-fibrations of complete type after a finite base extension were already constructed in [Reference Dubouloz and Kishimoto1]. The following example illustrates the fact that a similar phenomenon occurs for
![]() $\mathbb{A}^{1}$
-fibrations of affine type, providing in particular a negative answer to [Reference Gurjar, Masuda and Miyanishi3, Problem 3.13].
$\mathbb{A}^{1}$
-fibrations of affine type, providing in particular a negative answer to [Reference Gurjar, Masuda and Miyanishi3, Problem 3.13].
Example 3. Let
![]() $B\subset \mathbb{P}_{k}^{2}=\text{Proj}(k[x,y,z])$
be a smooth conic without
$B\subset \mathbb{P}_{k}^{2}=\text{Proj}(k[x,y,z])$
be a smooth conic without
![]() $k$
-rational point defined by a quadratic form
$k$
-rational point defined by a quadratic form
![]() $q=x^{2}+ay^{2}+bz^{2}$
, where
$q=x^{2}+ay^{2}+bz^{2}$
, where
![]() $a,b\in k^{\ast }$
, and let
$a,b\in k^{\ast }$
, and let
![]() $\overline{X}\subset \mathbb{P}_{k}^{3}=\text{Proj}(k[x,y,z,t])$
be the smooth quadric surface defined by the equation
$\overline{X}\subset \mathbb{P}_{k}^{3}=\text{Proj}(k[x,y,z,t])$
be the smooth quadric surface defined by the equation
![]() $q(x,y,z)-t^{2}=0$
. The complement
$q(x,y,z)-t^{2}=0$
. The complement
![]() $X\subset \overline{X}$
of the hyperplane section
$X\subset \overline{X}$
of the hyperplane section
![]() $\left\{t=0\right\}$
is a
$\left\{t=0\right\}$
is a
![]() $k$
-rational smooth affine surface with
$k$
-rational smooth affine surface with
![]() $\unicode[STIX]{x1D705}(X)<0$
, which does not admit any
$\unicode[STIX]{x1D705}(X)<0$
, which does not admit any
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow C$
over a smooth, affine or projective curve
$\unicode[STIX]{x1D70C}:X\rightarrow C$
over a smooth, affine or projective curve
![]() $C$
. Indeed, if such a fibration existed then a smooth projective model of
$C$
. Indeed, if such a fibration existed then a smooth projective model of
![]() $C$
would be isomorphic to
$C$
would be isomorphic to
![]() $\mathbb{P}_{k}^{1}$
; since the fiber of
$\mathbb{P}_{k}^{1}$
; since the fiber of
![]() $\unicode[STIX]{x1D70C}$
over a general
$\unicode[STIX]{x1D70C}$
over a general
![]() $k$
-rational point of
$k$
-rational point of
![]() $C$
is isomorphic to
$C$
is isomorphic to
![]() $\mathbb{A}_{k}^{1}$
, its closure in
$\mathbb{A}_{k}^{1}$
, its closure in
![]() $\overline{X}$
would intersect the boundary
$\overline{X}$
would intersect the boundary
![]() $\overline{X}\setminus X\simeq B$
in a unique point, necessarily
$\overline{X}\setminus X\simeq B$
in a unique point, necessarily
![]() $k$
-rational, in contradiction with the choice of
$k$
-rational, in contradiction with the choice of
![]() $B$
.
$B$
.
In contrast, for a suitable finite extension
![]() $k\subset k^{\prime }$
, the surface
$k\subset k^{\prime }$
, the surface
![]() $X_{k^{\prime }}$
becomes isomorphic to the complement of the diagonal in
$X_{k^{\prime }}$
becomes isomorphic to the complement of the diagonal in
![]() $\overline{X}_{k^{\prime }}\simeq \mathbb{P}_{k^{\prime }}^{1}\times \mathbb{P}_{k^{\prime }}^{1}$
and hence, it admits at least two distinct
$\overline{X}_{k^{\prime }}\simeq \mathbb{P}_{k^{\prime }}^{1}\times \mathbb{P}_{k^{\prime }}^{1}$
and hence, it admits at least two distinct
![]() $\mathbb{A}^{1}$
-fibrations over
$\mathbb{A}^{1}$
-fibrations over
![]() $\mathbb{P}_{k^{\prime }}^{1}$
, induced by the restriction of the first and second projections from
$\mathbb{P}_{k^{\prime }}^{1}$
, induced by the restriction of the first and second projections from
![]() $\overline{X}_{k^{\prime }}$
. Furthermore, since
$\overline{X}_{k^{\prime }}$
. Furthermore, since
![]() $X_{k^{\prime }}$
is isomorphic to the smooth affine quadric in
$X_{k^{\prime }}$
is isomorphic to the smooth affine quadric in
![]() $\mathbb{A}_{k^{\prime }}^{3}=\text{Spec}(k^{\prime }[u,v,w])$
with equation
$\mathbb{A}_{k^{\prime }}^{3}=\text{Spec}(k^{\prime }[u,v,w])$
with equation
![]() $uv-w^{2}=1$
, it also admits two distinct
$uv-w^{2}=1$
, it also admits two distinct
![]() $\mathbb{A}^{1}$
-fibrations over
$\mathbb{A}^{1}$
-fibrations over
![]() $\mathbb{A}_{k^{\prime }}^{1}$
, induced by the restrictions of the projections
$\mathbb{A}_{k^{\prime }}^{1}$
, induced by the restrictions of the projections
![]() $\text{pr}_{u}$
and
$\text{pr}_{u}$
and
![]() $\text{pr}_{v}$
.
$\text{pr}_{v}$
.
1.3 Existence of
 $\mathbb{A}^{1}$
-fibrations defined over the base field
$\mathbb{A}^{1}$
-fibrations defined over the base field
1.3.1. The previous example illustrates the general fact that if
![]() $X$
is a smooth geometrically connected affine surface with
$X$
is a smooth geometrically connected affine surface with
![]() $\unicode[STIX]{x1D705}(X)<0$
which does not admit any
$\unicode[STIX]{x1D705}(X)<0$
which does not admit any
![]() $\mathbb{A}^{1}$
-fibration, then there exists a finite extension
$\mathbb{A}^{1}$
-fibration, then there exists a finite extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
such that
$k$
such that
![]() $X_{k^{\prime }}$
admits at least two
$X_{k^{\prime }}$
admits at least two
![]() $\mathbb{A}^{1}$
-fibrations of the same type, either affine or complete, with distinct general fibers. Indeed, by virtue of Theorem 2, there exists a finite extension
$\mathbb{A}^{1}$
-fibrations of the same type, either affine or complete, with distinct general fibers. Indeed, by virtue of Theorem 2, there exists a finite extension
![]() $k_{0}$
of
$k_{0}$
of
![]() $k$
such that
$k$
such that
![]() $X_{k_{0}}$
admits an
$X_{k_{0}}$
admits an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow C$
. Let
$\unicode[STIX]{x1D70C}:X_{k_{0}}\rightarrow C$
. Let
![]() $k^{\prime }$
be the Galois closure of
$k^{\prime }$
be the Galois closure of
![]() $k_{0}$
in an algebraic closure of
$k_{0}$
in an algebraic closure of
![]() $k$
and let
$k$
and let
![]() $\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
be the
$\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
be the
![]() $\mathbb{A}^{1}$
-fibration deduced from
$\mathbb{A}^{1}$
-fibration deduced from
![]() $\unicode[STIX]{x1D70C}$
. If
$\unicode[STIX]{x1D70C}$
. If
![]() $\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is globally invariant under the action of the Galois group
$\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is globally invariant under the action of the Galois group
![]() $\text{Gal}(k^{\prime }/k)$
on
$\text{Gal}(k^{\prime }/k)$
on
![]() $X_{k^{\prime }}$
, in the sense that for every
$X_{k^{\prime }}$
, in the sense that for every
![]() $\unicode[STIX]{x1D6F7}\in \text{Gal}(k^{\prime }/k)$
considered as a Galois automorphism of
$\unicode[STIX]{x1D6F7}\in \text{Gal}(k^{\prime }/k)$
considered as a Galois automorphism of
![]() $X_{k^{\prime }}$
there exists a commutative diagram
$X_{k^{\prime }}$
there exists a commutative diagram
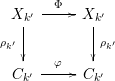
for a certain
![]() $k^{\prime }$
-automorphism
$k^{\prime }$
-automorphism
![]() $\unicode[STIX]{x1D719}$
of
$\unicode[STIX]{x1D719}$
of
![]() $C_{k^{\prime }}$
, then we would obtain a Galois action of
$C_{k^{\prime }}$
, then we would obtain a Galois action of
![]() $\text{Gal}(k^{\prime }/k)$
on
$\text{Gal}(k^{\prime }/k)$
on
![]() $C_{k^{\prime }}$
for which
$C_{k^{\prime }}$
for which
![]() $\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
becomes an equivariant morphism. Since
$\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
becomes an equivariant morphism. Since
![]() $C_{k^{\prime }}$
is quasi-projective and
$C_{k^{\prime }}$
is quasi-projective and
![]() $\unicode[STIX]{x1D70C}_{k}^{\prime }$
is affine, it would follow from Galois descent that there exist a curve
$\unicode[STIX]{x1D70C}_{k}^{\prime }$
is affine, it would follow from Galois descent that there exist a curve
![]() $\tilde{C}$
defined over
$\tilde{C}$
defined over
![]() $k$
and a morphism
$k$
and a morphism
![]() $q:X\rightarrow \tilde{C}$
defined over
$q:X\rightarrow \tilde{C}$
defined over
![]() $k$
such that
$k$
such that
![]() $\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is obtained from
$\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is obtained from
![]() $q$
by the base change
$q$
by the base change
![]() $\text{Spec}(k^{\prime })\rightarrow \text{Spec}(k)$
. Since by virtue of Example 1 the affine line does not have any nontrivial form, the generic fiber of
$\text{Spec}(k^{\prime })\rightarrow \text{Spec}(k)$
. Since by virtue of Example 1 the affine line does not have any nontrivial form, the generic fiber of
![]() $q$
would be isomorphic to the affine line over the field of rational functions of
$q$
would be isomorphic to the affine line over the field of rational functions of
![]() $\tilde{C}$
and so,
$\tilde{C}$
and so,
![]() $q:X\rightarrow \tilde{C}$
would be an
$q:X\rightarrow \tilde{C}$
would be an
![]() $\mathbb{A}^{1}$
-fibration defined over
$\mathbb{A}^{1}$
-fibration defined over
![]() $k$
, in contradiction with our hypothesis. So there exists at least an element
$k$
, in contradiction with our hypothesis. So there exists at least an element
![]() $\unicode[STIX]{x1D6F7}\in \text{Gal}(k^{\prime }/k)$
considered as a
$\unicode[STIX]{x1D6F7}\in \text{Gal}(k^{\prime }/k)$
considered as a
![]() $k$
-automorphism of
$k$
-automorphism of
![]() $X_{k^{\prime }}$
such that the
$X_{k^{\prime }}$
such that the
![]() $\mathbb{A}^{1}$
-fibrations
$\mathbb{A}^{1}$
-fibrations
![]() $\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
and
$\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
and
![]() $\unicode[STIX]{x1D70C}_{k^{\prime }}\circ \unicode[STIX]{x1D719}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
have distinct general fibers.
$\unicode[STIX]{x1D70C}_{k^{\prime }}\circ \unicode[STIX]{x1D719}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
have distinct general fibers.
Arguing backward, we obtain the following criterion:
Proposition 4. Let
![]() $X$
be a smooth geometrically connected affine surface with
$X$
be a smooth geometrically connected affine surface with
![]() $\unicode[STIX]{x1D705}(X)<0$
. If there exists a finite Galois extension
$\unicode[STIX]{x1D705}(X)<0$
. If there exists a finite Galois extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
such that
$k$
such that
![]() $X_{k^{\prime }}$
admits a unique
$X_{k^{\prime }}$
admits a unique
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
up to composition by automorphisms of
$\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
up to composition by automorphisms of
![]() $C_{k^{\prime }}$
, then
$C_{k^{\prime }}$
, then
![]() $\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is obtained by base extension from an
$\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is obtained by base extension from an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow C$
defined over
$\unicode[STIX]{x1D70C}:X\rightarrow C$
defined over
![]() $k$
.
$k$
.
Corollary 5. A smooth geometrically connected irrational affine surface
![]() $X$
has negative Kodaira dimension if and only if it admits an
$X$
has negative Kodaira dimension if and only if it admits an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow C$
over a smooth irrational curve
$\unicode[STIX]{x1D70C}:X\rightarrow C$
over a smooth irrational curve
![]() $C$
defined over the base field
$C$
defined over the base field
![]() $k$
. Furthermore for every extension
$k$
. Furthermore for every extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
,
$k$
,
![]() $\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is the unique
$\unicode[STIX]{x1D70C}_{k^{\prime }}:X_{k^{\prime }}\rightarrow C_{k^{\prime }}$
is the unique
![]() $\mathbb{A}^{1}$
-fibration on
$\mathbb{A}^{1}$
-fibration on
![]() $X_{k^{\prime }}$
up to composition by automorphisms of
$X_{k^{\prime }}$
up to composition by automorphisms of
![]() $C_{k^{\prime }}$
.
$C_{k^{\prime }}$
.
Proof. Uniqueness is clear since otherwise
![]() $C_{k^{\prime }}$
would be dominated by a general fiber of another
$C_{k^{\prime }}$
would be dominated by a general fiber of another
![]() $\mathbb{A}^{1}$
-fibration on
$\mathbb{A}^{1}$
-fibration on
![]() $X_{k^{\prime }}$
, and hence would be rational, implying in turn the rationality of
$X_{k^{\prime }}$
, and hence would be rational, implying in turn the rationality of
![]() $X$
. By virtue of Theorem 2, there exist a finite Galois extension
$X$
. By virtue of Theorem 2, there exist a finite Galois extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
and an
$k$
and an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C^{\prime }$
over a smooth curve
$\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C^{\prime }$
over a smooth curve
![]() $C^{\prime }$
. The latter is irrational as
$C^{\prime }$
. The latter is irrational as
![]() $X$
is irrational, which implies that
$X$
is irrational, which implies that
![]() $\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C^{\prime }$
is the unique
$\unicode[STIX]{x1D70C}^{\prime }:X_{k^{\prime }}\rightarrow C^{\prime }$
is the unique
![]() $\mathbb{A}^{1}$
-fibration on
$\mathbb{A}^{1}$
-fibration on
![]() $X_{k^{\prime }}$
. So
$X_{k^{\prime }}$
. So
![]() $\unicode[STIX]{x1D70C}^{\prime }$
descend to an
$\unicode[STIX]{x1D70C}^{\prime }$
descend to an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow C$
over a smooth irrational curve
$\unicode[STIX]{x1D70C}:X\rightarrow C$
over a smooth irrational curve
![]() $C$
defined over
$C$
defined over
![]() $k$
.◻
$k$
.◻
The following example shows that the irrationality hypothesis cannot be weakened to the property that
![]() $X$
is geometrically rational but not
$X$
is geometrically rational but not
![]() $k$
-rational.
$k$
-rational.
Example 6. Let
![]() $a\in \mathbb{Q}$
be a rational number which is not a cube and let
$a\in \mathbb{Q}$
be a rational number which is not a cube and let
![]() $S=S_{a}\subset \mathbb{P}_{\mathbb{Q}}^{3}=\text{Proj}_{\mathbb{Q}}(\mathbb{Q}[x,y,z,t])$
be the smooth cubic surface defined by the equation
$S=S_{a}\subset \mathbb{P}_{\mathbb{Q}}^{3}=\text{Proj}_{\mathbb{Q}}(\mathbb{Q}[x,y,z,t])$
be the smooth cubic surface defined by the equation
![]() $x^{3}+y^{3}+z^{3}+at^{3}=0$
. All lines on
$x^{3}+y^{3}+z^{3}+at^{3}=0$
. All lines on
![]() $S$
are defined over the splitting field
$S$
are defined over the splitting field
![]() $K$
of the polynomial
$K$
of the polynomial
![]() $u^{3}+a\in \mathbb{Q}[u]$
, and one checks by direct computation that no orbit of the action of the Galois group
$u^{3}+a\in \mathbb{Q}[u]$
, and one checks by direct computation that no orbit of the action of the Galois group
![]() $\text{Gal}(K/\mathbb{Q})\simeq \mathfrak{S}_{3}$
on
$\text{Gal}(K/\mathbb{Q})\simeq \mathfrak{S}_{3}$
on
![]() $S_{K}$
consists of a disjoint union of such lines. It follows that the Picard number
$S_{K}$
consists of a disjoint union of such lines. It follows that the Picard number
![]() $\unicode[STIX]{x1D70C}(S)$
of
$\unicode[STIX]{x1D70C}(S)$
of
![]() $S$
is equal to
$S$
is equal to
![]() $1$
, hence by Segree–Manin Theorem that
$1$
, hence by Segree–Manin Theorem that
![]() $S$
is rational but not
$S$
is rational but not
![]() $\mathbb{Q}$
-rational (see e.g., [Reference Kollár, Smith and Corti12, Exercise 2.18 and Theorem 2.1]). Let
$\mathbb{Q}$
-rational (see e.g., [Reference Kollár, Smith and Corti12, Exercise 2.18 and Theorem 2.1]). Let
![]() $H=\left\{x+y=0\right\}\subset \mathbb{P}_{\mathbb{Q}}^{3}$
be the tangent hyperplane to
$H=\left\{x+y=0\right\}\subset \mathbb{P}_{\mathbb{Q}}^{3}$
be the tangent hyperplane to
![]() $S$
at the point
$S$
at the point
![]() $p=\left[1:-1:0:0\right]$
and let
$p=\left[1:-1:0:0\right]$
and let
![]() $X=S\setminus (H\cap S)$
. So
$X=S\setminus (H\cap S)$
. So
![]() $X$
is a smooth affine surface defined over
$X$
is a smooth affine surface defined over
![]() $\mathbb{Q}$
, and since the intersection of
$\mathbb{Q}$
, and since the intersection of
![]() $H_{\mathbb{C}}$
with
$H_{\mathbb{C}}$
with
![]() $S_{\mathbb{C}}$
consists of three lines meeting at the Eckardt point
$S_{\mathbb{C}}$
consists of three lines meeting at the Eckardt point
![]() $p$
, one checks easily that
$p$
, one checks easily that
![]() $\unicode[STIX]{x1D705}(X)=\unicode[STIX]{x1D705}(X_{\mathbb{C}})=-\infty$
. Thus
$\unicode[STIX]{x1D705}(X)=\unicode[STIX]{x1D705}(X_{\mathbb{C}})=-\infty$
. Thus
![]() $X_{\mathbb{C}}$
admits an
$X_{\mathbb{C}}$
admits an
![]() $\mathbb{A}^{1}$
-fibration by virtue of [Reference Miyanishi and Sugie14], but we claim that
$\mathbb{A}^{1}$
-fibration by virtue of [Reference Miyanishi and Sugie14], but we claim that
![]() $X$
does not admit any such fibration defined over
$X$
does not admit any such fibration defined over
![]() $\mathbb{Q}$
. Indeed, suppose on the contrary that
$\mathbb{Q}$
. Indeed, suppose on the contrary that
![]() $\unicode[STIX]{x1D70B}:X\rightarrow C$
is an
$\unicode[STIX]{x1D70B}:X\rightarrow C$
is an
![]() $\mathbb{A}^{1}$
-fibration over a smooth curve defined over
$\mathbb{A}^{1}$
-fibration over a smooth curve defined over
![]() $\mathbb{Q}$
. Since
$\mathbb{Q}$
. Since
![]() $C$
is geometrically rational and contains a
$C$
is geometrically rational and contains a
![]() $\mathbb{Q}$
-rational point, for instance the image by
$\mathbb{Q}$
-rational point, for instance the image by
![]() $\unicode[STIX]{x1D70B}$
of the point
$\unicode[STIX]{x1D70B}$
of the point
![]() $[0:-1:1:0]\in X(\mathbb{Q})$
, it is
$[0:-1:1:0]\in X(\mathbb{Q})$
, it is
![]() $\mathbb{Q}$
-rational. But then
$\mathbb{Q}$
-rational. But then
![]() $X$
whence
$X$
whence
![]() $S$
would be
$S$
would be
![]() $\mathbb{Q}$
-rational, a contradiction.
$\mathbb{Q}$
-rational, a contradiction.
2 Families of
 $\mathbb{A}^{1}$
-ruled affine surfaces
$\mathbb{A}^{1}$
-ruled affine surfaces
2.1 Existence of étale
 $\mathbb{A}^{1}$
-cylinders
$\mathbb{A}^{1}$
-cylinders
This subsection is devoted to the proof of the following:
Theorem 7. Let
![]() $X$
and
$X$
and
![]() $S$
be normal algebraic varieties defined over a field
$S$
be normal algebraic varieties defined over a field
![]() $k$
of infinite transcendence degree over
$k$
of infinite transcendence degree over
![]() $\mathbb{Q}$
, and let
$\mathbb{Q}$
, and let
![]() $f:X\rightarrow S$
be a dominant affine morphism with the property that for a general closed point
$f:X\rightarrow S$
be a dominant affine morphism with the property that for a general closed point
![]() $s\in S$
, the fiber
$s\in S$
, the fiber
![]() $X_{s}$
is a smooth geometrically connected affine surface with negative Kodaira dimension. Then there exist an open subset
$X_{s}$
is a smooth geometrically connected affine surface with negative Kodaira dimension. Then there exist an open subset
![]() $S_{\ast }\subset S$
, a finite étale morphism
$S_{\ast }\subset S$
, a finite étale morphism
![]() $T\rightarrow S_{\ast }$
and a normal
$T\rightarrow S_{\ast }$
and a normal
![]() $T$
-scheme
$T$
-scheme
![]() $h:Y\rightarrow T$
such that
$h:Y\rightarrow T$
such that
![]() $f_{T}=\text{p}r_{T}:X_{T}=X\times _{S_{\ast }}T\rightarrow T$
factors as
$f_{T}=\text{p}r_{T}:X_{T}=X\times _{S_{\ast }}T\rightarrow T$
factors as
where
![]() $\unicode[STIX]{x1D70C}:X_{T}\rightarrow Y$
is an
$\unicode[STIX]{x1D70C}:X_{T}\rightarrow Y$
is an
![]() $\mathbb{A}^{1}$
-fibration.
$\mathbb{A}^{1}$
-fibration.
Proof. Shrinking
![]() $S$
if necessary, we may assume that
$S$
if necessary, we may assume that
![]() $S$
is affine, that
$S$
is affine, that
![]() $f:X\rightarrow S$
is smooth and that
$f:X\rightarrow S$
is smooth and that
![]() $\unicode[STIX]{x1D705}(X_{s})<0$
for every closed point
$\unicode[STIX]{x1D705}(X_{s})<0$
for every closed point
![]() $s\in S$
. It is enough to show that the fiber
$s\in S$
. It is enough to show that the fiber
![]() $X_{\unicode[STIX]{x1D702}}$
of
$X_{\unicode[STIX]{x1D702}}$
of
![]() $f$
over the generic point
$f$
over the generic point
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $S$
is geometrically connected, with negative Kodaira dimension. Indeed, if so, then by Theorem 2 above, there exist a finite extension
$S$
is geometrically connected, with negative Kodaira dimension. Indeed, if so, then by Theorem 2 above, there exist a finite extension
![]() $L$
of
$L$
of
![]() $K=\text{Frac}(\unicode[STIX]{x1D6E4}(S,{\mathcal{O}}_{S}))$
and an
$K=\text{Frac}(\unicode[STIX]{x1D6E4}(S,{\mathcal{O}}_{S}))$
and an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)\rightarrow C$
onto a smooth curve
$\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)\rightarrow C$
onto a smooth curve
![]() $C$
defined over
$C$
defined over
![]() $L$
. Letting
$L$
. Letting
![]() $T$
be the normalization of
$T$
be the normalization of
![]() $S$
in
$S$
in
![]() $L$
and shrinking
$L$
and shrinking
![]() $T$
again if necessary, we obtain a finite étale morphism
$T$
again if necessary, we obtain a finite étale morphism
![]() $T\rightarrow S$
such that the generic fiber of
$T\rightarrow S$
such that the generic fiber of
![]() $\text{pr}_{T}:X_{T}\rightarrow T$
is isomorphic to the
$\text{pr}_{T}:X_{T}\rightarrow T$
is isomorphic to the
![]() $\mathbb{A}^{1}$
-fibered surface
$\mathbb{A}^{1}$
-fibered surface
![]() $\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)\rightarrow C$
and then the assertion follows from Lemma 8 below.
$\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\times _{\text{Spec}(K)}\text{Spec}(L)\rightarrow C$
and then the assertion follows from Lemma 8 below.
The properties of being geometrically connectedness and having negative Kodaira dimension are invariant under finite algebraic extensions of the base field. So letting
![]() $\overline{k}$
be an algebraic closure of
$\overline{k}$
be an algebraic closure of
![]() $k$
, it is enough to show that the generic fiber of the induced morphism
$k$
, it is enough to show that the generic fiber of the induced morphism
![]() $f_{\overline{k}}:X_{\overline{k}}\rightarrow S_{\overline{k}}$
is geometrically connected, of negative Kodaira dimension. We may thus assume from now on that
$f_{\overline{k}}:X_{\overline{k}}\rightarrow S_{\overline{k}}$
is geometrically connected, of negative Kodaira dimension. We may thus assume from now on that
![]() $k$
is algebraically closed. Since
$k$
is algebraically closed. Since
![]() $X$
and
$X$
and
![]() $S$
are affine and of finite type over
$S$
are affine and of finite type over
![]() $k$
, there exist a subfield
$k$
, there exist a subfield
![]() $k_{0}$
of
$k_{0}$
of
![]() $k$
of finite transcendence degree over
$k$
of finite transcendence degree over
![]() $\mathbb{Q}$
, and a smooth morphism
$\mathbb{Q}$
, and a smooth morphism
![]() $f_{0}:X_{0}\rightarrow S_{0}$
of
$f_{0}:X_{0}\rightarrow S_{0}$
of
![]() $k_{0}$
-varieties such that
$k_{0}$
-varieties such that
![]() $f:X\rightarrow S$
is obtained from
$f:X\rightarrow S$
is obtained from
![]() $f_{0}:X_{0}\rightarrow S_{0}$
by the base extension
$f_{0}:X_{0}\rightarrow S_{0}$
by the base extension
![]() $\text{Spec}\left(k\right)\rightarrow \text{Spec}(k_{0})$
. The field
$\text{Spec}\left(k\right)\rightarrow \text{Spec}(k_{0})$
. The field
![]() $K_{0}=\text{Frac}(\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}}))$
has finite transcendence degree over
$K_{0}=\text{Frac}(\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}}))$
has finite transcendence degree over
![]() $\mathbb{Q}$
and hence, it admits a
$\mathbb{Q}$
and hence, it admits a
![]() $k_{0}$
-embedding
$k_{0}$
-embedding
![]() $\unicode[STIX]{x1D709}:K_{0}{\hookrightarrow}k$
. Letting
$\unicode[STIX]{x1D709}:K_{0}{\hookrightarrow}k$
. Letting
![]() $(X_{0})_{\unicode[STIX]{x1D702}_{0}}$
be the fiber of
$(X_{0})_{\unicode[STIX]{x1D702}_{0}}$
be the fiber of
![]() $f_{0}$
over the generic point
$f_{0}$
over the generic point
![]() $\unicode[STIX]{x1D702}_{0}:\text{Spec}(K_{0})\rightarrow S_{0}$
of
$\unicode[STIX]{x1D702}_{0}:\text{Spec}(K_{0})\rightarrow S_{0}$
of
![]() $S_{0}$
, the composition
$S_{0}$
, the composition
![]() $\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}}){\hookrightarrow}K_{0}{\hookrightarrow}k$
induces a
$\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}}){\hookrightarrow}K_{0}{\hookrightarrow}k$
induces a
![]() $k$
-homomorphism
$k$
-homomorphism
![]() $\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}})\otimes _{k_{0}}k\rightarrow k$
defining a closed point
$\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}})\otimes _{k_{0}}k\rightarrow k$
defining a closed point
![]() $s:\text{Spec}(k)\rightarrow \text{Spec}(\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}})\otimes _{k_{0}}k)=S$
of
$s:\text{Spec}(k)\rightarrow \text{Spec}(\unicode[STIX]{x1D6E4}(S_{0},{\mathcal{O}}_{S_{0}})\otimes _{k_{0}}k)=S$
of
![]() $S$
for which we obtain the following commutative diagram
$S$
for which we obtain the following commutative diagram
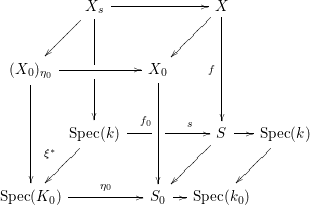
The bottom square of the cube being Cartesian by construction, we deduce that
Since by assumption,
![]() $X_{s}$
is geometrically connected with
$X_{s}$
is geometrically connected with
![]() $\unicode[STIX]{x1D705}(X_{s})<0$
, we conclude that
$\unicode[STIX]{x1D705}(X_{s})<0$
, we conclude that
![]() $(X_{0})_{\unicode[STIX]{x1D702}_{0}}$
is geometrically connected and has negative Kodaira dimension. This implies in turn that
$(X_{0})_{\unicode[STIX]{x1D702}_{0}}$
is geometrically connected and has negative Kodaira dimension. This implies in turn that
![]() $X_{\unicode[STIX]{x1D702}}$
is geometrically connected and that
$X_{\unicode[STIX]{x1D702}}$
is geometrically connected and that
![]() $\unicode[STIX]{x1D705}(X_{\unicode[STIX]{x1D702}})<0$
as desired.◻
$\unicode[STIX]{x1D705}(X_{\unicode[STIX]{x1D702}})<0$
as desired.◻
In the proof of the above theorem, we used the following lemma:
Lemma 8. Let
![]() $f:X\rightarrow S$
be a dominant affine morphism between normal varieties defined over a field
$f:X\rightarrow S$
be a dominant affine morphism between normal varieties defined over a field
![]() $k$
of characteristic zero. Then the following are equivalent:
$k$
of characteristic zero. Then the following are equivalent:
-
(a) The generic fiber
 $X_{\unicode[STIX]{x1D702}}$
of
$X_{\unicode[STIX]{x1D702}}$
of
 $f$
admits an
$f$
admits an
 $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
 $q:X_{\unicode[STIX]{x1D702}}\rightarrow C$
over a smooth curve
$q:X_{\unicode[STIX]{x1D702}}\rightarrow C$
over a smooth curve
 $C$
defined over the fraction field
$C$
defined over the fraction field
 $K$
of
$K$
of
 $S$
.
$S$
. -
(b) There exist an open subset
 $S_{\ast }$
of
$S_{\ast }$
of
 $S$
and a normal
$S$
and a normal
 $S_{\ast }$
-scheme
$S_{\ast }$
-scheme
 $h:Y\rightarrow S_{\ast }$
of relative dimension
$h:Y\rightarrow S_{\ast }$
of relative dimension
 $1$
such that the restriction of
$1$
such that the restriction of
 $f$
to
$f$
to
 $V=f^{-1}(S_{\ast })$
factors as
$V=f^{-1}(S_{\ast })$
factors as
 $f\mid _{V}=h\circ \unicode[STIX]{x1D70C}:V\rightarrow Y\rightarrow S_{\ast }$
where
$f\mid _{V}=h\circ \unicode[STIX]{x1D70C}:V\rightarrow Y\rightarrow S_{\ast }$
where
 $\unicode[STIX]{x1D70C}:V\rightarrow Y$
is an
$\unicode[STIX]{x1D70C}:V\rightarrow Y$
is an
 $\mathbb{A}^{1}$
-fibration.
$\mathbb{A}^{1}$
-fibration.
Proof. If (b) holds then letting
![]() $L$
be the fraction field of
$L$
be the fraction field of
![]() $Y$
, we have a commutative diagram
$Y$
, we have a commutative diagram
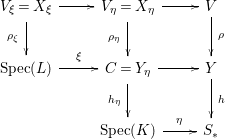
in which each square is Cartesian. It follows that
![]() $h_{\unicode[STIX]{x1D702}}:C\rightarrow \text{Spec}(K)$
is a normal whence smooth curve defined over
$h_{\unicode[STIX]{x1D702}}:C\rightarrow \text{Spec}(K)$
is a normal whence smooth curve defined over
![]() $K$
and that
$K$
and that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D702}}:X_{\unicode[STIX]{x1D702}}\rightarrow C$
is an
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D702}}:X_{\unicode[STIX]{x1D702}}\rightarrow C$
is an
![]() $\mathbb{A}^{1}$
-fibration. Conversely, suppose that
$\mathbb{A}^{1}$
-fibration. Conversely, suppose that
![]() $X_{\unicode[STIX]{x1D702}}$
admits an
$X_{\unicode[STIX]{x1D702}}$
admits an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $q:X_{\unicode[STIX]{x1D702}}\rightarrow C$
and let
$q:X_{\unicode[STIX]{x1D702}}\rightarrow C$
and let
![]() $\overline{C}$
be a smooth projective model of
$\overline{C}$
be a smooth projective model of
![]() $C$
over
$C$
over
![]() $K$
. Then there exist an open subset
$K$
. Then there exist an open subset
![]() $S_{0}$
of
$S_{0}$
of
![]() $S$
and a projective
$S$
and a projective
![]() $S_{0}$
-scheme
$S_{0}$
-scheme
![]() $h:Y\rightarrow S_{0}$
whose generic fiber is isomorphic to
$h:Y\rightarrow S_{0}$
whose generic fiber is isomorphic to
![]() $\overline{C}$
. After shrinking
$\overline{C}$
. After shrinking
![]() $S_{0}$
if necessary, the rational map
$S_{0}$
if necessary, the rational map
![]() $\unicode[STIX]{x1D70C}:V{\dashrightarrow}Y$
of
$\unicode[STIX]{x1D70C}:V{\dashrightarrow}Y$
of
![]() $S_{0}$
-schemes induced by
$S_{0}$
-schemes induced by
![]() $q$
becomes a morphism and we obtain a factorization
$q$
becomes a morphism and we obtain a factorization
![]() $f\mid _{V}=h\circ \unicode[STIX]{x1D70C}$
. By construction, the generic fiber
$f\mid _{V}=h\circ \unicode[STIX]{x1D70C}$
. By construction, the generic fiber
![]() $V_{\unicode[STIX]{x1D709}}$
of
$V_{\unicode[STIX]{x1D709}}$
of
![]() $\unicode[STIX]{x1D70C}:V\rightarrow Y$
is isomorphic to
$\unicode[STIX]{x1D70C}:V\rightarrow Y$
is isomorphic to
since
![]() $V\times _{Y}C\simeq V_{\unicode[STIX]{x1D702}}\simeq X_{\unicode[STIX]{x1D702}}$
and
$V\times _{Y}C\simeq V_{\unicode[STIX]{x1D702}}\simeq X_{\unicode[STIX]{x1D702}}$
and
![]() $\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\rightarrow C{\hookrightarrow}\overline{C}$
is an
$\unicode[STIX]{x1D70C}:X_{\unicode[STIX]{x1D702}}\rightarrow C{\hookrightarrow}\overline{C}$
is an
![]() $\mathbb{A}^{1}$
-fibration. So
$\mathbb{A}^{1}$
-fibration. So
![]() $\unicode[STIX]{x1D70C}:V\rightarrow Y$
is an
$\unicode[STIX]{x1D70C}:V\rightarrow Y$
is an
![]() $\mathbb{A}^{1}$
-fibration.◻
$\mathbb{A}^{1}$
-fibration.◻
Example 9. Let
![]() $R=\mathbb{C}[s^{\pm 1},t^{\pm 1}]$
,
$R=\mathbb{C}[s^{\pm 1},t^{\pm 1}]$
,
![]() $S=\text{Spec}(R)$
and let
$S=\text{Spec}(R)$
and let
![]() $D$
be the relatively ample divisor in
$D$
be the relatively ample divisor in
![]() $\mathbb{P}_{S}^{2}=\text{Proj}_{R}(R[x,y,z])$
defined by the equation
$\mathbb{P}_{S}^{2}=\text{Proj}_{R}(R[x,y,z])$
defined by the equation
![]() $x^{2}+sy^{2}+tz^{2}=0$
. The restriction
$x^{2}+sy^{2}+tz^{2}=0$
. The restriction
![]() $h:X=\mathbb{P}_{S}^{2}\setminus D\rightarrow S$
of the structure morphism defines a family of smooth affine surfaces with the property that for every closed point
$h:X=\mathbb{P}_{S}^{2}\setminus D\rightarrow S$
of the structure morphism defines a family of smooth affine surfaces with the property that for every closed point
![]() $s\in S$
,
$s\in S$
,
![]() $X_{s}$
is isomorphic to the complement in
$X_{s}$
is isomorphic to the complement in
![]() $\mathbb{P}_{\mathbb{C}}^{2}$
of the smooth conic
$\mathbb{P}_{\mathbb{C}}^{2}$
of the smooth conic
![]() $D_{s}$
. In particular,
$D_{s}$
. In particular,
![]() $X_{s}$
admits a continuum of pairwise distinct
$X_{s}$
admits a continuum of pairwise distinct
![]() $\mathbb{A}^{1}$
-fibrations
$\mathbb{A}^{1}$
-fibrations
![]() $X_{s}\rightarrow \mathbb{A}_{\mathbb{C}}^{1}$
, induced by the restrictions to
$X_{s}\rightarrow \mathbb{A}_{\mathbb{C}}^{1}$
, induced by the restrictions to
![]() $X_{s}$
of the rational pencils on
$X_{s}$
of the rational pencils on
![]() $\mathbb{P}_{\mathbb{C}}^{2}$
generated by
$\mathbb{P}_{\mathbb{C}}^{2}$
generated by
![]() $D_{s}$
and twice its tangent line at an arbitrary closed point
$D_{s}$
and twice its tangent line at an arbitrary closed point
![]() $p_{s}\in D_{s}$
. On the other hand, the fiber of
$p_{s}\in D_{s}$
. On the other hand, the fiber of
![]() $D$
over the generic point
$D$
over the generic point
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $S$
is a conic without
$S$
is a conic without
![]() $\mathbb{C}(s,t)$
-rational point in
$\mathbb{C}(s,t)$
-rational point in
![]() $\mathbb{P}_{\mathbb{C}(s,t)}^{2}$
and hence, we conclude by a similar argument as in Example 3 that
$\mathbb{P}_{\mathbb{C}(s,t)}^{2}$
and hence, we conclude by a similar argument as in Example 3 that
![]() $X_{\unicode[STIX]{x1D702}}$
does not admit any
$X_{\unicode[STIX]{x1D702}}$
does not admit any
![]() $\mathbb{A}^{1}$
-fibration defined over
$\mathbb{A}^{1}$
-fibration defined over
![]() $\mathbb{C}(s,t)$
. Therefore there is no open subset
$\mathbb{C}(s,t)$
. Therefore there is no open subset
![]() $S_{\ast }$
of
$S_{\ast }$
of
![]() $S$
over which
$S$
over which
![]() $h$
can be factored through an
$h$
can be factored through an
![]() $\mathbb{A}^{1}$
-fibration.
$\mathbb{A}^{1}$
-fibration.
2.2 Deformations of irrational
 $\mathbb{A}^{1}$
-ruled affine surfaces
$\mathbb{A}^{1}$
-ruled affine surfaces
In this subsection, we consider the particular situation of a flat family
![]() $f:X\rightarrow S$
over a normal variety
$f:X\rightarrow S$
over a normal variety
![]() $S$
whose general fibers are irrational
$S$
whose general fibers are irrational
![]() $\mathbb{A}^{1}$
-ruled affine surfaces. A combination of Corollary 5 and Theorem 7 above implies that if
$\mathbb{A}^{1}$
-ruled affine surfaces. A combination of Corollary 5 and Theorem 7 above implies that if
![]() $f:X\rightarrow S$
is smooth and defined over a field of infinite transcendence degree over
$f:X\rightarrow S$
is smooth and defined over a field of infinite transcendence degree over
![]() $\mathbb{Q}$
, then the generic fiber
$\mathbb{Q}$
, then the generic fiber
![]() $X_{\unicode[STIX]{x1D702}}$
of
$X_{\unicode[STIX]{x1D702}}$
of
![]() $f$
is
$f$
is
![]() $\mathbb{A}^{1}$
-ruled. Equivalently, there exist an open subset
$\mathbb{A}^{1}$
-ruled. Equivalently, there exist an open subset
![]() $S_{\ast }\subset S$
and a normal
$S_{\ast }\subset S$
and a normal
![]() $S_{\ast }$
-scheme
$S_{\ast }$
-scheme
![]() $h:Y\rightarrow S_{\ast }$
such that the restriction of
$h:Y\rightarrow S_{\ast }$
such that the restriction of
![]() $f$
to
$f$
to
![]() $X_{\ast }=X\times _{S}S_{\ast }$
factors through an
$X_{\ast }=X\times _{S}S_{\ast }$
factors through an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X_{\ast }\rightarrow Y$
(see Lemma 8). The restriction of
$\unicode[STIX]{x1D70C}:X_{\ast }\rightarrow Y$
(see Lemma 8). The restriction of
![]() $\unicode[STIX]{x1D70C}$
to the fiber of
$\unicode[STIX]{x1D70C}$
to the fiber of
![]() $f$
over a general closed point
$f$
over a general closed point
![]() $s\in S_{0}$
is an
$s\in S_{0}$
is an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
over the normal, whence smooth, curve
$\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
over the normal, whence smooth, curve
![]() $Y_{s}$
. Since
$Y_{s}$
. Since
![]() $X_{s}$
is irrational,
$X_{s}$
is irrational,
![]() $Y_{s}$
is irrational, and so
$Y_{s}$
is irrational, and so
![]() $\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
is the unique
$\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
is the unique
![]() $\mathbb{A}^{1}$
-fibration on
$\mathbb{A}^{1}$
-fibration on
![]() $X_{s}$
up to composition by automorphisms of
$X_{s}$
up to composition by automorphisms of
![]() $Y_{s}$
. So in this case, we can identify
$Y_{s}$
. So in this case, we can identify
![]() $\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
with the Maximally Rationally Connected fibration (MRC-fibration)
$\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
with the Maximally Rationally Connected fibration (MRC-fibration)
![]() $\unicode[STIX]{x1D719}:\overline{X}_{s}{\dashrightarrow}Y_{s}$
of a smooth projective model
$\unicode[STIX]{x1D719}:\overline{X}_{s}{\dashrightarrow}Y_{s}$
of a smooth projective model
![]() $\overline{X}_{s}$
of
$\overline{X}_{s}$
of
![]() $X_{s}$
in the sense of [Reference Kollár11, IV.5]: recall that
$X_{s}$
in the sense of [Reference Kollár11, IV.5]: recall that
![]() $\unicode[STIX]{x1D719}$
is unique, characterized by the property that its general fibers are rationally connected and that for a very general point
$\unicode[STIX]{x1D719}$
is unique, characterized by the property that its general fibers are rationally connected and that for a very general point
![]() $y\in Y_{s}$
any rational curve in
$y\in Y_{s}$
any rational curve in
![]() $\overline{X}_{s}$
which meets
$\overline{X}_{s}$
which meets
![]() $\overline{X}_{y}$
is actually contained in
$\overline{X}_{y}$
is actually contained in
![]() $\overline{X}_{y}$
. The
$\overline{X}_{y}$
. The
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X_{\ast }\rightarrow Y$
can therefore be re-interpreted as being the MRC-fibration of a relative smooth projective model
$\unicode[STIX]{x1D70C}:X_{\ast }\rightarrow Y$
can therefore be re-interpreted as being the MRC-fibration of a relative smooth projective model
![]() $\overline{X}$
of
$\overline{X}$
of
![]() $X$
over
$X$
over
![]() $S$
.
$S$
.
Reversing the argument, general existence and uniqueness results for MRC-fibrations allow actually to get rid of the smoothness hypothesis of a general fiber of
![]() $f:X\rightarrow S$
and to extend the conclusion of Theorem 7 to arbitrary base fields of characteristic zero. Namely, we obtain the following characterization:
$f:X\rightarrow S$
and to extend the conclusion of Theorem 7 to arbitrary base fields of characteristic zero. Namely, we obtain the following characterization:
Theorem 10. Let
![]() $X$
and
$X$
and
![]() $S$
be normal varieties defined over a field
$S$
be normal varieties defined over a field
![]() $k$
of characteristic zero and let
$k$
of characteristic zero and let
![]() $f:X\rightarrow S$
be a dominant affine morphism with the property that for a general closed point
$f:X\rightarrow S$
be a dominant affine morphism with the property that for a general closed point
![]() $s\in S$
, the fiber
$s\in S$
, the fiber
![]() $X_{s}$
is an irrational
$X_{s}$
is an irrational
![]() $\mathbb{A}^{1}$
-ruled surface. Then there exist a dense open subset
$\mathbb{A}^{1}$
-ruled surface. Then there exist a dense open subset
![]() $S_{\ast }$
of
$S_{\ast }$
of
![]() $S$
and a normal
$S$
and a normal
![]() $S_{\ast }$
-scheme
$S_{\ast }$
-scheme
![]() $h:Y\rightarrow S_{\ast }$
such that the restriction of
$h:Y\rightarrow S_{\ast }$
such that the restriction of
![]() $f$
to
$f$
to
![]() $X_{\ast }=X\times _{S}S_{\ast }$
factors as
$X_{\ast }=X\times _{S}S_{\ast }$
factors as
where
![]() $\unicode[STIX]{x1D70C}:X_{\ast }\rightarrow Y$
is an
$\unicode[STIX]{x1D70C}:X_{\ast }\rightarrow Y$
is an
![]() $\mathbb{A}^{1}$
-fibration.
$\mathbb{A}^{1}$
-fibration.
Proof. Shrinking
![]() $S$
if necessary, we may assume that it is smooth and that for every closed point
$S$
if necessary, we may assume that it is smooth and that for every closed point
![]() $s\in S$
,
$s\in S$
,
![]() $X_{s}$
is irrational and
$X_{s}$
is irrational and
![]() $\mathbb{A}^{1}$
-ruled, hence carrying a unique
$\mathbb{A}^{1}$
-ruled, hence carrying a unique
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{s}:X_{s}\rightarrow C_{s}$
over an irrational normal curve
$\unicode[STIX]{x1D70B}_{s}:X_{s}\rightarrow C_{s}$
over an irrational normal curve
![]() $C_{s}$
. Since
$C_{s}$
. Since
![]() $f:X\rightarrow S$
is affine, there exist a normal projective
$f:X\rightarrow S$
is affine, there exist a normal projective
![]() $S$
-scheme
$S$
-scheme
![]() $\overline{X}\rightarrow S$
and an open embedding
$\overline{X}\rightarrow S$
and an open embedding
![]() $X{\hookrightarrow}\overline{X}$
of schemes over
$X{\hookrightarrow}\overline{X}$
of schemes over
![]() $S$
. Letting
$S$
. Letting
![]() $W\rightarrow \overline{X}$
be a resolution of the singularities of
$W\rightarrow \overline{X}$
be a resolution of the singularities of
![]() $\overline{X}$
, hence in particular of those of
$\overline{X}$
, hence in particular of those of
![]() $X$
, we may assume up to shrinking
$X$
, we may assume up to shrinking
![]() $S$
again if necessary that
$S$
again if necessary that
![]() $W\rightarrow S$
is a smooth morphism. We let
$W\rightarrow S$
is a smooth morphism. We let
![]() $j:X{\dashrightarrow}W$
be the birational map of
$j:X{\dashrightarrow}W$
be the birational map of
![]() $S$
-schemes induced by the embedding
$S$
-schemes induced by the embedding
![]() $X{\hookrightarrow}\overline{X}$
. By virtue of [Reference Kollár11, Theorem 5.9], there exist an open subset
$X{\hookrightarrow}\overline{X}$
. By virtue of [Reference Kollár11, Theorem 5.9], there exist an open subset
![]() $W^{\prime }$
of
$W^{\prime }$
of
![]() $W$
, an
$W$
, an
![]() $S$
-scheme
$S$
-scheme
![]() $h:Z\rightarrow S$
and a proper morphism
$h:Z\rightarrow S$
and a proper morphism
![]() $\overline{q}:W^{\prime }\rightarrow Z$
such that for every
$\overline{q}:W^{\prime }\rightarrow Z$
such that for every
![]() $s\in S$
, the induced rational map
$s\in S$
, the induced rational map
![]() $\overline{q}_{s}:W_{s}{\dashrightarrow}Z_{s}$
is the MRC-fibration for
$\overline{q}_{s}:W_{s}{\dashrightarrow}Z_{s}$
is the MRC-fibration for
![]() $W_{s}$
. On the other hand, since
$W_{s}$
. On the other hand, since
![]() $W_{s}$
is a smooth projective model of
$W_{s}$
is a smooth projective model of
![]() $X_{s}$
, the induced rational map
$X_{s}$
, the induced rational map
![]() $\unicode[STIX]{x1D70B}_{s}:\overline{X}_{s}{\dashrightarrow}C_{s}$
is the MRC-fibration for
$\unicode[STIX]{x1D70B}_{s}:\overline{X}_{s}{\dashrightarrow}C_{s}$
is the MRC-fibration for
![]() $W_{s}$
. Consequently, for a general closed point
$W_{s}$
. Consequently, for a general closed point
![]() $z\in Z$
with
$z\in Z$
with
![]() $h(z)=s$
, the fiber
$h(z)=s$
, the fiber
![]() $W_{z}$
of
$W_{z}$
of
![]() $\overline{q}_{s}$
, which is an irreducible proper rational curve contained in
$\overline{q}_{s}$
, which is an irreducible proper rational curve contained in
![]() $W_{s}$
, must coincide with the closure of the image by
$W_{s}$
, must coincide with the closure of the image by
![]() $j$
of a general closed fiber of
$j$
of a general closed fiber of
![]() $\unicode[STIX]{x1D70B}_{s}$
. The latter being isomorphic to the affine line
$\unicode[STIX]{x1D70B}_{s}$
. The latter being isomorphic to the affine line
![]() $\mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
over the residue field
$\mathbb{A}_{\unicode[STIX]{x1D705}}^{1}$
over the residue field
![]() $\unicode[STIX]{x1D705}$
of the corresponding point of
$\unicode[STIX]{x1D705}$
of the corresponding point of
![]() $C_{s}$
, we conclude that there exists an affine open subset
$C_{s}$
, we conclude that there exists an affine open subset
![]() $U$
of
$U$
of
![]() $X$
on which the composition
$X$
on which the composition
![]() $\overline{q}\circ j:U\rightarrow Z$
is a well-defined morphism with general closed fibers isomorphic to affine lines over the corresponding residue fields. So
$\overline{q}\circ j:U\rightarrow Z$
is a well-defined morphism with general closed fibers isomorphic to affine lines over the corresponding residue fields. So
![]() $\overline{q}\circ j:U\rightarrow Z$
is an
$\overline{q}\circ j:U\rightarrow Z$
is an
![]() $\mathbb{A}^{1}$
-fibration by virtue of [Reference Kambayashi and Miyanishi9]. The generic fiber of
$\mathbb{A}^{1}$
-fibration by virtue of [Reference Kambayashi and Miyanishi9]. The generic fiber of
![]() $f:X\rightarrow S$
is thus
$f:X\rightarrow S$
is thus
![]() $\mathbb{A}^{1}$
-ruled and the assertion follows from Lemma 8 above.◻
$\mathbb{A}^{1}$
-ruled and the assertion follows from Lemma 8 above.◻
Example 11. Let
![]() $h:Y\rightarrow S$
be a smooth family of complex projective curves of genus
$h:Y\rightarrow S$
be a smooth family of complex projective curves of genus
![]() $g\geqslant 2$
over a normal affine base
$g\geqslant 2$
over a normal affine base
![]() $S$
and let
$S$
and let
![]() ${\mathcal{T}}_{Y/S}$
be the relative tangent sheaf of
${\mathcal{T}}_{Y/S}$
be the relative tangent sheaf of
![]() $h$
. Since by Riemman–Roch
$h$
. Since by Riemman–Roch
![]() $H^{0}(Y_{s},{\mathcal{T}}_{Y/S,s})=0$
and
$H^{0}(Y_{s},{\mathcal{T}}_{Y/S,s})=0$
and
![]() $\dim H^{1}(Y_{s},{\mathcal{T}}_{Y/S,s})=3g-3$
for every point
$\dim H^{1}(Y_{s},{\mathcal{T}}_{Y/S,s})=3g-3$
for every point
![]() $s\in S$
,
$s\in S$
,
![]() $h_{\ast }{\mathcal{T}}_{Y/S,s}=0$
,
$h_{\ast }{\mathcal{T}}_{Y/S,s}=0$
,
![]() $R^{1}h_{\ast }{\mathcal{T}}_{Y/S}$
is locally free of rank
$R^{1}h_{\ast }{\mathcal{T}}_{Y/S}$
is locally free of rank
![]() $3g-3$
[Reference Hartshorne4, Corollary III.12.9] and so,
$3g-3$
[Reference Hartshorne4, Corollary III.12.9] and so,
![]() $H^{1}(Y,{\mathcal{T}}_{Y/S})\simeq H^{0}(S,R^{1}h_{\ast }{\mathcal{T}}_{Y/S})$
by the Leray spectral sequence. Replacing
$H^{1}(Y,{\mathcal{T}}_{Y/S})\simeq H^{0}(S,R^{1}h_{\ast }{\mathcal{T}}_{Y/S})$
by the Leray spectral sequence. Replacing
![]() $S$
by an open subset, we may assume that
$S$
by an open subset, we may assume that
![]() $R^{1}h_{\ast }{\mathcal{T}}_{Y/S}$
admits a nowhere vanishing global section
$R^{1}h_{\ast }{\mathcal{T}}_{Y/S}$
admits a nowhere vanishing global section
![]() $\unicode[STIX]{x1D70E}$
. Via the isomorphism
$\unicode[STIX]{x1D70E}$
. Via the isomorphism
![]() $H^{1}(Y,{\mathcal{T}}_{Y/S})\simeq \text{Ext}_{Y}^{1}({\mathcal{O}}_{Y},{\mathcal{T}}_{Y/S})$
, we may interpret this section as the class of a nontrivial extension
$H^{1}(Y,{\mathcal{T}}_{Y/S})\simeq \text{Ext}_{Y}^{1}({\mathcal{O}}_{Y},{\mathcal{T}}_{Y/S})$
, we may interpret this section as the class of a nontrivial extension
![]() $0\rightarrow {\mathcal{T}}_{Y/S}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{O}}_{Y}\rightarrow 0$
of locally free sheaves over
$0\rightarrow {\mathcal{T}}_{Y/S}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{O}}_{Y}\rightarrow 0$
of locally free sheaves over
![]() $Y$
. The inclusion
$Y$
. The inclusion
![]() ${\mathcal{T}}_{Y/S}\rightarrow {\mathcal{E}}$
defines a section
${\mathcal{T}}_{Y/S}\rightarrow {\mathcal{E}}$
defines a section
![]() $D$
of the locally trivial
$D$
of the locally trivial
![]() $\mathbb{P}^{1}$
-bundle
$\mathbb{P}^{1}$
-bundle
![]() $\overline{\unicode[STIX]{x1D70C}}:\overline{X}=\text{Proj}(\text{Sym}_{{\mathcal{O}}_{Y}}{\mathcal{E}}^{\vee })\rightarrow Y$
and the nonvanishing of
$\overline{\unicode[STIX]{x1D70C}}:\overline{X}=\text{Proj}(\text{Sym}_{{\mathcal{O}}_{Y}}{\mathcal{E}}^{\vee })\rightarrow Y$
and the nonvanishing of
![]() $\unicode[STIX]{x1D70E}$
guarantees that
$\unicode[STIX]{x1D70E}$
guarantees that
![]() $D$
is the support of an
$D$
is the support of an
![]() $S$
-ample divisor. Indeed the
$S$
-ample divisor. Indeed the
![]() $S$
-ampleness of
$S$
-ampleness of
![]() $D$
is equivalent to the property that for every
$D$
is equivalent to the property that for every
![]() $s\in S$
the induced section
$s\in S$
the induced section
![]() $D_{s}$
of the
$D_{s}$
of the
![]() $\mathbb{P}^{1}$
-bundle
$\mathbb{P}^{1}$
-bundle
![]() $\overline{\unicode[STIX]{x1D70C}}_{s}:\overline{X}_{s}\rightarrow Y_{s}$
over the smooth projective curve
$\overline{\unicode[STIX]{x1D70C}}_{s}:\overline{X}_{s}\rightarrow Y_{s}$
over the smooth projective curve
![]() $Y_{s}$
is ample. Since by construction,
$Y_{s}$
is ample. Since by construction,
![]() $\overline{\unicode[STIX]{x1D70C}}_{s}\mid _{\overline{X}_{s}\setminus D_{s}}:\overline{X}_{s}\setminus D_{s}\rightarrow Y_{s}$
is a nontrivial torsor under the line bundle
$\overline{\unicode[STIX]{x1D70C}}_{s}\mid _{\overline{X}_{s}\setminus D_{s}}:\overline{X}_{s}\setminus D_{s}\rightarrow Y_{s}$
is a nontrivial torsor under the line bundle
![]() $\text{Spec}(\text{Sym}{\mathcal{T}}_{Y_{s}}^{\vee })\rightarrow Y_{s}$
, it follows that
$\text{Spec}(\text{Sym}{\mathcal{T}}_{Y_{s}}^{\vee })\rightarrow Y_{s}$
, it follows that
![]() $D_{s}$
intersects positively every section
$D_{s}$
intersects positively every section
![]() $D$
of
$D$
of
![]() $\overline{\unicode[STIX]{x1D70C}}_{s}$
except maybe
$\overline{\unicode[STIX]{x1D70C}}_{s}$
except maybe
![]() $D_{s}$
itself. On the other hand, we have
$D_{s}$
itself. On the other hand, we have
![]() $(D_{s}^{2})=-\text{deg}\,{\mathcal{T}}_{Y_{s}}=2g(Y_{s})-2>0$
, and so the ampleness of
$(D_{s}^{2})=-\text{deg}\,{\mathcal{T}}_{Y_{s}}=2g(Y_{s})-2>0$
, and so the ampleness of
![]() $D_{s}$
follows from the Nakai–Moishezon criterion and the description of the cone effective cycles on an irrational projective ruled surface given in [Reference Hartshorne4, Propositions 2.20–2.21].
$D_{s}$
follows from the Nakai–Moishezon criterion and the description of the cone effective cycles on an irrational projective ruled surface given in [Reference Hartshorne4, Propositions 2.20–2.21].
Letting
![]() $X=\overline{X}\setminus D$
, we obtain a smooth family
$X=\overline{X}\setminus D$
, we obtain a smooth family
where
![]() $\overline{\unicode[STIX]{x1D70C}}\mid _{X}:X\rightarrow Y$
is a nontrivial, locally trivial,
$\overline{\unicode[STIX]{x1D70C}}\mid _{X}:X\rightarrow Y$
is a nontrivial, locally trivial,
![]() $\mathbb{A}^{1}$
-bundle such that for every
$\mathbb{A}^{1}$
-bundle such that for every
![]() $s\in S$
,
$s\in S$
,
![]() $X_{s}$
is an affine surface with an
$X_{s}$
is an affine surface with an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
of complete type.
$\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow Y_{s}$
of complete type.
In contrast with the previous example, the following proposition shows in particular that if the total space of a family of irrational
![]() $\mathbb{A}^{1}$
-ruled affine surfaces
$\mathbb{A}^{1}$
-ruled affine surfaces
![]() $f:X\rightarrow S$
has finite divisor class group, then the induced
$f:X\rightarrow S$
has finite divisor class group, then the induced
![]() $\mathbb{A}^{1}$
-fibration on a general fiber of
$\mathbb{A}^{1}$
-fibration on a general fiber of
![]() $f:X\rightarrow S$
is necessarily of affine type.
$f:X\rightarrow S$
is necessarily of affine type.
Proposition 12. Let
![]() $X$
be a geometrically integral normal affine variety with finite divisor class group
$X$
be a geometrically integral normal affine variety with finite divisor class group
![]() $\text{Cl}(X)$
and let
$\text{Cl}(X)$
and let
![]() $f:X\rightarrow S$
be a dominant affine morphism to a normal variety
$f:X\rightarrow S$
be a dominant affine morphism to a normal variety
![]() $S$
with the property that for a general closed point
$S$
with the property that for a general closed point
![]() $s\in S$
, the fiber
$s\in S$
, the fiber
![]() $X_{s}$
is an irrational
$X_{s}$
is an irrational
![]() $\mathbb{A}^{1}$
-ruled surface, say with unique
$\mathbb{A}^{1}$
-ruled surface, say with unique
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{s}:X_{s}\rightarrow C_{s}$
. Then there exists an effective action of the additive group scheme
$\unicode[STIX]{x1D70B}_{s}:X_{s}\rightarrow C_{s}$
. Then there exists an effective action of the additive group scheme
![]() $\mathbb{G}_{a,S}$
on
$\mathbb{G}_{a,S}$
on
![]() $X$
such that for a general closed point
$X$
such that for a general closed point
![]() $s\in S$
, the
$s\in S$
, the
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{s}:X_{s}\rightarrow C_{s}$
factors through the algebraic quotient
$\unicode[STIX]{x1D70B}_{s}:X_{s}\rightarrow C_{s}$
factors through the algebraic quotient
![]() $\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow X_{s}/\!/\mathbb{G}_{a,s}=\text{Spec}(\unicode[STIX]{x1D6E4}(X_{s},{\mathcal{O}}_{X_{s}})^{\mathbb{G}_{a,s}})$
.
$\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow X_{s}/\!/\mathbb{G}_{a,s}=\text{Spec}(\unicode[STIX]{x1D6E4}(X_{s},{\mathcal{O}}_{X_{s}})^{\mathbb{G}_{a,s}})$
.
Proof. Let
![]() $f\mid _{X_{\ast }}=h\circ \unicode[STIX]{x1D70C}:X_{\ast }\stackrel{\unicode[STIX]{x1D70C}}{\longrightarrow }Y\stackrel{h}{\longrightarrow }S_{\ast }$
be as in Theorem 10. Since
$f\mid _{X_{\ast }}=h\circ \unicode[STIX]{x1D70C}:X_{\ast }\stackrel{\unicode[STIX]{x1D70C}}{\longrightarrow }Y\stackrel{h}{\longrightarrow }S_{\ast }$
be as in Theorem 10. Since
![]() $\unicode[STIX]{x1D70C}$
is an
$\unicode[STIX]{x1D70C}$
is an
![]() $\mathbb{A}^{1}$
-fibration, there exists an affine open subset
$\mathbb{A}^{1}$
-fibration, there exists an affine open subset
![]() $U\subset Y$
such that
$U\subset Y$
such that
![]() $\unicode[STIX]{x1D70C}^{-1}(U)\simeq U\times \mathbb{A}^{1}$
as schemes over
$\unicode[STIX]{x1D70C}^{-1}(U)\simeq U\times \mathbb{A}^{1}$
as schemes over
![]() $U$
. Since
$U$
. Since
![]() $\unicode[STIX]{x1D70C}^{-1}(U)$
is affine, its complement in
$\unicode[STIX]{x1D70C}^{-1}(U)$
is affine, its complement in
![]() $X$
is of pure codimension
$X$
is of pure codimension
![]() $1$
, and the finiteness of
$1$
, and the finiteness of
![]() $\text{Cl}(X)$
implies that it is actually the support of an effective principal divisor
$\text{Cl}(X)$
implies that it is actually the support of an effective principal divisor
![]() $\text{div}_{X}(a)$
for some
$\text{div}_{X}(a)$
for some
![]() $a\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
. Let
$a\in \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
. Let
![]() $\unicode[STIX]{x2202}_{0}$
be the locally nilpotent derivation of
$\unicode[STIX]{x2202}_{0}$
be the locally nilpotent derivation of
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70C}^{-1}(U),{\mathcal{O}}_{X})\simeq \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})_{a}$
corresponding to the
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70C}^{-1}(U),{\mathcal{O}}_{X})\simeq \unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})_{a}$
corresponding to the
![]() $\mathbb{G}_{a,U}$
-action by translations on the second factor. Since
$\mathbb{G}_{a,U}$
-action by translations on the second factor. Since
![]() $a$
is invertible in
$a$
is invertible in
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70C}^{-1}(U),{\mathcal{O}}_{X})$
, it belongs to the kernel of
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70C}^{-1}(U),{\mathcal{O}}_{X})$
, it belongs to the kernel of
![]() $\unicode[STIX]{x2202}_{0}$
, and the finite generation of
$\unicode[STIX]{x2202}_{0}$
, and the finite generation of
![]() $\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
guarantees that for a suitably chosen
$\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
guarantees that for a suitably chosen
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
![]() $a^{n}\unicode[STIX]{x2202}_{0}$
is a locally nilpotent derivation
$a^{n}\unicode[STIX]{x2202}_{0}$
is a locally nilpotent derivation
![]() $\unicode[STIX]{x2202}$
of
$\unicode[STIX]{x2202}$
of
![]() $\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
. By construction, the restriction of
$\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})$
. By construction, the restriction of
![]() $f$
to the dense open subset
$f$
to the dense open subset
![]() $\unicode[STIX]{x1D70C}^{-1}(U)$
of
$\unicode[STIX]{x1D70C}^{-1}(U)$
of
![]() $X$
is invariant under the corresponding
$X$
is invariant under the corresponding
![]() $\mathbb{G}_{a}$
-action, and so
$\mathbb{G}_{a}$
-action, and so
![]() $f:X\rightarrow S$
is
$f:X\rightarrow S$
is
![]() $\mathbb{G}_{a}$
-invariant. For a general closed point
$\mathbb{G}_{a}$
-invariant. For a general closed point
![]() $s\in S$
, the induced
$s\in S$
, the induced
![]() $\mathbb{G}_{a}$
-action on
$\mathbb{G}_{a}$
-action on
![]() $X_{s}$
is nontrivial, and its algebraic quotient
$X_{s}$
is nontrivial, and its algebraic quotient
![]() $\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow X_{s}/\!/\mathbb{G}_{a}=\text{Spec}(\unicode[STIX]{x1D6E4}(X_{s},{\mathcal{O}}_{X_{s}})^{\mathbb{G}_{a}})$
is a surjective
$\unicode[STIX]{x1D70C}_{s}:X_{s}\rightarrow X_{s}/\!/\mathbb{G}_{a}=\text{Spec}(\unicode[STIX]{x1D6E4}(X_{s},{\mathcal{O}}_{X_{s}})^{\mathbb{G}_{a}})$
is a surjective
![]() $\mathbb{A}^{1}$
-fibration onto a normal affine curve
$\mathbb{A}^{1}$
-fibration onto a normal affine curve
![]() $X_{s}/\!/\mathbb{G}_{a}$
. Since
$X_{s}/\!/\mathbb{G}_{a}$
. Since
![]() $C_{s}$
is irrational, the general fibers of
$C_{s}$
is irrational, the general fibers of
![]() $\unicode[STIX]{x1D70C}_{s}$
and
$\unicode[STIX]{x1D70C}_{s}$
and
![]() $\unicode[STIX]{x1D70B}_{s}$
must coincide. It follows that
$\unicode[STIX]{x1D70B}_{s}$
must coincide. It follows that
![]() $\unicode[STIX]{x1D70B}_{s}$
is
$\unicode[STIX]{x1D70B}_{s}$
is
![]() $\mathbb{G}_{a}$
-invariant, whence factors through
$\mathbb{G}_{a}$
-invariant, whence factors through
![]() $\unicode[STIX]{x1D70C}_{s}$
.◻
$\unicode[STIX]{x1D70C}_{s}$
.◻
3 Affine threefolds fibered in irrational
 $\mathbb{A}^{1}$
-ruled surfaces
$\mathbb{A}^{1}$
-ruled surfaces
In this section, we consider in more detail the case of normal complex affine threefolds
![]() $X$
admitting a fibration
$X$
admitting a fibration
![]() $f:X\rightarrow B$
by irrational
$f:X\rightarrow B$
by irrational
![]() $\mathbb{A}^{1}$
-ruled surfaces, over a smooth curve
$\mathbb{A}^{1}$
-ruled surfaces, over a smooth curve
![]() $B$
. We explain how to derive the variety
$B$
. We explain how to derive the variety
![]() $h:Y\rightarrow B$
for which
$h:Y\rightarrow B$
for which
![]() $f$
factors through an
$f$
factors through an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
from a relative minimal model program applied to a suitable projective model of
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
from a relative minimal model program applied to a suitable projective model of
![]() $X$
over
$X$
over
![]() $B$
. In the case where the divisor class group of
$B$
. In the case where the divisor class group of
![]() $X$
is finite, we provide a complete classification of such fibrations in terms of additive group actions on
$X$
is finite, we provide a complete classification of such fibrations in terms of additive group actions on
![]() $X$
.
$X$
.
3.1
 $\mathbb{A}^{1}$
-cylinders via relative minimal model program
$\mathbb{A}^{1}$
-cylinders via relative minimal model program
Let
![]() $X$
be a normal complex affine threefold and let
$X$
be a normal complex affine threefold and let
![]() $f:X\rightarrow B$
be a flat morphism onto a smooth curve
$f:X\rightarrow B$
be a flat morphism onto a smooth curve
![]() $B$
with the property that a general closed fiber
$B$
with the property that a general closed fiber
![]() $X_{b}$
of
$X_{b}$
of
![]() $f$
is an irreducible irrational
$f$
is an irreducible irrational
![]() $\mathbb{A}^{1}$
-ruled surface. We let
$\mathbb{A}^{1}$
-ruled surface. We let
![]() $\overline{f}:W\rightarrow B$
be a smooth projective model of
$\overline{f}:W\rightarrow B$
be a smooth projective model of
![]() $X$
over
$X$
over
![]() $B$
obtained from an arbitrary normal relative projective completion
$B$
obtained from an arbitrary normal relative projective completion
![]() $X{\hookrightarrow}\overline{X}$
of
$X{\hookrightarrow}\overline{X}$
of
![]() $X$
over
$X$
over
![]() $B$
by resolving the singularities. We let
$B$
by resolving the singularities. We let
![]() $j:X{\dashrightarrow}W$
be the birational map induced by the open immersion
$j:X{\dashrightarrow}W$
be the birational map induced by the open immersion
![]() $X{\hookrightarrow}\overline{X}$
.
$X{\hookrightarrow}\overline{X}$
.
By applying a minimal model program for
![]() $W$
over
$W$
over
![]() $B$
, we obtain a sequence of birational
$B$
, we obtain a sequence of birational
![]() $B$
-maps
$B$
-maps
between
![]() $B$
-schemes
$B$
-schemes
![]() $\overline{f}_{i}:W_{i}\rightarrow B$
, where
$\overline{f}_{i}:W_{i}\rightarrow B$
, where
![]() $\unicode[STIX]{x1D719}_{i}:W_{i}{\dashrightarrow}W_{i+1}$
is either a divisorial contraction or a flip, and the rightmost variety
$\unicode[STIX]{x1D719}_{i}:W_{i}{\dashrightarrow}W_{i+1}$
is either a divisorial contraction or a flip, and the rightmost variety
![]() $W^{\prime }$
is the output of a minimal model program over
$W^{\prime }$
is the output of a minimal model program over
![]() $B$
. The hypotheses imply that
$B$
. The hypotheses imply that
![]() $W^{\prime }$
has the structure of a Mori conic bundle
$W^{\prime }$
has the structure of a Mori conic bundle
![]() $\overline{\unicode[STIX]{x1D70C}}:W^{\prime }\rightarrow Y$
over a projective
$\overline{\unicode[STIX]{x1D70C}}:W^{\prime }\rightarrow Y$
over a projective
![]() $B$
-scheme
$B$
-scheme
![]() $h:Y\rightarrow B$
corresponding to the contraction of an extremal ray of
$h:Y\rightarrow B$
corresponding to the contraction of an extremal ray of
![]() $\overline{\text{NE}}(W^{\prime }/B)$
. Indeed, a general fiber of
$\overline{\text{NE}}(W^{\prime }/B)$
. Indeed, a general fiber of
![]() $\overline{f}$
being a birationally ruled projective surface, the output
$\overline{f}$
being a birationally ruled projective surface, the output
![]() $W^{\prime }$
is not a minimal model of
$W^{\prime }$
is not a minimal model of
![]() $W$
over
$W$
over
![]() $B$
. So
$B$
. So
![]() $W^{\prime }$
is either a Mori conic bundle over a
$W^{\prime }$
is either a Mori conic bundle over a
![]() $B$
-scheme
$B$
-scheme
![]() $Y$
of dimension
$Y$
of dimension
![]() $2$
or a del Pezzo fibration over
$2$
or a del Pezzo fibration over
![]() $B$
, the second case being excluded by the fact that the general fibers of
$B$
, the second case being excluded by the fact that the general fibers of
![]() $\overline{f}$
are irrational.
$\overline{f}$
are irrational.
Proposition 13. The induced map
![]() $\unicode[STIX]{x1D70C}=\overline{\unicode[STIX]{x1D70C}}\mid _{X}:X{\dashrightarrow}Y$
is a rational
$\unicode[STIX]{x1D70C}=\overline{\unicode[STIX]{x1D70C}}\mid _{X}:X{\dashrightarrow}Y$
is a rational
![]() $\mathbb{A}^{1}$
-fibration.
$\mathbb{A}^{1}$
-fibration.
Proof. Since a general closed fiber
![]() $X_{b}$
is a normal affine surface with an
$X_{b}$
is a normal affine surface with an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
over a certain irrational smooth curve
$\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
over a certain irrational smooth curve
![]() $C_{b}$
, it follows that there exists a unique maximal affine open subset
$C_{b}$
, it follows that there exists a unique maximal affine open subset
![]() $U_{b}$
of
$U_{b}$
of
![]() $C_{b}$
such that
$C_{b}$
such that
![]() $\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b})\simeq U_{b}\times \mathbb{A}^{1}$
and such that the rational map
$\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b})\simeq U_{b}\times \mathbb{A}^{1}$
and such that the rational map
![]() $j_{b}:\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b}){\dashrightarrow}W_{b}$
induced by
$j_{b}:\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b}){\dashrightarrow}W_{b}$
induced by
![]() $j$
is regular, inducing an isomorphism between
$j$
is regular, inducing an isomorphism between
![]() $\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b})$
and its image. Each step
$\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b})$
and its image. Each step
![]() $\unicode[STIX]{x1D719}_{i}:W_{i}{\dashrightarrow}W_{i+1}$
consists of either a flip whose flipping and flipped curves are contained in fibers of
$\unicode[STIX]{x1D719}_{i}:W_{i}{\dashrightarrow}W_{i+1}$
consists of either a flip whose flipping and flipped curves are contained in fibers of
![]() $\overline{f}_{i}:W_{i}\rightarrow B$
and
$\overline{f}_{i}:W_{i}\rightarrow B$
and
![]() $\overline{f}_{i+1}:W_{i+1}\rightarrow B$
respectively, or a divisorial contraction whose exceptional divisor is contained in a fiber of
$\overline{f}_{i+1}:W_{i+1}\rightarrow B$
respectively, or a divisorial contraction whose exceptional divisor is contained in a fiber of
![]() $\overline{f}_{i}:W_{i}\rightarrow B$
, or a divisorial contraction whose exceptional divisor intersects a general fiber of
$\overline{f}_{i}:W_{i}\rightarrow B$
, or a divisorial contraction whose exceptional divisor intersects a general fiber of
![]() $\overline{f}_{i}:W_{i}\rightarrow B$
. Clearly, a general closed fiber of
$\overline{f}_{i}:W_{i}\rightarrow B$
. Clearly, a general closed fiber of
![]() $\overline{f}_{i}:W_{i}\rightarrow B$
is not affected by the first two types of birational maps. On the other hand, if
$\overline{f}_{i}:W_{i}\rightarrow B$
is not affected by the first two types of birational maps. On the other hand, if
![]() $\unicode[STIX]{x1D719}_{i}:W_{i}\rightarrow W_{i+1}$
is the contraction of a divisor
$\unicode[STIX]{x1D719}_{i}:W_{i}\rightarrow W_{i+1}$
is the contraction of a divisor
![]() $E_{i}\subset W_{i}$
which dominates
$E_{i}\subset W_{i}$
which dominates
![]() $B$
, then a general fiber of
$B$
, then a general fiber of
![]() $\unicode[STIX]{x1D719}_{i}\mid _{E_{i}}$
is a smooth proper rational curve. The intersection of
$\unicode[STIX]{x1D719}_{i}\mid _{E_{i}}$
is a smooth proper rational curve. The intersection of
![]() $E_{i}$
with a general closed fiber
$E_{i}$
with a general closed fiber
![]() $W_{i,b}$
of
$W_{i,b}$
of
![]() $\overline{f}_{i}$
thus consists of proper rational curves, and its intersection with the image of the maximal affine cylinder like open subset
$\overline{f}_{i}$
thus consists of proper rational curves, and its intersection with the image of the maximal affine cylinder like open subset
![]() $\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b})$
of
$\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b})$
of
![]() $X_{b}$
is either empty or composed of affine rational curves. Since
$X_{b}$
is either empty or composed of affine rational curves. Since
![]() $U_{b}$
is an irrational curve, it follows that each irreducible component of
$U_{b}$
is an irrational curve, it follows that each irreducible component of
![]() $E_{i}\cap (\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b}))$
is contained in a fiber of
$E_{i}\cap (\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b}))$
is contained in a fiber of
![]() $\unicode[STIX]{x1D70B}_{b}$
. This implies that there exists an open subset
$\unicode[STIX]{x1D70B}_{b}$
. This implies that there exists an open subset
![]() $U_{b,0}$
of
$U_{b,0}$
of
![]() $U_{b}$
with the property that for every
$U_{b}$
with the property that for every
![]() $i=1,\ldots ,\ell$
, the restriction of
$i=1,\ldots ,\ell$
, the restriction of
![]() $\unicode[STIX]{x1D719}_{i}\circ \cdots \circ \unicode[STIX]{x1D719}_{1}\circ j$
to
$\unicode[STIX]{x1D719}_{i}\circ \cdots \circ \unicode[STIX]{x1D719}_{1}\circ j$
to
![]() $\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b,0})\subset X_{b}$
is an isomorphism onto its image in
$\unicode[STIX]{x1D70B}_{b}^{-1}(U_{b,0})\subset X_{b}$
is an isomorphism onto its image in
![]() $W_{i,b}$
. A general fiber of
$W_{i,b}$
. A general fiber of
![]() $\overline{\unicode[STIX]{x1D70C}}:W^{\prime }\rightarrow Y$
over a closed point
$\overline{\unicode[STIX]{x1D70C}}:W^{\prime }\rightarrow Y$
over a closed point
![]() $y\in Y$
being a smooth proper rational curve, its intersection with
$y\in Y$
being a smooth proper rational curve, its intersection with
![]() $\unicode[STIX]{x1D70B}_{h(y)}^{-1}(U_{h(y),0})$
viewed as an open subset of
$\unicode[STIX]{x1D70B}_{h(y)}^{-1}(U_{h(y),0})$
viewed as an open subset of
![]() $W_{h(y)}^{\prime }$
, is thus either empty or equal to a fiber of
$W_{h(y)}^{\prime }$
, is thus either empty or equal to a fiber of
![]() $\unicode[STIX]{x1D70B}_{h(y)}$
. So by virtue of [Reference Kambayashi and Miyanishi9], there exists an open subset
$\unicode[STIX]{x1D70B}_{h(y)}$
. So by virtue of [Reference Kambayashi and Miyanishi9], there exists an open subset
![]() $V$
of
$V$
of
![]() $X$
on which
$X$
on which
![]() $\overline{\unicode[STIX]{x1D70C}}$
restricts to an
$\overline{\unicode[STIX]{x1D70C}}$
restricts to an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\overline{\unicode[STIX]{x1D70C}}\mid _{V}:V\rightarrow Y$
.◻
$\overline{\unicode[STIX]{x1D70C}}\mid _{V}:V\rightarrow Y$
.◻
Corollary 14. Let
![]() $X$
be a normal complex affine threefold
$X$
be a normal complex affine threefold
![]() $X$
equipped with a morphism
$X$
equipped with a morphism
![]() $f:X\rightarrow B$
onto a smooth curve
$f:X\rightarrow B$
onto a smooth curve
![]() $B$
whose general closed fibers are irrational
$B$
whose general closed fibers are irrational
![]() $\mathbb{A}^{1}$
-ruled surfaces. Then
$\mathbb{A}^{1}$
-ruled surfaces. Then
![]() $X$
is birationally equivalent to the product of
$X$
is birationally equivalent to the product of
![]() $\mathbb{P}^{1}$
with a family
$\mathbb{P}^{1}$
with a family
![]() $h_{0}:{\mathcal{C}}_{0}\rightarrow B_{0}$
of smooth projective curves of genus
$h_{0}:{\mathcal{C}}_{0}\rightarrow B_{0}$
of smooth projective curves of genus
![]() $g\geqslant 1$
over an open subset
$g\geqslant 1$
over an open subset
![]() $B_{0}\subset B$
.
$B_{0}\subset B$
.
Proof. By the previous Proposition,
![]() $X$
has the structure of a rational
$X$
has the structure of a rational
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70C}:X{\dashrightarrow}Y$
over a
$\unicode[STIX]{x1D70C}:X{\dashrightarrow}Y$
over a
![]() $2$
-dimensional normal proper
$2$
-dimensional normal proper
![]() $B$
-scheme
$B$
-scheme
![]() $h:Y\rightarrow B$
. In particular,
$h:Y\rightarrow B$
. In particular,
![]() $X$
is birational to
$X$
is birational to
![]() $Y\times \mathbb{P}^{1}$
. On the other hand, for a general closed point
$Y\times \mathbb{P}^{1}$
. On the other hand, for a general closed point
![]() $b\in B$
, the curve
$b\in B$
, the curve
![]() $Y_{b}$
is birational to the base
$Y_{b}$
is birational to the base
![]() $C_{b}$
of the unique
$C_{b}$
of the unique
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
on the irrational affine surface
$\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
on the irrational affine surface
![]() $X_{b}$
. Letting
$X_{b}$
. Letting
![]() $\unicode[STIX]{x1D70E}:{\tilde{Y}}\rightarrow Y$
be a desingularization of
$\unicode[STIX]{x1D70E}:{\tilde{Y}}\rightarrow Y$
be a desingularization of
![]() $Y$
, there exists an open subset
$Y$
, there exists an open subset
![]() $B_{0}$
of
$B_{0}$
of
![]() $B$
over which the composition
$B$
over which the composition
![]() $h\circ \unicode[STIX]{x1D70E}:{\tilde{Y}}\rightarrow Y$
restricts to a smooth family
$h\circ \unicode[STIX]{x1D70E}:{\tilde{Y}}\rightarrow Y$
restricts to a smooth family
![]() $h_{0}:{\mathcal{C}}_{0}\rightarrow B_{0}$
of projective curves of a certain genus
$h_{0}:{\mathcal{C}}_{0}\rightarrow B_{0}$
of projective curves of a certain genus
![]() $g\geqslant 1$
. By construction,
$g\geqslant 1$
. By construction,
![]() $X$
is birational to
$X$
is birational to
![]() ${\mathcal{C}}_{0}\times \mathbb{P}^{1}$
.◻
${\mathcal{C}}_{0}\times \mathbb{P}^{1}$
.◻
Remark 15. Example 11 above shows conversely that for every smooth family
![]() $h:{\mathcal{C}}\rightarrow B$
of projective curves of genus
$h:{\mathcal{C}}\rightarrow B$
of projective curves of genus
![]() $g\geqslant 2$
, there exists a smooth
$g\geqslant 2$
, there exists a smooth
![]() $\mathbb{A}^{1}$
-ruled affine threefold
$\mathbb{A}^{1}$
-ruled affine threefold
![]() $X$
birationally equivalent to
$X$
birationally equivalent to
![]() ${\mathcal{C}}\times \mathbb{P}^{1}$
. Actually, in the setting of the previous Corollary 14, if we assume further that a general fiber of
${\mathcal{C}}\times \mathbb{P}^{1}$
. Actually, in the setting of the previous Corollary 14, if we assume further that a general fiber of
![]() $f:X\rightarrow B$
carries an
$f:X\rightarrow B$
carries an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
over a smooth curve
$\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
over a smooth curve
![]() $C_{b}$
whose smooth projective model has genus
$C_{b}$
whose smooth projective model has genus
![]() $g\geqslant 2$
, then there exists a uniquely determined family
$g\geqslant 2$
, then there exists a uniquely determined family
![]() $h:{\mathcal{C}}\rightarrow B$
of proper stable curves of genus
$h:{\mathcal{C}}\rightarrow B$
of proper stable curves of genus
![]() $g$
such that
$g$
such that
![]() $X$
is birationally equivalent to
$X$
is birationally equivalent to
![]() ${\mathcal{C}}\times \mathbb{P}^{1}$
: indeed, the moduli stack
${\mathcal{C}}\times \mathbb{P}^{1}$
: indeed, the moduli stack
![]() $\overline{{\mathcal{M}}}_{g}$
of stable curves of genus
$\overline{{\mathcal{M}}}_{g}$
of stable curves of genus
![]() $g\geqslant 2$
being proper and separated, the smooth family
$g\geqslant 2$
being proper and separated, the smooth family
![]() $h_{0}:{\mathcal{C}}_{0}\rightarrow B_{0}$
extends in a unique way to a family
$h_{0}:{\mathcal{C}}_{0}\rightarrow B_{0}$
extends in a unique way to a family
![]() $h:{\mathcal{C}}\rightarrow B$
of stable curves of genus
$h:{\mathcal{C}}\rightarrow B$
of stable curves of genus
![]() $g$
.
$g$
.
3.2 Factorial affine threefolds
Proposition 16. Let
![]() $X$
be a normal affine threefold with finite divisor class group
$X$
be a normal affine threefold with finite divisor class group
![]() $\text{Cl}(X)$
and let
$\text{Cl}(X)$
and let
![]() $f:X\rightarrow B$
be a morphism onto a smooth curve
$f:X\rightarrow B$
be a morphism onto a smooth curve
![]() $B$
whose general closed fibers are irrational
$B$
whose general closed fibers are irrational
![]() $\mathbb{A}^{1}$
-ruled surfaces. Then there exists a factorization
$\mathbb{A}^{1}$
-ruled surfaces. Then there exists a factorization
![]() $f=h\circ \unicode[STIX]{x1D70C}:X\rightarrow Y\rightarrow B$
where
$f=h\circ \unicode[STIX]{x1D70C}:X\rightarrow Y\rightarrow B$
where
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y$
is the algebraic quotient morphism of an effective
$\unicode[STIX]{x1D70C}:X\rightarrow Y$
is the algebraic quotient morphism of an effective
![]() $\mathbb{G}_{a,B}$
-action on
$\mathbb{G}_{a,B}$
-action on
![]() $X$
. In particular, a general fiber of
$X$
. In particular, a general fiber of
![]() $f$
admits an
$f$
admits an
![]() $\mathbb{A}^{1}$
-fibration of affine type.
$\mathbb{A}^{1}$
-fibration of affine type.
Proof. By virtue of Proposition 12, there exists an effective
![]() $\mathbb{G}_{a,B}$
-action on
$\mathbb{G}_{a,B}$
-action on
![]() $X$
such that for a general closed point
$X$
such that for a general closed point
![]() $b\in B$
, the
$b\in B$
, the
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
on
$\unicode[STIX]{x1D70B}_{b}:X_{b}\rightarrow C_{b}$
on
![]() $X_{b}$
factors through the algebraic quotient
$X_{b}$
factors through the algebraic quotient
Since
![]() $X$
is a threefold, the ring of invariants
$X$
is a threefold, the ring of invariants
![]() $\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})^{\mathbb{G}_{a,B}}$
is finitely generated [Reference Zariski16]. The quotient morphism
$\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})^{\mathbb{G}_{a,B}}$
is finitely generated [Reference Zariski16]. The quotient morphism
![]() $\unicode[STIX]{x1D70C}:X\rightarrow Y=\text{Spec}(\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})^{\mathbb{G}_{a,B}})$
is an
$\unicode[STIX]{x1D70C}:X\rightarrow Y=\text{Spec}(\unicode[STIX]{x1D6E4}(X,{\mathcal{O}}_{X})^{\mathbb{G}_{a,B}})$
is an
![]() $\mathbb{A}^{1}$
-fibration, and since
$\mathbb{A}^{1}$
-fibration, and since
![]() $Y$
is a categorical quotient in the category of algebraic varieties, the invariant morphism
$Y$
is a categorical quotient in the category of algebraic varieties, the invariant morphism
![]() $f:X\rightarrow B$
factors through
$f:X\rightarrow B$
factors through
![]() $\unicode[STIX]{x1D70C}$
.◻
$\unicode[STIX]{x1D70C}$
.◻
Corollary 17. Let
![]() $f:\mathbb{A}^{3}\rightarrow B$
be a morphism onto a smooth curve
$f:\mathbb{A}^{3}\rightarrow B$
be a morphism onto a smooth curve
![]() $B$
with irrational
$B$
with irrational
![]() $\mathbb{A}^{1}$
-ruled general fibers. Then
$\mathbb{A}^{1}$
-ruled general fibers. Then
![]() $B$
is isomorphic to either
$B$
is isomorphic to either
![]() $\mathbb{P}^{1}$
or
$\mathbb{P}^{1}$
or
![]() $\mathbb{A}^{1}$
and there exists a factorization
$\mathbb{A}^{1}$
and there exists a factorization
![]() $f=h\circ \unicode[STIX]{x1D70C}:\mathbb{A}^{3}\rightarrow \mathbb{A}^{2}\rightarrow B$
, where
$f=h\circ \unicode[STIX]{x1D70C}:\mathbb{A}^{3}\rightarrow \mathbb{A}^{2}\rightarrow B$
, where
![]() $\unicode[STIX]{x1D70C}:\mathbb{A}^{3}\rightarrow \mathbb{A}^{2}$
is the quotient morphism of an effective
$\unicode[STIX]{x1D70C}:\mathbb{A}^{3}\rightarrow \mathbb{A}^{2}$
is the quotient morphism of an effective
![]() $\mathbb{G}_{a,B}$
-action on
$\mathbb{G}_{a,B}$
-action on
![]() $\mathbb{A}^{3}$
.
$\mathbb{A}^{3}$
.
Proof. Since
![]() $B$
is dominated by a general line in
$B$
is dominated by a general line in
![]() $\mathbb{A}^{3}$
, it is necessarily isomorphic to
$\mathbb{A}^{3}$
, it is necessarily isomorphic to
![]() $\mathbb{P}^{1}$
or
$\mathbb{P}^{1}$
or
![]() $\mathbb{A}^{1}$
. The second assertion follows from Proposition 16 and the fact that the algebraic quotient of every nontrivial
$\mathbb{A}^{1}$
. The second assertion follows from Proposition 16 and the fact that the algebraic quotient of every nontrivial
![]() $\mathbb{G}_{a}$
-action on
$\mathbb{G}_{a}$
-action on
![]() $\mathbb{A}^{3}$
is isomorphic to
$\mathbb{A}^{3}$
is isomorphic to
![]() $\mathbb{A}^{2}$
[Reference Miyanishi13].◻
$\mathbb{A}^{2}$
[Reference Miyanishi13].◻
Example 18. In Corollary 17 above, the base curve
![]() $B$
need not be affine. For instance, the morphism
$B$
need not be affine. For instance, the morphism
defines a family whose general member is isomorphic to the product
![]() $C_{\unicode[STIX]{x1D706}}\times \mathbb{A}^{1}$
where
$C_{\unicode[STIX]{x1D706}}\times \mathbb{A}^{1}$
where
![]() $C_{\unicode[STIX]{x1D706}}\subset \mathbb{A}^{2}=\text{Spec}(\mathbb{C}[xz-y^{2},x])$
is the affine elliptic curve with equation
$C_{\unicode[STIX]{x1D706}}\subset \mathbb{A}^{2}=\text{Spec}(\mathbb{C}[xz-y^{2},x])$
is the affine elliptic curve with equation
![]() $(xz-y^{2})^{3}+\unicode[STIX]{x1D706}((xz-y^{2})x^{2}+1)=0$
. The subring
$(xz-y^{2})^{3}+\unicode[STIX]{x1D706}((xz-y^{2})x^{2}+1)=0$
. The subring
![]() $\mathbb{C}[xz-y^{2},x]$
of
$\mathbb{C}[xz-y^{2},x]$
of
![]() $\mathbb{C}[x,y,z]$
coincides with the ring of invariants of the
$\mathbb{C}[x,y,z]$
coincides with the ring of invariants of the
![]() $\mathbb{G}_{a}$
-action associated with the locally nilpotent
$\mathbb{G}_{a}$
-action associated with the locally nilpotent
![]() $\mathbb{C}[x]$
-derivation
$\mathbb{C}[x]$
-derivation
![]() $x\unicode[STIX]{x2202}_{y}+2y\unicode[STIX]{x2202}_{z}$
and
$x\unicode[STIX]{x2202}_{y}+2y\unicode[STIX]{x2202}_{z}$
and
![]() $f$
is the composition of the quotient morphism
$f$
is the composition of the quotient morphism
![]() $\unicode[STIX]{x1D70C}:\mathbb{A}^{3}\rightarrow \mathbb{A}^{2}=\mathbb{A}^{3}/\!/\mathbb{G}_{a}=\text{Spec}(\mathbb{C}[u,v])$
defined by
$\unicode[STIX]{x1D70C}:\mathbb{A}^{3}\rightarrow \mathbb{A}^{2}=\mathbb{A}^{3}/\!/\mathbb{G}_{a}=\text{Spec}(\mathbb{C}[u,v])$
defined by
![]() $(x,y,z)\mapsto (xz-y^{2},x)$
and of the morphism
$(x,y,z)\mapsto (xz-y^{2},x)$
and of the morphism
![]() $h:\mathbb{A}^{2}=\text{Spec}(\mathbb{C}[u,v])\rightarrow \mathbb{P}^{1}$
defined by
$h:\mathbb{A}^{2}=\text{Spec}(\mathbb{C}[u,v])\rightarrow \mathbb{P}^{1}$
defined by
![]() $\left(u,v\right)\mapsto [uv^{2}+1:u^{3}]$
.
$\left(u,v\right)\mapsto [uv^{2}+1:u^{3}]$
.
Corollary 17 above implies in particular that if a general fiber of a regular function
![]() $f:\mathbb{A}^{3}\rightarrow \mathbb{A}^{1}$
is irrational and admits an
$f:\mathbb{A}^{3}\rightarrow \mathbb{A}^{1}$
is irrational and admits an
![]() $\mathbb{A}^{1}$
-fibration, then the latter is necessarily of affine type. In contrast, regular functions
$\mathbb{A}^{1}$
-fibration, then the latter is necessarily of affine type. In contrast, regular functions
![]() $f:\mathbb{A}^{3}\rightarrow \mathbb{A}^{1}$
whose general fibers are rational and equipped with
$f:\mathbb{A}^{3}\rightarrow \mathbb{A}^{1}$
whose general fibers are rational and equipped with
![]() $\mathbb{A}^{1}$
-fibrations of complete type only do exist, as illustrated by the following example.
$\mathbb{A}^{1}$
-fibrations of complete type only do exist, as illustrated by the following example.
Example 19. Let
![]() $f=x^{3}-y^{3}+z(z+1)\in \mathbb{C}[x,y,z]$
and let
$f=x^{3}-y^{3}+z(z+1)\in \mathbb{C}[x,y,z]$
and let
![]() $f:\mathbb{A}^{3}=\text{Spec}(\mathbb{C}[x,y,z])\rightarrow \mathbb{A}^{1}=\text{Spec}(\mathbb{C}[\unicode[STIX]{x1D706}])$
be the corresponding morphism. The closure
$f:\mathbb{A}^{3}=\text{Spec}(\mathbb{C}[x,y,z])\rightarrow \mathbb{A}^{1}=\text{Spec}(\mathbb{C}[\unicode[STIX]{x1D706}])$
be the corresponding morphism. The closure
![]() $\overline{S}_{\unicode[STIX]{x1D706}}$
in
$\overline{S}_{\unicode[STIX]{x1D706}}$
in
![]() $\mathbb{P}^{3}=\text{Proj}(\mathbb{C}[x,y,z,t])$
of a general fiber
$\mathbb{P}^{3}=\text{Proj}(\mathbb{C}[x,y,z,t])$
of a general fiber
![]() $S_{\unicode[STIX]{x1D706}}=f^{\ast }(\unicode[STIX]{x1D706})$
of
$S_{\unicode[STIX]{x1D706}}=f^{\ast }(\unicode[STIX]{x1D706})$
of
![]() $f$
is a smooth cubic surface which intersects the hyperplane
$f$
is a smooth cubic surface which intersects the hyperplane
![]() $H_{\infty }=\left\{t=0\right\}$
along the union
$H_{\infty }=\left\{t=0\right\}$
along the union
![]() $B_{\unicode[STIX]{x1D706}}$
of three lines meeting at the Eckardt point
$B_{\unicode[STIX]{x1D706}}$
of three lines meeting at the Eckardt point
![]() $p=\left[0:0:1:0\right]$
. Thus
$p=\left[0:0:1:0\right]$
. Thus
![]() $S_{\unicode[STIX]{x1D706}}$
is rational and a direct computation reveals that
$S_{\unicode[STIX]{x1D706}}$
is rational and a direct computation reveals that
![]() $\unicode[STIX]{x1D705}(S_{\unicode[STIX]{x1D706}})=-\infty$
. So by virtue of [Reference Miyanishi and Sugie14],
$\unicode[STIX]{x1D705}(S_{\unicode[STIX]{x1D706}})=-\infty$
. So by virtue of [Reference Miyanishi and Sugie14],
![]() $S_{\unicode[STIX]{x1D706}}$
admits an
$S_{\unicode[STIX]{x1D706}}$
admits an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:S_{\unicode[STIX]{x1D706}}\rightarrow C_{\unicode[STIX]{x1D706}}$
over a smooth rational curve
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:S_{\unicode[STIX]{x1D706}}\rightarrow C_{\unicode[STIX]{x1D706}}$
over a smooth rational curve
![]() $C_{\unicode[STIX]{x1D706}}$
. If
$C_{\unicode[STIX]{x1D706}}$
. If
![]() $C_{\unicode[STIX]{x1D706}}$
was affine, then there would exist a nontrivial
$C_{\unicode[STIX]{x1D706}}$
was affine, then there would exist a nontrivial
![]() $\mathbb{G}_{a}$
-action on
$\mathbb{G}_{a}$
-action on
![]() $S_{\unicode[STIX]{x1D706}}$
having the general fibers of
$S_{\unicode[STIX]{x1D706}}$
having the general fibers of
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
as general orbits. But it is straightforward to check that every automorphism of
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
as general orbits. But it is straightforward to check that every automorphism of
![]() $S_{\unicode[STIX]{x1D706}}$
considered as a birational self-map of
$S_{\unicode[STIX]{x1D706}}$
considered as a birational self-map of
![]() $\overline{S}_{\unicode[STIX]{x1D706}}$
is in fact a biregular automorphism of
$\overline{S}_{\unicode[STIX]{x1D706}}$
is in fact a biregular automorphism of
![]() $\overline{S}_{\unicode[STIX]{x1D706}}$
preserving the boundary
$\overline{S}_{\unicode[STIX]{x1D706}}$
preserving the boundary
![]() $B_{\unicode[STIX]{x1D706}}$
. So the automorphism group of
$B_{\unicode[STIX]{x1D706}}$
. So the automorphism group of
![]() $S_{\unicode[STIX]{x1D706}}$
injects into the group
$S_{\unicode[STIX]{x1D706}}$
injects into the group
![]() $\text{Aut}(\overline{S}_{\unicode[STIX]{x1D706}},B_{\unicode[STIX]{x1D706}})$
of automorphisms of the pair
$\text{Aut}(\overline{S}_{\unicode[STIX]{x1D706}},B_{\unicode[STIX]{x1D706}})$
of automorphisms of the pair
![]() $(\overline{S}_{\unicode[STIX]{x1D706}},B_{\unicode[STIX]{x1D706}})$
. The latter being a finite group, we conclude that no such
$(\overline{S}_{\unicode[STIX]{x1D706}},B_{\unicode[STIX]{x1D706}})$
. The latter being a finite group, we conclude that no such
![]() $\mathbb{G}_{a}$
-action exists, and hence that
$\mathbb{G}_{a}$
-action exists, and hence that
![]() $S_{\unicode[STIX]{x1D706}}$
only admits
$S_{\unicode[STIX]{x1D706}}$
only admits
![]() $\mathbb{A}^{1}$
-fibrations of complete type. An
$\mathbb{A}^{1}$
-fibrations of complete type. An
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:S_{\unicode[STIX]{x1D706}}\rightarrow \mathbb{P}^{1}$
can be obtained as follows: letting
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:S_{\unicode[STIX]{x1D706}}\rightarrow \mathbb{P}^{1}$
can be obtained as follows: letting
![]() $B_{\unicode[STIX]{x1D706}}=L_{1}\cup L_{2}\cup L_{3}$
,
$B_{\unicode[STIX]{x1D706}}=L_{1}\cup L_{2}\cup L_{3}$
,
![]() $L_{1}$
is a member of a
$L_{1}$
is a member of a
![]() $6$
-tuple of pairwise disjoint lines whose simultaneous contraction realizes
$6$
-tuple of pairwise disjoint lines whose simultaneous contraction realizes
![]() $\overline{S}_{\unicode[STIX]{x1D706}}$
as a blow-up
$\overline{S}_{\unicode[STIX]{x1D706}}$
as a blow-up
![]() $\unicode[STIX]{x1D70E}:\overline{S}_{\unicode[STIX]{x1D706}}\rightarrow \mathbb{P}^{2}$
of
$\unicode[STIX]{x1D70E}:\overline{S}_{\unicode[STIX]{x1D706}}\rightarrow \mathbb{P}^{2}$
of
![]() $\mathbb{P}^{2}$
in such a way that
$\mathbb{P}^{2}$
in such a way that
![]() $\unicode[STIX]{x1D70E}(L_{2})$
and
$\unicode[STIX]{x1D70E}(L_{2})$
and
![]() $\unicode[STIX]{x1D70E}(L_{3})$
are respectively a smooth conic and its tangent line at the point
$\unicode[STIX]{x1D70E}(L_{3})$
are respectively a smooth conic and its tangent line at the point
![]() $p=\unicode[STIX]{x1D70E}(L_{1})$
. The birational transform
$p=\unicode[STIX]{x1D70E}(L_{1})$
. The birational transform
![]() $\overline{\unicode[STIX]{x1D70B}}_{\unicode[STIX]{x1D706}}:\overline{S}_{\unicode[STIX]{x1D706}}{\dashrightarrow}\mathbb{P}^{1}$
on
$\overline{\unicode[STIX]{x1D70B}}_{\unicode[STIX]{x1D706}}:\overline{S}_{\unicode[STIX]{x1D706}}{\dashrightarrow}\mathbb{P}^{1}$
on
![]() $\overline{S}_{\unicode[STIX]{x1D706}}$
of the pencil generated by
$\overline{S}_{\unicode[STIX]{x1D706}}$
of the pencil generated by
![]() $\unicode[STIX]{x1D70E}(L_{2})$
and
$\unicode[STIX]{x1D70E}(L_{2})$
and
![]() $2\unicode[STIX]{x1D70E}(L_{3})$
restricts to an
$2\unicode[STIX]{x1D70E}(L_{3})$
restricts to an
![]() $\mathbb{A}^{1}$
-fibration
$\mathbb{A}^{1}$
-fibration
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:S_{\unicode[STIX]{x1D706}}\rightarrow \mathbb{P}^{1}$
with two degenerate fibers: an irreducible one, of multiplicity two, consisting of the intersection with
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:S_{\unicode[STIX]{x1D706}}\rightarrow \mathbb{P}^{1}$
with two degenerate fibers: an irreducible one, of multiplicity two, consisting of the intersection with
![]() $S_{\unicode[STIX]{x1D706}}$
of the unique exceptional divisor of
$S_{\unicode[STIX]{x1D706}}$
of the unique exceptional divisor of
![]() $\unicode[STIX]{x1D70E}$
whose center is supported on
$\unicode[STIX]{x1D70E}$
whose center is supported on
![]() $\unicode[STIX]{x1D70E}(L_{3})\setminus \{p\}$
, and a smooth one consisting of the intersection with
$\unicode[STIX]{x1D70E}(L_{3})\setminus \{p\}$
, and a smooth one consisting of the intersection with
![]() $S_{\unicode[STIX]{x1D706}}$
of the four exceptional divisors of
$S_{\unicode[STIX]{x1D706}}$
of the four exceptional divisors of
![]() $\unicode[STIX]{x1D70E}$
with centers supported on
$\unicode[STIX]{x1D70E}$
with centers supported on
![]() $\unicode[STIX]{x1D70E}(L_{2})\setminus \left\{p\right\}$
.
$\unicode[STIX]{x1D70E}(L_{2})\setminus \left\{p\right\}$
.
Acknowledgement
The research was done during a visit of the first author at the University of Saitama. The authors thank this institution for its generous support and the excellent working conditions.