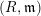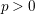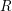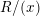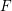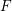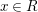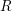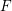1 Introduction
Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of prime characteristic
$(R,\mathfrak{m})$
be a Noetherian local ring of prime characteristic
![]() $p>0$
. We have the Frobenius endomorphism
$p>0$
. We have the Frobenius endomorphism
![]() $F:R\rightarrow R$
,
$F:R\rightarrow R$
,
![]() $x\mapsto x^{p}$
. The
$x\mapsto x^{p}$
. The
![]() $F$
-singularities are certain singularities defined via this Frobenius map. They appear in the theory of tight closure (cf. [Reference Huneke13] for its introduction), which was systematically introduced by Hochster and Huneke [Reference Hochster and Huneke9] and developed by many researchers, including Hara, Schwede, Smith, Takagi, Watanabe, Yoshida and others. A recent active research of
$F$
-singularities are certain singularities defined via this Frobenius map. They appear in the theory of tight closure (cf. [Reference Huneke13] for its introduction), which was systematically introduced by Hochster and Huneke [Reference Hochster and Huneke9] and developed by many researchers, including Hara, Schwede, Smith, Takagi, Watanabe, Yoshida and others. A recent active research of
![]() $F$
-singularities is centered around the correspondence with the singularities of the minimal model program. We recommend [Reference Takagi and Watanabe25] as an excellent survey for recent developments.
$F$
-singularities is centered around the correspondence with the singularities of the minimal model program. We recommend [Reference Takagi and Watanabe25] as an excellent survey for recent developments.
In this paper we study the deformation of
![]() $F$
-singularities. That is, we consider the problem: if
$F$
-singularities. That is, we consider the problem: if
![]() $R/(x)$
has certain property P for a regular element
$R/(x)$
has certain property P for a regular element
![]() $x\in R$
, then does
$x\in R$
, then does
![]() $R$
has the property P? The classical objects of
$R$
has the property P? The classical objects of
![]() $F$
-singularities are
$F$
-singularities are
![]() $F$
-regularity,
$F$
-regularity,
![]() $F$
-rationality,
$F$
-rationality,
![]() $F$
-purity and
$F$
-purity and
![]() $F$
-injectivity (cf. [Reference Huneke13, Reference Takagi and Watanabe25]). It is well known that
$F$
-injectivity (cf. [Reference Huneke13, Reference Takagi and Watanabe25]). It is well known that
![]() $F$
-rationality always deforms while
$F$
-rationality always deforms while
![]() $F$
-regularity and
$F$
-regularity and
![]() $F$
-purity do not deform in general [Reference Singh22, Reference Singh23]. Whether
$F$
-purity do not deform in general [Reference Singh22, Reference Singh23]. Whether
![]() $F$
-injectivity deforms is a long- standing open problem [Reference Fedder6] (for recent developments, we refer to [Reference Horiuchi, Miller and Shimomoto11, Reference Ma, Schwede and Shimomoto18]). Recall that the Frobenius endomorphism induces a natural Frobenius action on every local cohomology module,
$F$
-injectivity deforms is a long- standing open problem [Reference Fedder6] (for recent developments, we refer to [Reference Horiuchi, Miller and Shimomoto11, Reference Ma, Schwede and Shimomoto18]). Recall that the Frobenius endomorphism induces a natural Frobenius action on every local cohomology module,
![]() $F$
:
$F$
:
![]() $H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
. The ring
$H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
. The ring
![]() $R$
is called
$R$
is called
![]() $F$
-injective if this Frobenius action
$F$
-injective if this Frobenius action
![]() $F$
is injective for every
$F$
is injective for every
![]() $i\geqslant 0$
. The class of
$i\geqslant 0$
. The class of
![]() $F$
-injective singularities contains other classes of
$F$
-injective singularities contains other classes of
![]() $F$
-singularities. For an ideal-theoretic characterization of
$F$
-singularities. For an ideal-theoretic characterization of
![]() $F$
-injectivity, see [Reference Quy and Shimomoto20, Main Theorem D]. We consider this paper as a step toward a solution of the deformation of
$F$
-injectivity, see [Reference Quy and Shimomoto20, Main Theorem D]. We consider this paper as a step toward a solution of the deformation of
![]() $F$
-injectivity.
$F$
-injectivity.
We introduce two conditions:
![]() $F$
-full and
$F$
-full and
![]() $F$
-anti-nilpotent singularities, in terms of the Frobenius actions on local cohomology modules of
$F$
-anti-nilpotent singularities, in terms of the Frobenius actions on local cohomology modules of
![]() $R$
(we refer to Section 2 for detailed definitions). The first condition is motivated by recent results on Du Bois singularities [Reference Ma, Schwede and Shimomoto18]. The second condition has been studied in [Reference Enescu and Hochster5, Reference Ma16], and is known to be equivalent to stably FH-finite, which means all local cohomology modules of
$R$
(we refer to Section 2 for detailed definitions). The first condition is motivated by recent results on Du Bois singularities [Reference Ma, Schwede and Shimomoto18]. The second condition has been studied in [Reference Enescu and Hochster5, Reference Ma16], and is known to be equivalent to stably FH-finite, which means all local cohomology modules of
![]() $R$
and
$R$
and
![]() $R[[x_{1},\ldots ,x_{n}]]$
supported at the maximal ideals have only finitely many Frobenius stable submodules. We prove that
$R[[x_{1},\ldots ,x_{n}]]$
supported at the maximal ideals have only finitely many Frobenius stable submodules. We prove that
![]() $F$
-fullness and
$F$
-fullness and
![]() $F$
-anti-nilpotency both deform, and we obtain more evidence on deformation of
$F$
-anti-nilpotency both deform, and we obtain more evidence on deformation of
![]() $F$
-injectivity. Our results largely generalize earlier results of [Reference Horiuchi, Miller and Shimomoto11] in this direction. We list some of our main results here:
$F$
-injectivity. Our results largely generalize earlier results of [Reference Horiuchi, Miller and Shimomoto11] in this direction. We list some of our main results here:
Theorem 1.1. (Theorem 4.2, Corollary 5.16)
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
$(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
![]() $p>0$
and
$p>0$
and
![]() $x$
a regular element of
$x$
a regular element of
![]() $R$
. Then we have:
$R$
. Then we have:
(1) if
 $R/(x)$
is
$R/(x)$
is
 $F$
-anti-nilpotent, then so is
$F$
-anti-nilpotent, then so is
 $R$
;
$R$
;(2) if
 $R/(x)$
is
$R/(x)$
is
 $F$
-full, then so is
$F$
-full, then so is
 $R$
;
$R$
;(3) if
 $R/(x)$
is
$R/(x)$
is
 $F$
-full and
$F$
-full and
 $F$
-injective, then so is
$F$
-injective, then so is
 $R$
.
$R$
.
Theorem 1.2. (Theorem 5.11)
Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
$(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
![]() $p>0$
. Suppose the residue field
$p>0$
. Suppose the residue field
![]() $k=R/\mathfrak{m}$
is perfect. Let
$k=R/\mathfrak{m}$
is perfect. Let
![]() $x$
be a regular element of
$x$
be a regular element of
![]() $R$
such that
$R$
such that
![]() $\operatorname{Coker}(H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R))$
has finite length for every
$\operatorname{Coker}(H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R))$
has finite length for every
![]() $i$
. If
$i$
. If
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective, then the map
$F$
-injective, then the map
![]() $x^{p-1}F$
:
$x^{p-1}F$
:
![]() $H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for every
$H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for every
![]() $i$
, in particular
$i$
, in particular
![]() $R$
is
$R$
is
![]() $F$
-injective.
$F$
-injective.
2 Definitions and basic properties
2.1 Modules with Frobenius structure
Let
![]() $(R,\mathfrak{m})$
be a local ring of characteristic
$(R,\mathfrak{m})$
be a local ring of characteristic
![]() $p>0$
. A Frobenius action on an
$p>0$
. A Frobenius action on an
![]() $R$
-module
$R$
-module
![]() $M$
,
$M$
,
![]() $F$
:
$F$
:
![]() $M\rightarrow M$
, is an additive map such that for all
$M\rightarrow M$
, is an additive map such that for all
![]() $u\in M$
and
$u\in M$
and
![]() $r\in R$
,
$r\in R$
,
![]() $F(ru)=r^{p}u$
. Such an action induces a natural
$F(ru)=r^{p}u$
. Such an action induces a natural
![]() $R$
-linear map
$R$
-linear map
![]() $\mathscr{F}_{R}(M)\rightarrow M$
,Footnote
1
where
$\mathscr{F}_{R}(M)\rightarrow M$
,Footnote
1
where
![]() $\mathscr{F}_{R}(-)$
denotes the Peskine–Szpiro’s Frobenius functor. We say
$\mathscr{F}_{R}(-)$
denotes the Peskine–Szpiro’s Frobenius functor. We say
![]() $N$
is an
$N$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $M$
if
$M$
if
![]() $F(N)\subseteq N$
. We say the Frobenius action on
$F(N)\subseteq N$
. We say the Frobenius action on
![]() $M$
is nilpotent if
$M$
is nilpotent if
![]() $F^{e}(M)=0$
for some
$F^{e}(M)=0$
for some
![]() $e$
.
$e$
.
We note that having a Frobenius action on
![]() $M$
is the same as saying that
$M$
is the same as saying that
![]() $M$
is a left module over the ring
$M$
is a left module over the ring
![]() $R\{F\}$
, which may be viewed as a noncommutative ring generated over
$R\{F\}$
, which may be viewed as a noncommutative ring generated over
![]() $R$
by the symbols
$R$
by the symbols
![]() $1,F,F^{2},\ldots \,$
by requiring that
$1,F,F^{2},\ldots \,$
by requiring that
![]() $Fr=r^{p}F$
for
$Fr=r^{p}F$
for
![]() $r\in R$
. Moreover,
$r\in R$
. Moreover,
![]() $N$
is an
$N$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $M$
equivalent to requiring that
$M$
equivalent to requiring that
![]() $N$
is an
$N$
is an
![]() $R\{F\}$
-submodule of
$R\{F\}$
-submodule of
![]() $M$
. We will not use this viewpoint in this article though.
$M$
. We will not use this viewpoint in this article though.
Let
![]() $M$
be an (typically Artinian)
$M$
be an (typically Artinian)
![]() $R$
-module with a Frobenius action
$R$
-module with a Frobenius action
![]() $F$
. We say the Frobenius action on
$F$
. We say the Frobenius action on
![]() $M$
is full (or simply
$M$
is full (or simply
![]() $M$
is full), if the map
$M$
is full), if the map
![]() $\mathscr{F}_{R}^{e}(M)\rightarrow M$
is surjective for some (equivalently, every)
$\mathscr{F}_{R}^{e}(M)\rightarrow M$
is surjective for some (equivalently, every)
![]() $e\geqslant 1$
. This is the same as saying that the
$e\geqslant 1$
. This is the same as saying that the
![]() $R$
-span of all the elements of the form
$R$
-span of all the elements of the form
![]() $F^{e}(u)$
is the whole
$F^{e}(u)$
is the whole
![]() $M$
for some (equivalently, every)
$M$
for some (equivalently, every)
![]() $e\geqslant 1$
. We say the Frobenius action on
$e\geqslant 1$
. We say the Frobenius action on
![]() $M$
is anti-nilpotent (or simply
$M$
is anti-nilpotent (or simply
![]() $M$
is anti-nilpotent), if for any
$M$
is anti-nilpotent), if for any
![]() $F$
-stable submodule
$F$
-stable submodule
![]() $N\subseteq M$
, the induced Frobenius action
$N\subseteq M$
, the induced Frobenius action
![]() $F$
on
$F$
on
![]() $M/N$
is injective (note that this in particular implies that
$M/N$
is injective (note that this in particular implies that
![]() $F$
acts injectively on
$F$
acts injectively on
![]() $M$
).
$M$
).
Lemma 2.1. The Frobenius action on
![]() $M$
is anti-nilpotent if and only if every
$M$
is anti-nilpotent if and only if every
![]() $F$
-stable submodule
$F$
-stable submodule
![]() $N\subseteq M$
is full. In particular, if
$N\subseteq M$
is full. In particular, if
![]() $M$
anti-nilpotent, then
$M$
anti-nilpotent, then
![]() $M$
is full.
$M$
is full.
Proof. Suppose
![]() $M$
is anti-nilpotent. Let
$M$
is anti-nilpotent. Let
![]() $N\subseteq M$
be an
$N\subseteq M$
be an
![]() $F$
-stable submodule. Consider the
$F$
-stable submodule. Consider the
![]() $R$
-span of
$R$
-span of
![]() $F(N)$
, call it
$F(N)$
, call it
![]() $N^{\prime }$
. Clearly,
$N^{\prime }$
. Clearly,
![]() $N^{\prime }\subseteq N$
is another
$N^{\prime }\subseteq N$
is another
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $M$
and
$M$
and
![]() $F(N)\subseteq N^{\prime }$
. But since
$F(N)\subseteq N^{\prime }$
. But since
![]() $M$
is anti-nilpotent,
$M$
is anti-nilpotent,
![]() $F$
acts injectively on
$F$
acts injectively on
![]() $M/N^{\prime }$
. Thus we have
$M/N^{\prime }$
. Thus we have
![]() $N=N^{\prime }$
and hence
$N=N^{\prime }$
and hence
![]() $N$
is full.
$N$
is full.
Conversely, suppose every
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $M$
is full. Suppose there exists an
$M$
is full. Suppose there exists an
![]() $F$
-stable submodule
$F$
-stable submodule
![]() $N\subseteq M$
such that the Frobenius action on
$N\subseteq M$
such that the Frobenius action on
![]() $M/N$
is not injective. Pick
$M/N$
is not injective. Pick
![]() $y\notin N$
such that
$y\notin N$
such that
![]() $F(y)\in N$
. Let
$F(y)\in N$
. Let
![]() $N^{\prime \prime }=N+Ry$
. It is clear that
$N^{\prime \prime }=N+Ry$
. It is clear that
![]() $N^{\prime \prime }$
is an
$N^{\prime \prime }$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $M$
and the
$M$
and the
![]() $R$
-span of
$R$
-span of
![]() $F(N^{\prime \prime })$
is contained in
$F(N^{\prime \prime })$
is contained in
![]() $N\subsetneq N^{\prime \prime }$
. This shows
$N\subsetneq N^{\prime \prime }$
. This shows
![]() $N^{\prime \prime }$
is not full, a contradiction.◻
$N^{\prime \prime }$
is not full, a contradiction.◻
We also mention that whenever
![]() $M$
is endowed with a Frobenius action
$M$
is endowed with a Frobenius action
![]() $F$
, then
$F$
, then
![]() $\widetilde{F}=rF$
defines another Frobenius action on
$\widetilde{F}=rF$
defines another Frobenius action on
![]() $M$
for every
$M$
for every
![]() $r\in R$
. It is easy to check that if the action
$r\in R$
. It is easy to check that if the action
![]() $\widetilde{F}$
is full or anti-nilpotent, then so is
$\widetilde{F}$
is full or anti-nilpotent, then so is
![]() $F$
.
$F$
.
2.2
 $F$
-singularities
$F$
-singularities
We collect some definitions about singularities in positive characteristic. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
$(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
![]() $p>0$
with the Frobenius endomorphism
$p>0$
with the Frobenius endomorphism
![]() $F:R\rightarrow R;x\mapsto x^{p}$
.
$F:R\rightarrow R;x\mapsto x^{p}$
.
![]() $R$
is called
$R$
is called
![]() $F$
-finite if
$F$
-finite if
![]() $R$
is a finitely generated as an
$R$
is a finitely generated as an
![]() $R$
-module via the homomorphism
$R$
-module via the homomorphism
![]() $F$
.
$F$
.
![]() $R$
is called
$R$
is called
![]() $F$
-pure if the Frobenius endomorphism is pure.Footnote
2
It is worth to note that if
$F$
-pure if the Frobenius endomorphism is pure.Footnote
2
It is worth to note that if
![]() $R$
is either
$R$
is either
![]() $F$
-finite or complete, then
$F$
-finite or complete, then
![]() $R$
being
$R$
being
![]() $F$
-pure is equivalent to the condition that the Frobenius endomorphism
$F$
-pure is equivalent to the condition that the Frobenius endomorphism
![]() $F:R\rightarrow R$
is split [Reference Hochster and Roberts12]. Let
$F:R\rightarrow R$
is split [Reference Hochster and Roberts12]. Let
![]() $I=(x_{1},\ldots ,x_{t})$
be an ideal of
$I=(x_{1},\ldots ,x_{t})$
be an ideal of
![]() $R$
. Then we denote by
$R$
. Then we denote by
![]() $H_{I}^{i}(R)$
the
$H_{I}^{i}(R)$
the
![]() $i$
th local cohomology module with support at
$i$
th local cohomology module with support at
![]() $I$
(we refer to [Reference Brodmann and Sharp3] for the general theory of local cohomology modules). Recall that local cohomology may be computed as the cohomology of the Čech complex
$I$
(we refer to [Reference Brodmann and Sharp3] for the general theory of local cohomology modules). Recall that local cohomology may be computed as the cohomology of the Čech complex
The Frobenius endomorphism
![]() $F:R\rightarrow R$
induces a natural Frobenius action
$F:R\rightarrow R$
induces a natural Frobenius action
![]() $F:H_{I}^{i}(R)\rightarrow H_{I^{[p]}}^{i}(R)\cong H_{I}^{i}(R)$
. A local ring
$F:H_{I}^{i}(R)\rightarrow H_{I^{[p]}}^{i}(R)\cong H_{I}^{i}(R)$
. A local ring
![]() $(R,\mathfrak{m})$
is called
$(R,\mathfrak{m})$
is called
![]() $F$
-injective if the Frobenius action on
$F$
-injective if the Frobenius action on
![]() $H_{\mathfrak{m}}^{i}(R)$
is injective for all
$H_{\mathfrak{m}}^{i}(R)$
is injective for all
![]() $i\geqslant 0$
. This is the case if
$i\geqslant 0$
. This is the case if
![]() $R$
is
$R$
is
![]() $F$
-pure [Reference Hochster and Roberts12, Lemma 2.2]. One can also characterize
$F$
-pure [Reference Hochster and Roberts12, Lemma 2.2]. One can also characterize
![]() $F$
-injectivity using certain ideal closure operations (see [Reference Ma17, Reference Quy and Shimomoto20] for more details).
$F$
-injectivity using certain ideal closure operations (see [Reference Ma17, Reference Quy and Shimomoto20] for more details).
Example 2.2. Let
![]() $I=(x_{1},\ldots ,x_{t})\subseteq R$
be an ideal generated by
$I=(x_{1},\ldots ,x_{t})\subseteq R$
be an ideal generated by
![]() $t$
elements. By the above discussion we have
$t$
elements. By the above discussion we have
and the natural Frobenius action on
![]() $H_{I}^{t}(R)$
sends
$H_{I}^{t}(R)$
sends
![]() $1/(x_{1}\cdots x_{t})$
to
$1/(x_{1}\cdots x_{t})$
to
![]() $1/(x_{1}^{p}\cdots x_{t}^{p})$
. Therefore, it is easy to see the Frobenius action on
$1/(x_{1}^{p}\cdots x_{t}^{p})$
. Therefore, it is easy to see the Frobenius action on
![]() $H_{I}^{t}(R)$
is full (in fact,
$H_{I}^{t}(R)$
is full (in fact,
![]() $\mathscr{F}_{R}(H_{I}^{t}(R))\rightarrow H_{I}^{t}(R)$
is an isomorphism). On the other hand, one cannot expect
$\mathscr{F}_{R}(H_{I}^{t}(R))\rightarrow H_{I}^{t}(R)$
is an isomorphism). On the other hand, one cannot expect
![]() $H_{I}^{t}(R)$
is always anti-nilpotent even when
$H_{I}^{t}(R)$
is always anti-nilpotent even when
![]() $R$
is regular. For example, let
$R$
is regular. For example, let
![]() $R=k[[x,y]]$
be a formal power series ring in two variables and
$R=k[[x,y]]$
be a formal power series ring in two variables and
![]() $I=(x)$
. We have
$I=(x)$
. We have
Let
![]() $N$
be the submodule of
$N$
be the submodule of
![]() $H_{(x)}^{1}(R)$
generated by
$H_{(x)}^{1}(R)$
generated by
![]() $\{y^{2}x^{-n}\}_{n=1}^{\infty }$
, then it is easy to see
$\{y^{2}x^{-n}\}_{n=1}^{\infty }$
, then it is easy to see
![]() $N$
is an
$N$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $H_{(x)}^{1}(R)$
. However,
$H_{(x)}^{1}(R)$
. However,
![]() $F(yx^{-1})=y^{p}x^{-p}\in N$
while
$F(yx^{-1})=y^{p}x^{-p}\in N$
while
![]() $yx^{-1}\notin N$
. So the Frobenius action on
$yx^{-1}\notin N$
. So the Frobenius action on
![]() $H_{(x)}^{1}(R)/N$
is not injective and hence
$H_{(x)}^{1}(R)/N$
is not injective and hence
![]() $H_{(x)}^{1}(R)$
is not anti-nilpotent.
$H_{(x)}^{1}(R)$
is not anti-nilpotent.
We are mostly interested in the Frobenius actions on local cohomology modules of
![]() $R$
supported at the maximal ideal. We introduce two notions of
$R$
supported at the maximal ideal. We introduce two notions of
![]() $F$
-singularities.
$F$
-singularities.
Definition 2.3.
(1) We say that
 $(R,\mathfrak{m})$
is
$(R,\mathfrak{m})$
is
 $F$
-full, if the Frobenius action on
$F$
-full, if the Frobenius action on
 $H_{\mathfrak{m}}^{i}(R)$
is full for every
$H_{\mathfrak{m}}^{i}(R)$
is full for every
 $i\geqslant 0$
. This means
$i\geqslant 0$
. This means
 $\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))\rightarrow H_{\mathfrak{m}}^{i}(R)$
is surjective for every
$\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))\rightarrow H_{\mathfrak{m}}^{i}(R)$
is surjective for every
 $i\geqslant 0$
.
$i\geqslant 0$
.(2) We say that
 $(R,\mathfrak{m})$
is
$(R,\mathfrak{m})$
is
 $F$
-anti-nilpotent, if the Frobenius action on
$F$
-anti-nilpotent, if the Frobenius action on
 $H_{\mathfrak{m}}^{i}(R)$
is anti-nilpotent for every
$H_{\mathfrak{m}}^{i}(R)$
is anti-nilpotent for every
 $i\geqslant 0$
.
$i\geqslant 0$
.
The concept of
![]() $F$
-anti-nilpotency is not new, it was introduced and studied in [Reference Enescu and Hochster5] and [Reference Ma16] under the name stably FH-finite: that is, all local cohomology modules of
$F$
-anti-nilpotency is not new, it was introduced and studied in [Reference Enescu and Hochster5] and [Reference Ma16] under the name stably FH-finite: that is, all local cohomology modules of
![]() $R$
and
$R$
and
![]() $R[[x_{1},\ldots ,x_{n}]]$
supported at their maximal ideals have only finitely many
$R[[x_{1},\ldots ,x_{n}]]$
supported at their maximal ideals have only finitely many
![]() $F$
-stable submodules. It is a nontrivial result [Reference Enescu and Hochster5, Theorem 4.15] that this is equivalent to
$F$
-stable submodules. It is a nontrivial result [Reference Enescu and Hochster5, Theorem 4.15] that this is equivalent to
![]() $R$
being
$R$
being
![]() $F$
-anti-nilpotent.
$F$
-anti-nilpotent.
Remark 2.4.
(1) It is clear that
 $F$
-anti-nilpotent implies
$F$
-anti-nilpotent implies
 $F$
-injective and
$F$
-injective and
 $F$
-full (see Lemma 2.1). Moreover,
$F$
-full (see Lemma 2.1). Moreover,
 $F$
-pure local rings are
$F$
-pure local rings are
 $F$
-anti-nilpotent [Reference Ma16, Theorem 1.1]. In particular,
$F$
-anti-nilpotent [Reference Ma16, Theorem 1.1]. In particular,
 $F$
-pure local rings are
$F$
-pure local rings are
 $F$
-full.
$F$
-full.(2) We can construct many
 $F$
-anti-nilpotent (equivalently, stably FH-finite) rings that are not
$F$
-anti-nilpotent (equivalently, stably FH-finite) rings that are not
 $F$
-pure [Reference Quy and Shimomoto20, Sections 5 and 6].
$F$
-pure [Reference Quy and Shimomoto20, Sections 5 and 6].(3) Cohen–Macaulay rings are automatically
 $F$
-full, since
$F$
-full, since
 $\mathscr{F}_{R}(H_{\mathfrak{m}}^{d}(R))\rightarrow H_{\mathfrak{m}}^{d}(R)$
is an isomorphism. But even
$\mathscr{F}_{R}(H_{\mathfrak{m}}^{d}(R))\rightarrow H_{\mathfrak{m}}^{d}(R)$
is an isomorphism. But even
 $F$
-injective Cohen–Macaulay rings are not necessarily
$F$
-injective Cohen–Macaulay rings are not necessarily
 $F$
-anti-nilpotent [Reference Enescu and Hochster5, Example 2.16].
$F$
-anti-nilpotent [Reference Enescu and Hochster5, Example 2.16].
We give some simple examples of rings that are not
![]() $F$
-full, we see a family of such rings in Example 3.6.
$F$
-full, we see a family of such rings in Example 3.6.
Example 2.5.
(1) Let
 $R=k[s^{4},s^{3}t,st^{3},t^{4}]$
where
$R=k[s^{4},s^{3}t,st^{3},t^{4}]$
where
 $k$
is a field of characteristic
$k$
is a field of characteristic
 $p>0$
. Then
$p>0$
. Then
 $R$
is a graded ring with
$R$
is a graded ring with
 $s^{4},t^{4}$
a homogeneous system of parameters. A simple computation shows that the class spans the local cohomology module
$s^{4},t^{4}$
a homogeneous system of parameters. A simple computation shows that the class spans the local cohomology module $$\begin{eqnarray}\left[\frac{(s^{3}t)^{2}}{s^{4}},-\frac{(st^{3})^{2}}{t^{4}}\right]\in R_{s^{4}}\oplus R_{t^{4}}\end{eqnarray}$$
$$\begin{eqnarray}\left[\frac{(s^{3}t)^{2}}{s^{4}},-\frac{(st^{3})^{2}}{t^{4}}\right]\in R_{s^{4}}\oplus R_{t^{4}}\end{eqnarray}$$
 $H_{\mathfrak{m}}^{1}(R)$
. In particular,
$H_{\mathfrak{m}}^{1}(R)$
. In particular,
 $[H_{\mathfrak{m}}^{1}(R)]$
sits only in degree 2 and thus the natural Frobenius map kills
$[H_{\mathfrak{m}}^{1}(R)]$
sits only in degree 2 and thus the natural Frobenius map kills
 $H_{\mathfrak{m}}^{1}(R)$
.
$H_{\mathfrak{m}}^{1}(R)$
.
 $R$
is not
$R$
is not
 $F$
-full.
$F$
-full.(2) Let
 $R=(k[x,y,z]/(x^{3}+y^{3}+z^{3}))\#k[s,t]$
be the Segre product of
$R=(k[x,y,z]/(x^{3}+y^{3}+z^{3}))\#k[s,t]$
be the Segre product of
 $A=(k[x,y,z]/(x^{3}+y^{3}+z^{3}))$
and
$A=(k[x,y,z]/(x^{3}+y^{3}+z^{3}))$
and
 $B=k[s,t]$
, where
$B=k[s,t]$
, where
 $k$
is a field of characteristic
$k$
is a field of characteristic
 $p>0$
with
$p>0$
with
 $p\equiv 2$
mod
$p\equiv 2$
mod
 $3$
. Then
$3$
. Then
 $R$
is a normal domain, since it is a direct summand of
$R$
is a normal domain, since it is a direct summand of
 $A\otimes _{k}B=A[s,t]$
. Moreover, a direct computation (for example see [Reference Ma, Schwede and Shimomoto18, Examples 4.11 and 4.16]) shows that Since
$A\otimes _{k}B=A[s,t]$
. Moreover, a direct computation (for example see [Reference Ma, Schwede and Shimomoto18, Examples 4.11 and 4.16]) shows that Since $$\begin{eqnarray}H_{\mathfrak{m}_{R}}^{2}(R)=[H_{\mathfrak{ m}_{R}}^{2}(R)]_{0}\cong [H_{\mathfrak{m}_{A}}^{2}(A)]_{0}=k.\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{m}_{R}}^{2}(R)=[H_{\mathfrak{ m}_{R}}^{2}(R)]_{0}\cong [H_{\mathfrak{m}_{A}}^{2}(A)]_{0}=k.\end{eqnarray}$$
 $p\equiv 2$
mod 3, we know the natural Frobenius map kills
$p\equiv 2$
mod 3, we know the natural Frobenius map kills
 $[H_{\mathfrak{m}_{A}}^{2}(A)]_{0}$
. Hence
$[H_{\mathfrak{m}_{A}}^{2}(A)]_{0}$
. Hence
 $R$
is not
$R$
is not
 $F$
-full. On the other hand, if
$F$
-full. On the other hand, if
 $p\equiv 1$
mod
$p\equiv 1$
mod
 $3$
, then it is well known that
$3$
, then it is well known that
 $R$
is
$R$
is
 $F$
-pure (since
$F$
-pure (since
 $A$
is) and hence
$A$
is) and hence
 $F$
-anti-nilpotent [Reference Ma16, Theorem 1.1].
$F$
-anti-nilpotent [Reference Ma16, Theorem 1.1].
Remark 2.6.
(1) When
 $R$
is a homomorphic image of a regular ring
$R$
is a homomorphic image of a regular ring
 $A$
, say
$A$
, say
 $R=A/I$
,
$R=A/I$
,
 $R$
is
$R$
is
 $F$
-full if and only if
$F$
-full if and only if
 $H_{\mathfrak{m}}^{i}(A/J)\rightarrow H_{\mathfrak{m}}^{i}(A/I)$
is surjective for every
$H_{\mathfrak{m}}^{i}(A/J)\rightarrow H_{\mathfrak{m}}^{i}(A/I)$
is surjective for every
 $J\subseteq I\subseteq \sqrt{J}$
. This is because by [Reference Lyubeznik15, Lemma 2.2], the
$J\subseteq I\subseteq \sqrt{J}$
. This is because by [Reference Lyubeznik15, Lemma 2.2], the
 $R$
-span of
$R$
-span of
 $F^{e}(H_{\mathfrak{m}}^{i}(R))$
is the same as the image
$F^{e}(H_{\mathfrak{m}}^{i}(R))$
is the same as the image
 $H_{\mathfrak{m}}^{i}(A/I^{[p^{e}]})\rightarrow H_{\mathfrak{m}}^{i}(A/I)$
, and for every
$H_{\mathfrak{m}}^{i}(A/I^{[p^{e}]})\rightarrow H_{\mathfrak{m}}^{i}(A/I)$
, and for every
 $J\subseteq I\subseteq \sqrt{J}$
,
$J\subseteq I\subseteq \sqrt{J}$
,
 $I^{[p^{e}]}\subseteq J$
for
$I^{[p^{e}]}\subseteq J$
for
 $e\gg 0$
. As an application, when
$e\gg 0$
. As an application, when
 $R=A/I$
is
$R=A/I$
is
 $F$
-full, we have
$F$
-full, we have
 $H_{\mathfrak{m}}^{i}(A/I)=0$
provided
$H_{\mathfrak{m}}^{i}(A/I)=0$
provided
 $H_{\mathfrak{m}}^{i}(A/J)=0$
. Hence
$H_{\mathfrak{m}}^{i}(A/J)=0$
. Hence
 $\operatorname{depth}A/I\geqslant \operatorname{depth}A/J$
for every
$\operatorname{depth}A/I\geqslant \operatorname{depth}A/J$
for every
 $J\subseteq I\subseteq \sqrt{J}$
.
$J\subseteq I\subseteq \sqrt{J}$
.(2) Suppose
 $R$
is a local ring essentially of finite type over
$R$
is a local ring essentially of finite type over
 $\mathbb{C}$
and
$\mathbb{C}$
and
 $R$
is Du Bois (we refer to [Reference Schwede21] or [Reference Ma, Schwede and Shimomoto18] for the definition and basic properties of Du Bois singularities). In this case we do have
$R$
is Du Bois (we refer to [Reference Schwede21] or [Reference Ma, Schwede and Shimomoto18] for the definition and basic properties of Du Bois singularities). In this case we do have
 $H_{\mathfrak{m}}^{i}(A/J)\rightarrow H_{\mathfrak{m}}^{i}(A/I)$
is surjective for every
$H_{\mathfrak{m}}^{i}(A/J)\rightarrow H_{\mathfrak{m}}^{i}(A/I)$
is surjective for every
 $J\subseteq I=\sqrt{J}$
[Reference Ma, Schwede and Shimomoto18, Lemma 3.3]. This is the main ingredient in proving singularities of dense
$J\subseteq I=\sqrt{J}$
[Reference Ma, Schwede and Shimomoto18, Lemma 3.3]. This is the main ingredient in proving singularities of dense
 $F$
-injective type deform [Reference Ma, Schwede and Shimomoto18, Theorem C].
$F$
-injective type deform [Reference Ma, Schwede and Shimomoto18, Theorem C].(3) Since
 $F$
-injective singularity is the conjectured characteristic
$F$
-injective singularity is the conjectured characteristic
 $p>0$
analog of Du Bois singularity [Reference Bhatt, Schwede and Takagi1, Reference Schwede21], it is thus quite natural to ask whether
$p>0$
analog of Du Bois singularity [Reference Bhatt, Schwede and Takagi1, Reference Schwede21], it is thus quite natural to ask whether
 $F$
-injective local rings are always
$F$
-injective local rings are always
 $F$
-full. It turns out that this is false in general [Reference Ma, Schwede and Shimomoto18, Example 3.5]. However, constructing such examples seems hard. In fact, [Reference Enescu and Hochster5, Example 2.16] (or its variants like [Reference Ma, Schwede and Shimomoto18, Example 3.5]) is the only example we know that is
$F$
-full. It turns out that this is false in general [Reference Ma, Schwede and Shimomoto18, Example 3.5]. However, constructing such examples seems hard. In fact, [Reference Enescu and Hochster5, Example 2.16] (or its variants like [Reference Ma, Schwede and Shimomoto18, Example 3.5]) is the only example we know that is
 $F$
-injective but not
$F$
-injective but not
 $F$
-anti-nilpotent.
$F$
-anti-nilpotent.
The above remarks motivate us to introduce and study
![]() $F$
-fullness and a stronger notion of
$F$
-fullness and a stronger notion of
![]() $F$
-injectivity (see Section 5).
$F$
-injectivity (see Section 5).
We end this subsection by proving that
![]() $F$
-full rings localize. Note that it is proved in [Reference Ma16, Theorem 5.10] that
$F$
-full rings localize. Note that it is proved in [Reference Ma16, Theorem 5.10] that
![]() $F$
-anti-nilpotent rings localize.
$F$
-anti-nilpotent rings localize.
For convenience, we use
![]() $R^{(1)}$
to denote the target ring of the Frobenius map
$R^{(1)}$
to denote the target ring of the Frobenius map
![]() $R\overset{F}{\rightarrow }R^{(1)}$
. If
$R\overset{F}{\rightarrow }R^{(1)}$
. If
![]() $M$
is an
$M$
is an
![]() $R$
-module, then
$R$
-module, then
![]() $\operatorname{Hom}_{R}(R^{(1)},M)$
has a structure of an
$\operatorname{Hom}_{R}(R^{(1)},M)$
has a structure of an
![]() $R^{(1)}$
-module. We can then identify
$R^{(1)}$
-module. We can then identify
![]() $R^{(1)}$
with
$R^{(1)}$
with
![]() $R$
, and
$R$
, and
![]() $\operatorname{Hom}_{R}(R^{(1)},M)$
corresponds to an
$\operatorname{Hom}_{R}(R^{(1)},M)$
corresponds to an
![]() $R$
-module which we call
$R$
-module which we call
![]() $F^{\flat }(M)$
(we refer to [Reference Blickle and Böckle2, Section 2.3] for more details on this). When
$F^{\flat }(M)$
(we refer to [Reference Blickle and Böckle2, Section 2.3] for more details on this). When
![]() $R$
is
$R$
is
![]() $F$
-finite, we have
$F$
-finite, we have
![]() $\operatorname{Hom}_{R}(R^{(1)},E_{R})\cong E_{R^{(1)}}$
and
$\operatorname{Hom}_{R}(R^{(1)},E_{R})\cong E_{R^{(1)}}$
and
![]() $F^{\flat }(E)\cong E_{R}$
, where
$F^{\flat }(E)\cong E_{R}$
, where
![]() $E_{R}$
denotes the injective hull of the residue field of
$E_{R}$
denotes the injective hull of the residue field of
![]() $(R,\mathfrak{m})$
.
$(R,\mathfrak{m})$
.
Proposition 2.7. Let
![]() $(R,\mathfrak{m})$
be an
$(R,\mathfrak{m})$
be an
![]() $F$
-finite and
$F$
-finite and
![]() $F$
-full local ring. Then
$F$
-full local ring. Then
![]() $R_{\mathfrak{p}}$
is also
$R_{\mathfrak{p}}$
is also
![]() $F$
-full for every
$F$
-full for every
![]() $\mathfrak{p}\in \operatorname{Spec}R$
.
$\mathfrak{p}\in \operatorname{Spec}R$
.
Proof. By a result of Gabber [Reference Gabber7, Remark 13.6],
![]() $R$
is a homomorphic image of a regular ring
$R$
is a homomorphic image of a regular ring
![]() $A$
. Let
$A$
. Let
![]() $n=\dim A$
. We have
$n=\dim A$
. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Hom}_{R^{(1)}}(\operatorname{Hom}_{R}(R^{(1)},\operatorname{Ext}_{A}^{n-i}(R,A)),E_{R^{(1)}})\nonumber\\ \displaystyle & & \displaystyle \quad \cong \operatorname{Hom}_{R^{(1)}}(\operatorname{Hom}_{R}(R^{(1)},\operatorname{Ext}_{A}^{n-i}(R,A)),\operatorname{Hom}_{R}(R^{(1)},E_{R}))\nonumber\\ \displaystyle & & \displaystyle \quad \cong \operatorname{Hom}_{R}(\operatorname{Hom}_{R}(R^{(1)},\operatorname{Ext}_{A}^{n-i}(R,A)),E_{R})\nonumber\\ \displaystyle & & \displaystyle \quad \cong R^{(1)}\otimes \operatorname{Hom}_{R}(\operatorname{Ext}_{A}^{n-i}(R,A),E_{R})\nonumber\\ \displaystyle & & \displaystyle \quad \cong R^{(1)}\otimes H_{\mathfrak{m}}^{i}(R)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Hom}_{R^{(1)}}(\operatorname{Hom}_{R}(R^{(1)},\operatorname{Ext}_{A}^{n-i}(R,A)),E_{R^{(1)}})\nonumber\\ \displaystyle & & \displaystyle \quad \cong \operatorname{Hom}_{R^{(1)}}(\operatorname{Hom}_{R}(R^{(1)},\operatorname{Ext}_{A}^{n-i}(R,A)),\operatorname{Hom}_{R}(R^{(1)},E_{R}))\nonumber\\ \displaystyle & & \displaystyle \quad \cong \operatorname{Hom}_{R}(\operatorname{Hom}_{R}(R^{(1)},\operatorname{Ext}_{A}^{n-i}(R,A)),E_{R})\nonumber\\ \displaystyle & & \displaystyle \quad \cong R^{(1)}\otimes \operatorname{Hom}_{R}(\operatorname{Ext}_{A}^{n-i}(R,A),E_{R})\nonumber\\ \displaystyle & & \displaystyle \quad \cong R^{(1)}\otimes H_{\mathfrak{m}}^{i}(R)\nonumber\end{eqnarray}$$
where the last isomorphism is by local duality. Thus after identifying
![]() $R^{(1)}$
with
$R^{(1)}$
with
![]() $R$
, we have
$R$
, we have
![]() $\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))$
is the Matlis dual of
$\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))$
is the Matlis dual of
![]() $F^{\flat }(\operatorname{Ext}_{A}^{n-i}(R,A))$
. So
$F^{\flat }(\operatorname{Ext}_{A}^{n-i}(R,A))$
. So
![]() $\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))\rightarrow H_{\mathfrak{m}}^{i}(R)$
is surjective for every
$\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))\rightarrow H_{\mathfrak{m}}^{i}(R)$
is surjective for every
![]() $i$
if and only if
$i$
if and only if
![]() $\operatorname{Ext}_{A}^{n-i}(R,A)\rightarrow F^{\flat }(\operatorname{Ext}_{A}^{n-i}(R,A))$
is injective for every
$\operatorname{Ext}_{A}^{n-i}(R,A)\rightarrow F^{\flat }(\operatorname{Ext}_{A}^{n-i}(R,A))$
is injective for every
![]() $i$
. The latter condition clearly localizes. So
$i$
. The latter condition clearly localizes. So
![]() $R$
is
$R$
is
![]() $F$
-full implies
$F$
-full implies
![]() $R_{\mathfrak{p}}$
is
$R_{\mathfrak{p}}$
is
![]() $F$
-full for every
$F$
-full for every
![]() $\mathfrak{p}\in \operatorname{Spec}R$
.◻
$\mathfrak{p}\in \operatorname{Spec}R$
.◻
3 On surjective elements
The following definition was introduced in [Reference Horiuchi, Miller and Shimomoto11] and was the key tool in [Reference Horiuchi, Miller and Shimomoto11].
Definition 3.1. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring and
$(R,\mathfrak{m})$
be a Noetherian local ring and
![]() $x$
a regular element of
$x$
a regular element of
![]() $R$
.
$R$
.
![]() $x$
is called a surjective element if the natural map on the local cohomology module
$x$
is called a surjective element if the natural map on the local cohomology module
![]() $H_{\mathfrak{m}}^{i}(R/(x^{n}))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
induced by
$H_{\mathfrak{m}}^{i}(R/(x^{n}))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
induced by
![]() $R/(x^{n})\rightarrow R/(x)$
is surjective for all
$R/(x^{n})\rightarrow R/(x)$
is surjective for all
![]() $n>0$
and
$n>0$
and
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
The next proposition is a restatement of [Reference Horiuchi, Miller and Shimomoto11, Lemma 3.2], so we omit the proof.
Proposition 3.2. The following are equivalent:
(i)
 $x$
is a surjective element.
$x$
is a surjective element.(ii) For all
 $0<h\leqslant k$
the multiplication map induces an injection
$0<h\leqslant k$
the multiplication map induces an injection $$\begin{eqnarray}R/(x^{h})\overset{x^{k-h}}{\rightarrow }R/(x^{k})\end{eqnarray}$$
for each
$$\begin{eqnarray}R/(x^{h})\overset{x^{k-h}}{\rightarrow }R/(x^{k})\end{eqnarray}$$
for each $$\begin{eqnarray}H_{\mathfrak{m}}^{i}(R/(x^{h}))\rightarrow H_{\mathfrak{ m}}^{i}(R/(x^{k}))\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{m}}^{i}(R/(x^{h}))\rightarrow H_{\mathfrak{ m}}^{i}(R/(x^{k}))\end{eqnarray}$$
 $i\geqslant 0$
.
$i\geqslant 0$
.(iii) For all
 $0<h\leqslant k$
the short exact sequence induces a short exact sequence
$0<h\leqslant k$
the short exact sequence induces a short exact sequence $$\begin{eqnarray}0\rightarrow R/(x^{h})\overset{x^{k-h}}{\rightarrow }R/(x^{k})\rightarrow R/(x^{k-h})\rightarrow 0\end{eqnarray}$$
for each
$$\begin{eqnarray}0\rightarrow R/(x^{h})\overset{x^{k-h}}{\rightarrow }R/(x^{k})\rightarrow R/(x^{k-h})\rightarrow 0\end{eqnarray}$$
for each $$\begin{eqnarray}0\rightarrow H_{\mathfrak{m}}^{i}(R/(x^{h}))\rightarrow H_{\mathfrak{ m}}^{i}(R/(x^{k}))\rightarrow H_{\mathfrak{ m}}^{i}(R/(x^{k-h}))\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{\mathfrak{m}}^{i}(R/(x^{h}))\rightarrow H_{\mathfrak{ m}}^{i}(R/(x^{k}))\rightarrow H_{\mathfrak{ m}}^{i}(R/(x^{k-h}))\rightarrow 0\end{eqnarray}$$
 $i\geqslant 0$
.
$i\geqslant 0$
.
Proposition 3.3. The following are equivalent:
(i)
 $x$
is a surjective element.
$x$
is a surjective element.(ii) The multiplication map
 $H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for all
$H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for all
 $i\geqslant 0$
.
$i\geqslant 0$
.
Proof. By Proposition 3.2,
![]() $x$
is a surjective element if and only if all maps in the direct limit system
$x$
is a surjective element if and only if all maps in the direct limit system
![]() $\{H_{\mathfrak{m}}^{i}(R/(x^{h}))\}_{h\geqslant 1}$
are injective. This is equivalent to the condition
$\{H_{\mathfrak{m}}^{i}(R/(x^{h}))\}_{h\geqslant 1}$
are injective. This is equivalent to the condition
is injective for all
![]() $h\geqslant 1$
and all
$h\geqslant 1$
and all
![]() $i\geqslant 0$
(the last isomorphism comes from an easy computation using local cohomology spectral sequences and noting that
$i\geqslant 0$
(the last isomorphism comes from an easy computation using local cohomology spectral sequences and noting that
![]() $x$
is a nonzero divisor on
$x$
is a nonzero divisor on
![]() $R$
, see also [Reference Horiuchi, Miller and Shimomoto11, Lemma 2.2]).
$R$
, see also [Reference Horiuchi, Miller and Shimomoto11, Lemma 2.2]).
Claim 3.4.
![]() $\unicode[STIX]{x1D719}_{h}$
is exactly the connection maps in the long exact sequence of local cohomology induced by
$\unicode[STIX]{x1D719}_{h}$
is exactly the connection maps in the long exact sequence of local cohomology induced by
![]() $0\rightarrow R\xrightarrow[{}]{\cdot x^{h}}R\rightarrow R/(x^{h})\rightarrow 0$
:
$0\rightarrow R\xrightarrow[{}]{\cdot x^{h}}R\rightarrow R/(x^{h})\rightarrow 0$
:
Proof of claim.
Observe that by definition,
![]() $\unicode[STIX]{x1D719}_{h}$
is the natural map in the long exact sequence of local cohomology
$\unicode[STIX]{x1D719}_{h}$
is the natural map in the long exact sequence of local cohomology
which is induced by
![]() $0\rightarrow R/(x^{h})\rightarrow R_{x}/R\xrightarrow[{}]{\cdot x^{h}}R_{x}/R\rightarrow 0$
(note that
$0\rightarrow R/(x^{h})\rightarrow R_{x}/R\xrightarrow[{}]{\cdot x^{h}}R_{x}/R\rightarrow 0$
(note that
![]() $x^{h}$
is a nonzero divisor on
$x^{h}$
is a nonzero divisor on
![]() $R$
and
$R$
and
![]() $H_{x}^{1}(R)\cong R_{x}/R$
). However, it is easy to see that the multiplication by
$H_{x}^{1}(R)\cong R_{x}/R$
). However, it is easy to see that the multiplication by
![]() $x^{h}$
map
$x^{h}$
map
![]() $H_{\mathfrak{m}}^{i}(R_{x}/R)\xrightarrow[{}]{\cdot x^{h}}H_{\mathfrak{m}}^{i}(R_{x}/R)$
can be identified with the multiplication by
$H_{\mathfrak{m}}^{i}(R_{x}/R)\xrightarrow[{}]{\cdot x^{h}}H_{\mathfrak{m}}^{i}(R_{x}/R)$
can be identified with the multiplication by
![]() $x^{h}$
map
$x^{h}$
map
![]() $H_{\mathfrak{m}}^{i+1}(R)\xrightarrow[{}]{\cdot x^{h}}H_{\mathfrak{m}}^{i+1}(R)$
because we have a natural identification
$H_{\mathfrak{m}}^{i+1}(R)\xrightarrow[{}]{\cdot x^{h}}H_{\mathfrak{m}}^{i+1}(R)$
because we have a natural identification
![]() $H_{\mathfrak{m}}^{i}(R_{x}/R)\cong H_{\mathfrak{m}}^{i}(H_{x}^{1}(R))\cong H_{\mathfrak{m}}^{i+1}(R)$
(see for example [Reference Horiuchi, Miller and Shimomoto11, Lemma 2.2]). This finishes the proof of the claim.◻
$H_{\mathfrak{m}}^{i}(R_{x}/R)\cong H_{\mathfrak{m}}^{i}(H_{x}^{1}(R))\cong H_{\mathfrak{m}}^{i+1}(R)$
(see for example [Reference Horiuchi, Miller and Shimomoto11, Lemma 2.2]). This finishes the proof of the claim.◻
From the claim it is immediate that
![]() $x$
is a surjective element if and only if the long exact sequence splits into short exact sequences:
$x$
is a surjective element if and only if the long exact sequence splits into short exact sequences:
But this is equivalent to saying that the multiplication map
![]() $H_{\mathfrak{m}}^{i}(R)\overset{x^{h}}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for all
$H_{\mathfrak{m}}^{i}(R)\overset{x^{h}}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for all
![]() $h\geqslant 1$
and
$h\geqslant 1$
and
![]() $i\geqslant 0$
, and also equivalent to
$i\geqslant 0$
, and also equivalent to
![]() $H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for all
$H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for all
![]() $i\geqslant 0$
.◻
$i\geqslant 0$
.◻
We next link the notion of surjective element with
![]() $F$
-fullness. This is inspired by [Reference Ma, Schwede and Shimomoto18, Reference Singh and Walther24].
$F$
-fullness. This is inspired by [Reference Ma, Schwede and Shimomoto18, Reference Singh and Walther24].
Proposition 3.5. Let
![]() $x$
be a regular element of
$x$
be a regular element of
![]() $(R,\mathfrak{m})$
. If
$(R,\mathfrak{m})$
. If
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-full, then
$F$
-full, then
![]() $x$
is a surjective element. In particular, if
$x$
is a surjective element. In particular, if
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-anti-nilpotent, then
$F$
-anti-nilpotent, then
![]() $x$
is a surjective element.
$x$
is a surjective element.
Proof. We have natural maps:
 $$\begin{eqnarray}\displaystyle \mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x))) & \xrightarrow[{}]{\unicode[STIX]{x1D6FC}_{e}} & \displaystyle R/(x)\otimes _{R}\mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\cong \mathscr{F}_{R/(x)}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\nonumber\\ \displaystyle & \xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{e}} & \displaystyle H_{\mathfrak{m}}^{i}(R/(x)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x))) & \xrightarrow[{}]{\unicode[STIX]{x1D6FC}_{e}} & \displaystyle R/(x)\otimes _{R}\mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\cong \mathscr{F}_{R/(x)}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\nonumber\\ \displaystyle & \xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{e}} & \displaystyle H_{\mathfrak{m}}^{i}(R/(x)).\nonumber\end{eqnarray}$$
If
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-full, then
$F$
-full, then
![]() $\unicode[STIX]{x1D6FD}_{e}$
is surjective for every
$\unicode[STIX]{x1D6FD}_{e}$
is surjective for every
![]() $e$
. Since
$e$
. Since
![]() $\unicode[STIX]{x1D6FC}_{e}$
is always surjective, the natural map
$\unicode[STIX]{x1D6FC}_{e}$
is always surjective, the natural map
![]() $\mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
is surjective for every
$\mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
is surjective for every
![]() $e$
. Now simply notice that for every
$e$
. Now simply notice that for every
![]() $e>0$
, the map
$e>0$
, the map
![]() $\mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
factors through
$\mathscr{F}_{R}^{e}(H_{\mathfrak{m}}^{i}(R/(x)))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
factors through
![]() $H_{\mathfrak{m}}^{i}(R/(x^{p^{e}}))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
, so
$H_{\mathfrak{m}}^{i}(R/(x^{p^{e}}))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
, so
![]() $H_{\mathfrak{m}}^{i}(R/(x^{p^{e}}))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
is surjective for every
$H_{\mathfrak{m}}^{i}(R/(x^{p^{e}}))\rightarrow H_{\mathfrak{m}}^{i}(R/(x))$
is surjective for every
![]() $e>0$
. This clearly implies that
$e>0$
. This clearly implies that
![]() $x$
is a surjective element.◻
$x$
is a surjective element.◻
The above propositions allow us to construct a family of non
![]() $F$
-full local rings:
$F$
-full local rings:
Example 3.6. Let
![]() $(R,\mathfrak{m})$
be a local ring with finite length cohomology, that is,
$(R,\mathfrak{m})$
be a local ring with finite length cohomology, that is,
![]() $H_{\mathfrak{m}}^{i}(R)$
has finite length for every
$H_{\mathfrak{m}}^{i}(R)$
has finite length for every
![]() $i<\dim R$
(under mild conditions, this is equivalent to saying that
$i<\dim R$
(under mild conditions, this is equivalent to saying that
![]() $R$
is Cohen–Macaulay on the punctured spectrum). Let
$R$
is Cohen–Macaulay on the punctured spectrum). Let
![]() $x$
be an arbitrary regular element in
$x$
be an arbitrary regular element in
![]() $R$
. If
$R$
. If
![]() $R$
is not Cohen–Macaulay, then we claim that
$R$
is not Cohen–Macaulay, then we claim that
![]() $R/(x)$
is not
$R/(x)$
is not
![]() $F$
-full (and hence not
$F$
-full (and hence not
![]() $F$
-anti-nilpotent). For suppose it is, then
$F$
-anti-nilpotent). For suppose it is, then
![]() $x$
is a surjective element by Proposition 3.5, hence
$x$
is a surjective element by Proposition 3.5, hence
![]() $H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for every
$H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for every
![]() $i$
by Proposition 3.3. But since
$i$
by Proposition 3.3. But since
![]() $R$
has finite length cohomology, we also know that a power of
$R$
has finite length cohomology, we also know that a power of
![]() $x$
annihilates
$x$
annihilates
![]() $H_{\mathfrak{m}}^{i}(R)$
for every
$H_{\mathfrak{m}}^{i}(R)$
for every
![]() $i<\dim R$
. This implies
$i<\dim R$
. This implies
![]() $H_{\mathfrak{m}}^{i}(R)=0$
for every
$H_{\mathfrak{m}}^{i}(R)=0$
for every
![]() $i<\dim R$
. So
$i<\dim R$
. So
![]() $R$
is Cohen–Macaulay, a contradiction.
$R$
is Cohen–Macaulay, a contradiction.
We learned the following argument from [Reference Horiuchi, Miller and Shimomoto11, Lemma A.1]. Since it is a crucial technique of this paper, we provide a detailed proof.
Proposition 3.7. Let
![]() $(R,\mathfrak{m})$
be a local ring of prime characteristic
$(R,\mathfrak{m})$
be a local ring of prime characteristic
![]() $p$
and
$p$
and
![]() $x$
a regular element of
$x$
a regular element of
![]() $R$
. Let
$R$
. Let
![]() $s$
be a positive integer such that the map
$s$
be a positive integer such that the map
![]() $H_{\mathfrak{m}}^{s-1}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s-1}(R)$
is surjective and the Frobenius action on
$H_{\mathfrak{m}}^{s-1}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s-1}(R)$
is surjective and the Frobenius action on
![]() $H_{\mathfrak{m}}^{s-1}(R/(x))$
is injective, then the map
$H_{\mathfrak{m}}^{s-1}(R/(x))$
is injective, then the map
is injective.
Proof. The natural commutative diagram

induces the following commutative diagram (the left most
![]() $0$
comes from our hypothesis that the map
$0$
comes from our hypothesis that the map
![]() $H_{\mathfrak{m}}^{s-1}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s-1}(R)$
is surjective):
$H_{\mathfrak{m}}^{s-1}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s-1}(R)$
is surjective):

Suppose
![]() $y\in \operatorname{Ker}(x^{p-1}F)\cap \text{Soc}(H_{\mathfrak{m}}^{s}(R))$
. Then we have
$y\in \operatorname{Ker}(x^{p-1}F)\cap \text{Soc}(H_{\mathfrak{m}}^{s}(R))$
. Then we have
![]() $x\cdot y=0$
so there exists
$x\cdot y=0$
so there exists
![]() $z\in H_{\mathfrak{m}}^{s-1}(R/(x))$
such that
$z\in H_{\mathfrak{m}}^{s-1}(R/(x))$
such that
![]() $\unicode[STIX]{x1D6FC}(z)=y$
. Following the above commutative diagram we have
$\unicode[STIX]{x1D6FC}(z)=y$
. Following the above commutative diagram we have
However, since both
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D6FC}$
are injective, we have
$\unicode[STIX]{x1D6FC}$
are injective, we have
![]() $z=0$
and hence
$z=0$
and hence
![]() $y=0$
. This shows
$y=0$
. This shows
![]() $x^{p-1}F$
is injective and hence completes the proof.◻
$x^{p-1}F$
is injective and hence completes the proof.◻
Proposition 3.7 immediately generalizes the main result of [Reference Horiuchi, Miller and Shimomoto11]:
Corollary 3.8. (Compare with [Reference Horiuchi, Miller and Shimomoto11], Main Theorem)
Let
![]() $(R,\mathfrak{m})$
be a local ring of prime characteristic
$(R,\mathfrak{m})$
be a local ring of prime characteristic
![]() $p$
and
$p$
and
![]() $x$
a regular element of
$x$
a regular element of
![]() $R$
. Suppose
$R$
. Suppose
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective. Then we have
$F$
-injective. Then we have
(i) The map
 $H_{\mathfrak{m}}^{t}(R)\overset{x^{p-1}F}{\longrightarrow }H_{\mathfrak{m}}^{t}(R)$
is injective where
$H_{\mathfrak{m}}^{t}(R)\overset{x^{p-1}F}{\longrightarrow }H_{\mathfrak{m}}^{t}(R)$
is injective where
 $t=\operatorname{depth}R$
. In particular, the natural Frobenius action on
$t=\operatorname{depth}R$
. In particular, the natural Frobenius action on
 $H_{\mathfrak{m}}^{t}(R)$
is injective.
$H_{\mathfrak{m}}^{t}(R)$
is injective.(ii) Suppose
 $x$
is a surjective element. Then the map
$x$
is a surjective element. Then the map
 $H_{\mathfrak{m}}^{i}(R)\overset{x^{p-1}F}{\longrightarrow }H_{\mathfrak{m}}^{i}(R)$
is injective for all
$H_{\mathfrak{m}}^{i}(R)\overset{x^{p-1}F}{\longrightarrow }H_{\mathfrak{m}}^{i}(R)$
is injective for all
 $i\geqslant 0$
. In particular,
$i\geqslant 0$
. In particular,
 $R$
is
$R$
is
 $F$
-injective.
$F$
-injective.(iii) If
 $R/(x)$
is
$R/(x)$
is
 $F$
-full (e.g.,
$F$
-full (e.g.,
 $R$
is
$R$
is
 $F$
-anti-nilpotent or
$F$
-anti-nilpotent or
 $R$
is
$R$
is
 $F$
-pure), then
$F$
-pure), then
 $R$
is
$R$
is
 $F$
-injective.
$F$
-injective.
Proof. (i) Follows from Proposition 3.7 applied to
![]() $s=t$
, (ii) also follows from Proposition 3.7 (because
$s=t$
, (ii) also follows from Proposition 3.7 (because
![]() $H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for every
$H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R)$
is surjective for every
![]() $i\geqslant 0$
by Proposition 3.3), (iii) follows from (ii), because we know
$i\geqslant 0$
by Proposition 3.3), (iii) follows from (ii), because we know
![]() $x$
is a surjective element by Proposition 3.5.◻
$x$
is a surjective element by Proposition 3.5.◻
In the next two sections, we show that
![]() $F$
-full and
$F$
-full and
![]() $F$
-anti-nilpotent singularities both deform. We also prove new cases of deformation of
$F$
-anti-nilpotent singularities both deform. We also prove new cases of deformation of
![]() $F$
-injectivity. These results are generalizations of Proposition 3.7 and Corollary 3.8.
$F$
-injectivity. These results are generalizations of Proposition 3.7 and Corollary 3.8.
4 Deformation of
 $F$
-full and
$F$
-full and
 $F$
-anti-nilpotent singularities
$F$
-anti-nilpotent singularities
In this section we prove that the condition
![]() $F$
-full and
$F$
-full and
![]() $F$
-anti-nilpotent both deform. Throughout this section we assume that
$F$
-anti-nilpotent both deform. Throughout this section we assume that
![]() $(R,\mathfrak{m})$
is a local ring of prime characteristic
$(R,\mathfrak{m})$
is a local ring of prime characteristic
![]() $p$
. We begin with a crucial lemma.
$p$
. We begin with a crucial lemma.
Lemma 4.1. Let
![]() $x$
be a surjective element of
$x$
be a surjective element of
![]() $R$
. Let
$R$
. Let
![]() $N\subseteq H_{\mathfrak{m}}^{i}(R)$
be an
$N\subseteq H_{\mathfrak{m}}^{i}(R)$
be an
![]() $F$
-stable submodule. Let
$F$
-stable submodule. Let
![]() $L=\bigcap _{t}x^{t}N$
. Then
$L=\bigcap _{t}x^{t}N$
. Then
![]() $L$
is an
$L$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $H_{\mathfrak{m}}^{i}(R)$
and we have the following commutative diagram (for every
$H_{\mathfrak{m}}^{i}(R)$
and we have the following commutative diagram (for every
![]() $e\geqslant 1$
):
$e\geqslant 1$
):

where
![]() $\unicode[STIX]{x1D719}$
is the map
$\unicode[STIX]{x1D719}$
is the map
![]() $H_{\mathfrak{m}}^{i-1}(R/(x))\rightarrow H_{\mathfrak{m}}^{i}(R)$
.
$H_{\mathfrak{m}}^{i-1}(R/(x))\rightarrow H_{\mathfrak{m}}^{i}(R)$
.
Proof. Since
![]() $x$
is a surjective element, by Proposition 3.3 we know that the map
$x$
is a surjective element, by Proposition 3.3 we know that the map
Applying the local cohomology functor to the following commutative diagram:

we have the following commutative diagram:

for all
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
![]() $e\geqslant 1$
, where the rows are short exact sequences by
$e\geqslant 1$
, where the rows are short exact sequences by
![]() $(\star )$
.
$(\star )$
.
Therefore, to prove the lemma, it suffices to show that
![]() $L$
is
$L$
is
![]() $F$
-stable and
$F$
-stable and
is exact. It is clear that
![]() $L$
is
$L$
is
![]() $F$
-stable since it is an intersection of
$F$
-stable since it is an intersection of
![]() $F$
-stable submodules of
$F$
-stable submodules of
![]() $H_{\mathfrak{m}}^{i}(R)$
. To see the exactness of the above sequence, first note that
$H_{\mathfrak{m}}^{i}(R)$
. To see the exactness of the above sequence, first note that
![]() $\operatorname{Im}(\unicode[STIX]{x1D719})=0:_{H_{\mathfrak{m}}^{i}(R)}x$
, so
$\operatorname{Im}(\unicode[STIX]{x1D719})=0:_{H_{\mathfrak{m}}^{i}(R)}x$
, so
![]() $L+\operatorname{Im}(\unicode[STIX]{x1D719})\subseteq L:_{H_{\mathfrak{m}}^{i}(R)}x$
. Thus it is enough to check that
$L+\operatorname{Im}(\unicode[STIX]{x1D719})\subseteq L:_{H_{\mathfrak{m}}^{i}(R)}x$
. Thus it is enough to check that
![]() $L:_{H_{\mathfrak{m}}^{i}(R)}x\subseteq L+\operatorname{Im}(\unicode[STIX]{x1D719})$
. Let
$L:_{H_{\mathfrak{m}}^{i}(R)}x\subseteq L+\operatorname{Im}(\unicode[STIX]{x1D719})$
. Let
![]() $y$
be an element such that
$y$
be an element such that
![]() $xy\in L$
. Since
$xy\in L$
. Since
![]() $L=xL$
by the construction of
$L=xL$
by the construction of
![]() $L$
, there exists
$L$
, there exists
![]() $z\in L$
such that
$z\in L$
such that
![]() $xy=xz$
. So
$xy=xz$
. So
![]() $y-z\in \operatorname{Im}(\unicode[STIX]{x1D719})$
and hence
$y-z\in \operatorname{Im}(\unicode[STIX]{x1D719})$
and hence
![]() $y\in L+\operatorname{Im}(\unicode[STIX]{x1D719})$
, as desired.◻
$y\in L+\operatorname{Im}(\unicode[STIX]{x1D719})$
, as desired.◻
We are ready to prove the main result of this section. This answers [Reference Quy and Shimomoto20, Problem 4] for stably FH-finiteness.
Theorem 4.2.
![]() $(R,\mathfrak{m})$
be a local ring of positive characteristic
$(R,\mathfrak{m})$
be a local ring of positive characteristic
![]() $p$
and
$p$
and
![]() $x$
a regular element of
$x$
a regular element of
![]() $R$
. Then we have:
$R$
. Then we have:
(i) if
 $R/(x)$
is
$R/(x)$
is
 $F$
-anti-nilpotent, then so is
$F$
-anti-nilpotent, then so is
 $R$
;
$R$
;(ii) if
 $R/(x)$
is
$R/(x)$
is
 $F$
-full, then so is
$F$
-full, then so is
 $R$
.
$R$
.
Proof. We first prove (i). Let
![]() $N$
be an
$N$
be an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $H_{\mathfrak{m}}^{i}(R)$
. We want to show that the induced Frobenius action on
$H_{\mathfrak{m}}^{i}(R)$
. We want to show that the induced Frobenius action on
![]() $H_{\mathfrak{m}}^{i}(R)/N$
is injective. Since
$H_{\mathfrak{m}}^{i}(R)/N$
is injective. Since
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-anti-nilpotent,
$F$
-anti-nilpotent,
![]() $x$
is a surjective element by Proposition 3.5. Let
$x$
is a surjective element by Proposition 3.5. Let
![]() $L=\bigcap _{t}x^{t}N$
. By Lemma 4.1, we have the following commutative diagram:
$L=\bigcap _{t}x^{t}N$
. By Lemma 4.1, we have the following commutative diagram:

We first claim that the middle map
![]() $x^{p^{e}-1}F^{e}:H_{\mathfrak{m}}^{i}(R)/L\rightarrow H_{\mathfrak{m}}^{i}(R)/L$
is injective. Let
$x^{p^{e}-1}F^{e}:H_{\mathfrak{m}}^{i}(R)/L\rightarrow H_{\mathfrak{m}}^{i}(R)/L$
is injective. Let
![]() $y\in \operatorname{Ker}(x^{p^{e}-1}F^{e})\cap \text{Soc}(H_{\mathfrak{m}}^{i}(R)/L)$
. We have
$y\in \operatorname{Ker}(x^{p^{e}-1}F^{e})\cap \text{Soc}(H_{\mathfrak{m}}^{i}(R)/L)$
. We have
![]() $x\cdot y=0$
, so
$x\cdot y=0$
, so
![]() $y=\unicode[STIX]{x1D719}(z)$
for some
$y=\unicode[STIX]{x1D719}(z)$
for some
![]() $z\in H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
. It is easy to see that
$z\in H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
. It is easy to see that
![]() $\unicode[STIX]{x1D719}^{-1}(L)$
is an
$\unicode[STIX]{x1D719}^{-1}(L)$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $H_{\mathfrak{m}}^{i-1}(R/(x))$
and
$H_{\mathfrak{m}}^{i-1}(R/(x))$
and
![]() $F^{e}(z)=0$
. Since
$F^{e}(z)=0$
. Since
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-anti-nilpotent, we know the Frobenius action
$F$
-anti-nilpotent, we know the Frobenius action
![]() $F$
, and hence its iterate
$F$
, and hence its iterate
![]() $F^{e}$
, on
$F^{e}$
, on
![]() $H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
is injective. Therefore,
$H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
is injective. Therefore,
![]() $z=0$
and hence
$z=0$
and hence
![]() $y=0$
. This proves that
$y=0$
. This proves that
![]() $x^{p^{e}-1}F^{e}$
and hence
$x^{p^{e}-1}F^{e}$
and hence
![]() $F$
acts injectively on
$F$
acts injectively on
![]() $H_{\mathfrak{m}}^{i}(R)/L$
.
$H_{\mathfrak{m}}^{i}(R)/L$
.
Note that we have a descending chain
![]() $N\supseteq xN\supseteq x^{2}N\supseteq \cdots \,.$
Since
$N\supseteq xN\supseteq x^{2}N\supseteq \cdots \,.$
Since
![]() $H_{\mathfrak{m}}^{i}(R)$
is Artinian,
$H_{\mathfrak{m}}^{i}(R)$
is Artinian,
![]() $L=\bigcap _{t}x^{t}N=x^{n}N$
for all
$L=\bigcap _{t}x^{t}N=x^{n}N$
for all
![]() $n\gg 0$
. We next claim that
$n\gg 0$
. We next claim that
![]() $L=N$
, this will finish the proof because we already showed
$L=N$
, this will finish the proof because we already showed
![]() $F$
acts injectively on
$F$
acts injectively on
![]() $H_{\mathfrak{m}}^{i}(R)/L$
. We have
$H_{\mathfrak{m}}^{i}(R)/L$
. We have
![]() $x^{p^{e}-1}F^{e}(N)\subseteq x^{p^{e}-1}N=L$
for
$x^{p^{e}-1}F^{e}(N)\subseteq x^{p^{e}-1}N=L$
for
![]() $e\gg 0$
, but the map
$e\gg 0$
, but the map
![]() $x^{p^{e}-1}F^{e}:H_{\mathfrak{m}}^{i}(R)/L\rightarrow H_{\mathfrak{m}}^{i}(R)/L$
is injective by the above paragraph. So we must have
$x^{p^{e}-1}F^{e}:H_{\mathfrak{m}}^{i}(R)/L\rightarrow H_{\mathfrak{m}}^{i}(R)/L$
is injective by the above paragraph. So we must have
![]() $N\subseteq L$
and thus
$N\subseteq L$
and thus
![]() $L=N$
. This completes the proof of (1).
$L=N$
. This completes the proof of (1).
Next we prove (ii). The method is similar to that of (i). Let
![]() $N$
be the
$N$
be the
![]() $R$
-span of
$R$
-span of
![]() $F(H_{\mathfrak{m}}^{i}(R))$
in
$F(H_{\mathfrak{m}}^{i}(R))$
in
![]() $H_{\mathfrak{m}}^{i}(R)$
, this is the same as the image of
$H_{\mathfrak{m}}^{i}(R)$
, this is the same as the image of
![]() $\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))\rightarrow H_{\mathfrak{m}}^{i}(R)$
. It is clear that
$\mathscr{F}_{R}(H_{\mathfrak{m}}^{i}(R))\rightarrow H_{\mathfrak{m}}^{i}(R)$
. It is clear that
![]() $N$
is an
$N$
is an
![]() $F$
-stable submodule. We want to show
$F$
-stable submodule. We want to show
![]() $N=H_{\mathfrak{m}}^{i}(R)$
. Since
$N=H_{\mathfrak{m}}^{i}(R)$
. Since
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-full,
$F$
-full,
![]() $x$
is a surjective element by Proposition 3.5. Let
$x$
is a surjective element by Proposition 3.5. Let
![]() $L=\bigcap _{t}x^{t}N$
. By Lemma 4.1, we have the following commutative diagram:
$L=\bigcap _{t}x^{t}N$
. By Lemma 4.1, we have the following commutative diagram:

The descending chain
![]() $N\supseteq xN\supseteq x^{2}N\supseteq \cdots \,$
stabilizes because
$N\supseteq xN\supseteq x^{2}N\supseteq \cdots \,$
stabilizes because
![]() $H_{\mathfrak{m}}^{i}(R)$
is Artinian. So
$H_{\mathfrak{m}}^{i}(R)$
is Artinian. So
![]() $L=\bigcap _{t}x^{t}N=x^{n}N$
for
$L=\bigcap _{t}x^{t}N=x^{n}N$
for
![]() $n\gg 0$
. The key point is that in the above diagram, the middle Frobenius action
$n\gg 0$
. The key point is that in the above diagram, the middle Frobenius action
![]() $x^{p^{e}-1}F^{e}$
is the zero map on
$x^{p^{e}-1}F^{e}$
is the zero map on
![]() $H_{\mathfrak{m}}^{i}(R)/L$
for
$H_{\mathfrak{m}}^{i}(R)/L$
for
![]() $e\gg 0$
, because for any
$e\gg 0$
, because for any
![]() $y\in H_{\mathfrak{m}}^{i}(R)$
,
$y\in H_{\mathfrak{m}}^{i}(R)$
,
![]() $F^{e}(y)\in N$
and thus
$F^{e}(y)\in N$
and thus
![]() $x^{p^{e}-1}F^{e}(y)\in L$
for
$x^{p^{e}-1}F^{e}(y)\in L$
for
![]() $e\gg 0$
. But then since
$e\gg 0$
. But then since
![]() $H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
can be viewed as a submodule of
$H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
can be viewed as a submodule of
![]() $H_{\mathfrak{m}}^{i}(R)/L$
by the above commutative diagram, the natural Frobenius action
$H_{\mathfrak{m}}^{i}(R)/L$
by the above commutative diagram, the natural Frobenius action
![]() $F^{e}$
on
$F^{e}$
on
![]() $H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
is zero, that is,
$H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
is zero, that is,
![]() $F$
is nilpotent on
$F$
is nilpotent on
![]() $H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
.
$H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
.
Since
![]() $F$
is nilpotent on
$F$
is nilpotent on
![]() $H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
, we know that
$H_{\mathfrak{m}}^{i-1}(R/(x))/\unicode[STIX]{x1D719}^{-1}(L)$
, we know that
![]() $\unicode[STIX]{x1D719}^{-1}(L)$
must contain all elements
$\unicode[STIX]{x1D719}^{-1}(L)$
must contain all elements
![]() $F^{e}(H_{\mathfrak{m}}^{i}(R/(x)))$
, hence it contains the
$F^{e}(H_{\mathfrak{m}}^{i}(R/(x)))$
, hence it contains the
![]() $R$
-span of
$R$
-span of
![]() $F^{e}(H_{\mathfrak{m}}^{i}(R/(x)))$
. But
$F^{e}(H_{\mathfrak{m}}^{i}(R/(x)))$
. But
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-full, so we must have
$F$
-full, so we must have
![]() $\unicode[STIX]{x1D719}^{-1}(L)=H_{\mathfrak{m}}^{i-1}(R/(x))$
. But this means the map
$\unicode[STIX]{x1D719}^{-1}(L)=H_{\mathfrak{m}}^{i-1}(R/(x))$
. But this means the map
is an isomorphism, which is impossible unless
![]() $H_{\mathfrak{m}}^{i}(R)=L$
(since otherwise any nonzero socle element of
$H_{\mathfrak{m}}^{i}(R)=L$
(since otherwise any nonzero socle element of
![]() $H_{\mathfrak{m}}^{i}(R)/L$
maps to zero). Therefore, we have
$H_{\mathfrak{m}}^{i}(R)/L$
maps to zero). Therefore, we have
![]() $H_{\mathfrak{m}}^{i}(R)=N=L$
. This proves
$H_{\mathfrak{m}}^{i}(R)=N=L$
. This proves
![]() $R$
is
$R$
is
![]() $F$
-full and hence finished the proof of (2).◻
$F$
-full and hence finished the proof of (2).◻
The following is a well-known counter-example of Fedder [Reference Fedder6] and Singh [Reference Singh22] for the deformation of
![]() $F$
-purity.
$F$
-purity.
Example 4.3. (Compare with [Reference Quy and Shimomoto20, Lemma 6.1])
Let
![]() $K$
be a perfect field of characteristic
$K$
be a perfect field of characteristic
![]() $p>0$
and let
$p>0$
and let
Let
![]() $u,v,y$
and
$u,v,y$
and
![]() $z$
denote the image of
$z$
denote the image of
![]() $U,V,Y$
and
$U,V,Y$
and
![]() $Z$
in
$Z$
in
![]() $R$
(and its quotients), respectively. Then
$R$
(and its quotients), respectively. Then
![]() $y$
is a regular element of
$y$
is a regular element of
![]() $R$
and
$R$
and
![]() $R/(y)\cong K[[U,V,Z]]/(UV,UZ,VZ)$
is
$R/(y)\cong K[[U,V,Z]]/(UV,UZ,VZ)$
is
![]() $F$
-pure by [Reference Hochster and Roberts12, Proposition 5.38]. So
$F$
-pure by [Reference Hochster and Roberts12, Proposition 5.38]. So
![]() $R/(y)$
is
$R/(y)$
is
![]() $F$
-anti-nilpotent by [Reference Ma16, Theorem 1.1]. By Theorem 4.2 we have
$F$
-anti-nilpotent by [Reference Ma16, Theorem 1.1]. By Theorem 4.2 we have
![]() $R$
is also
$R$
is also
![]() $F$
-anti-nilpotent, or equivalently,
$F$
-anti-nilpotent, or equivalently,
![]() $R$
is stably
$R$
is stably
![]() $FH$
-finite.
$FH$
-finite.
5
 $F$
-injectivity
$F$
-injectivity
5.1
 $F$
-injectivity and depth
$F$
-injectivity and depth
We start with the following definition.
Definition 5.1. (Cf. [Reference Brodmann and Sharp3, Definition 9.1.3]) Let
![]() $M$
be a finitely generated module over a local ring
$M$
be a finitely generated module over a local ring
![]() $(R,\mathfrak{m})$
. The finiteness dimension
$(R,\mathfrak{m})$
. The finiteness dimension
![]() $f_{\mathfrak{m}}(M)$
of
$f_{\mathfrak{m}}(M)$
of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathfrak{m}$
is defined as follows:
$\mathfrak{m}$
is defined as follows:
Remark 5.2.
(i) Assume that
 $\dim M=0$
or
$\dim M=0$
or
 $M=0$
(recall that a trivial module has dimension
$M=0$
(recall that a trivial module has dimension
 $-1$
). In this case,
$-1$
). In this case,
 $H_{\mathfrak{m}}^{i}(M)$
is finitely generated for all
$H_{\mathfrak{m}}^{i}(M)$
is finitely generated for all
 $i$
and
$i$
and
 $f_{\mathfrak{m}}(M)$
is equal to
$f_{\mathfrak{m}}(M)$
is equal to
 $\infty$
. It will be essential to know when the finiteness dimension is a positive integer. We mention the following result. Let
$\infty$
. It will be essential to know when the finiteness dimension is a positive integer. We mention the following result. Let
 $(R,\mathfrak{m})$
be a local ring and let
$(R,\mathfrak{m})$
be a local ring and let
 $M$
be a finitely generated
$M$
be a finitely generated
 $R$
-module. If
$R$
-module. If
 $d=\dim M>0$
, then the local cohomology module
$d=\dim M>0$
, then the local cohomology module
 $H_{\mathfrak{m}}^{d}(M)$
is not finitely generated. For the proof of this result, see [Reference Brodmann and Sharp3, Corollary 7.3.3].
$H_{\mathfrak{m}}^{d}(M)$
is not finitely generated. For the proof of this result, see [Reference Brodmann and Sharp3, Corollary 7.3.3].(ii) Suppose
 $(R,\mathfrak{m})$
is an image of a Cohen–Macaulay local ring. By the Grothendieck finiteness theorem (cf. [Reference Brodmann and Sharp3, Theorem 9.5.2]) we have
$(R,\mathfrak{m})$
is an image of a Cohen–Macaulay local ring. By the Grothendieck finiteness theorem (cf. [Reference Brodmann and Sharp3, Theorem 9.5.2]) we have  $$\begin{eqnarray}f_{\mathfrak{m}}(M)=\min \{\operatorname{depth}M_{\mathfrak{p}}+\dim R/\mathfrak{p}\,:\,\mathfrak{p}\in \text{Supp}(M)\setminus \{\mathfrak{m}\}\}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\mathfrak{m}}(M)=\min \{\operatorname{depth}M_{\mathfrak{p}}+\dim R/\mathfrak{p}\,:\,\mathfrak{p}\in \text{Supp}(M)\setminus \{\mathfrak{m}\}\}.\end{eqnarray}$$
(iii)
 $M$
is generalized Cohen–Macaulay if and only if
$M$
is generalized Cohen–Macaulay if and only if
 $\dim M=f_{\mathfrak{m}}(M)$
.
$\dim M=f_{\mathfrak{m}}(M)$
.
It is clear that
![]() $\operatorname{depth}R\leqslant f_{\mathfrak{m}}(R)\leqslant \dim R$
. The following result says that if
$\operatorname{depth}R\leqslant f_{\mathfrak{m}}(R)\leqslant \dim R$
. The following result says that if
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective, then
$F$
-injective, then
![]() $R$
has ‘good’ depth.
$R$
has ‘good’ depth.
Theorem 5.3. If
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective, then
$F$
-injective, then
![]() $\operatorname{depth}R=f_{\mathfrak{m}}(R)$
.
$\operatorname{depth}R=f_{\mathfrak{m}}(R)$
.
Proof. Suppose
![]() $t=\operatorname{depth}R<f_{\mathfrak{m}}(R)$
. The commutative diagram
$t=\operatorname{depth}R<f_{\mathfrak{m}}(R)$
. The commutative diagram

induces the following commutative diagram

where both
![]() $\unicode[STIX]{x1D6FC}$
and the left vertical map are injective. But
$\unicode[STIX]{x1D6FC}$
and the left vertical map are injective. But
![]() $H_{\mathfrak{m}}^{t}(R)$
has finite length,
$H_{\mathfrak{m}}^{t}(R)$
has finite length,
![]() $x^{p^{e}-1}F^{e}:H_{\mathfrak{m}}^{t}(R)\rightarrow H_{\mathfrak{m}}^{t}(R)$
vanishes for
$x^{p^{e}-1}F^{e}:H_{\mathfrak{m}}^{t}(R)\rightarrow H_{\mathfrak{m}}^{t}(R)$
vanishes for
![]() $e\gg 0$
, which is a contradiction.◻
$e\gg 0$
, which is a contradiction.◻
Remark 5.4. The assertion of Theorem 5.3 also holds true if
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-full. Indeed, by Proposition 3.5 we have
$F$
-full. Indeed, by Proposition 3.5 we have
![]() $x$
is a surjective element. Hence there is no nonzero
$x$
is a surjective element. Hence there is no nonzero
![]() $H_{\mathfrak{m}}^{i}(R)$
of finite length. Thus
$H_{\mathfrak{m}}^{i}(R)$
of finite length. Thus
![]() $\operatorname{depth}R=f_{\mathfrak{m}}(R)$
.
$\operatorname{depth}R=f_{\mathfrak{m}}(R)$
.
Remark 5.5. The above result is closely related to the work of Schwede and Singh in [Reference Horiuchi, Miller and Shimomoto11, Appendix]. In the proof of [Reference Horiuchi, Miller and Shimomoto11, Lemma A.2, Theorem A.3], it is claimed that if
![]() $R_{\mathfrak{p}}$
satisfies the Serre condition
$R_{\mathfrak{p}}$
satisfies the Serre condition
![]() $(S_{k})$
for all
$(S_{k})$
for all
![]() $\mathfrak{p}$
in
$\mathfrak{p}$
in
![]() $\text{Spec}^{\circ }(R)$
, the punctured spectrum of
$\text{Spec}^{\circ }(R)$
, the punctured spectrum of
![]() $R$
, and
$R$
, and
![]() $\operatorname{depth}R=t<k$
, then
$\operatorname{depth}R=t<k$
, then
![]() $H_{\mathfrak{m}}^{t}(R)$
is finitely generated. But this fact may not be true if
$H_{\mathfrak{m}}^{t}(R)$
is finitely generated. But this fact may not be true if
![]() $R$
is not equidimensional. For instance, let
$R$
is not equidimensional. For instance, let
![]() $R=K[[a,b,c,d]]/(a)\cap (b,c,d)$
with
$R=K[[a,b,c,d]]/(a)\cap (b,c,d)$
with
![]() $K$
a field. We have
$K$
a field. We have
![]() $\operatorname{depth}R=1$
and
$\operatorname{depth}R=1$
and
![]() $R_{\mathfrak{p}}$
satisfies
$R_{\mathfrak{p}}$
satisfies
![]() $(S_{2})$
for all
$(S_{2})$
for all
![]() $\mathfrak{p}\in \text{Spec}^{\circ }(R)$
. However,
$\mathfrak{p}\in \text{Spec}^{\circ }(R)$
. However,
![]() $H_{\mathfrak{m}}^{1}(R)$
is not finitely generated.
$H_{\mathfrak{m}}^{1}(R)$
is not finitely generated.
The assertion of [Reference Horiuchi, Miller and Shimomoto11, Lemma A.2] (and hence [Reference Horiuchi, Miller and Shimomoto11, Theorem A.3]) is still true. In fact, we can reduce it to the case that
![]() $R$
is equidimensional. We fill this gap below.
$R$
is equidimensional. We fill this gap below.
Corollary 5.6. [Reference Horiuchi, Miller and Shimomoto11, Lemma A.2]
Let
![]() $(R,\mathfrak{m})$
be an
$(R,\mathfrak{m})$
be an
![]() $F$
-finite local ring. Suppose there exists a regular element
$F$
-finite local ring. Suppose there exists a regular element
![]() $x$
such that
$x$
such that
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective. If
$F$
-injective. If
![]() $R_{\mathfrak{p}}$
satisfies the Serre condition
$R_{\mathfrak{p}}$
satisfies the Serre condition
![]() $(S_{k})$
for all
$(S_{k})$
for all
![]() $\mathfrak{p}\in \text{Spec}^{\circ }(R)$
, then
$\mathfrak{p}\in \text{Spec}^{\circ }(R)$
, then
![]() $R$
is
$R$
is
![]() $(S_{k})$
.
$(S_{k})$
.
Proof. We can assume that
![]() $k\leqslant d=\dim R$
. In fact, we need only to prove that
$k\leqslant d=\dim R$
. In fact, we need only to prove that
![]() $t:=\operatorname{depth}R\geqslant k$
. The case
$t:=\operatorname{depth}R\geqslant k$
. The case
![]() $k=1$
is trivial since
$k=1$
is trivial since
![]() $R$
contains a regular element
$R$
contains a regular element
![]() $x$
. For
$x$
. For
![]() $k\geqslant 2$
, since
$k\geqslant 2$
, since
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective we have
$F$
-injective we have
![]() $R/(x)$
is reduced (cf. [Reference Schwede21, Proposition 4.3]). Hence
$R/(x)$
is reduced (cf. [Reference Schwede21, Proposition 4.3]). Hence
![]() $\operatorname{depth}(R/(x))\geqslant 1$
, so
$\operatorname{depth}(R/(x))\geqslant 1$
, so
![]() $\operatorname{depth}R\geqslant 2$
. Thus
$\operatorname{depth}R\geqslant 2$
. Thus
![]() $R$
satisfies the Serre condition
$R$
satisfies the Serre condition
![]() $(S_{2})$
. On the other hand, since
$(S_{2})$
. On the other hand, since
![]() $R$
is
$R$
is
![]() $F$
-finite,
$F$
-finite,
![]() $R$
is a homomorphic image of a regular ring by a result of Gabber [Reference Gabber7, Remark 13.6]. In particular,
$R$
is a homomorphic image of a regular ring by a result of Gabber [Reference Gabber7, Remark 13.6]. In particular,
![]() $R$
is universally catenary.Footnote
3
But if a universally catenary ring satisfies
$R$
is universally catenary.Footnote
3
But if a universally catenary ring satisfies
![]() $(S_{2})$
, then it is equidimensional (see [Reference Hochster and Huneke10, Remark 2.2(h)]). By Theorem 5.3 and Remark 5.2(ii), there exists a prime ideal
$(S_{2})$
, then it is equidimensional (see [Reference Hochster and Huneke10, Remark 2.2(h)]). By Theorem 5.3 and Remark 5.2(ii), there exists a prime ideal
![]() $\mathfrak{p}\in \text{Spec}^{\circ }(R)$
such that
$\mathfrak{p}\in \text{Spec}^{\circ }(R)$
such that
![]() $\operatorname{depth}R=\operatorname{depth}R_{\mathfrak{p}}+\dim R/\mathfrak{p}$
. It is then easy to see that
$\operatorname{depth}R=\operatorname{depth}R_{\mathfrak{p}}+\dim R/\mathfrak{p}$
. It is then easy to see that
![]() $\operatorname{depth}R\geqslant \min \{d,k+1\}\geqslant k$
. The proof is complete.◻
$\operatorname{depth}R\geqslant \min \{d,k+1\}\geqslant k$
. The proof is complete.◻
Remark 5.7. In the above argument, we actually proved that if
![]() $k<d$
, then
$k<d$
, then
![]() $\operatorname{depth}R\geqslant k+1$
.
$\operatorname{depth}R\geqslant k+1$
.
5.2 Deformation of
 $F$
-injectivity
$F$
-injectivity
We begin with the following generalization of the notion of surjective elements.
Definition 5.8. (Cf. [Reference Cuong, Morales and Nhan4])
A regular element
![]() $x$
is called a strictly filter regular element if
$x$
is called a strictly filter regular element if
has finite length for all
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
Lemma 5.9. Let
![]() $(R,\mathfrak{m})$
be a local ring of characteristic
$(R,\mathfrak{m})$
be a local ring of characteristic
![]() $p>0$
. Suppose the residue field
$p>0$
. Suppose the residue field
![]() $k=R/\mathfrak{m}$
is perfect. Let
$k=R/\mathfrak{m}$
is perfect. Let
![]() $M$
be an
$M$
be an
![]() $R$
-module with an injective Frobenius action
$R$
-module with an injective Frobenius action
![]() $F$
. Suppose
$F$
. Suppose
![]() $L$
is an
$L$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $M$
of finite length. Then the induced Frobenius action on
$M$
of finite length. Then the induced Frobenius action on
![]() $M/L$
is injective.
$M/L$
is injective.
Proof. First we note that
![]() $L$
is killed by
$L$
is killed by
![]() $\mathfrak{m}$
: suppose
$\mathfrak{m}$
: suppose
![]() $x\in L$
, then
$x\in L$
, then
![]() $F^{e}(\mathfrak{m}\cdot x)=\mathfrak{m}^{[p^{e}]}\cdot x=0$
for
$F^{e}(\mathfrak{m}\cdot x)=\mathfrak{m}^{[p^{e}]}\cdot x=0$
for
![]() $e\gg 0$
since
$e\gg 0$
since
![]() $L$
has finite length. But then
$L$
has finite length. But then
![]() $\mathfrak{m}\cdot x=0$
since
$\mathfrak{m}\cdot x=0$
since
![]() $F$
acts injectively. Now we have a Frobenius action
$F$
acts injectively. Now we have a Frobenius action
![]() $F$
on a
$F$
on a
![]() $k$
-vector space
$k$
-vector space
![]() $L$
. Call the image of
$L$
. Call the image of
![]() $L^{\prime }\subseteq L$
(which is a
$L^{\prime }\subseteq L$
(which is a
![]() $k^{p}$
-vector subspace of
$k^{p}$
-vector subspace of
![]() $L$
). Since
$L$
). Since
![]() $F$
is injective, the
$F$
is injective, the
![]() $k^{p}$
-vector space dimension of
$k^{p}$
-vector space dimension of
![]() $L^{\prime }$
is equal to the
$L^{\prime }$
is equal to the
![]() $k$
-vector space dimension of
$k$
-vector space dimension of
![]() $L$
. But since
$L$
. But since
![]() $k^{p}=k$
, this implies
$k^{p}=k$
, this implies
![]() $L^{\prime }=L$
and thus
$L^{\prime }=L$
and thus
![]() $F$
is surjective, hence
$F$
is surjective, hence
![]() $F$
is bijective. Now by the injectivity of
$F$
is bijective. Now by the injectivity of
![]() $F$
again we have
$F$
again we have
![]() $F(x)\notin L$
for all
$F(x)\notin L$
for all
![]() $x\notin L$
. Thus
$x\notin L$
. Thus
![]() $F:M/L\rightarrow M/L$
is injective.◻
$F:M/L\rightarrow M/L$
is injective.◻
Example 5.10. The perfectness of the residue field in Lemma 5.9 is necessary. Let
![]() $A=\mathbb{F}_{p}[t]$
and
$A=\mathbb{F}_{p}[t]$
and
![]() $R=k=\mathbb{F}_{p}(t)$
, where
$R=k=\mathbb{F}_{p}(t)$
, where
![]() $t$
is an indeterminate. We consider the Frobenius action on the
$t$
is an indeterminate. We consider the Frobenius action on the
![]() $A$
-module
$A$
-module
![]() $Ae_{1}\oplus Ae_{2}$
defined by
$Ae_{1}\oplus Ae_{2}$
defined by
It is clear that
![]() $F$
is injective. Moreover,
$F$
is injective. Moreover,
![]() $Ae_{1}\oplus 0$
is an
$Ae_{1}\oplus 0$
is an
![]() $F$
-stable submodule of
$F$
-stable submodule of
![]() $Ae_{1}\oplus Ae_{2}$
. Since
$Ae_{1}\oplus Ae_{2}$
. Since
![]() $F(Ae_{1}\oplus Ae_{2})\subseteq Ae_{1}\oplus 0$
, the induced Frobenius action on
$F(Ae_{1}\oplus Ae_{2})\subseteq Ae_{1}\oplus 0$
, the induced Frobenius action on
![]() $(Ae_{1}\oplus Ae_{2})/(Ae_{1}\oplus 0)$
is the zero map. By localizing, we obtain an injective Frobenius action on
$(Ae_{1}\oplus Ae_{2})/(Ae_{1}\oplus 0)$
is the zero map. By localizing, we obtain an injective Frobenius action on
![]() $M=k\cdot e_{1}\oplus k\cdot e_{2}$
with
$M=k\cdot e_{1}\oplus k\cdot e_{2}$
with
![]() $L=k\cdot e_{1}\oplus 0$
is an
$L=k\cdot e_{1}\oplus 0$
is an
![]() $F$
-stable submodule of finite length, but the induced Frobenius action on
$F$
-stable submodule of finite length, but the induced Frobenius action on
![]() $M/L$
is not injective.
$M/L$
is not injective.
The following is a generalization of the main result of [Reference Horiuchi, Miller and Shimomoto11] when
![]() $R/\mathfrak{m}$
is perfect.
$R/\mathfrak{m}$
is perfect.
Theorem 5.11. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
$(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
![]() $p>0$
. Suppose the residue field
$p>0$
. Suppose the residue field
![]() $k=R/\mathfrak{m}$
is perfect. Let
$k=R/\mathfrak{m}$
is perfect. Let
![]() $x$
be a strictly filter regular element. If
$x$
be a strictly filter regular element. If
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective, then the map
$F$
-injective, then the map
![]() $x^{p-1}F$
:
$x^{p-1}F$
:
![]() $H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for every
$H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for every
![]() $i$
, in particular
$i$
, in particular
![]() $R$
is
$R$
is
![]() $F$
-injective.
$F$
-injective.
Proof. Let
![]() $L_{i}:=\operatorname{Coker}(H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R))$
, we have
$L_{i}:=\operatorname{Coker}(H_{\mathfrak{m}}^{i}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{i}(R))$
, we have
![]() $L_{i}$
has finite length for all
$L_{i}$
has finite length for all
![]() $i\geqslant 0$
. The commutative diagram
$i\geqslant 0$
. The commutative diagram

induces the following commutative diagram

Therefore, we have the following commutative diagram

with the Frobenius action
![]() $F:H_{\mathfrak{m}}^{i-1}(R/(x))/L_{i-1}\rightarrow H_{\mathfrak{m}}^{i-1}(R/(x))/L_{i-1}$
is injective by Lemma 5.9. Now by the same method as in the proof of Proposition 3.7 or Theorem 4.2(i), we conclude that the map
$F:H_{\mathfrak{m}}^{i-1}(R/(x))/L_{i-1}\rightarrow H_{\mathfrak{m}}^{i-1}(R/(x))/L_{i-1}$
is injective by Lemma 5.9. Now by the same method as in the proof of Proposition 3.7 or Theorem 4.2(i), we conclude that the map
![]() $x^{p-1}F:H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for all
$x^{p-1}F:H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for all
![]() $i\geqslant 0$
.◻
$i\geqslant 0$
.◻
Similarly, we have the following:
Proposition 5.12. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
$(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
![]() $p>0$
. Suppose the residue field
$p>0$
. Suppose the residue field
![]() $k=R/\mathfrak{m}$
is perfect. Let
$k=R/\mathfrak{m}$
is perfect. Let
![]() $x$
be a regular element such that
$x$
be a regular element such that
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective. Let
$F$
-injective. Let
![]() $s$
be a positive integer such that
$s$
be a positive integer such that
![]() $H_{\mathfrak{m}}^{s-1}(R/(x))$
has finite length. Then the map
$H_{\mathfrak{m}}^{s-1}(R/(x))$
has finite length. Then the map
![]() $x^{p-1}F:H_{\mathfrak{m}}^{s+1}(R)\rightarrow H_{\mathfrak{m}}^{s+1}(R)$
is injective.
$x^{p-1}F:H_{\mathfrak{m}}^{s+1}(R)\rightarrow H_{\mathfrak{m}}^{s+1}(R)$
is injective.
Proof. The short exact sequence
induces the exact sequence
Since
![]() $H_{\mathfrak{m}}^{s-1}(R/(x))$
has finite length, so is
$H_{\mathfrak{m}}^{s-1}(R/(x))$
has finite length, so is
![]() $\operatorname{Ker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
. We claim that
$\operatorname{Ker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
. We claim that
also has finite length: to see this we may assume
![]() $R$
is complete, since
$R$
is complete, since
![]() $\operatorname{Ker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
has finite length, this means
$\operatorname{Ker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
has finite length, this means
![]() $H_{\mathfrak{m}}^{s}(R)^{\vee }\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R)^{\vee }$
is surjective when localizing at any
$H_{\mathfrak{m}}^{s}(R)^{\vee }\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R)^{\vee }$
is surjective when localizing at any
![]() $\mathfrak{p}\neq \mathfrak{m}$
. But by [Reference Matsumura19, Theorem 2.4] this implies
$\mathfrak{p}\neq \mathfrak{m}$
. But by [Reference Matsumura19, Theorem 2.4] this implies
![]() $H_{\mathfrak{m}}^{s}(R)^{\vee }\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R)^{\vee }$
is an isomorphism when localizing at any
$H_{\mathfrak{m}}^{s}(R)^{\vee }\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R)^{\vee }$
is an isomorphism when localizing at any
![]() $\mathfrak{p}\neq \mathfrak{m}$
. Thus
$\mathfrak{p}\neq \mathfrak{m}$
. Thus
![]() $\operatorname{Ker}(H_{\mathfrak{m}}^{s}(R)^{\vee }\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R)^{\vee })$
has finite length which, after dualizing, shows that
$\operatorname{Ker}(H_{\mathfrak{m}}^{s}(R)^{\vee }\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R)^{\vee })$
has finite length which, after dualizing, shows that
![]() $\operatorname{Coker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
has finite length.
$\operatorname{Coker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
has finite length.
We have proved
![]() $L_{s}=\operatorname{Coker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
has finite length. Now the map
$L_{s}=\operatorname{Coker}(H_{\mathfrak{m}}^{s}(R)\overset{x}{\rightarrow }H_{\mathfrak{m}}^{s}(R))$
has finite length. Now the map
![]() $x^{p-1}F:H_{\mathfrak{m}}^{s+1}(R)\rightarrow H_{\mathfrak{m}}^{s+1}(R)$
is injective by the same argument as in Theorem 5.11.◻
$x^{p-1}F:H_{\mathfrak{m}}^{s+1}(R)\rightarrow H_{\mathfrak{m}}^{s+1}(R)$
is injective by the same argument as in Theorem 5.11.◻
The following immediate corollary of the above proposition recovers (and in fact generalizes) results in [Reference Horiuchi, Miller and Shimomoto11].
Corollary 5.13. [Reference Horiuchi, Miller and Shimomoto11, Corollary 4.7]
Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
$(R,\mathfrak{m})$
be a Noetherian local ring of characteristic
![]() $p>0$
. Suppose the residue field
$p>0$
. Suppose the residue field
![]() $k=R/\mathfrak{m}$
is perfect. Let
$k=R/\mathfrak{m}$
is perfect. Let
![]() $x$
be a regular element such that
$x$
be a regular element such that
![]() $R/(x)$
is
$R/(x)$
is
![]() $F$
-injective. Then the map
$F$
-injective. Then the map
![]() $x^{p-1}F:H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for all
$x^{p-1}F:H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is injective for all
![]() $i\leqslant f_{\mathfrak{m}}(R/(x))+1$
. In particular, if
$i\leqslant f_{\mathfrak{m}}(R/(x))+1$
. In particular, if
![]() $R/(x)$
is generalized Cohen–Macaulay, then
$R/(x)$
is generalized Cohen–Macaulay, then
![]() $R$
is
$R$
is
![]() $F$
-injective.
$F$
-injective.
Because of the deep connections between
![]() $F$
-injective and Du Bois singularities [Reference Bhatt, Schwede and Takagi1, Reference Schwede21] and Remark 2.6, we believe that it is rarely the case that an
$F$
-injective and Du Bois singularities [Reference Bhatt, Schwede and Takagi1, Reference Schwede21] and Remark 2.6, we believe that it is rarely the case that an
![]() $F$
-injective ring fails to be
$F$
-injective ring fails to be
![]() $F$
-full (again, the only example we know this happens is [Reference Ma, Schwede and Shimomoto18, Example 3.5], which is based on the construction of [Reference Enescu and Hochster5, Example 2.16]). Therefore, we introduce:
$F$
-full (again, the only example we know this happens is [Reference Ma, Schwede and Shimomoto18, Example 3.5], which is based on the construction of [Reference Enescu and Hochster5, Example 2.16]). Therefore, we introduce:
Definition 5.14. We say
![]() $(R,\mathfrak{m})$
is strongly
$(R,\mathfrak{m})$
is strongly
![]() $F$
-injective if
$F$
-injective if
![]() $R$
is
$R$
is
![]() $F$
-injective and
$F$
-injective and
![]() $F$
-full.
$F$
-full.
Remark 5.15. In general we have:
![]() $F$
-anti-nilpotent
$F$
-anti-nilpotent
![]() $\Rightarrow$
strongly
$\Rightarrow$
strongly
![]() $F$
-injective
$F$
-injective
![]() $\Rightarrow$
$\Rightarrow$
![]() $F$
-injective. Moreover, when
$F$
-injective. Moreover, when
![]() $R$
is Cohen–Macaulay, strongly
$R$
is Cohen–Macaulay, strongly
![]() $F$
-injective is equivalent to
$F$
-injective is equivalent to
![]() $F$
-injective.
$F$
-injective.
We can prove that strong
![]() $F$
-injectivity deform.
$F$
-injectivity deform.
Corollary 5.16. Let
![]() $x$
be a regular element on
$x$
be a regular element on
![]() $(R,\mathfrak{m})$
. If
$(R,\mathfrak{m})$
. If
![]() $R/(x)$
is strongly
$R/(x)$
is strongly
![]() $F$
-injective, then
$F$
-injective, then
![]() $R$
is strongly
$R$
is strongly
![]() $F$
-injective.
$F$
-injective.