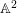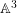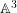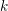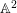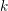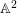1 Introduction
For any commutative ring ![]() $R$, we will use the notation
$R$, we will use the notation ![]() $A=R^{[n]}$ to mean that
$A=R^{[n]}$ to mean that ![]() $A$ is a polynomial ring in
$A$ is a polynomial ring in ![]() $n$ variables over
$n$ variables over ![]() $R$. Now let
$R$. Now let ![]() $k$ be a field with algebraic closure
$k$ be a field with algebraic closure ![]() $\bar{k}$ and
$\bar{k}$ and ![]() $A$ be a
$A$ be a ![]() $k$-algebra. We say that
$k$-algebra. We say that ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{n}$-form over
$\mathbb{A}^{n}$-form over ![]() $k$ if
$k$ if ![]() $A\otimes _{k}\bar{k}=\bar{k}^{[n]}$. It is well known that separable
$A\otimes _{k}\bar{k}=\bar{k}^{[n]}$. It is well known that separable ![]() $\mathbb{A}^{1}$-forms are trivial (i.e.,
$\mathbb{A}^{1}$-forms are trivial (i.e., ![]() $k^{[1]}$) and that there exist nontrivial purely inseparable
$k^{[1]}$) and that there exist nontrivial purely inseparable ![]() $\mathbb{A}^{1}$-forms over fields of positive characteristic. An extensive study of such algebras was made by Asanuma in [Reference Asanuma3]. Kambayashi established [Reference Kambayashi18] that separable
$\mathbb{A}^{1}$-forms over fields of positive characteristic. An extensive study of such algebras was made by Asanuma in [Reference Asanuma3]. Kambayashi established [Reference Kambayashi18] that separable ![]() $\mathbb{A}^{2}$-forms over a field
$\mathbb{A}^{2}$-forms over a field ![]() $k$ are trivial. Over any field of positive characteristic, the nontrivial purely inseparable
$k$ are trivial. Over any field of positive characteristic, the nontrivial purely inseparable ![]() $\mathbb{A}^{1}$-forms can be used to give examples of nontrivial
$\mathbb{A}^{1}$-forms can be used to give examples of nontrivial ![]() $\mathbb{A}^{n}$-forms for any integer
$\mathbb{A}^{n}$-forms for any integer ![]() $n>1$. However, the problem of the existence of nontrivial separable
$n>1$. However, the problem of the existence of nontrivial separable ![]() $\mathbb{A}^{3}$-forms over a field is still open in general. A few recent partial results on the triviality of separable
$\mathbb{A}^{3}$-forms over a field is still open in general. A few recent partial results on the triviality of separable ![]() $\mathbb{A}^{3}$-forms are mentioned in Remark 3.3.
$\mathbb{A}^{3}$-forms are mentioned in Remark 3.3.
Now let ![]() $R$ be a ring containing a field
$R$ be a ring containing a field ![]() $k$. An
$k$. An ![]() $R$-algebra
$R$-algebra ![]() $A$ is said to be an
$A$ is said to be an ![]() $\mathbb{A}^{n}$-form over
$\mathbb{A}^{n}$-form over ![]() $R$ with respect to
$R$ with respect to ![]() $k$ if
$k$ if ![]() $A\otimes _{k}\bar{k}=(R\otimes _{k}\bar{k})^{[n]}$, where
$A\otimes _{k}\bar{k}=(R\otimes _{k}\bar{k})^{[n]}$, where ![]() $\bar{k}$ denotes the algebraic closure of
$\bar{k}$ denotes the algebraic closure of ![]() $k$. In [Reference Dutta10], Dutta investigated separable
$k$. In [Reference Dutta10], Dutta investigated separable ![]() $\mathbb{A}^{1}$-forms over any ring
$\mathbb{A}^{1}$-forms over any ring ![]() $R$ containing a field
$R$ containing a field ![]() $k$ and obtained Theorem 2.9. He also observed Theorem 2.10 for
$k$ and obtained Theorem 2.9. He also observed Theorem 2.10 for ![]() $\mathbb{A}^{2}$-forms over any Principal Ideal Domain (PID) containing
$\mathbb{A}^{2}$-forms over any Principal Ideal Domain (PID) containing ![]() $\mathbb{Q}$.
$\mathbb{Q}$.
In this paper, we prove a partial result on separable ![]() $\mathbb{A}^{3}$-forms over a field
$\mathbb{A}^{3}$-forms over a field ![]() $k$ (Theorem 3.2) and extend the results on
$k$ (Theorem 3.2) and extend the results on ![]() $\mathbb{A}^{2}$-forms (Theorems 2.8 and 2.10) to any one-dimensional Noetherian
$\mathbb{A}^{2}$-forms (Theorems 2.8 and 2.10) to any one-dimensional Noetherian ![]() $\mathbb{Q}$-algebra (Theorem 3.7) and to any
$\mathbb{Q}$-algebra (Theorem 3.7) and to any ![]() $\mathbb{Q}$-algebra having a fixed point free locally nilpotent derivation (Theorem 3.8). After receiving a preprint of our paper, Prof. M. Miyanishi informed us that a part of Theorem 3.2 has also been obtained recently in [Reference Gurjar, Masuda and Miyanishi13] by a different approach (see Remark 3.3 (4) for a precise statement).
$\mathbb{Q}$-algebra having a fixed point free locally nilpotent derivation (Theorem 3.8). After receiving a preprint of our paper, Prof. M. Miyanishi informed us that a part of Theorem 3.2 has also been obtained recently in [Reference Gurjar, Masuda and Miyanishi13] by a different approach (see Remark 3.3 (4) for a precise statement).
2 Preliminaries
In this section we recall a few definitions and well-known results. All rings will be assumed to be commutative containing unity.
Definition 2.1. An ![]() $R$-algebra
$R$-algebra ![]() $A$ is said to be an
$A$ is said to be an ![]() $\mathbb{A}^{r}$-fibration over
$\mathbb{A}^{r}$-fibration over ![]() $R$ if the following hold:
$R$ if the following hold:
(i)
 $A$ is finitely generated over
$A$ is finitely generated over  $R$.
$R$.(ii)
 $A$ is flat over
$A$ is flat over  $R$.
$R$.(iii)
 for every prime ideal
for every prime ideal  of
of  $R$.
$R$.
Definition 2.2. Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $p$
$p$![]() $({\geqslant}0)$ with algebraic closure
$({\geqslant}0)$ with algebraic closure ![]() $\bar{k}$ and
$\bar{k}$ and ![]() $R$ a
$R$ a ![]() $k$-algebra. An
$k$-algebra. An ![]() $R$-algebra
$R$-algebra ![]() $A$ is said to be an
$A$ is said to be an ![]() $\mathbb{A}^{n}$-form over
$\mathbb{A}^{n}$-form over ![]() $R$ (with respect to
$R$ (with respect to ![]() $k$) if
$k$) if ![]() $A\otimes _{k}\bar{k}=(R\otimes _{k}\bar{k})^{[n]}$.
$A\otimes _{k}\bar{k}=(R\otimes _{k}\bar{k})^{[n]}$.
Definition 2.3. Let ![]() $A=R^{[n]}$ and
$A=R^{[n]}$ and ![]() $F\in A$.
$F\in A$. ![]() $F$ is said to be a residual coordinate in
$F$ is said to be a residual coordinate in ![]() $A$ if, for every prime ideal
$A$ if, for every prime ideal ![]() of
of ![]() $R$,
$R$, ![]() , where
, where ![]() $\bar{F}$ denotes the image of
$\bar{F}$ denotes the image of ![]() $F$ in
$F$ in ![]() .
.
Definition 2.4. A derivation ![]() $D$ on a ring
$D$ on a ring ![]() $A$ is said to be a locally nilpotent derivation if, for each
$A$ is said to be a locally nilpotent derivation if, for each ![]() $a\in A$, there exists an integer
$a\in A$, there exists an integer ![]() $n\geqslant 0$ (depending on
$n\geqslant 0$ (depending on ![]() $a$), such that
$a$), such that ![]() $D^{n}(a)=0$.
$D^{n}(a)=0$.
Definition 2.5. We say that a locally nilpotent derivation ![]() $D$ on a ring
$D$ on a ring ![]() $A$ admits a slice if there exists
$A$ admits a slice if there exists ![]() $s$ in
$s$ in ![]() $A$ for which
$A$ for which ![]() $D(s)=1$.
$D(s)=1$.
Definition 2.6. A locally nilpotent derivation ![]() $D$ on a ring
$D$ on a ring ![]() $A$ is said to be fixed point free if
$A$ is said to be fixed point free if ![]() $(DA)=A$, where
$(DA)=A$, where ![]() $(DA)$ is the ideal of
$(DA)$ is the ideal of ![]() $A$ generated by
$A$ generated by ![]() $D(A)$.
$D(A)$.
Definition 2.7. Let ![]() $R$ be a ring and
$R$ be a ring and ![]() $D$ a locally nilpotent
$D$ a locally nilpotent ![]() $R$-derivation on the polynomial ring
$R$-derivation on the polynomial ring ![]() $A=R^{[n]}$. Then the rank of the derivation
$A=R^{[n]}$. Then the rank of the derivation ![]() $D$, denoted by
$D$, denoted by ![]() $\text{rk}~(D)$, is defined to be the least integer
$\text{rk}~(D)$, is defined to be the least integer ![]() $i$ such that there exist
$i$ such that there exist ![]() $X_{1},\ldots ,X_{n-i}\in \text{ker}\,D$ satisfying
$X_{1},\ldots ,X_{n-i}\in \text{ker}\,D$ satisfying ![]() $A=R[X_{1},\ldots ,X_{n-i}]^{[i]}$.
$A=R[X_{1},\ldots ,X_{n-i}]^{[i]}$.
We first state Kambayashi’s theorem [Reference Kambayashi18, Theorem 3] on the triviality of separable ![]() $\mathbb{A}^{2}$-forms over fields.
$\mathbb{A}^{2}$-forms over fields.
Theorem 2.8. Let ![]() $k$ and
$k$ and ![]() $L$ be fields such that
$L$ be fields such that ![]() $L$ is separably algebraic over
$L$ is separably algebraic over ![]() $k$. Suppose
$k$. Suppose ![]() $A$ is a
$A$ is a ![]() $k$-algebra such that
$k$-algebra such that ![]() $A\otimes _{k}L=L^{[2]}$. Then
$A\otimes _{k}L=L^{[2]}$. Then ![]() $A=k^{[2]}$.
$A=k^{[2]}$.
We now state a theorem on separable ![]() $\mathbb{A}^{1}$-forms over rings and a theorem on
$\mathbb{A}^{1}$-forms over rings and a theorem on ![]() $\mathbb{A}^{2}$-forms over a PID due to Dutta [Reference Dutta10, Theorem 7 and Remark 8].
$\mathbb{A}^{2}$-forms over a PID due to Dutta [Reference Dutta10, Theorem 7 and Remark 8].
Theorem 2.9. Let ![]() $k$ be a field,
$k$ be a field, ![]() $L$ a separable field extension of
$L$ a separable field extension of ![]() $k$,
$k$, ![]() $R$ a
$R$ a ![]() $k$-algebra and
$k$-algebra and ![]() $A$ an
$A$ an ![]() $R$-algebra such that
$R$-algebra such that ![]() $A\otimes _{k}L$ is isomorphic to the symmetric algebra of a finitely generated rank one projective module over
$A\otimes _{k}L$ is isomorphic to the symmetric algebra of a finitely generated rank one projective module over ![]() $R\otimes _{k}L$. Then
$R\otimes _{k}L$. Then ![]() $A$ is isomorphic to the symmetric algebra of a finitely generated rank one projective module over
$A$ is isomorphic to the symmetric algebra of a finitely generated rank one projective module over ![]() $R$.
$R$.
Theorem 2.10. Let ![]() $k$ be a field of characteristic zero,
$k$ be a field of characteristic zero, ![]() $R$ a PID containing
$R$ a PID containing ![]() $k$ and
$k$ and ![]() $A$ an
$A$ an ![]() $R$-algebra such that
$R$-algebra such that ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{2}$-form over
$\mathbb{A}^{2}$-form over ![]() $R$ with respect to
$R$ with respect to ![]() $k$. Then
$k$. Then ![]() $A=R^{[2]}$.
$A=R^{[2]}$.
Next we quote a result on ![]() $\mathbb{A}^{2}$-fibrations due to Asanuma and Bhatwadekar [Reference Asanuma and Bhatwadekar2, Theorem 3.8 and Remark 3.13].
$\mathbb{A}^{2}$-fibrations due to Asanuma and Bhatwadekar [Reference Asanuma and Bhatwadekar2, Theorem 3.8 and Remark 3.13].
Theorem 2.11. Let ![]() $R$ be a one-dimensional Noetherian
$R$ be a one-dimensional Noetherian ![]() $\mathbb{Q}$-algebra. Let
$\mathbb{Q}$-algebra. Let ![]() $A$ be an
$A$ be an ![]() $\mathbb{A}^{2}$-fibration over
$\mathbb{A}^{2}$-fibration over ![]() $R$. Then there exists
$R$. Then there exists ![]() $H\in A$ such that
$H\in A$ such that ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{1}$-fibration over
$\mathbb{A}^{1}$-fibration over ![]() $R[H]$.
$R[H]$.
The following result on residual coordinates was proved by Bhatwadekar and Dutta for Noetherian rings containing ![]() $\mathbb{Q}$ [Reference Bhatwadekar and Dutta5, Theorem 3.2] and later generalized by van den Essen and van Rossum for general
$\mathbb{Q}$ [Reference Bhatwadekar and Dutta5, Theorem 3.2] and later generalized by van den Essen and van Rossum for general ![]() $\mathbb{Q}$-algebras [Reference van den Essen and van Rossum11, Theorem 3.4].
$\mathbb{Q}$-algebras [Reference van den Essen and van Rossum11, Theorem 3.4].
Theorem 2.12. Let ![]() $R$ be a
$R$ be a ![]() $\mathbb{Q}$-algebra,
$\mathbb{Q}$-algebra, ![]() $A=R^{[2]}$ and
$A=R^{[2]}$ and ![]() $F\in A$. If
$F\in A$. If ![]() $F$ is a residual coordinate in
$F$ is a residual coordinate in ![]() $A$ then
$A$ then ![]() $A=R[F]^{[1]}$.
$A=R[F]^{[1]}$.
Next we state a theorem which follows from a fundamental result in the theory of locally nilpotent derivations [Reference Freudenburg12, Corollary 1.26].
Theorem 2.13. Let ![]() $k$ be a field of characteristic zero,
$k$ be a field of characteristic zero, ![]() $A$ a
$A$ a ![]() $k$-algebra,
$k$-algebra, ![]() $D$ a locally nilpotent derivation on
$D$ a locally nilpotent derivation on ![]() $A$ and
$A$ and ![]() $B:=\text{ker}\,D$. Then the following are equivalent:
$B:=\text{ker}\,D$. Then the following are equivalent:
(1)
 $D$ admits a slice
$D$ admits a slice  $s$.
$s$.(2)
 $A=B[s]=B^{[1]}$ and
$A=B[s]=B^{[1]}$ and  $D=d/ds$ on
$D=d/ds$ on  $A$.
$A$.(3)
 $D(A)=A$.
$D(A)=A$.
The following rigidity theorem is due to Daigle [Reference Daigle8, Theorem ![]() $2.5$].
$2.5$].
Theorem 2.14. Let ![]() $k$ be a field of characteristic zero and
$k$ be a field of characteristic zero and ![]() $D$ be a locally nilpotent derivation on the polynomial ring
$D$ be a locally nilpotent derivation on the polynomial ring ![]() $A=k^{[3]}$ with
$A=k^{[3]}$ with ![]() $\text{rk}\,(D)=2$. Let
$\text{rk}\,(D)=2$. Let ![]() $X,W\in \text{ker}\,D$ be such that
$X,W\in \text{ker}\,D$ be such that ![]() $A=k[X]^{[2]}=k[W]^{[2]}$. Then
$A=k[X]^{[2]}=k[W]^{[2]}$. Then ![]() $k[X]=k[W]$.
$k[X]=k[W]$.
The following result on fixed point free locally nilpotent derivations was obtained by Bhatwadekar and Dutta [Reference Bhatwadekar and Dutta6, Theorem 4.7] for any Noetherian ![]() $\mathbb{Q}$-algebra and later generalized to any
$\mathbb{Q}$-algebra and later generalized to any ![]() $\mathbb{Q}$-algebra by Berson et al. [Reference Berson, van den Essen and Maubach4, Theorem 3.5]; [Reference Freudenburg12, Theorem 4.15].
$\mathbb{Q}$-algebra by Berson et al. [Reference Berson, van den Essen and Maubach4, Theorem 3.5]; [Reference Freudenburg12, Theorem 4.15].
Theorem 2.15. Let ![]() $R$ be a
$R$ be a ![]() $\mathbb{Q}$-algebra,
$\mathbb{Q}$-algebra, ![]() $A=R[X,Y]=R^{[2]}$,
$A=R[X,Y]=R^{[2]}$, ![]() $D$ a fixed point free locally nilpotent
$D$ a fixed point free locally nilpotent ![]() $R$-derivation of
$R$-derivation of ![]() $A$ and
$A$ and ![]() $B=\text{ker}~D$. Then
$B=\text{ker}~D$. Then ![]() $D$ admits a slice,
$D$ admits a slice, ![]() $B=R^{[1]}$ and
$B=R^{[1]}$ and ![]() $A=B^{[1]}$.
$A=B^{[1]}$.
Remark 2.16. A fixed point free locally nilpotent derivation on ![]() $k[X,Y,Z]$ has a slice [Reference Kaliman17]. But a fixed point free locally nilpotent
$k[X,Y,Z]$ has a slice [Reference Kaliman17]. But a fixed point free locally nilpotent ![]() $R$-derivation on
$R$-derivation on ![]() $R[X,Y,Z]$ need not have a slice even if
$R[X,Y,Z]$ need not have a slice even if ![]() $R$ is a PID [Reference Bhatwadekar, Gupta and Lokhande7, Example 5.6].
$R$ is a PID [Reference Bhatwadekar, Gupta and Lokhande7, Example 5.6].
3 Main results
In this section we will prove our main results. Note that if ![]() $k$ is a field of characteristic zero,
$k$ is a field of characteristic zero, ![]() $A$ a
$A$ a ![]() $k$-algebra and
$k$-algebra and ![]() $L$ a field extension of
$L$ a field extension of ![]() $k$, then any
$k$, then any ![]() $k$-linear locally nilpotent derivation
$k$-linear locally nilpotent derivation ![]() $D$ on
$D$ on ![]() $A$ can be extended to a locally nilpotent derivation
$A$ can be extended to a locally nilpotent derivation ![]() $D\otimes 1_{L}$ on
$D\otimes 1_{L}$ on ![]() $A\otimes _{k}L$ such that
$A\otimes _{k}L$ such that ![]() $(D\otimes 1_{L})(a\otimes \unicode[STIX]{x1D706})=D(a)\otimes \unicode[STIX]{x1D706}$ for all
$(D\otimes 1_{L})(a\otimes \unicode[STIX]{x1D706})=D(a)\otimes \unicode[STIX]{x1D706}$ for all ![]() $a\in A$ and
$a\in A$ and ![]() $\unicode[STIX]{x1D706}\in L$. We will first establish our main theorem on
$\unicode[STIX]{x1D706}\in L$. We will first establish our main theorem on ![]() $\mathbb{A}^{3}$-forms over
$\mathbb{A}^{3}$-forms over ![]() $k$ (Theorem 3.2). We begin with a special case of this result which holds for
$k$ (Theorem 3.2). We begin with a special case of this result which holds for ![]() $\mathbb{A}^{3}$-forms over a PID
$\mathbb{A}^{3}$-forms over a PID ![]() $R$ with respect to
$R$ with respect to ![]() $k$.
$k$.
Proposition 3.1. Let ![]() $k$ be a field of characteristic zero with algebraic closure
$k$ be a field of characteristic zero with algebraic closure ![]() $\bar{k}$,
$\bar{k}$, ![]() $R$ a PID containing
$R$ a PID containing ![]() $k$ and
$k$ and ![]() $A$ be an
$A$ be an ![]() $\mathbb{A}^{3}$-form over
$\mathbb{A}^{3}$-form over ![]() $R$ with respect to
$R$ with respect to ![]() $k$. Suppose that there exists an
$k$. Suppose that there exists an ![]() $R$-linear locally nilpotent derivation
$R$-linear locally nilpotent derivation ![]() $D$ on
$D$ on ![]() $A$ such that
$A$ such that ![]() $\text{rk}\,(D\otimes 1_{\bar{k}})=1$. Then
$\text{rk}\,(D\otimes 1_{\bar{k}})=1$. Then ![]() $A=R^{[3]}$.
$A=R^{[3]}$.
Proof. Since ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{3}$-form over
$\mathbb{A}^{3}$-form over ![]() $R$ with respect to
$R$ with respect to ![]() $k$, there exists a finite extension
$k$, there exists a finite extension ![]() $L$ over
$L$ over ![]() $k$ such that
$k$ such that ![]() $A\otimes _{k}L=(R\otimes _{k}L)^{[3]}$ and
$A\otimes _{k}L=(R\otimes _{k}L)^{[3]}$ and ![]() $\text{rk}\,(D\otimes _{k}1_{L})=1$. Let
$\text{rk}\,(D\otimes _{k}1_{L})=1$. Let ![]() $B=\text{ker}\,D$. Set
$B=\text{ker}\,D$. Set ![]() $\bar{R}:=R\otimes _{k}L$,
$\bar{R}:=R\otimes _{k}L$, ![]() $\bar{A}:=A\otimes _{k}L$,
$\bar{A}:=A\otimes _{k}L$, ![]() $\bar{B}:=B\otimes _{k}L$ and
$\bar{B}:=B\otimes _{k}L$ and ![]() $\bar{D}:=D\otimes 1_{L}$. Then
$\bar{D}:=D\otimes 1_{L}$. Then ![]() $\bar{A}=\bar{R}^{[3]}$ and
$\bar{A}=\bar{R}^{[3]}$ and ![]() $\text{ker}\,\bar{D}=\bar{B}$. Since
$\text{ker}\,\bar{D}=\bar{B}$. Since ![]() $\text{rk}(\bar{D})=1$, we have
$\text{rk}(\bar{D})=1$, we have ![]() $\bar{A}=\bar{B}^{[1]}$ and
$\bar{A}=\bar{B}^{[1]}$ and ![]() $\bar{B}=\bar{R}^{[2]}$. Hence,
$\bar{B}=\bar{R}^{[2]}$. Hence, ![]() $B=R^{[2]}$ by Theorem 2.10. As
$B=R^{[2]}$ by Theorem 2.10. As ![]() $\text{Pic}(B)$ is trivial,
$\text{Pic}(B)$ is trivial, ![]() $A=B^{[1]}$ by Theorem 2.9. Thus,
$A=B^{[1]}$ by Theorem 2.9. Thus, ![]() $A=R^{[3]}$.◻
$A=R^{[3]}$.◻
We now prove our main result on ![]() $\mathbb{A}^{3}$-forms.
$\mathbb{A}^{3}$-forms.
Theorem 3.2. Let ![]() $k$ be a field of characteristic zero with algebraic closure
$k$ be a field of characteristic zero with algebraic closure ![]() $\bar{k}$ and
$\bar{k}$ and ![]() $A$ be an
$A$ be an ![]() $\mathbb{A}^{3}$-form over
$\mathbb{A}^{3}$-form over ![]() $k$. Suppose that there exists a
$k$. Suppose that there exists a ![]() $k$-linear locally nilpotent derivation
$k$-linear locally nilpotent derivation ![]() $D$ on
$D$ on ![]() $A$ such that
$A$ such that ![]() $\text{rk}\,(D\otimes 1_{\bar{k}})\leqslant 2$. Then
$\text{rk}\,(D\otimes 1_{\bar{k}})\leqslant 2$. Then ![]() $A=k^{[3]}$.
$A=k^{[3]}$.
Proof. Since ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{3}$-form over
$\mathbb{A}^{3}$-form over ![]() $k$, there exists a finite Galois extension
$k$, there exists a finite Galois extension ![]() $L$ over
$L$ over ![]() $k$ with Galois group
$k$ with Galois group ![]() $G$ such that
$G$ such that ![]() $A\otimes _{k}L=L^{[3]}$ and
$A\otimes _{k}L=L^{[3]}$ and ![]() $\text{rk}\,(D\otimes _{k}1_{L})\leqslant 2$. Let
$\text{rk}\,(D\otimes _{k}1_{L})\leqslant 2$. Let ![]() $B=\text{ker}\,D$. Set
$B=\text{ker}\,D$. Set ![]() $\bar{A}:=A\otimes _{k}L$,
$\bar{A}:=A\otimes _{k}L$, ![]() $\bar{B}:=B\otimes _{k}L$ and
$\bar{B}:=B\otimes _{k}L$ and ![]() $\bar{D}:=D\otimes 1_{L}$. Then
$\bar{D}:=D\otimes 1_{L}$. Then ![]() $\bar{A}=L^{[3]}$ and
$\bar{A}=L^{[3]}$ and ![]() $\text{ker}\,\bar{D}=\bar{B}$.
$\text{ker}\,\bar{D}=\bar{B}$.
If ![]() $\text{rk}(\bar{D})=1$, then
$\text{rk}(\bar{D})=1$, then ![]() $A=k^{[3]}$ by Proposition 3.1 (taking
$A=k^{[3]}$ by Proposition 3.1 (taking ![]() $R=k$).
$R=k$).
We now consider the case ![]() $\text{rk}\,(\bar{D})=2$. We then have
$\text{rk}\,(\bar{D})=2$. We then have ![]() $X\in \bar{B}$ such that
$X\in \bar{B}$ such that ![]() $\bar{A}=L[X]^{[2]}$. We show that there exists
$\bar{A}=L[X]^{[2]}$. We show that there exists ![]() $W\in L[X]\cap A$ such that
$W\in L[X]\cap A$ such that ![]() $L[X]=L[W]$.
$L[X]=L[W]$.
We identify ![]() $A$ with its image in
$A$ with its image in ![]() $\bar{A}$ under the map
$\bar{A}$ under the map ![]() $a\rightarrow a\otimes 1$. Any
$a\rightarrow a\otimes 1$. Any ![]() $\unicode[STIX]{x1D70E}\in G$ can be extended to an
$\unicode[STIX]{x1D70E}\in G$ can be extended to an ![]() $A$-automorphism of
$A$-automorphism of ![]() $\bar{A}$ by defining
$\bar{A}$ by defining ![]() $\unicode[STIX]{x1D70E}(a\otimes l)=a\otimes \unicode[STIX]{x1D70E}(l)$, for all
$\unicode[STIX]{x1D70E}(a\otimes l)=a\otimes \unicode[STIX]{x1D70E}(l)$, for all ![]() $a\in A$ and
$a\in A$ and ![]() $l\in L$. Let
$l\in L$. Let
where ![]() $1,e_{1},\ldots ,e_{r}$ form a part of a
$1,e_{1},\ldots ,e_{r}$ form a part of a ![]() $k$-basis of
$k$-basis of ![]() $A$ and
$A$ and ![]() $l_{i}$’s are in
$l_{i}$’s are in ![]() $L$. Since the bilinear map
$L$. Since the bilinear map ![]() $L\times L\longrightarrow k$ given by
$L\times L\longrightarrow k$ given by ![]() $(x,y)\mapsto \text{Tr}(xy)$ is nondegenerate (where
$(x,y)\mapsto \text{Tr}(xy)$ is nondegenerate (where ![]() $\text{Tr}(a):=\text{Trace}(a)$ for all
$\text{Tr}(a):=\text{Trace}(a)$ for all ![]() $a$ in
$a$ in ![]() $L$), replacing
$L$), replacing ![]() $X$ by
$X$ by ![]() $lX$ (for some
$lX$ (for some ![]() $l\in L$) if necessary we can assume that
$l\in L$) if necessary we can assume that ![]() $\text{Tr}(l_{i})\neq 0$ for some
$\text{Tr}(l_{i})\neq 0$ for some ![]() $i\geqslant 1$. Thus
$i\geqslant 1$. Thus
is an element of ![]() $A\setminus k$. Note that
$A\setminus k$. Note that ![]() $\unicode[STIX]{x1D70E}\bar{D}=\bar{D}\unicode[STIX]{x1D70E}$ and hence
$\unicode[STIX]{x1D70E}\bar{D}=\bar{D}\unicode[STIX]{x1D70E}$ and hence ![]() $\unicode[STIX]{x1D70E}(X)\in \bar{B}$. Since
$\unicode[STIX]{x1D70E}(X)\in \bar{B}$. Since ![]() $\unicode[STIX]{x1D70E}$ is an automorphism of
$\unicode[STIX]{x1D70E}$ is an automorphism of ![]() $\bar{A}$, by Theorem 2.14,
$\bar{A}$, by Theorem 2.14, ![]() $L[X]=L[\unicode[STIX]{x1D70E}(X)]$. Hence
$L[X]=L[\unicode[STIX]{x1D70E}(X)]$. Hence ![]() $\unicode[STIX]{x1D70E}(X)$ is linear in
$\unicode[STIX]{x1D70E}(X)$ is linear in ![]() $X$ for each
$X$ for each ![]() $\unicode[STIX]{x1D70E}$ and hence
$\unicode[STIX]{x1D70E}$ and hence ![]() $\text{deg}_{X}W\leqslant 1$. But as
$\text{deg}_{X}W\leqslant 1$. But as ![]() $B\cap L=k$,
$B\cap L=k$, ![]() $W\notin L$, so that
$W\notin L$, so that ![]() $\text{deg}_{X}W=1$ which implies
$\text{deg}_{X}W=1$ which implies ![]() $L[X]=L[W]$.
$L[X]=L[W]$.
So ![]() $\bar{A}=L[W]^{[2]}=(k[W]\otimes _{k}L)^{[2]}$. By Theorem 2.10, we get
$\bar{A}=L[W]^{[2]}=(k[W]\otimes _{k}L)^{[2]}$. By Theorem 2.10, we get ![]() $A=k[W]^{[2]}$.◻
$A=k[W]^{[2]}$.◻
Remark 3.3. Let ![]() $k$ be a field of characteristic zero with algebraic closure
$k$ be a field of characteristic zero with algebraic closure ![]() $\bar{k}$ and
$\bar{k}$ and ![]() $A$ an
$A$ an ![]() $\mathbb{A}^{3}$-form over
$\mathbb{A}^{3}$-form over ![]() $k$. We record below a few other results on the triviality of
$k$. We record below a few other results on the triviality of ![]() $A$.
$A$.
(1) Daigle and Kaliman have proved [Reference Daigle and Kaliman9, Corollary 3.3] that if ![]() $A$ admits a fixed point free locally nilpotent derivation
$A$ admits a fixed point free locally nilpotent derivation ![]() $D$, then
$D$, then ![]() $A=k^{[3]}$.
$A=k^{[3]}$.
(2) Daigle and Kaliman have also proved [Reference Daigle and Kaliman9, Proposition 4.9] that if ![]() $A$ contains an element
$A$ contains an element ![]() $f$ which is a coordinate of
$f$ which is a coordinate of ![]() $A\otimes _{k}\bar{k}$, then
$A\otimes _{k}\bar{k}$, then ![]() $A=k^{[3]}$ and
$A=k^{[3]}$ and ![]() $f$ is a coordinate of
$f$ is a coordinate of ![]() $A$.
$A$.
(3) Koras and Russell have proved [Reference Koras and Russell19, Theorem C] that if ![]() $A$ admits an effective action of a reductive algebraic
$A$ admits an effective action of a reductive algebraic ![]() $k$-group of positive dimension, then
$k$-group of positive dimension, then ![]() $A=k^{[3]}$.
$A=k^{[3]}$.
(4) Recently, Gurjar, Masuda and Miyanishi have shown [Reference Gurjar, Masuda and Miyanishi13] that ![]() $A=k^{[3]}$ if
$A=k^{[3]}$ if ![]() $A$ admits either a fixed point free locally nilpotent derivation or a nonconfluent action of a unipotent group of dimension two. Their results give an alternative approach to Theorem 3.2 for the case
$A$ admits either a fixed point free locally nilpotent derivation or a nonconfluent action of a unipotent group of dimension two. Their results give an alternative approach to Theorem 3.2 for the case ![]() $\text{rk}\,(\bar{D})=1$.
$\text{rk}\,(\bar{D})=1$.
We now extend Theorems 2.8 and 2.10 to more general rings. For convenience, we first record a few easy lemmas.
Lemma 3.4. Let ![]() $R$ be a ring containing
$R$ be a ring containing ![]() $\mathbb{Q}$ and
$\mathbb{Q}$ and ![]() $A=R^{[2]}$. If
$A=R^{[2]}$. If ![]() $H\in A$ is such that
$H\in A$ is such that ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{1}$-fibration over
$\mathbb{A}^{1}$-fibration over ![]() $R[H]$, then
$R[H]$, then ![]() $A=R[H]^{[1]}$.
$A=R[H]^{[1]}$.
Proof. Let ![]() be a prime ideal of
be a prime ideal of ![]() $R$ and let
$R$ and let ![]() $\bar{H}$ denote the image of
$\bar{H}$ denote the image of ![]() $H$ in
$H$ in ![]() . Then
. Then ![]() is an
is an ![]() $\mathbb{A}^{1}$-fibration over the PID
$\mathbb{A}^{1}$-fibration over the PID ![]() and hence
and hence ![]() . Thus,
. Thus, ![]() $H$ is a residual coordinate of
$H$ is a residual coordinate of ![]() $A$. Hence, by Theorem 2.12,
$A$. Hence, by Theorem 2.12, ![]() $A=R[H]^{[1]}$.◻
$A=R[H]^{[1]}$.◻
We now observe that Theorem 2.8 extends to separable ![]() $\mathbb{A}^{2}$-forms over a field
$\mathbb{A}^{2}$-forms over a field ![]() $K$ with respect to a subfield
$K$ with respect to a subfield ![]() $k$.
$k$.
Lemma 3.5. Let ![]() $k$ be a field and
$k$ be a field and ![]() $K$ a field extension of
$K$ a field extension of ![]() $k$. Let
$k$. Let ![]() $A$ be a
$A$ be a ![]() $K$-algebra such that
$K$-algebra such that ![]() $A\otimes _{k}L=(K\otimes _{k}L)^{[2]}$, for some finite separable field extension
$A\otimes _{k}L=(K\otimes _{k}L)^{[2]}$, for some finite separable field extension ![]() $L$ of
$L$ of ![]() $k$. Then
$k$. Then ![]() $A=K^{[2]}$.
$A=K^{[2]}$.
Proof. By hypothesis, we have ![]() $A\otimes _{K}(K\otimes _{k}L)=(K\otimes _{k}L)^{[2]}$. Since
$A\otimes _{K}(K\otimes _{k}L)=(K\otimes _{k}L)^{[2]}$. Since ![]() $L$ over
$L$ over ![]() $k$ is a finite separable extension,
$k$ is a finite separable extension, ![]() $K\otimes _{k}L$ is a finite direct product of separable extensions
$K\otimes _{k}L$ is a finite direct product of separable extensions ![]() $L_{i}$ over
$L_{i}$ over ![]() $K$. Hence, we have
$K$. Hence, we have ![]() $A\otimes _{K}L_{i}={L_{i}}^{[2]}$ (for each
$A\otimes _{K}L_{i}={L_{i}}^{[2]}$ (for each ![]() $i$), which implies
$i$), which implies ![]() $A=K^{[2]}$ by Theorem 2.8.◻
$A=K^{[2]}$ by Theorem 2.8.◻
We now show that ![]() $\mathbb{A}^{2}$-forms are
$\mathbb{A}^{2}$-forms are ![]() $\mathbb{A}^{2}$-fibrations.
$\mathbb{A}^{2}$-fibrations.
Lemma 3.6. Let ![]() $k$ be a field of characteristic zero,
$k$ be a field of characteristic zero, ![]() $R$ be a
$R$ be a ![]() $k$-algebra and
$k$-algebra and ![]() $A$ be an
$A$ be an ![]() $R$-algebra. Let
$R$-algebra. Let ![]() $A$ be an
$A$ be an ![]() $\mathbb{A}^{2}$-form over
$\mathbb{A}^{2}$-form over ![]() $R$ with respect to
$R$ with respect to ![]() $k$. Then
$k$. Then ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{2}$-fibration over
$\mathbb{A}^{2}$-fibration over ![]() $R$.
$R$.
Proof. Let ![]() $A\otimes _{k}\bar{k}=(R\otimes _{k}\bar{k})[X,Y]$, where
$A\otimes _{k}\bar{k}=(R\otimes _{k}\bar{k})[X,Y]$, where ![]() $\bar{k}$ is an algebraic closure of
$\bar{k}$ is an algebraic closure of ![]() $k$. Let
$k$. Let ![]() $X=\sum _{i=0}^{n}a_{i}\otimes \unicode[STIX]{x1D706}_{i}$ and
$X=\sum _{i=0}^{n}a_{i}\otimes \unicode[STIX]{x1D706}_{i}$ and ![]() $Y=\sum _{i=0}^{m}b_{i}\otimes \unicode[STIX]{x1D707}_{i}$, where
$Y=\sum _{i=0}^{m}b_{i}\otimes \unicode[STIX]{x1D707}_{i}$, where ![]() $a_{i},b_{i}\in A$ and
$a_{i},b_{i}\in A$ and ![]() $\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D707}_{i}\in \bar{k}$. Then
$\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D707}_{i}\in \bar{k}$. Then ![]() $R[a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{m}]\subseteq A$ and the induced map
$R[a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{m}]\subseteq A$ and the induced map ![]() $R[a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{m}]\otimes _{k}\bar{k}\longrightarrow A\otimes _{k}\bar{k}$ is an isomorphism. Hence
$R[a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{m}]\otimes _{k}\bar{k}\longrightarrow A\otimes _{k}\bar{k}$ is an isomorphism. Hence ![]() $\bar{k}$ being faithfully flat over
$\bar{k}$ being faithfully flat over ![]() $k$, we have
$k$, we have ![]() $A=R[a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{m}]$. Thus
$A=R[a_{1},\ldots ,a_{n},b_{1},\ldots ,b_{m}]$. Thus ![]() $A$ is a finitely generated
$A$ is a finitely generated ![]() $R$-algebra. Again, as
$R$-algebra. Again, as ![]() $A\otimes _{k}\bar{k}$ is faithfully flat over
$A\otimes _{k}\bar{k}$ is faithfully flat over ![]() $R\otimes _{k}\bar{k}$ and
$R\otimes _{k}\bar{k}$ and ![]() $\bar{k}$ is faithfully flat over
$\bar{k}$ is faithfully flat over ![]() $k$,
$k$, ![]() $A$ is flat over
$A$ is flat over ![]() $R$. Now it suffices to show
$R$. Now it suffices to show ![]() , for each prime ideal
, for each prime ideal ![]() of
of ![]() $R$.
$R$.
Let ![]() be an arbitrary prime ideal of
be an arbitrary prime ideal of ![]() $R$. By hypothesis there exists a finite separable extension
$R$. By hypothesis there exists a finite separable extension ![]() $L$ of
$L$ of ![]() $k$ such that
$k$ such that ![]() $A\otimes _{k}L=(R\otimes _{k}L)^{[2]}$. Hence,
$A\otimes _{k}L=(R\otimes _{k}L)^{[2]}$. Hence, ![]() . Hence by Lemma 3.5,
. Hence by Lemma 3.5, ![]() .
.
Thus, ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{2}$-fibration over
$\mathbb{A}^{2}$-fibration over ![]() $R$.◻
$R$.◻
We now extend Theorems 2.8 and 2.10 to any one-dimensional Noetherian ring containing a field of characteristic zero.
Theorem 3.7. Let ![]() $k$ be a field of characteristic zero and
$k$ be a field of characteristic zero and ![]() $R$ a one-dimensional Noetherian
$R$ a one-dimensional Noetherian ![]() $k$-algebra. If
$k$-algebra. If ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{2}$-form over
$\mathbb{A}^{2}$-form over ![]() $R$ with respect to
$R$ with respect to ![]() $k$, then there exists a finitely generated rank one projective
$k$, then there exists a finitely generated rank one projective ![]() $R$-module
$R$-module ![]() $Q$ such that
$Q$ such that ![]() $A\cong (\text{Sym}_{R}(Q))^{[1]}$.
$A\cong (\text{Sym}_{R}(Q))^{[1]}$.
Proof. By Lemma 3.6, ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{2}$-fibration over
$\mathbb{A}^{2}$-fibration over ![]() $R$ and hence by Theorem 2.11, there exists
$R$ and hence by Theorem 2.11, there exists ![]() $H\in A$ such that
$H\in A$ such that ![]() $A$ is an
$A$ is an ![]() $\mathbb{A}^{1}$-fibration over
$\mathbb{A}^{1}$-fibration over ![]() $R[H]$. Let
$R[H]$. Let ![]() $\bar{k}$ be an algebraic closure of
$\bar{k}$ be an algebraic closure of ![]() $k$,
$k$, ![]() $\bar{A}:=A\otimes \bar{k}$ and
$\bar{A}:=A\otimes \bar{k}$ and ![]() $\bar{R}:=R\otimes \bar{k}$. Since
$\bar{R}:=R\otimes \bar{k}$. Since ![]() $\bar{A}=\bar{R}^{[2]}$ and
$\bar{A}=\bar{R}^{[2]}$ and ![]() $\bar{A}$ is an
$\bar{A}$ is an ![]() $\mathbb{A}^{1}$-fibration over
$\mathbb{A}^{1}$-fibration over ![]() $\bar{R}[H]$, we have
$\bar{R}[H]$, we have ![]() $\bar{A}=\bar{R}[H]^{[1]}$ by Lemma 3.4. Thus by Theorem 2.9,
$\bar{A}=\bar{R}[H]^{[1]}$ by Lemma 3.4. Thus by Theorem 2.9, ![]() $A\cong \text{Sym}_{R[H]}(Q_{1})$, for some finitely generated rank one projective
$A\cong \text{Sym}_{R[H]}(Q_{1})$, for some finitely generated rank one projective ![]() $R[H]$-module
$R[H]$-module ![]() $Q_{1}$. Set
$Q_{1}$. Set ![]() $R_{\text{red}}:=R/nil(R)$. Now
$R_{\text{red}}:=R/nil(R)$. Now
Now by [Reference Itoh14, Section 2, Lemma 1], there exists a finitely generated rank one projective ![]() $R_{\text{red}}$-module
$R_{\text{red}}$-module ![]() $Q^{\prime }$ such that
$Q^{\prime }$ such that ![]() $Q_{1}\otimes _{R}(R_{\text{red}})=Q^{\prime }\otimes _{R_{\text{red}}}R_{\text{red}}[H]$. Thus,
$Q_{1}\otimes _{R}(R_{\text{red}})=Q^{\prime }\otimes _{R_{\text{red}}}R_{\text{red}}[H]$. Thus,
Now by [Reference Ischebeck and Rao15, Proposition 2.3.5], there exists a finitely generated rank one projective ![]() $R$-module
$R$-module ![]() $Q$ such that
$Q$ such that ![]() $Q\otimes _{R}R_{\text{red}}=Q^{\prime }$ and hence
$Q\otimes _{R}R_{\text{red}}=Q^{\prime }$ and hence ![]() $A=(\text{Sym}_{R}(Q))^{[1]}$.◻
$A=(\text{Sym}_{R}(Q))^{[1]}$.◻
The following result shows that under the additional hypothesis that ![]() $A$ has a fixed point free locally nilpotent
$A$ has a fixed point free locally nilpotent ![]() $R$-derivation, Theorem 3.7 can be extended to any ring containing a field of characteristic zero.
$R$-derivation, Theorem 3.7 can be extended to any ring containing a field of characteristic zero.
Theorem 3.8. Let ![]() $k$ be a field of characteristic zero,
$k$ be a field of characteristic zero, ![]() $R$ a ring containing
$R$ a ring containing ![]() $k$ and
$k$ and ![]() $A$ be an
$A$ be an ![]() $\mathbb{A}^{2}$-form over
$\mathbb{A}^{2}$-form over ![]() $R$ with respect to
$R$ with respect to ![]() $k$. Suppose
$k$. Suppose ![]() $A$ has a fixed point free locally nilpotent
$A$ has a fixed point free locally nilpotent ![]() $R$-derivation. Then there exists a finitely generated rank one projective
$R$-derivation. Then there exists a finitely generated rank one projective ![]() $R$-module
$R$-module ![]() $Q$ such that
$Q$ such that ![]() $A\cong (\text{Sym}_{R}(Q))^{[1]}$.
$A\cong (\text{Sym}_{R}(Q))^{[1]}$.
Proof. Let ![]() $L$ be a finite extension of
$L$ be a finite extension of ![]() $k$ such that
$k$ such that ![]() $A\otimes _{k}L=(R\otimes _{k}L)^{[2]}$. Let
$A\otimes _{k}L=(R\otimes _{k}L)^{[2]}$. Let ![]() $D$ be a fixed point free locally nilpotent
$D$ be a fixed point free locally nilpotent ![]() $R$-derivation of
$R$-derivation of ![]() $A$ and
$A$ and ![]() $B=\text{ker}~D$. Set
$B=\text{ker}~D$. Set ![]() $\bar{R}:=R\otimes _{k}L$,
$\bar{R}:=R\otimes _{k}L$, ![]() $\bar{A}:=A\otimes _{k}L$,
$\bar{A}:=A\otimes _{k}L$, ![]() $\bar{B}:=B\otimes _{k}L$ and
$\bar{B}:=B\otimes _{k}L$ and ![]() $\bar{D}:=D\otimes 1_{L}$. Then
$\bar{D}:=D\otimes 1_{L}$. Then ![]() $\bar{A}=\bar{R}^{[2]}$,
$\bar{A}=\bar{R}^{[2]}$, ![]() $\text{ker}\,\bar{D}=\bar{B}$ and
$\text{ker}\,\bar{D}=\bar{B}$ and ![]() $\bar{D}$ is a fixed point free locally nilpotent derivation of
$\bar{D}$ is a fixed point free locally nilpotent derivation of ![]() $\bar{A}$. Hence, by Theorem 2.15,
$\bar{A}$. Hence, by Theorem 2.15, ![]() $\bar{D}$ has a slice and
$\bar{D}$ has a slice and ![]() $\bar{B}=\bar{R}^{[1]}$. Now, by Theorem 2.13,
$\bar{B}=\bar{R}^{[1]}$. Now, by Theorem 2.13, ![]() $D(\bar{A})=\bar{A}$. Thus,
$D(\bar{A})=\bar{A}$. Thus, ![]() $D(A)\otimes _{k}L=D(\bar{A})=\bar{A}=A\otimes _{k}L$. Hence, by faithful flatness of
$D(A)\otimes _{k}L=D(\bar{A})=\bar{A}=A\otimes _{k}L$. Hence, by faithful flatness of ![]() $L$ over
$L$ over ![]() $k$,
$k$, ![]() $D(A)=A$. So
$D(A)=A$. So ![]() $A=B^{[1]}$ by Theorem 2.13. Since
$A=B^{[1]}$ by Theorem 2.13. Since ![]() $\bar{B}=\bar{R}^{[1]}$, by Theorem 2.9,
$\bar{B}=\bar{R}^{[1]}$, by Theorem 2.9, ![]() $B=\text{Sym}_{R}(Q)$ and hence
$B=\text{Sym}_{R}(Q)$ and hence ![]() $A=(\text{Sym}_{R}(Q))^{[1]}$, for some finitely generated rank one projective
$A=(\text{Sym}_{R}(Q))^{[1]}$, for some finitely generated rank one projective ![]() $R$-module
$R$-module ![]() $Q$.◻
$Q$.◻
Remark 3.9. Kahoui and Ouali have shown [Reference Kahoui and Ouali16, Corollary 3.2] that when ![]() $R$ is regular the above result holds for any
$R$ is regular the above result holds for any ![]() $\mathbb{A}^{2}$-fibration over
$\mathbb{A}^{2}$-fibration over ![]() $R$.
$R$.
Acknowledgments
The authors thank S. M. Bhatwadekar for the current version of Theorem 3.8 and also for his useful comments and suggestions. The second author acknowledges the Department of Science and Technology for their SwarnaJayanti Fellowship. The third author also acknowledges Council of Scientific and Industrial Research (CSIR) for their grant.