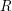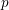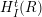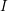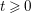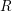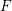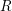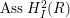1 Introduction
Throughout this paper, let
![]() $R$
be a commutative Noetherian ring and
$R$
be a commutative Noetherian ring and
![]() $I$
an ideal of
$I$
an ideal of
![]() $R$
. Local cohomology, introduced by Grothendieck, is an important tool in both algebraic geometry and commutative algebra (cf. [Reference Brodmann and Sharp5]). In general, the local cohomology module
$R$
. Local cohomology, introduced by Grothendieck, is an important tool in both algebraic geometry and commutative algebra (cf. [Reference Brodmann and Sharp5]). In general, the local cohomology module
![]() $H_{I}^{t}(R)$
is not finitely generated as an
$H_{I}^{t}(R)$
is not finitely generated as an
![]() $R$
-module. Therefore an important problem is identifying finiteness properties of local cohomology. Huneke in [Reference Huneke7] raised the question of whether local cohomology modules of Noetherian rings always have finitely many associated primes. This problem is an active research area in commutative algebra in the last two decades.
$R$
-module. Therefore an important problem is identifying finiteness properties of local cohomology. Huneke in [Reference Huneke7] raised the question of whether local cohomology modules of Noetherian rings always have finitely many associated primes. This problem is an active research area in commutative algebra in the last two decades.
Nowadays, we know that Huneke’s question has a negative answer in general; many interesting counterexamples were constructed by Katzman [Reference Katzman10], Singh [Reference Singh20], and Singh and Swanson [Reference Singh and Swanson21], even for a hypersurface
![]() $R$
with “good” singularities. On the other hand, affirmative results have been obtained for nice classes of
$R$
with “good” singularities. On the other hand, affirmative results have been obtained for nice classes of
![]() $R$
, typically with small singular loci. In particular, Huneke’s question has been largely settled when
$R$
, typically with small singular loci. In particular, Huneke’s question has been largely settled when
![]() $R$
is regular (cf. [Reference Bhatt, Blickle, Lyubeznik, Singh and Zhang3, Reference Huneke and Sharp9, Reference Lyubeznik12, Reference Lyubeznik13]), although important cases remain open, see Remark 2.9. Many partial affirmative results for singular
$R$
is regular (cf. [Reference Bhatt, Blickle, Lyubeznik, Singh and Zhang3, Reference Huneke and Sharp9, Reference Lyubeznik12, Reference Lyubeznik13]), although important cases remain open, see Remark 2.9. Many partial affirmative results for singular
![]() $R$
have also been proved, for example see [Reference Brodmann and Faghani4, Reference Marley14, Reference Quy18, Reference Takagi and Takahashi23].
$R$
have also been proved, for example see [Reference Brodmann and Faghani4, Reference Marley14, Reference Quy18, Reference Takagi and Takahashi23].
In this paper, we first consider Huneke’s problem when
![]() $R$
contains a field of prime characteristic
$R$
contains a field of prime characteristic
![]() $p$
. In this situation perhaps the most significant result to date in the singular situation came from the work of Takagi and Takahashi [Reference Takagi and Takahashi23], who showed that Huneke’s question has an affirmative answer when
$p$
. In this situation perhaps the most significant result to date in the singular situation came from the work of Takagi and Takahashi [Reference Takagi and Takahashi23], who showed that Huneke’s question has an affirmative answer when
![]() $R$
is a Gorenstein ring with finite
$R$
is a Gorenstein ring with finite
![]() $F$
-representation type. The notion of finite
$F$
-representation type. The notion of finite
![]() $F$
-representation type was introduced by Smith and Van den Bergh in [Reference Smith and Van den Bergh22] as a characteristic
$F$
-representation type was introduced by Smith and Van den Bergh in [Reference Smith and Van den Bergh22] as a characteristic
![]() $p$
analogue of the notion of finite representation type. One part of our main theorem extends their result by dropping the Gorenstein condition.
$p$
analogue of the notion of finite representation type. One part of our main theorem extends their result by dropping the Gorenstein condition.
Main Theorem. Let
![]() $R$
be a Noetherian ring of prime characteristic
$R$
be a Noetherian ring of prime characteristic
![]() $p$
that has finite
$p$
that has finite
![]() $F$
-representation type or finite singular locus. Then
$F$
-representation type or finite singular locus. Then
![]() $H_{I}^{t}(R)$
has only finitely many associated prime ideals for any ideal
$H_{I}^{t}(R)$
has only finitely many associated prime ideals for any ideal
![]() $I$
and for any
$I$
and for any
![]() $t\geqslant 0$
. Consequently,
$t\geqslant 0$
. Consequently,
![]() $H_{I}^{t}(R)$
has closed support for any ideal
$H_{I}^{t}(R)$
has closed support for any ideal
![]() $I$
and for any
$I$
and for any
![]() $t\geqslant 0$
.
$t\geqslant 0$
.
Remark 1.1. We have been informed that Mel Hochster and Luis Núñez-Betancourt have obtained the same result above with different method in [Reference Hochster and Núñez-Betancourt6].
Our main result yields affirmative answers of Huneke’s problem for many important classes of rings. The proof is rather short, the main ingredient being the theory of filter regular sequence and an extremely useful isomorphism of local cohomology modules by Nagel–Schenzel, see Lemma 2.6.
In the last section, we use the same approach to study the problem of when
![]() $\operatorname{Ass}H_{I}^{2}(R)$
is always finite and give a sufficient condition on the singularities of
$\operatorname{Ass}H_{I}^{2}(R)$
is always finite and give a sufficient condition on the singularities of
![]() $R$
in any characteristic, see Theorem 3.3.
$R$
in any characteristic, see Theorem 3.3.
2 Results in positive characteristic
In this section, we always assume that
![]() $R$
contains a field of prime characteristic
$R$
contains a field of prime characteristic
![]() $p>0$
. For such a ring, we have the Frobenius homomorphism
$p>0$
. For such a ring, we have the Frobenius homomorphism
![]() $F:R\rightarrow R;x\mapsto x^{p}$
. We also denote
$F:R\rightarrow R;x\mapsto x^{p}$
. We also denote
![]() $F^{e}=F\circ \cdots \circ F$
(iterated
$F^{e}=F\circ \cdots \circ F$
(iterated
![]() $e$
times) for all
$e$
times) for all
![]() $e\geqslant 0$
. For any
$e\geqslant 0$
. For any
![]() $R$
-module
$R$
-module
![]() $M$
, we denote by
$M$
, we denote by
![]() $^{e}M$
the module
$^{e}M$
the module
![]() $M$
with its
$M$
with its
![]() $R$
-module structure pulled back via
$R$
-module structure pulled back via
![]() $F^{e}$
. That is,
$F^{e}$
. That is,
![]() $^{e}M$
is just
$^{e}M$
is just
![]() $M$
as an abelian group, but its
$M$
as an abelian group, but its
![]() $R$
-module structure is determined by
$R$
-module structure is determined by
![]() $r\cdot m=r^{p^{e}}m$
for all
$r\cdot m=r^{p^{e}}m$
for all
![]() $r\in R$
and
$r\in R$
and
![]() $m\in M$
. We say
$m\in M$
. We say
![]() $R$
is
$R$
is
![]() $F$
-finite if
$F$
-finite if
![]() $^{1}R$
is a finitely generated
$^{1}R$
is a finitely generated
![]() $R$
-module. Let
$R$
-module. Let
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $R$
. For each
$R$
. For each
![]() $q=p^{e}$
we denote
$q=p^{e}$
we denote
![]() $I^{[q]}=(a^{q}\,|\,a\in I)$
. It is easy to see that
$I^{[q]}=(a^{q}\,|\,a\in I)$
. It is easy to see that
The following is useful in the sequel (cf. [Reference Takagi and Takahashi23, Lemma 3.1]).
Lemma 2.1. Suppose that
![]() $R$
is a ring of prime characteristic. Let
$R$
is a ring of prime characteristic. Let
![]() $M$
be an
$M$
be an
![]() $R$
-module. Then
$R$
-module. Then
![]() $\text{Ass}_{R}M=\text{Ass}_{R}\text{}^{e}M$
for all
$\text{Ass}_{R}M=\text{Ass}_{R}\text{}^{e}M$
for all
![]() $e\geqslant 1$
.
$e\geqslant 1$
.
Rings with finite
![]() $F$
-representation type were first introduced by Smith and Van den Bergh in [Reference Smith and Van den Bergh22], under the assumption that the Krull–Schmidt theorem holds for them. Yao [Reference Yao24] studied these rings in a more general setting.
$F$
-representation type were first introduced by Smith and Van den Bergh in [Reference Smith and Van den Bergh22], under the assumption that the Krull–Schmidt theorem holds for them. Yao [Reference Yao24] studied these rings in a more general setting.
Definition 2.2. Let
![]() $R$
be a Noetherian ring of prime characteristic
$R$
be a Noetherian ring of prime characteristic
![]() $p$
. We say that
$p$
. We say that
![]() $R$
has finite
$R$
has finite
![]() $F$
-representation type by finitely generated
$F$
-representation type by finitely generated
![]() $R$
-modules
$R$
-modules
![]() $M_{1},\ldots ,M_{s}$
if for every
$M_{1},\ldots ,M_{s}$
if for every
![]() $e\geqslant 0$
, the
$e\geqslant 0$
, the
![]() $R$
-module
$R$
-module
![]() $^{e}R$
is isomorphic to a finite direct sum of the
$^{e}R$
is isomorphic to a finite direct sum of the
![]() $R$
-modules
$R$
-modules
![]() $M_{1},\ldots ,M_{s}$
, that is, there exist nonnegative integers
$M_{1},\ldots ,M_{s}$
, that is, there exist nonnegative integers
![]() $n_{e1},\ldots ,n_{es}$
such that
$n_{e1},\ldots ,n_{es}$
such that
We simply say that
![]() $R$
has finite
$R$
has finite
![]() $F$
-representation type if there exist finitely generated
$F$
-representation type if there exist finitely generated
![]() $R$
-modules
$R$
-modules
![]() $M_{1},\ldots ,M_{s}$
by which
$M_{1},\ldots ,M_{s}$
by which
![]() $R$
has finite
$R$
has finite
![]() $F$
-representation type.
$F$
-representation type.
It is clear that if the ring
![]() $R$
has finite
$R$
has finite
![]() $F$
-representation type, then
$F$
-representation type, then
![]() $R$
is
$R$
is
![]() $F$
-finite. We collect here some examples of rings with finite
$F$
-finite. We collect here some examples of rings with finite
![]() $F$
-representation type. For the details, see [Reference Takagi and Takahashi23, Example 1.3].
$F$
-representation type. For the details, see [Reference Takagi and Takahashi23, Example 1.3].
Example 2.3.
(i) Let
 $R$
be an
$R$
be an
 $F$
-finite regular local ring of characteristic
$F$
-finite regular local ring of characteristic
 $p>0$
(resp. a polynomial ring
$p>0$
(resp. a polynomial ring
 $k[X_{1},\ldots ,X_{n}]$
over a field
$k[X_{1},\ldots ,X_{n}]$
over a field
 $k$
of characteristic
$k$
of characteristic
 $p>0$
such that
$p>0$
such that
 $[k:k^{p}]<\infty$
). Then
$[k:k^{p}]<\infty$
). Then
 $R$
has finite
$R$
has finite
 $F$
-representation type by the
$F$
-representation type by the
 $R$
-module
$R$
-module
 $R$
.
$R$
.(ii) Let
 $R$
be a Cohen–Macaulay local ring of prime characteristic
$R$
be a Cohen–Macaulay local ring of prime characteristic
 $p$
with finite representation type. Then
$p$
with finite representation type. Then
 $R$
has finite
$R$
has finite
 $F$
-representation type.
$F$
-representation type.(iii) Let
 $S=k[X_{1},\ldots ,X_{n}]$
be a polynomial ring over a field
$S=k[X_{1},\ldots ,X_{n}]$
be a polynomial ring over a field
 $k$
of characteristic
$k$
of characteristic
 $p>0$
such that
$p>0$
such that
 $[k:k^{p}]<\infty$
and
$[k:k^{p}]<\infty$
and
 $\mathfrak{a}$
a monomial ideal of
$\mathfrak{a}$
a monomial ideal of
 $S$
. Then the quotient ring
$S$
. Then the quotient ring
 $R=S/\mathfrak{a}$
has finite
$R=S/\mathfrak{a}$
has finite
 $F$
-representation type.
$F$
-representation type.(iv) Let
 $R{\hookrightarrow}S$
be a finite local homomorphism of Noetherian local rings of prime characteristic
$R{\hookrightarrow}S$
be a finite local homomorphism of Noetherian local rings of prime characteristic
 $p$
such that
$p$
such that
 $R$
is an
$R$
is an
 $R$
-module direct summand of
$R$
-module direct summand of
 $S$
. If
$S$
. If
 $S$
has finite
$S$
has finite
 $F$
-representation type, so does
$F$
-representation type, so does
 $R$
.
$R$
.(v) A normal semigroup ring over a field
 $k$
of characteristic
$k$
of characteristic
 $p>0$
such that
$p>0$
such that
 $[k:k^{p}]<\infty$
has finite
$[k:k^{p}]<\infty$
has finite
 $F$
-representation type. Also, rings of invariants of linearly reductive groups over such field have finite
$F$
-representation type. Also, rings of invariants of linearly reductive groups over such field have finite
 $F$
-representation type.
$F$
-representation type.
Remark 2.4. It is easy to see that if
![]() $R$
has finite
$R$
has finite
![]() $F$
-representation type, then so do
$F$
-representation type, then so do
![]() $R[X]$
and
$R[X]$
and
![]() $R[[X]]$
, as well as localizations and completions of
$R[[X]]$
, as well as localizations and completions of
![]() $R$
. Combining this fact and the above examples we can produce many interesting examples of rings with finite
$R$
. Combining this fact and the above examples we can produce many interesting examples of rings with finite
![]() $F$
-representation type.
$F$
-representation type.
We next recall the notion of
![]() $I$
-filter regular sequence of
$I$
-filter regular sequence of
![]() $R$
and its relation with local cohomology.
$R$
and its relation with local cohomology.
Definition 2.5. Let
![]() $I$
be an ideal of a Noetherian ring
$I$
be an ideal of a Noetherian ring
![]() $R$
. We say a sequence
$R$
. We say a sequence
![]() $x_{1},\ldots ,x_{t}$
of elements contained in
$x_{1},\ldots ,x_{t}$
of elements contained in
![]() $I$
is an
$I$
is an
![]() $I$
-filter regular sequence of
$I$
-filter regular sequence of
![]() $R$
if
$R$
if
for all
![]() $i=1,\ldots ,t$
, where
$i=1,\ldots ,t$
, where
![]() $V(I)$
denotes the set of prime ideals containing
$V(I)$
denotes the set of prime ideals containing
![]() $I$
. This condition is equivalent to
$I$
. This condition is equivalent to
![]() $x_{i}\notin \mathfrak{p}$
for all
$x_{i}\notin \mathfrak{p}$
for all
![]() $\mathfrak{p}\in \text{Ass}_{R}R/(x_{1},\ldots ,x_{i-1})\setminus V(I)$
and for all
$\mathfrak{p}\in \text{Ass}_{R}R/(x_{1},\ldots ,x_{i-1})\setminus V(I)$
and for all
![]() $i=1,\ldots ,t$
.
$i=1,\ldots ,t$
.
The following is very useful to analyze the local cohomology modules by filter regular sequences (cf. [Reference Nagel and Schenzel15, Proposition 3.4] for the original version when
![]() $I$
is the maximal ideal, and [Reference Asadollahi and Schenzel1, Proposition 2.3] for the general version below). More applications can be found in [Reference Quy and Shimomoto19].
$I$
is the maximal ideal, and [Reference Asadollahi and Schenzel1, Proposition 2.3] for the general version below). More applications can be found in [Reference Quy and Shimomoto19].
Lemma 2.6. (Nagel–Schenzel’s isomorphism)
Let
![]() $I$
be an ideal of a Noetherian ring
$I$
be an ideal of a Noetherian ring
![]() $R$
and
$R$
and
![]() $x_{1},\ldots ,x_{t}$
an
$x_{1},\ldots ,x_{t}$
an
![]() $I$
-filter regular sequence of
$I$
-filter regular sequence of
![]() $R$
. Then we have
$R$
. Then we have
Remark 2.7. It should be noted that the notion of filter regular sequence and the Nagel–Schenzel isomorphism are not dependent on the characteristic of the ring. Moreover, for any
![]() $t\geqslant 1$
we always can choose an
$t\geqslant 1$
we always can choose an
![]() $I$
-filter regular sequence of
$I$
-filter regular sequence of
![]() $x_{1},\ldots ,x_{t}$
. Indeed, by the prime avoidance lemma we can choose
$x_{1},\ldots ,x_{t}$
. Indeed, by the prime avoidance lemma we can choose
![]() $x_{1}\in I$
and
$x_{1}\in I$
and
![]() $x_{1}\notin \mathfrak{p}$
for all
$x_{1}\notin \mathfrak{p}$
for all
![]() $\mathfrak{p}\in \text{Ass}_{R}R\setminus V(I)$
. For
$\mathfrak{p}\in \text{Ass}_{R}R\setminus V(I)$
. For
![]() $i>1$
assume that we have
$i>1$
assume that we have
![]() $x_{1},\ldots ,x_{i-1}$
, then we choose
$x_{1},\ldots ,x_{i-1}$
, then we choose
![]() $x_{i}\in I$
and
$x_{i}\in I$
and
![]() $x_{i}\notin \mathfrak{p}$
for all
$x_{i}\notin \mathfrak{p}$
for all
![]() $\mathfrak{p}\in \text{Ass}_{R}R/(x_{1},\ldots ,x_{i-1})\setminus V(I)$
by the prime avoidance lemma again. For more details, see [Reference Asadollahi and Schenzel1, Section 2].
$\mathfrak{p}\in \text{Ass}_{R}R/(x_{1},\ldots ,x_{i-1})\setminus V(I)$
by the prime avoidance lemma again. For more details, see [Reference Asadollahi and Schenzel1, Section 2].
Lemma 2.8. Let
![]() $R$
be a commutative Noetherian ring of characteristic
$R$
be a commutative Noetherian ring of characteristic
![]() $p>0$
and
$p>0$
and
![]() $\mathfrak{a}$
is an ideal. Then
$\mathfrak{a}$
is an ideal. Then
Proof. Let
![]() $\mathfrak{p}\in \operatorname{Ass}R/\mathfrak{a}^{[q]}$
for some
$\mathfrak{p}\in \operatorname{Ass}R/\mathfrak{a}^{[q]}$
for some
![]() $q=p^{e}$
. If
$q=p^{e}$
. If
![]() $\mathfrak{p}\in \operatorname{Ass}R/\mathfrak{a}$
, we are done. If not, we need to show that
$\mathfrak{p}\in \operatorname{Ass}R/\mathfrak{a}$
, we are done. If not, we need to show that
![]() $\mathfrak{p}\in \operatorname{Sing}(R)$
. Suppose not, then
$\mathfrak{p}\in \operatorname{Sing}(R)$
. Suppose not, then
![]() $R_{\mathfrak{p}}$
is regular. As Frobenius localizes and is flat over a regular ring, we have that
$R_{\mathfrak{p}}$
is regular. As Frobenius localizes and is flat over a regular ring, we have that
![]() $\operatorname{depth}(R/\mathfrak{a}^{[q]})_{\mathfrak{p}}=\operatorname{depth}(R/\mathfrak{a})_{\mathfrak{p}}>0$
, a contradiction.◻
$\operatorname{depth}(R/\mathfrak{a}^{[q]})_{\mathfrak{p}}=\operatorname{depth}(R/\mathfrak{a})_{\mathfrak{p}}>0$
, a contradiction.◻
We are now ready to prove the main theorem which we mentioned in the introduction.
Proof of Main Theorem.
For any ideal
![]() $I$
and any
$I$
and any
![]() $t\geqslant 0$
we prove that
$t\geqslant 0$
we prove that
![]() $\text{Ass}_{R}H_{I}^{i}(R)$
is finite provided
$\text{Ass}_{R}H_{I}^{i}(R)$
is finite provided
![]() $R$
has finite
$R$
has finite
![]() $F$
-representation type. The case
$F$
-representation type. The case
![]() $t=0$
is trivial. For
$t=0$
is trivial. For
![]() $t\geqslant 1$
, by Remark 2.7 we can choose an
$t\geqslant 1$
, by Remark 2.7 we can choose an
![]() $I$
-filter regular sequence
$I$
-filter regular sequence
![]() $x_{1},\ldots ,x_{t}$
of
$x_{1},\ldots ,x_{t}$
of
![]() $R$
. Set
$R$
. Set
![]() $\mathfrak{a}=(x_{1},\ldots ,x_{t})$
, by Lemma 2.6 we have
$\mathfrak{a}=(x_{1},\ldots ,x_{t})$
, by Lemma 2.6 we have
Therefore
![]() $\text{Ass}_{R}H_{I}^{t}(R)\subseteq \text{Ass}_{R}H_{\mathfrak{a}}^{t}(R)$
. Consider local cohomology as the direct limit of Koszul cohomologies, then we have
$\text{Ass}_{R}H_{I}^{t}(R)\subseteq \text{Ass}_{R}H_{\mathfrak{a}}^{t}(R)$
. Consider local cohomology as the direct limit of Koszul cohomologies, then we have
In the case our ring is of prime characteristic
![]() $p>0$
we have the following isomorphism
$p>0$
we have the following isomorphism
where
![]() $q=p^{e}$
,
$q=p^{e}$
,
![]() $e\geqslant 0$
. It is not hard to check that
$e\geqslant 0$
. It is not hard to check that
Hence it is enough to prove that
![]() $\bigcup _{q}\text{Ass}_{R}R/\mathfrak{a}^{[q]}$
is a finite set. On the other hand, let
$\bigcup _{q}\text{Ass}_{R}R/\mathfrak{a}^{[q]}$
is a finite set. On the other hand, let
![]() $M_{1},\ldots ,M_{s}$
be the finitely generated
$M_{1},\ldots ,M_{s}$
be the finitely generated
![]() $R$
-modules by which
$R$
-modules by which
![]() $R$
has finite
$R$
has finite
![]() $F$
-representation type. For all
$F$
-representation type. For all
![]() $e\geqslant 0$
we have
$e\geqslant 0$
we have
By Lemma 2.1 we have
for all
![]() $q=p^{e}$
. Since
$q=p^{e}$
. Since
![]() $M_{i}$
is finitely generated for all
$M_{i}$
is finitely generated for all
![]() $1\leqslant i\leqslant s$
, the proof is complete.
$1\leqslant i\leqslant s$
, the proof is complete.
When
![]() $\operatorname{Sing}(R)$
is finite, the proof is the same until (*), then we can invoke Lemma 2.8.◻
$\operatorname{Sing}(R)$
is finite, the proof is the same until (*), then we can invoke Lemma 2.8.◻
Remark 2.9. We can also prove the assertion of our theorem when
![]() $\operatorname{Sing}(R)$
is finite by the localization at countably infinitely many primes technique in [Reference Bahmanpour and Quy2]. To prove that assume
$\operatorname{Sing}(R)$
is finite by the localization at countably infinitely many primes technique in [Reference Bahmanpour and Quy2]. To prove that assume
![]() $\text{Ass}_{R}H_{I}^{t}(R)$
is an infinite set for some ideal
$\text{Ass}_{R}H_{I}^{t}(R)$
is an infinite set for some ideal
![]() $I$
and some
$I$
and some
![]() $t\geqslant 0$
. Since
$t\geqslant 0$
. Since
![]() $\text{Sing}(R)$
is finite, we can choose a countably infinitely many set
$\text{Sing}(R)$
is finite, we can choose a countably infinitely many set
![]() $\{{\mathfrak{p}_{i}\}}_{i\in \mathbb{N}}\subseteq \text{Ass}_{R}H_{I}^{t}(R)$
such that
$\{{\mathfrak{p}_{i}\}}_{i\in \mathbb{N}}\subseteq \text{Ass}_{R}H_{I}^{t}(R)$
such that
![]() $R_{\mathfrak{p}_{i}}$
is regular for all
$R_{\mathfrak{p}_{i}}$
is regular for all
![]() $i\geqslant 1$
. Using the localization at countably infinitely many primes technique (if necessary) as in [Reference Bahmanpour and Quy2, Lemma 1.1] we obtain a regular ring
$i\geqslant 1$
. Using the localization at countably infinitely many primes technique (if necessary) as in [Reference Bahmanpour and Quy2, Lemma 1.1] we obtain a regular ring
![]() $T$
of prime characteristic such that
$T$
of prime characteristic such that
![]() $\text{Ass}_{T}H_{IT}^{t}(T)$
is infinite. This is a contradiction. This proof would work in all characteristic, but even in characteristic
$\text{Ass}_{T}H_{IT}^{t}(T)$
is infinite. This is a contradiction. This proof would work in all characteristic, but even in characteristic
![]() $0$
we do not know if finiteness of associated primes holds for all regular rings.
$0$
we do not know if finiteness of associated primes holds for all regular rings.
Corollary 2.10. Let
![]() $R\rightarrow S$
be a homomorphism of commutative Noetherian rings of characteristic
$R\rightarrow S$
be a homomorphism of commutative Noetherian rings of characteristic
![]() $p>0$
that splits as
$p>0$
that splits as
![]() $R$
-modules. Assume that
$R$
-modules. Assume that
![]() $\operatorname{Sing}(S)$
is a finite set. Then
$\operatorname{Sing}(S)$
is a finite set. Then
![]() $H_{I}^{t}(R)$
has only finitely many associated prime ideals for any ideal
$H_{I}^{t}(R)$
has only finitely many associated prime ideals for any ideal
![]() $I$
and for any
$I$
and for any
![]() $t\geqslant 0$
.
$t\geqslant 0$
.
Proof. One can use our main theorem together with [Reference Núñez-Betancourt16]. ◻
3 On
 $\operatorname{Ass}H_{I}^{2}(R)$
$\operatorname{Ass}H_{I}^{2}(R)$
In this section, we consider rings of any characteristic. Despite all the positive and negative results we have mentioned, it remains mysterious to understand the associated primes of
![]() $H_{I}^{2}(R)$
, the first nontrivial case. It can be infinite even for a hypersurface domain [Reference Singh and Swanson21, Remark 4.2]. On the other hand, we do not know if this set is always finite if
$H_{I}^{2}(R)$
, the first nontrivial case. It can be infinite even for a hypersurface domain [Reference Singh and Swanson21, Remark 4.2]. On the other hand, we do not know if this set is always finite if
![]() $R$
is an excellent normal domain (however, it is finite if
$R$
is an excellent normal domain (however, it is finite if
![]() $\dim R\leqslant 4$
, [Reference Huneke, Katz and Marley8, Reference Marley14]). In this section, we analyze this question a bit further and identify an interesting condition that guarantees the finiteness of
$\dim R\leqslant 4$
, [Reference Huneke, Katz and Marley8, Reference Marley14]). In this section, we analyze this question a bit further and identify an interesting condition that guarantees the finiteness of
![]() $\operatorname{Ass}H_{I}^{2}(R)$
.
$\operatorname{Ass}H_{I}^{2}(R)$
.
Definition 3.1. A local normal domain
![]() $R$
is said to satisfy condition
$R$
is said to satisfy condition
![]() $(D3)$
if for any reflexive ideal
$(D3)$
if for any reflexive ideal
![]() $I$
,
$I$
,
![]() $\operatorname{depth}I\geqslant \min \{\dim R,3\}$
.
$\operatorname{depth}I\geqslant \min \{\dim R,3\}$
.
Remark 3.2. The following local rings satisfy condition
![]() $(D3)$
: any normal domain of dimension at most
$(D3)$
: any normal domain of dimension at most
![]() $2$
, any UFD of depth at least
$2$
, any UFD of depth at least
![]() $3$
. In particular, any complete intersection regular in codimension
$3$
. In particular, any complete intersection regular in codimension
![]() $3$
is
$3$
is
![]() $(D3)$
. More interestingly,
$(D3)$
. More interestingly,
![]() $R$
is
$R$
is
![]() $(D3)$
if it is
$(D3)$
if it is
![]() $\mathbb{Q}$
-factorial and is strongly
$\mathbb{Q}$
-factorial and is strongly
![]() $F$
-regular (positive characteristic) or has log-terminal singularities (characteristic
$F$
-regular (positive characteristic) or has log-terminal singularities (characteristic
![]() $0$
), see [Reference Patakfalvi and Schwede17, Theorem 3.1].
$0$
), see [Reference Patakfalvi and Schwede17, Theorem 3.1].
Theorem 3.3. Suppose
![]() $R$
is a normal domain such that the set
$R$
is a normal domain such that the set
is finite. Then
![]() $\operatorname{Ass}H_{I}^{2}(R)$
is finite for any ideal
$\operatorname{Ass}H_{I}^{2}(R)$
is finite for any ideal
![]() $I$
.
$I$
.
Proof. We begin by claiming that the set
![]() $\{\mathfrak{p}\in \operatorname{Ass}H_{I}^{2}(R),\operatorname{ht}\mathfrak{p}\leqslant 2\}$
is finite. Obviously, for
$\{\mathfrak{p}\in \operatorname{Ass}H_{I}^{2}(R),\operatorname{ht}\mathfrak{p}\leqslant 2\}$
is finite. Obviously, for
![]() $\mathfrak{p}$
in such set,
$\mathfrak{p}$
in such set,
![]() $\operatorname{ht}\mathfrak{p}=2$
. Then our claim follows from [Reference Bahmanpour and Quy2, Theorem 3.6].
$\operatorname{ht}\mathfrak{p}=2$
. Then our claim follows from [Reference Bahmanpour and Quy2, Theorem 3.6].
If
![]() $R$
is excellent the claim also follows from the proof of [Reference Huneke, Katz and Marley8, Corollary 2.8]. Let
$R$
is excellent the claim also follows from the proof of [Reference Huneke, Katz and Marley8, Corollary 2.8]. Let
![]() $\sqrt{I}=J\cap K$
where
$\sqrt{I}=J\cap K$
where
![]() $\operatorname{ht}J=1$
,
$\operatorname{ht}J=1$
,
![]() $\operatorname{ht}K\geqslant 2$
. If
$\operatorname{ht}K\geqslant 2$
. If
![]() $K\subseteq \mathfrak{p}$
, we are done. If not, then
$K\subseteq \mathfrak{p}$
, we are done. If not, then
![]() $H_{I_{\mathfrak{p}}}^{2}(R_{\mathfrak{p}})=H_{J_{\mathfrak{p}}}^{2}(R_{\mathfrak{p}})$
. But as
$H_{I_{\mathfrak{p}}}^{2}(R_{\mathfrak{p}})=H_{J_{\mathfrak{p}}}^{2}(R_{\mathfrak{p}})$
. But as
![]() $R$
is an excellent normal domain,
$R$
is an excellent normal domain,
![]() $R_{\mathfrak{p}}$
is analytically irreducible, so
$R_{\mathfrak{p}}$
is analytically irreducible, so
![]() $H_{J_{\mathfrak{p}}}^{2}(R_{\mathfrak{p}})=0$
by the Hartshorne–Lichtenbaum vanishing theorem, a contradiction.
$H_{J_{\mathfrak{p}}}^{2}(R_{\mathfrak{p}})=0$
by the Hartshorne–Lichtenbaum vanishing theorem, a contradiction.
Next we show that the set
![]() $\{\mathfrak{p}\in \operatorname{Ass}H_{I}^{2}(R),\operatorname{ht}\mathfrak{p}\geqslant 3\}$
is a subset of
$\{\mathfrak{p}\in \operatorname{Ass}H_{I}^{2}(R),\operatorname{ht}\mathfrak{p}\geqslant 3\}$
is a subset of
![]() $N$
, finishing the proof. By the Nagel–Schenzel trick as in the proof of the main theorem (or [Reference Huneke, Katz and Marley8, Proposition 2.7]), we can assume that
$N$
, finishing the proof. By the Nagel–Schenzel trick as in the proof of the main theorem (or [Reference Huneke, Katz and Marley8, Proposition 2.7]), we can assume that
![]() $\mathfrak{p}\in \operatorname{Ass}R/(x^{n},y^{n})$
for some
$\mathfrak{p}\in \operatorname{Ass}R/(x^{n},y^{n})$
for some
![]() $n\geqslant 0$
. We need to show
$n\geqslant 0$
. We need to show
![]() $R_{\mathfrak{p}}$
is not
$R_{\mathfrak{p}}$
is not
![]() $(D3)$
. Suppose it is. There is an exact sequence:
$(D3)$
. Suppose it is. There is an exact sequence:
By localizing and counting depth, it is clear that
![]() $(x^{n}:y^{n})$
satisfies Serre’s condition
$(x^{n}:y^{n})$
satisfies Serre’s condition
![]() $(S_{2})$
, so it is a reflexive ideal. As
$(S_{2})$
, so it is a reflexive ideal. As
![]() $\dim R_{\mathfrak{p}}\geqslant 3$
and it is
$\dim R_{\mathfrak{p}}\geqslant 3$
and it is
![]() $(D3)$
, it follows that
$(D3)$
, it follows that
![]() $\operatorname{depth}R_{\mathfrak{p}}/(x^{n}:y^{n})_{\mathfrak{p}}\geqslant 2$
. Counting depth again shows that
$\operatorname{depth}R_{\mathfrak{p}}/(x^{n}:y^{n})_{\mathfrak{p}}\geqslant 2$
. Counting depth again shows that
![]() $\operatorname{depth}R_{\mathfrak{p}}/(x^{n},y^{n})_{\mathfrak{p}}>0$
, contradicting the fact that
$\operatorname{depth}R_{\mathfrak{p}}/(x^{n},y^{n})_{\mathfrak{p}}>0$
, contradicting the fact that
![]() $\mathfrak{p}\in \operatorname{Ass}R/(x^{n},y^{n})$
.◻
$\mathfrak{p}\in \operatorname{Ass}R/(x^{n},y^{n})$
.◻
Corollary 3.4. Let
![]() $R$
be a commutative domain which is regular in codimension
$R$
be a commutative domain which is regular in codimension
![]() $3$
and is locally a complete intersection. Then
$3$
and is locally a complete intersection. Then
![]() $\operatorname{Ass}H_{I}^{2}(R)$
is finite for any ideal
$\operatorname{Ass}H_{I}^{2}(R)$
is finite for any ideal
![]() $I$
in
$I$
in
![]() $R$
.
$R$
.
Remark 3.5. Under mild conditions, the properties that guarantee condition
![]() $(D3)$
, as explained in Remark 3.2, are open properties on
$(D3)$
, as explained in Remark 3.2, are open properties on
![]() $\operatorname{Spec}R$
. Thus, in such situation Theorem 3.3 would yield statements such as “if
$\operatorname{Spec}R$
. Thus, in such situation Theorem 3.3 would yield statements such as “if
![]() $R$
is a local normal domain which is
$R$
is a local normal domain which is
![]() $\mathbb{Q}$
-factorial and has log-terminal singularities in codimension
$\mathbb{Q}$
-factorial and has log-terminal singularities in codimension
![]() $\dim R-2$
, then
$\dim R-2$
, then
![]() $\operatorname{Ass}H_{I}^{2}(R)$
is always finite”.
$\operatorname{Ass}H_{I}^{2}(R)$
is always finite”.
Remark 3.6. Singh and Swanson constructed [Reference Singh and Swanson21, Theorem 5.1] a
![]() $F$
-regular hypersurface UFD
$F$
-regular hypersurface UFD
![]() $R$
and an ideal
$R$
and an ideal
![]() $I$
such that
$I$
such that
![]() $\operatorname{Ass}H_{I}^{3}(R)$
is infinite. This shows that having good singularities alone may not help for higher local cohomology. However, in view of Theorem 3.3, it is plausible that if
$\operatorname{Ass}H_{I}^{3}(R)$
is infinite. This shows that having good singularities alone may not help for higher local cohomology. However, in view of Theorem 3.3, it is plausible that if
![]() $R$
is regular in codimension
$R$
is regular in codimension
![]() $c$
and has nice singularities, then
$c$
and has nice singularities, then
![]() $\operatorname{Ass}H_{I}^{t}(R)$
is finite for
$\operatorname{Ass}H_{I}^{t}(R)$
is finite for
![]() $t$
small relative to
$t$
small relative to
![]() $c$
. The example in [Reference Singh and Swanson21] is normal but not
$c$
. The example in [Reference Singh and Swanson21] is normal but not
![]() $(R_{2})$
.
$(R_{2})$
.
Acknowledgments
The second author would like to thank the VIASM for hospitality and financial support. He is supported by the Vietnam National Foundation for Science and Technology Development (Nafosted) under grant numbers 101.04-2017.10.