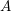1 Introduction
The study of the cohomology groups of local systems is an important subject in algebraic geometry, hyperplane arrangements, topology and hypergeometric functions of several variables. Many mathematicians are interested in the conditions for which we have their concentrations in the middle degrees. (For a review of this subject, see, for example, [Reference Dimca4, Section 6.4].) Here, let us consider this problem in the following situation. Let
![]() $B=\{b(1),b(2),\ldots ,b(N)\}\subset \mathbb{Z}^{n-1}$
be a finite subset of the lattice
$B=\{b(1),b(2),\ldots ,b(N)\}\subset \mathbb{Z}^{n-1}$
be a finite subset of the lattice
![]() $\mathbb{Z}^{n-1}$
. Assume that the affine lattice generated by
$\mathbb{Z}^{n-1}$
. Assume that the affine lattice generated by
![]() $B$
in
$B$
in
![]() $\mathbb{Z}^{n-1}$
coincides with
$\mathbb{Z}^{n-1}$
coincides with
![]() $\mathbb{Z}^{n-1}$
. For
$\mathbb{Z}^{n-1}$
. For
![]() $z=(z_{1},\ldots ,z_{N})\in \mathbb{C}^{N}$
, we consider Laurent polynomials
$z=(z_{1},\ldots ,z_{N})\in \mathbb{C}^{N}$
, we consider Laurent polynomials
![]() $P(x)$
on the algebraic torus
$P(x)$
on the algebraic torus
![]() $T_{0}=(\mathbb{C}^{\ast })^{n-1}$
defined by
$T_{0}=(\mathbb{C}^{\ast })^{n-1}$
defined by
![]() $P(x)=\sum _{j=1}^{N}z_{j}x^{b(j)}$
(
$P(x)=\sum _{j=1}^{N}z_{j}x^{b(j)}$
(
![]() $x=(x_{1},\ldots ,x_{n-1})\in T_{0}=(\mathbb{C}^{\ast })^{n-1}$
). Then, for
$x=(x_{1},\ldots ,x_{n-1})\in T_{0}=(\mathbb{C}^{\ast })^{n-1}$
). Then, for
![]() $c=(c_{1},\ldots ,c_{n})\in \mathbb{C}^{n}$
, we obtain a possibly multivalued function
$c=(c_{1},\ldots ,c_{n})\in \mathbb{C}^{n}$
, we obtain a possibly multivalued function
![]() $P(x)^{-c_{n}}x_{1}^{c_{1}-1}\cdots x_{n-1}^{c_{n-1}-1}$
on
$P(x)^{-c_{n}}x_{1}^{c_{1}-1}\cdots x_{n-1}^{c_{n-1}-1}$
on
![]() $W=T_{0}\setminus P^{-1}(0)$
. It generates the rank-one local system
$W=T_{0}\setminus P^{-1}(0)$
. It generates the rank-one local system
on
![]() $W$
. Under the nonresonance condition (see Definition 3.1) on
$W$
. Under the nonresonance condition (see Definition 3.1) on
![]() $c\in \mathbb{C}^{n}$
, Gelfand et al. [Reference Gelfand, Kapranov and Zelevinsky10] proved that we have the concentration
$c\in \mathbb{C}^{n}$
, Gelfand et al. [Reference Gelfand, Kapranov and Zelevinsky10] proved that we have the concentration
for nondegenerate Laurent polynomials
![]() $P(x)$
. This result was obtained as a byproduct of their study on the integral representations of
$P(x)$
. This result was obtained as a byproduct of their study on the integral representations of
![]() $A$
-hypergeometric functions in [Reference Gelfand, Kapranov and Zelevinsky10]. Since their proof of this concentration heavily relies on the framework of the
$A$
-hypergeometric functions in [Reference Gelfand, Kapranov and Zelevinsky10]. Since their proof of this concentration heavily relies on the framework of the
![]() ${\mathcal{D}}$
-module theory, it is desirable to prove it more directly. In this paper, by applying the twisted Morse theory to perverse sheaves, we extend the result of Gelfand–Kapranov–Zelevinsky to various directions.
${\mathcal{D}}$
-module theory, it is desirable to prove it more directly. In this paper, by applying the twisted Morse theory to perverse sheaves, we extend the result of Gelfand–Kapranov–Zelevinsky to various directions.
First, in Theorem 3.3, we relax the nondegeneracy condition on
![]() $P(x)$
by replacing it with a weaker one (see Definition 3.2). We thus extend the result of [Reference Gelfand, Kapranov and Zelevinsky10] to the case where the hypersurface
$P(x)$
by replacing it with a weaker one (see Definition 3.2). We thus extend the result of [Reference Gelfand, Kapranov and Zelevinsky10] to the case where the hypersurface
![]() $P^{-1}(0)\subset T_{0}$
may have isolated singular points in
$P^{-1}(0)\subset T_{0}$
may have isolated singular points in
![]() $T_{0}$
. In fact, in Theorem 3.3, we relax also the condition that
$T_{0}$
. In fact, in Theorem 3.3, we relax also the condition that
![]() $B$
generates
$B$
generates
![]() $\mathbb{Z}^{n-1}$
to a weaker one that the dimension of the convex hull
$\mathbb{Z}^{n-1}$
to a weaker one that the dimension of the convex hull
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-1}$
of
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-1}$
of
![]() $B$
in
$B$
in
![]() $\mathbb{R}^{n-1}$
is
$\mathbb{R}^{n-1}$
is
![]() $n-1$
. In Theorem 3.11, we extend these results to more general local systems associated to several Laurent polynomials. Namely, we obtain a vanishing theorem for arrangements of toric hypersurfaces with isolated singular points. Our proofs of Theorems 3.3 and 3.11 are very natural and are obtained by taking (possibly singular) “minimal” toric compactifications of
$n-1$
. In Theorem 3.11, we extend these results to more general local systems associated to several Laurent polynomials. Namely, we obtain a vanishing theorem for arrangements of toric hypersurfaces with isolated singular points. Our proofs of Theorems 3.3 and 3.11 are very natural and are obtained by taking (possibly singular) “minimal” toric compactifications of
![]() $T_{0}$
. In order to work on such singular varieties, we use our previous idea in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2]. See Section 3 for the details. Moreover, in Theorem 5.1 (assuming the nondegeneracy of Gelfand et al. [Reference Gelfand, Kapranov and Zelevinsky10] for Laurent polynomials), we relax the nonresonance condition of
$T_{0}$
. In order to work on such singular varieties, we use our previous idea in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2]. See Section 3 for the details. Moreover, in Theorem 5.1 (assuming the nondegeneracy of Gelfand et al. [Reference Gelfand, Kapranov and Zelevinsky10] for Laurent polynomials), we relax the nonresonance condition of
![]() $c\in \mathbb{C}^{n}$
in Theorem 3.11 by replacing it with the much weaker one
$c\in \mathbb{C}^{n}$
in Theorem 3.11 by replacing it with the much weaker one
![]() $c\notin \mathbb{Z}^{n}$
. To prove Theorem 5.1, we first perturb Laurent polynomials by multiplying monomials. Then, we apply the twisted Morse theory to the real-valued functions associated to them by using some standard properties of vanishing cycles of perverse sheaves. See Sections 4 and 5 for the details. In the course of the proof of Theorem 5.1, we obtain also the following result which might be of independent interest. Let
$c\notin \mathbb{Z}^{n}$
. To prove Theorem 5.1, we first perturb Laurent polynomials by multiplying monomials. Then, we apply the twisted Morse theory to the real-valued functions associated to them by using some standard properties of vanishing cycles of perverse sheaves. See Sections 4 and 5 for the details. In the course of the proof of Theorem 5.1, we obtain also the following result which might be of independent interest. Let
![]() $Q_{1},\ldots ,Q_{l}$
be Laurent polynomials on
$Q_{1},\ldots ,Q_{l}$
be Laurent polynomials on
![]() $T=(\mathbb{C}^{\ast })^{n}$
, and for
$T=(\mathbb{C}^{\ast })^{n}$
, and for
![]() $1\leqslant i\leqslant l$
denote by
$1\leqslant i\leqslant l$
denote by
![]() $\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n}$
the Newton polytope
$\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n}$
the Newton polytope
![]() $NP(Q_{i})$
of
$NP(Q_{i})$
of
![]() $Q_{i}$
. Set
$Q_{i}$
. Set
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{l}$
.
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{l}$
.
Theorem 1.1. Let
![]() ${\mathcal{L}}$
be a nontrivial local system of rank one on
${\mathcal{L}}$
be a nontrivial local system of rank one on
![]() $T=(\mathbb{C}^{\ast })^{n}$
. Assume that for any
$T=(\mathbb{C}^{\ast })^{n}$
. Assume that for any
![]() $1\leqslant i\leqslant l$
we have
$1\leqslant i\leqslant l$
we have
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}_{i}=n$
, and the subvariety
$\operatorname{dim}\unicode[STIX]{x1D6E5}_{i}=n$
, and the subvariety
of
![]() $T$
is a nondegenerate complete intersection. Then, for any
$T$
is a nondegenerate complete intersection. Then, for any
![]() $1\leqslant i\leqslant l$
, we have the concentration
$1\leqslant i\leqslant l$
, we have the concentration
Moreover, we have
where
![]() $\operatorname{Vol}_{\mathbb{Z}}(\underbrace{\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{1}}_{m_{1}\text{-times}},\ldots ,\underbrace{\unicode[STIX]{x1D6E5}_{i},\ldots ,\unicode[STIX]{x1D6E5}_{i}}_{m_{i}\text{-times}})\in \mathbb{Z}$
is the normalized
$\operatorname{Vol}_{\mathbb{Z}}(\underbrace{\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{1}}_{m_{1}\text{-times}},\ldots ,\underbrace{\unicode[STIX]{x1D6E5}_{i},\ldots ,\unicode[STIX]{x1D6E5}_{i}}_{m_{i}\text{-times}})\in \mathbb{Z}$
is the normalized
![]() $n$
-dimensional mixed volume with respect to the lattice
$n$
-dimensional mixed volume with respect to the lattice
![]() $\mathbb{Z}^{n}\subset \mathbb{R}^{n}$
.
$\mathbb{Z}^{n}\subset \mathbb{R}^{n}$
.
Note that this result can be considered as a refinement of the classical Bernstein–Khovanskii–Kushnirenko theorem (see [Reference Khovanskii13]). On the other hand, Matusevich et al. [Reference Matusevich, Miller and Walther21] and Saito et al. [Reference Saito, Sturmfels and Takayama26] studied the condition on the parameter vector
![]() $c\in \mathbb{C}^{n}$
, for which the corresponding local system of
$c\in \mathbb{C}^{n}$
, for which the corresponding local system of
![]() $A$
-hypergeometric functions is non-rank-jumping. They also relaxed the nonresonance condition of
$A$
-hypergeometric functions is non-rank-jumping. They also relaxed the nonresonance condition of
![]() $c\in \mathbb{C}^{n}$
. It would be an interesting problem to study the relationship between Theorem 5.1 and their results.
$c\in \mathbb{C}^{n}$
. It would be an interesting problem to study the relationship between Theorem 5.1 and their results.
2 Preliminary results
In this section, we recall basic notions and results which are used in this paper. In this paper, we essentially follow the terminology of [Reference Dimca4], [Reference Hotta, Takeuchi and Tanisaki12], etc. For example, for a topological space
![]() $X$
, we denote by
$X$
, we denote by
![]() $\mathbf{D}^{b}(X)$
the derived category whose objects are bounded complexes of sheaves of
$\mathbf{D}^{b}(X)$
the derived category whose objects are bounded complexes of sheaves of
![]() $\mathbb{C}_{X}$
-modules on
$\mathbb{C}_{X}$
-modules on
![]() $X$
. We denote by
$X$
. We denote by
![]() $\mathbf{D}_{c}^{b}(X)$
the full subcategory of
$\mathbf{D}_{c}^{b}(X)$
the full subcategory of
![]() $\mathbf{D}^{b}(X)$
consisting of constructible objects. Let
$\mathbf{D}^{b}(X)$
consisting of constructible objects. Let
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n}$
be a lattice polytope in
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n}$
be a lattice polytope in
![]() $\mathbb{R}^{n}$
. For an element
$\mathbb{R}^{n}$
. For an element
![]() $u\in \mathbb{R}^{n}$
of (the dual vector space of)
$u\in \mathbb{R}^{n}$
of (the dual vector space of)
![]() $\mathbb{R}^{n}$
, we define the supporting face
$\mathbb{R}^{n}$
, we define the supporting face
![]() $\unicode[STIX]{x1D6FE}_{u}\prec \unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6FE}_{u}\prec \unicode[STIX]{x1D6E5}$
of
![]() $u$
in
$u$
in
![]() $\unicode[STIX]{x1D6E5}$
by
$\unicode[STIX]{x1D6E5}$
by
where for
![]() $u=(u_{1},\ldots ,u_{n})$
and
$u=(u_{1},\ldots ,u_{n})$
and
![]() $v=(v_{1},\ldots ,v_{n})$
we set
$v=(v_{1},\ldots ,v_{n})$
we set
![]() $\langle u,v\rangle =\sum _{i=1}^{n}u_{i}v_{i}$
. For a face
$\langle u,v\rangle =\sum _{i=1}^{n}u_{i}v_{i}$
. For a face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
, we set
$\unicode[STIX]{x1D6E5}$
, we set
Then,
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
is an
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
is an
![]() $(n-\operatorname{dim}\unicode[STIX]{x1D6FE})$
-dimensional rational convex polyhedral cone in
$(n-\operatorname{dim}\unicode[STIX]{x1D6FE})$
-dimensional rational convex polyhedral cone in
![]() $\mathbb{R}^{n}$
. Moreover, the family
$\mathbb{R}^{n}$
. Moreover, the family
![]() $\{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\mid \unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}\}$
of cones in
$\{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})\mid \unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}\}$
of cones in
![]() $\mathbb{R}^{n}$
thus obtained is a subdivision of
$\mathbb{R}^{n}$
thus obtained is a subdivision of
![]() $\mathbb{R}^{n}$
. We call it the dual subdivision of
$\mathbb{R}^{n}$
. We call it the dual subdivision of
![]() $\mathbb{R}^{n}$
by
$\mathbb{R}^{n}$
by
![]() $\unicode[STIX]{x1D6E5}$
. If
$\unicode[STIX]{x1D6E5}$
. If
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n$
, it satisfies the axiom of fans (see [Reference Fulton8] and [Reference Oda22], etc.). We call it the dual fan of
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n$
, it satisfies the axiom of fans (see [Reference Fulton8] and [Reference Oda22], etc.). We call it the dual fan of
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
Let
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{p}\subset \mathbb{R}^{n}$
be lattice polytopes in
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{p}\subset \mathbb{R}^{n}$
be lattice polytopes in
![]() $\mathbb{R}^{n}$
, and let
$\mathbb{R}^{n}$
, and let
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{p}\subset \mathbb{R}^{n}$
be their Minkowski sum. For a face
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{p}\subset \mathbb{R}^{n}$
be their Minkowski sum. For a face
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
of
![]() $\unicode[STIX]{x1D6E5}$
, by taking a point
$\unicode[STIX]{x1D6E5}$
, by taking a point
![]() $u\in \mathbb{R}^{n}$
in the relative interior of its dual cone
$u\in \mathbb{R}^{n}$
in the relative interior of its dual cone
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
, we define the supporting face
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FE})$
, we define the supporting face
![]() $\unicode[STIX]{x1D6FE}_{i}\prec \unicode[STIX]{x1D6E5}_{i}$
of
$\unicode[STIX]{x1D6FE}_{i}\prec \unicode[STIX]{x1D6E5}_{i}$
of
![]() $u$
in
$u$
in
![]() $\unicode[STIX]{x1D6E5}_{i}$
. Then, it is easy to see that
$\unicode[STIX]{x1D6E5}_{i}$
. Then, it is easy to see that
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{p}$
. Now, we recall Bernstein–Khovanskii–Kushnirenko’s theorem [Reference Khovanskii13].
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{p}$
. Now, we recall Bernstein–Khovanskii–Kushnirenko’s theorem [Reference Khovanskii13].
Definition 2.1. Let
![]() $g(x)=\sum _{v\in \mathbb{Z}^{n}}c_{v}x^{v}$
be a Laurent polynomial on the algebraic torus
$g(x)=\sum _{v\in \mathbb{Z}^{n}}c_{v}x^{v}$
be a Laurent polynomial on the algebraic torus
![]() $T=(\mathbb{C}^{\ast })^{n}$
(
$T=(\mathbb{C}^{\ast })^{n}$
(
![]() $c_{v}\in \mathbb{C}$
).
$c_{v}\in \mathbb{C}$
).
(1) We call the convex hull of
 $\operatorname{supp}(g):=\{v\in \mathbb{Z}^{n}\mid c_{v}\neq 0\}\subset \mathbb{Z}^{n}\subset \mathbb{R}^{n}$
in
$\operatorname{supp}(g):=\{v\in \mathbb{Z}^{n}\mid c_{v}\neq 0\}\subset \mathbb{Z}^{n}\subset \mathbb{R}^{n}$
in
 $\mathbb{R}^{n}$
the Newton polytope of
$\mathbb{R}^{n}$
the Newton polytope of
 $g$
and denote it by
$g$
and denote it by
 $NP(g)$
.
$NP(g)$
.(2) For a face
 $\unicode[STIX]{x1D6FE}\prec NP(g)$
of
$\unicode[STIX]{x1D6FE}\prec NP(g)$
of
 $NP(g)$
, we define the
$NP(g)$
, we define the
 $\unicode[STIX]{x1D6FE}$
-part
$\unicode[STIX]{x1D6FE}$
-part
 $g^{\unicode[STIX]{x1D6FE}}$
of
$g^{\unicode[STIX]{x1D6FE}}$
of
 $g$
by
$g$
by
 $g^{\unicode[STIX]{x1D6FE}}(x):=\sum _{v\in \unicode[STIX]{x1D6FE}}c_{v}x^{v}$
.
$g^{\unicode[STIX]{x1D6FE}}(x):=\sum _{v\in \unicode[STIX]{x1D6FE}}c_{v}x^{v}$
.
Definition 2.2. (see [Reference Khovanskii14], [Reference Oka23], etc.)
Let
![]() $g_{1},g_{2},\ldots ,g_{p}$
be Laurent polynomials on
$g_{1},g_{2},\ldots ,g_{p}$
be Laurent polynomials on
![]() $T=(\mathbb{C}^{\ast })^{n}$
. Set
$T=(\mathbb{C}^{\ast })^{n}$
. Set
![]() $\unicode[STIX]{x1D6E5}_{i}=NP(g_{i})$
$\unicode[STIX]{x1D6E5}_{i}=NP(g_{i})$
![]() $(i=1,\ldots ,p)$
and
$(i=1,\ldots ,p)$
and
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{p}$
. Then, we say that the subvariety
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{p}$
. Then, we say that the subvariety
![]() $Z=\{x\in T=(\mathbb{C}^{\ast })^{n}\mid g_{1}(x)=g_{2}(x)=\cdots =g_{p}(x)=0\}$
of
$Z=\{x\in T=(\mathbb{C}^{\ast })^{n}\mid g_{1}(x)=g_{2}(x)=\cdots =g_{p}(x)=0\}$
of
![]() $T=(\mathbb{C}^{\ast })^{n}$
is a nondegenerate complete intersection if for any face
$T=(\mathbb{C}^{\ast })^{n}$
is a nondegenerate complete intersection if for any face
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
of
![]() $\unicode[STIX]{x1D6E5}$
the
$\unicode[STIX]{x1D6E5}$
the
![]() $p$
-form
$p$
-form
![]() $dg_{1}^{\unicode[STIX]{x1D6FE}_{1}}\wedge dg_{2}^{\unicode[STIX]{x1D6FE}_{2}}\wedge \cdots \wedge dg_{p}^{\unicode[STIX]{x1D6FE}_{p}}$
does not vanish on
$dg_{1}^{\unicode[STIX]{x1D6FE}_{1}}\wedge dg_{2}^{\unicode[STIX]{x1D6FE}_{2}}\wedge \cdots \wedge dg_{p}^{\unicode[STIX]{x1D6FE}_{p}}$
does not vanish on
![]() $\{x\in T=(\mathbb{C}^{\ast })^{n}\mid g_{1}^{\unicode[STIX]{x1D6FE}_{1}}(x)=\cdots =g_{p}^{\unicode[STIX]{x1D6FE}_{p}}(x)=0\}$
.
$\{x\in T=(\mathbb{C}^{\ast })^{n}\mid g_{1}^{\unicode[STIX]{x1D6FE}_{1}}(x)=\cdots =g_{p}^{\unicode[STIX]{x1D6FE}_{p}}(x)=0\}$
.
Definition 2.3. Let
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{n}$
be lattice polytopes in
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{n}$
be lattice polytopes in
![]() $\mathbb{R}^{n}$
. Then, their normalized
$\mathbb{R}^{n}$
. Then, their normalized
![]() $n$
-dimensional mixed volume
$n$
-dimensional mixed volume
![]() $\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{n})\in \mathbb{Z}$
is defined by the formula
$\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{n})\in \mathbb{Z}$
is defined by the formula
 $$\begin{eqnarray}\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{n})=\frac{1}{n!}\mathop{\sum }_{k=1}^{n}(-1)^{n-k}\mathop{\sum }_{\substack{ I\subset \{1,\ldots ,n\} \\ \sharp I=k}}\operatorname{Vol}_{\mathbb{Z}}\left(\mathop{\sum }_{i\in I}\unicode[STIX]{x1D6E5}_{i}\right),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{n})=\frac{1}{n!}\mathop{\sum }_{k=1}^{n}(-1)^{n-k}\mathop{\sum }_{\substack{ I\subset \{1,\ldots ,n\} \\ \sharp I=k}}\operatorname{Vol}_{\mathbb{Z}}\left(\mathop{\sum }_{i\in I}\unicode[STIX]{x1D6E5}_{i}\right),\end{eqnarray}$$
where
![]() $\operatorname{Vol}_{\mathbb{Z}}(\cdot )=n!\operatorname{Vol}(\cdot )\in \mathbb{Z}$
is the normalized
$\operatorname{Vol}_{\mathbb{Z}}(\cdot )=n!\operatorname{Vol}(\cdot )\in \mathbb{Z}$
is the normalized
![]() $n$
-dimensional volume with respect to the lattice
$n$
-dimensional volume with respect to the lattice
![]() $\mathbb{Z}^{n}\subset \mathbb{R}^{n}$
.
$\mathbb{Z}^{n}\subset \mathbb{R}^{n}$
.
Theorem 2.4. [Reference Khovanskii13]
Let
![]() $g_{1},g_{2},\ldots ,g_{p}$
be Laurent polynomials on
$g_{1},g_{2},\ldots ,g_{p}$
be Laurent polynomials on
![]() $T=(\mathbb{C}^{\ast })^{n}$
. Assume that the subvariety
$T=(\mathbb{C}^{\ast })^{n}$
. Assume that the subvariety
![]() $Z=\{x\in T=(\mathbb{C}^{\ast })^{n}\mid g_{1}(x)=g_{2}(x)=\cdots =g_{p}(x)=0\}$
of
$Z=\{x\in T=(\mathbb{C}^{\ast })^{n}\mid g_{1}(x)=g_{2}(x)=\cdots =g_{p}(x)=0\}$
of
![]() $T=(\mathbb{C}^{\ast })^{n}$
is a nondegenerate complete intersection. Set
$T=(\mathbb{C}^{\ast })^{n}$
is a nondegenerate complete intersection. Set
![]() $\unicode[STIX]{x1D6E5}_{i}=NP(g_{i})$
$\unicode[STIX]{x1D6E5}_{i}=NP(g_{i})$
![]() $(i=1,\ldots ,p)$
. Then, we have
$(i=1,\ldots ,p)$
. Then, we have
where
![]() $\operatorname{Vol}_{\mathbb{Z}}(\underbrace{\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{1}}_{m_{1}\text{-times}},\ldots ,\underbrace{\unicode[STIX]{x1D6E5}_{p},\ldots ,\unicode[STIX]{x1D6E5}_{p}}_{m_{p}\text{-times}})\in \mathbb{Z}$
is the normalized
$\operatorname{Vol}_{\mathbb{Z}}(\underbrace{\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{1}}_{m_{1}\text{-times}},\ldots ,\underbrace{\unicode[STIX]{x1D6E5}_{p},\ldots ,\unicode[STIX]{x1D6E5}_{p}}_{m_{p}\text{-times}})\in \mathbb{Z}$
is the normalized
![]() $n$
-dimensional mixed volume with respect to the lattice
$n$
-dimensional mixed volume with respect to the lattice
![]() $\mathbb{Z}^{n}\subset \mathbb{R}^{n}$
.
$\mathbb{Z}^{n}\subset \mathbb{R}^{n}$
.
3 A vanishing theorem for local systems
Let
![]() $B=\{b(1),b(2),\ldots ,b(N)\}\subset \mathbb{Z}^{n-1}$
be a finite subset of the lattice
$B=\{b(1),b(2),\ldots ,b(N)\}\subset \mathbb{Z}^{n-1}$
be a finite subset of the lattice
![]() $\mathbb{Z}^{n-1}$
. Let
$\mathbb{Z}^{n-1}$
. Let
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-1}$
be the convex hull of
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-1}$
be the convex hull of
![]() $B$
in
$B$
in
![]() $\mathbb{R}^{n-1}$
. Assume that
$\mathbb{R}^{n-1}$
. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
. For
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
. For
![]() $z=(z_{1},\ldots ,z_{N})\in \mathbb{C}^{N}$
, we define a Laurent polynomial
$z=(z_{1},\ldots ,z_{N})\in \mathbb{C}^{N}$
, we define a Laurent polynomial
![]() $P(x)$
on
$P(x)$
on
![]() $T_{0}=(\mathbb{C}^{\ast })^{n-1}$
by
$T_{0}=(\mathbb{C}^{\ast })^{n-1}$
by
![]() $P(x)=\sum _{j=1}^{N}z_{j}x^{b(j)}$
(
$P(x)=\sum _{j=1}^{N}z_{j}x^{b(j)}$
(
![]() $x=(x_{1},\ldots ,x_{n-1})\in T_{0}=(\mathbb{C}^{\ast })^{n-1}$
). Then, for
$x=(x_{1},\ldots ,x_{n-1})\in T_{0}=(\mathbb{C}^{\ast })^{n-1}$
). Then, for
![]() $c=(c_{1},\ldots ,c_{n})\in \mathbb{C}^{n}$
, the possibly multivalued function
$c=(c_{1},\ldots ,c_{n})\in \mathbb{C}^{n}$
, the possibly multivalued function
![]() $P(x)^{-c_{n}}x_{1}^{c_{1}-1}\cdots x_{n-1}^{c_{n-1}-1}$
on
$P(x)^{-c_{n}}x_{1}^{c_{1}-1}\cdots x_{n-1}^{c_{n-1}-1}$
on
![]() $W=T_{0}\setminus P^{-1}(0)$
generates the local system
$W=T_{0}\setminus P^{-1}(0)$
generates the local system
Set
![]() $a(j)=(b(j),1)\in \mathbb{Z}^{n}$
(
$a(j)=(b(j),1)\in \mathbb{Z}^{n}$
(
![]() $1\leqslant j\leqslant N$
) and
$1\leqslant j\leqslant N$
) and
![]() $A=\{a(1),a(2),\ldots ,a(N)\}\subset \mathbb{Z}^{n}$
. Then,
$A=\{a(1),a(2),\ldots ,a(N)\}\subset \mathbb{Z}^{n}$
. Then,
![]() $K=\mathbb{R}_{+}A\subset \mathbb{R}^{n}$
is an
$K=\mathbb{R}_{+}A\subset \mathbb{R}^{n}$
is an
![]() $n$
-dimensional closed convex polyhedral cone in
$n$
-dimensional closed convex polyhedral cone in
![]() $\mathbb{R}^{n}$
. For a face
$\mathbb{R}^{n}$
. For a face
![]() $\unicode[STIX]{x1D6E4}\prec K$
of
$\unicode[STIX]{x1D6E4}\prec K$
of
![]() $K$
, let
$K$
, let
![]() $\operatorname{Lin}(\unicode[STIX]{x1D6E4})\simeq \mathbb{C}^{\operatorname{dim}\unicode[STIX]{x1D6E4}}\subset \mathbb{C}^{n}$
be the
$\operatorname{Lin}(\unicode[STIX]{x1D6E4})\simeq \mathbb{C}^{\operatorname{dim}\unicode[STIX]{x1D6E4}}\subset \mathbb{C}^{n}$
be the
![]() $\mathbb{C}$
-linear subspace of
$\mathbb{C}$
-linear subspace of
![]() $\mathbb{C}^{n}$
generated by
$\mathbb{C}^{n}$
generated by
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Definition 3.1. (Gelfand et al. [Reference Gelfand, Kapranov and Zelevinsky10, page 262])
We say that the parameter vector
![]() $c\in \mathbb{C}^{n}$
is nonresonant (with respect to
$c\in \mathbb{C}^{n}$
is nonresonant (with respect to
![]() $A$
) if for any face
$A$
) if for any face
![]() $\unicode[STIX]{x1D6E4}\prec K$
of
$\unicode[STIX]{x1D6E4}\prec K$
of
![]() $K$
such that
$K$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E4}=n-1$
we have
$\operatorname{dim}\unicode[STIX]{x1D6E4}=n-1$
we have
![]() $c\notin \{\mathbb{Z}^{n}+\operatorname{Lin}(\unicode[STIX]{x1D6E4})\}$
.
$c\notin \{\mathbb{Z}^{n}+\operatorname{Lin}(\unicode[STIX]{x1D6E4})\}$
.
The following definition is essentially weaker than the usual (Kouchnirenko) nondegeneracy (see [Reference Khovanskii14], [Reference Oka23], etc.).
Definition 3.2. We say that the Laurent polynomial
![]() $P(x)=\sum _{j=1}^{N}z_{j}x^{b(j)}$
is “weakly” nondegenerate if for any face
$P(x)=\sum _{j=1}^{N}z_{j}x^{b(j)}$
is “weakly” nondegenerate if for any face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
, the hypersurface
$\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
, the hypersurface
is smooth and reduced.
Let
![]() $\unicode[STIX]{x1D704}:W=T_{0}\setminus P^{-1}(0){\hookrightarrow}T_{0}$
be the inclusion map, and set
$\unicode[STIX]{x1D704}:W=T_{0}\setminus P^{-1}(0){\hookrightarrow}T_{0}$
be the inclusion map, and set
![]() ${\mathcal{M}}=R\unicode[STIX]{x1D704}_{\ast }{\mathcal{L}}\in \mathbf{D}_{c}^{b}(T_{0})$
. Then, the following theorem generalizes one of the results in Gelfand et al. [Reference Gelfand, Kapranov and Zelevinsky10] to the case where the hypersurface
${\mathcal{M}}=R\unicode[STIX]{x1D704}_{\ast }{\mathcal{L}}\in \mathbf{D}_{c}^{b}(T_{0})$
. Then, the following theorem generalizes one of the results in Gelfand et al. [Reference Gelfand, Kapranov and Zelevinsky10] to the case where the hypersurface
![]() $P^{-1}(0)\subset T_{0}$
may have isolated singular points.
$P^{-1}(0)\subset T_{0}$
may have isolated singular points.
Theorem 3.3. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
, the parameter vector
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
, the parameter vector
![]() $c\in \mathbb{C}^{n}$
is nonresonant and the Laurent polynomial
$c\in \mathbb{C}^{n}$
is nonresonant and the Laurent polynomial
![]() $P(x)$
is weakly nondegenerate. Then, there exists an isomorphism
$P(x)$
is weakly nondegenerate. Then, there exists an isomorphism
for any
![]() $j\in \mathbb{Z}$
. Moreover, we have the concentration
$j\in \mathbb{Z}$
. Moreover, we have the concentration
Proof. Let
![]() $\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of
$\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of
![]() $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
![]() $\mathbb{R}^{n-1}$
, and let
$\mathbb{R}^{n-1}$
, and let
![]() $X$
be the (possibly singular) toric variety associated to it. Then, there exists a natural action of
$X$
be the (possibly singular) toric variety associated to it. Then, there exists a natural action of
![]() $T_{0}$
on
$T_{0}$
on
![]() $X$
whose orbits are parametrized by the faces of
$X$
whose orbits are parametrized by the faces of
![]() $\unicode[STIX]{x1D6E5}$
. For a face
$\unicode[STIX]{x1D6E5}$
. For a face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
, denote by
$\unicode[STIX]{x1D6E5}$
, denote by
![]() $X_{\unicode[STIX]{x1D6FE}}\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
the
$X_{\unicode[STIX]{x1D6FE}}\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
the
![]() $T_{0}$
-orbit associated to
$T_{0}$
-orbit associated to
![]() $\unicode[STIX]{x1D6FE}$
. Note that
$\unicode[STIX]{x1D6FE}$
. Note that
![]() $X_{\unicode[STIX]{x1D6E5}}\simeq T_{0}$
is the unique open dense
$X_{\unicode[STIX]{x1D6E5}}\simeq T_{0}$
is the unique open dense
![]() $T_{0}$
-orbit in
$T_{0}$
-orbit in
![]() $X$
and its complement
$X$
and its complement
![]() $X\setminus X_{\unicode[STIX]{x1D6E5}}$
is the union of
$X\setminus X_{\unicode[STIX]{x1D6E5}}$
is the union of
![]() $X_{\unicode[STIX]{x1D6FE}}$
for
$X_{\unicode[STIX]{x1D6FE}}$
for
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}<n-1$
. Let
$\operatorname{dim}\unicode[STIX]{x1D6FE}<n-1$
. Let
![]() $i:X_{\unicode[STIX]{x1D6E5}}\simeq T_{0}{\hookrightarrow}X$
be the inclusion map. Then, by the weak nondegeneracy of
$i:X_{\unicode[STIX]{x1D6E5}}\simeq T_{0}{\hookrightarrow}X$
be the inclusion map. Then, by the weak nondegeneracy of
![]() $P(x)$
, the closure
$P(x)$
, the closure
![]() $S=\overline{i(P^{-1}(0))}\subset X$
of the hypersurface
$S=\overline{i(P^{-1}(0))}\subset X$
of the hypersurface
![]() $i(P^{-1}(0))\subset i(T_{0})$
in
$i(P^{-1}(0))\subset i(T_{0})$
in
![]() $X$
intersects
$X$
intersects
![]() $T_{0}$
-orbits
$T_{0}$
-orbits
![]() $X_{\unicode[STIX]{x1D6FE}}$
in
$X_{\unicode[STIX]{x1D6FE}}$
in
![]() $X\setminus X_{\unicode[STIX]{x1D6E5}}$
transversely. Moreover, by the nonresonance of
$X\setminus X_{\unicode[STIX]{x1D6E5}}$
transversely. Moreover, by the nonresonance of
![]() $c\in \mathbb{C}^{n}$
, for any
$c\in \mathbb{C}^{n}$
, for any
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}=n-2$
, the monodromy of the local system
$\operatorname{dim}\unicode[STIX]{x1D6FE}=n-2$
, the monodromy of the local system
![]() ${\mathcal{L}}$
around the codimension-one
${\mathcal{L}}$
around the codimension-one
![]() $T_{0}$
-orbit
$T_{0}$
-orbit
![]() $X_{\unicode[STIX]{x1D6FE}}\subset X$
in
$X_{\unicode[STIX]{x1D6FE}}\subset X$
in
![]() $X$
is nontrivial. Indeed, let
$X$
is nontrivial. Indeed, let
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
be such a facet of
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
be such a facet of
![]() $\unicode[STIX]{x1D6E5}$
. We denote by
$\unicode[STIX]{x1D6E5}$
. We denote by
![]() $\unicode[STIX]{x1D6E4}$
the facet of the cone
$\unicode[STIX]{x1D6E4}$
the facet of the cone
![]() $K=\mathbb{R}_{+}A$
generated by
$K=\mathbb{R}_{+}A$
generated by
![]() $\unicode[STIX]{x1D6FE}\times \{1\}\subset K$
. Let
$\unicode[STIX]{x1D6FE}\times \{1\}\subset K$
. Let
![]() $\unicode[STIX]{x1D708}\in \mathbb{Z}^{n-1}\setminus \{0\}$
be the primitive inner conormal vector of the facet
$\unicode[STIX]{x1D708}\in \mathbb{Z}^{n-1}\setminus \{0\}$
be the primitive inner conormal vector of the facet
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-1}$
, and set
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-1}$
, and set
Then, the primitive inner conormal vector
![]() $\widetilde{\unicode[STIX]{x1D708}}\in \mathbb{Z}^{n}\setminus \{0\}$
of the facet
$\widetilde{\unicode[STIX]{x1D708}}\in \mathbb{Z}^{n}\setminus \{0\}$
of the facet
![]() $\unicode[STIX]{x1D6E4}$
of
$\unicode[STIX]{x1D6E4}$
of
![]() $K\subset \mathbb{R}^{n}$
is explicitly given by the formula
$K\subset \mathbb{R}^{n}$
is explicitly given by the formula
and the condition
![]() $c=(c_{1},\ldots ,c_{n-1},c_{n})\notin \{\mathbb{Z}^{n}+\operatorname{Lin}(\unicode[STIX]{x1D6E4})\}$
is equivalent to the one
$c=(c_{1},\ldots ,c_{n-1},c_{n})\notin \{\mathbb{Z}^{n}+\operatorname{Lin}(\unicode[STIX]{x1D6E4})\}$
is equivalent to the one
 $$\begin{eqnarray}m(\unicode[STIX]{x1D6FE}):=\left\langle \unicode[STIX]{x1D708},\left(\begin{array}{@{}c@{}}c_{1}-1\\ \vdots \\ c_{n-1}-1\end{array}\right)\right\rangle -m\cdot c_{n}\quad \notin \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}m(\unicode[STIX]{x1D6FE}):=\left\langle \unicode[STIX]{x1D708},\left(\begin{array}{@{}c@{}}c_{1}-1\\ \vdots \\ c_{n-1}-1\end{array}\right)\right\rangle -m\cdot c_{n}\quad \notin \mathbb{Z}.\end{eqnarray}$$
We can easily see that the order of the (multivalued) function
![]() $P(x)^{-c_{n}}x_{1}^{c_{1}-1}\cdots x_{n-1}^{c_{n-1}-1}$
along the codimension-one
$P(x)^{-c_{n}}x_{1}^{c_{1}-1}\cdots x_{n-1}^{c_{n-1}-1}$
along the codimension-one
![]() $T_{0}$
-orbit
$T_{0}$
-orbit
![]() $X_{\unicode[STIX]{x1D6FE}}\subset X$
in
$X_{\unicode[STIX]{x1D6FE}}\subset X$
in
![]() $X$
is equal to
$X$
is equal to
![]() $m(\unicode[STIX]{x1D6FE})\notin \mathbb{Z}$
. Then, by constructing suitable distance functions as in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2], we can show that for the open embedding
$m(\unicode[STIX]{x1D6FE})\notin \mathbb{Z}$
. Then, by constructing suitable distance functions as in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2], we can show that for the open embedding
![]() $i:T_{0}{\hookrightarrow}X$
we have
$i:T_{0}{\hookrightarrow}X$
we have
as follows. Let us first assume that the point
![]() $p\in X\setminus i(T_{0})$
lies in a
$p\in X\setminus i(T_{0})$
lies in a
![]() $0$
-dimensional
$0$
-dimensional
![]() $T_{0}$
-orbit
$T_{0}$
-orbit
![]() $X_{\unicode[STIX]{x1D6FE}}$
. Let
$X_{\unicode[STIX]{x1D6FE}}$
. Let
![]() $U_{\unicode[STIX]{x1D6FE}}\subset X$
be an
$U_{\unicode[STIX]{x1D6FE}}\subset X$
be an
![]() $(n-1)$
-dimensional affine toric variety containing
$(n-1)$
-dimensional affine toric variety containing
![]() $\{p\}=X_{\unicode[STIX]{x1D6FE}}$
, and regard it as a subvariety of
$\{p\}=X_{\unicode[STIX]{x1D6FE}}$
, and regard it as a subvariety of
![]() $\mathbb{C}_{\unicode[STIX]{x1D701}}^{l}$
for some
$\mathbb{C}_{\unicode[STIX]{x1D701}}^{l}$
for some
![]() $l$
. Let
$l$
. Let
![]() $a=(a_{1},\ldots ,a_{n-1})\in \mathbb{Z}^{n-1}$
be the coordinate of the vertex
$a=(a_{1},\ldots ,a_{n-1})\in \mathbb{Z}^{n-1}$
be the coordinate of the vertex
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
, and define a (nontrivial) rank-one local system
$\unicode[STIX]{x1D6E5}$
, and define a (nontrivial) rank-one local system
![]() $\widetilde{{\mathcal{L}}}$
on
$\widetilde{{\mathcal{L}}}$
on
![]() $T_{0}$
by
$T_{0}$
by
Then, on a neighborhood of the point
![]() $p$
in
$p$
in
![]() $U_{\unicode[STIX]{x1D6FE}}\subset \mathbb{C}_{\unicode[STIX]{x1D701}}^{l}$
,
$U_{\unicode[STIX]{x1D6FE}}\subset \mathbb{C}_{\unicode[STIX]{x1D701}}^{l}$
,
![]() $Ri_{\ast }{\mathcal{M}}$
is isomorphic to
$Ri_{\ast }{\mathcal{M}}$
is isomorphic to
![]() $Ri_{\ast }\widetilde{{\mathcal{L}}}$
. Next, as in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2], we construct a real-valued function
$Ri_{\ast }\widetilde{{\mathcal{L}}}$
. Next, as in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2], we construct a real-valued function
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $\mathbb{C}_{\unicode[STIX]{x1D701}}^{l}$
whose level sets
$\mathbb{C}_{\unicode[STIX]{x1D701}}^{l}$
whose level sets
![]() $\unicode[STIX]{x1D6FA}_{t}=\{\unicode[STIX]{x1D701}\in \mathbb{C}^{l}\mid \unicode[STIX]{x1D711}(\unicode[STIX]{x1D701})<t\}$
(
$\unicode[STIX]{x1D6FA}_{t}=\{\unicode[STIX]{x1D701}\in \mathbb{C}^{l}\mid \unicode[STIX]{x1D711}(\unicode[STIX]{x1D701})<t\}$
(
![]() $t\in \mathbb{R}_{{>}0}$
) satisfy the conditions
$t\in \mathbb{R}_{{>}0}$
) satisfy the conditions
![]() $\bigcap _{t>0}\unicode[STIX]{x1D6FA}_{t}=\{p\}=X_{\unicode[STIX]{x1D6FE}}$
and
$\bigcap _{t>0}\unicode[STIX]{x1D6FA}_{t}=\{p\}=X_{\unicode[STIX]{x1D6FE}}$
and
![]() $(\bigcup _{t>0}\unicode[STIX]{x1D6FA}_{t})\cap T_{0}=T_{0}$
, and use it to show the isomorphism
$(\bigcup _{t>0}\unicode[STIX]{x1D6FA}_{t})\cap T_{0}=T_{0}$
, and use it to show the isomorphism
by the twisted Morse theory. We thus obtain the isomorphism
![]() $(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
. When the point
$(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
. When the point
![]() $p\in X\setminus i(T_{0})$
lies in a
$p\in X\setminus i(T_{0})$
lies in a
![]() $T_{0}$
-orbit
$T_{0}$
-orbit
![]() $X_{\unicode[STIX]{x1D6FE}}$
such that
$X_{\unicode[STIX]{x1D6FE}}$
such that
![]() $\operatorname{dim}X_{\unicode[STIX]{x1D6FE}}=\operatorname{dim}\unicode[STIX]{x1D6FE}>0$
, by taking a normal slice of
$\operatorname{dim}X_{\unicode[STIX]{x1D6FE}}=\operatorname{dim}\unicode[STIX]{x1D6FE}>0$
, by taking a normal slice of
![]() $X_{\unicode[STIX]{x1D6FE}}$
in
$X_{\unicode[STIX]{x1D6FE}}$
in
![]() $X$
, we can reduce the problem to the case where
$X$
, we can reduce the problem to the case where
![]() $\operatorname{dim}X_{\unicode[STIX]{x1D6FE}}=0$
. We thus obtain an isomorphism
$\operatorname{dim}X_{\unicode[STIX]{x1D6FE}}=0$
. We thus obtain an isomorphism
![]() $i_{!}{\mathcal{M}}\simeq Ri_{\ast }{\mathcal{M}}$
in
$i_{!}{\mathcal{M}}\simeq Ri_{\ast }{\mathcal{M}}$
in
![]() $\mathbf{D}_{c}^{b}(X)$
. Applying the functor
$\mathbf{D}_{c}^{b}(X)$
. Applying the functor
![]() $R\unicode[STIX]{x1D6E4}_{c}(X;\cdot )=R\unicode[STIX]{x1D6E4}(X;\cdot )$
to it, we obtain the desired isomorphisms
$R\unicode[STIX]{x1D6E4}_{c}(X;\cdot )=R\unicode[STIX]{x1D6E4}(X;\cdot )$
to it, we obtain the desired isomorphisms
for
![]() $j\in \mathbb{Z}$
. Now, recall that
$j\in \mathbb{Z}$
. Now, recall that
![]() $T_{0}$
is an affine variety, and
$T_{0}$
is an affine variety, and
![]() ${\mathcal{M}}\in \mathbf{D}_{c}^{b}(T_{0})$
is a perverse sheaf on it (up to some shift). Then, by Artin’s vanishing theorem for perverse sheaves over affine varieties (see [Reference Dimca4, Corollaries 5.2.18 and 5.2.19], etc.), we have
${\mathcal{M}}\in \mathbf{D}_{c}^{b}(T_{0})$
is a perverse sheaf on it (up to some shift). Then, by Artin’s vanishing theorem for perverse sheaves over affine varieties (see [Reference Dimca4, Corollaries 5.2.18 and 5.2.19], etc.), we have
and
from which the last assertion immediately follows. This completes the proof. ◻
By Theorem 2.4, we obtain the following corollary of Theorem 3.3.
Corollary 3.4. In the situation of Theorem 3.3, let
![]() $p_{1},\ldots ,p_{r}\in P^{-1}(0)$
be the (isolated) singular points of
$p_{1},\ldots ,p_{r}\in P^{-1}(0)$
be the (isolated) singular points of
![]() $P^{-1}(0)\subset T_{0}$
, and for
$P^{-1}(0)\subset T_{0}$
, and for
![]() $1\leqslant i\leqslant r$
, let
$1\leqslant i\leqslant r$
, let
![]() $\unicode[STIX]{x1D707}_{i}>0$
be the Milnor number of
$\unicode[STIX]{x1D707}_{i}>0$
be the Milnor number of
![]() $P^{-1}(0)$
at
$P^{-1}(0)$
at
![]() $p_{i}$
. Then, we have
$p_{i}$
. Then, we have
Proof. By multiplying a monomial
![]() $x^{a}$
(
$x^{a}$
(
![]() $a\in \mathbb{Z}^{n-1}$
) to
$a\in \mathbb{Z}^{n-1}$
) to
![]() $P(x)$
, we may assume that the Newton polytope
$P(x)$
, we may assume that the Newton polytope
![]() $\unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6E5}$
of
![]() $P$
contains the origin
$P$
contains the origin
![]() $0\in \mathbb{R}^{n-1}$
. Then, by Sard’s theorem, the generic fiber
$0\in \mathbb{R}^{n-1}$
. Then, by Sard’s theorem, the generic fiber
![]() $P^{-1}(t)\subset T_{0}$
(
$P^{-1}(t)\subset T_{0}$
(
![]() $t\not =0$
) of the map
$t\not =0$
) of the map
![]() $P:T_{0}\longrightarrow \mathbb{C}$
is a nondegenerate hypersurface of
$P:T_{0}\longrightarrow \mathbb{C}$
is a nondegenerate hypersurface of
![]() $T_{0}$
in the sense of Definition 2.2. Hence, it follows from Theorem 2.4 that its Euler characteristic
$T_{0}$
in the sense of Definition 2.2. Hence, it follows from Theorem 2.4 that its Euler characteristic
![]() $\unicode[STIX]{x1D712}(P^{-1}(t))$
is equal to
$\unicode[STIX]{x1D712}(P^{-1}(t))$
is equal to
![]() $(-1)^{n-1-1}\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5})=(-1)^{n-2}\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5})$
. It is also well known that we have
$(-1)^{n-1-1}\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5})=(-1)^{n-2}\operatorname{Vol}_{\mathbb{Z}}(\unicode[STIX]{x1D6E5})$
. It is also well known that we have
For the open set
![]() $W=T_{0}\setminus P^{-1}(0)$
of
$W=T_{0}\setminus P^{-1}(0)$
of
![]() $T_{0}$
, by
$T_{0}$
, by
![]() $\unicode[STIX]{x1D712}(T_{0})=0$
, we thus obtain the equality
$\unicode[STIX]{x1D712}(T_{0})=0$
, we thus obtain the equality
Moreover, by applying the Mayer–Vietoris argument to the rank-one local system
![]() ${\mathcal{L}}$
, we have
${\mathcal{L}}$
, we have
![]() $\unicode[STIX]{x1D712}(W)=\sum _{j\in \mathbb{Z}}(-1)^{j}\operatorname{dim}H^{j}(W;{\mathcal{L}})$
. Then, the assertion follows immediately from Theorem 3.3.◻
$\unicode[STIX]{x1D712}(W)=\sum _{j\in \mathbb{Z}}(-1)^{j}\operatorname{dim}H^{j}(W;{\mathcal{L}})$
. Then, the assertion follows immediately from Theorem 3.3.◻
We can generalize Theorem 3.3 to the case where the hypersurface
![]() $S=\overline{i(P^{-1}(0))}\subset X$
has (stratified) isolated singular points
$S=\overline{i(P^{-1}(0))}\subset X$
has (stratified) isolated singular points
![]() $p$
also in
$p$
also in
![]() $T_{0}$
-orbits
$T_{0}$
-orbits
![]() $X_{\unicode[STIX]{x1D6FE}}\subset X\setminus i(T_{0})$
as follows. For such a point
$X_{\unicode[STIX]{x1D6FE}}\subset X\setminus i(T_{0})$
as follows. For such a point
![]() $p\in S\cap X_{\unicode[STIX]{x1D6FE}}$
of
$p\in S\cap X_{\unicode[STIX]{x1D6FE}}$
of
![]() $S$
, let us show that we have the vanishing
$S$
, let us show that we have the vanishing
![]() $(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
in general. First, consider the case where the codimension of
$(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
in general. First, consider the case where the codimension of
![]() $X_{\unicode[STIX]{x1D6FE}}$
in
$X_{\unicode[STIX]{x1D6FE}}$
in
![]() $X$
is one. The question being local, it suffices to consider the case where
$X$
is one. The question being local, it suffices to consider the case where
![]() $X=\mathbb{C}_{y}^{n-1}\supset X_{\unicode[STIX]{x1D6FE}}=\{y_{n-1}=0\}$
,
$X=\mathbb{C}_{y}^{n-1}\supset X_{\unicode[STIX]{x1D6FE}}=\{y_{n-1}=0\}$
,
![]() $S=\{f(y)=0\}\ni p=0$
,
$S=\{f(y)=0\}\ni p=0$
,
![]() $T_{0}=\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}$
,
$T_{0}=\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}$
,
![]() $i:\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}{\hookrightarrow}\mathbb{C}^{n-1}$
and
$i:\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}{\hookrightarrow}\mathbb{C}^{n-1}$
and
for
![]() $\unicode[STIX]{x1D6FC}=-c_{n}$
and some
$\unicode[STIX]{x1D6FC}=-c_{n}$
and some
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{C}$
. (By the notation in the proof of Theorem 3.3, we have
$\unicode[STIX]{x1D6FD}\in \mathbb{C}$
. (By the notation in the proof of Theorem 3.3, we have
![]() $\unicode[STIX]{x1D6FD}=m(\unicode[STIX]{x1D6FE})$
.) Here,
$\unicode[STIX]{x1D6FD}=m(\unicode[STIX]{x1D6FE})$
.) Here,
![]() $f(y)$
is a polynomial on
$f(y)$
is a polynomial on
![]() $\mathbb{C}^{n-1}$
such that
$\mathbb{C}^{n-1}$
such that
![]() $S=f^{-1}(0)$
has a (stratified) isolated singular point at
$S=f^{-1}(0)$
has a (stratified) isolated singular point at
![]() $p=0\in S\cap X_{\unicode[STIX]{x1D6FE}}$
. Moreover, for the inclusion map
$p=0\in S\cap X_{\unicode[STIX]{x1D6FE}}$
. Moreover, for the inclusion map
![]() $\unicode[STIX]{x1D704}:\mathbb{C}^{n-1}\setminus \{f(y)\cdot y_{n-1}=0\}{\hookrightarrow}\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}$
, we have
$\unicode[STIX]{x1D704}:\mathbb{C}^{n-1}\setminus \{f(y)\cdot y_{n-1}=0\}{\hookrightarrow}\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}$
, we have
![]() ${\mathcal{M}}\simeq R\unicode[STIX]{x1D704}_{\ast }{\mathcal{L}}$
. By the nonresonance of
${\mathcal{M}}\simeq R\unicode[STIX]{x1D704}_{\ast }{\mathcal{L}}$
. By the nonresonance of
![]() $c\in \mathbb{C}^{n}$
, we have
$c\in \mathbb{C}^{n}$
, we have
![]() $\unicode[STIX]{x1D6FD}=m(\unicode[STIX]{x1D6FE})\notin \mathbb{Z}$
, and there exists an isomorphism
$\unicode[STIX]{x1D6FD}=m(\unicode[STIX]{x1D6FE})\notin \mathbb{Z}$
, and there exists an isomorphism
Set
![]() ${\mathcal{N}}=i_{!}(\mathbb{C}_{\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}}y_{n-1}^{\unicode[STIX]{x1D6FD}})$
. Then,
${\mathcal{N}}=i_{!}(\mathbb{C}_{\mathbb{C}^{n-1}\setminus \{y_{n-1}=0\}}y_{n-1}^{\unicode[STIX]{x1D6FD}})$
. Then,
![]() ${\mathcal{N}}$
is a perverse sheaf (up to some shift) on
${\mathcal{N}}$
is a perverse sheaf (up to some shift) on
![]() $X=\mathbb{C}^{n-1}$
and satisfies the condition
$X=\mathbb{C}^{n-1}$
and satisfies the condition
![]() $\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}\simeq \unicode[STIX]{x1D719}_{f}({\mathcal{N}})_{p}$
(using Equation (3.18)), where
$\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}\simeq \unicode[STIX]{x1D719}_{f}({\mathcal{N}})_{p}$
(using Equation (3.18)), where
are the nearby and vanishing cycle functors associated to
![]() $f$
respectively (see [Reference Dimca4], etc.). By the
$f$
respectively (see [Reference Dimca4], etc.). By the
![]() $t$
-exactness of the functor
$t$
-exactness of the functor
![]() $\unicode[STIX]{x1D719}_{f}$
, the constructible sheaf
$\unicode[STIX]{x1D719}_{f}$
, the constructible sheaf
![]() $\unicode[STIX]{x1D719}_{f}({\mathcal{N}})$
on
$\unicode[STIX]{x1D719}_{f}({\mathcal{N}})$
on
![]() $S=f^{-1}(0)$
is perverse (up to some shift). Moreover, by our assumption, its support is contained in the point
$S=f^{-1}(0)$
is perverse (up to some shift). Moreover, by our assumption, its support is contained in the point
![]() $\{p\}=\{0\}\subset X=\mathbb{C}^{n-1}$
. This implies that we have the concentration
$\{p\}=\{0\}\subset X=\mathbb{C}^{n-1}$
. This implies that we have the concentration
Namely, for the Milnor fiber
![]() $F_{p}$
of
$F_{p}$
of
![]() $f$
at
$f$
at
![]() $p=0\in \mathbb{C}^{n-1}$
, we have
$p=0\in \mathbb{C}^{n-1}$
, we have
Let
![]() $B(p;\unicode[STIX]{x1D700})\subset \mathbb{C}^{n-1}$
be a small open ball in
$B(p;\unicode[STIX]{x1D700})\subset \mathbb{C}^{n-1}$
be a small open ball in
![]() $\mathbb{C}^{n-1}$
centered at
$\mathbb{C}^{n-1}$
centered at
![]() $p=0$
, and for
$p=0$
, and for
![]() $0<\unicode[STIX]{x1D702}\ll \unicode[STIX]{x1D700}$
set
$0<\unicode[STIX]{x1D702}\ll \unicode[STIX]{x1D700}$
set
Then, in order to show the vanishing
![]() $(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
, it suffices to prove the one
$(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
, it suffices to prove the one
![]() $R\unicode[STIX]{x1D6E4}(G;Ri_{\ast }{\mathcal{M}})\simeq 0$
for the constructible sheaf
$R\unicode[STIX]{x1D6E4}(G;Ri_{\ast }{\mathcal{M}})\simeq 0$
for the constructible sheaf
on
![]() $G$
, where
$G$
, where
![]() ${\mathcal{L}}^{\prime }$
is the rank-one local system on the punctured disk
${\mathcal{L}}^{\prime }$
is the rank-one local system on the punctured disk
![]() $D_{\unicode[STIX]{x1D702}}^{\ast }=\{t\in \mathbb{C}\mid 0<|t|<\unicode[STIX]{x1D702}\}\subset \mathbb{C}$
generated by the function
$D_{\unicode[STIX]{x1D702}}^{\ast }=\{t\in \mathbb{C}\mid 0<|t|<\unicode[STIX]{x1D702}\}\subset \mathbb{C}$
generated by the function
![]() $t^{\unicode[STIX]{x1D6FC}}$
. By the projection formula, we have
$t^{\unicode[STIX]{x1D6FC}}$
. By the projection formula, we have
Note that
![]() $H^{j}R(f|_{G})_{\ast }({\mathcal{N}}|_{G})\simeq 0$
(
$H^{j}R(f|_{G})_{\ast }({\mathcal{N}}|_{G})\simeq 0$
(
![]() $j\not =n-2$
), and
$j\not =n-2$
), and
![]() $H^{n-2}R(f|_{G})_{\ast }({\mathcal{N}}|_{G})$
is a local system on
$H^{n-2}R(f|_{G})_{\ast }({\mathcal{N}}|_{G})$
is a local system on
![]() $D_{\unicode[STIX]{x1D702}}^{\ast }$
whose stalks are isomorphic to
$D_{\unicode[STIX]{x1D702}}^{\ast }$
whose stalks are isomorphic to
![]() $H^{n-2}(F_{p};{\mathcal{N}})\simeq H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}$
. Hence, in order to show the vanishing
$H^{n-2}(F_{p};{\mathcal{N}})\simeq H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}$
. Hence, in order to show the vanishing
![]() $(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
, it suffices to prove that the monodromy operator
$(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
, it suffices to prove that the monodromy operator
![]() $\unicode[STIX]{x1D6F7}:H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}\overset{{\sim}}{\longrightarrow }H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}$
does not have the eigenvalue
$\unicode[STIX]{x1D6F7}:H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}\overset{{\sim}}{\longrightarrow }H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}$
does not have the eigenvalue
![]() $\exp (-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC})$
. For this purpose, we use the results in [Reference Matsui and Takeuchi18, Section 5]. Let
$\exp (-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC})$
. For this purpose, we use the results in [Reference Matsui and Takeuchi18, Section 5]. Let
![]() $\unicode[STIX]{x1D6E4}_{+}(f)\subset \mathbb{R}_{+}^{n-1}$
be the convex hull of
$\unicode[STIX]{x1D6E4}_{+}(f)\subset \mathbb{R}_{+}^{n-1}$
be the convex hull of
![]() $\bigcup _{v\in \operatorname{supp}(f)}(v+\mathbb{R}_{+}^{n-1})$
in
$\bigcup _{v\in \operatorname{supp}(f)}(v+\mathbb{R}_{+}^{n-1})$
in
![]() $\mathbb{R}_{+}^{n-1}$
. We call it the Newton polyhedron of
$\mathbb{R}_{+}^{n-1}$
. We call it the Newton polyhedron of
![]() $f$
at the origin
$f$
at the origin
![]() $p=0\in \mathbb{C}^{n-1}$
.
$p=0\in \mathbb{C}^{n-1}$
.
Definition 3.5. (see [Reference Khovanskii14], [Reference Oka23], etc.)
We say that
![]() $f$
is Newton nondegenerate at the origin
$f$
is Newton nondegenerate at the origin
![]() $p=0\in \mathbb{C}^{n-1}$
if for any compact face
$p=0\in \mathbb{C}^{n-1}$
if for any compact face
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E4}_{+}(f)$
of
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E4}_{+}(f)$
of
![]() $\unicode[STIX]{x1D6E4}_{+}(f)$
the hypersurface
$\unicode[STIX]{x1D6E4}_{+}(f)$
the hypersurface
![]() $\{y\in (\mathbb{C}^{\ast })^{n-1}\mid f^{\unicode[STIX]{x1D6FE}}(y)=0\}$
of
$\{y\in (\mathbb{C}^{\ast })^{n-1}\mid f^{\unicode[STIX]{x1D6FE}}(y)=0\}$
of
![]() $(\mathbb{C}^{\ast })^{n-1}$
is smooth and reduced.
$(\mathbb{C}^{\ast })^{n-1}$
is smooth and reduced.
For each subset
![]() $I\subset \{1,2,\ldots ,n-1\}$
, we set
$I\subset \{1,2,\ldots ,n-1\}$
, we set
Let
![]() $\unicode[STIX]{x1D6FE}_{1}^{I},\ldots ,\unicode[STIX]{x1D6FE}_{n(I)}^{I}\prec \unicode[STIX]{x1D6E4}_{+}(f)\cap \mathbb{R}_{+}^{I}$
be the compact facets of
$\unicode[STIX]{x1D6FE}_{1}^{I},\ldots ,\unicode[STIX]{x1D6FE}_{n(I)}^{I}\prec \unicode[STIX]{x1D6E4}_{+}(f)\cap \mathbb{R}_{+}^{I}$
be the compact facets of
![]() $\unicode[STIX]{x1D6E4}_{+}(f)\cap \mathbb{R}_{+}^{I}$
. For
$\unicode[STIX]{x1D6E4}_{+}(f)\cap \mathbb{R}_{+}^{I}$
. For
![]() $1\leqslant i\leqslant n(I)$
, denote by
$1\leqslant i\leqslant n(I)$
, denote by
![]() $d_{i}^{I}\in \mathbb{Z}_{{>}0}$
the lattice distance of
$d_{i}^{I}\in \mathbb{Z}_{{>}0}$
the lattice distance of
![]() $\unicode[STIX]{x1D6FE}_{i}^{I}$
from the origin
$\unicode[STIX]{x1D6FE}_{i}^{I}$
from the origin
![]() $0\in \mathbb{R}_{+}^{I}$
, and let
$0\in \mathbb{R}_{+}^{I}$
, and let
![]() $u_{i}^{I}=(u_{i,1}^{I},\ldots ,u_{i,n-1}^{I})\in \mathbb{R}_{+}^{I}\cap \mathbb{Z}^{n-1}$
be the unique (nonzero) primitive vector which takes its minimum exactly on
$u_{i}^{I}=(u_{i,1}^{I},\ldots ,u_{i,n-1}^{I})\in \mathbb{R}_{+}^{I}\cap \mathbb{Z}^{n-1}$
be the unique (nonzero) primitive vector which takes its minimum exactly on
![]() $\unicode[STIX]{x1D6FE}_{i}^{I}$
. For simplicity, we set
$\unicode[STIX]{x1D6FE}_{i}^{I}$
. For simplicity, we set
![]() $\unicode[STIX]{x1D6FF}_{i}^{I}:=u_{i,n-1}^{I}$
. Finally, we define a finite subset
$\unicode[STIX]{x1D6FF}_{i}^{I}:=u_{i,n-1}^{I}$
. Finally, we define a finite subset
![]() $E_{p}\subset \mathbb{C}$
of
$E_{p}\subset \mathbb{C}$
of
![]() $\mathbb{C}$
by
$\mathbb{C}$
by
Then, the following result is a special case of [Reference Matsui and Takeuchi18, Theorem 5.5].
Proposition 3.6. In the above situation, assume moreover that
![]() $f$
is Newton nondegenerate at the origin
$f$
is Newton nondegenerate at the origin
![]() $p=0\in \mathbb{C}^{n-1}$
. Then, the set of the eigenvalues of the monodromy operator
$p=0\in \mathbb{C}^{n-1}$
. Then, the set of the eigenvalues of the monodromy operator
![]() $\unicode[STIX]{x1D6F7}:H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}\overset{{\sim}}{\longrightarrow }H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}$
is contained in
$\unicode[STIX]{x1D6F7}:H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}\overset{{\sim}}{\longrightarrow }H^{n-2}\unicode[STIX]{x1D713}_{f}({\mathcal{N}})_{p}$
is contained in
![]() $E_{p}$
.
$E_{p}$
.
Corollary 3.7. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
,
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
,
![]() $c\in \mathbb{C}^{n}$
is nonresonant,
$c\in \mathbb{C}^{n}$
is nonresonant,
![]() $\exp (-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D6FC})=\exp (2\unicode[STIX]{x1D70B}\sqrt{-1}c_{n})\notin E_{p}$
and
$\exp (-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D6FC})=\exp (2\unicode[STIX]{x1D70B}\sqrt{-1}c_{n})\notin E_{p}$
and
![]() $f$
is Newton nondegenerate at the origin
$f$
is Newton nondegenerate at the origin
![]() $p=0\in \mathbb{C}^{n-1}$
. Then, we have
$p=0\in \mathbb{C}^{n-1}$
. Then, we have
![]() $(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
.
$(Ri_{\ast }{\mathcal{M}})_{p}\simeq 0$
.
In fact, by [Reference Matsui and Takeuchi18, Theorem 5.5], we can generalize this corollary to the case where the codimension of the
![]() $T_{0}$
-orbit
$T_{0}$
-orbit
![]() $X_{\unicode[STIX]{x1D6FE}}$
in
$X_{\unicode[STIX]{x1D6FE}}$
in
![]() $X_{\unicode[STIX]{x1D6FE}}\subset X\setminus i(T_{0})$
containing the (stratified) isolated singular point
$X_{\unicode[STIX]{x1D6FE}}\subset X\setminus i(T_{0})$
containing the (stratified) isolated singular point
![]() $p$
of
$p$
of
![]() $S$
is larger than one. We leave the precise formulation to the reader and omit the details here. In this way, our Theorem 3.3 can be generalized to the case where
$S$
is larger than one. We leave the precise formulation to the reader and omit the details here. In this way, our Theorem 3.3 can be generalized to the case where
![]() $S$
has (stratified) isolated singular points
$S$
has (stratified) isolated singular points
![]() $p$
also in
$p$
also in
![]() $T_{0}$
-orbits
$T_{0}$
-orbits
![]() $X_{\unicode[STIX]{x1D6FE}}\subset X\setminus i(T_{0})$
. In particular, we have the following result. For a face
$X_{\unicode[STIX]{x1D6FE}}\subset X\setminus i(T_{0})$
. In particular, we have the following result. For a face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6E5}$
, let
![]() $L_{\unicode[STIX]{x1D6FE}}\simeq \mathbb{R}^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
be the linear subspace of
$L_{\unicode[STIX]{x1D6FE}}\simeq \mathbb{R}^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
be the linear subspace of
![]() $\mathbb{R}^{n-1}$
parallel to the affine span of
$\mathbb{R}^{n-1}$
parallel to the affine span of
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\mathbb{R}^{n-1}$
, and consider the
$\mathbb{R}^{n-1}$
, and consider the
![]() $\unicode[STIX]{x1D6FE}$
-part
$\unicode[STIX]{x1D6FE}$
-part
![]() $P^{\unicode[STIX]{x1D6FE}}$
of
$P^{\unicode[STIX]{x1D6FE}}$
of
![]() $P$
as a function on
$P$
as a function on
![]() $T_{\unicode[STIX]{x1D6FE}}=\operatorname{Spec}(\mathbb{C}[L_{\unicode[STIX]{x1D6FE}}\cap \mathbb{Z}^{n-1}])\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
.
$T_{\unicode[STIX]{x1D6FE}}=\operatorname{Spec}(\mathbb{C}[L_{\unicode[STIX]{x1D6FE}}\cap \mathbb{Z}^{n-1}])\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
.
Theorem 3.8. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
, and for any face
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-1$
, and for any face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
, the hypersurface
$\unicode[STIX]{x1D6E5}$
, the hypersurface
![]() $(P^{\unicode[STIX]{x1D6FE}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
$(P^{\unicode[STIX]{x1D6FE}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
![]() $T_{\unicode[STIX]{x1D6FE}}$
has only isolated singular points. Then, for generic parameter vectors
$T_{\unicode[STIX]{x1D6FE}}$
has only isolated singular points. Then, for generic parameter vectors
![]() $c\in \mathbb{C}^{n}$
, we have the concentration
$c\in \mathbb{C}^{n}$
, we have the concentration
From now on, let us generalize Theorem 3.3 to the following more general situation. For
![]() $0<k<n$
, let
$0<k<n$
, let
![]() $B_{i}=\{b_{i}(1),b_{i}(2),\ldots ,b_{i}(N_{i})\}\subset \mathbb{Z}^{n-k}$
(
$B_{i}=\{b_{i}(1),b_{i}(2),\ldots ,b_{i}(N_{i})\}\subset \mathbb{Z}^{n-k}$
(
![]() $1\leqslant i\leqslant k$
) be
$1\leqslant i\leqslant k$
) be
![]() $k$
finite subsets of the lattice
$k$
finite subsets of the lattice
![]() $\mathbb{Z}^{n-k}$
, and set
$\mathbb{Z}^{n-k}$
, and set
![]() $N=N_{1}+N_{2}+\cdots +N_{k}$
. For
$N=N_{1}+N_{2}+\cdots +N_{k}$
. For
![]() $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
![]() $(z_{i1},\ldots ,z_{iN_{i}})\in \mathbb{C}^{N_{i}}$
, we define a Laurent polynomial
$(z_{i1},\ldots ,z_{iN_{i}})\in \mathbb{C}^{N_{i}}$
, we define a Laurent polynomial
![]() $P_{i}(x)$
on
$P_{i}(x)$
on
![]() $T_{0}=(\mathbb{C}^{\ast })^{n-k}$
by
$T_{0}=(\mathbb{C}^{\ast })^{n-k}$
by
![]() $P_{i}(x)=\sum _{j=1}^{N_{i}}z_{ij}x^{b_{i}(j)}$
(
$P_{i}(x)=\sum _{j=1}^{N_{i}}z_{ij}x^{b_{i}(j)}$
(
![]() $x=(x_{1},\ldots ,x_{n-k})\in T_{0}=(\mathbb{C}^{\ast })^{n-k}$
). Let us set
$x=(x_{1},\ldots ,x_{n-k})\in T_{0}=(\mathbb{C}^{\ast })^{n-k}$
). Let us set
![]() $W=T_{0}\setminus \bigcup _{i=1}^{k}P_{i}^{-1}(0)$
. Then, for
$W=T_{0}\setminus \bigcup _{i=1}^{k}P_{i}^{-1}(0)$
. Then, for
![]() $c=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\in \mathbb{C}^{n}$
, the possibly multivalued function
$c=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\in \mathbb{C}^{n}$
, the possibly multivalued function
on
![]() $W$
generates the local system
$W$
generates the local system
Let
![]() $e_{i}=(0,0,\ldots ,0,1,0,\ldots ,0)\in \mathbb{Z}^{k}$
(
$e_{i}=(0,0,\ldots ,0,1,0,\ldots ,0)\in \mathbb{Z}^{k}$
(
![]() $1\leqslant i\leqslant k$
) be the standard basis of
$1\leqslant i\leqslant k$
) be the standard basis of
![]() $\mathbb{Z}^{k}$
, and set
$\mathbb{Z}^{k}$
, and set
![]() $a_{i}(j)=(b_{i}(j),e_{i})\in \mathbb{Z}^{n-k}\times \mathbb{Z}^{k}=\mathbb{Z}^{n}$
(
$a_{i}(j)=(b_{i}(j),e_{i})\in \mathbb{Z}^{n-k}\times \mathbb{Z}^{k}=\mathbb{Z}^{n}$
(
![]() $1\leqslant i\leqslant k$
,
$1\leqslant i\leqslant k$
,
![]() $1\leqslant j\leqslant N_{i}$
) and
$1\leqslant j\leqslant N_{i}$
) and
For
![]() $1\leqslant i\leqslant k$
, let
$1\leqslant i\leqslant k$
, let
![]() $\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n-k}$
be the convex hull of
$\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n-k}$
be the convex hull of
![]() $B_{i}$
in
$B_{i}$
in
![]() $\mathbb{R}^{n-k}$
. Denote by
$\mathbb{R}^{n-k}$
. Denote by
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-k}$
their Minkowski sum
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-k}$
their Minkowski sum
![]() $\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$
. Assume that
$\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$
. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
. Then, by using the
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
. Then, by using the
![]() $n$
-dimensional closed convex polyhedral cone
$n$
-dimensional closed convex polyhedral cone
![]() $K=\mathbb{R}_{+}A\subset \mathbb{R}^{n}$
generated by
$K=\mathbb{R}_{+}A\subset \mathbb{R}^{n}$
generated by
![]() $A$
in
$A$
in
![]() $\mathbb{R}^{n}$
, we can define the nonresonance of the parameter
$\mathbb{R}^{n}$
, we can define the nonresonance of the parameter
![]() $c\in \mathbb{C}^{n}$
as in Definition 3.1. For a face
$c\in \mathbb{C}^{n}$
as in Definition 3.1. For a face
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
of
![]() $\unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6E5}$
, let
![]() $\unicode[STIX]{x1D6FE}_{i}\prec \unicode[STIX]{x1D6E5}_{i}$
be the faces of
$\unicode[STIX]{x1D6FE}_{i}\prec \unicode[STIX]{x1D6E5}_{i}$
be the faces of
![]() $\unicode[STIX]{x1D6E5}_{i}$
(
$\unicode[STIX]{x1D6E5}_{i}$
(
![]() $1\leqslant i\leqslant k$
) canonically associated to
$1\leqslant i\leqslant k$
) canonically associated to
![]() $\unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}$
such that
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{k}$
.
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{k}$
.
Definition 3.9. We say that the
![]() $k$
-tuple of the Laurent polynomials
$k$
-tuple of the Laurent polynomials
![]() $(P_{1},\ldots ,P_{k})$
is “weakly” (resp. “strongly”) nondegenerate if for any face
$(P_{1},\ldots ,P_{k})$
is “weakly” (resp. “strongly”) nondegenerate if for any face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
(resp.
$\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
(resp.
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}\leqslant \operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
) and nonempty subset
$\operatorname{dim}\unicode[STIX]{x1D6FE}\leqslant \operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
) and nonempty subset
![]() $J\subset \{1,2,\ldots ,k\}$
, the subvariety
$J\subset \{1,2,\ldots ,k\}$
, the subvariety
is a nondegenerate complete intersection.
Remark 3.10. Denote the convex hull of
![]() $\bigcup _{i=1}^{k}(\unicode[STIX]{x1D6E5}_{i}\times \{e_{i}\})\subset \mathbb{R}^{n-k}\times \mathbb{R}^{k}=\mathbb{R}^{n}$
in
$\bigcup _{i=1}^{k}(\unicode[STIX]{x1D6E5}_{i}\times \{e_{i}\})\subset \mathbb{R}^{n-k}\times \mathbb{R}^{k}=\mathbb{R}^{n}$
in
![]() $\mathbb{R}^{n}$
by
$\mathbb{R}^{n}$
by
![]() $\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
. Then,
$\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
. Then,
![]() $\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
is naturally identified with the Newton polytope of the Laurent polynomial
$\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
is naturally identified with the Newton polytope of the Laurent polynomial
![]() $R(x,t)=\sum _{i=1}^{k}P_{i}(x)t_{i}$
on
$R(x,t)=\sum _{i=1}^{k}P_{i}(x)t_{i}$
on
![]() $\widetilde{T_{0}}:=T_{0}\times (\mathbb{C}^{\ast })_{t}^{k}\simeq (\mathbb{C}^{\ast })_{x,t}^{n}$
. In [Reference Gelfand, Kapranov and Zelevinsky10], the authors considered the condition that for any face
$\widetilde{T_{0}}:=T_{0}\times (\mathbb{C}^{\ast })_{t}^{k}\simeq (\mathbb{C}^{\ast })_{x,t}^{n}$
. In [Reference Gelfand, Kapranov and Zelevinsky10], the authors considered the condition that for any face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
, the hypersurface
$\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
, the hypersurface
![]() $\{(x,t)\in \widetilde{T_{0}}\mid R^{\unicode[STIX]{x1D6FE}}(x,t)=0\}\subset \widetilde{T_{0}}$
of
$\{(x,t)\in \widetilde{T_{0}}\mid R^{\unicode[STIX]{x1D6FE}}(x,t)=0\}\subset \widetilde{T_{0}}$
of
![]() $\widetilde{T_{0}}$
is smooth and reduced. It is easy to see that our strong nondegeneracy of the
$\widetilde{T_{0}}$
is smooth and reduced. It is easy to see that our strong nondegeneracy of the
![]() $k$
-tuple
$k$
-tuple
![]() $(P_{1},\ldots ,P_{k})$
in Definition 3.9 is equivalent to their condition.
$(P_{1},\ldots ,P_{k})$
in Definition 3.9 is equivalent to their condition.
Let
![]() $\unicode[STIX]{x1D704}:W=T_{0}\setminus \bigcup _{i=1}^{k}P_{i}^{-1}(0)\longrightarrow T_{0}$
be the inclusion map, and set
$\unicode[STIX]{x1D704}:W=T_{0}\setminus \bigcup _{i=1}^{k}P_{i}^{-1}(0)\longrightarrow T_{0}$
be the inclusion map, and set
![]() ${\mathcal{M}}=R\unicode[STIX]{x1D704}_{\ast }{\mathcal{L}}\in \mathbf{D}_{c}^{b}(T_{0})$
.
${\mathcal{M}}=R\unicode[STIX]{x1D704}_{\ast }{\mathcal{L}}\in \mathbf{D}_{c}^{b}(T_{0})$
.
Theorem 3.11. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
, the parameter vector
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
, the parameter vector
![]() $c\in \mathbb{C}^{n}$
is nonresonant and
$c\in \mathbb{C}^{n}$
is nonresonant and
![]() $(P_{1},\ldots ,P_{k})$
is weakly nondegenerate. Then, there exists an isomorphism
$(P_{1},\ldots ,P_{k})$
is weakly nondegenerate. Then, there exists an isomorphism
for any
![]() $j\in \mathbb{Z}$
. Moreover, we have the concentration
$j\in \mathbb{Z}$
. Moreover, we have the concentration
Proof. The proof is similar to that of Theorem 3.3. Let
![]() $\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of
$\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of
![]() $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
![]() $\mathbb{R}^{n-k}$
, and let
$\mathbb{R}^{n-k}$
, and let
![]() $X$
be the (possibly singular) toric variety associated to it. For a face
$X$
be the (possibly singular) toric variety associated to it. For a face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
, we denote by
$\unicode[STIX]{x1D6E5}$
, we denote by
![]() $X_{\unicode[STIX]{x1D6FE}}\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
the
$X_{\unicode[STIX]{x1D6FE}}\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
the
![]() $T_{0}$
-orbit associated to
$T_{0}$
-orbit associated to
![]() $\unicode[STIX]{x1D6FE}$
. Let
$\unicode[STIX]{x1D6FE}$
. Let
![]() $i:X_{\unicode[STIX]{x1D6E5}}\simeq T_{0}{\hookrightarrow}X$
be the inclusion map. Then, by the weak nondegeneracy of the
$i:X_{\unicode[STIX]{x1D6E5}}\simeq T_{0}{\hookrightarrow}X$
be the inclusion map. Then, by the weak nondegeneracy of the
![]() $k$
-tuple
$k$
-tuple
![]() $(P_{1},\ldots ,P_{k})$
, for any
$(P_{1},\ldots ,P_{k})$
, for any
![]() $T_{0}$
-orbits
$T_{0}$
-orbits
![]() $X_{\unicode[STIX]{x1D6FE}}$
in
$X_{\unicode[STIX]{x1D6FE}}$
in
![]() $X\setminus X_{\unicode[STIX]{x1D6E5}}$
and the closure
$X\setminus X_{\unicode[STIX]{x1D6E5}}$
and the closure
![]() $S=\overline{i(\bigcup _{i=1}^{k}P_{i}^{-1}(0))}\subset X$
of the hypersurface
$S=\overline{i(\bigcup _{i=1}^{k}P_{i}^{-1}(0))}\subset X$
of the hypersurface
![]() $i(\bigcup _{i=1}^{k}P_{i}^{-1}(0))\subset i(T_{0})$
in
$i(\bigcup _{i=1}^{k}P_{i}^{-1}(0))\subset i(T_{0})$
in
![]() $X$
, their intersection
$X$
, their intersection
![]() $S\cap X_{\unicode[STIX]{x1D6FE}}\subset X_{\unicode[STIX]{x1D6FE}}$
is a normal crossing divisor in
$S\cap X_{\unicode[STIX]{x1D6FE}}\subset X_{\unicode[STIX]{x1D6FE}}$
is a normal crossing divisor in
![]() $X_{\unicode[STIX]{x1D6FE}}$
. In fact,
$X_{\unicode[STIX]{x1D6FE}}$
. In fact,
![]() $S$
itself is normal crossing on a neighborhood of such
$S$
itself is normal crossing on a neighborhood of such
![]() $X_{\unicode[STIX]{x1D6FE}}$
, and any irreducible component of it intersects
$X_{\unicode[STIX]{x1D6FE}}$
, and any irreducible component of it intersects
![]() $X_{\unicode[STIX]{x1D6FE}}$
transversely. Moreover, by the nonresonance of
$X_{\unicode[STIX]{x1D6FE}}$
transversely. Moreover, by the nonresonance of
![]() $c\in \mathbb{C}^{n}$
, for any
$c\in \mathbb{C}^{n}$
, for any
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}=n-k-1$
, the monodromy of the local system
$\operatorname{dim}\unicode[STIX]{x1D6FE}=n-k-1$
, the monodromy of the local system
![]() ${\mathcal{L}}$
around the codimension-one
${\mathcal{L}}$
around the codimension-one
![]() $T_{0}$
-orbit
$T_{0}$
-orbit
![]() $X_{\unicode[STIX]{x1D6FE}}\subset X$
in
$X_{\unicode[STIX]{x1D6FE}}\subset X$
in
![]() $X$
is nontrivial. Indeed, let
$X$
is nontrivial. Indeed, let
![]() $\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
be such a facet of
$\unicode[STIX]{x1D6FE}\prec \unicode[STIX]{x1D6E5}$
be such a facet of
![]() $\unicode[STIX]{x1D6E5}$
, and let
$\unicode[STIX]{x1D6E5}$
, and let
![]() $\unicode[STIX]{x1D6FE}_{i}\prec \unicode[STIX]{x1D6E5}_{i}$
be the faces of
$\unicode[STIX]{x1D6FE}_{i}\prec \unicode[STIX]{x1D6E5}_{i}$
be the faces of
![]() $\unicode[STIX]{x1D6E5}_{i}$
(
$\unicode[STIX]{x1D6E5}_{i}$
(
![]() $1\leqslant i\leqslant k$
) associated to
$1\leqslant i\leqslant k$
) associated to
![]() $\unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}$
such that
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{k}$
. We denote the convex hull of
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{k}$
. We denote the convex hull of
![]() $\bigcup _{i=1}^{k}(\unicode[STIX]{x1D6E5}_{i}\times \{e_{i}\})$
(resp.
$\bigcup _{i=1}^{k}(\unicode[STIX]{x1D6E5}_{i}\times \{e_{i}\})$
(resp.
![]() $\bigcup _{i=1}^{k}(\unicode[STIX]{x1D6FE}_{i}\times \{e_{i}\})$
)
$\bigcup _{i=1}^{k}(\unicode[STIX]{x1D6FE}_{i}\times \{e_{i}\})$
)
![]() $\subset \mathbb{R}^{n-k}\times \mathbb{R}^{k}=\mathbb{R}^{n}$
in
$\subset \mathbb{R}^{n-k}\times \mathbb{R}^{k}=\mathbb{R}^{n}$
in
![]() $\mathbb{R}^{n}$
by
$\mathbb{R}^{n}$
by
![]() $\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
(resp.
$\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
(resp.
![]() $\unicode[STIX]{x1D6FE}_{1}\ast \cdots \ast \unicode[STIX]{x1D6FE}_{k}$
). Then,
$\unicode[STIX]{x1D6FE}_{1}\ast \cdots \ast \unicode[STIX]{x1D6FE}_{k}$
). Then,
![]() $\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
is the join of
$\unicode[STIX]{x1D6E5}_{1}\ast \cdots \ast \unicode[STIX]{x1D6E5}_{k}$
is the join of
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
and
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
and
![]() $\unicode[STIX]{x1D6FE}_{1}\ast \cdots \ast \unicode[STIX]{x1D6FE}_{k}$
is its facet. We denote by
$\unicode[STIX]{x1D6FE}_{1}\ast \cdots \ast \unicode[STIX]{x1D6FE}_{k}$
is its facet. We denote by
![]() $\unicode[STIX]{x1D6E4}$
the facet of the cone
$\unicode[STIX]{x1D6E4}$
the facet of the cone
![]() $K=\mathbb{R}_{+}A$
generated by
$K=\mathbb{R}_{+}A$
generated by
![]() $\unicode[STIX]{x1D6FE}_{1}\ast \cdots \ast \unicode[STIX]{x1D6FE}_{k}\subset K$
. Let
$\unicode[STIX]{x1D6FE}_{1}\ast \cdots \ast \unicode[STIX]{x1D6FE}_{k}\subset K$
. Let
![]() $\unicode[STIX]{x1D708}\in \mathbb{Z}^{n-k}\setminus \{0\}$
be the primitive inner conormal vector of the facet
$\unicode[STIX]{x1D708}\in \mathbb{Z}^{n-k}\setminus \{0\}$
be the primitive inner conormal vector of the facet
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-k}$
, and for
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{n-k}$
, and for
![]() $1\leqslant i\leqslant k$
set
$1\leqslant i\leqslant k$
set
Then, the primitive inner conormal vector
![]() $\widetilde{\unicode[STIX]{x1D708}}\in \mathbb{Z}^{n}\setminus \{0\}$
of the facet
$\widetilde{\unicode[STIX]{x1D708}}\in \mathbb{Z}^{n}\setminus \{0\}$
of the facet
![]() $\unicode[STIX]{x1D6E4}$
of
$\unicode[STIX]{x1D6E4}$
of
![]() $K\subset \mathbb{R}^{n}$
is explicitly given by the formula
$K\subset \mathbb{R}^{n}$
is explicitly given by the formula
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D708}}=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D708}\\ -m_{1}\\ \vdots \\ -m_{k}\end{array}\right)\in \mathbb{Z}^{n}\setminus \{0\},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D708}}=\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D708}\\ -m_{1}\\ \vdots \\ -m_{k}\end{array}\right)\in \mathbb{Z}^{n}\setminus \{0\},\end{eqnarray}$$
and the condition
![]() $c=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \{\mathbb{Z}^{n}+\operatorname{Lin}(\unicode[STIX]{x1D6E4})\}$
is equivalent to the one
$c=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \{\mathbb{Z}^{n}+\operatorname{Lin}(\unicode[STIX]{x1D6E4})\}$
is equivalent to the one
 $$\begin{eqnarray}m(\unicode[STIX]{x1D6FE}):=\left\langle \unicode[STIX]{x1D708},\left(\begin{array}{@{}c@{}}c_{1}-1\\ \vdots \\ c_{n-k}-1\end{array}\right)\right\rangle -\mathop{\sum }_{i=1}^{k}m_{i}\cdot \widetilde{c_{i}}\quad \notin \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}m(\unicode[STIX]{x1D6FE}):=\left\langle \unicode[STIX]{x1D708},\left(\begin{array}{@{}c@{}}c_{1}-1\\ \vdots \\ c_{n-k}-1\end{array}\right)\right\rangle -\mathop{\sum }_{i=1}^{k}m_{i}\cdot \widetilde{c_{i}}\quad \notin \mathbb{Z}.\end{eqnarray}$$
Moreover, we can easily see that the order of the (multivalued) function
along the codimension-one
![]() $T_{0}$
-orbit
$T_{0}$
-orbit
![]() $X_{\unicode[STIX]{x1D6FE}}\subset X$
in
$X_{\unicode[STIX]{x1D6FE}}\subset X$
in
![]() $X$
is equal to
$X$
is equal to
![]() $m(\unicode[STIX]{x1D6FE})\notin \mathbb{Z}$
. Finally, by constructing suitable distance functions as in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2], we can show that
$m(\unicode[STIX]{x1D6FE})\notin \mathbb{Z}$
. Finally, by constructing suitable distance functions as in the proof of [Reference Esterov and Takeuchi7, Lemma 4.2], we can show that
Namely, there exists an isomorphism
![]() $i_{!}{\mathcal{M}}\simeq Ri_{\ast }{\mathcal{M}}$
in
$i_{!}{\mathcal{M}}\simeq Ri_{\ast }{\mathcal{M}}$
in
![]() $\mathbf{D}_{c}^{b}(X)$
. Applying the functor
$\mathbf{D}_{c}^{b}(X)$
. Applying the functor
![]() $R\unicode[STIX]{x1D6E4}_{c}(X;\cdot )=R\unicode[STIX]{x1D6E4}(X;\cdot )$
to it, we obtain the desired isomorphisms
$R\unicode[STIX]{x1D6E4}_{c}(X;\cdot )=R\unicode[STIX]{x1D6E4}(X;\cdot )$
to it, we obtain the desired isomorphisms
for
![]() $j\in \mathbb{Z}$
. Then, the remaining assertion can be proved as in the proof of Theorem 3.3. This completes the proof.◻
$j\in \mathbb{Z}$
. Then, the remaining assertion can be proved as in the proof of Theorem 3.3. This completes the proof.◻
In the situation of Theorem 3.11, for any
![]() $1\leqslant i\leqslant k$
, the hypersurface
$1\leqslant i\leqslant k$
, the hypersurface
![]() $P_{i}^{-1}(0)\subset T_{0}$
has only isolated singular points. Assume moreover that the hypersurface
$P_{i}^{-1}(0)\subset T_{0}$
has only isolated singular points. Assume moreover that the hypersurface
![]() $\bigcup _{i=1}^{k}P_{i}^{-1}(0)\subset T_{0}$
is normal crossing outside them. Then, as in Corollary 3.4, by Theorem 2.4, we can also express the dimension of
$\bigcup _{i=1}^{k}P_{i}^{-1}(0)\subset T_{0}$
is normal crossing outside them. Then, as in Corollary 3.4, by Theorem 2.4, we can also express the dimension of
![]() $H^{n-k}(W;{\mathcal{L}})$
in terms of some mixed volumes of the polytopes
$H^{n-k}(W;{\mathcal{L}})$
in terms of some mixed volumes of the polytopes
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
and the Milnor numbers of the isolated singular points. Since the statement of this result is involved, we leave its precise formulation to the reader.
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
and the Milnor numbers of the isolated singular points. Since the statement of this result is involved, we leave its precise formulation to the reader.
As in the case where
![]() $k=1$
, we have the following result. For a face
$k=1$
, we have the following result. For a face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6E5}$
, let
![]() $L_{\unicode[STIX]{x1D6FE}}\simeq \mathbb{R}^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
be the linear subspace of
$L_{\unicode[STIX]{x1D6FE}}\simeq \mathbb{R}^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
be the linear subspace of
![]() $\mathbb{R}^{n-k}$
parallel to the affine span of
$\mathbb{R}^{n-k}$
parallel to the affine span of
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\mathbb{R}^{n-k}$
, and for
$\mathbb{R}^{n-k}$
, and for
![]() $1\leqslant i\leqslant k$
, consider the
$1\leqslant i\leqslant k$
, consider the
![]() $\unicode[STIX]{x1D6FE}_{i}$
-part
$\unicode[STIX]{x1D6FE}_{i}$
-part
![]() $P_{i}^{\unicode[STIX]{x1D6FE}_{i}}$
of
$P_{i}^{\unicode[STIX]{x1D6FE}_{i}}$
of
![]() $P_{i}$
as a function on
$P_{i}$
as a function on
![]() $T_{\unicode[STIX]{x1D6FE}}=\operatorname{Spec}(\mathbb{C}[L_{\unicode[STIX]{x1D6FE}}\cap \mathbb{Z}^{n-k}])\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
.
$T_{\unicode[STIX]{x1D6FE}}=\operatorname{Spec}(\mathbb{C}[L_{\unicode[STIX]{x1D6FE}}\cap \mathbb{Z}^{n-k}])\simeq (\mathbb{C}^{\ast })^{\operatorname{dim}\unicode[STIX]{x1D6FE}}$
.
Theorem 3.12. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
, and for any
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
, and for any
![]() $1\leqslant i\leqslant k$
, the hypersurface
$1\leqslant i\leqslant k$
, the hypersurface
![]() $P_{i}^{-1}(0)\subset T_{0}$
of
$P_{i}^{-1}(0)\subset T_{0}$
of
![]() $T_{0}$
has only isolated singular points. Assume moreover that for any face
$T_{0}$
has only isolated singular points. Assume moreover that for any face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
and nonempty subset
$\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
and nonempty subset
![]() $J\subset \{1,2,\ldots ,k\}$
, the
$J\subset \{1,2,\ldots ,k\}$
, the
![]() $k$
-tuple of the Laurent polynomials
$k$
-tuple of the Laurent polynomials
![]() $(P_{1},\ldots ,P_{k})$
satisfies the following condition.
$(P_{1},\ldots ,P_{k})$
satisfies the following condition.
If
 $J=\{i\}$
for some
$J=\{i\}$
for some
 $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
 $\operatorname{dim}\unicode[STIX]{x1D6FE}_{i}=\operatorname{dim}\unicode[STIX]{x1D6FE}=\operatorname{dim}\unicode[STIX]{x1D6E5}-1=n-k-1$
, the hypersurface
$\operatorname{dim}\unicode[STIX]{x1D6FE}_{i}=\operatorname{dim}\unicode[STIX]{x1D6FE}=\operatorname{dim}\unicode[STIX]{x1D6E5}-1=n-k-1$
, the hypersurface
 $(P_{i}^{\unicode[STIX]{x1D6FE}_{i}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
$(P_{i}^{\unicode[STIX]{x1D6FE}_{i}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
 $T_{\unicode[STIX]{x1D6FE}}$
has only isolated singular points. Otherwise, the subvariety (3.40)
$T_{\unicode[STIX]{x1D6FE}}$
has only isolated singular points. Otherwise, the subvariety (3.40) $$\begin{eqnarray}\{x\in T_{0}=(\mathbb{C}^{\ast })^{n-k}\mid P_{i}^{\unicode[STIX]{x1D6FE}_{i}}(x)=0~(i\in J)\}\subset T_{0}\end{eqnarray}$$
$$\begin{eqnarray}\{x\in T_{0}=(\mathbb{C}^{\ast })^{n-k}\mid P_{i}^{\unicode[STIX]{x1D6FE}_{i}}(x)=0~(i\in J)\}\subset T_{0}\end{eqnarray}$$
of
 $T_{0}$
is a nondegenerate complete intersection.
$T_{0}$
is a nondegenerate complete intersection.
Then, for generic parameter vectors
![]() $c\in \mathbb{C}^{n}$
, we have the concentration
$c\in \mathbb{C}^{n}$
, we have the concentration
Proof. Let
![]() $\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of
$\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of
![]() $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
![]() $\mathbb{R}^{n-k}$
, and let
$\mathbb{R}^{n-k}$
, and let
![]() $X$
be the (possibly singular) toric variety associated to it. Then, our assumptions imply that for any
$X$
be the (possibly singular) toric variety associated to it. Then, our assumptions imply that for any
![]() $1\leqslant i\leqslant k$
, the hypersurface
$1\leqslant i\leqslant k$
, the hypersurface
![]() $S_{i}=\overline{i(P_{i}^{-1}(0))}\subset X$
has only stratified isolated singular points in
$S_{i}=\overline{i(P_{i}^{-1}(0))}\subset X$
has only stratified isolated singular points in
![]() $X$
, and we can prove the assertion following the proofs of Theorems 3.8 and 3.11.◻
$X$
, and we can prove the assertion following the proofs of Theorems 3.8 and 3.11.◻
For a face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $1\leqslant i\leqslant k$
such that
$1\leqslant i\leqslant k$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}_{i}<\operatorname{dim}\unicode[STIX]{x1D6FE}\leqslant n-k-1$
, the hypersurface
$\operatorname{dim}\unicode[STIX]{x1D6FE}_{i}<\operatorname{dim}\unicode[STIX]{x1D6FE}\leqslant n-k-1$
, the hypersurface
![]() $(P_{i}^{\unicode[STIX]{x1D6FE}_{i}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
$(P_{i}^{\unicode[STIX]{x1D6FE}_{i}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
![]() $T_{\unicode[STIX]{x1D6FE}}$
is smooth or has nonisolated singularities. In the latter case, we cannot prove the concentration in Theorem 3.12 by our methods. This is the reason why we do not allow such cases in our assumptions of Theorem 3.12. However, in the very special case where the Newton polytopes
$T_{\unicode[STIX]{x1D6FE}}$
is smooth or has nonisolated singularities. In the latter case, we cannot prove the concentration in Theorem 3.12 by our methods. This is the reason why we do not allow such cases in our assumptions of Theorem 3.12. However, in the very special case where the Newton polytopes
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
are similar to each other, we do not have this problem and obtain the following simpler result.
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
are similar to each other, we do not have this problem and obtain the following simpler result.
Theorem 3.13. Assume that
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
, the Newton polytopes
$\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
, the Newton polytopes
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
are similar to each other, and for any face
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
are similar to each other, and for any face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $1\leqslant i\leqslant k$
, the hypersurface
$1\leqslant i\leqslant k$
, the hypersurface
![]() $(P_{i}^{\unicode[STIX]{x1D6FE}_{i}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
$(P_{i}^{\unicode[STIX]{x1D6FE}_{i}})^{-1}(0)\subset T_{\unicode[STIX]{x1D6FE}}$
of
![]() $T_{\unicode[STIX]{x1D6FE}}$
has only isolated singular points. Assume moreover that for any face
$T_{\unicode[STIX]{x1D6FE}}$
has only isolated singular points. Assume moreover that for any face
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
![]() $\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
and any subset
$\operatorname{dim}\unicode[STIX]{x1D6FE}<\operatorname{dim}\unicode[STIX]{x1D6E5}=n-k$
and any subset
![]() $J\subset \{1,2,\ldots ,k\}$
such that
$J\subset \{1,2,\ldots ,k\}$
such that
![]() $\sharp J\geqslant 2$
, the subvariety
$\sharp J\geqslant 2$
, the subvariety
of
![]() $T_{0}$
is a nondegenerate complete intersection. Then, for generic parameter vectors
$T_{0}$
is a nondegenerate complete intersection. Then, for generic parameter vectors
![]() $c\in \mathbb{C}^{n}$
, we have the concentration
$c\in \mathbb{C}^{n}$
, we have the concentration
4 Some results on the twisted Morse theory
In this section, we prepare some auxiliary results on the twisted Morse theory which will be used in Section 5. The following proposition is a refinement of the results in [Reference Esterov5, page 10]. See also [Reference Esterov and Takeuchi7, Proposition 7.1].
Proposition 4.1. Let
![]() $T$
be an algebraic torus
$T$
be an algebraic torus
![]() $(\mathbb{C}^{\ast })_{x}^{n}$
, and let
$(\mathbb{C}^{\ast })_{x}^{n}$
, and let
![]() $T=\sqcup _{\unicode[STIX]{x1D6FC}}Z_{\unicode[STIX]{x1D6FC}}$
be its algebraic stratification. In particular, we assume that each stratum
$T=\sqcup _{\unicode[STIX]{x1D6FC}}Z_{\unicode[STIX]{x1D6FC}}$
be its algebraic stratification. In particular, we assume that each stratum
![]() $Z_{\unicode[STIX]{x1D6FC}}$
in it is smooth. Let
$Z_{\unicode[STIX]{x1D6FC}}$
in it is smooth. Let
![]() $h(x)$
be a Laurent polynomial on
$h(x)$
be a Laurent polynomial on
![]() $T=(\mathbb{C}^{\ast })_{x}^{n}$
such that the hypersurface
$T=(\mathbb{C}^{\ast })_{x}^{n}$
such that the hypersurface
![]() $\{h=0\}\subset T$
intersects
$\{h=0\}\subset T$
intersects
![]() $Z_{\unicode[STIX]{x1D6FC}}$
transversely for any
$Z_{\unicode[STIX]{x1D6FC}}$
transversely for any
![]() $\unicode[STIX]{x1D6FC}$
. For
$\unicode[STIX]{x1D6FC}$
. For
![]() $a\in \mathbb{C}^{n}$
, consider the (possibly multivalued) function
$a\in \mathbb{C}^{n}$
, consider the (possibly multivalued) function
![]() $g_{a}(x):=h(x)x^{-a}$
on
$g_{a}(x):=h(x)x^{-a}$
on
![]() $T$
. Then, there exists a nonempty Zariski open subset
$T$
. Then, there exists a nonempty Zariski open subset
![]() $\unicode[STIX]{x1D6FA}\subset \mathbb{C}^{n}$
of
$\unicode[STIX]{x1D6FA}\subset \mathbb{C}^{n}$
of
![]() $\mathbb{C}^{n}$
such that the restriction
$\mathbb{C}^{n}$
such that the restriction
![]() $g_{a}|_{Z_{\unicode[STIX]{x1D6FC}}}:Z_{\unicode[STIX]{x1D6FC}}\longrightarrow \mathbb{C}$
of
$g_{a}|_{Z_{\unicode[STIX]{x1D6FC}}}:Z_{\unicode[STIX]{x1D6FC}}\longrightarrow \mathbb{C}$
of
![]() $g_{a}$
to
$g_{a}$
to
![]() $Z_{\unicode[STIX]{x1D6FC}}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
$Z_{\unicode[STIX]{x1D6FC}}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
![]() $a\in \unicode[STIX]{x1D6FA}\subset \mathbb{C}^{n}$
and
$a\in \unicode[STIX]{x1D6FA}\subset \mathbb{C}^{n}$
and
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Proof. We may assume that each stratum
![]() $Z_{\unicode[STIX]{x1D6FC}}$
is connected. We fix a stratum
$Z_{\unicode[STIX]{x1D6FC}}$
is connected. We fix a stratum
![]() $Z_{\unicode[STIX]{x1D6FC}}$
and set
$Z_{\unicode[STIX]{x1D6FC}}$
and set
![]() $k=\operatorname{dim}Z_{\unicode[STIX]{x1D6FC}}$
. For a subset
$k=\operatorname{dim}Z_{\unicode[STIX]{x1D6FC}}$
. For a subset
![]() $I\subset \{1,2,\ldots ,n\}$
such that
$I\subset \{1,2,\ldots ,n\}$
such that
![]() $|I|=k=\operatorname{dim}Z_{\unicode[STIX]{x1D6FC}}$
, denote by
$|I|=k=\operatorname{dim}Z_{\unicode[STIX]{x1D6FC}}$
, denote by
![]() $\unicode[STIX]{x1D70B}_{I}:T=(\mathbb{C}^{\ast })_{x}^{n}\longrightarrow (\mathbb{C}^{\ast })^{k}$
the projection associated to
$\unicode[STIX]{x1D70B}_{I}:T=(\mathbb{C}^{\ast })_{x}^{n}\longrightarrow (\mathbb{C}^{\ast })^{k}$
the projection associated to
![]() $I$
. We also denote by
$I$
. We also denote by
![]() $Z_{\unicode[STIX]{x1D6FC},I}\subset Z_{\unicode[STIX]{x1D6FC}}$
the maximal Zariski open subset of
$Z_{\unicode[STIX]{x1D6FC},I}\subset Z_{\unicode[STIX]{x1D6FC}}$
the maximal Zariski open subset of
![]() $Z_{\unicode[STIX]{x1D6FC}}$
such that the restriction of
$Z_{\unicode[STIX]{x1D6FC}}$
such that the restriction of
![]() $\unicode[STIX]{x1D70B}_{I}$
to it is locally biholomorphic. By the implicit function theorem, the variety
$\unicode[STIX]{x1D70B}_{I}$
to it is locally biholomorphic. By the implicit function theorem, the variety
![]() $Z_{\unicode[STIX]{x1D6FC}}$
is covered by such open subsets
$Z_{\unicode[STIX]{x1D6FC}}$
is covered by such open subsets
![]() $Z_{\unicode[STIX]{x1D6FC},I}$
. For simplicity, let us consider the case where
$Z_{\unicode[STIX]{x1D6FC},I}$
. For simplicity, let us consider the case where
![]() $I=\{1,2,\ldots ,k\}\subset \{1,2,\ldots ,n\}$
. Then, we may regard
$I=\{1,2,\ldots ,k\}\subset \{1,2,\ldots ,n\}$
. Then, we may regard
![]() $g_{a}|_{Z_{\unicode[STIX]{x1D6FC}}}$
locally as a function
$g_{a}|_{Z_{\unicode[STIX]{x1D6FC}}}$
locally as a function
![]() $g_{a,\unicode[STIX]{x1D6FC},I}(x_{1},\ldots ,x_{k})$
on the Zariski open subset
$g_{a,\unicode[STIX]{x1D6FC},I}(x_{1},\ldots ,x_{k})$
on the Zariski open subset
![]() $\unicode[STIX]{x1D70B}_{I}(Z_{\unicode[STIX]{x1D6FC},I})\subset (\mathbb{C}^{\ast })^{k}$
of the form
$\unicode[STIX]{x1D70B}_{I}(Z_{\unicode[STIX]{x1D6FC},I})\subset (\mathbb{C}^{\ast })^{k}$
of the form
By our assumption, the hypersurface
![]() $\{h_{a,\unicode[STIX]{x1D6FC},I}=0\}\subset \unicode[STIX]{x1D70B}_{I}(Z_{\unicode[STIX]{x1D6FC},I})\subset (\mathbb{C}^{\ast })^{k}$
is smooth. Then, as in the proof of [Reference Esterov and Takeuchi7, Proposition 7.1], we can show that there exists a nonempty Zariski open subset
$\{h_{a,\unicode[STIX]{x1D6FC},I}=0\}\subset \unicode[STIX]{x1D70B}_{I}(Z_{\unicode[STIX]{x1D6FC},I})\subset (\mathbb{C}^{\ast })^{k}$
is smooth. Then, as in the proof of [Reference Esterov and Takeuchi7, Proposition 7.1], we can show that there exists a nonempty Zariski open subset
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},I}\subset \mathbb{C}^{n}$
such that the (possibly multivalued) function
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},I}\subset \mathbb{C}^{n}$
such that the (possibly multivalued) function
![]() $g_{a,\unicode[STIX]{x1D6FC},I}(x_{1},\ldots ,x_{k})$
on
$g_{a,\unicode[STIX]{x1D6FC},I}(x_{1},\ldots ,x_{k})$
on
![]() $\unicode[STIX]{x1D70B}_{I}(Z_{\unicode[STIX]{x1D6FC},I})\subset (\mathbb{C}^{\ast })^{k}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
$\unicode[STIX]{x1D70B}_{I}(Z_{\unicode[STIX]{x1D6FC},I})\subset (\mathbb{C}^{\ast })^{k}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
![]() $a\in \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},I}\subset \mathbb{C}^{n}$
. This completes the proof.◻
$a\in \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},I}\subset \mathbb{C}^{n}$
. This completes the proof.◻
Corollary 4.2. In the situation of Proposition 4.1, assume moreover that for the Newton polytope
![]() $NP(h)\subset \mathbb{R}^{n}$
of
$NP(h)\subset \mathbb{R}^{n}$
of
![]() $h$
, we have
$h$
, we have
![]() $\operatorname{dim}NP(h)=n$
. Then, there exists
$\operatorname{dim}NP(h)=n$
. Then, there exists
![]() $a\in \operatorname{Int}NP(h)$
such that the restriction
$a\in \operatorname{Int}NP(h)$
such that the restriction
![]() $g_{a}|_{Z_{\unicode[STIX]{x1D6FC}}}:Z_{\unicode[STIX]{x1D6FC}}\longrightarrow \mathbb{C}$
of
$g_{a}|_{Z_{\unicode[STIX]{x1D6FC}}}:Z_{\unicode[STIX]{x1D6FC}}\longrightarrow \mathbb{C}$
of
![]() $g_{a}$
to
$g_{a}$
to
![]() $Z_{\unicode[STIX]{x1D6FC}}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
$Z_{\unicode[STIX]{x1D6FC}}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Now, let
![]() $Q_{1},\ldots ,Q_{l}$
be Laurent polynomials on
$Q_{1},\ldots ,Q_{l}$
be Laurent polynomials on
![]() $T=(\mathbb{C}^{\ast })^{n}$
, and for
$T=(\mathbb{C}^{\ast })^{n}$
, and for
![]() $1\leqslant i\leqslant l$
, denote by
$1\leqslant i\leqslant l$
, denote by
![]() $\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n}$
the Newton polytope
$\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n}$
the Newton polytope
![]() $NP(Q_{i})$
of
$NP(Q_{i})$
of
![]() $Q_{i}$
. Set
$Q_{i}$
. Set
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{l}$
. Then, by Corollary 4.2, we obtain the following result which might be of independent interest.
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{l}$
. Then, by Corollary 4.2, we obtain the following result which might be of independent interest.
Theorem 4.3. Let
![]() ${\mathcal{L}}$
be a nontrivial local system of rank one on
${\mathcal{L}}$
be a nontrivial local system of rank one on
![]() $T=(\mathbb{C}^{\ast })^{n}$
. Assume that for any
$T=(\mathbb{C}^{\ast })^{n}$
. Assume that for any
![]() $1\leqslant i\leqslant l$
, we have
$1\leqslant i\leqslant l$
, we have
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}_{i}=n$
, and the subvariety
$\operatorname{dim}\unicode[STIX]{x1D6E5}_{i}=n$
, and the subvariety
of
![]() $T$
is a nondegenerate complete intersection. Then, for any
$T$
is a nondegenerate complete intersection. Then, for any
![]() $1\leqslant i\leqslant l$
, we have the concentration
$1\leqslant i\leqslant l$
, we have the concentration
Moreover, we have
Proof. We prove the assertion by induction on
![]() $i$
. For
$i$
. For
![]() $i=0$
, we have
$i=0$
, we have
![]() $Z_{i}=T$
and the assertion is obvious. Since
$Z_{i}=T$
and the assertion is obvious. Since
![]() $Z_{i}\subset T$
is affine, by Artin’s vanishing theorem, we have the concentration
$Z_{i}\subset T$
is affine, by Artin’s vanishing theorem, we have the concentration
On the other hand, by Corollary 4.2, there exists
![]() $a_{i}\in \operatorname{Int}NP(Q_{i})\subset \mathbb{R}^{n}$
such that the real-valued function
$a_{i}\in \operatorname{Int}NP(Q_{i})\subset \mathbb{R}^{n}$
such that the real-valued function
has only isolated nondegenerate (Morse type) critical points. Note that the Morse index of
![]() $g_{i}$
at each critical point is
$g_{i}$
at each critical point is
![]() $\operatorname{dim}Z_{i-1}=n-i+1$
. Let
$\operatorname{dim}Z_{i-1}=n-i+1$
. Let
![]() $\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of the
$\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of the
![]() $n$
-dimensional polytope
$n$
-dimensional polytope
![]() $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
![]() $\mathbb{R}^{n}$
, and let
$\mathbb{R}^{n}$
, and let
![]() $\unicode[STIX]{x1D6F4}$
be its smooth subdivision. We denote by
$\unicode[STIX]{x1D6F4}$
be its smooth subdivision. We denote by
![]() $X_{\unicode[STIX]{x1D6F4}}$
the toric variety associated to
$X_{\unicode[STIX]{x1D6F4}}$
the toric variety associated to
![]() $\unicode[STIX]{x1D6F4}$
. Then,
$\unicode[STIX]{x1D6F4}$
. Then,
![]() $X_{\unicode[STIX]{x1D6F4}}$
is a smooth compactification of
$X_{\unicode[STIX]{x1D6F4}}$
is a smooth compactification of
![]() $T$
such that
$T$
such that
![]() $D=X_{\unicode[STIX]{x1D6F4}}\setminus T$
is a normal crossing divisor in it. By our assumption, the closures
$D=X_{\unicode[STIX]{x1D6F4}}\setminus T$
is a normal crossing divisor in it. By our assumption, the closures
![]() $\overline{Z_{i-1}},\overline{Z_{i}}\subset X_{\unicode[STIX]{x1D6F4}}$
of
$\overline{Z_{i-1}},\overline{Z_{i}}\subset X_{\unicode[STIX]{x1D6F4}}$
of
![]() $Z_{i-1},Z_{i}$
in
$Z_{i-1},Z_{i}$
in
![]() $X_{\unicode[STIX]{x1D6F4}}$
are smooth. Moreover, they intersect
$X_{\unicode[STIX]{x1D6F4}}$
are smooth. Moreover, they intersect
![]() $D$
, etc. transversely. Let
$D$
, etc. transversely. Let
![]() $U$
be a sufficiently small tubular neighborhood of
$U$
be a sufficiently small tubular neighborhood of
![]() $\overline{Z_{i}}\cap D$
in
$\overline{Z_{i}}\cap D$
in
![]() $\overline{Z_{i-1}}$
. Then, by [Reference Zaharia28, Section 3.5] (see also [Reference Libgober and Sperber16]), for any
$\overline{Z_{i-1}}$
. Then, by [Reference Zaharia28, Section 3.5] (see also [Reference Libgober and Sperber16]), for any
![]() $t\in \mathbb{R}_{+}$
, there exist isomorphisms
$t\in \mathbb{R}_{+}$
, there exist isomorphisms
Moreover, the level set
![]() $g_{i}^{-1}(t)\cap (Z_{i-1}\setminus U)$
of
$g_{i}^{-1}(t)\cap (Z_{i-1}\setminus U)$
of
![]() $g_{i}$
in
$g_{i}$
in
![]() $Z_{i-1}\setminus U$
is compact in
$Z_{i-1}\setminus U$
is compact in
![]() $Z_{i-1}$
and intersects
$Z_{i-1}$
and intersects
![]() $\unicode[STIX]{x2202}U$
transversely for any
$\unicode[STIX]{x2202}U$
transversely for any
![]() $t\in \mathbb{R}_{+}$
. Hence, for
$t\in \mathbb{R}_{+}$
. Hence, for
![]() $t\gg 0$
, we have isomorphisms
$t\gg 0$
, we have isomorphisms
Moreover, for
![]() $0<t\ll 1$
, we have isomorphisms
$0<t\ll 1$
, we have isomorphisms
When
![]() $t\in \mathbb{R}$
decreases passing through one of the critical values of
$t\in \mathbb{R}$
decreases passing through one of the critical values of
![]() $g_{i}$
, only the dimensions of
$g_{i}$
, only the dimensions of
![]() $H^{n-i+1}(\{g_{i}<t\};{\mathcal{L}})$
and
$H^{n-i+1}(\{g_{i}<t\};{\mathcal{L}})$
and
![]() $H^{n-i}(\{g_{i}<t\};{\mathcal{L}})$
may change, and the other cohomology groups
$H^{n-i}(\{g_{i}<t\};{\mathcal{L}})$
may change, and the other cohomology groups
![]() $H^{j}(\{g_{i}<t\};{\mathcal{L}})$
$H^{j}(\{g_{i}<t\};{\mathcal{L}})$
![]() $(j\not =n-i+1,n-i)$
remain the same. Then, by our induction hypothesis for
$(j\not =n-i+1,n-i)$
remain the same. Then, by our induction hypothesis for
![]() $i-1$
and Equation (4.5), we obtain the desired concentration
$i-1$
and Equation (4.5), we obtain the desired concentration
Moreover, the last assertion follows from Theorem 2.4. This completes the proof. ◻
From now on, assume also that the
![]() $l$
-tuple
$l$
-tuple
![]() $(Q_{1},\ldots ,Q_{l})$
is strongly nondegenerate, and
$(Q_{1},\ldots ,Q_{l})$
is strongly nondegenerate, and
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}_{l}=n$
. Let
$\operatorname{dim}\unicode[STIX]{x1D6E5}_{l}=n$
. Let
![]() $T=\bigsqcup _{\unicode[STIX]{x1D6FC}}Z_{\unicode[STIX]{x1D6FC}}$
be the algebraic stratification of
$T=\bigsqcup _{\unicode[STIX]{x1D6FC}}Z_{\unicode[STIX]{x1D6FC}}$
be the algebraic stratification of
![]() $T$
associated to the hypersurface
$T$
associated to the hypersurface
![]() $S=\bigcup _{i=1}^{l-1}Q_{i}^{-1}(0)\subset T$
, and set
$S=\bigcup _{i=1}^{l-1}Q_{i}^{-1}(0)\subset T$
, and set
![]() $M=T\setminus S$
. Then, by Corollary 4.2, there exists
$M=T\setminus S$
. Then, by Corollary 4.2, there exists
![]() $a\in \operatorname{Int}(\unicode[STIX]{x1D6E5}_{l})$
such that the restriction of the (possibly multivalued) function
$a\in \operatorname{Int}(\unicode[STIX]{x1D6E5}_{l})$
such that the restriction of the (possibly multivalued) function
![]() $Q_{l}(x)x^{-a}$
to
$Q_{l}(x)x^{-a}$
to
![]() $Z_{\unicode[STIX]{x1D6FC}}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
$Z_{\unicode[STIX]{x1D6FC}}$
has only isolated nondegenerate (i.e., Morse type) critical points for any
![]() $\unicode[STIX]{x1D6FC}$
. In particular, it has only stratified isolated singular points. We fix such
$\unicode[STIX]{x1D6FC}$
. In particular, it has only stratified isolated singular points. We fix such
![]() $a\in \operatorname{Int}(\unicode[STIX]{x1D6E5}_{l})$
and define a real-valued function
$a\in \operatorname{Int}(\unicode[STIX]{x1D6E5}_{l})$
and define a real-valued function
![]() $g:T\longrightarrow \mathbb{R}_{+}$
by
$g:T\longrightarrow \mathbb{R}_{+}$
by
![]() $g(x)=|Q_{l}(x)x^{-a}|$
. For
$g(x)=|Q_{l}(x)x^{-a}|$
. For
![]() $t\in \mathbb{R}_{+}$
, we set also
$t\in \mathbb{R}_{+}$
, we set also
Then, we have the following result.
Lemma 4.4. Let
![]() ${\mathcal{L}}$
be a local system on
${\mathcal{L}}$
be a local system on
![]() $M=T\setminus S$
. Then, for any
$M=T\setminus S$
. Then, for any
![]() $c>0$
, there exists a sufficiently small
$c>0$
, there exists a sufficiently small
![]() $0<\unicode[STIX]{x1D700}\ll 1$
such that we have the concentration
$0<\unicode[STIX]{x1D700}\ll 1$
such that we have the concentration
Proof. Let
![]() $\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of the
$\unicode[STIX]{x1D6F4}_{0}$
be the dual fan of the
![]() $n$
-dimensional polytope
$n$
-dimensional polytope
![]() $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
![]() $\mathbb{R}^{n}$
, and let
$\mathbb{R}^{n}$
, and let
![]() $\unicode[STIX]{x1D6F4}$
be its smooth subdivision. We denote by
$\unicode[STIX]{x1D6F4}$
be its smooth subdivision. We denote by
![]() $X_{\unicode[STIX]{x1D6F4}}$
the toric variety associated to
$X_{\unicode[STIX]{x1D6F4}}$
the toric variety associated to
![]() $\unicode[STIX]{x1D6F4}$
. Then,
$\unicode[STIX]{x1D6F4}$
. Then,
![]() $X_{\unicode[STIX]{x1D6F4}}$
is a smooth compactification of
$X_{\unicode[STIX]{x1D6F4}}$
is a smooth compactification of
![]() $T$
such that
$T$
such that
![]() $D=X_{\unicode[STIX]{x1D6F4}}\setminus T$
is a normal crossing divisor in it. By the strong nondegeneracy of
$D=X_{\unicode[STIX]{x1D6F4}}\setminus T$
is a normal crossing divisor in it. By the strong nondegeneracy of
![]() $(Q_{1},\ldots ,Q_{l})$
, the hypersurface
$(Q_{1},\ldots ,Q_{l})$
, the hypersurface
![]() $\overline{Q_{l}^{-1}(0)}\subset X_{\unicode[STIX]{x1D6F4}}$
intersects
$\overline{Q_{l}^{-1}(0)}\subset X_{\unicode[STIX]{x1D6F4}}$
intersects
![]() $D$
, etc. transversely. Let
$D$
, etc. transversely. Let
![]() $U$
be a sufficiently small tubular neighborhood of
$U$
be a sufficiently small tubular neighborhood of
![]() $\overline{Q_{l}^{-1}(0)}\cap D$
in
$\overline{Q_{l}^{-1}(0)}\cap D$
in
![]() $X_{\unicode[STIX]{x1D6F4}}$
, and for
$X_{\unicode[STIX]{x1D6F4}}$
, and for
![]() $t\in \mathbb{R}_{+}$
, set
$t\in \mathbb{R}_{+}$
, set
![]() $M_{t}^{\prime }=M_{t}\setminus U$
. Then, by [Reference Zaharia28, Section 3.5], for any
$M_{t}^{\prime }=M_{t}\setminus U$
. Then, by [Reference Zaharia28, Section 3.5], for any
![]() $t\in \mathbb{R}_{+}$
, there exist isomorphisms
$t\in \mathbb{R}_{+}$
, there exist isomorphisms
Moreover, the level set
![]() $g^{-1}(t)\cap (T\setminus U)$
of
$g^{-1}(t)\cap (T\setminus U)$
of
![]() $g$
in
$g$
in
![]() $T\setminus U$
is compact in
$T\setminus U$
is compact in
![]() $T$
and intersects
$T$
and intersects
![]() $\unicode[STIX]{x2202}U$
transversely for any
$\unicode[STIX]{x2202}U$
transversely for any
![]() $t\in \mathbb{R}_{+}$
. For
$t\in \mathbb{R}_{+}$
. For
![]() $c>0$
, let
$c>0$
, let
![]() $p_{1},\ldots ,p_{r}\in T\setminus g^{-1}(0)=T\setminus Q_{l}^{-1}(0)$
be the stratified isolated singular points of the function
$p_{1},\ldots ,p_{r}\in T\setminus g^{-1}(0)=T\setminus Q_{l}^{-1}(0)$
be the stratified isolated singular points of the function
![]() $h(x)=Q_{l}(x)x^{-a}$
in
$h(x)=Q_{l}(x)x^{-a}$
in
![]() $T$
such that
$T$
such that
![]() $g(p_{i})=|h(p_{i})|=c$
. Note that we have
$g(p_{i})=|h(p_{i})|=c$
. Note that we have
Then, there exist small open balls
![]() $B_{i}$
centered at
$B_{i}$
centered at
![]() $p_{i}$
in
$p_{i}$
in
![]() $T$
and
$T$
and
![]() $0<\unicode[STIX]{x1D700}\ll 1$
such that we have isomorphisms
$0<\unicode[STIX]{x1D700}\ll 1$
such that we have isomorphisms
For
![]() $1\leqslant i\leqslant r$
, by taking a local branch
$1\leqslant i\leqslant r$
, by taking a local branch
![]() $\log h$
of the logarithm of the function
$\log h$
of the logarithm of the function
![]() $h\not =0$
on a neighborhood of
$h\not =0$
on a neighborhood of
![]() $p_{i}\in T\setminus h^{-1}(0)$
, we set
$p_{i}\in T\setminus h^{-1}(0)$
, we set
![]() $f_{i}=\log h-\log h(p_{i})$
. Then,
$f_{i}=\log h-\log h(p_{i})$
. Then,
![]() $f_{i}$
has also a stratified isolated singular point at
$f_{i}$
has also a stratified isolated singular point at
![]() $p_{i}$
. Let
$p_{i}$
. Let
![]() $F_{i}\subset B_{i}$
be the Milnor fiber of
$F_{i}\subset B_{i}$
be the Milnor fiber of
![]() $f_{i}$
at
$f_{i}$
at
![]() $p_{i}\in f_{i}^{-1}(0)$
. Then, for any
$p_{i}\in f_{i}^{-1}(0)$
. Then, for any
![]() $1\leqslant i\leqslant r$
, by shrinking
$1\leqslant i\leqslant r$
, by shrinking
![]() $B_{i}$
if necessary, we can easily prove the isomorphisms
$B_{i}$
if necessary, we can easily prove the isomorphisms
Let
![]() $j:M=T\setminus S{\hookrightarrow}T$
be the inclusion. Since the Milnor fibers
$j:M=T\setminus S{\hookrightarrow}T$
be the inclusion. Since the Milnor fibers
![]() $F_{i}\subset B_{i}$
intersect each stratum
$F_{i}\subset B_{i}$
intersect each stratum
![]() $Z_{\unicode[STIX]{x1D6FC}}$
transversely, we have also isomorphisms
$Z_{\unicode[STIX]{x1D6FC}}$
transversely, we have also isomorphisms
where
![]() $\unicode[STIX]{x1D719}_{f_{i}}$
are Deligne’s vanishing cycle functors. Hence, by (the proof of) [Reference Dimca4, Proposition 6.1.1], the assertion follows from
$\unicode[STIX]{x1D719}_{f_{i}}$
are Deligne’s vanishing cycle functors. Hence, by (the proof of) [Reference Dimca4, Proposition 6.1.1], the assertion follows from
and the fact that
![]() $Rj_{\ast }{\mathcal{L}}$
and
$Rj_{\ast }{\mathcal{L}}$
and
![]() $\unicode[STIX]{x1D719}_{f_{i}}(Rj_{\ast }{\mathcal{L}})$
are perverse sheaves (up to some shifts). This completes the proof.◻
$\unicode[STIX]{x1D719}_{f_{i}}(Rj_{\ast }{\mathcal{L}})$
are perverse sheaves (up to some shifts). This completes the proof.◻
5 A new vanishing theorem
Now, let
![]() $P_{1},\ldots ,P_{k}$
be Laurent polynomials on
$P_{1},\ldots ,P_{k}$
be Laurent polynomials on
![]() $T_{0}=(\mathbb{C}^{\ast })^{n-k}$
, and for
$T_{0}=(\mathbb{C}^{\ast })^{n-k}$
, and for
![]() $1\leqslant i\leqslant k$
, denote by
$1\leqslant i\leqslant k$
, denote by
![]() $\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n-k}$
the Newton polytope
$\unicode[STIX]{x1D6E5}_{i}\subset \mathbb{R}^{n-k}$
the Newton polytope
![]() $NP(P_{i})$
of
$NP(P_{i})$
of
![]() $P_{i}$
. Set
$P_{i}$
. Set
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$
. Let us set
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$
. Let us set
![]() $W=T_{0}\setminus \bigcup _{i=1}^{k}P_{i}^{-1}(0)$
, and for
$W=T_{0}\setminus \bigcup _{i=1}^{k}P_{i}^{-1}(0)$
, and for
![]() $(c,\widetilde{c})=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\in \mathbb{C}^{n}$
consider the local system
$(c,\widetilde{c})=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\in \mathbb{C}^{n}$
consider the local system
on
![]() $W$
.
$W$
.
Theorem 5.1. Assume that the
![]() $k$
-tuple of the Laurent polynomials
$k$
-tuple of the Laurent polynomials
![]() $(P_{1},\ldots ,P_{k})$
is strongly nondegenerate,
$(P_{1},\ldots ,P_{k})$
is strongly nondegenerate,
![]() $(c,\widetilde{c})=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \mathbb{Z}^{n}$
, and for any
$(c,\widetilde{c})=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \mathbb{Z}^{n}$
, and for any
![]() $1\leqslant i\leqslant k$
, we have
$1\leqslant i\leqslant k$
, we have
![]() $\operatorname{dim}\unicode[STIX]{x1D6E5}_{i}=n-k$
. Then, we have the concentration
$\operatorname{dim}\unicode[STIX]{x1D6E5}_{i}=n-k$
. Then, we have the concentration
Proof. Set
![]() $T=T_{0}\times (\mathbb{C}^{\ast })_{t_{1},\ldots ,t_{k}}^{k}\simeq (\mathbb{C}^{\ast })_{x,t}^{n}$
, and consider the Laurent polynomials
$T=T_{0}\times (\mathbb{C}^{\ast })_{t_{1},\ldots ,t_{k}}^{k}\simeq (\mathbb{C}^{\ast })_{x,t}^{n}$
, and consider the Laurent polynomials
on
![]() $T$
. For
$T$
. For
![]() $1\leqslant i\leqslant k$
, we set also
$1\leqslant i\leqslant k$
, we set also
We define a local system
![]() $\widetilde{{\mathcal{L}}}$
on
$\widetilde{{\mathcal{L}}}$
on
![]() $T$
by
$T$
by
Then,
![]() $Z_{k}\simeq W$
, and we have isomorphisms
$Z_{k}\simeq W$
, and we have isomorphisms
First, let us consider the case where
![]() $\widetilde{c}=(\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \mathbb{Z}^{k}$
. In this case, without loss of generality, we may assume that
$\widetilde{c}=(\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \mathbb{Z}^{k}$
. In this case, without loss of generality, we may assume that
![]() $\widetilde{c_{k}}\notin \mathbb{Z}$
. Then, by the Künneth formula, for
$\widetilde{c_{k}}\notin \mathbb{Z}$
. Then, by the Künneth formula, for
![]() $i=1,2,\ldots ,k-1$
, we have the vanishings
$i=1,2,\ldots ,k-1$
, we have the vanishings
Moreover, we can naturally identify
![]() $Z_{k-1}\subset T$
with
$Z_{k-1}\subset T$
with
![]() $(T_{0}\setminus \bigcup _{i=1}^{k-1}P_{i}^{-1}(0))$
$(T_{0}\setminus \bigcup _{i=1}^{k-1}P_{i}^{-1}(0))$
![]() $\times \,\mathbb{C}_{t_{k}}^{\ast }$
. Consider
$\times \,\mathbb{C}_{t_{k}}^{\ast }$
. Consider
![]() $\widetilde{P_{k}}$
as a Laurent polynomial on
$\widetilde{P_{k}}$
as a Laurent polynomial on
![]() $T_{1}=T_{0}\times \mathbb{C}_{t_{k}}^{\ast }\simeq (\mathbb{C}^{\ast })^{n-k+1}$
. Note that we have
$T_{1}=T_{0}\times \mathbb{C}_{t_{k}}^{\ast }\simeq (\mathbb{C}^{\ast })^{n-k+1}$
. Note that we have
![]() $\operatorname{dim}NP(\widetilde{P_{k}})=n-k+1=\operatorname{dim}T_{1}$
. By taking a sufficiently generic
$\operatorname{dim}NP(\widetilde{P_{k}})=n-k+1=\operatorname{dim}T_{1}$
. By taking a sufficiently generic
we define a real-valued function
![]() $g$
on
$g$
on
![]() $T_{1}=T_{0}\times \mathbb{C}_{t_{k}}^{\ast }$
by
$T_{1}=T_{0}\times \mathbb{C}_{t_{k}}^{\ast }$
by
Then, by applying Lemma 4.4 to the Morse function
![]() $g:T_{1}=T_{0}\times \mathbb{C}^{\ast }\longrightarrow \mathbb{R}$
and arguing as in the proof of Theorem 4.3, we obtain the desired concentration
$g:T_{1}=T_{0}\times \mathbb{C}^{\ast }\longrightarrow \mathbb{R}$
and arguing as in the proof of Theorem 4.3, we obtain the desired concentration
The proof for the remaining case where
![]() $(c,\widetilde{c})=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \mathbb{Z}^{n}$
and
$(c,\widetilde{c})=(c_{1},\ldots ,c_{n-k},\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\notin \mathbb{Z}^{n}$
and
![]() $\widetilde{c}=(\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\in \mathbb{Z}^{k}$
is similar. In this case,
$\widetilde{c}=(\widetilde{c_{1}},\ldots ,\widetilde{c_{k}})\in \mathbb{Z}^{k}$
is similar. In this case,
![]() $Z_{1}\subset T$
is isomorphic to the product
$Z_{1}\subset T$
is isomorphic to the product
![]() $Z_{1}^{\prime }\times (\mathbb{C}^{\ast })^{k-1}$
for a hypersurface
$Z_{1}^{\prime }\times (\mathbb{C}^{\ast })^{k-1}$
for a hypersurface
![]() $Z_{1}^{\prime }$
in
$Z_{1}^{\prime }$
in
![]() $T_{0}\times \mathbb{C}_{t_{1}}^{\ast }$
, and
$T_{0}\times \mathbb{C}_{t_{1}}^{\ast }$
, and
![]() $\widetilde{{\mathcal{L}}}$
is isomoprhic to the pullback of a local system on
$\widetilde{{\mathcal{L}}}$
is isomoprhic to the pullback of a local system on
![]() $T_{0}\times \mathbb{C}_{t_{1}}^{\ast }$
. Hence, by the Künneth formula and the proof of Theorem 4.3, we obtain the concentration
$T_{0}\times \mathbb{C}_{t_{1}}^{\ast }$
. Hence, by the Künneth formula and the proof of Theorem 4.3, we obtain the concentration
Repeating this argument with the help of Lemma 4.4 and the proof of Theorem 4.3, we obtain also
Then, the assertion is obtained by applying Artin’s vanishing theorem to the
![]() $(n-k)$
-dimensional affine variety
$(n-k)$
-dimensional affine variety
![]() $Z_{k}\subset T$
. This completes the proof.◻
$Z_{k}\subset T$
. This completes the proof.◻
Acknowledgments
We express our hearty gratitude to Professor N. Takayama for drawing our attention to this problem. Moreover, some discussions with Professor M. Yoshinaga were very useful during the preparation of this paper. We also thank the referee for giving us many valuable suggestions.