Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mizuta, Yoshihiro
and
Nagai, Toshitaka
1977.
Potential theoretic properties of the subdifferential of a convex function.
Hiroshima Mathematical Journal,
Vol. 7,
Issue. 1,
Calvert, Bruce
and
Picard, Colette
1978.
Opérateurs accrétifs et $\phi $-accrétifs dans un espace de Banach.
Hiroshima Mathematical Journal,
Vol. 8,
Issue. 1,
Attouch, Hédy
and
Picard, Colette
1979.
Problèmes variationnels et théorie du potentiel non linéaire.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 1,
Issue. 2,
p.
89.
Benilan, Philippe
and
Picard, Colette
1979.
Séminaire de Théorie du Potentiel Paris, No. 4.
Vol. 713,
Issue. ,
p.
1.
van Beusekom, Petra
1994.
ICPT ’91.
p.
179.
Stefanelli, Ulisse
2006.
Nonlocal quasivariational evolution problems.
Journal of Differential Equations,
Vol. 229,
Issue. 1,
p.
204.

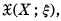 we discussed potential theoretic properties of the gradient
we discussed potential theoretic properties of the gradient 