Article contents
THE SECOND FUNDAMENTAL THEOREM OF INVARIANT THEORY FOR THE ORTHOSYMPLECTIC SUPERGROUP
Published online by Cambridge University Press: 04 December 2019
Abstract
The first fundamental theorem of invariant theory for the orthosymplectic supergroup scheme 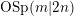 $\text{OSp}(m|2n)$ states that there is a full functor from the Brauer category with parameter
$\text{OSp}(m|2n)$ states that there is a full functor from the Brauer category with parameter  $m-2n$ to the category of tensor representations of
$m-2n$ to the category of tensor representations of 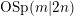 $\text{OSp}(m|2n)$. This has recently been proved using algebraic supergeometry to relate the problem to the invariant theory of the general linear supergroup. In this work, we use the same circle of ideas to prove the second fundamental theorem for the orthosymplectic supergroup. Specifically, we give a linear description of the kernel of the surjective homomorphism from the Brauer algebra to endomorphisms of tensor space, which commute with the orthosymplectic supergroup. The main result has a clear and succinct formulation in terms of Brauer diagrams. Our proof includes, as special cases, new proofs of the corresponding second fundamental theorems for the classical orthogonal and symplectic groups, as well as their quantum analogues, which are independent of the Capelli identities. The results of this paper have led to the result that the map from the Brauer algebra
$\text{OSp}(m|2n)$. This has recently been proved using algebraic supergeometry to relate the problem to the invariant theory of the general linear supergroup. In this work, we use the same circle of ideas to prove the second fundamental theorem for the orthosymplectic supergroup. Specifically, we give a linear description of the kernel of the surjective homomorphism from the Brauer algebra to endomorphisms of tensor space, which commute with the orthosymplectic supergroup. The main result has a clear and succinct formulation in terms of Brauer diagrams. Our proof includes, as special cases, new proofs of the corresponding second fundamental theorems for the classical orthogonal and symplectic groups, as well as their quantum analogues, which are independent of the Capelli identities. The results of this paper have led to the result that the map from the Brauer algebra 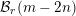 ${\mathcal{B}}_{r}(m-2n)$ to endomorphisms of
${\mathcal{B}}_{r}(m-2n)$ to endomorphisms of 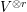 $V^{\otimes r}$ is an isomorphism if and only if
$V^{\otimes r}$ is an isomorphism if and only if 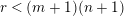 $r<(m+1)(n+1)$.
$r<(m+1)(n+1)$.
Information
- Type
- Article
- Information
- Copyright
- © 2019 Foundation Nagoya Mathematical Journal
Footnotes
This work has been supported by the Australian Research Council.
References
- 2
- Cited by


