Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kaji, Hajime
and
Yasukura, Osami
2004.
Projective geometry of Freudenthal's varieties of certain type.
Michigan Mathematical Journal,
Vol. 52,
Issue. 3,

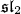 triples. Secondly for a graded decomposition of contact type
triples. Secondly for a graded decomposition of contact type 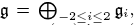 we show that the intersection of
we show that the intersection of 