1 Introduction
Optimality Theory (OT) was developed as a response to a ‘conceptual crisis at the center of phonological thought’ (Prince & Smolensky Reference Prince and Smolensky2004: 2). The problem with classical rule-based theory was not its inability to analyse emergent phonological patterns, but rather the lack of explanation for why phonological rules which do not have anything in common seem to cooperate and serve a single purpose. Various output constraints have been introduced since the early 1970s, but general conditions on their use have remained unclear, as they have been used sometimes as blockers and sometimes as triggers of phonological rules.
OT introduced constraints and constraint hierarchies, claiming that rules are unnecessary. The blocking–triggering inconsistency of constraints was resolved, but new problems arose. The best-known challenge for OT is opacity, for which the number of proposed solutions is so large that a comprehensive overview would call for a monograph. All of these proposals require more complex mechanisms than simple reranking of violable constraints. However, any of those can cover just a subset of opacity phenomena. For example, local conjunction (Kirchner Reference Kirchner1996, Baković Reference Baković2000), comparative markedness (McCarthy Reference McCarthy2003), turbid output representations (Goldrick Reference Goldrick2000) and contrast-preserving constraints (Łubowicz Reference Łubowicz2012) are not relevant to counterbleeding opacity; intercandidate sympathy (McCarthy Reference McCarthy1999) and targeted constraints (Burzio Reference Burzio2001, Wilson Reference Wilson2001) cannot explain mutual feeding and chain shifts; output–output correspondence (Benua Reference Benua1997) is designed for morphological opacity only; and, while stratal OT (Bermúdez-Otero Reference Bermúdez-Otero1999, Kiparsky Reference Kiparsky2000) can formally account for any kind of opacity, in many cases it is difficult to justify multi-level analyses.
The most recent version of OT is Harmonic Serialism (HS). In HS, surface forms are generated from underlying forms in a series of optimising steps. At each step, a generated candidate can differ from the input in only one respect. The winner of each generate-and-evaluate step is submitted as the input to the next step. This loop continues until nothing can be done to improve harmony (Prince & Smolensky Reference Prince and Smolensky2004: 6, McCarthy Reference McCarthy2008, Reference McCarthy2010a, Reference McCarthyb).
Unfortunately, serialism is not the key to solving the opacity problem. Despite its similarities to rule-based derivation, the HS version of OT is not successful at handling opacity. In the case of counterfeeding, the derivation will not converge until all possible processes that improve harmony have been applied. In the case of counterbleeding opacity, on the other hand, the derivation converges too early (McCarthy Reference McCarthy2000).
There have also been attempts to account for opacity in HS, yet these too are only able to address certain types of opacity. They also modify some basic assumptions of HS. For instance, Hauser et al. (Reference Hauser, Hughto, Somerday, Albright and Fullwood2015) propose a special kind of faithfulness constraint to handle counterfeeding opacity – UO-faithfulness. UO-faithfulness constraints compare candidates with the underlying form, not with the input form of the current derivational step. UO-faithfulness effectively preserves underlying contrast, yet this solution is not available if the property to be preserved is not present in the underlying form, for example in opaque stress placement preceding epenthesis in Tiberian Hebrew, where input /CVCC/ surfaces as [ˈCVCVC], not as [CVˈCVC], even though final closed syllables are normally stressed (Idsardi Reference Idsardi2000). Counterbleeding opacity is even more difficult to account for. Although cases where syllabification is involved can be analysed if the operations available to the generator are decomposed into more primitive operations (Torres-Tamarit Reference Torres-Tamarit2016), there is no general solution to the opacity problem in OT.
Attempts to account for opacity within OT have led to a situation similar to that of several decades ago, when attempts were made to formalise blocking, a challenging task for rule-based theories, using for example the Revised Alternation Condition (Kiparsky Reference Kiparsky and Fujimura1973a), the Elsewhere Condition, and disjunctive blocking (Kiparsky Reference Kiparsky, Anderson and Kiparsky1973b, Halle & Idsardi Reference Halle, Idsardi and Roca1997).
Both blocking and opacity are common in languages, and an adequate theory of phonology should be able to account for them without any modifications. Work by Idsardi (Reference Idsardi2000), Calabrese (Reference Calabrese2005) and Baković (Reference Baković2013) has concluded that there is no crucial evidence to decide in favour of rules or constraints.
In the current paper, a theory that adopts the best of both approaches is introduced: processes and relations (PRR) theory. In PRR theory, every phonological process consists of a triggering markedness constraint and a repair. Markedness constraints are violable by surface forms, exactly as in OT. But, unlike OT, complete processes interact, not markedness and faithfulness constraints independently (see §2). Phonological processes may be in a feeding or bleeding relation (Kiparsky Reference Kiparsky, Bach and Harms1968). Both opacity and blocking effects are consequences of these two basic relations and the order of application of the processes. Bleeding, feeding, counterbleeding and counterfeeding are discussed in §3, and more complicated relations (e.g. Duke-of-York derivations, mutual feeding and mutual bleeding, derived environment effects and blocking) in §4 and §5. I will focus primarily on formal relations between processes; full case studies, detailed definitions of constraints and establishing the right set of processes are beyond the scope of this paper.
2 Processes as pairs of constraints
2.1 General description of processes
Markedness and faithfulness constraints in OT are functionally very different, and a theory that treats them alike may not be ideal. Markedness (M) and faithfulness (F) constraints operate in pairs, and the need to satisfy an M constraint triggers a change that causes a violation of an F constraint. F constraints are violated only when this improves harmony for markedness, and are never triggers; their usual informal meaning is ‘do not do anything’, which cannot initiate an action in any logically meaningful sense. If an M constraint dominates a relevant F constraint, a change occurs. Such pairs, where an M constraint functions as a trigger and a F constraint denotes a suitable repair (R), constitute minimal phonological processes, represented schematically in (1).
(1)

In standard OT analyses, there are various M constraints whose satisfaction does not imply violations of F constraints, namely the prosodic M constraints (e.g. FootBinarity, Trochaic, Onset and NoCoda). However, satisfying a prosodic M constraint is not possible without some change. Input forms are usually neither syllabified nor footed – the structure has to be built. Consequently, output candidates have more structure than the input form, and therefore violate a constraint against adding prosodic constituents, say Dep(structure) (cf. Prince & Smolensky Reference Prince and Smolensky2004: 30, n. 13).Footnote 1 In addition, F constraints that demand faithfulness between output forms (including base and reduplicant) function in OT analyses as M constraints; for example, in Paamese (Russell Reference Russell, Archangeli and Terry Langendoen1997), the base form /luhi/ reduplicates as [luhu-luhu] ‘plant’, because /i/ changes to [u] in non-final positions, and base–reduplicant identity triggers the same change in the base.
Positional faithfulness (PF) constraints are another type of F constraint in OT whose validity has been questioned. Formally, PF constraints can be replaced by positional markedness (PM) constraints. For example, a factorial typology including a PF constraint, such as Ident[vce]ons, Ident[vce] and *VcdObstr (from Beckman Reference Beckman1998), generates the same output patterns as a typology with the PM constraint *VcdCoda instead of Ident[vce]ons. PF constraints demand preservation of lexical contrast in prominent positions; corresponding PM constraints prohibit non-prominent features in non-prominent positions. To avoid referring to non-prominent positions, these PM constraints can be reformulated as ‘if prominent feature, then in prominent position’. For example, *VcdCoda can be reformulated as ‘if voiced obstruent, then in onset position’.Footnote 2
As a process, an M–R pair consists of two parts: it has a structural description as well as a structural change, which makes it similar to a phonological rule. However, classical rules are language-specific, while M constraints are universal. I also assume that repairs available for each M constraint are universally determined, an idea also found in OT (e.g. Lombardi Reference Lombardi and Lombardi2001, Steriade Reference Steriade, Hanson and Inkelas2009).
A repair can be switched on or off in particular languages. Any repair which is switched on actualises a process. A child acquiring a language has to figure out which M constraints are active (i.e. need to be satisfied) in that language. The child has to switch off all other repairs. The switching-off of repairs is comparable with the constraint-demotion algorithm in OT (Tesar & Smolensky Reference Tesar and Smolensky1998). In OT terms, to switch a repair off means to demote an M constraint below an F constraint, but in OT, all F constraints – that is, all kinds of repairs – are accessible without restrictions.
Calabrese (Reference Calabrese2005) proposes a theory of M constraints and triggered repairs, and also discusses both process ordering and blocking. In his theory, negative M constraints and rules interact. Rules are positive instructions that a given structure must be modified in a given way, but M constraints have many universally possible ranked repairs. M constraints trigger repairs, or block the application of processes (similarly to the approach found in Paradis Reference Paradis1988). The highest-ranked repair is always attempted first; the next one applies only when a licit outcome cannot be produced otherwise.
The theory presented in the following sections can be considered as a further development of Calabrese's theory. The goal is to define different interactions between phonological processes. Several questions about processes will be left open here; for example, how to integrate positional constraints (possibly, processes can be actualised only for certain phonological positions) or how to take markedness hierarchies into account (conceivably, repairs that insert segments can be defined unambiguously by means of markedness hierarchies). To the best of my understanding, these issues do not cast doubt on the foundations of the theory.
2.2 Universality of repairs
In this section, I will explain an important property of repairs, to ensure a better understanding of interactions. It follows from the architecture of standard OT that, within one invariable grammar, an M constraint can never be satisfied using different repairs. Even if many suitable F constraints are ranked below the M constraint, only the lowest-ranking of them will be violated. To allow any additional method to satisfy the M constraint, some other M constraint must be involved.
For example, *σ μμμ, a constraint against trimoraic syllables, may be satisfied by degemination, which violates Max(C)μ, or by long-vowel shortening, which violates Max(V)μ. However, no language permits both ways of satisfying *σ μμμ. If Max(V)μ is ranked higher than Max(C)μ, then the coda consonant will lose its mora; if Max(C)μ is ranked higher, then the long vowel will shorten. Both strategies will emerge within one grammar if another M constraint triggers the alternative repair. In the case of satisfying *σ μμμ, a constraint against long high vowels, *LongHigh (from Baković Reference Baković2007), may function as such a trigger. If these four constraints form the hierarchy *σ μμμ, *LongHigh ⪼ Max(V)μ ⪼ Max(C)μ, then *σ μμμ is satisfied by coda shortening, except in superheavy syllables with long high vowels, where it is satisfied by vowel shortening. However, vowel shortening is actually triggered by *LongHigh – that it also satisfies *σ μμμ is just a coincidence. The repair for *σ μμμ in this system is still Max(C)μ; this constraint must be ranked lower than *σ μμμ. Max(V)μ may be ranked higher than *σ μμμ if *LongHigh is ranked even higher.
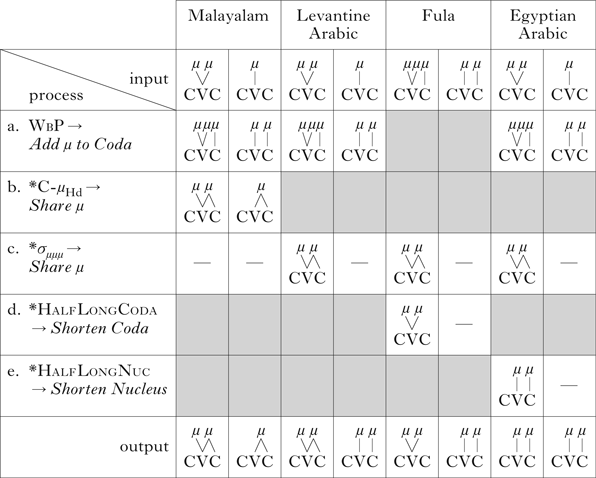
The question now arises whether there exists only one repair for every M constraint universally, so that a given M constraint is repaired in the same way in every language where the M constraint is active. Let us further analyse the apparent repair strategies of *σ μμμ. Many methods to satisfy *σ μμμ are considered by Broselow et al. (Reference Broselow, Chen and Huffman1997), who conclude that four types of languages exist: Hindi allows trimoraic syllables, Malayalam shares every coda mora with the nucleus, even in CVC syllables, Levantine Arabic shares the coda mora only in CVVC syllables and Egyptian Arabic shortens the vowel in CVVC syllables. This factorial typology is computed using the three M constraints σ μμμ (‘syllables are maximally bimoraic’), *Shared-μ (‘moras are linked to single segments’) and *C-μ Hd (‘the head of a mora is a vowel’), together with the F constraint Faith-μ, which is violated when the number of moras linked to the input segment and the number of moras linked to the corresponding output segment are not equal (Broselow et al. Reference Broselow, Chen and Huffman1997).
I will add one further type of language to the typology, those which satisfy *σ μμμ by degemination (Paradis Reference Paradis1988, Baković Reference Baković and Akinlabi1995). Fula, which I consider in §2.3, is such a language. Broselow et al. were actually investigating a subset of strategies to satisfy Weight-by-Position (WbyP), a widely used constraint that requires all codas to be moraic. Thus their analysis does not include inputs with trimoraic syllables (except Malayalam geminates). Furthermore, they do not consider candidates with non-moraic codas, because they assume WbyP to be at the top of the hierarchy. If we add WbyP and candidates with non-moraic codas to the system, the number of possible output patterns increases to ten. Analysing these and searching for real-language examples would require a thorough separate study. Fortunately, this is not essential for my aim here, which is to show that it is possible to generate the ‘homogeneity of target, heterogeneity of process’ effect without freely rerankable F constraints.
Factorial typologies in OT are not an easy way to predict which patterns cannot occur in languages, because F constraints can be freely added to the typologies. It cannot be determined which repair will be used for which M constraint. In Broselow et al. (Reference Broselow, Chen and Huffman1997), the Egyptian Arabic pattern (long-vowel shortening) emerges, because WbyP demands that coda consonants are moraic; however, this would generate trimoraic syllables, which cannot be repaired by mora sharing, since the constraint against shared moras is relatively high-ranked. The only possibility left is vowel shortening (the corresponding OT hierarchy is WbyP, *σ μμμ, *Shared-μ ⪼ Faith-μ). The problem is that we are free to add a candidate without a coda consonant, a resyllabified candidate, a methathetic candidate or anything else. Every one of those can be an actual output if the corresponding F constraint is sufficiently low-ranked; see (2), where Xμ = moraic segment and X = non-moraic segment.
(2)

I have been unable to find any languages that delete codas in the context of superheavy syllables or use metathesis to avoid such syllables. In at least one language, Finnish, certain CVVC sequences are syllabified as .CV.VC., and VV sequences at similar positions as .VV., but this difference in syllabification is due to the avoidance of stressed light syllables, and does not count as a repair strategy for *σ μμμ (see Anttila & Tachikawa Shapiro Reference Anttila and Shapiro2017).
The ‘too many solutions problem’ is well known in OT (e.g. Lombardi Reference Lombardi and Lombardi2001, Steriade Reference Steriade, Hanson and Inkelas2009). In HS, the problem can be resolved in particular situations where positional faithfulness is involved. However, this solution needs new types of PF constraints (Jesney Reference Jesney2011). Furthermore, syllable-building operations must be treated as unfaithful, i.e. as autonomous operations that cannot occur together with other operations at the same derivational stage. This contrasts with the general view, that syllabification is faithful. A single modification in HS is generally defined in terms of a single violation of a ‘basic’ faithfulness constraint, and syllabification does not add violations to any faithfulness constraints (McCarthy Reference McCarthy2010b, Reference McCarthy2016). It is possible that syllabification and resyllabification in HS should be dealt with differently; see Torres-Tamarit (Reference Torres-Tamarit2016), who treats mora insertion in certain cases as a faithful operation. What counts in HS as ‘a single violation of a basic faithfulness constraint’ is still a matter of debate.
In PRR theory, the question of ‘single violations’ does not arise, since, in OT terms, a repair may violate several F constraints. If in all languages an active M constraint is satisfied by the same subset of basic operations, then all these basic operations together form one single repair. If some languages need only a subset of these operations, the minimal subset of universally needed operations is the repair of the M constraint.
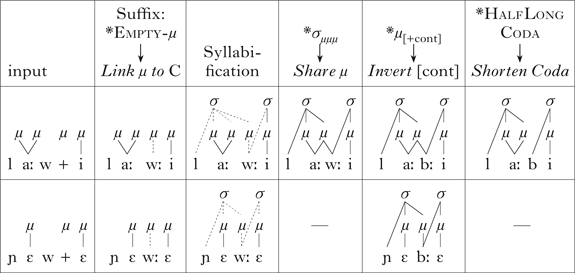
The universal repair for WbyP most likely consists of two operations: inserting a mora into the syllable, and linking it to the coda consonant (Add μ to Coda); see Table Ia. In languages in which WbyP is active, CVC syllables are generally heavy. Thus WbyP is universally not satisfied by mora sharing. Linking the coda to its own mora inevitably violates *C-μ Hd, the constraint proposed by Broselow et al. (Reference Broselow, Chen and Huffman1997) to analyse Malayalam. Malayalam satisfies *C-μ Hd by mora sharing, as in (b), and this may well be the universal repair for this constraint. The universal repair for *σ μμμ is also mora sharing (between the coda and the nucleus, as in (c)), as this is the only available repair that preserves lexical length contrasts. Mora sharing, in turn, is repaired by delinking the shared mora from the coda consonant, as in (d). Delinking from the vowel would generate syllables with non-moraic nuclei (but moraic codas) in the case of CVC syllables, which can hardly be an outcome of a universal process. I use *HalfLongCoda instead of *Shared-μ, because in certain languages (e.g. Icelandic; see Árnason Reference Árnason2011), diphthongs are shortened in closed syllables, and I assume that short diphthongs consist of two vowels sharing one mora. So far, no processes have been found which shorten a long vowel or diphthong in a superheavy syllable. It is possible that a constraint against half-long nuclei also exists, as in (e) (Kirchner Reference Kirchner1997 proposes a constraint against half-long vowels, but for different structures).
Table I Avoiding trimoraic syllables in different languages. A grey cell denotes an inactive process, and ‘–’ indicates that a process does not apply because the triggering M constraint is not violated.
Most OT hierarchies can easily be modified in the way described here: the hierarchy of M and F constraints is replaced with ordered processes (i.e. M constraints that trigger repairs). A similar point is made in Baković (Reference Baković2013), but in a different context.
The relations between processes are best represented as a schema, as in Fig. 1. Note that the schema does not indicate the order of application of the processes, just the relations between them. They may apply in different sequences in different languages. One process may even apply many times if it is triggered by some other process (triggering is discussed in §5). In the schema, every repair is placed directly under its M constraint. The M constraint and its repair are connected with an arrow. All the other arrows indicate relations between processes. The directions of relational arrows are of no importance here (except that they are always pointing from repairs towards M constraints). They are labelled with a minus or a plus sign. Minus indicates that the repair increases violations of the M constraint, and plus indicates that the repair is able to satisfy the M constraint. Traditionally, such relations are referred to as ‘feeding’ and ‘bleeding’ respectively (after Kiparsky Reference Kiparsky, Bach and Harms1968).
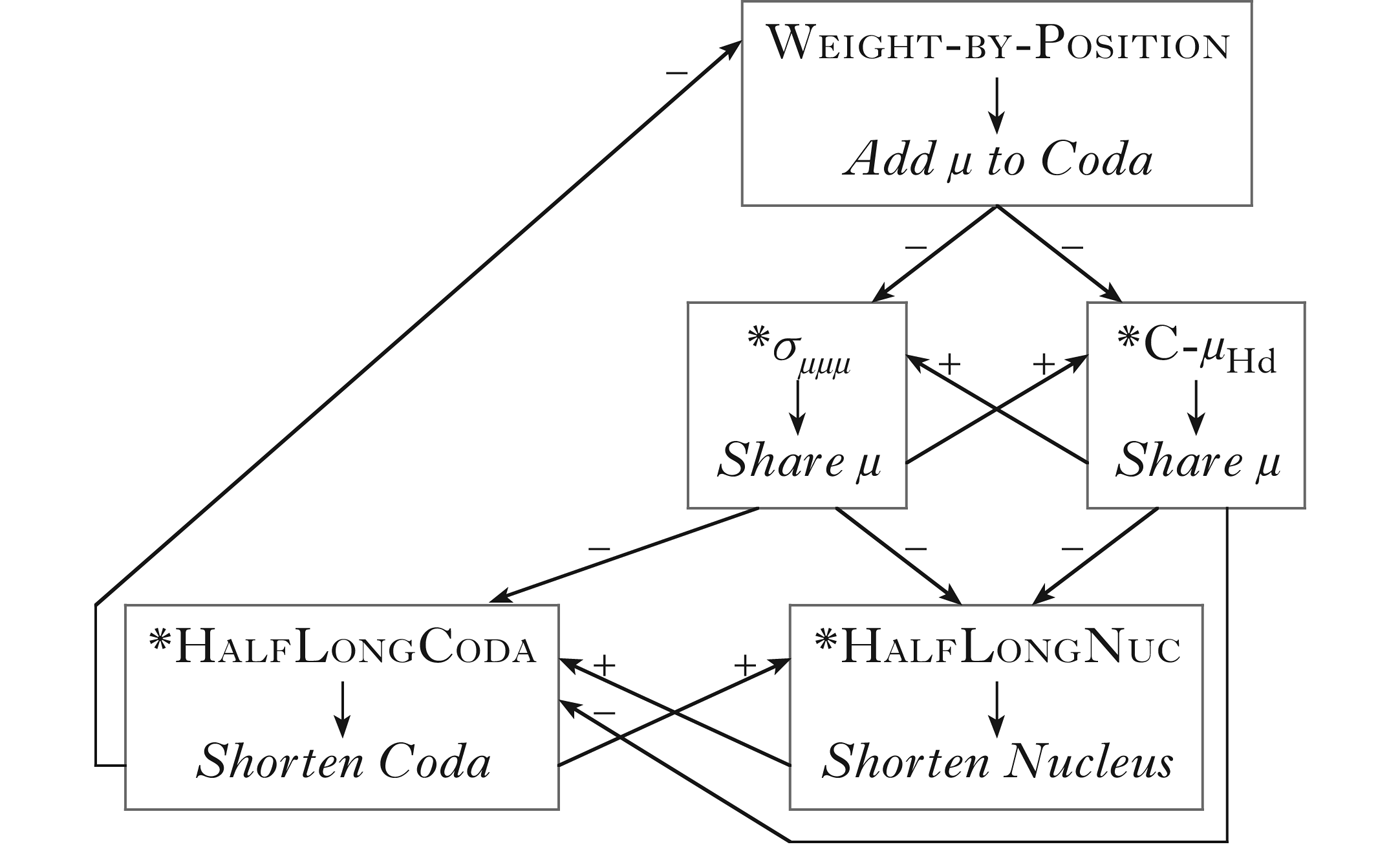
Figure 1 Relational schema showing bleeding and feeding relations between the processes that control the trimoraicity of syllables.
If we are interested in which alternative strategies exist to satisfy an M constraint, we have to look at the ‘+’-arrows that lead to the constraint, and at the ‘―’-arrows that lead away from its repair. Every ‘+’-arrow connects an M constraint with an alternative repair. For example, *HalfLongCoda can alternatively be satisfied by nucleus shortening, and *HalfLongNuc by coda shortening. Every ‘―’-arrow connects a repair with an M constraint to which it may generate violations (for example, Share μ generates violations to *HalfLongCoda, and also to *HalfLongNuc, if the syllable has a long vowel or diphthong). The repair of an M constraint may also be an alternative repair to the M constraint that triggered the first repair. For example, *σ μμμ is repaired by its own repair, mora sharing, which generates further violations to *HalfLongNuc and *HalfLongCoda, and therefore may be further repaired by the shortening of half-long segments.
(2) above shows that *σ μμμ and WbyP can be satisfied by coda deletion in OT. However, I am not aware of any OT analysis claiming that there are languages without closed syllables because of WbyP and *σ μμμ. Though counterintuitive, this claim would be formally correct within the framework of OT. The situation is similar with *σ μμμ in Malayalam. Malayalam shares every coda mora because of *C-μ Hd; the ranking of *σ μμμ is of no importance, and it would be misguided to conclude that Malayalam uses mora sharing to satisfy *σ μμμ.
In the phonological literature, there are many examples of ‘homogeneity of target, heterogeneity of process’. The ability to explain the phenomenon has been considered a benefit of OT, although it comes at a cost: the ‘too many solutions problem’. In PRR theory, this kind of overgeneration does not occur. However, if every repair needs its own M constraint, it may appear that too many M constraints are required.
Let us consider briefly another example: hiatus resolution. Languages use many different strategies to avoid hiatus: glide formation, vowel deletion, consonant epenthesis, elision and diphthongisation. Furthermore, several of these strategies may coexist in the same language (Casali Reference Casali1996). However, like the strategies to satisfy *σ μμμ, different strategies to resolve hiatus also cannot emerge solely due to a single M constraint (e.g. *V.V). In his hiatus-resolving typology, Casali (Reference Casali1996: 36, 69) introduces Onset, *Diphthong, *Cj, *Cw and Glidehood (to prevent [+low] glides and glides that are not [+front] or [+round]). The relations between these constraints are shown in Fig. 2.
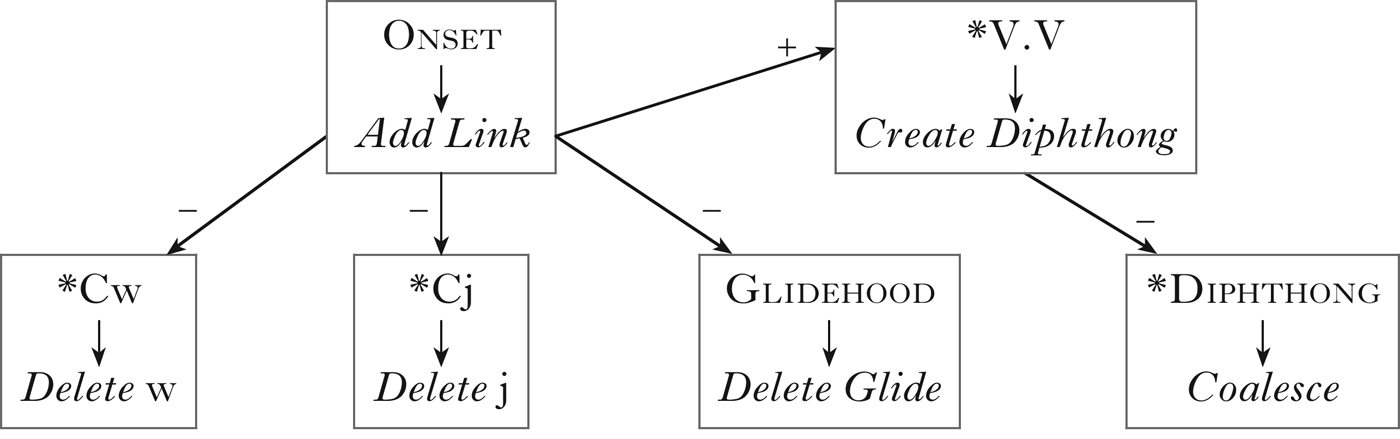
Figure 2 Relational schema for hiatus resolution.
According to Fig. 2, hiatus is generally resolved by diphthongisation. Related processes may induce vowel coalescence, gliding or elision. For example, in Xhosa, Onset → Add Link generates glides, but in the case of /a.V/, gliding is blocked by Glidehood (blocking will be discussed in §5.1). *V.V forces /a.V/ to become a diphthong, which further coalesces to [e]. *Cj deletes the glide /j/ after consonant, but *Cw is inactive in Xhosa. In sum, /wa-inkosi/ ‘on the chiefs’ surfaces as [wenkosi] (coalescence), /ni-enza/ ‘you make’ as [nenza] (elision) and /uku-ahlula/ ‘to divide’ as [ukwahlula] (gliding), exactly as reported by Casali (Reference Casali1996: 117–118).
Even if a typological OT analysis ranks only one M constraint against several F constraints to explain variable repairs in different languages, other analyses of related phenomena often introduce further M constraints. Pater (Reference Pater1999) discusses four strategies to satisfy *NT (‘no nasal–voiceless obstruent sequences’): fusion, postnasal voicing, nasal deletion and denasalisation. *NT induces devoicing, *ND (‘no nasal–voiced obstruent sequences’) may cause fusion (see Hyman Reference Hyman, Hume and Johnson2001) and *Nasal, *NasalCoda (Golston Reference Golston1996), *MoraicNasal (Morén Reference Morén2000) and similar constraints may be responsible for deletion and denasalisation.
Of course, a few preliminary examples cannot prove that, universally, every phonological M constraint has exactly one repair. The aim of the theory is not to find a single repair for every M constraint, but to systematise the repairs. The number of repairs does not affect the theory of relations between processes as described in subsequent sections, because only one repair is available in any specific case. If an M constraint has several repairs, then the actualisation of a process means choosing one of them and switching it on.
2.3 A case study: degemination in Fula
Paradis (Reference Paradis1988) presents an account of degemination in Fula (Niger-Congo) to illustrate her theory of constraints and repair strategies. The same data is also analysed by Prince & Smolensky (Reference Prince and Smolensky2004: §10.3.4), who concede that OT relies on Paradis (Reference Paradis1988), who argues for increasing the role of constraints; OT further increases their role. My work here is based on both Paradis’ theory and OT; I therefore employ the same example.
According to Paradis (Reference Paradis1988: 76–79), any consonant in Fula, except the continuants ([f s h w j r]), can be a geminate, as in [radːo] ‘hunt’, [golːaːde] ‘to work’. Gemination occurs in a certain set of continuant-final stems when the plural suffix is added. Since geminate continuants are prohibited, they occlusivise and surface as geminate stops (3a). After long vowels, geminate stops degeminate; the actual forms are [laːbi] and [lεːcε], with opaquely applied occlusivisation (3b).
(3)

Although the output forms in Fula are opaque, they can be analysed in the original version of OT (see Prince & Smolensky Reference Prince and Smolensky2004: §10.3.4), in which every output candidate is assumed to contain all the material from the input. Deletion is implemented as non-parsing, and epenthesis as filling of empty positions. M constraints can therefore see deleted or inserted elements, and certain cases of counterbleeding opacity can be accounted for. This version of OT has been replaced by Correspondence Theory (developed in McCarthy & Prince Reference McCarthy, Prince, Beckman, Dickey and Urbanczyk1995, Reference McCarthy and Prince1999), the current standard theory of faithfulness within OT. The most important innovation of Correspondence Theory is that input and output no longer have to contain exactly the same material. An undesirable consequence of this is that the now standard version of OT cannot deal with even those cases of opacity, such as Fula, which were analysable within the original version.
Gemination in Fula is triggered by the weak form of the plural suffix /-ɗV/, which consists of an initial empty mora followed by a vowel attached to its own mora (Paradis Reference Paradis1988, Baković Reference Baković and Akinlabi1995).Footnote 3 But empty moras cannot surface in Fula (*Empty-μ must be satisfied). Trimoraic syllables and moraic continuants are also prohibited (*σ μμμ and *μ [+cont] must be satisfied). The problem for standard OT is that *σ μμμ is satisfied by mora deletion, which also satisfies *Empty-μ and *μ [+cont]. There is therefore nothing to force occlusivisation; see (4).
(4)

In PRR, *σ μμμ is satisfied by mora sharing, not deletion. Fula also needs *HalfLongCoda → Shorten Coda. These two processes, if applied in sequence, cause degemination (see §2.2). Another process in Fula, *μ [+cont] → Invert [cont], occlusivises moraic continuants by changing [+continuant] to [―continuant].
To satisfy the constraint against empty moras (*Empty-μ), the mora must be attached to a segment. In Fula, the mora will be linked to the stem-final consonant. Cross-linguistically, vowel lengthening (compensatory lengthening) is more common, and the most likely universal repair of *Empty-μ is Link μ to V. Consonant lengthening seems to occur only in specific morphological environments (see Samek-Lodovici Reference Samek-Lodovici, Ackema and Schoorlemmer1994). I will therefore label the process Suffix: *Empty-μ → Link μ to C.Footnote 4
Relations between the processes are represented in Fig. 3. (The feeding relation between Suffix: *Empty-μ → Link μ to C and *μ [+cont] → Invert [cont] will be discussed further in §3.1, and the bleeding relation between *HalfLongCoda → Shorten Coda and *μ [+cont] → Invert [cont] in §3.2.)
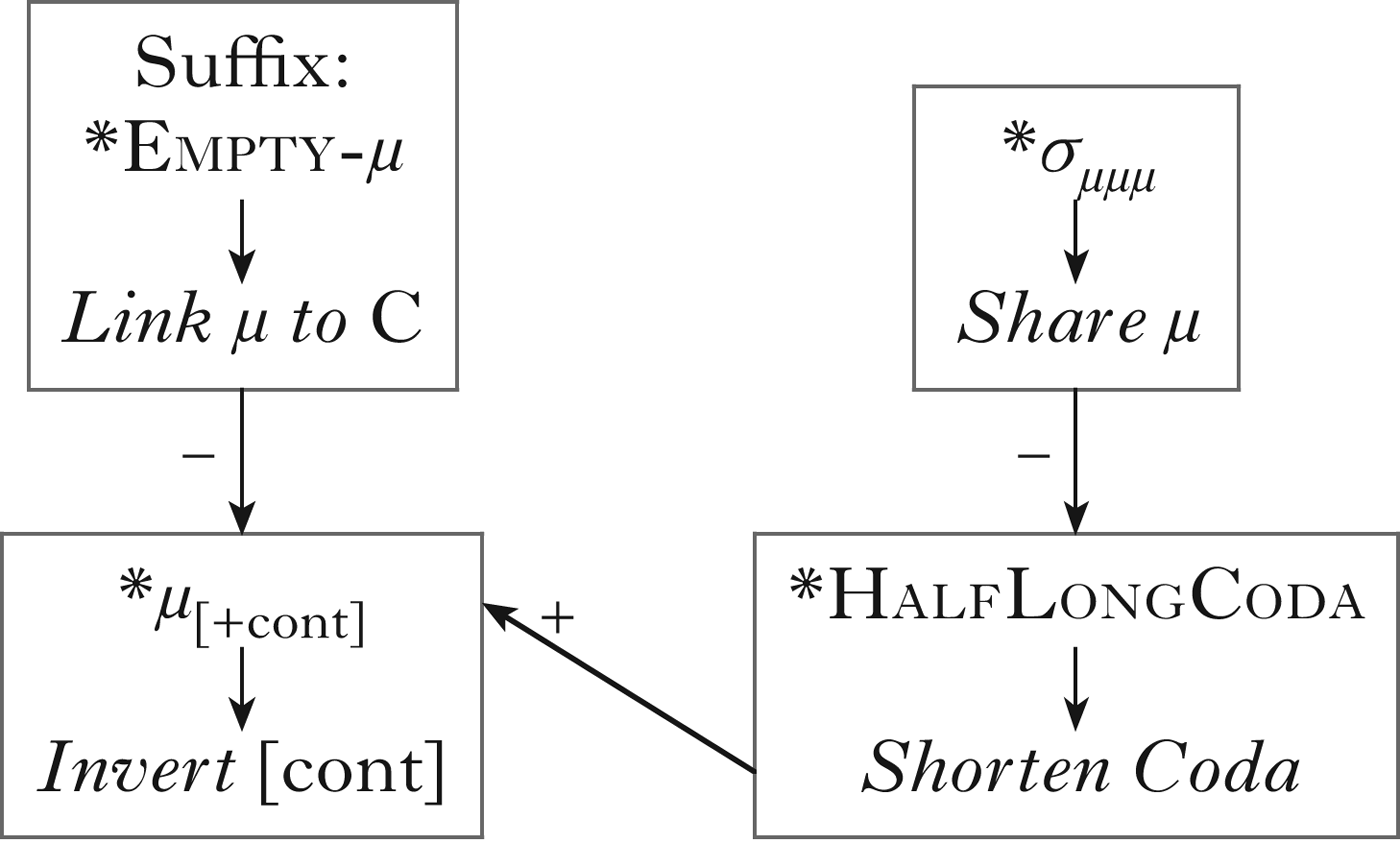
Figure 3 Relational schema for processes in Fula.
The analysis of Fula geminates cannot be completed without an account of syllabification processes. I assume here that syllabification does not count moras; it just seeks sonority peaks. A complete account of syllabification in PRR has not yet been developed (note that the same is true for HS; see §2.2).
Table II represents the processes considered above and their outcomes in Fula. Processes are given in their order of application, from left to right. The output of one process is the input to the next. Both underlying representations violate the first M constraint, *Empty-μ, and are repaired by Link μ to C, producing moraic continuants which violate *μ [+cont] and are repaired by occlusivisation. In the case of the first input form, Link μ to C and syllabification together also create violations to *σ μμμ, which induce degemination. Note that the order of application of related processes cannot be changed, since this would produce a different outcome (I will consider different ordering effects in subsequent sections). The order of unrelated processes is not crucial.
Table II Applying the processes in Fula. ‘—’ indicates that the process does not apply because the triggering M constraint is not violated.
3 Unidirectional relationships between two processes
In grammars, processes interact, rather than M and F constraints independently. OT-like F constraints are unnecessary, yet, just as in OT, M constraints are universal, and violable by surface forms. However, the violability comes from serial derivation: an M constraint which was satisfied in some earlier stage of the derivation can be violated again by a subsequent process. Although the processes are blind to other processes during the derivation, they can interact and even conjoin, thus generating opacity and blocking effects.
Different processes are intrinsically related to each other if they influence the same phonological elements. These are feeding and bleeding relations. Feeding means that the repair of one M constraint causes new violations of some other M constraint. In the case of bleeding, the repair of one M constraint is also capable of satisfying some other M constraint. As before, a feeding relation is indicated schematically by an arrow with a minus sign, and a bleeding relation by an arrow with a plus sign. In relational schemas such as Fig. 3, the direction of the arrows is irrelevant. To save space, relational schemas and derivational tables such as Table II are combined in the following sections, as shown in (5), where ↗ arrows indicate that processes apply in feeding or bleeding order, and ↖ arrows indicate that processes apply in counterfeeding or counterbleeding order. Irrespective of the direction of the relational arrow, the order of application of the processes represented in derivational tables is always from left to right.
(5)

3.1 Feeding
Consider first two different examples of the situation where the satisfaction of one M constraint can cause violations of some other M constraint, i.e. feeding, as in (5a): occlusivisation in Fula and devoicing in Isthmus Nahuat.
(6a) illustrates gemination feeding occlusivisation in Fula, as described in §2.3 (cf. Fig. 3 and Table II); mora sharing is irrelevant here. Reordering of the processes would cause counterfeeding opacity: the input form /ɲεw+(μ)ε/, where (μ) is an empty mora, would surface as [ɲεwːε], i.e. with a moraic continuant, whereas underlying moraic continuants would not survive; see (6b).
(6)

An OT tableau for the feeding order is given in (7). There are five OT rankings that yield the correct output, but these rankings cannot be written out in one single linear order, because only the pairwise rankings *μ [+cont] ⪼ Ident[cont] and *Empty-μ ⪼ Dep-μ -Link, Ident[cont] are crucial. The counterfeeding pattern in (6b) is unachievable in OT: [ɲεwːε] from /ɲεw+(μ)ε/ is possible only under the ranking Ident[cont] ⪼ *μ [+cont], but this ranking inevitably eliminates /ɲεwːε/ → [ɲεbːε].Footnote 5
(7)

Isthmus Nahuat, a dialect of the Uto-Aztecan language Nahuat, offers an example of counterfeeding. In this dialect, word-final unstressed vowels are optionally deleted after voiced sonorants (/l j w m/). Another process devoices word-final /l j w/, but does not apply to apocopated words (Kenstowicz & Kisseberth Reference Kenstowicz and Kisseberth1979: 299). Following Kager (Reference Kager1999: 372–377), I adopt the triggering M constraints FinalC and *VcdCoda. Though these constraints are somewhat inaccurate, they are adequate for present purposes. The essential processes, which are related in the same way as those in (6b), are given in (8a). Obviously, applying them in reverse order would produce transparent forms, as in (8b).
(8)

Chain shifts provide a special case of counterfeeding: underlying /A/ becomes surface [B], while /B/ becomes [C]. As an example, consider vowel raising in Nzεbi, a Bantu language spoken in Gabon (for an OT analysis that uses local conjunction, see Kirchner Reference Kirchner1996). In certain Nzεbi verb forms (the exact conditions are not important here), the vowel /a/, specified as [+low, ―high, ―ATR], raises to [ε] ([―low, ―high, ―ATR]). At the same time, /ε/ changes to [e] ([―low, ―high, +ATR]), and /e/ to [i] ([―low, +high, +ATR]). The processes apply in counterfeeding order, as in (9a).
(9)

If we change the order of some of these processes, a step in the chain shift is skipped. For example, in Basaa, vowel raising is otherwise identical to Nzεbi, except that /a/ and /ε/ both raise to [e] (Kirchner Reference Kirchner1996). In this language, *[+ low] → Invert [low] feeds *[―low, ―ATR] → Invert [ATR], as in (9b).
3.2 Bleeding
The source of counterbleeding opacity is also a relation between processes, involving relation type (5b), where the repair of one M constraint can eliminate the violations of some other M constraint. The transparent ordering will be exemplified by English plural formation (adapted from Gussenhoven & Jacobs Reference Gussenhoven and Jacobs2011: 52–56). The opaque ordering is also observable in Fula degemination.
The English plural suffix is /z/, but after sibilants it changes to [ɪz], and after voiceless sounds other than sibilants to [s] (e.g. [aɪz] eyes, [kɪsɪz] kisses, [bæks] backs). English words cannot end in sibilant sequences – the M constraint *[+strid][+strid] must be satisfied – and cannot end in an obstruent cluster in which one consonant is voiceless and the other voiced – that is, *[αvce][―αvce] must also be satisfied. *[+strid][+strid] triggers epenthesis and *[αvce][―αvce] triggers devoicing. *[αvce][―αvce] could also be satisfied by epenthesis, but devoicing does not help to satisfy *[+strid][+strid], since changing a voiced sibilant to voiceless (or vice versa) does not make it a non-sibilant.
The relations between processes are shown in (10a), with example derivations.
(10)

A corresponding OT tableau is given in (11). In OT, there are three hierarchies that yield the desired output, and the structurally similar interactions between the processes of English and Fula are not revealed.
(11)

No matter how the OT-constraints in (11) are reordered, [kɪsɪs] will never win: violations incurred by [kɪsɪz] are a proper subset of those incurred by [kɪsɪs]. However, this is not in itself an advantage for OT. If the English processes in (10a) applied in reverse order, an opaque pattern would occur, as in (10b). Such patterns are common in natural languages.
Consider once again degemination in Fula. The necessary constraints and repairs are related in the same way as the constraints and repairs in the analysis of English plurals. What is different is the order of application of the processes. In the case of transparent ordering, as in English, the repair that satisfies both M constraints comes first. Therefore, inputs that violate both M constraints are fully satisfied at the first step of the derivation, and do not need further repairs. In opaque cases, the reversed order of processes leads to doubly repaired output forms, although only one of the repairs would suffice; see (12).
(12)

Note that if two processes are in a bleeding relation, there must exist some potential form that violates both M constraints. For example, in English, /kɪs + z/ violates both *[+strid][+strid] and *[αvce][―αvce]; in Fula, /laːwːi/ violates *μ [+cont] and *HalfLongCoda. If such a form is impossible, the processes are not in a bleeding relation. Consider the schema in (13), which seems to represent bleeding: Change B undoubtedly satisfies both *AB and *CB. However, the outcome of these processes is exactly the same as it is with the same processes in reverse order. The processes are actually independent of each other, since Change B can never satisfy *AB and *CB simultaneously. A bleeding relation requires the trigger of the bleeding process to refer to a subset of those elements that are referred to by the trigger of the subsequent process. AB clearly is not a subset of CB, but [+strid][+strid] is a possible subset of [αvce][―αvce] (every [+strident] segment also has the feature [±voice]). This issue becomes important in cases like fed counterbleeding; see §4.3.
(13)

3.3 Summary
The phenomena in Fula, English and Isthmus Nahuat examined above represent the simplest relations between two phonological processes. In all these cases, the repair of one M constraint is related to another M constraint. The type of relation and the order of application of the processes give four different surface patterns: bleeding, feeding, counterbleeding and counterfeeding (cf. Kiparsky Reference Kiparsky and Fujimura1973a). All four patterns are easily produced in a derivational model with ordered processes, while a treatment of counterfeeding and counterbleeding within OT requires extensions to the theory.
4 Bidirectional relationships between two processes
As pointed out by Newton (Reference Newton1971), Shrofel (Reference Shrofel1980), Kiparsky (Reference Kiparsky1982), Baković (Reference Baković2007), Kavitskaya & Staroverov (Reference Kavitskaya and Staroverov2010) and many others, phonological processes can be in a mutually bleeding or mutually feeding relationship, schematised in (14a). Additionally, fed counterbleeding and bled counterfeeding have been argued to exist. However, a closer look (explained in §4.3) reveals that these relationships, schematised in (14b), lead to contradictions, and thus never arise in actual grammars. The relationships in (14b) are still worth analysing, since their existence is predicted by OT.
(14)

4.1 Mutual feeding
The mutual feeding relationship schematised in (14a.i), also known as fed counterfeeding, is found in Lardil, an Australian Tangkic language, where trimoraic or longer nouns undergo final vowel apocope and non-apical consonants are deleted in word-final position. The first process repairs the violations of FinalC by Delete V. (I ignore here the fact that apocope is blocked in shorter words, to avoid adding another process to the example in (15).) Deleting a word-final vowel following a non-apical consonant creates a structure that violates Final[apical], the trigger of the second process, which demands that word-final consonants be [+coronal, ―distributed]. Thus *FinalC → Delete V feeds the second process. Final[apical] is repaired by Delete C, but deletion of the consonant places the preceding vowel in the word-final position, hence Final[apical] → Delete C counterfeeds the first process; see the schema and derivations in (15) (cf. Hale Reference Hale and Sebeok1973, Prince & Smolensky Reference Prince and Smolensky2004: 122, Kavitskaya & Staroverov Reference Kavitskaya and Staroverov2010: 2).
(15)

A special case of mutual feeding is provided by ‘Duke-of-York derivations’, which have the general form /A/ → //B// → [A]: underlying A is unnecessarily changed to B and then back to A (Pullum Reference Pullum1976). Since the intermediate step is indeterminate, it has been argued that Duke-of-York derivations should be ruled out by the theory.
A simple example of a Duke-of-York derivation comes from Kashubian, a Slavic minority language spoken in Poland. Kashubian palatalises consonants before front non-low vowels, e.g. błësk [k] ‘flash’ – błëszcz+e+c [ʧ’ε] ‘to shine’. Since palatalised [ʦ’ ʣ’ s’ z’] do not occur in the surface inventory of Kashubian, palatalisation is argued to be accompanied by context-free depalatalisation of coronals (Rubach Reference Rubach2003, Kosecka Reference Kosecka2014). As the phonetic details of Kashubian palatalisation are irrelevant here, I will use the ad hoc constraints *Cε ‘consonants are palatalised before front non-low vowels’ and *s’ ‘no palatalised coronals’, as in (16).
(16)

As indicated in (16), the first process changes the underlying sequence /sε/ (see Kosecka Reference Kosecka2014: 148) to intermediate //s’ε//, and the second process changes it back to [sε]. The intermediate step is completely vacuous; it could be skipped without any resultant change in the output form.
The Duke-of-York derivation problem can arise whenever two processes are in a mutual feeding relation, and one repair does exactly the opposite of what the second repair does. As a non-derivational theory, OT nicely eliminates the vacuous intermediate step. Its ability to handle Duke-of-York derivations – despite them involving counterfeeding – comes from the fact that the input form of a Duke-of-York derivation is allowed to be changed only in one way. In the case of Kashubian, the input /s/ can be altered only to [s’], and /s’/ can be altered only to [s]. Thus there are only two competing output candidates, and the top-ranked M constraint alone selects the winner. Whatever the lower-ranked M constraint demands, it is blocked by the top-ranked M constraint.
I return to the analysis of Kashubian in §5.1, after introducing the mechanism of process conjunction.
4.2 Mutual bleeding
Mutual bleeding (see (14a.ii) above) has been discussed by Shrofel (Reference Shrofel1980), Kiparsky (Reference Kiparsky1982) and Baković (Reference Baković, Goldsmith, Riggle and Yu2011), among others. A well-known example comes from Standard German, where one process deletes /g/ after nasals (*ŋg → Delete g) and a second process devoices final obstruents (*VcdCoda → Devoice). The second process never changes forms that are repaired by the first process, because Delete g bleeds *VcdCoda, as in (17a). In Colloquial Northern German, the processes apply in reverse order, as illustrated in (17b). This is also a case of mutual bleeding (cf. Kiparsky Reference Kiparsky1982: 66, Ito & Mester Reference Ito, Mester, Féry and van de Vijver2003: 279).
(17)

Mutual bleeding does not involve opacity; output forms are not doubly repaired. Nevertheless, the pattern is not analysable in standard OT. The hierarchy Ident[vce] ⪼ Max[g] generates the correct Standard German output [dɪŋ], but also generates [taː] instead of [taːk]. To generate [taːk], we would need to reverse the ranking, which would, however, generate *[dɪŋk]. For Colloquial Northern German, the hierarchy Max[g] ⪼ Ident[vce] is not appropriate, since it generates the incorrect plural form *[dɪŋkə].
Stratal OT can account for both varieties of German. However, it is difficult to justify a multilevel analysis, because, at least in Standard German, the problematic forms [dɪŋ] and [taːk] are morphologically uninflected (see Ito & Mester Reference Ito, Mester, Féry and van de Vijver2003: 283–284 for additional arguments).
Ito & Mester (Reference Ito, Mester, Féry and van de Vijver2003) advocate an analysis using constraint conjunction. However, conjunction alone does not suffice; they also have to modify the *ŋg constraint in such a way that it also penalises [ŋk] sequences (formulated here as *ŋK, where K=[g] or [k]). A closer examination reveals that the solution still does not work. We need Max[g] and Max[k] as separate constraints (Ito & Mester use just Max), since the hierarchy Max ⪼ *ŋK, which is needed for [baŋk], produces the unwanted output [dɪŋgə], as in (18d). [dɪŋgə] does not violate *VcdCoda; it does violate *ŋK, but this constraint is ranked too low to exclude it.Footnote 6 This example shows that even transparent patterns like mutual bleeding can be problematical for OT and its extensions.
(18)

4.3 Fed counterbleeding and bled counterfeeding
Fed counterbleeding and bled counterfeeding cannot emerge in real languages. As noted in §3.2, if two processes are in a bleeding relationship, there must be some potential input that violates both M constraints. For example, in English, /kɪs+z/ violates both *[+strid][+strid] and *[αvce][―αvce]; in German, /dɪŋg/ violates *ŋg and *VcdCoda. In the case of feeding, however, violations of one M constraint are generated only by applying the other process: the input /sε/ in Kashubian violates just *Cε, while the violation of *s’ is generated by the repair of *Cε.
A formal schema of a supposedly mutual bleeding–feeding relationship is given in (19). Delete B can satisfy both *B and *AB; thus *B → Delete B bleeds *AB → Delete A. *AB → Delete A seems to feed *B → Delete B, because, if A in the AB sequence is deleted, the remaining B undoubtedly violates *B. However, it is not feeding: the AB sequence violates *B irrespective of A-deletion; no additional violations of *B are generated by *AB → Delete A. If we define *B such that it is not violated by AB, i.e. only an isolated B is prohibited, then the two processes are no longer in a real bleeding relationship: no input can violate *B while violating *AB.
(19)

Consider the example from Turkish in (20). The processes involved are vowel epenthesis and intervocalic k-deletion (Kager Reference Kager1999: 373–377, Baković Reference Baković2007: 226–230). *CC → Insert ɨ applies first, feeding *VkV → Delete k, which in turn seems to counterbleed *CC → Insert ɨ. It is not a real bleeding relation, since *VkV cannot be violated by a CC sequence. Baković (Reference Baković2007) also argues that this is not a case of counterbleeding, because reversing the processes does not lead to bleeding. He uses the label ‘self-destructive feeding’.
(20)

The problems with classifying and analysing such cases are specific to OT. Feeding should be analysable, but OT fails to generate the correct Turkish forms because it treats Delete k as a possible repair for *CC; see (21). Its failure to account for simple feeding cases is yet another argument against OT.
(21)

4.4 Summary
The analyses of mutual feeding and mutual bleeding confirm the conclusion that ordered processes are a more concise way to describe grammars than a theory with ordered M and F constraints like OT. Furthermore, OT creates an insoluble problem with non-existent relations like bled counterfeeding. However, it seems to be better than process ordering in one specific case, Duke-of-York derivations. This advantage disappears if we introduce the possibility of process conjunction into PRR theory, as I will demonstrate in the next section.
5 Conjoined processes
The main advantage of OT over rule-based theories lies in its ability to handle blocking effects. A rule applies whenever its context meets certain circumstances and it is its turn to apply. There are no sufficiently general ways of blocking a rule. In PRR theory, however, processes can be blocked if they are conjoined.
5.1 Triggering by feeding and blocked counterfeeding
Feeding means that the first process creates new violations of the trigger of the second process, and thus forces the second process to apply. If the processes are conjoined, the second process applies if and only if the first process generates new violations of the trigger of the second process. The situation may be called ‘triggering by feeding’.
In §3.1, feeding was exemplified by apocope and final devoicing (cf. the example from Isthmus Nahuat in (8)). The same processes and examples are used in (22) to illustrate the ‘triggering by feeding’ situation. Conjoined processes are indicated by borders. In (22), the input /ʃikɑ-ˈkili/ loses its final vowel because of the first process. This triggers the second process, which devoices final /l/, producing the output [ʃikɑˈkil̥]. The first process does not apply to /ˈtajoːl/, so the second process is not triggered and also does not apply (indicated by ‘|’).
(22)

The ‘triggering by feeding’ situation is usually described as blocking in underived environments. An example of this type comes from Finnish (Kiparsky Reference Kiparsky, Anderson and Kiparsky1973b). The two processes in feeding order are word-final vowel raising, where /e/ raises to [i], and assibilation of /t/ to [s] before [i]; see (23). Assibilation applies only to underlyingly /e/-final nouns. Though the case at hand does not involve counterbleeding or counterfeeding, it cannot be analysed in the standard version of OT. The reason for this is the underapplication of the process *ti → Assibilate.
(23)

There is one further way in which processes that are in a feeding relationship may be conjoined. The processes in (24) apply in counterfeeding order. Avoiding the generation of new violations to the first process can be achieved by blocking: the counterfeeding process does not apply if it would generate new violations to the trigger of the related previously applied process. In (24), *VcdCoda blocks apocope, but triggers devoicing (here and below, blocked forms which are not generated are enclosed within {}).
(24)

An example of ‘blocked counterfeeding’ is found in the history of Estonian. The two interacting processes are word-final vowel apocope (Viitso Reference Viitso and Erelt2003: 183) and the lengthening of monomoraic lexical words. The latter is emergent in borrowings. Relevant derivations are shown in (25).
(25)

Baković (Reference Baković2007) describes an unusual blocking interaction in Lithuanian. One process assimilates the final consonant of the verbal prefixes /at/ and /ap/ to an adjacent stem-initial consonant, such as [at-koːpjtji] ‘to climb up’ and [ad-gautji] ‘to get back’. The other process adds [i] between the prefix and the stem if the initial consonant of the stem and the final consonant of the prefix are identical, or differ only in terms of voicing or palatalisation, such as [atji-taikjiːtji] ‘to make fit well’ (palatalisation before [i] is automatic). These facts can be analysed with two ordered rules, epenthesis and assimilation. However, epenthesis should be stated as applying between consonants that differ at most in voicing and/or palatalisation, such as [atji-taikjiːtji] and [apji-bjerjtji], but [at-koːpjtji]. As Baković (Reference Baković2007: 235) notes, ‘crucially missing in this descriptively satisfactory analysis, however, is a successful explanation of the fact that the assimilation rule is bled in precisely those contexts where it would otherwise create pairs of completely identical adjacent consonants’. In Lithuanian, the constraint *CiCi (‘no sequences of identical consonants’) must be satisfied.Footnote 7 Baković (Reference Baković2007) calls this type of interaction ‘cross-derivational feeding’, and argues for an analysis within OT which can describe the generalisation about the distribution of the epenthetic vowel in Lithuanian (automatic palatalisation and the direction of the assimilation are ignored as contextually irrelevant refinements); see (26) (from Baković Reference Baković2007).
(26)

The situation can be equally well explained in PRR theory, as in (27). In Lithuanian, assimilation is blocked by *CiCi, but the process does not just underapply: epenthesis is used as an alternative repair. The processes in Lithuanian apply in counterfeeding order. The first process does not bleed the second, since no input can violate both *CiCi and Agree (see §4.3). Assimilation in /ap-bjertji/ is blocked by *CiCi. However, Agree still wants to be satisfied, and the repair of *CiCi is the only one available. This is one way in which non-universal repairs can emerge. Nevertheless, at every derivational step, the algorithm sees only those M constraints and repairs which are connected to the trigger of the current process. Agree cannot directly trigger Insert V, but it can trigger it through *CiCi, as determined by the relational arrows. In the cases in (24) and (25), no useful alternative repair exists: changing voice or inserting a mora does not satisfy FinalC.
(27)

Another interesting situation where a blocker is needed is the Duke-of-York derivation discussed in §4.1. Consider again the Kashubian example in (16). Without a blocker, the first process changes /sε/ to //s’ε//, and the second process changes it back to [sε]. In this case, we have a simple grammar, but a somewhat complicated derivation, with a vacuous step. If the first M constraint functions as a blocker, the derivation is the simplest possible (/sε/ → [sε]), but the grammar is more complicated, as in (28).Footnote 8
(28)

We might argue that the vacuous intermediate step is still created, in order to evaluate whether it satisfies the blocking constraint. On this line of argument, OT also generates vacuous intermediate forms (with an unlimited set of other output candidates), and the Duke-of-York derivation is actually the simplest.
‘Blocked counterfeeding’ is the only case of blocking that standard OT can handle. In an OT tableau, the constraints of the blocking process must outrank the constraints of the other process. This ensures that all output candidates that violate the blocker are banned from surfacing, as shown in (29).
(29)

Furthermore, OT can generate a pattern where apocope is blocked by *VcdCoda, yet *VcdCoda itself does not function as a trigger, i.e. the F constraint Ident[vce] outranks *VcdCoda, and devoicing does not occur; see (30).
(30)

In PRR theory, the same situation can be represented as in (31). The blocking M constraint in the hypothetical language is not powerful enough to trigger a repair for itself (the deactivated repair is shaded). The language tolerates only underlying violations of the constraint; generating new violations by other processes is banned.
(31)

I have been unable to find any clear language examples of this sort.Footnote 9 It is the only type of conjoined process where an M constraint is active despite its repair being switched off. If such exceptional cases do not in fact exist, this would be an argument in favour of PRR, because PRR rules them out by allowing only whole processes to interact.
Allophonic variation is a common case of ‘blocked counterfeeding’ (Baković Reference Baković2013). Consider a textbook example from Kager (Reference Kager1999: 27): in many dialects of English, vowels are generally oral, except before a tautosyllabic nasal stop, as in cat [kæt], but can't [kænt]. The processes are mutually feeding, and the repairs are the opposites of each other, exactly as in Kashubian; compare (28) and (32). Blocking avoids the generation of the vacuous intermediate form //an//.
(32)

The corresponding constraint hierarchy in OT is *V[oral]N ⪼ *V[nas] ⪼ Ident[nas]. More generally, if a context-sensitive M constraint blocks a context-free M constraint, allophonic variation occurs. In OT, the two M constraints and the F constraint generate six different hierarchies and four different output patterns. The hierarchy *V[nas] ⪼ *V[oral]N, Ident[nas] produces a language where all vowels are oral, i.e. where underlying nasal vowels denasalise. The same can be achieved with *V[nas] → Denasalise alone; *V[oral]N → Nasalise in such a language is inactive. The hierarchy *V[oral]N ⪼ Ident[nas] ⪼ *V[nas] creates positional neutralisation: vowels are nasalised before nasals, and underlying contrasts are preserved in other contexts. This situation is equivalent to one in which only *V[oral]N → Nasalise applies. In the fourth possible case, both processes are inactive, and all underlying contrasts in vowel nasality are maintained in the surface forms. In OT, the corresponding hierarchy is Ident[nas] ⪼ *V[oral]N, *V[nas] (cf. Kager Reference Kager1999: 27–40).
A question that now arises is whether PRR theory allows the same output patterns as OT. Languages where underlying contrasts are preserved solely before nasal stops, but in which vowels are oral in other contexts, are impossible to generate within standard OT, and it has been claimed that languages of this kind do not exist (Kager Reference Kager1999: 34–35). However, as shown in (30) above, OT can create patterns where an M constraint functions solely as a blocker, without triggering any repairs. In this case, underlying contrasts survive even if this violates the blocking M constraint, but no repair is allowed to add violations to the constraint. The pattern /ãl al/ → [al], /ãn/ → [ãn], /an/ → [an] (i.e. underlying contrasts preserved only before nasal stops) exactly meets the description: denasalisation applies only if it does not violate *V[oral]N, but *V[oral]N does not trigger nasalisation; see (33). In PRR, such patterns are ruled out, as only whole processes interact.
(33)

OT cannot create the pattern in (33), because both repairs (Nasalise and Denasalise) violate only one F constraint: Ident[nas]. However, similar patterns of blocked counterfeeding can be generated if the repairs violate different F constraints (for example, Ident[vce] and Del(V) in (29) and (30)). If, for instance, Ident[nas] were replaced by Max[nas] and Dep[nas] or by Ident[+nas] and Ident[―nas], the output pattern [ãn an al] would be produced, as confirmed by (34). Many phonologists have introduced such constraints; for example, Lombardi (Reference Lombardi and Lombardi2001) provides an argument for privative [voice] and Max[vce], and Butska (Reference Butska, Artstein and Holler1998) uses Faith[vce] and Faith[voiceless]. OT per se does not eliminate the output pattern in question; this depends on the F constraints used.
(34)

5.2 Triggering by bleeding and blocked counterbleeding
The English plural suffix, analysed in (10) above, and in (35) as involving process conjunction, provides an example of a blocker that develops from a bleeding relation. The result of such conjunction is ‘blocked counterbleeding’: the counterbleeding process will not apply if the other process has applied, thus avoiding overapplication. This situation is also referred to as ‘blocking in derived environments’.
(35)

A blocked counterbleeding process is found in Diola Fogny (Niger-Congo), spoken in Senegal and neighbouring countries. In this language, nasals assimilate in place to following non-continuants; other preconsonantal consonants are deleted (Kiparsky Reference Kiparsky, Anderson and Kiparsky1973b, Piggott Reference Piggott1999, Baković Reference Baković, Goldsmith, Riggle and Yu2011); see (36). If the processes apply serially, no consonant cluster will survive, regardless of the order of the processes: every nasal followed by a consonant violates *CC, and is therefore deleted. To save the NC clusters, deletion must be blocked, as shown in (36).
(36)

A bleeding order can develop to a ‘triggering by bleeding’ relation, represented in (37). In that case, the bled process will be applied instead of the bleeding process if the trigger of the bleeding process is violated. The inputs /kɪs+z/ and /nəʊz+z/ violate *[+strid][+strid]. Despite this, Insert V does not apply, but forces *[αvce][―αvce] → Devoice to apply. Thus, /kɪs+z/ changes to [kɪss], but /nəʊz+z/ is left unchanged, because it does not violate *[αvce][―αvce]. The input /bæk+z/ also does not change, since it satisfies *[+strid][+strid], and so *[αvce][―αvce] → Devoice is not triggered. Altogether, ‘triggering by bleeding’ means that only the repair of the bled process applies, and only if both M constraints are violated. (This is not the only formally possible interpretation of ‘triggering by bleeding’, but it is the only one for the language examples I am familiar with.)
(37)

A triggering by bleeding situation is found in Japanese (Farris-Trimble Reference Farris-Trimble2008, Pater Reference Pater2009), where only a single voiced obstruent is permitted within a word. This rule is known as Lyman's Law. Another restriction in Japanese prohibits voiced geminates. However, in loanwords, multiple voiced obstruents are allowed (e.g. [bagu] ‘bug’). Furthermore, loanwords may contain voiced geminates (e.g. [webːu] ‘web’). When a loanword contains both a voiced geminate and a voiced obstruent, the geminate is optionally devoiced (e.g. [gudːo] ~ [gutːo] ‘good’); see (38). Such devoicing is unacceptable outside the context of Lyman's Law.
(38)

Neither of the examples in current subsection can be analysed within standard OT, because of underapplication. If [kɪss] wins, then [nəʊzɪz] cannot win, since Dep-V ⪼ *[+strid][+strid] prefers [nəʊzz]. Similarly, if [kɪss] and [nəʊzz] win, then [bækz] is impossible. As well as Harmonic Grammar, many variations of OT have been proposed for accounting for similar patterns, such as the Split Additive Model (Albright et al. Reference Albright, Magri, Michaels, Chan, Jacob and Kapia2008) or Linear OT (Keller Reference Keller, Fanselow, Féry, Vogel and Schlesewsky2006). PRR theory does not require augmentation to analyse this pattern.
5.3 Emergence of new processes
There is at least one way in which related processes can develop further. In the case of counterbleeding, the first process overapplies. Overapplication can be avoided not only by conjoining the processes, but also by creating a new process that repairs the M constraint of the first process by applying the repair of the second process; note the reversed arrow and the shaded repair in (39). Compared to triggering by bleeding, only the alternative repair is triggered, not the whole process.
(39)

A counterfeeding order also may evolve to a new process, as shown in (40). The linking arrow is reversed, and triggers a repair which is the opposite of the repair of the original counterfeeding process. Thus the original counterfeeding process must be deactivated.
(40)

The history of German provides a similar example, given in (41). In East Central German, word-final schwas were deleted, except after voiced obstruents, as in spæte > spät and küele > kühl, but not weize > *weiz. Final schwa was restored in certain morphological forms, such as in the imperatives. This may have begun with the formation of the ‘false’ process *VcdCoda → Insert ə (cf. Gress-Wright Reference Gress-Wright2010).
(41)

5.4 Summary
Process conjunction generates four surface patterns in addition to bleeding, counterbleeding, feeding, counterfeeding, mutual bleeding and mutual feeding. All four are found in languages. In PRR theory, all the patterns can be described uniformly, relying just on ordered processes and the feeding and bleeding relations between them. Two of the patterns are best characterised as blocking effects, and the other two as triggerings in certain circumstances. All the possibilities are shown in (42). In contrast, OT can only account for the ‘blocked counterfeeding’ situation.
(42)

6 Conclusion
In recent decades, OT has become the most widely used generative theory in phonology. It has advantages over rule-based serialism, which generally cannot handle blocking effects, and yet has difficulties with dealing with opacity, since it cannot distinguish derived from non-derived environments. Various extensions to standard OT have therefore been proposed. Modifying OT is not the only way of solving the opacity problem. In this paper, I have proposed a unification of rule-based serialism and OT. The unified theory of processes and relations between them (PRR theory) can describe both opacity and blocking effects. I have focused here on the relations between phonological processes, rather than on the processes themselves.
In PRR theory, a phonological process consists of a trigger and a repair. Triggers are OT-like M constraints, and repairs are equivalents to F constraints. Processes may be independent of each other and apply in any order, or they may be in a feeding or bleeding relation. A feeding relation (see the example schema in (43a)) can produce seven different output patterns, all of which are attested in languages.
(43)

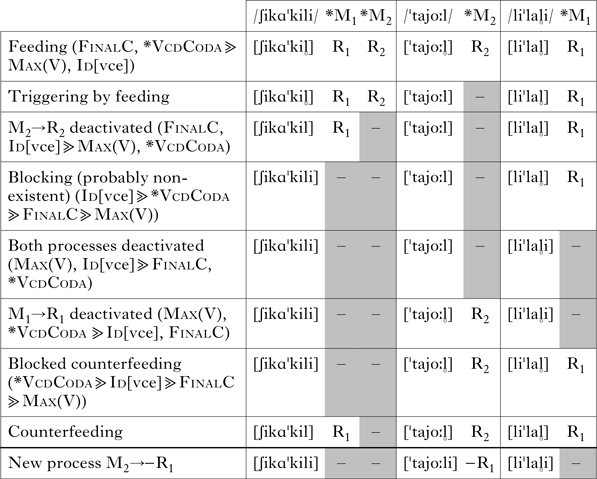
The patterns are listed in Table III, with OT hierarchies where possible. The first underlying form /ʃikɑˈkili/ violates the first M constraint FinalC (M1), and potentially violates *VcdCoda (M2) as well. /ˈtajoːl/ violates only M2, and /liˈlal̥i/ only M1. R1 and R2 in the table cells indicate which repairs are used to satisfy the M constraints. ―R1 signifies that the repair is the opposite of R1 (for example, if R1 deletes a vowel, then ―R1 inserts the vowel, and vice versa). The possible output patterns are arranged so that they form a chain from feeding to counterfeeding. Note that output patterns where R1 applies solely to *M1*M2 inputs are not generated. PRR theory is not as restrictive as OT, and yet still does not produce every combinatorically possible output.
Table III Typology of feeding relations.
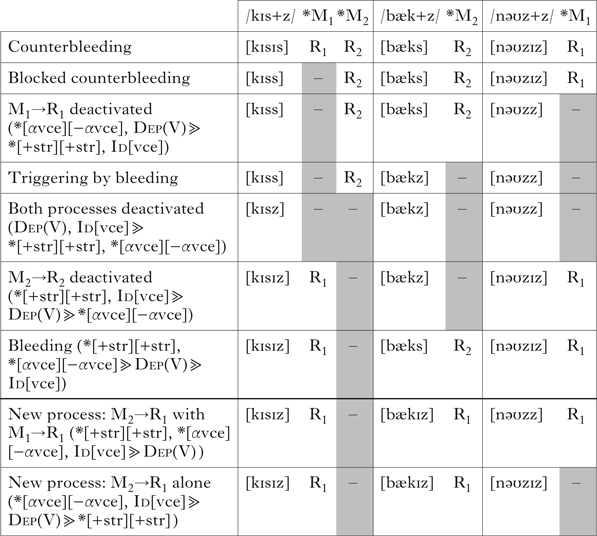
The typology for bleeding relations in (43b) is represented in Table IV. All the listed output patterns are attested in languages. Standard OT can generate only six of these patterns.
Table IV Typology of bleeding relations.
Compared to OT, PRR theory enables a better understanding of the possible interactions between phonological processes and the universality of processes.


















































