I. INTRODUCTION
Indexing is the first obvious door to open successfully when one is concerned with a structure determination by powder diffractometry (SDPD). For that purpose, the old good 1960–1990 generation of indexing programs has proven its efficiency. Three programs emerge by a high frequency of use: ITO (Visser, Reference Visser1969), TREOR (Werner et al., 1985) and DICVOL (Boultif and Louër, Reference Boultif and Louër1991) (see references for previous TREOR and DICVOL versions inside of these papers). Because they have different limitations, using all these complementary programs, not only one, is generally recommended (Werner, Reference Werner, Eriksson and Westdahl2002). The citation numbers (ISI Web of Science) of the previous references is an order of magnitude larger than any other publication about indexing software (581, 511 and 278 citations in the ranges 1975–2000, 1986–2000 and 1992–2000, for ITO, TREOR and DICVOL, respectively). These three famous programs are complemented with several others into the CRYSFIRE suite (Shirley, 1999), adding more chances of success. In spite of the availability of this impressive package, there is a renewed recent interest in trying to improve our indexing capacity. Several new programs have appeared on the market, making use of different either new or old approaches: genetic algorithm with AUTOX-MRIAAU (Zlokazov, Reference Zlokazov1992) and GAIN (Kariuki et al., Reference Kariuki, Belmonte, McMahon, Johnston, Harris and Nelmes1999), the latter using whole profile fitting by the Le Bail method (Le Bail et al., Reference Le Bail, Duroy and Fourquet1988); EFLECH/INDEX (Bergmann and Kleeberg, Reference Bergmann and Kleeberg1999) using also the original profile, extracting both line positions and a covariance matrix; iterative use of singular value decomposition with SVD-index within TOPAS (Coelho, Reference Coelho2003); and dichotomy procedure (as in DICVOL) with X-Cell within the Materials Studio suite (Neumann, Reference Neumann2003). These efforts have their origin certainly in part in the increase of the computer power. As a consequence of the expansion of SDPD, the indexing step is appearing more as a bottleneck due to some known difficulties associated with bad data (zeropoint error, inaccuracy, impurities,…) or special cases (flat cells, ill-crystallized compounds). The powder diffraction community has adopted some well known sentences about indexing which are highlighting these difficulties. Some texts in the program manuals or advice in the output files have passed in the usual language: “indexing is more an art than a science,” “it is entirely the users responsibility to decide whether any of the suggested unit cells is the correct cell” (ITO), “powder indexing works beautifully on good data, but with poor data it will usually not work at all” (Shirley, Reference Shirley1980), “DICVOL proposes solutions, the user disposes of them” (DICVOL), etc. These sentences are a bit discouraging to newcomers in the field, facing a huge list of more or less improbable cells with low figures of merit. Users do not always have the chance to record their own patterns and may feel disarmed. So, there is a real need for new programs able to solve those reputed impossible cases: mixtures where many impurity lines are present, patterns with big zeropoint error (though this should not occur), or when line broadening intrinsic to the sample is making synchrotron radiation almost useless. Users now want solutions fast, without thinking too much, ignoring that “part of the beauty of SDPD does consist in its complexity, i.e., in the lack of complete automatism as well as in the necessity of a careful and sagacious human interpretation of the experimental data,” as said by an anonymous reviewer of the present manuscript.
The McMaille (the French word “maille” means cell, pronounce “MacMy”) computer program code was written up by the end of 2002 in order to explore the Monte Carlo possibilities (Le Bail, 2002) for indexing powder patterns, bearing in mind the main indexing problems leading to failure, and trying to overcome them.
II. THE CRYSTALLOGRAPHIC PROBLEM
The basic principles were described many times, in almost all references given in the Introduction, and in several review papers (for instance, Louër, Reference Louër1992, Werner, 2002, Shirley, Reference Shirley2003). For the method used here, it is sufficient to know that McMaille operates in the parameters space. Once a set of cell parameters is selected randomly, the corresponding peak positions can be calculated directly by the usual formula, and compared to the observed ones, and the Miller indices are assigned.
III. McMAILLE ALGORITHM
In a first approach, it was expected to model the raw whole powder pattern, like it is done in the GAIN program (Kariuki et al., Reference Kariuki, Belmonte, McMahon, Johnston, Harris and Nelmes1999). But in spite of the use of the Le Bail profile-fitting procedure (Le Bail et al., Reference Le Bail, Duroy and Fourquet1988), which is orders of magnitude faster than least-squares fitting of individual intensities [Pawley method (Pawley, Reference Pawley1981)], the GAIN program seems to remain slow, so that only small tetragonal and orthorhombic cells were shown to be indexable (with cell parameters smaller than 6 Å). Fitting the raw powder pattern needs to use sophisticated profile shapes, reproducing the background, and this is paid by heavy calculations which are not a real problem if only tens of iterations are concerned (when extracting peak intensities or refining structures), but indexing may need to test millions of cell parameter combinations. Rather than retain whole-raw-profile fitting, a first McMaille version tried to fit a pseudo powder pattern built up by using a Gaussian peak shape and full widths at half maximum (FWHM) following the (U, V, W) Caglioti law characterizing standard patterns from the used diffractometer, the peaks having positions and intensities obtained from the application of a peak hunting software, for instance, PowderX (Dong, Reference Dong1999) or WinPlotr (Roisnel and Rodriguez-Carvajal, Reference Roisnel and Rodriguez-Carvajal2001). It was found that a Monte Carlo process, which will randomly propose cell parameters, would have better chances of success if the FWHM were enlarged rather than narrowed. This does not mean at all that data would not have to be accurate. On the contrary, this just means that using enlarged peaks, centered around a very accurate position, would give more chance for the process to detect quickly a minima in the figure of merit (FoM) surface, starting from cell parameters decisively more different from the final ones than if the FWHM were too narrow. The more the “observed” peaks of the idealized powder profile are large, the more you have chances to intercept them by the calculated peaks. But at the cell refinement stage, it is mainly the position accuracy which is important. It will lead effectively to low R values (exact overlapping corresponds to R=0,) allowing us to distinguish the true solution from bad proposals. As FoM, the conventional Rietveld (Reference Rietveld1969) RP value was retained. A problem was that the yet simple Gaussian peak shape, combined with three to four iterations of the Rietveld (Reference Rietveld1969) decomposition formula (the so-called Le Bail method) for fitting the pattern, needed too much computer time. There is no idea of the time needed for indexing a small orthorhombic cell in the Kariuki et al. paper (Reference Kariuki, Belmonte, McMahon, Johnston, Harris and Nelmes1999). By using a computer running McMaille at 2.4 GHz, on a fragment of pseudo powder pattern built up from 20 peak positions and intensities, it was possible to test 103 cells per second in cubic symmetry and much less in lower symmetries (300 cells per second in triclinic). This was really not fast enough.
Then, an even simpler columnar peak shape was tested, not applying any Le Bail fit, but the R factor was estimated from the percentage of inclusion of the calculated columns inside of the “observed” ones. Of course, the calculated column intensities were set equal to the “observed” ones (Figure 1). The calculations were 20 times faster (20 000 tests per second in cubic cases and 6000 in triclinic), leading to possibilities for indexing in any crystal system in more reasonable times (in a matter of seconds for high symmetry and
Figure 1. Comparison between a real pattern and the idealized pattern (zero-background, columnar peak-shape) on which is working McMaille. This case is sample 3 (C61Br2) of the SDPD Round Robin 2 (Le Bail and Cranswick, Reference Le Bail and Cranswick2003), http://www.cristal.org/sdpdrr2/.
minutes for low symmetries including monoclinic and triclinic cells). However, such times are relevant to the examination of a restricted domain of volume (ΔV=500 Å3) and of cell parameters (<20 Å). Examining all symmetries in a quite large domain, from 20 starting lines, may require hours, if not a night of calculations, testing up to 109 cell parameter combinations. Also, these times are true only if there is no tolerated impurity line. Allowing for extraneous peaks considerably decreases the speed.
Four tricks have a part in the success of the Monte Carlo process, changing randomly one parameter at a time, that parameter being itself selected randomly, depending on the symmetry (from one to six parameters, zeropoint fixed):
a—Cells are retained for further examination if R is smaller than a user defined value (R1∼50%).
b—Cells are also retained for further examination if all the N observed peaks (minus a number of tolerated impurity peaks N′ defined by the user) are “explained,” whatever the R value.
c—Further examination means that if a or b conditions are fulfilled, then the cell parameters are adjusted by a Monte Carlo process, testing randomly 200 to 5000 small parameter changes (cubic to triclinic case, respectively). That way, R can decrease from 50% (case a) or larger (possibly in case b) to the minima (usually less than 10%), which a least-square refinement process would not have allowed.
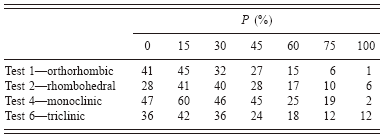
d—Memory is kept of new parameters if they improve R in 85% of the cases (in order to escape from false minima). Tests of efficiency of the process were made for various percentages (Table I).
The flow diagram for McMaille is shown in Figure 2. The user also decides on a limit R2 for R below which a cell proposal will be kept in the final list, and on a limit R3 below which a solution is considered as being very probably the correct solution so that the program can stop.
McMaille can run in two main modes. A press-button automated “black-box” mode for which very little information is provided by the user: 20 lines positions and intensities, the wavelength, an estimated zeropoint and the program then uses default values in order to explore all symmetries within predefined cell parameters and volumes ranges (Table II). This is practical for a first exploration. If this automated mode fails, then the manual mode is recommended, allowing one to explore outside of the default values.
TABLE I. Optimization effects with various probability values (probability P to accept a new cell parameter if the fit is not improved) are given the number of times the correct answer is found for the same number of Monte Carlo steps. The tendency is to work better with P∼15%, as a mean, avoiding being trapped in a false minima. Tests 1–6 are the filenames of example cases in the distributed McMaille package. P: a value of 15 means that for 15% of the cells tested, a parameter change may be accepted even if that change does not lead to any R decrease or number of indexed reflections improvement (no change means that you keep the previous parameter unchanged). P=100: change always accepted even if it does not improve the fit. P=0: change not accepted at all if it does not improve the fit.
A cumbersome grid-search approach is also implemented, sometimes useful in special cases. For instance, if a flat cell has been detected, this grid-search mode allows one to fix the two large cell parameters and to explore only the difficult-to-find small parameter.
IV. SPECIAL FEATURES
At the end of the automated “black box” mode execution, McMaille produces a file ready for the manual mode, which needs more details (R1, R2, R3 values, etc.).
In order to save computing time with the generation of Miller indices, lists of hkl are predetermined (400 to 1000 triplets) for every crystal system and saved in files read once at the beginning. Their attribution to the experimental peaks does not necessitate any reordering (which would be too long). If a calculated profile does not intercept any observed one, then the corresponding hkl set is simply considered as unobserved, and not taken into account.
Due to these possible long executing times, there is an on-screen summary appearing, and it is possible to cancel the job, whereas saving the results by pressing the K (capital letter) keystroke, the program checks for this occurence every 30 000 Monte Carlo cell combinations.
Figure 2. Flow diagram for McMaille.
TABLE II. Default conditions in the automated “black-box” mode. Maximum number of Monte Carlo events, maximum cell parameters (P max), maximum volumes (V max). In orthorhombic, monoclinic and triclinic symmetries, the volumes are explored in four parts, successively.

A strategy for trying index large cells (proteins for instance) is to rescale the data by dividing the wavelength by a factor up to 10, overcoming the default maximum cell volumes, and allowing one to use the automated mode. However, there is no such need for rescaling in the manual mode.
The fact that the program does not produce a list of possible space groups for the most probable cells may be considered as a limitation, and that process could be implemented in the next version updates.
V. IMPURITY LINES AND BEYOND: INDEXING MULTIPHASE PATTERNS
In automated mode, the default is to tolerate three impurity lines. In manual mode, the user decides by two control parameters, N′, the maximum number of unindexed lines, and R2, allowing consideration of only proposals with R<R2. Fixing R2 at 15% means that cell proposals explaining at least 85% of the peak’s total intensity will be listed. An impurity should not concern more than 10%–15% of the total intensity. But the number of (small) peaks belonging to the impurity can be high. The main problem here with McMaille is that the speed decreases for large N′ values. However, this relative insensitivity to impurities is a strong point of McMaille. The systematic study of impurity line inclusion has shown that, provided the total intensity of the impurity lines is less than 15% of the grand total intensity, then we have the following.
(i) With less than 35% (in number) of the impurity lines, McMaille generally provides the correct cell in top position. However, the figures of merit decrease.
(ii) With 35%–50% of the impurity lines, McMaille may still propose the correct cell, but generally not in first position. Thus it is more difficult to locate it.
Tests for indexing simultaneously two phases in a mixture were also made. Multiple synthesis in varying conditions, or thermal behavior, should reveal the multiphase nature of a sample. It is much better to adjust the synthesis conditions, and even if the phases cannot be prepared as pure phases, intensity variations should allow one to define the peaks belonging to one or the other phase. But if really one wants to attempt indexing of a mixture, then there is a cost to pay when using McMaille. In the one-phase mode, McMaille tests for Ni>N−N′ (Ni being the number of indexed lines that should be larger than the difference between the total number of lines N and the number of tolerated unindexed lines N′). In a two-phase mode, N′ has to be larger than N/2,
TABLE III. Unit-cell dimensions as suggested by McMaille for selected PDF-2 powder patterns (most of them Grant-in-Aid, unindexed) in automated mode (unless specified). N/U are the total number of lines and the number of unindexed lines. All these cases would need further work (recording a new powder pattern) for confirmation. These results are taken from the UPPW round robin (Unindexed Powder Pattern of the Week) http://sdpd.univ-lemans.fr/uppw/.

so that this considerably increases the number of possibilities that will have to be examined, and adjusted by the Monte Carlo process. The same effect is due to the necessary increase of R1 to more than 50%. The consequence is a dramatic decrease of the program speed, so that examining low-symmetry two-phase cases becomes prohibitive. The limits R2 and R3 themselves have to be increased to more than 50%. McMaille finally examines all the combinations of the suggested cells two by two so as to locate the best global fit. The conclusions about two-phase indexing with McMaille are that, provided at least 30 lines are examined with 13–17 lines belonging to each phase, and 40%–60% of the total intensity distributed to each phase, then the program appears to be able to produce solutions in reasonable times (<1 h) for combinations of two phases either cubic or hexagonal or tetragonal or orthorhombic. The monoclinic and triclinic cases were not examined (being too long).
VI. ZEROPOINT
Due to a W parameter defined in McMaille, a kind of enlarged peak width that it is preferable to set at two or three times more than the real FWHM, the program is able to provide some tolerance to a zeropoint error. Imagine that there is a ±0.03°(2θ) zeropoint error, and that W=0.30°(2θ) (suggested by the program for a 1.54056 Å wavelength). Then at least the R value can be already as low as 10%, and will be in fact lower, since there will be some accomodation of the cell parameters in order to decrease R (some of the calculated reflections will match better than this 0.03 error). So, it is estimated that McMaille has a natural tolerance to a zeropoint error up to 0.05°(2θ). Note, however, that the suggested W value in automated mode is [(0.3*λ)/1.54056], so that for a wavelength close to 0.7 Å, as frequently retained for synchrotron radiation, the above tolerance will be reduced by a factor of 2. Fortunately, zero-point errors are usually very small with synchrotron data because of the parallel beam and optimized geometry.
VII. TEST CASES
Several test cases are distributed with McMaille, most of them taken from the other indexing programs package. A more recent example is described below, the case of bethanechol chloride C7H17ClN2O2, also called carbamyl-β-methylcholine chloride. That compound was the subject of two ICDD Grant-in-Aids (43-1748 and 46-1964) and was included in the list of UPPWs (Unindexed Powder Pattern of the Week), a kind of permanent indexing round robin on the Internet (http://sdpd.univ-lemans.fr/uppw/), reported in Table III. No competitor could provide any convincing indexation, not even McMaille. So, it was decided to record a new pattern. The sample was from the Sératec Company. When one disposes only of Bragg Brentano geometry-based diffractometers, it is advisable for SDPD purpose to perform at least two powder patterns, one with a sample pressed in order to have the better resolution (Figure 3) for indexing and the other managed for limiting preferred orientation effects (Figure 4) for structure solving. Not having access to spray drying, you can apply a technique of dusting your sample through a fine sieve on a frosty glass holder—because this is much better than using a vertically side-loaded
Figure 3. Powder pattern of bethanechol chloride used for peak position extraction prior to indexing. Sample pressed with huge preferred orientation effect, silicium zero-background holder. Bragg-Brentano, CuKα, corrected for Kα2, FWHM∼0.10(2θ)° (0.04 for LaB6 in the same conditions).
Figure 4. Le Bail fit on the powder pattern of bethanechol chloride (using FULLPROF, P21/n space group). Sample dusted through a sieve on a silicium zero-background holder with a slight pressure by a sheet of paper in order to obtain a better plane surface. Preferred orientation is not completely removed, these conditions lead to a lower resolution with FWHM∼0.25(2θ)°.
horizontal holder. Anyway, with these new powder patterns of bethanechol chloride, every competitor succeeded easily in finding the cell. The results from McMaille in automated mode were a=8.875(4) (Å), b=16.407(7) (Å), c=7.141(3) (Å), β=93.82(2)(°), M(20)=52, F(20)=127 (0.005, 31). (These FoM would be even better if the P21/n space group systematic extinctions were considered in calculating the number of theoretical lines.) Going back to the ICDD entries, it was observed that both presented many impurity lines and had a zeropoint of the order-of −0.10°(2θ). Any self-calibration from these original data failed to estimate that zeropoint error. It may seem easy afterward to consider how a failure could have been avoided, but let us have a look back to these 43-1748 and 46-1964 entries; at least, was it possible to index knowing the correct zeropoint? The answer is yes with McMaille in spite of the impurity lines (Table III). There were 8 impurity lines among the first 26 lines for the 43-1748 entry (Figure 5) and 3 impurity lines among the first 35 for the 46-1964 entry. This means that
Figure 5. Idealized powder pattern with Gaussian peak shape, reconstructed from PDF 43-1748, bethanechol chloride, at the end of the McMaille execution (after correction of a −0.10(2θ)° zeropoint), displayed by WinPLOTR. There are 8 unexplained lines among the first 26 observed ones. The first four lines at low diffraction angle are half of these impurity lines. This does not preclude McMaille to find the correct cell in first position.
finding the solution with an automatic process would need to examine possible zeropoint errors larger than those naturally tolerated by the program algorithm [McMaille can find solutions in spite of a zeropoint error of the order of |0.05|°(2θ), maximum]. Given the current slowness of McMaille, it would be prohibitive to add this systematic exploration of zeropoint values in the automated process. Adding the zeropoint as a supplementary parameter in the Monte Carlo calculations is also very demanding in time and was not made. The zeropoint problem is really something to be solved before indexing, either by self-calibration or, if this results in a dubious estimation, by mixing the sample with a reference compound. Finally, it was considered to write a new table of dobs, dcalc and I’s from this study of bethanechol chloride in order to replace these 43-1748 and 46-1964 PDF entries. However, owing to that preferred orientation problem, the dobs would have to be taken from the high resolution pattern (Figure 3) and the Iobs from the low resolution pattern (Figure 4), a kind of impossible task. It seems better to wait for the crystal structure determination (Le Bail and Stephens, to be published) and its inclusion into the Cambridge Structural Database from which ICDD will calculate the powder pattern.
VIII. SOFTWARE
A. Software environment
McMaille is written in Fortran 77 and has been implemented under the Microsoft Windows operating system as a console application by using the Compaq Visual Fortran compiler.
B. Program specifications
Input: In automated mode, the input resumes to a text title line, a second line with three values, the wavelength, the zeropoint and a code (=3) specifying the use of the “black-box” mode, then further lines giving couples of 2θ [or d(Å)] and intensities values are required. In manual mode, the input is more complex, requiring upper and lower limits R1, R2, R3 for the Monte Carlo search, as well as the definition of the symmetries in which the indexing will be performed, the peak width W, the number of tolerated unindexed peaks N′, and the maximum numbers of Monte Carlo events.
Output: The information used as input above is shown, and the results of the indexing are listed classified according to the R values, the volume, and the number of time a same solution was found. The most probable cell parameters are finally least-squared refined together with a zeropoint and the M(20) and F(20) figures of merit are calculated (DeWolf, Reference DeWolf1968; Smith and Snyder, Reference Smith and Snyder1979). A final plot is produced by McMaille, which can be displayed by WinPLOTR. Other software compatible with the McMaille outputs are CHEKCELL and CRYSFIRE. A recommended next step for establishing the cell veracity is to extract the intensities by whole profile fitting, using either the Pawley or Le Bail methods (Figure 4), for instance by applying FULLPROF (Rodriguez-Carvajal, 1990). And the final proof will be obtained if the structure is solved, whatever the method, and then finally refined by the Rietveld method.
C. Documentation and availability
The program can be downloaded through the Internet, distributed under the GNU Public license (open source). It can be used free of charge for academic research purposes. The URL of the program is http://www.cristal.org/McMaille/. Documentation, including examples, is available at this URL. There is a full manual and a shortened one for the simplified automated mode users.
IX. CONCLUSION
Again, it is emphasized here that accurate data are essential when facing a powder pattern indexation problem. The method used in McMaille appears to be promising. The program is already quite efficient if the user is not in too much of a hurry and possesses a fast computer. A faster algorithm would be required, or faster computers, for considering impurity lines and two-phase problems (options in McMaille which are recommended to be used cautiously). The program needs some skills in manual mode, but there is almost nothing to do in the automated mode (except finding the zeropoint). Users with computing knowledge may decide to improve the available source code. Exploiting completely the potential of the method by using really the raw profile instead of an idealized one will have to wait for much faster computers. As a final comment, it must be said that, like most indexing programs, McMaille will not always present the correct solution in first position. For recognizing the very best solution in the output, the user has to find the cell proposal corresponding to the smallest R factor, with highest symmetry and smallest volume, indexing the largest number of peaks. This is sometimes not an easy task, although ordered lists of most probable cells are proposed for each of these above criteria.
ACKNOWLEDGMENT
Part of this paper has been presented at the SSPD’03 Conference, Stara Lesna, Slovakia, September 2003.





